MetaTrader 5 / 統計と分析
English Русский Deutsch
preview
MQL5における単変量時系列への動的モード分解の適用

MQL5における単変量時系列への動的モード分解の適用

MetaTrader 5 — 統計と分析 |
71 0
Francis Dube
Francis Dube

はじめに

動的モード分解(DMD: Dynamic Mode Decomposition)は、複雑な動的システムを分析するための手法です。工学分野では、DMDは流体解析において時空間構造を抽出する技術として利用されています。DMDは、時系列データを固有モードと呼ばれる線形動的表現へ分解します。各モードは固有の空間的形状を持ち、それぞれ異なる振動周波数や成長・減衰率を示します。これにより、しばしば解くことが難しい支配方程式を扱うことなく、流体系の根本的な力学を分析することが可能になります。

時空間構造とは、時間と空間にわたり形状や特性を保ちながら存在し続けるパターンを指します。たとえば、空中を漂う煙の輪を思い浮かべてください。煙の輪は周囲の空気が動いていてもその形を保ちながら一体となって移動する構造です。

エンジニアは、このような複雑な流れの中に存在する時空間構造を特定し分析するために、DMDのような手法を使用します。本稿では、MetaTrader 5におけるDMDの実装について解説します。実際のコード例を通じて、新しい行列メソッドDynamicModeDecomposition()の使い方を学びます。また、その入力仕様の説明に加え、得られた出力を処理するために必要な基本的なコードユーティリティについても紹介します。 



DMDアルゴリズム

DMDアルゴリズムは、Peter SchmidとJoern Sesterhennによって流体力学解析のために開発された手法です。DMDは本質的に次元削減手法であり、データ中に存在する振動成分を特定できる点が特徴で、PCA（主成分分析）とフーリエ変換による信号検出を組み合わせたような性質を持ちます。この手法の大きな利点のひとつは、対象データに対して特別な仮定を置かないことです。非定常な時系列データでも動作し、近年のバリエーションでは不均一な時間間隔で取得されたデータにも対応できます。DMDで最も重要な要件は、データそのものの構造であり、十分に高次元なデータセットであることが推奨されます。

DMDは、ある動的システムから時間とともに取得された一連の「スナップショット」に基づいています。これらのスナップショット（システムに関連する任意のデータ）は、行列として整理され、各列が特定時刻の状態に対応します。

X行列のスナップショット


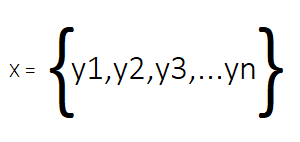
この行列Xの各列がシステムのスナップショットになります。実世界のDMDデータセットは高次元であることが多く、各時点で数百から数千の変数が計測されます。そのため、多くの場合、行数（変数または特徴量数）が列数（スナップショット数）より大きくなります。

初期スナップショットのX1行列


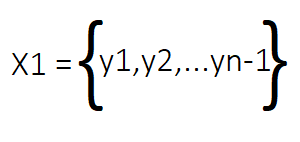
行列Xから、X1とX2の2つの行列を構成します。これらは動的システムの時間進行を表すペアとなります。X1はXの最後の列を除くすべての列で構成され、システムの初期時刻の状態を表します。逆に、X2はXの2列目から最後の列までで構成され、X1の次の時刻の状態に相当します。

後続のスナップショットのX2行列


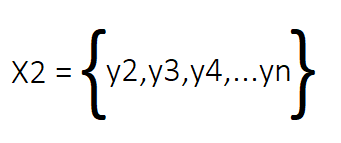
DMDの数学的基盤は、 X1およびX2​の間に「ある行列Aが存在し、AX1がX2を十分に近似する」という関係が成り立つと仮定する点にあります。DMDの目的は、このAを明示的に求めることなく、Aの固有構造（固有値と固有ベクトル）を推定することです。

X1とX2の関係

この目的のために、DMDではレイリー・リッツ法型の手順を用います。これは、大規模行列の固有値・固有ベクトルを近似するための標準的な線形代数手法です。問題をデータに基づいて慎重に選んだ低次元部分空間へ射影することで解を求めます。DMDでは、この部分空間としてX1の列空間の一部を使用します。その構成にはX1の特異値分解(SVD)から得られる最大左特異ベクトルが使われます。

X1のSVD

X1のSVDの結果とX2を用いて、 行列Aの近似を形成します。ここでランクの打ち切りはkとして示されます。 

DMD行列式

この作用素行列Aの近似は、DMD行列またはレイリー商と呼ばれます。この小さな行列の固有値はリッツ値またはDMD固有値と呼ばれ、対応する固有ベクトルはリッツベクトルやProjected DMDモードを計算するために使用されます。

DMD行列の固有値分解

リッツベクトルの式

リッツ値とリッツベクトルはリッツペアを形成し、これはデータセットの動的モード分解を表します。これらのモードは、システムのダイナミクスを低ランクかつデータ駆動で近似したものを提供します。

リッツペア

この近似の質は部分空間の選択に直接結びついており、その部分空間はDMDではスナップショットデータと本質的に関連しています。DMDモードは、DMD固有値に従って時間とともに変化するパターンを記述します。つまり、モードが構造を表し、固有値がその構造が特定の時点でどのように変化するかを決定します。

モードの時間的進化は、そのダイナミクスを計算することで可視化できます。  そしてこれは、モードの振幅を計算することを必要とします。振幅は初期の重みまたは係数として機能し、各モードがシステムの初期状態や全体の進化にどれだけ寄与しているかを示します。大きな振幅を持つモードはシステムのダイナミクスにおける主要な特徴となり、小さな振幅のモードは挙動への影響が小さくなります。モード、固有値、振幅を組み合わせることで、DMDはシステムの近似モデルを構築できます。この再構築されたモデルは時間方向に外挿することもでき、システムの将来状態を予測するために利用できます。



時間遅延埋め込み

古典的なDMDアルゴリズムに加えて、特定のデータセットやユースケースに対応するために開発された他のバリエーションも存在します。多くのバリエーションは、基本手法を強化するために前処理や後処理の手順を組み込む点で古典的DMDと異なります。たとえば、時間遅延埋め込みは、システムの状態空間を拡張するための手法であり、DMDによる解析により適した形にします。

標準的なDMDは、システムのダイナミクスが一つのスナップショットから次のスナップショットへ線形に近似できると仮定します。この仮定は、強い非線形性を持つシステムや、空間変数（行）が少ないデータでは成立しないことがあります。過去の観測値を現在の状態ベクトルに埋め込むことで、遅延座標は複雑なダイナミクスを展開することができます。これにより、DMDで用いられるような線形近似でも、非線形またはカオス的なシステムの本質的な特徴を捉えることが可能になります。つまり、十分に高次元でないデータセットに対してもDMDを適用できる可能性が広がることを意味します。

ここでの考え方は、拡張データ行列を作成することです。各タイムステップに単一のスナップショットを使用する代わりに、現在のスナップショットと過去のいくつかのスナップショットを含む新しい「状態」ベクトルを作成します。過去のスナップショットはそれぞれ特定の時間間隔または遅延だけ遅らせます。これは、特異スペクトル解析で軌跡行列を構築することに似ています。以下のコードでは、行列に対して時間遅延埋め込みを適用するための関数time_delay_embedding()を定義しています。

//+------------------------------------------------------------------+
//|  pseudo hankelization                                            |
//+------------------------------------------------------------------+
matrix time_delay_embedding(matrix &data, ulong delay=2)
  {

   if(delay>=data.Cols() || delay<1)
     {
      Print(__FUNCTION__, " invalid input parameters ");
      return matrix::Zeros(0,0);
     }

   ulong rows = data.Rows();
   matrix matrices;

   matrix out(rows*delay,data.Cols()-(delay-1));

   for(ulong i = 0; i<delay; i++)
     {
      matrices = np::sliceMatrixCols(data,long(i),long(i+data.Cols()-(delay-1)));
      if(!np::matrixCopyRows(out,matrices,long(i*rows),long((i*rows)+matrices.Rows())))
        {
         Print(__FUNCTION__, " failed copy operation ");
         return matrix::Zeros(0,0);
        }
     }

   return out;
  

関数time_delay_reconstruction()は、時間遅延埋め込みで前処理されたデータセットに対するDMDの再構築結果や予測結果に使用でき、データセットを元の形状に戻すことを可能にします。

//+------------------------------------------------------------------+
//| rebuild original shape of data after augmentation                |
//+------------------------------------------------------------------+
matrix time_delay_reconstruction(matrix &data, ulong delay)
  {

   ulong rows = data.Rows();
   ulong cols = data.Cols();

   if(rows<delay)
     {
      Print(__FUNCTION__," invalid inputs");
      return data;
     }

   matrix out(rows/delay,cols + delay - 1);

   matrix splitted[];

   ulong splits = data.Hsplit(delay,splitted);

   for(ulong i = 0; i<splits; i++)
      if(!np::matrixCopyCols(out,splitted[i],long(i),long(i+cols)))
        {
         Print(__FUNCTION__, " failed copy operation ");
         return data;
        }

   return out;
  }

使用するDMDのバリエーションに関わらず、最終的に得られる出力は似ており、DMD固有値、DMDモード、DMD振幅となります。DMD解析の肝は、これらの出力、特にDMD固有値の解釈にあります。DMDの結果の解釈方法を示す最良の方法は例を用いることであり、そのためにはコードを詳しく見ていく必要があります。



MQL5のDMD

MetaTraderがOpenBLASルーチンのサポートを拡張したことにより、DMDを実装する2つのメソッドが導入されました。1つ目のDynamicModeDecomposition()は標準的なSVDベースのDMDアルゴリズムを実装しており、DynamicModeDecompositionQR()はQR分解ベースの実装を使用します。本稿ではSVDベースのバージョンに焦点を当てます。以下のコードスニペットで示される作例の時系列を分解しながら、この手法について解説します。

//+------------------------------------------------------------------+
//| univariate process                                               |
//+------------------------------------------------------------------+
vector f(vector &in)
  {
   return cos(in)*sin(cos(in))*cos(in*0.2);
  }

このコードは、3つの異なる振動成分の積として構成される時系列を示しており、その結果、振幅と周波数が変化する複雑な波が生成されます。

時系列の例

3成分の組み合わせにより、周期的ではありますが単純な調和波ではない複雑なパターンが作られます。cos(x)*sin(cos(x))による高速振動は、より遅いcos(0.2*x)成分によって「引き伸ばされ」「圧縮され」、グラフに示される複雑な波形を生み出します。この時系列の分解は、スクリプト「DMD_Demo.mq5」でおこなわれます。分解はまず、時系列を適切なコンテナに格納して、分解の準備をおこなうところから始まります。 

//+------------------------------------------------------------------+
//|                                                     DMD_Demo.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
//---
#include<np.mqh>
#include<cmath.mqh>
//---
input ENUM_DMD_SCALE jobs = DMDSCALE_N;
input ENUM_DMD_EIGV jobz = DMDEIGV_V;
input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R;
input ENUM_DMD_REFINE jobf = DMDREFINE_R;
input ENUM_SVD_ALG whtsvd = SVDALG_1;
input long nrnk = -1;
input double tol_ = 1.e-9;//tol
input ulong Delay = 50;//apply time delay embedding
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   ulong series_len = 100;
   double dt = 0.1010101;
   double first_time_point = 0.0;
   vector t = np::arange(series_len,first_time_point,dt);
   vector F = f(t);
   matrix X(1,series_len);
   X.Row(F,0);

MQL5のDynamicModeDecomposition()は行列ベースのメソッドであり、分解の成功または失敗を示すブール値を返します。ドキュメントを見ると、このメソッドにはいくつかの必須入力があり、その中には最終結果に大きな影響を与えるため慎重に選択する必要があるものもあります。以下では、DynamicModeDecomposition()メソッドのパラメータについて解説します。

//---
   if(Delay)
      X = time_delay_embedding(X,Delay);
//---
   Print("X shape is ", X.Rows(),":",X.Cols());
//---
   matrix X1 = np::sliceMatrixCols(X,0,X.Cols()-1);
   matrix X2 = np::sliceMatrixCols(X,1);
//---
   vectorc eigen_values;
   matrix W;
   matrix B;
   vector residuals;
   matrix left_vectors;
   matrix res_vectors;
   matrix Z,S;

   if(!X1.DynamicModeDecomposition(X2,jobs,jobz,jobr,jobf,whtsvd,nrnk,tol_,eigen_values,left_vectors,Z,residuals,res_vectors,B,W,S))
     {
      Print(" DMD error ",GetLastError());
      return;
    

DynamicModeDecomposition()は、まず行列自体から始めると、入力として2つの行列を必要とします。1つ目は初期スナップショットの行列で、メソッドはこの行列に対して呼び出されます。次のスナップショットの行列は、メソッドの最初のパラメータとして渡されます。行列に関する唯一の要件は、十分に高次元であることです。メソッドは「縦長」または「細長い」行列を想定しています。もし行列の列数が行数を上回った場合、実行時にエラーが発生します。時間遅延埋め込みを適用する場合は、適切な形状の拡張行列が生成される必要があります。埋め込みの次元が拡張行列の行数を決定します。

今回の例を考えると、行列に変形した際に1行100列（スナップショット数）の行列になります。ここに次元50の時間遅延埋め込みを適用すると、拡張行列は50行（元の行数 × 埋め込み次元）および51列（元の列数 − 埋め込み次元 + 1）になります。適切な時間遅延埋め込みの選択は、状態空間を拡張することと、効果的な解析をおこなうために十分なスナップショット数を確保することとのバランスになります。

input ENUM_DMD_SCALE jobs = DMDSCALE_N

DynamicModeDecomposition()の2つ目のパラメータは、組み込みの前処理ステップを指定するための列挙型です。これにより、データに適用するスケーリング手法を選択できます。スケーリングなしを含めて4つの選択肢があります。すべての列を同程度のスケールに揃えることで、非常に大きなノルムを持つ一部の列がアルゴリズム全体を支配してしまう可能性を下げ、よりバランスの取れた数値的に安定した計算が可能になります。これにより、各スナップショットが全体のダイナミクスに均等に寄与するようになり、少数の大きな値を持つ事象に結果が偏ることを防ぎます。したがって、アルゴリズムは時系列全体にわたって重要なモードを識別でき、より小さなスケールの現象に関連するモードであっても検出できるようになります。

input ENUM_SVD_ALG whtsvd = SVDALG_1;

whtsvdパラメータはENUM_SVD_ALG列挙型であり、DMD処理で使用する4種類のSVD実装のいずれかを指定できます。SVDの実装は精度の点で違いがあり、最終的な結果に影響を与える可能性があります。

input long nrnk = -1;

nrnkパラメータは、縮約モデルの基盤となる列部分空間を明示的に定義するために使用できます。これは正の値として指定でき、データセットの列数以下である必要があります。別の方法として、このパラメータを-1または-2に設定すると、tolパラメータを用いたデータ駆動型のランク打ち切り手法が適用されます。

input double tol_ = 1.e-9;//tol

許容値は、SVDによって得られる特異値に対して適用されるしきい値であり、データセットの最適ランクを決定するために用いられます。残りの入力パラメータは、この処理から得られる出力に関するものです。これらについては、分解結果を確認しながら説明していきます。すべてのパラメータが定義されたら、プログラムを実行し、まずはDMD固有値から結果を観察できます。


固有値解析

DMD固有値（リッツ値）は、eigen_valuesというベクトルのパラメータとして返されます。これらの固有値は、システムの時間的な振る舞いを決定します。固有値は複素数であり、それぞれのモードの一般的な傾向を符号化しています。固有値の数は、DMDによって計算された縮約次数モデルのランクに相当します。固有値の虚部は振動の周波数を示し、実部はモードの安定性を示します。

モードの安定性は固有値の絶対値によって推測できます。

  • 絶対値 > 1：モードは不安定で、時間とともに成長します。
  • 絶対値 < 1：モードは安定と見なされ、時間が経つにつれて減衰する傾向があります。
  • 絶対値 = 1：モードは安定で、増加も減衰もせずに振動します。これは純粋に周期的、または定常的な挙動を示す典型です。

別の視点として、複素平面上にリッツ値をプロットすることでモードの安定性を評価できます。この可視化の目的は、固有値が単位円に対してどこに位置するのかを確認することです。望ましいのは比較的安定したモードであり、これは一貫した構造やパターンの存在を示します。安定したモードの固有値は、単位円の近くに位置します。以下は本例に対する固有値のプロットです。

固有値プロット


周波数について補足すると、実数値の振動は複素共役の固有値ペアとして表現されます。これは、実数値データがサインとコサインの組み合わせであり、単一の複素指数関数では表現できないためです。オイラーの公式に従えば、実数値関数を表現するには複素指数関数のペアが必要となるため、DMDでも複素共役のペアが現れます。今回の合成データセットには複数の周期成分が含まれているため、DMDがそれらの周期に対応する複数の複素共役固有値ペアを出力することが期待されます。さらに、固有値の虚部は、各モードが表す成分の特徴付けにも利用できます。虚部が0に近い固有値は、トレンド成分やゆっくり変化する成分を表すことが多いです。 

IN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      DMD eigenvalues or Ritz values
NF      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.5094085277495803,0.8361736631055409)
MR      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.5094085277495803,-0.8361736631055409)
LH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9997963823571733,0.02020000684364618)
IG      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9997963823571733,-0.02020000684364618)
CQ      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9835155147230954,0.1808172385894571)
DN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9835155147230954,-0.1808172385894571)
RG      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9754097172453285,0.2203989043734001)
QS      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9754097172453285,-0.2203989043734001)
LL      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9272204223699192,0.3744766566706951)
CE      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9272204223699192,-0.3744766566706951)
MR      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9113505757240357,0.4116425317268657)
FO      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.9113505757240357,-0.4116425317268657)
LH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.8329207590629218,0.5528761024511968)
KP      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.8329207590629218,-0.5528761024511968)
KN      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.810278335748567,0.5863411580059696)
NI      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.810278335748567,-0.5863411580059696)
CP      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6775746857433339,0.740515480806191)
JL      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6775746857433339,-0.740515480806191)
JH      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6991117585413807,0.7090540641602167)
QQ      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      (0.6991117585413807,-0.7090540641602167)
CM      0       20:48:41.719    DMD_univariate (AUDUSD,D1)      Eigenvalues shape - (20,)


スナップショットの取得間隔が分かっている場合にのみ、振動モードの周波数を決定できます。これはDynamicModeDecomposition()メソッドではあまり強調されていない点です。連続するスナップショット間の時間間隔は重要で、DMDが離散時間の作用素を求める以上、スナップショット間隔は離散的な結果を連続時間の力学へと結び付ける役割を果たします。この情報がなければ、離散時間の固有値を連続時間における意味のある周波数や成長・減衰率へ正確に変換することはできません。周波数や成長/減衰率は、スナップショットの時間間隔を用いて以下の式で計算されます。

周波数の式


成長率/減衰率の計算式


左特異ベクトル

left_vectorsパラメータで返される行列には、初期スナップショット行列X1のSVDから得られた左特異ベクトルがすべて格納されます。left_vectors行列の各列は、データセットのPOD（固有値直交分解、Proper Orthogonal Decomposition）モードと呼ばれます。POD は工学分野で用いられる用語で、統計学における主成分分析と概念的に類似しています。

Left singular vectors -> left_vectors 
[[-0.2186571002130553,0.2532378192042484,-0.03145683319876429,-0.08784983133100939,0.3705873208513075,0.2206528031484838,0.1522505585095688,0.2508786634158028,0.4005453375455179,-0.2070914249820868,-0.256938973254042,0.1083123043478309,0.3743749436717269,-0.08325285604985129,0.2153162921311084,0.03514527602276374,0.2660964556173894,-0.02288502160553232,0.08420865568250724,-0.1244960454833032,-0.05915206418948179,0.1412740898453582,-0.06378450251683798,0.05225051446648973,0.04596520897629693,0.05533900119077329,-0.03035343487604242,0.01632904421933207,0.02488201223142909,0.009443994581533457,0.003233076671905151,-0.007000002498680975,-0.0003763343596269273,-0.002249960643275939,0.006083378336102527,0.002738028494735405,-0.003071412428518359,0.007630930463007241,0.0006780866248171729,-0.001537236018891231,0.001097628276266037,0.002549189417918068,-0.00121555935468654,0.0002914617225681344,-0.001329425380550676,-0.0008417462519557183,-0.0001925572219431676,0.0006672631970817051,1.658425254616608e-07,-0.003517246244801298]
,[-0.2120650337138182,0.2460711108749398,0.02614922665855949,-0.06095346519256405,0.316287819867838,0.1367332022924505,0.1608350411867044,0.08971817028514953,0.1591329520755127,0.016649392674401,-0.02435104895770137,-0.1166535735451681,-0.1350117043919009,0.1534878122543588,-0.2129032230923289,0.07705593536128043,-0.375021818402949,-0.07706813579203413,-0.1050339399444373,0.2860161516006371,0.08475158498594149,-0.3855235413551042,0.1862630616541108,-0.1991183017470892,-0.1509536720131326,-0.2375913171609213,0.1371371152602869,-0.0898699217072978,-0.1292195766965235,-0.06648667026234195,-0.01812981549697532,0.0417051043959161,0.009525456359058087,0.01011521692378288,-0.03803922672356531,-0.02106190474509607,0.01766810797476536,-0.04822406797849837,-0.003057210631146539,0.006231539022859201,-0.006288330102253714,-0.0156751476701437,0.009093777375705452,-0.003891906142160671,0.01113869460673238,0.005700478320541056,0.001323281173233992,-0.004963029289243439,0.002210166681645755,0.01885563684292829]
,[-0.2050754583292416,0.2276848333084614,0.08120826878905353,-0.0401725018668373,0.255713699260657,0.06031724967005543,0.1260872837922681,-0.05233055144856189,-0.02895470981613132,0.1414817752150981,0.1496548155010341,-0.1633919339675757,-0.2909072792943354,0.1170695606024898,-0.2104477264601786,-0.05761666740975601,-0.1642196356337907,0.09376106622320569,-0.09917019230808037,-0.0512314209072473,0.07533085329520638,0.2045397680225845,-0.1172476831676734,0.2373535055615748,0.1327391899523122,0.363322598165184,-0.2353759964165236,0.2001199525018012,0.2797917856739792,0.2087875622138012,0.03391328469051902,-0.1093628961879368,-0.04980659874835306,-0.009841138497083401,0.1071536601377198,0.07721338502591252,-0.04348696114962958,0.1359693579381065,0.005776723545380768,-0.00329638274325811,0.01197007184135679,0.04141926298403621,-0.03188888672341144,0.02029703016126579,-0.0411903406233533,-0.02103491458905859,-0.004064246582866178,0.01736432751085308,-0.01540381295312496,-0.04519633129179929]
,[-0.197864304332741,0.198939547987894,0.1313736616978487,-0.02558290784786304,0.1925995771445337,-0.006134276320507245,0.05852103373207649,-0.1566416078904816,-0.1489006796224137,0.1767605998850408,0.2187235587134117,-0.08102546015612813,-0.2025179789413045,-0.02467023236462294,0.007177707826474537,-0.1394599646494139,0.1774528338997285,0.1254318761473469,0.06991185536803274,-0.2322392434345509,-0.1022804195006251,0.2595084087385101,-0.1385151209344889,0.02231602330043558,0.08496345787013258,-0.1181672772615679,0.1251167503291135,-0.1942278207520568,-0.2798025229501522,-0.3656598349104803,0.01139657187065844,0.1552588902748942,0.1253960619854343,-0.03868294575932402,-0.1774709498310883,-0.172412195179344,0.05203395600508887,-0.2094389089818375,-0.004270301693629558,-0.03143829332941872,0.006497267040059443,-0.05389031613821053,0.06861563190685697,-0.0601060573479536,0.08699077151177441,0.05297098886227182,0.005414702197319015,-0.03549882813964893,0.05199258221374336,0.05778558739229585…]
Left singular vectors shape - (50,50)



DMDモード

Projected DMDモード、つまりリッツベクトルは出力行列Zに返されます。パラメータjobzはENUM_DMD_EIGV列挙型であり、Zにどのような内容を出力するかを制御するために使われます。これにより、必要がなければモードを計算しないように指定することもできます。合成データセットの分解から得られたモードを確認すると、注意深い読者は、対応する固有値が複素数であるにもかかわらず、パラメータZが実行列として返されていることに気付くはずです。これはどういうことなのでしょうか。実は、モード自体は本来複素数です。DynamicModeDecomposition()メソッドは、複素数のモードをコンパクト形式で返しているのです。

KN      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      Z
MJ      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[-0.2115833899347683,0.04066707935807452,0.1309479910169292,-0.05340607539953211,-0.1311407627226479,-0.05294578413949149,0.1307327748372062,-0.05393554251234634,0.1300831102003118,0.05561343290756637,0.05476143012438625,0.1303708466035617,-0.0602971275669671,0.1290171409159042,0.1325833779653352,-0.0474567460410165,0.03953679964167294,0.1224969410523646,-0.08648845700023616,0.1302991571594397]
KL      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.1410082298469801,-0.1561422002553993,0.1320001302525303,-0.05075005112167052,-0.1194054633670081,-0.07578550974758559,0.1394053542006602,-0.02379589291884476,0.09978976936668775,0.1002790127266047,-0.003759313795174276,0.1413556653516757,-0.1215537937113269,0.07412474322962503,0.1352548790995219,0.03928642939266112,-0.06394467904383667,0.1123039293425674,-0.1528368724559976,0.02980086078332629]
KE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.0571288895384227,-0.1979205129165305,0.1329984050115342,-0.0480733131719782,-0.1037338006863208,-0.09612679258491226,0.1412219243613748,0.007514043825130007,0.05497499123596727,0.1303496653103515,-0.06161407873237246,0.1272770978516157,-0.1422252875452086,-0.00546499036287681,0.08655973711477287,0.1111375957285514,-0.1264360522083525,0.02869970692204134,-0.1280036213687715,-0.0876039346033588]
QM      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1946438003924811,-0.0523269950779746,0.1339424057467836,-0.04537695566367969,-0.08464242182804624,-0.1132990516514234,0.1360931500665304,0.03845442944292374,0.002161029940774177,0.1414497110787759,-0.1085446923168975,0.09063109173113748,-0.1154409995132384,-0.08318535501859128,0.004972784147358847,0.1408055296621761,-0.1069381563322531,-0.07420079524911123,-0.02739821515064329,-0.1519997996523627]
MD      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1442714745004026,0.1362363903857534,0.1348317466067521,-0.04266207939022894,-0.06276071186776834,-0.1267361823950489,0.1242712682729774,0.06750360361706979,-0.05096588923209126,0.1319643397659119,-0.1362298611687498,0.03791506074287562,-0.0501630100812688,-0.133110472474709,-0.07853144874233632,0.1170082970122646,-0.01755245167388933,-0.1294221063050899,0.08865106243357559,-0.1256351416263412]
FO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.03992077677928203,0.1893519332890936,0.1356660661019982,-0.03992979099864888,-0.03881004602829696,-0.1359952192100831,0.10633768314148,0.09323292091368418,-0.09667419061156554,0.1032745163734511,-0.139760607057441,-0.02152411345851591,0.0318114520997212,-0.1386035419997053,-0.1322392470005959,0.04876382240238289,0.08394555153666447,-0.1006538267573124,0.1510967437027885,-0.02495855075802432]
IE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.1796559181414814,0.06272269832359235,0.1364450246963949,-0.03718120464898366,-0.01358000327434823,-0.1407709344456745,0.08317437492830956,0.1143770068564059,-0.1283121621102718,0.05955600024366348,-0.1185106827077816,-0.07714740932760773,0.103127741913013,-0.09785844890997622,-0.1357422735154563,-0.03802553162801222,0.1314496877308521,-0.006061975670165805,0.123318478664932,0.08964429318551075]
ON      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [-0.145052625469143,-0.1177739752477081,0.1371683036826087,-0.03441744261256562,0.01209766591051641,-0.140905898452734,0.05592052522418876,0.1298959869971385,-0.1412759661384557,0.007171600964583176,-0.07624763897835488,-0.1190923437906344,0.1400016038285632,-0.02449262903763641,-0.08769262768666558,-0.1104036026020508,0.09357636250498216,0.09318079023848276,0.02260518070773477,0.1500697490161283]
OD      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.02477722278466908,-0.1806550663349361,0.1378356065274133,-0.03163963382212003,0.03737645720044752,-0.1363956708335061,0.02591649044609354,0.1390266308270787,-0.1336795590605116,-0.04625490379734653,-0.02046485321417844,-0.1399216409042799,0.1301514645240822,0.05700280745582626,-0.006321464342295452,-0.1408756808015346,-0.00561461203492375,0.1324202843066922,-0.09062222999370595,0.1209556314953582]
FO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.1648424157584578,-0.07139540484283648,0.1384466607105591,-0.02884891198589165,0.06142301561190965,-0.1273889490658437,-0.005362119258359672,0.141319891110143,-0.1066290580133119,-0.09294834217094237,0.03894705870314489,-0.1359418964516609,0.0768895241650633,0.1194373735899043,0.0774784937512529,-0.1178541799925052,-0.1018942505428861,0.08561003773138477,-0.149086741625562,0.0203522730386399…]
ID      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      Z shape - (50,20)

各モード（Zの各列）について、対応する固有値が非ゼロの虚部を持つ場合、そのモードの虚部はZの次の列 に格納されています。これは同時に、その複素固有ベクトルと共役な別の固有ベクトルが存在することも意味します。一方、固有値に虚部がない場合（実固有値の場合）、隣の列はまったく別の固有値に対応する列となります。以下のコードでは、ユーティリティ関数compact_to_complex()を定義しています。この関数は、コンパクト形式で格納された実数コンテナ（実数部と虚数部が縦に並んだ形）および複素数ベクトル（複素数を復元するためのキー）を入力として受け取り、実際の複素数に復元したコンテナを返します。 

//+------------------------------------------------------------------+
//|process vector representing complex numbers in compact form       |
//+------------------------------------------------------------------+
vectorc compact_to_complex(vector& v,vectorc& bp)
  {
   vectorc v_out = vectorc::Zeros(v.Size());

   for(ulong i = 0; i<v.Size() && i<bp.Size();)
     {
      if(bp[i].imag)
        {
         v_out[i].real = v[i];
         if(i+1 < v.Size())
           {
            v_out[i].imag = v[i+1];
            v_out[i+1].real = v_out[i].real;
            v_out[i+1].imag = -1.0*v_out[i].imag;
            i+=2;
           }
        }
      else
        {
         v_out[i].real = v[i];
         i+=1;
        }
     }

   return v_out;
  }
//+------------------------------------------------------------------+
//| process matrix representing complex numbers in compact form      |
//+------------------------------------------------------------------+
matrixc compact_to_complex(matrix& m, vectorc& bp)
  {
   matrixc m_out = matrixc::Zeros(m.Rows(), m.Cols());

   for(ulong i = 0; i<m.Rows(); i++)
     {
      vector row = m.Row(i);
      vectorc row_c = compact_to_complex(row,bp);
      m_out.Row(row_c,i);
     }
   return m_out;
  }

以下に、コンパクト形式のモードと実際の複素モード形式の違いを示します。

CF      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD modes or Ritz Vectors -> Z
PS      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[(-0.2115833899347683,0.04066707935807452),(-0.2115833899347683,-0.04066707935807452),(0.1309479910169292,-0.05340607539953211),(0.1309479910169292,0.05340607539953211),(-0.1311407627226479,-0.05294578413949149),(-0.1311407627226479,0.05294578413949149),(0.1307327748372062,-0.05393554251234634),(0.1307327748372062,0.05393554251234634),(0.1300831102003118,0.05561343290756637),(0.1300831102003118,-0.05561343290756637),(0.05476143012438625,0.1303708466035617),(0.05476143012438625,-0.1303708466035617),(-0.0602971275669671,0.1290171409159042),(-0.0602971275669671,-0.1290171409159042),(0.1325833779653352,-0.0474567460410165),(0.1325833779653352,0.0474567460410165),(0.03953679964167294,0.1224969410523646),(0.03953679964167294,-0.1224969410523646),(-0.08648845700023616,0.1302991571594397),(-0.08648845700023616,-0.1302991571594397)]
OO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(-0.1410082298469801,-0.1561422002553993),(-0.1410082298469801,0.1561422002553993),(0.1320001302525303,-0.05075005112167052),(0.1320001302525303,0.05075005112167052),(-0.1194054633670081,-0.07578550974758559),(-0.1194054633670081,0.07578550974758559),(0.1394053542006602,-0.02379589291884476),(0.1394053542006602,0.02379589291884476),(0.09978976936668775,0.1002790127266047),(0.09978976936668775,-0.1002790127266047),(-0.003759313795174276,0.1413556653516757),(-0.003759313795174276,-0.1413556653516757),(-0.1215537937113269,0.07412474322962503),(-0.1215537937113269,-0.07412474322962503),(0.1352548790995219,0.03928642939266112),(0.1352548790995219,-0.03928642939266112),(-0.06394467904383667,0.1123039293425674),(-0.06394467904383667,-0.1123039293425674),(-0.1528368724559976,0.02980086078332629),(-0.1528368724559976,-0.02980086078332629)]
MN      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.0571288895384227,-0.1979205129165305),(0.0571288895384227,0.1979205129165305),(0.1329984050115342,-0.0480733131719782),(0.1329984050115342,0.0480733131719782),(-0.1037338006863208,-0.09612679258491226),(-0.1037338006863208,0.09612679258491226),(0.1412219243613748,0.007514043825130007),(0.1412219243613748,-0.007514043825130007),(0.05497499123596727,0.1303496653103515),(0.05497499123596727,-0.1303496653103515),(-0.06161407873237246,0.1272770978516157),(-0.06161407873237246,-0.1272770978516157),(-0.1422252875452086,-0.00546499036287681),(-0.1422252875452086,0.00546499036287681),(0.08655973711477287,0.1111375957285514),(0.08655973711477287,-0.1111375957285514),(-0.1264360522083525,0.02869970692204134),(-0.1264360522083525,-0.02869970692204134),(-0.1280036213687715,-0.0876039346033588),(-0.1280036213687715,0.0876039346033588)]
OI      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.1946438003924811,-0.0523269950779746),(0.1946438003924811,0.0523269950779746),(0.1339424057467836,-0.04537695566367969),(0.1339424057467836,0.04537695566367969),(-0.08464242182804624,-0.1132990516514234),(-0.08464242182804624,0.1132990516514234),(0.1360931500665304,0.03845442944292374),(0.1360931500665304,-0.03845442944292374),(0.002161029940774177,0.1414497110787759),(0.002161029940774177,-0.1414497110787759),(-0.1085446923168975,0.09063109173113748),(-0.1085446923168975,-0.09063109173113748),(-0.1154409995132384,-0.08318535501859128),(-0.1154409995132384,0.08318535501859128),(0.004972784147358847,0.1408055296621761),(0.004972784147358847,-0.1408055296621761),(-0.1069381563322531,-0.07420079524911123),(-0.1069381563322531,0.07420079524911123),(-0.02739821515064329,-0.1519997996523627),(-0.02739821515064329,0.1519997996523627)]
CH      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [(0.1442714745004026,0.1362363903857534),(0.1442714745004026,-0.1362363903857534),(0.1348317466067521,-0.04266207939022894),(0.1348317466067521,0.04266207939022894),(-0.06276071186776834,-0.1267361823950489),(-0.06276071186776834,0.1267361823950489),(0.1242712682729774,0.06750360361706979),(0.1242712682729774,-0.06750360361706979),(-0.05096588923209126,0.1319643397659119),(-0.05096588923209126,-0.1319643397659119),(-0.1362298611687498,0.03791506074287562),(-0.1362298611687498,-0.03791506074287562),(-0.0501630100812688,-0.133110472474709),(-0.0501630100812688,0.133110472474709),(-0.07853144874233632,0.1170082970122646),(-0.07853144874233632,-0.1170082970122646),…]
KG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD modes or Ritz Vectors shape (50,20)


残差

次の2つの出力パラメータresidualsとres_vectorsは関連しています。residualsベクトルの各値は、res_vectors行列の対応する列ベクトルのユークリッドノルムです。各データスナップショットに対する残差ベクトルは、実際のスナップショットとDMDモデルによって予測されたスナップショットとの差分であり、ある時刻における誤差ベクトルを表します。残差ベクトルのノルムは、通常、誤差の定量的指標として用いられます。一般的に、ノルムが0に近いほど、モデルの精度は高いと判断できます。 

CD      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      Residual norms -> residuals
FO      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      [0.008836676346169272,0.008836676346169272,9.235187494765224e-09,9.235187494765224e-09,1.742579533919419e-08,1.742579533919419e-08,1.653443663139743e-08,1.653443663139743e-08,2.597847624528849e-07,2.597847624528849e-07,2.320987987120818e-07,2.320987987120818e-07,9.788834713137558e-06,9.788834713137558e-06,8.123609086522145e-06,8.123609086522145e-06,0.0004010758671648529,0.0004010758671648529,0.0004371025994576595,0.0004371025994576595]
EN      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      Residuals shape - (20,)

residuals出力パラメータは実数のベクトルであるのに対し、res_vectorsはコンパクト形式の複素数行列です。

CD      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      Residual vectors -> res_vectors
OR      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      [[(0.0007788944957199118,6.210241253423732E-05),(0.0007788944957199118,-6.210241253423732E-05),(-5.316966866786288E-10,-4.560266955722092E-10),(-5.316966866786288E-10,4.560266955722092E-10),(9.00277352666734E-10,9.748073598325746E-10),(9.00277352666734E-10,-9.748073598325746E-10),(7.854966954656817E-10,-9.872156113421848E-10),(7.854966954656817E-10,9.872156113421848E-10),(-1.459522849800443E-08,1.377941803715199E-08),(-1.459522849800443E-08,-1.377941803715199E-08),(1.069276902784799E-08,-1.449544934084557E-08),(1.069276902784799E-08,1.449544934084557E-08),(-5.704307382975449E-07,5.291619083608312E-07),(-5.704307382975449E-07,-5.291619083608312E-07),(-4.031761563494385E-07,5.112246791380559E-07),(-4.031761563494385E-07,-5.112246791380559E-07),(-2.293253034875431E-05,2.549073482446818E-05),(-2.293253034875431E-05,-2.549073482446818E-05),(1.737165621398806E-05,3.217988337436348E-05),(1.737165621398806E-05,-3.217988337436348E-05)]
PH      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(-0.001602312423460747,-0.0004729759518786458),(-0.001602312423460747,0.0004729759518786458),(9.344054696658333E-10,8.094462253249723E-10),(9.344054696658333E-10,-8.094462253249723E-10),(-1.519821102302643E-09,-1.798446391809705E-09),(-1.519821102302643E-09,1.798446391809705E-09),(-1.489875889326697E-09,1.679088970293896E-09),(-1.489875889326697E-09,-1.679088970293896E-09),(2.855568843884715E-08,-2.24272293236627E-08),(2.855568843884715E-08,2.24272293236627E-08),(-2.198151384524838E-08,2.429971562856181E-08),(-2.198151384524838E-08,-2.429971562856181E-08),(1.189711697907603E-06,-8.400539607544832E-07),(1.189711697907603E-06,8.400539607544832E-07),(8.892800195531292E-07,-8.493346006915869E-07),(8.892800195531292E-07,8.493346006915869E-07),(5.40418365579387E-05,-4.256796091403961E-05),(5.40418365579387E-05,4.256796091403961E-05),(-2.314522858359869E-05,-6.846121833149754E-05),(-2.314522858359869E-05,6.846121833149754E-05)]
FG      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(4.593660886884066E-05,0.0007257275432220045),(4.593660886884066E-05,-0.0007257275432220045),(3.019065830667245E-10,2.421602848801108E-10),(3.019065830667245E-10,-2.421602848801108E-10),(-6.415215442201472E-10,-3.751031429910512E-10),(-6.415215442201472E-10,3.751031429910512E-10),(-2.171667012884626E-10,6.773338626087089E-10),(-2.171667012884626E-10,-6.773338626087089E-10),(2.210737475895341E-09,-1.156460674445192E-08),(2.210737475895341E-09,1.156460674445192E-08),(5.990476170669723E-10,1.068699011230745E-08),(5.990476170669723E-10,-1.068699011230745E-08),(-6.762525454895307E-08,-4.884491409673508E-07),(-6.762525454895307E-08,4.884491409673508E-07),(-1.490076587543424E-07,-3.929403302738166E-07),(-1.490076587543424E-07,3.929403302738166E-07),(-1.571073502396048E-05,-1.913611580105223E-05),(-1.571073502396048E-05,1.913611580105223E-05),(-2.530414087616173E-05,6.629116600515017E-06),(-2.530414087616173E-05,-6.629116600515017E-06)]
DS      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(0.001363806542495044,0.0001361882900650091),(0.001363806542495044,-0.0001361882900650091),(-9.180490534443919E-10,-7.880395988535405E-10),(-9.180490534443919E-10,7.880395988535405E-10),(1.549437189662939E-09,1.690010908994566E-09),(1.549437189662939E-09,-1.690010908994566E-09),(1.36508163106619E-09,-1.700071097787692E-09),(1.36508163106619E-09,1.700071097787692E-09),(-2.543471129545782E-08,2.364815934741138E-08),(-2.543471129545782E-08,-2.364815934741138E-08),(1.871941607278771E-08,-2.493395216685013E-08),(1.871941607278771E-08,2.493395216685013E-08),(-1.000003475026823E-06,9.064440836814569E-07),(-1.000003475026823E-06,-9.064440836814569E-07),(-7.106895980740768E-07,8.787577454316686E-07),(-7.106895980740768E-07,-8.787577454316686E-07),(-4.07015728396895E-05,4.38344900164922E-05),(-4.07015728396895E-05,-4.38344900164922E-05),(2.940113570619463E-05,5.652142258574799E-05),(2.940113570619463E-05,-5.652142258574799E-05)]
OK      0       20:54:02.690    DMD_univariate (AUDUSD,D1)       [(0.0005033857628483629,-0.0006840539757191899),(0.0005033857628483629,0.0006840539757191899),(-6.779790617805759E-10,-5.646610123921647E-10),(-6.779790617805759E-10,5.646610123921647E-10),(1.278677420890606E-09,1.06406300437456E-09),(1.278677420890606E-09,-1.06406300437456E-09),…]
PG      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      
OJ      0       20:54:02.690    DMD_univariate (AUDUSD,D1)      Residual vectors shape - (50,20)

ENUM_DMD_RESIDUALS列挙型パラメータjobrは、残差ベクトルの計算方式を指定するオプションであり、必要に応じて残差計算を無効化できます。


リッツ補正とExact DMDモード

パラメータjobfは列挙型ENUM_DMD_REFINEで、行列Bの出力内容を決定します。
  • jobf = DMDREFINE_Nの場合、行列Bは空になります。
  • jobf = DMDREFINE_Eの場合、BにはExact DMDモードの複素数が格納されます。Exact DMDモードとProjected DMDモードの違いは、システムのダイナミクスを近似する線形作用素との関係にあります。両者は同じ固有値を生成しますが、空間構造（モード自体）は異なります。Projected DMDモードは、基底ベクトル集合への射影の結果として得られるため、近似であり、最適な線形作用素の真の固有ベクトルではありません。一方、Exact DMDモードの計算方法は、同じ問題を解く別のアプローチです。この方法では射影ステップを省略し、線形作用素の固有ベクトルを直接求めます。その結果得られるモードは、システムの最適線形近似の真の固有ベクトルであるため「正確」と見なされます。初期スナップショットのデータ範囲に制約されることもありません。
  • jobf = DMDREFINE_Rの場合、行列Bにはリッツ補正(Ritz refinement)と呼ばれる後処理手順で使用する値が格納されます。リッツペアは線形作用素Aの近似に基づいて計算されます。リッツ補正は、リッツベクトルをさらに改善する方法であり、行列Bには初期残差を最小化するために必要な値が含まれます。リッツ補正の詳細は本記事の範囲外ですが、主に将来予測の精度向上に役立つステップです。


レイリー商

出力パラメータWも、コンパクト形式の複素数を格納した行列です。

DQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      DMD matrix eigenvectors - W 
CQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      [[(0.03397841954159109,0.03317980055719008),(0.03397841954159109,-0.03317980055719008),(-0.9002396504998079,0),(-0.9002396504998079,-0),(0.01119040053117125,0.1182840538877034),(0.01119040053117125,-0.1182840538877034),(-0.08933258155433688,-0.07445561873978643),(-0.08933258155433688,0.07445561873978643),(0.002252288602000291,-0.07268070968789277),(0.002252288602000291,0.07268070968789277),(0.06363962546273101,-0.06242908185135146),(0.06363962546273101,0.06242908185135146),(0.05937239512593095,0.01490455626039135),(0.05937239512593095,-0.01490455626039135),(-0.02589857176991502,-0.03197379959572326),(-0.02589857176991502,0.03197379959572326),(0.03403147435273887,-0.02518975096744712),(0.03403147435273887,0.02518975096744712),(0.04814500369424651,0.0006646006481806285),(0.04814500369424651,-0.0006646006481806285)]
LK      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(-0.03856865140041035,-0.04728745684412225),(-0.03856865140041035,0.04728745684412225),(-0.07418687400224905,-0.02671782636983063),(-0.07418687400224905,0.02671782636983063),(-0.6278925369875541,0),(-0.6278925369875541,-0),(0.6611296439031247,0),(0.6611296439031247,-0),(-0.01948319607116129,0.1638582051901045),(-0.01948319607116129,-0.1638582051901045),(-0.1160509917189585,0.04684553196764583),(-0.1160509917189585,-0.04684553196764583),(-0.06080699466607752,-0.007252509160005485),(-0.06080699466607752,0.007252509160005485),(0.04824148800646633,0.0544753020238296),(0.04824148800646633,-0.0544753020238296),(-0.02631424783289801,0.02396317634823539),(-0.02631424783289801,-0.02396317634823539),(-0.05371125803952446,-0.01772350219292688),(-0.05371125803952446,0.01772350219292688)]
JS      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(0.01927996329670138,-0.003323809768950481),(0.01927996329670138,0.003323809768950481),(-0.001092132447284393,-0.08813408560005521),(-0.001092132447284393,0.08813408560005521),(-0.01686362521399225,-0.6191005830078983),(-0.01686362521399225,0.6191005830078983),(0.02637345886634726,0.5944648032143058),(0.02637345886634726,-0.5944648032143058),(-0.1052128591626567,-0.008385210070686162),(-0.1052128591626567,0.008385210070686162),(-0.004565995041448841,-0.09830093201273357),(-0.004565995041448841,0.09830093201273357),(0.02484135400580122,-0.004386892506558514),(0.02484135400580122,0.004386892506558514),(-0.01604018998961423,0.01817361621091497),(-0.01604018998961423,-0.01817361621091497),(0.01513765754343997,-0.01442045062996068),(0.01513765754343997,0.01442045062996068),(0.02301961366729926,-0.02281949313848668),(0.02301961366729926,0.02281949313848668)]
DQ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(0.01349178032453495,0.04031036542801018),(0.01349178032453495,-0.04031036542801018),(0.2800915230663114,0.2610589921860959),(0.2800915230663114,-0.2610589921860959),(0.07750855775646105,-0.2950535943034701),(0.07750855775646105,0.2950535943034701),(-0.2337105682364486,0.0040858569402831),(-0.2337105682364486,-0.0040858569402831),(0.06293226732327413,-0.1508577239678987),(0.06293226732327413,0.1508577239678987),(-0.03484731631897012,0.1006710384526284),(-0.03484731631897012,-0.1006710384526284),(-0.01073717194453397,-0.1026561241299194),(-0.01073717194453397,0.1026561241299194),(-0.08143509356008606,-0.07823035735671989),(-0.08143509356008606,0.07823035735671989),(-0.06786249180652332,-0.01131117739979555),(-0.06786249180652332,0.01131117739979555),(-0.01459517002905221,0.04968638335424509),(-0.01459517002905221,-0.04968638335424509)]
DS      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [(-0.06312195367435448,-0.05788238216619907),(-0.06312195367435448,0.05788238216619907),(-0.106179393196619,-0.1067792237431208),(-0.106179393196619,0.1067792237431208),(0.2228105336536818,-0.09464986022387956),(0.2228105336536818,0.09464986022387956),(-0.1223565828897724,-0.2665717534473687),(-0.1223565828897724,0.2665717534473687),(0.0407625323894802,0.0608679763109657),(0.0407625323894802,-0.0608679763109657),(-0.0236347933639726,0.2167362736925585),(-0.0236347933639726,-0.2167362736925585),(-0.1397842805702028,0.002686549243340094),(-0.1397842805702028,-0.002686549243340094),(0.0494448535458599,0.07175076524193082),(0.0494448535458599,-0.07175076524193082),(-0.05089933082548433,0.06350343732496355),…]
LP      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      
FK      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      W shape - (20,20)

この行列Wには、レイリー商の評価から得られる行列の固有ベクトルが格納されています。出力行列Sは、対応するレイリー商の結果を格納するために使用されます。レイリー商は、本文脈では次のような形式の式で表されます。

レイリー商の式

この結果として得られるのは正方行列であり、線形作用素Aの近似として利用されます。

RF      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      DMD matrix or Rayleigh Quotient -> S
HR      0       20:54:02.688    DMD_univariate (AUDUSD,D1)      [[0.5094085277495803,-0.8604610082897919,0.0002006138033779966,0.04760027059805147,-0.002803306343440372,-0.0391415882078795,-0.0003134843372287616,0.07893996206869613,0.001757225544053047,0.05891514022091245,0.1021418500890567,0.0154878531271508,0.08161025402145326,-0.01322727684398736,0.05289807915719862,0.1366031199179701,0.09067443894366256,0.02387635894976379,-0.1337617534319445,0.3158438887995204]
GG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0.8125718517577054,0.5094085277495803,0.03212818037482736,0.07731373949333104,-0.004523461571676836,-0.06365727084560829,0.07166331416570983,0.1149560436517001,0.0417897026770658,0.0807703163043338,0.1168290328074077,-0.07784523729378179,0.08134266010864513,0.0457586690177342,-0.05281322289935021,0.1041166865025129,0.06016908821880863,-0.02262883866060445,0.01864963663274376,0.1592958144288718]
QM      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0.9997963823571733,-0.06841114291664024,0.003677630227929817,0.05134906476950822,0.001010343646915456,-0.1036712695688504,-0.001982116115745312,-0.07741467176450138,-0.1344061700387433,-0.02117211346836873,-0.1074879052755059,0.01790950142871103,-0.07054528189524574,-0.180179648794732,-0.1196714016226133,-0.0318305136919558,0.177441519638216,-0.4172515456746314]
PO      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0.005964529447791189,0.9997963823571733,-6.130430193796907e-05,0.0001608255296355939,-0.1417177910594132,0.02603215499459065,-0.07645245784783392,0.02929171223870932,0.09632863544056425,0.2022679146534209,0.1005224694321643,-0.1320544694433864,0.2724705351116244,0.2311524902397419,0.1709822160686499,0.1206265129749707,-0.4633910086326531,0.6944803173283216]
RG      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0.9835155147230954,-0.1807872789366,-0.01287650437961382,0.002273054758487322,-0.006948726541217937,0.002592615695004415,0.008633127046368962,0.01836065518926932,0.009038166070419178,-0.01198352209799287,0.02469606203936868,0.02084314801005234,0.01542969758433841,0.01093290292806937,-0.04194970752430172,0.06273377057840418]
OE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0.1808472032071591,0.9835155147230954,0.1161226589750725,-0.02159149420945333,0.06263828964805583,-0.02419610245484403,-0.07926824162748283,-0.1657867613281642,-0.08263670791881386,0.1082473436056935,-0.2234334894897005,-0.1898550808858993,-0.1404004467922538,-0.09891860736477874,0.3801384435040523,-0.5700922000360884]
QE      0       20:54:02.688    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0.9754097172453285,-0.3671559385031988,-0.005735330959573934,-0.1752131166062669,-0.3034665524406584,-0.0447757385532624,-0.2423096107440454,0.03850758043656835,-0.1556886673590776,-0.4051646386927485,-0.2688190825258632,-0.07028522559611267,0.3951927856107862,-0.935685263814825]
ES      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0.1323025776105538,0.9754097172453285,-0.1277498034867074,0.01635682016747238,0.1038905065841927,0.3269719154788018,0.122074385755231,-0.211766280182049,0.4229381295746578,0.3086378423896532,0.2339698855185775,0.1869911903713443,-0.6953365989256011,0.9790102802912404]
EJ      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0.9272204223699192,-0.4253756556605945,-0.1675761806365016,-0.0322689202475039,-0.1347517961361585,0.0260709867621285,-0.09491983678538948,-0.2278476057705441,-0.1518792160120434,-0.04275596295515771,0.2317849265989918,-0.532635511016381]
FM      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0.3296680581625781,0.9272204223699192,0.05633171550556969,0.2408424337338481,0.07416894629162182,-0.1553200191742876,0.3047043287502109,0.2020029040523848,0.1558084075499993,0.1346159453957157,-0.4912332208887085,0.6651615829764952]
HG      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0.9113505757240357,-0.2568972073981867,0.05055669367035209,-0.2566052078814798,0.4776439687989247,0.2195895146754944,0.1834173442058648,0.2105372198999828,-0.7236933009079901,0.8511605081274156]
JD      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0.6596006848134373,0.9113505757240357,0.3140920520023247,-0.01324336135550369,0.1361348333013918,0.5052672912884386,0.3296699228616658,0.06220880832355302,-0.4176612853765882,1.116102030438296]
JE      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0,0,0.8329207590629218,0.4624722437908844,0.355960803548531,0.1072881843791952,0.1013740688581597,0.1566216030021757,-0.5124168716630659,0.5231145883642944]
LP      0       20:54:02.689    DMD_univariate (AUDUSD,D1)       [0,0,0,0,0,0,0,0,0,0,0,0,-0.6609520652656545,0.8329207590629218,-0.07009147383110947,-0.3140620624168415,-0.2035214647743208,-0.03229751959115882…]
NH      0       20:54:02.689    DMD_univariate (AUDUSD,D1)      S shape - (20,20)

これで、DynamicModeDecomposition()のパラメータの説明は終わりです。次に、これらの結果を組み合わせて 再構築、フィルタリング、予測をおこなう方法を示します。しかし、その前にMQL5における複素数サポートの制限について触れておく必要があります。MQL5の組み込み関数の多くは複素数を引数として扱えないため、独自のユーティリティを実装する必要があります。このために、cmath.mqhに定義されているcmathライブラリを導入します。


MQL5での複素数の扱い

ファイルcmath.mqhには、複素数を扱うための各種ユーティリティが定義されています。複素配列、ベクトル、行列から虚部や実部を抽出する関数も用意されています。

//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
void real(complex& data[],double& out[])
  {
   ArrayResize(out,data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].real;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
void imaginary(complex& data[],double& out[])
  {
   ArrayResize(out,data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].imag;
  }

//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
vector real(vectorc& data)
  {
   vector out=vector::Zeros(data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].real;
   return out;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
vector imaginary(vectorc& data)
  {
   vector out=vector::Zeros(data.Size());
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = data[i].imag;
   return out;
  }
//+------------------------------------------------------------------+
//| get real part from container of complex numbers                  |
//+------------------------------------------------------------------+
matrix real(matrixc& data)
  {
   matrix out=matrix::Zeros(data.Rows(),data.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
      for(ulong j = 0; j<out.Cols(); j++)
         out[i,j] = data[i,j].real;
   return out;
  }
//+-------------------------------------------------------------------+
//| get imaginary part from container of complex numbers              |
//+-------------------------------------------------------------------+
matrix imaginary(matrixc& data)
  {
   matrix out=matrix::Zeros(data.Rows(),data.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
      for(ulong j = 0; j<out.Cols(); j++)
         out[i,j] = data[i,j].imag;
   return out;
  }

また、実数のコンテナを複素数に変換したり、その逆をおこなうルーチンも用意されています。

//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
vectorc as_complex(vector& re,vector& im)
  {
   vectorc out = vectorc::Zeros(MathMax(re.Size(),im.Size()));
   for(ulong i = 0; i<out.Size(); i++)
     {
      out[i].real = i<re.Size()?re[i]:0.0;
      out[i].imag = i<im.Size()?im[i]:0.0;
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
matrixc as_complex(matrix& re,matrix& im)
  {
   matrixc out = matrixc::Zeros((ulong)MathMax(re.Rows(),im.Rows()),(ulong)MathMax(re.Cols(),im.Cols()));
   for(ulong i = 0; i<out.Rows(); i++)
     {
      for(ulong j = 0; j<out.Cols(); j++)
        {
         out[i,j].real = (i<re.Rows() && j<re.Cols())?re[i,j]:0.0;
         out[i,j].imag = (i<im.Rows() && j<im.Cols())?im[i,j]:0.0;
        }
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
vectorc as_complex(vector& re)
  {
   vectorc out = vectorc::Zeros(re.Size());
   for(ulong i = 0; i<out.Size(); i++)
     {
      out[i].real = re[i];
      out[i].imag = 0.0;
     }
   return out;
  }
//+------------------------------------------------------------------+
//| create complex containers from real numbers                      |
//+------------------------------------------------------------------+
matrixc as_complex(matrix& re)
  {
   matrixc out = matrixc::Zeros(re.Rows(),re.Cols());
   for(ulong i = 0; i<out.Rows(); i++)
     {
      for(ulong j = 0; j<out.Cols(); j++)
        {
         out[i,j].real = re[i,j];
         out[i,j].imag = 0.0;
        }
     }
   return out;
  

最後に、このライブラリには複素数および複素数コンテナに対する 指数関数、べき乗、絶対値、自然対数の実装も含まれています。

//+------------------------------------------------------------------+
//|        power of complex number                                   |
//+------------------------------------------------------------------+
complex c_pow(complex base, complex exponent)
  {
   return c_exp(exponent*c_log(base));
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
vectorc c_pow(vectorc &vect, complex exponent)
  {
   vectorc out(vect.Size());
   for(ulong i = 0; i<vect.Size(); i++)
      out[i] = c_pow(vect[i],exponent);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
matrixc c_pow(matrixc &matrx, complex exponent)
  {
   matrixc out(matrx.Rows(),matrx.Cols());
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_pow(matrx.Col(i),exponent),i);
   return out;
  }


//+------------------------------------------------------------------+
//|        power of complex number                                   |
//+------------------------------------------------------------------+
complex c_pow(complex value, double alpha)
  {
   complex out = value;
   double r = c_abs(value);
   double theta = atan2(value.imag,value.real);
   double n_r = pow(r,alpha);
   double n_theta = alpha*theta;

   out.real = n_r*cos(n_theta);
   out.imag = n_r*sin(n_theta);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
vectorc c_pow(vectorc &vect, double alpha)
  {
   vectorc out(vect.Size());
   for(ulong i = 0; i<vect.Size(); i++)
      out[i] = c_pow(vect[i],alpha);
   return out;
  }
//+------------------------------------------------------------------+
//| simple power of complex number                                   |
//+------------------------------------------------------------------+
matrixc c_pow(matrixc &matrx, double alpha)
  {
   matrixc out(matrx.Rows(),matrx.Cols());
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_pow(matrx.Col(i),alpha),i);
   return out;
  }

//+------------------------------------------------------------------+
//|  Complex Signum Function                                         |
//+------------------------------------------------------------------+
complex signum(complex z)
  {
   double magnitude = sqrt((z.real*z.real) + (z.imag*z.imag));
   if(!magnitude)
      return 0+0i;
   complex magz;
   magz.real = magnitude;
   magz.imag = 0.0;

   return z/magz;
  }

//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
double c_abs(complex z)
  {
   return sqrt((z.real*z.real) + (z.imag*z.imag));
  }
//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
vector c_abs(vectorc &z)
  {
   CComplexVector v(z);
   return sqrt((v.re*v.re) + (v.im*v.im));
  }
//+------------------------------------------------------------------+
//| absolute value of a complex number (magnitude)                   |
//+------------------------------------------------------------------+
matrix abs(matrixc &z)
  {
   CComplexMatrix v(z);
   return sqrt((v.re*v.re) + (v.im*v.im));
  }
//+------------------------------------------------------------------+
//| sqrt of complex number                                           |
//+------------------------------------------------------------------+
complex c_sqrt(complex z)
  {
   double mag_z = c_abs(z);
   mag_z=sqrt(mag_z);
   double theta = atan2(z.imag,z.real);
   complex out;
   out.real = mag_z*cos(theta/2.0);
   out.imag = mag_z*sin(theta/2.0);
   return out;
  }
//+------------------------------------------------------------------+
//| sqrt of complex vector                                           |
//+------------------------------------------------------------------+
vectorc c_sqrt(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_sqrt(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//| sqrt of complex vector                                           |
//+------------------------------------------------------------------+
matrixc c_sqrt(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_sqrt(z.Col(i)),i);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
complex c_log(complex z)
  {
   complex out;
   out.real = c_abs(z);
   out.imag = atan2(z.imag,z.real);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
vectorc c_log(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_log(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//|  log of complex number                                           |
//+------------------------------------------------------------------+
matrixc c_log(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_log(z.Col(i)),i);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
complex c_exp(complex z)
  {
   complex out;
   out.real = exp(z.real)*cos(z.imag);
   out.imag = exp(z.real)*sin(z.imag);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
vectorc c_exp(vectorc &z)
  {
   vectorc out = z;
   for(ulong i = 0; i<out.Size(); i++)
      out[i] = c_exp(z[i]);
   return out;
  }
//+------------------------------------------------------------------+
//|  exp function of complex number                                  |
//+------------------------------------------------------------------+
matrixc c_exp(matrixc &z)
  {
   matrixc out = z;
   for(ulong i = 0; i<out.Cols(); i++)
      out.Col(c_exp(z.Col(i)),i);
   return out;
  }


振幅とモードのダイナミクス

DMDにおける 再構築 とは、分解から導かれたモードのみを用いて入力データを再現することを指します。フィルタリング は、入力データを特定のモードのみで再構築することです。予測は、再構築を時間方向に外挿する操作です。これらをおこなうには、各モードの 振幅とダイナミクスを計算する必要があります。振幅はDynamicModeDecomposition()の直接の出力ではなく、別のステップでモードをスナップショットに当てはめることで求めます。通常は最小二乗法またはモードの疑似逆行列を用いて計算されます。

複素数で非対称な行列に対する最小二乗問題の解を求めるには、正規方程式のLU分解を利用できます。正規方程式は、過剰決定系を解ける正方系に変換します。これは、以下のコードスニペットのようにAlglibライブラリ のユーティリティを使って実現できます。

//+------------------------------------------------------------------+
//|  compute the DMD amplitudes                                      |
//+------------------------------------------------------------------+
vectorc              compute_amplitudes(matrix& snapshots, matrixc& modes)
  {
   vectorc amplitudes(0);

   vectorc x0 = as_complex(snapshots.Col(0));
   matrixc A_h = modes.TransposeConjugate();
   matrixc B = np::matmul(A_h,modes);
   vectorc c = np::matmul(A_h,x0);
   complex right_side[], solution[];
   int pivots[];
   CMatrixComplex lua = B;

   if(!np::vecAsArray(c,right_side))
     {
      Print(__FUNCTION__, " vector as array failure ");
      return amplitudes;
     }

   vector check_pivots;
   ResetLastError();
   CAlglib::CMatrixLU(lua,lua.Rows(),lua.Cols(),pivots);
   int info;
   check_pivots.Assign(pivots);
   if(check_pivots.Max() == check_pivots.Min())
     {
      Print(__FUNCTION__," CAlglib::CMatrixLU()  failure ", GetLastError());
      return amplitudes;
     }

   CDenseSolverReportShell shell;

   CAlglib::CMatrixLUSolve(lua,pivots,int(pivots.Size()),right_side,info,shell,solution);

   if(info < 1)
     {
      Print(__FUNCTION__, " modes matrix is singular, or VERY close to singular. ", GetLastError());
      return amplitudes;
     }

   amplitudes.Assign(solution);

   return amplitudes;

  

このコードでは、スナップショット行列とモードを入力として 振幅を計算する関数 が定義されています。ここでは例として最初のスナップショットを使用していますが、任意の時刻のスナップショットを使うことも可能です。最小二乗法で計算された解が振幅となり、振幅は複素数です。振幅を用いることで、DMDによって明らかにされた最も支配的なモードを計算することもできます。これは振幅の絶対値を計算することでおこないます。この情報はフィルタリングの際にも活用できます。

//---
   vector abs_dmd_amplitudes = c_abs(dmd_amplitudes);
//---
   long amp_indices[];
   if(!np::arange(amp_indices,int(abs_dmd_amplitudes.Size())) ||
      !np::quickSortIndices(abs_dmd_amplitudes,false,amp_indices,amp_indices[0],amp_indices[amp_indices.Size()-1]))
     {
      Print(" error ");
      return;
     }
//---

得られた振幅を用いて、各モードのダイナミクスを計算できます。DMDダイナミクスの行列はヴヴァンデルモンドの行列となり、各行がモードの時間発展を表します。この計算では、スナップショットの離散的な時刻とDMD固有値が必要になります。固有値は列ベクトルとして並べられ、データセット内の各離散時刻に対してべき乗を計算します。最後に、各列ベクトルに振幅を掛け合わせます。関数compute_dynamics()は、振幅、リッツ値、およびスナップショットの時刻ベクトルを与えることで、DMDダイナミクス行列を計算します。

//+------------------------------------------------------------------+
//|   calculate the mode dynamics                                    |
//+------------------------------------------------------------------+
matrixc           compute_dynamics(vectorc& amplitudes,vectorc& eigs, vector& timesteps)
  {
   matrixc mat_eigs = np::repeat_vector_as_rows_cols(eigs,timesteps.Size(),false);
   vector tpow = (timesteps - timesteps[0])/(timesteps[1] - timesteps[0]);
   matrixc dyn = mat_eigs;

   for(ulong i = 0; i<mat_eigs.Cols(); i++)
     {
      vectorc column = mat_eigs.Col(i);
      column = c_pow(column,tpow[i]);
      column*=amplitudes;
      dyn.Col(column,i);
     }

   return dyn;
  }

下図は、本例における最も支配的なモードの時間発展を示したプロットです。このグラフィックは、スクリプト DMD_Mode_Dynamics.ex5によって生成したものです。 

支配的モードダイナミック


再構成と予測

DMDモード、振幅、固有値を組み合わせることで、入力データの近似を構成できます。再構成されたデータセットは、元のデータの支配的なダイナミクスを捉えた低ランク表現になります。これは、モードにダイナミクスを掛け合わせることで実現されます。

//+------------------------------------------------------------------+
//|  reconstruct the input data based on the dominant dmd dynamics   |
//+------------------------------------------------------------------+
matrixc            reconstructed_data(matrixc& dynamics, matrixc& modes)
  {
   return np::matmul(modes,dynamics);
  }

下図は、DMDモデルによって定義された再構成系列です。

再構築系列

データをフィルタリングしたい場合は、除去したいモードを「オフ」にする必要があります。これは、対象のモード（列）をゼロに設定し、そのうえでダイナミクスと掛け合わせることで実現できます。

//---
   vector time_steps = np::arange(X1.Cols()+1,t[0],dt);
   matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps);
   matrixc masked_modes;
//---
   if(NumTop)
     {
      double min_amp = abs_dmd_amplitudes[amp_indices[NumTop]];
      masked_modes = matrixc::Zeros(dmd_modes.Rows(),dmd_modes.Cols());
      for(ulong i = 0; i<dmd_modes.Cols(); i++)
        {
         bool select = c_abs(dmd_amplitudes[i])>min_amp;
         if(select)
            masked_modes.Col(dmd_modes.Col(i),i);
        }
     }
   else
      masked_modes = dmd_modes;
//---
   matrixc reconstructed = reconstructed_data(dmd_dynamics,masked_modes);
//---
   matrix real_rec = real(reconstructed);
//---
   real_rec = time_delay_reconstruction(real_rec,Delay);
//--

下の図は、最も支配的なモードのみを使用してフィルタリングされた再構成を示しています。

フィルタ再構成デモ

予測は、ダイナミクスを計算する際に、入力データの末端を超えて離散時刻を拡張することでおこないます。DMDモデルは、モードを時間方向に外挿することで予測を生成します。予測精度は、DMD によって得られる線形モデルが実際のシステムダイナミクスをどれだけ適切に表現しているかに依存します。

//---
   vector time_steps = np::arange((X1.Cols())+Num_future_points+1,first_time_point,dt);
//---
   matrixc dmd_dynamics = compute_dynamics(dmd_amplitudes,eigen_values,time_steps);
//---
   matrixc reconstruction = reconstructed_data(dmd_dynamics,dmd_modes);
//--

ここでは、10ステップ先まで予測した結果を確認できます。

デモ系列の予測

なお、今回のデモではまったくノイズのない、非常にクリーンな信号を用いています。次のセクションでは、データにノイズが多く含まれる場合にDMDの予測がどのように振る舞うかを見ていきます。


価格データへのDMDの適用

スクリプトDMD_Price_Decomposition.ex5は、実世界のデータにDMDを適用する例を示しています。このスクリプトはクォートのサンプルをダウンロードし、系列を分解します。得られたDMDモデルは、ユーザーが指定したステップ数の予測をおこなうために使用されます。最後に、予測された系列を実際の価格クォートと並べて可視化し、比較できるようにします。 

//+------------------------------------------------------------------+
//|                                       DMD_Price_Decompostion.mq5 |
//|                                  Copyright 2025, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2025, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<dmd_utils.mqh>
//--- input parameters
input string   Symbol_="AUDUSD";
input ENUM_TIMEFRAMES   TimeFrame=PERIOD_D1;
input datetime StartDate=D'2025.06.02';
input ENUM_DMD_SCALE jobs = DMDSCALE_N;
input ENUM_DMD_EIGV jobz = DMDEIGV_V;
input ENUM_DMD_RESIDUALS jobr = DMDRESIDUALS_R;
input ENUM_DMD_REFINE jobf = DMDREFINE_R;
input ENUM_SVD_ALG whtsvd = SVDALG_1;
input long nrnk = 20;
input double tol_ = 1.e-9;//tol
input ulong Delay = 50;//apply time delay embedding
input ulong Num_Future_steps = 10;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   vector prices;
   if(!prices.CopyRates(Symbol_,TimeFrame,COPY_RATES_CLOSE,StartDate,100+Num_Future_steps))
    {
     Print(" failed to get close prices for ", Symbol_,". Error ", GetLastError());
     return;
    }
//---
   matrix X = matrix::Zeros(1,100);
   vector input_series = np::sliceVector(prices,0,100);
   X.Row(input_series,0);
   np::matrix2csv("AUDUSD.csv",X.Transpose());
//---
   CDmd dmd;
   if(!dmd.fit(X,1,tol_,nrnk,Delay,jobs,whtsvd,jobz,jobr,jobf))
      return;
   else
      Print(" It worked! ");
   
   vectorc egs = dmd.dmd_eigs();  
   Print("DMD eigenvalues or Ritz values\n",egs);
   
   matrix forecast = dmd.reconstructed_data(Num_Future_steps);
   vector time = np::arange(prices.Size(),0.0,dmd.dmd_time_delta());
   plot_forecast(prices,forecast.Row(0),time,Num_Future_steps," Price forecast",0,0,0,0,500,400,true,30);
  }

このプログラムは、dmd_utils.mqhに定義されているCDmdクラスを使用します。このクラスは、組み込みの DynamicModeDecomposition(メソッドの機能に、本文で説明する追加機能を付与したラッパークラスです。主要インターフェースはfit()メソッドで、DMD分解に必要なパラメータを受け取り、必要に応じて時間遅れ埋め込みを適用します。また、時間遅れ埋め込みを適用する機能も備えています。 

virtual bool              fit(matrix &X,double time_delta, double tolerance, long svd_rank = -1,ulong embedding_dimension = 0,ENUM_DMD_SCALE scale = DMDSCALE_N,ENUM_SVD_ALG svd_method = SVDALG_1, ENUM_DMD_EIGV eigv = DMDEIGV_V,ENUM_DMD_RESIDUALS resid = DMDRESIDUALS_R,ENUM_DMD_REFINE refine = DMDREFINE_R)
     {
      reset();

      matrix z,res_vectors,b,w,s;
      vector residuals;
      m_delay = embedding_dimension;
      matrix snapshots = m_delay>1?time_delay_embedding(X,m_delay):X;
      if(!snapshots.Cols())
         return false;
      m_snapshots_x = np::sliceMatrixCols(snapshots,0,snapshots.Cols()-1);
      m_snapshots_y = np::sliceMatrixCols(snapshots,1);
      if(!m_snapshots_x.DynamicModeDecomposition(m_snapshots_y,scale,eigv,resid,refine,svd_method,svd_rank,tolerance,m_eigs,m_left_vectors,z,m_residuals,res_vectors,b,w,s))
        {
         Print(__FUNCTION__, " DMD error ", GetLastError());
         return false;
        }

      if(eigv != DMDEIGV_N)
         m_modes = compact_to_complex(z,m_eigs);

      m_eigenvectors = compact_to_complex(w,m_eigs);

      if(refine == DMDREFINE_E)
        {
         m_modes = compact_to_complex(b,m_eigs);
         m_exact_modes = true;
        }
      else
         if(refine == DMDREFINE_R)
            m_residual_vectors = compact_to_complex(res_vectors,m_eigs);

      m_og_first = m_dmd_first = 0.0;
      m_og_dt = m_dmd_dt = time_delta;
      m_og_timesteps = m_dmd_timesteps = np::arange(m_snapshots_x.Cols()+1,m_dmd_first,m_dmd_dt);
      m_og_last = m_dmd_last = m_dmd_timesteps.Size()-1;

      m_fitted = compute_amplitudes() ;

      return m_fitted;
     }

モデルの適合が完了すると、下記のgetterメソッドを呼び出すことで、モデルのさまざまな情報を取得できます。 

matrixc           dmd_modes(void)
     {
      return m_modes;
     }
   double            dmd_time_delta(void)
     {
      return m_dmd_dt;
     }
   double            dmd_first_time(void)
     {
      return m_dmd_first;
     }
   ulong             dmd_last_time(void)
     {
      return m_dmd_last;
     }
   double            og_first_time(void)
     {
      return m_og_first;
     }
   ulong             og_last_time(void)
     {
      return m_og_last;
     }
   vector            dmd_time_steps(void)
     {
      return m_dmd_timesteps;
     }
   vector            og_time_steps(void)
     {
      return m_og_timesteps;
     }
   vectorc           dmd_eigs(void)
     {
      return m_eigs;
     }
   vectorc           dmd_amplitudes(void)
     {
      return m_amplitudes;
     }
   matrixc           exact_dmd_modes(void)
     {
      if(m_exact_modes)
         return m_modes;
      else
         return matrixc::Zeros(0,0);
     }
   matrixc           eigenvectors(void)
     {
      return m_eigenvectors;
     }
   vector            growth_rate(void)
     {
      return real(m_eigs)/m_dmd_dt;
     }

   vector            frequency(void)
     {
      vectorc f = c_log(m_eigs);
      return imaginary(f)/(2.0*M_PI*m_dmd_dt);
     }
   matrixc           residual_vectors(void)
     {
      return m_residual_vectors;
     }
   vector            residuals(void)
     {
      return m_residuals;
     }

再構成、予測、およびフィルタリング操作は、オーバーロードされたreconstructed_data()メソッドによって処理されます。いずれも出力は実数値のコンテナで、入力データと同じ形状を持ちます。オプションパラメータを1つだけ持つ reconstructed_data()のバージョンは、主にフィルタリングなしの予測や再構成に使用されます。オプションパラメータが0以外に設定されている場合、指定されたステップ数の予測を生成します。それ以外の場合は、入力データの再構成を出力します。 

matrix            reconstructed_data(ulong num_future_steps = 0)
     {
      if(num_future_steps)
        {
         m_dmd_last+=num_future_steps;
         m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt);
        }

      matrixc d = dynamics();
      matrixc data = np::matmul(m_modes,d);
      if(!num_future_steps)
         data = np::sliceMatrixCols(data,0,long(m_og_last+1));
      matrix rdata = real(data);
      if(m_delay>1)
         rdata = time_delay_reconstruction(rdata,m_delay);
      return rdata;
     }

reconstructed_data()のバージョン2は、追加でベクトルパラメータを受け取ります。このメソッドでは、ユーザーがモード数と同じサイズの1と0からなるベクトルを渡すことを想定しています。ベクトル内の0は対応するモードを破棄することを意味します。この操作は元のモード自体を変更するものではありませんが、フィルタリングされた予測や再構成の計算を可能にします。 

matrix            reconstructed_data(vector& modes_mask, ulong num_future_steps = 0)
     {
      if(num_future_steps)
        {
         m_dmd_last+=num_future_steps;
         m_dmd_timesteps = np::arange(m_dmd_last+1,m_dmd_first,m_dmd_dt);
        }

      matrixc d = dynamics();
      matrixc masked_modes = matrixc::Zeros(m_modes.Rows(),m_modes.Cols());
      if(modes_mask.Size() == m_modes.Cols())
        {
         for(ulong i = 0; i<masked_modes.Cols(); i++)
            if(modes_mask[i])
               masked_modes.Col(m_modes.Col(i),i);
        }
      matrixc data = np::matmul(masked_modes,d);
      if(!num_future_steps)
         data = np::sliceMatrixCols(data,0,long(m_og_last+1));
      matrix rdata = real(data);
      if(m_delay>1)
         rdata = time_delay_reconstruction(rdata,m_delay);
      return rdata;
     }

プログラムを実行すると、次の出力が得られます。

DMD再構築と価格予測

DMDは系列内のノイズの影響により、ダイナミクスの推定に苦労することがわかります。入力の数ステップを超える予測はほとんど不可能です。これは、DMDが本質的に短期予測にのみ有効であることを確認する結果となります。数ステップ以上先の予測では、モデルはすぐに精度を失い始めます。 


結論

この記事では、MQL5における単変量時系列への動的モード分解(DMT)の適用方法を、新しいDynamicModeDecomposition()行列メソッドを用いて紹介しました。本メソッドの入力項目や、出力の解釈および分析への活用方法についても解説しました。その過程で、複素数を扱うために必要な基本的なツールも提示しています。DMDはMQL5 における有用な手法となり得ますが、その効果を最大限に引き出すには、ユーザーにはかなりのドメイン知識が求められます。DMD自体の理解だけでなく、解析対象のデータセットについても十分な知識が必要です。この記事で参照されているすべてのコードは以下にリストされ、添付されています。
ファイル名  詳細
MQL5/include/np.mqhベクトルおよび行列操作のユーティリティ関数をまとめたヘッダファイル
MQL5/include/cmath.mqh複素数を扱う演算ユーティリティ関数のヘッダファイル
MQL5/include/dmd_utils.mqhCDmdクラス定義やDMD分析に役立つ各種関数を含むヘッダファイル
MQL5/scripts/DMD_Demo.mq5固有値プロットを作成するためのスクリプト
MQL5/scripts/DMD_Mode_Dynamics.mq5モードのダイナミクスの計算と表示を示すスクリプト
MQL5/scripts/DMD_Reconstruction.mq5DMDモデルの再構成およびフィルタリングへの応用を示すスクリプト
MQL5/scripts/DMD_Forecast_Demo.m5DMDモデルを用いた予測方法を示すスクリプト
MQL5/scripts/DMD_Price_Decomposition.mq5CDmdクラスの利用例と、実際の価格データへのDMD適用を示すスクリプト

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/19188

添付されたファイル |
ZIPをダウンロード
Mql5.zip (37.62 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。

この著者による他の記事

ディスカッションに移動
FVGをマスターする：ブレーカーと市場構造の変化によるフォーメーション、ロジック、自動取引 FVGをマスターする：ブレーカーと市場構造の変化によるフォーメーション、ロジック、自動取引
これは、FVG（Fair Value Gaps、フェアバリューギャップ）の発生の形成ロジックや、ブレーカーおよびMSS（Market Structure Shifts、市場構造の変化）を用いた自動取引について解説することを目的として執筆した記事です。
MQL5での取引戦略の自動化（第31回）：プライスアクションに基づくスリードライブハーモニックパターンシステムの作成 MQL5での取引戦略の自動化（第31回）：プライスアクションに基づくスリードライブハーモニックパターンシステムの作成
本記事では、MQL5においてピボットポイントとフィボナッチ比率に基づいて強気、弱気双方のスリードライブハーモニックパターンを識別し、ユーザーが選択できるカスタムエントリー、ストップロス、テイクプロフィット設定を用いて取引を実行するスリードライブパターンシステムを開発します。さらに、チャートオブジェクトによる視覚的フィードバックによって、トレーダーの洞察を強化します。
プライスアクション分析ツールキットの開発（第40回）：Market DNA Passport プライスアクション分析ツールキットの開発（第40回）：Market DNA Passport
本記事では、各通貨ペアが持つ固有のアイデンティティを、その過去のプライスアクションという視点から探ります。生物の設計図を記述するDNAの概念に着想を得て、本記事では市場にも同様の枠組みを適用し、プライスアクションを各通貨ペアのDNAとして扱います。ボラティリティ、スイング、リトレースメント、スパイク、セッション特性といった構造的挙動を分解することで、各ペアを他と区別する基礎的なプロファイルが浮かび上がります。このアプローチにより、市場行動に対するより深い洞察が得られ、トレーダーは各銘柄の特性に合った戦略を体系的に組み立てられるようになります。
共和分株式による統計的裁定取引（第4回）：リアルタイムモデル更新 共和分株式による統計的裁定取引（第4回）：リアルタイムモデル更新
本記事では、共和分関係にある株式バスケットを対象とした、シンプルでありながら包括的な統計的アービトラージのパイプラインについて解説します。データのダウンロードと保存を行うPythonスクリプト、相関検定、共和分検定、定常性検定、さらにデータベース更新用のMetatrader 5サービスの実装およびそれに対応するエキスパートアドバイザー(EA)も含まれています。また、いくつかの設計上の判断については、参考情報および実験の再現性向上のために本記事に記録しています。