Выборочные методы марковских цепей Монте-Карло. Алгоритм HMC

Введение

Байесовское моделирование и методы марковских цепей Монте-Карло (MCMC) лежат в основе решения сложных вероятностных задач машинного обучения. Однако традиционные MCMC-алгоритмы, основанные на случайном блуждании (например, Метрополис-Гастингс), сталкиваются с фундаментальной проблемой в высокоразмерных моделях — «проклятием размерности».

При увеличении числа оцениваемых параметров эти методы вынуждены делать чрезмерно маленькие шаги, чтобы сохранить разумную вероятность принятия. Это приводит к медленному исследованию пространства, высокой автокорреляции выборок и как следствие низкой производительности.

Гамильтонов алгоритм Монте-Карло (HMC) решает эту проблему, опираясь на принципы  гамильтоновой механики и информацию о градиенте логарифма целевой плотности. Вместо коротких, случайных шагов, HMC совершает большие, направленные траектории, эффективно перемещаясь к областям высокой вероятности. Как и в задаче оптимизации, доступ к градиенту радикально ускоряет поиск. Это позволяет HMC работать даже в пространствах высокой размерности, где традиционные методы терпят неудачу.

Для иллюстрации работы HMC используется сложный тестовый пример — сэмплирование 100-мерного коррелированного нормального распределения с сильно различающимися дисперсиями. Рассмотрены ключевые элементы, обеспечивающие  автономность и стабильность разработанной реализации:

• адаптивная настройки размера шага интегрирования epsilon и диагональной матрицы масс M,
• поиск оценки максимума апостериорной плотности (MAP) с помощью метода L-BFGS для ускорения  период прогрева.

Для оценки качества полученных выборок реализована  комплексная диагностика  (Rhat, ESS, MCSE, Mean, SD, квантили) и мониторинг процесса в реальном времени. 

Динамическая основа HMC

HMC это градиентный метод MCMC со вспомогательными величинами, пришедший из физики. В его основе лежит гамильтонова механика, которая позволяет создавать направленные траектории в пространстве параметров, избегая хаотичного случайного блуждания.

Основными элементами HMC являются:

• потенциальная энергия E(z): равна отрицательному логарифму целевой плотности вероятности: E(z) = - log p(z)
• вспомогательный импульс r: его как правило, берут из простого распределения, обычно многомерного нормального r ∼ N(0,M), где M — это матрица масс
• кинетическая энергия K(r): равна отрицательному логарифму распределения импульса
• полная энергия (Гамильтониан) H(z,r): определяет общую энергию системы

H(z, r) = E(z) + K(r)

Движение цепи HMC происходит в так называемом фазовом пространстве, которое представляет собой объединенное пространство параметров z (положение) и вспомогательного импульса r.

Гамильтонова динамика, описываемая ниже, создает детерминированную траекторию в этом (z, r) пространстве. Движение по этой траектории сохраняет полную энергию (Гамильтониан). Это свойство обеспечивает обратимость и сохранение объема в фазовом пространстве, что необходимо для корректности алгоритма Монте-Карло.

Эволюция  z(t) и r(t) во времени описывается двумя совместными дифференциальными уравнениями движения:

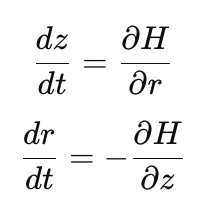
Рис. 1.  Гамильтоновы уравнения движения

Уравнение положения (dz/dt) определяет как быстро и в каком направлении меняется положение z. Скорость изменения положения z выражается через производную Гамильтониана по импульсу r. Поскольку H(z, r) зависит от r только через кинетическую энергию

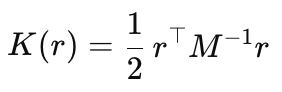
то частная производная ∂H/∂r равна обратной матрице масс умноженной на импульс.

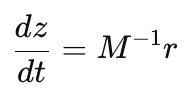
Матрица M в этом контексте определяет инертность (или "тяжесть") параметров. Если масса параметра высока, его движение замедляется. Это позволяет алгоритму управлять размером шага в разных измерениях, обеспечивая равномерное  исследование пространства. 

Уравнение импульса (dr/dt) определяет, как меняется импульс r в каждой точке пространства z. Скорость изменения импульса r пропорционально отрицательному градиенту потенциальной энергии -∇E(z), что по сути является градиентом логарифма целевой плотности. Таким образом, это уравнение описывает силу, которая направляет цепь в сторону увеличения целевой плотности, подталкивая сэмплы к областям высокой  вероятности.

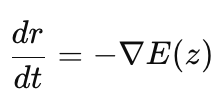
При идеальном (непрерывном) интегрировании гамильтоновых уравнений полная энергия H(z, r) сохраняется вдоль всей траектории. Это можно увидеть, если расписать полную производную Гамильтониана по времени:

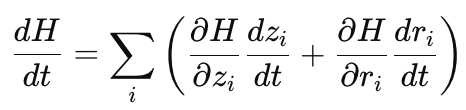
Теперь, если подставить уравнения движения в эту формулу, мы придем к выражению:

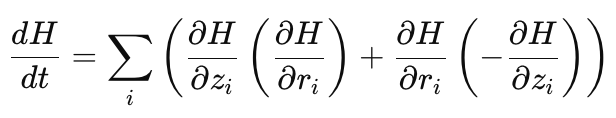
в котором слагаемые взаимно уничтожатся и, следовательно, производная по времени будет равна нулю. Значит, энергия остаётся постоянной и система не может перейти с одного уровня энергии на другой. Если в начале траектории полная энергия, допустим, равна 10, то и в конце траектории также будет 10 (в идеальном случае). Цепь параметров z движется, но только внутри одной энергетической поверхности — множества точек (z, r), где H(z, r)=10. Без смены уровня энергии цепь сэмплирует лишь малую часть целевого распределения.

Чтобы решить проблему застревания на одной энергетической поверхности, HMC в начале каждой итерации случайно выбирает новый вектор импульса r из нормального распределения p(r). Это меняет кинетическую энергию и, тем самым, меняется и полная энергия H. Цепь перепрыгивает на новую энергетическую поверхность и продолжает движение уже там. Так, шаг за шагом, она обходит все уровни энергии — и, соответственно, все области параметров z, соответствующие целевому распределению.

Численное интегрирование и схема «Чехарда» (Leapfrog)

На практике непрерывные гамильтоновы уравнения решают численно. Обычные методы, такие как метод Эйлера, вносят ошибки, которые нарушают сохранение энергии, искажают объем фазового пространства и делают траекторию необратимой, а это недопустимо для MCMC. Поэтому в HMC используется специальная схема интегрирования «чехарда» (Leapfrog). Ее преимущество в том, что она точно сохраняет объем фазового пространства, полностью обратима и обладает высокой точностью, благодаря чему выборки остаются несмещёнными даже при длинных траекториях.

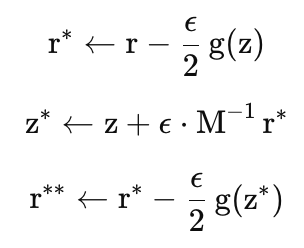
Рис. 2. Схема одного шага Leapfrog: чередование полушагов по импульсу и полного шага по положению

Один полный шаг размера ϵ  состоит из трёх этапов, которые чередуют обновление импульса и положения. Сначала импульс r обновляется на половину шага ϵ/2, используя отрицательный градиент потенциальной энергии в текущей точке z. Затем положение z сдвигается на полный шаг ϵ, используя уже обновленный импульс масштабированный обратной матрицей масс M. После этого вычисляем новый градиент потенциальной энергии g в новом положении z и выполняем второй полушаг по импульсу, снова на ϵ/2. Такая последовательность минимизирует ошибку и сохраняет симметрию траектории.

//--- Leapfrog шаги
         for(int l = 0; l < num_leapfrog; l++)
           {
            r = r - (epsilon / 2.0) * g_new; // Пол шага для импульса        
            z = z + epsilon * M_inv * r;     // Полный шаг положения z с учетом M^-1
            E(z, g_new, e, log_pdf, false);  // вычисляем новый градиент
            r = r - (epsilon / 2.0) * g_new; // Еще пол шага для импульса
           }

Тем не менее, даже схема Leapfrog не сохраняет полную энергию идеально, небольшие численные ошибки все таки накапливаются. Поэтому сохранение энергии корректируется с помощью критерия принятия Метрополиса-Гастингса. После построения траектории (серии шагов Leapfrog), мы получаем состояние-кандидат (z∗, r∗) и принимаем его с вероятностью, основанной на разнице полной энергии H до и после интегрирования:

min(1, exp { H(z, r) - H(z*, r*) })

Для численной стабильности это условие проверяется в эквивалентной логарифмической форме. Принятие кандидата происходит, если натуральный логарифм равномерно распределенного случайного числа u ∼ U(0,1) меньше разницы старой и новой энергий:

ln(u) < H(z, r) − H(z*, r*)

Если энергия почти не изменилась (H(z, r) ≈ H(z∗, r∗)), разница близка к нулю, и вероятность принятия будет близка к 100%. Если ошибка интегрирования велика — кандидат с большой вероятностью отклоняется. Таким образом, шаг Метрополиса корректирует неточности схемы Leapfrog, гарантируя, что все сэмплы остаются корректными и несмещёнными.

Поиск оценки MAP

Прежде чем приступать к основному этапу семплирования, полезно переместить начальную точку цепи в область высокой вероятности. Такой подход значительно сокращает период прогрева (Burn-in), поскольку наиболее выгодно начинать семплирование из области высоких значений плотности.

Оценка MAP (Maximum A Posteriori) — это точка z, в которой целевая плотность вероятности p(z) достигает своего максимума. Поскольку потенциальная энергия E(z) определяется как отрицательный логарифм плотности вероятности, задача поиска MAP сводится к эквивалентной задаче минимизации потенциальной энергии.

Для нахождения MAP в нашем коде используется метод оптимизации L-BFGS (библиотека Alglib). Оценка MAP, полученная после успешной минимизации, становится стартовой точкой для основного этапа семплирования или для этапа настройки матрицы масс. Таким образом поиск MAP гарантирует, что HMC начнет свою работу из наиболее перспективной области пространства параметров.

Настройка параметров HMC

Для обеспечения высокой эффективности HMC в реальных задачах, особенно в многомерном пространстве, требуется адаптивная настройка двух ключевых параметров: размера шага интегрирования epsilon и матрицы масс M.

Адаптация размера шага

Размер шага интегрирования epsilon (Leapfrog step size) — это ключевой параметр, от которого зависит точность численного решения гамильтоновых уравнений:

• слишком большой шаг приводит к значительной ошибке интегрирования, нарушению закона сохранения энергии и, как следствие, к низкой вероятности принятия,
• если epsilon слишком мал, требуется чрезмерно большое количество шагов L для построения одной траектории, из-за чего сэмплирование становится неоправданно медленным.

Цель адаптации — поддерживать фактическую вероятность принятия (acceptance) в оптимальном диапазоне (обычно 65%–95%). В нашем алгоритме это достигается с помощью экспоненциального скользящего среднего (EMA) фактической вероятности принятия. EMA сглаживает краткосрочные колебания, позволяя алгоритму плавно реагировать на изменения в пространстве вероятности:

• если EMA принятия выше целевого значения (слишком высокая точность интегрирования), epsilon немного увеличивается;
• если EMA принятия ниже целевого значения (много отклонений), epsilon уменьшается, чтобы снизить ошибку интегрирования и повысить шанс принятия.

Этот подход гарантирует, что HMC использует максимально возможный шаг epsilon, который позволяет быстро перемещаться по пространству, сохраняя при этом высокую и стабильную вероятность принятия.

Адаптация матрицы масс

Хотя адаптация размера шага позволяет управлять общей длиной траектории, она не решает проблему масштабирования в гетероскедастичном (неоднородном по дисперсии) пространстве. Если целевое распределение сильно вытянуто (например, дисперсия z1 = 100, а z2 = 0.01), единый шаг epsilon не может быть оптимальным сразу для обеих осей: он будет слишком маленьким для широкой оси z1 и слишком большим для узкой оси z2.

Именно здесь на помощь приходит матрица масс M. Она выступает в роли метрики пространства, которая перестраивает масштаб координат так, чтобы сэмплер видел распределение как изотропное — то есть близкое к сферическому. Это достигается за счёт того, что матрица масс управляет скоростью движения цепи по каждой оси отдельно. Оси с низкой дисперсией (узкие направления) получают большую массу, что замедляет движение и предотвращает резкие скачки через пик плотности. Напротив, оси с высокой дисперсией (широкие направления) получают малую массу, что позволяет цепи быстро и уверенно исследовать обширные области.

В идеале матрица масс должна быть пропорциональна обратной ковариационной матрице целевого распределения. Тогда вытянутое, коррелированное или гетероскедастичное распределение преобразуется в пространство, где все направления имеют примерно одинаковый масштаб. Благодаря этому теперь можно использовать один общий шаг epsilon, который будет адекватен для всех осей, без необходимости жертвовать точностью ради скорости или наоборот. В результате общая эффективность сэмплирования значительно возрастает.

В нашей реализации HMC используется два подхода к настройке диагональной матрицы масс:

• оценка по Гессиану в точке максимума апостериорной плотности (MAP),
• итеративное сэмплирование, которое постепенно уточняет оценки дисперсий по накопленным выборкам

Оба метода позволяют запустить основной этап сэмплирования с уже хорошо настроенной матрицей масс, что существенно ускоряет сходимость и повышает качество семплов.

Настройка по Гессиану в точке MAP

Наиболее прямой подход основан на том, что вблизи максимума, целевая функция p(z) часто аппроксимируется многомерным нормальным распределением. В этом случае ковариационная матрица Σ целевого распределения обратно пропорциональна Гессиану H потенциальной энергии E(z) : Σ = H^-1. Поскольку матрица масс должна быть пропорциональна обратной ковариации, получаем: M ≈ H. Таким образом оптимальная матрица масс — это Гессиан потенциальной энергии в точке MAP.

Так как вычисление полного Гессиана (матрицы вторых производных) слишком затратно, будем вычислять только его диагональные элементы, рассчитанные в точке максимума апостериорной плотности (MAP). Функция GetDiagonalHessian использует метод центральной разности для аппроксимации этих производных:

//+------------------------------------------------------------------+
//| Численно вычисляет диагональный Гессиан LogPDF                   |
//+------------------------------------------------------------------+
vector  GetDiagonalHessian(LogPDF *log_pdf, const vector &theta)
     {
      // Установка размера шага h.
      double h = 1e-5;
      
      int n = (int)theta.Size();
      vector Hdiag(n);

      // Вычисление fun(theta)
      double funtheta = log_pdf.LogTarget(theta);
      vector theta_h = theta;
      // 4. Вычисление диагональных элементов H_ii
      for(int i = 0; i < n; i++)
        {
         // f(x + 2h*e_i)
         theta_h[i] = theta[i] + 2.0 * h;
         double fun_plus_2h = log_pdf.LogTarget(theta_h);

         // f(x - 2h*e_i)
         theta_h[i] = theta[i] - 2.0 * h;
         double fun_minus_2h = log_pdf.LogTarget(theta_h);

         // Восстановление x_i
         theta_h[i] = theta[i];

         // Центральная разность: (f(x+2h) + f(x-2h) - 2f(x)) / (4h^2)
         Hdiag[i] = (fun_plus_2h + fun_minus_2h - 2.0 * funtheta) / (4.0 * h * h);
        }

      return Hdiag;
     }

   //+------------------------------------------------------------------+
   //| Адаптивно настраивает матрицу масс M на основе Гессиана LogPDF   |
   //+------------------------------------------------------------------+
   vector  TuneHessian(LogPDF *log_pdf, const vector &start_point)
     {
      // регуляризация
      double reg = 1e-3;

      // 1. Расчет отрицательного диагонального Гессиана LogPDF
      // M = -H
      vector negdiaghessian = -1.0 * GetDiagonalHessian(log_pdf, start_point);

      // 2. Регуляризация: massvec = max(reg, negdiaghessian).
      int n = (int)negdiaghessian.Size();
      vector massvec(n);
     
      for(int i = 0; i < n; i++)
        {
         if(negdiaghessian[i] < reg)
           {
            // Заменяем отрицательные или слишком маленькие значения на reg
            massvec[i] = reg;
           }
         else
           {
            massvec[i] = negdiaghessian[i];
           }
        }
      return massvec;
     }

Однако данный метод наиболее эффективен, когда целевое распределение p(z) действительно близко к нормальному. Если распределение имеет сложную форму (например, несколько мод), Гессиан, рассчитанный в одной точке, не может адекватно отразить это распределение. В таком случае более надежным является метод итеративного сэмплирования.

Итеративное cэмплирование (адаптация по выборочной дисперсии)

Метод итеративного сэмплирования — это эмпирический подход, который позволяет алгоритму адаптировать матрицу масс на основе фактического поведения цепи. Его основная идея заключается в том, чтобы постепенно повышать точность матрицы, используя выборки, которые цепь сама генерирует.

Процесс начинается с небольшого числа сэмплов и некоторой начальной матрицы M. На каждой итерации запускается HMC для генерации N выборок z. Затем вычисляется эмпирическая дисперсия Var(z(i)) этих выборок по каждой координате. Матрица обновляется на основе этой дисперсии по формуле:

M(i)=1 / (Var(z(i)) + λ)

где λ — небольшой регуляризатор для предотвращения деления на ноль.

Для повышения надежности оценки дисперсии, количество сэмплов на каждой последующей итерации увеличивается, а конечная точка предыдущей цепи используется как стартовая точка для следующей итерации.

//+------------------------------------------------------+
//| Настройка матрицы масс с помощью итеративной выборки |
//+------------------------------------------------------+
bool TuneIterativeSampling(
    LogPDF *log_pdf, 
    HMC_Params &params,
    const vector &initial_x, // Начальная точка для первой итерации
    vector &mass_vec_out,    // Финальный вектор масс
    vector &endpoint_out     // Конечная точка последней цепи
    )
{
    ulong n = initial_x.Size();
    
    // Создаем копию параметров
    HMC_Params current_params = params;    
    current_params.DisableEpsilonAdaptation  = true;
    current_params.burnin   = 0; // При настройке нам не нужен burnin период и прореживание
    current_params.ThinSize = 1; 
    current_params.num_print = 0; // отключим вывод информации
    
    // Начальный вектор масс: M = M_initial * Multiplier
    vector mass_vec = params.mass_vector * params.IterativeSamplingInitialMassMultiplier;
    current_params.mass_vector = mass_vec;   
    int num_samples = params.IterativeSamplingMinSamples;  
    matrix xsmpl_matrix;
    double acceptance_rate = 0.0;
    vector current_start_point = initial_x;
    vector current_endpoint(n); 
    
    PrintFormat("Итеративная настройка матрицы масс (%d итераций) ", params.IterativeSamplingIterations);
    for (int i = 1; i <= params.IterativeSamplingIterations; i++)
    {
        current_params.num_samples = num_samples;
        
        HMC(current_start_point, xsmpl_matrix, acceptance_rate, log_pdf, current_params, current_endpoint);

        vector variance_vec = xsmpl_matrix.Var(1,1);       
        vector new_mass_vec(n);                 
        new_mass_vec = 1.0 / (variance_vec + params.IterativeSamplingRegularizer);       
        mass_vec = new_mass_vec;
        current_params.mass_vector = mass_vec; // Обновляем M для следующей итерации HMC
        PrintFormat("  Итерация %d: Сэмплов=%d ", i, current_params.num_samples);        
        // Увеличение объема сэмплирования
        num_samples = MathMin(num_samples * 2, params.IterativeSamplingMaxSamples);       
        // Настройка стартовой точки для следующей итерации
        current_start_point = current_endpoint;
    }
    
    // Установка финальных значений
    mass_vec_out = mass_vec; 
    endpoint_out = current_endpoint;   
    params.mass_vector = mass_vec; 

    return true;
}

Этот подход позволяет подбирать оптимальное масштабирование параметров работающее и для негауссовых распределений.

Мониторинг сэмплирования в реальном времени

В процессе работы HMC предусмотрен вывод диагностической информации в журнал. За частоту такого вывода отвечает параметр num_print структуры HMC_Params:

• если num_print = 0, вывод отключен,
• если num_print — положительное целое число (например, 100), информация будет выводиться каждые 100 сохраненных сэмплов после завершения периода прогрева.

Оперативный мониторинг позволяет:

1. Проверять достижение стационарности (LOG PDF): Убедиться, что среднее значение логарифма плотности перестало расти и колеблется вокруг некоторого стабильного уровня. Это указывает на то, что цепь успешно достигла области высокой вероятности и начала сэмплировать из целевого распределения.
2. Следить за адаптацией размера шага (STEP SIZE), который автоматически корректируется для поддержания целевой вероятности принятия.
3. Контролировать среднюю вероятность принятия (ACC RATIO), которая должна оставаться вблизи целевого значения, заданного пользователем.
4. Отслеживать количество расхождений (DIVERGENT), то есть траекторий, в которых Гамильтониан не был сохранен (часто указывает на проблемы в модели или слишком большой шаг). Идеально когда расхождений нет.

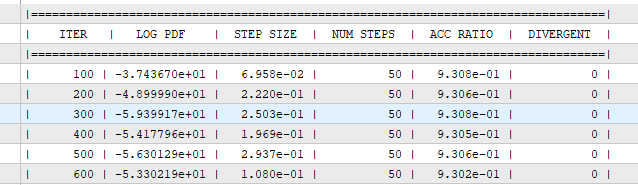
Рис.3. Пример вывода информации во время семплирования

Диагностические показатели MCMC

За вычисление и вывод в журнал статистики отвечает функция Diagnostics. Она оценивает ключевые метрики по всем цепям:

• оценка среднего (Mean)
• стандартное отклонение (SD)
• стандартная ошибка Монте-Карло (MCSE) — оценивает точность, с которой мы можем оценить среднее. MCSE = SD / sqrt (ESS). Чем ниже MCSE, тем точнее наша оценка среднего значения.

• Квантили (Q5, Q95)
• Эффективный размер выборки (Effective Sample Size, ESS) — определяет сколько независимых сэмплов эквивалентно по информативности всей MCMC-выборке. В MCMC сэмплы коррелируют (один сэмпл зависит от предыдущего), поэтому ESS < фактического размера выборки. Чем выше ESS, тем меньше автокорреляция и тем больше полезной информации в выборке.

• Статистика сходимости Гельмана-Рубина (R-hat)  — оценивает, насколько хорошо различные независимые цепи MCMC смешиваются и сходятся к одному и тому же целевому распределению. Значения R-hat, близкие к 1 (как правило, < 1.1), указывают на удовлетворительную сходимость, где вариация между цепями сравнима с вариацией внутри цепей.

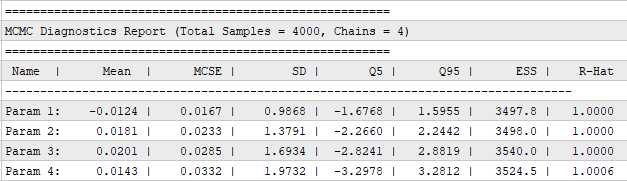
Рис. 4. Пример вывода итоговой статистики

Диагностика сходимости и эффективности HMC-семплера

Разобравшись с основами гамильтонова метода Монте-Карло, перейдем к оценке его практической эффективности. В качестве стресс-теста, демонстрирующего возможности HMC, рассмотрим 100-мерное коррелированное, гетероскедастичное нормальное распределение. Работа со столь сложным целевым распределением (где дисперсия линейно растет от 1 до 100, а корреляция между соседними параметрами составляет 0.9) является серьезным испытанием для большинства традиционных MCMC-алгоритмов. Данный пример наглядно покажет необходимость предварительной настройки матрицы масс для адекватной работы в пространствах с сильно различающимися масштабами параметров.

Для этого создадим класс NormalLogPDF унаследованный от абстрактный класса LogPDF, который реализует логарифм плотности и аналитический градиент необходимые для HMC:

#include <MCMC\HMC.mqh>

// --- ВХОДНЫЕ ПАРАМЕТРЫ HMC ---
input int    Inp_Dimension     = 100;   // Размерность пространства параметров D
input double Inp_Correlation   = 0.9;   // Коэффициент корреляции 
input int    Inp_NumChains     = 4;     // Количество цепей 
input int    Inp_NumSamples    = 1000;  // Количество сохраняемых сэмплов на одну цепь
input int    Inp_ThinSize      = 10;    // Интервал прореживания (Thinning)
input double Inp_StepSize      = 0.01;  // Начальный размер шага Leapfrog 
input int    Inp_NumLeapfrog   = 50;    // Количество шагов Leapfrog
input int    Inp_Burnin        = 1000;  // Период прогрева (Burn-in)
input double Inp_TargetAccept  = 0.93;  // Целевая вероятность принятия 
input TUNING Inp_MassTuning    = NONE;  // Метод настройки матрицы масс
input int    Inp_NumPrint      = 100;   // Частота вывода диагностической информации в журнал (0 - отключить)

//--- Пример реализации LogPDF (многомерное коррелированное нормальное распределение)
class NormalLogPDF : public LogPDF {
private:
    ulong size;        // Размерность D
    vector mu;         // Среднее значение 
    matrix sigma;      // Ковариационная матрица
    matrix inv_sigma;  // Обратная ковариационная матрица

public:
    NormalLogPDF(ulong dim, double correlation) {
        size = dim;
        mu = vector::Zeros(size);
        sigma = matrix::Zeros(size, size);
        
        // 1. Вводим вектор масштабирования дисперсий (от 1.0 до 100.0)
        vector k = vector::Zeros(size);
        for (int i = 0; i <(int) size; i++) {
            double variance_scale = 1.0 + (double)i / (double)(size - 1) * 99.0;
            k[i] = variance_scale;
        }

        // 2. Создаем коррелированную матрицу с разными дисперсиями
        for (int i = 0; i <(int) size; i++) {
            for (int j = 0; j <(int) size; j++) {
                // Ковариация Sigma[i, j] = sqrt(k[i] * k[j]) * correlation^|i-j|
                sigma[i, j] = MathSqrt(k[i] * k[j]) * MathPow(correlation, (double)MathAbs(i - j));
            }
        }
        
        // 3. Инвертирование матрицы ковариации
        inv_sigma = sigma.Inv(); 
    }
    
    double LogTarget(const vector &z) override {
        vector diff = z - mu;
        return -0.5 * diff @ inv_sigma @ diff;
    }

    vector GradLogTarget(const vector &z) override {
        vector diff = z - mu;
        return -1 * (inv_sigma @ diff);
    }
    
};

В первую очередь с помощью функции EstimateMAP найдем точку максимума плотности, которая послужит оптимальной стартовой позицией.

Для всесторонней оценки сходимости и качества полученной выборки сгенерируем 4 независимых цепи по 1000 сэмплов каждая (после периода прогрева) и вычислим ключевые статистики по всем цепям.

Для оценки практической значимости адаптивной настройки матрицы масс проведём сравнительный анализ двух стратегий:

• когда матрица масс не адаптируется и остаётся единичной — это стандартный подход по умолчанию, когда масштабирование параметров не учитывается,
• iterative sampling, при котором диагональные элементы матрицы масс оцениваются по дисперсиям сэмплов.

Хотя теоретически оптимальным подходом в гауссовском случае была бы настройка матрицы масс на основе Гессиана в точке MAP, в реальных задачах с отклонением от нормального распределения (тяжелые хвосты, мультимодальность, асимметрия), он не дает удовлетворительных результатов. Более надежным и универсальным подходом является iterative-sampling.

Поэтому, чтобы показать возможности HMC в реалистичных сценариях, будем использовать именно этот подход и сравним его результаты с базовой стратегией без адаптации.

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart() {
    int dim =        Inp_Dimension;
    int num_chains = Inp_NumChains;
    Print("--- Start HMC (D=", dim, ", Chains=", num_chains, ") ---");    
    
    // Создание объекта для целевой плотности
    NormalLogPDF log_pdf(dim, Inp_Correlation);
    
    // 1. Инициализация параметров HMC 
    HMC_Params params;
    
    params.num_samples        = Inp_NumSamples;
    params.ThinSize           = Inp_ThinSize;
    params.step_size          = Inp_StepSize;
    params.num_leapfrog       = Inp_NumLeapfrog;
    params.burnin             = Inp_Burnin;
    params.target_accept      = Inp_TargetAccept;
    params.mass_tuning_method = Inp_MassTuning; 
    params.num_print          = Inp_NumPrint;

    // Создаем семплер HMC
    HamiltonianSampler mcmc;
      
    // 2. Настройка матрицы масс M
    vector initial_point_for_tuning = vector::Ones(dim) * 5.0; // Смещенная начальная точка
    vector mass_vec_out;
    vector endpoint_out(dim); // Конечная точка после настройки масс/горячий старт

    if (params.mass_tuning_method != NONE)
    {
        Print("--- Estimate MAP Point --- ");
        // Результат MAP используем как стартовую точку для семплера
        initial_point_for_tuning = mcmc.EstimateMAP(&log_pdf, initial_point_for_tuning); 

        Print(" --- Tune Mass Matrix --- ");  
           if (params.mass_tuning_method == HESSIAN)
        {
             params.mass_vector = mcmc.TuneHessian(&log_pdf, initial_point_for_tuning);        
        } else if (params.mass_tuning_method == ITERATIVE)
        {
            mass_vec_out.Resize(dim);
            endpoint_out.Resize(dim);
            mcmc.TuneIterativeSampling(&log_pdf, params, initial_point_for_tuning, 
                mass_vec_out, endpoint_out);
             
            params.mass_vector = mass_vec_out; 
        }                      
        Print("Настройка матрицы масс завершена.(первые 5 и последние 5 элементов):");       
        int total_size = (int)params.mass_vector.Size();
        int limit_start = (int)MathMin(total_size, 5);       
        // Вывод первых 5 элементов
        for(int i = 0; i < limit_start; i++)
        {
            Print("M[", i, "] = ", params.mass_vector[i]);
        }
        
        if (total_size > 10) // и последние 5
        {
            Print("...");
            int start_index = total_size - 5;                     
            for(int i = start_index; i < total_size; i++) 
            {
                Print("M[", i, "] = ", params.mass_vector[i]);
            }
        }
    }
    // -------------------------------------------------------------    
    // 3. Запускаем HMC для заданного количества цепей
    // -------------------------------------------------------------   
    matrix samples_all[]; // Массив всех цепей
    ArrayResize(samples_all, num_chains);       
    uint start_time = GetTickCount(); 
    for (int chain_idx = 0; chain_idx < num_chains; chain_idx++) 
    {
        Print("\n" + "========================================");
        Print("Start chain #", chain_idx + 1, " из ", num_chains);
        Print("========================================");
        
        vector start_point(dim);      
        if (chain_idx == 0 && params.mass_tuning_method != NONE)
        {
            // Для первой цепи используем конечную точку после настройки
            start_point = endpoint_out;
            Print("Start point: after adaptation");
        }
        else
        {
            // Для остальных цепей используем случайную точку для проверки сходимости
            double rndn[];
            MathRandomNormal(0.0, 5.0, dim, rndn); 
            start_point.Assign(rndn);
            Print("Start point: Random");
        }

        matrix samples = matrix::Zeros(1,1);
        double accept_rate = 0.0;
        vector final_endpoint(dim);        
        mcmc.HMC(start_point, samples, accept_rate, &log_pdf, params, final_endpoint);
        samples_all[chain_idx] = samples;
        Print("--- Результаты HMC для цепи #", chain_idx + 1, " ---");
        Print("Вероятность принятия: ", DoubleToString(accept_rate * 100, 2), "%");
        // Запись семплов в csv файл
        string file_name = StringFormat("HMC/hmc_samples_chain_%d.csv", chain_idx + 1);
        MatrixToCSV(file_name, samples); 
    }  
    uint elapsed_time = GetTickCount() - start_time;
    Print("\nОбщее время вычисления сэмплов (", num_chains, " цепей): ", DoubleToString(elapsed_time / 1000.0, 3), " секунд");
     
    // 5. Выводим результаты статистики семплов в журнал 
    Diagnostics(samples_all,50, true);
}

После завершения семплирования проведем диагностику по всем цепям. 

Параметр	ESS  c M-настройкой	ESS без M (единичная матрица)
param 1	3370	3453
param 50	2414	2023
param 80	2915	1552
param 90	2534	1311
param 100	2669	1715

В первую очередь смотрим на ESS, так как он является ключевым показателем эффективности. Результаты подтверждают важность адаптации, особенно для параметров с высокой дисперсией. Прирост ESS достигает 50–100 % в случае использования настройки. Для параметра с минимальной дисперсией (Param 1) ESS составил 3370 с адаптацией и 3453 без неё — разница незначительна, поскольку единичная матрица масс уже близка к оптимальной в узких направлениях.

Критерий сходимости R-hat

Параметр	R-hat с M	R-hat без M
Все	1 - 1.0025	1 -1.0020

Обе стратегии демонстрируют отличную сходимость (R-Hat < 1.01), что означает, что все 4 цепи успешно сошлись к стационарному распределению. Однако как показывает ESS, сходимость не гарантирует эффективности: Rhat говорит о сходимости, но не о качестве полученных сэмплов.

Стандартная ошибка Монте-Карло (MCSE) ниже при использовании M-настройки, особенно для параметров с большим масштабом. Это означает, что при том же числе итераций настроенный HMC даёт более точные оценки среднего — особенно для параметров с большой дисперсией. 

Параметр	MCSE с M	MCSE без M
param 50	0.1456	0.1536
param 90	0.1859	0.2627
param 100	0.1930	0.2444

Оценки стандартного отклонения (SD) в обоих случаях оказались практически идентичными и очень близкими к теоретическим значениям:

Параметр	SD с M	SD без M
param 1	0.99	1.00
param 50	7.15	6.91
param 100	9.97	10.12

Небольшие расхождения (в пределах 1–3 %) статистически несущественны и лежат в пределах естественной вариации Монте-Карло. Оценка SD почти не зависит от адаптации, потому даже при высокой автокорреляции, если цепи сошлись (Rhat <1.01), дисперсия будет правильной — просто медленнее сходится.

Ключевое отличие проявляется не в SD, а в оценках среднего. Без M-настройки наблюдался заметный дрейф оценок среднего в отрицательную область (от -0.40 до -0.23), тогда как с M-настройкой средние значения оставались более симметричными и близкими к истинному нулю (от +0.05 до +0.27). Это является дополнительным признаком того, что адаптация M обеспечивает более полноценное исследование пространства состояний.

Таким образом, настройка матрицы масс критически важна для эффективной работы HMC в высокоразмерных, гетероскедастичных моделях. HMC очень чувствителен к масштабу параметров и без настройки массы "тяжелые" параметры (с большой дисперсией) двигаются медленно, вызывая высокий уровень автокорреляции и низкий ESS.

Хотя численные статистические показатели являются объективным доказательством успешности сэмплирования, также полезно визуально оценить результаты работы HMC, чтобы подтвердить сходимость и исследовать форму целевого распределения.

Для визуализации результатов используется два основных типа графиков:

• Corner Plot, который отображает маргинальные одномерные распределения  каждой переменной, а также парные двумерные распределения (т.е., ковариационные отношения между каждой парой переменных):

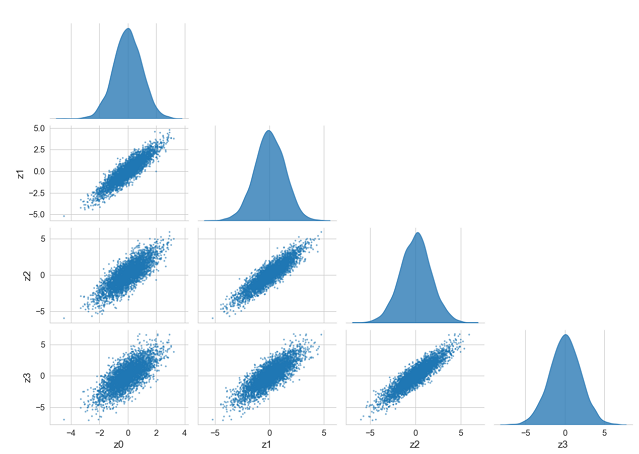
Рис. 5. Corner plot для первых четырёх параметров

• Trace Plot, который показывает эволюцию значений параметров по итерациям в каждой из четырёх цепей. Используется для визуальной проверки стационарности(отсутствие трендов), качества перемешивания и отсутствия автокорреляции:

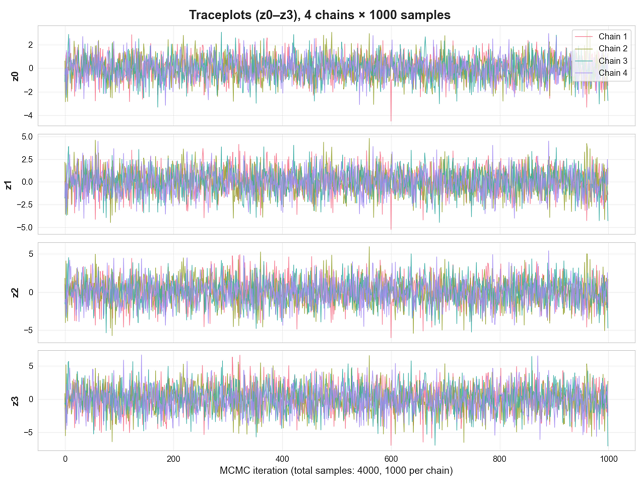
Рис. 6. Трассировочный граифик, 4 цепи для первых 4 переменных

Заключение

В данной статье была представлена базовая реализация гамильтонова алгоритма Монте-Карло (HMC) на языке MQL5. Эффективность разработанного градиентного сэмплера была успешно подтверждена на сложном тестовом примере — получении выборки из 100-мерного, коррелированного и гетероскедастичного нормального распределения.

Разработанный функционал представляет собой комплексное решение, включающее следующие важные компоненты:

• поиск стартовой точки (MAP) с помощью оптимизатора L-BFGS,
• проверку корректности вычисления градиента,
• методы настройки матрицы масс,
• комплексную диагностику качества семплов (Rhat, ESS, MCSE, квантили),
• мониторинг процесса сэмплирования в реальном времени

Всё это превращает HMC в готовый к практическому применению инструмент в реальных задачах машинного обучения. HMC не зря называют «золотым стандартом» в области MCMC. Он открывает двери для применения многопараметрических байесовских моделей, где традиционные MCMC-методы не могут обеспечить достаточную скорость и качество сэмплов.

Дальнейшее развитие данного метода может коснуться внедрения алгоритма NUTS (No-U-Turn Sampler), который автоматически настраивает оптимальную длину траектории, что позволит сделать HMC ещё более автономным и надёжным, устранив необходимость вручную настраивать количество шагов L.

Программы, используемые в статье

#	Имя	Тип	Описание
1	HMC.mqh	Включаемый файл	Алгоритм HMC, методы настройки матрицы масс, поиск MAP, диагностика семплов
2	HMC_D100.mq5	Скрипт	Пример семплирования с помощью HMC
3	Plot.py	Скрипт	Визкализация в Python