Critério de Independência de Hilbert-Schmidt (HSIC)

Introdução

A principal tarefa do trader ao trabalhar com cotações de instrumentos financeiros é a criação de um sistema de negociação (EA) com expectativa matemática positiva. Ao projetar esses sistemas, frequentemente se assume que existem dependências ocultas nos dados utilizados para aprendizado e posterior negociação. No entanto, a questão da verificação estatística dessa suposição geralmente não é considerada. Acredita-se que uma resposta indireta possa ser obtida por meio dos resultados de testes em dados fora da amostra (out-of-sample).

Enquanto isso, uma resposta estatisticamente fundamentada à questão da existência de relação entre os atributos e a variável-alvo tem importância fundamental. Uma resposta positiva dá confiança na viabilidade do uso de modelos preditivos, enquanto uma resposta negativa leva a refletir: o que exatamente o algoritmo está tentando prever?

Na estatística matemática, a questão da existência ou ausência de ligação probabilística entre variáveis aleatórias é respondida pelos critérios de independência. Um desses critérios é o teste estatístico HSIC — um poderoso método não paramétrico desenvolvido em 2005 pelo estatístico Arthur Gretton.

Diferentemente do coeficiente de correlação, que identifica apenas relações lineares, o HSIC é capaz de detectar tanto dependências lineares quanto não lineares. Graças a isso, ele é amplamente utilizado em aprendizado de máquina para seleção de atributos, análise de relações de causa e efeito e outras tarefas. Neste artigo, vamos analisar o princípio de funcionamento do HSIC e implementá-lo no ambiente MQL5.

O que é HSIC

HSIC é uma medida de dependência entre duas variáveis aleatórias X e Y, baseada na abordagem de kernels. O método utiliza a “magia” matemática das funções kernel, por exemplo, a gaussiana (fig.1), que transformam os dados em um espaço especial RKHS (Reproducing Kernel Hilbert Spaces), onde as dependências se tornam mais fáceis de detectar.

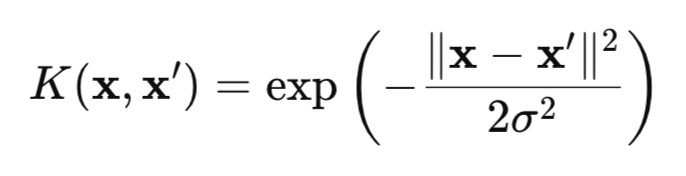
Figura 1 Núcleo gaussiano (RBF)

onde:

• x, x' são vetores (pontos) de observações,
• || ||² é o quadrado da norma euclidiana,
• σ é a largura do kernel.

Existem muitos kernels que podem ser usados para o teste HSIC, como kernels para dados categóricos ou o kernel de Laplace. No entanto, neste artigo, vamos concentrar nossa atenção no kernel gaussiano, pois ele é universal e possui a propriedade de caracteristicidade. Essa propriedade permite identificar quaisquer dependências nos dados, tornando o kernel gaussiano especialmente eficaz.

O HSIC clássico testa a independência par entre duas variáveis aleatórias X e Y, verificando se a condição P(X,Y) = P(X)P(Y) é satisfeita. Para isso, o HSIC analisa o desvio da distribuição conjunta em relação ao produto das distribuições marginais, utilizando matrizes kernel, isto é, uma tabela em que cada elemento reflete a similaridade entre pares de pontos de dados, calculada com o auxílio da função kernel.

Uma vantagem importante do HSIC está em sua capacidade de trabalhar com dados de qualquer dimensionalidade: escalares, vetoriais ou suas combinações. Isso é especialmente valioso em tarefas em que a construção explícita de distribuições conjuntas multidimensionais P(X,Y) é difícil devido à alta dimensionalidade dos dados.

Do ponto de vista matemático, o critério HSIC é definido como o quadrado da norma de Hilbert-Schmidt do operador de covariância cruzada no RKHS:

onde:

• K(X,X') é a função kernel para a variável aleatória X,
• L(Y,Y') é a função kernel para a variável aleatória Y,
• || ||HS - norma de Hilbert-Schmidt.

Aqui é apropriado comparar o HSIC com a covariância usual. A covariância clássica mede a relação linear entre as grandezas X e Y em seu espaço original, enquanto o HSIC trabalha com os mapeamentos de X e Y para o espaço de Hilbert reproduzível por kernels (RKHS), isto é, um espaço de funções, o que permite transformar os dados para revelar dependências não lineares complexas.

Na prática, não é necessário calcular diretamente a norma de Hilbert-Schmidt. Em vez disso, o HSIC é estimado por meio de uma estatística empírica, que se baseia em matrizes kernel construídas para a amostra de dados:

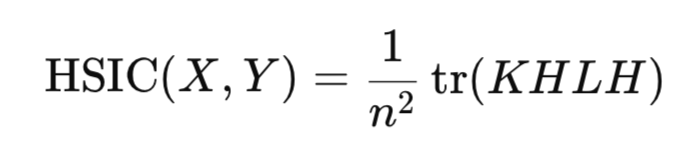
onde:

• K, L são matrizes de kernel n*n,
• H é a matriz de centralização n*n (I -1/n11^T),
• tr() é o traço da matriz,
• n é o número de observações.

De forma semelhante ao coeficiente de correlação, o HSIC avalia a presença de dependência entre as variáveis aleatórias X e Y utilizando estatística amostral, sem a necessidade de construir as distribuições dessas grandezas.

A estatística HSIC é sempre não negativa:

• valor de HSIC > 0 indica a presença de dependência,
• enquanto HSIC = 0 indica a independência dos dados.

Verificação da significância do HSIC

No entanto, para conclusões confiáveis, não basta calcular a estatística — é necessário confirmar sua significância estatística para excluir um resultado aleatório. Para a estatística HSIC, não existe uma forma analítica exata da distribuição sob a hipótese nula. Ou seja, não podemos simplesmente usar, por exemplo, a distribuição normal e obter de forma rápida e fácil, sem custos computacionais, um valor crítico ou p-value. Para resolver esse problema, são aplicadas duas abordagens principais:

• teste de permutação,
• aproximação gama.

O teste de permutação é o método principal e mais preciso para avaliar a distribuição do HSIC sob H0. Seu objetivo é destruir qualquer dependência entre X e Y por meio da permutação aleatória dos índices de uma das variáveis ou do embaralhamento da matriz kernel resultante dessa variável. Para obter um resultado preciso, é necessário realizar um número relativamente grande dessas permutações, em torno de 1000. Por isso, o teste de permutação é bastante custoso, pois exige o cálculo do HSIC para cada uma dessas permutações.

A principal vantagem do teste de permutação consiste no fato de que ele não requer qualquer suposição sobre a forma da distribuição dos dados; em vez disso, ele se baseia na distribuição empírica da estatística, obtida por meio das permutações. Em seguida, a distribuição empírica do HSIC é utilizada para obter uma estimativa do p-value. 

Para acelerar o cálculo da estatística, é utilizada a aproximação gama. Nesse enfoque, a estatística HSIC é escalada levando em conta o tamanho da amostra (n*HSIC), e os parâmetros da distribuição gama são estimados a partir dos momentos amostrais do HSIC (média e variância). Esse método é significativamente mais rápido do que o teste de permutação, porém sua precisão pode ser menor para amostras pequenas. Existem também outros métodos para estimar a distribuição do HSIC sob a hipótese nula de independência, mas eles são complexos de implementar e raramente utilizados na prática, portanto não são considerados neste artigo.

Implementação do HSIC Permutation em MQL5

O teste de permutação é implementado na função hsic_test.

//+------------------------------------------------------------------+
//| Функция для перестановочного теста                               |
//+------------------------------------------------------------------+
vector hsic_test(matrix &X,matrix &Y,const double alpha,bool Bootstrap = false,int n_permutations=1000)
{
vector ret = vector::Zeros(3);
int n = (int)X.Rows(); 

matrix K =  RBF_kernel(X); // матрица ядра для X
matrix L =  RBF_kernel(Y); // матрица ядра для Y
matrix H = matrix::Eye(n, n) - matrix::Ones(n, n)/n; // Центрирующая матрица
//--------------------------------------

// Kc центрированная ядерная матрица К
   matrix Kc(n, n);
   if(!Kc.GeMM(H, K, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Kc = H * K");
      return ret;
   }
   if(!Kc.GeMM(Kc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Kc * H");
      return ret;
   }
   Kc = Kc.Transpose();
   double coef = 1/pow(n,2);

// Вычисляем наблюдаемое значение статистики HSIC
   double  hsic_obs = compute_hsic(L,Kc,coef);
   ret[0]= hsic_obs;

  //------------ Перестановочный тест ------------------------------------
  if (Bootstrap == true){ 
    vector hsic_perms = vector::Zeros(n_permutations);   
    for ( int i = 0; i<n_permutations; i++)
    {        
        ShuffleMatrix(L); // Перемешиваем матрицу
        hsic_perms[i] = compute_hsic(L,Kc,coef);
    }
    
    int count = 0;
for(int i = 0; i < n_permutations; i++)
{
   if(hsic_perms[i] >= hsic_obs)
      count++;
}
   // Вычисляем p-value
double p_value = (n_permutations > 0) ? (double)count / n_permutations : 0.0;
    ret[1] = p_value; 
  
  // Вычисляем критическое значение
  double hsic_sort[];
  VectortoArray(hsic_perms,hsic_sort);
  ArraySort(hsic_sort);
  double CV = hsic_sort[(int)round((1-alpha)*n_permutations)];
    ret[2] = CV; 
    }
 //----------------------------------------------------------------------------------   
  return ret;  
}

• A função recebe dois conjuntos de dados X e Y (são matrizes de dimensão n*d, onde n é o número de observações e d é a dimensionalidade dos dados),

• o parâmetro alpha define o nível de significância (isso é o erro do tipo I, isto é, a probabilidade de rejeitar a hipótese nula quando ela é de fato verdadeira),

• o parâmetro Bootstrap (se true, o teste é calculado com permutações para obter o p-value, caso contrário, apenas o cálculo da estatística),

• n_permutations é o número de permutações aleatórias,

• a função retorna um vetor contendo o valor observado do HSIC, o p_value e o valor crítico da estatística para o nível alpha escolhido.

O cálculo da matriz do kernel gaussiano é realizado na função RBF_kernel.

//+------------------------------------------------------------------+
//| Гауссовское ядро                                                 |
//+------------------------------------------------------------------+ 
matrix RBF_kernel(const matrix &X) {
   int n = (int)X.Rows();
   
   // Вычисляем матрицу расстояний через скалярное произведение
   matrix XX(n, n); 
   if(!XX.GeMM(X, X.Transpose(), 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить XX = X * X^T");    
   }
   
 matrix diag(n,1);
 diag.Col(XX.Diag(),0);  // вектор диагональных элементов
 //  квадраты расстояний
 matrix D_sq = matrix::Ones(n, 1).MatMul(diag.Transpose()) + diag.MatMul(matrix::Ones(1, n)) - 2*XX;
   
   // Вычисляем sigma на первых n_sigma строках
   int n_sigma = MathMin(n, 100);
   int num_elements = (n_sigma * (n_sigma - 1)) / 2;
   vector upper_tri(num_elements);
   int idx = 0;
   for(int i = 0; i < n_sigma; i++) {
      for(int j = i + 1; j < n_sigma; j++) {
         upper_tri[idx] = D_sq[i, j]; 
         idx++;
      }
   }
  double sigma = MathSqrt(0.5 * upper_tri.Median());
   
   return MathExp((-1* D_sq) / (2 * sigma*sigma)); 
}

A função calcula os quadrados das distâncias entre os pontos de dados, a largura do kernel sigma e retorna a matriz de kernel desejada de tamanho n*n.

Para o cálculo eficiente dos quadrados das distâncias, é utilizada a forma matricial em vez de um laço comum:

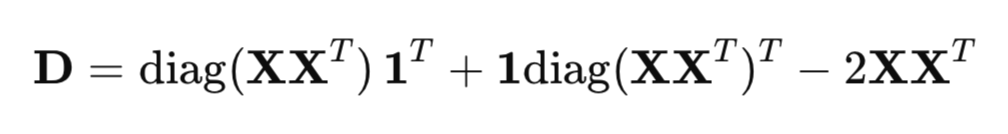
onde:

• XX^T é a matriz de Gram (matriz de produtos escalares),
• diag(XX^T) é o vetor dos elementos diagonais,
• 1 - vetor de uns.

O parâmetro sigma no kernel gaussiano define a largura do kernel e influencia significativamente a sensibilidade do HSIC na detecção de dependências nos dados. O parâmetro sigma define a escala de similaridade: valores grandes de sigma tornam o kernel mais amplo (pontos que estão mais distantes entre si ainda são considerados semelhantes), enquanto valores pequenos o tornam mais estreito (apenas pontos muito próximos são considerados semelhantes).

Um dos métodos mais comuns para a escolha de sigma é o uso da seguinte heurística da mediana:

O coeficiente 0,5 é adotado para que o denominador do kernel RBF seja igual à mediana dos quadrados das distâncias euclidianas entre os pontos de dados, o que garante uma estimativa adaptativa que leva em conta a escala dos dados. 

A variável n_sigma = MathMin(n, 100) limita a quantidade de dados para o cálculo de sigma a 100. Isso é feito para reduzir os custos computacionais em amostras grandes, mantendo ao mesmo tempo a representatividade para a estimativa de sigma.  No vetor upper_tri são copiados os quadrados das distâncias euclidianas utilizando apenas o triângulo superior da matriz de distâncias (sem a diagonal, i=j), para evitar duplicação e distâncias nulas.

A função para o cálculo da estatística HSIC é compute_hsic.

//+------------------------------------------------------------------+
//| Функция для вычисления HSIC                                      |
//+------------------------------------------------------------------+
double compute_hsic(const matrix &L, const matrix& Kc, const double coef){
matrix KcL= Kc*L;               
return coef*KcL.Sum();
}

Após o cálculo da estatística HSIC observada, é realizado o teste de permutação para verificar sua significância estatística. A função ShuffleMatrix (matrix &m) implementa essa permutação para a matriz de kernel L, correspondente à variável Y. Do ponto de vista estatístico, não há diferença entre embaralhar L ou K, pois o HSIC é simétrico em relação a X e Y, o que resulta em valores equivalentes no teste de permutação do HSIC. O embaralhamento da própria variável Y e o recálculo subsequente da matriz L para cada permutação é ineficiente.

//+------------------------------------------------------------------+
//| Функция для перемешивания данных матрицы                         |
//+------------------------------------------------------------------+
void ShuffleMatrix(matrix &m)
{
   int rows = (int)m.Rows();
   int cols = (int)m.Cols();
   
   if (rows != cols) {
   Print("Ошибка: Матрица должна быть квадратной");
}  
   int perm[];
   GeneratePermutation(rows, perm);  // Генерация случайной перестановки индексов
   matrix temp = m;  
   // Перестановка строк и столбцов
   for(int i = 0; i < rows; i++)
   {
      for(int j = 0; j < cols; j++)
      {
         m[i,j] = temp[perm[i], perm[j]];
      }
   }
}

A geração de índices aleatórios é realizada por meio da função GeneratePermutation.

//+------------------------------------------------------------------+
//| Функция для создания случайной перестановки индексов             |
//+------------------------------------------------------------------+ 
void GeneratePermutation(int size, int &perm[])
{
   MathSequence(0,size,1,perm);
   
   // Алгоритм Фишера-Йетса для перестановки
   for(int i = size - 1; i > 0; i--)
   {
      // Генерация случайного индекса от 0 до i
      int j = (int)(MathRand() / 32768.0 * (i + 1)); 
      int temp = perm[i];
      perm[i] = perm[j];
      perm[j] = temp;
   }
}

Após múltiplas permutações da matriz de kernel L, utilizando a função ShuffleMatrix, forma-se a distribuição empírica da estatística HSIC sob a hipótese nula de independência. O p-value é definido como a proporção dos valores permutados de HSIC que são maiores ou iguais à estatística observada. Se o p-value for menor que o nível de significância alpha, a hipótese nula de independência é rejeitada.

O valor crítico é escolhido como o quantil da distribuição empírica no nível 1−alpha, isto é, o valor acima do qual se encontram alpha⋅100 % dos cálculos permutados de HSIC.

Implementação do HSIC Gamma

O cálculo da aproximação gama é realizado pela função hsic_Gamma_test.

//+------------------------------------------------------------------+
//| Функция для Гамма-аппроксимации HSIC                             |
//+------------------------------------------------------------------+
double hsic_Gamma_test(matrix &X, matrix &Y, double &CV, double & pvalue)
{
int n = (int)X.Rows(); 

matrix K =  RBF_kernel(X); // матрица ядра для X
matrix L =  RBF_kernel(Y); // матрица ядра для Y
matrix H = matrix::Eye(n, n) - matrix::Ones(n, n)/n; // Центрирующая матрица

   matrix Kc(n, n); // Вычисляем центрированную матрицу ядра X  
   if(!Kc.GeMM(H, K, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Kc = H * K");
      return 0;
   }
   if(!Kc.GeMM(Kc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Kc * H");
      return 0;
   }   
   matrix KcT = Kc.Transpose();
     
   matrix Lc(n, n);  // Вычисляем центрированную матрицу ядра Y 
   if(!Lc.GeMM(H, L, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Lc = H * L");
      return 0;
   }
   
   if(!Lc.GeMM(Lc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Lc * H");
      return 0;
      }
              
   double m = (double)n; 
   double coef = 1/m;
   
// Вычисляем наблюдаемое значение HSIC
matrix KcLc;
double  hsic_obs = compute_hsic_Gamma(Lc,KcT,coef,KcLc); // n*HSIC

   matrix varHSIC_m = KcLc*KcLc;
   varHSIC_m = (1.0/36.0)*varHSIC_m;  
   double  varHSIC = 1/(m)/(m-1) * (varHSIC_m.Sum() - varHSIC_m.Trace() );
   varHSIC = 72*(m-4)*(m-5)/m/(m-1)/(m-2)/(m-3)  *  varHSIC; // Дисперсия HSIC
   
   matrix KD;
   KD.Diag(K.Diag(),0);
   matrix LD;
   LD.Diag(L.Diag(),0);
   K = K-KD;   
   L = L-LD;  
   matrix one = matrix::Ones(n,1);
   matrix a = 1/m/(m-1)*one.Transpose();
   matrix muX;
   muX.GeMM(a,K.MatMul(one),1,0);
   matrix  muY;
   muY.GeMM(a,L.MatMul(one),1,0);
   double mHSIC  = 1/m * ( 1 +muX[0,0]*muY[0,0]  - muX[0,0] - muY[0,0] ) ; // математическое ожидание HSIC

//параметры Гамма распределения
 double alphaG = mHSIC*mHSIC / varHSIC;
 double beta = varHSIC*m / mHSIC;   
 
 int err;
 CV = MathQuantileGamma(1-alpha_,alphaG,beta,err);  // Critical value
 pvalue = 1 - MathCumulativeDistributionGamma(hsic_obs,alphaG,beta,err); // p-value 
 //----------------------------------------------------------------------------------   
  return hsic_obs;  
}

Aqui calculamos a estatística HSIC, escalada pelo tamanho da amostra n (n*HSIC), à qual corresponde aproximadamente uma distribuição gama com parâmetros de forma (alpha) e escala (beta). Esses parâmetros são determinados com base na esperança matemática e na variância da estatística HSIC.

Verificação em dados sintéticos

Para avaliar a capacidade do HSIC de detectar dependências não lineares, vamos modelar um experimento típico de tarefas de trading. Consideremos dois atributos X={X1,X2}, que estão ligados de forma não linear à variável-alvo escalar Y, mas não apresentam correlação linear com ela (fig. 2). Essa situação reflete um problema real enfrentado pelo trader: verificar se os atributos selecionados influenciam a variável a ser prevista, antes de utilizá-los em um sistema de negociação.

Vamos gerar os dados da seguinte forma:

Y = X1^2 cos(π X2) + Noise

onde:

• X1 e X2 são variáveis independentes e uniformemente distribuídas no intervalo [-5,5],
• Noise é um ruído gaussiano,
• Y é a variável-alvo, ligada a X1 e X2 por uma dependência não linear.

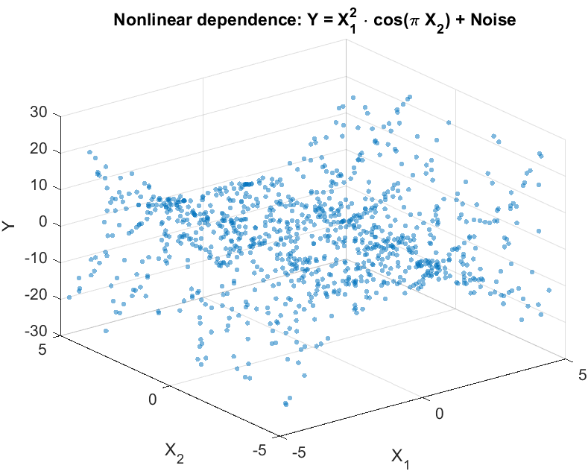
Fig.2 Gráfico de dispersão da variável-alvo Y e dos atributos X

O objetivo do experimento é testar a hipótese de independência na forma:

P(X1,X2,Y) = P(X1,X2)P(Y),

isto é, determinar se ambos os atributos influenciam conjuntamente a variável-alvo ou se não existe qualquer relação entre eles.

Em tarefas reais, onde o número de atributos pode ser grande, o HSIC permite verificar dependências de forma flexível: tanto para atributos individuais, por exemplo, X1 ou X2 com Y, quanto para subgrupos arbitrários de dados. Isso torna o método útil para a seleção de atributos informativos, por exemplo, por meio do ranqueamento pelo p-value, a fim de selecionar os mais significativos para a construção de um sistema de negociação.

Na fig.3 são apresentados os resultados do teste HSIC utilizando a aproximação gama. O valor obtido do HSIC, o p-value correspondente e o valor crítico confirmam uma dependência não linear estatisticamente significativa entre X e Y. Isso demonstra a capacidade do HSIC de identificar de forma eficaz relações complexas nos dados, o que é especialmente importante para a análise de cotações de mercado, onde os atributos frequentemente exercem influência não linear sobre a variável a ser prevista. Para comparação, o coeficiente de correlação calculado para X1, X2 e Y mostrou-se próximo de zero, não detectando qualquer relação linear.

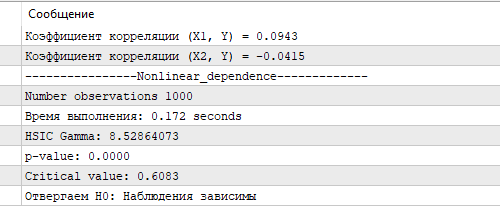
Fig.3 Resultados do teste HSIC, aproximação gama

O teste exato de permutação HSIC, executado em uma amostra do mesmo tamanho, levou 8,5 segundos em um computador bastante modesto para os padrões atuais do autor (Ryzen 3 de 4 núcleos). Ainda assim, o tempo de cálculo da aproximação gama é significativamente menor, o que a torna a escolha preferencial em tarefas onde a velocidade de computação é crucial, por exemplo, na análise de grandes volumes de dados financeiros em tempo real. A aproximação gama, apesar de possíveis imprecisões em amostras pequenas, fornece um equilíbrio entre velocidade e precisão, o que a torna uma ferramenta valiosa para a implementação do HSIC em algoritmos de negociação em MQL5.

Conclusão

Neste artigo, examinamos o HSIC (Hilbert-Schmidt Independence Criterion), um poderoso método não paramétrico para avaliar a dependência entre variáveis aleatórias. O HSIC utiliza uma abordagem baseada em kernels, o que permite detectar dependências não lineares complexas sem a necessidade de modelagem explícita das distribuições conjuntas.

Principais vantagens do HSIC:

• funciona com dados escalares e vetoriais de qualquer dimensionalidade,
• capta dependências não lineares complexas,
• é relativamente simples de implementar

No entanto, o método também apresenta limitações:

• sensibilidade à escolha do parâmetro de largura do kernel σ,
• dependência do tamanho da amostra: em amostras pequenas o teste de permutação pode ser menos poderoso, enquanto em amostras grandes o cálculo das matrizes de kernel K e L é bastante custoso em termos de tempo,
• o HSIC indica apenas a presença de dependência, mas não caracteriza sua intensidade, diferentemente do coeficiente de correlação.

No artigo, demonstramos a aplicação do HSIC em dados sintéticos com dependência não linear, confirmando sua capacidade de detectar relações inacessíveis a métodos tradicionais, como a correlação de Pearson. A implementação do HSIC em MQL5 mostrou sua aplicabilidade prática para a seleção de atributos informativos no desenvolvimento de sistemas de negociação.

Analisamos a versão básica do método com kernel gaussiano, porém o HSIC possui possibilidades mais amplas, incluindo o trabalho com dados categóricos e o teste de independência condicional. Essas direções abrem perspectivas para pesquisas futuras e para a aplicação do método em tarefas de trading, aprendizado de máquina e análise de dados.