Criterio de independencia de Hilbert-Schmidt (HSIC)

Introducción

La tarea principal de un tráder al trabajar con cotizaciones de instrumentos financieros es crear un sistema comercial (asesor) con una esperanza matemática positiva. Al diseñar dichos sistemas, con frecuencia se supone que existen dependencias ocultas en los datos usados para el entrenamiento y el comercio posterior. Sin embargo, normalmente no se analiza la cuestión de la comprobación estadística de esta suposición. Se considera que es posible obtener una respuesta indirecta probando los resultados con datos fuera de la muestra.

Mientras tanto, una respuesta estadísticamente sólida a la pregunta sobre si existe una relación entre las características y la variable objetivo resulta de vital importancia. Una respuesta positiva da confianza en la utilidad de los modelos predictivos, mientras que una respuesta negativa hace que uno se pregunte: ¿qué es exactamente lo que trata de predecir el algoritmo?

En estadística matemática, la cuestión sobre la presencia o ausencia de una relación probabilística entre variables aleatorias se responde mediante criterios de independencia. Uno de estos criterios es la prueba estadística HSIC, un poderoso método no paramétrico desarrollado en 2005 por el estadístico Arthur Gretton.

A diferencia del coeficiente de correlación, que solo identifica relaciones lineales, el HSIC es capaz de detectar relaciones tanto lineales como no lineales. Debido a esto, se usa ampliamente en el aprendizaje automático para la selección de características, el análisis de causa y efecto y otras tareas. En este artículo, analizaremos el principio de funcionamiento del HSIC y lo implementaremos en el entorno MQL5.

¿Qué es el HSIC?

El HSIC es una medida de la dependencia entre dos variables aleatorias X e Y basada en el enfoque del kernel. El método usa la "magia" matemática de las funciones de kernel (por ejemplo, Gaussiana (fig. 1)), que transforman los datos en un espacio RKHS (Reproducing Kernel Hilbert Spaces) especial, donde las dependencias se vuelven más fáciles de detectar.

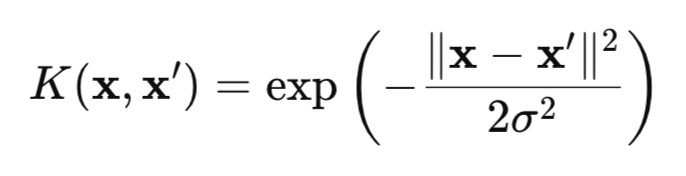
Figura 1 kernel gaussiano (kernel RBF)

donde:

• x, x' – vectores (puntos) de observaciones,
• ||   ||² – cuadrado de la norma euclidiana,
• σ — anchura del kernel.

Hay muchos kernels que se pueden usar para la prueba HSIC, como los kernels para datos categóricos o el kernel de Laplace. Sin embargo, en este artículo centraremos nuestra atención en el kernel gaussiano, ya que es universal y posee la propiedad característica. Esta propiedad nos permite identificar cualquier dependencia en los datos, lo que hace que el kernel gaussiano sea particularmente efectivo.

El HSIC clásico prueba la independencia por pares entre dos variables aleatorias X e Y verificando si se cumple la condición P(X,Y) = P(X)P(Y). Para ello, el HSIC analiza la desviación de la distribución conjunta respecto del producto de las distribuciones marginales utilizando matrices de kernel (una tabla donde cada elemento refleja la similitud entre pares de puntos de datos, calculada utilizando una función kernel).

Una ventaja importante del HSIC es su capacidad de trabajar con datos de cualquier dimensión: escalares, vectoriales o combinaciones de ambos. Esto resulta especialmente valioso en problemas donde construir explícitamente distribuciones conjuntas multidimensionales P(X,Y) resulta difícil debido a la alta dimensionalidad de los datos.

Desde un punto de vista matemático, el criterio HSIC se define como el cuadrado de la norma de Hilbert-Schmidt del operador de covarianza cruzada en RKHS:

donde:

• K(X,X') – función de kernel para una variable aleatoria X,
• L(Y,Y') – función de kernel para la variable aleatoria Y,
• || || HS – norma de Hilbert-Schmidt.

Aquí resulta apropiado comparar el HSIC con la covarianza habitual. La covarianza clásica mide la relación lineal entre las cantidades X e Y en su espacio original, mientras que HSIC trabaja con mapeos de X e Y en un espacio de Hilbert de kernel reproductor (RKHS), es decir, en un espacio de funciones que permite transformar los datos para revelar dependencias no lineales complejas.

En la práctica, no resulta necesario calcular directamente la norma de Hilbert-Schmidt. En cambio, el HSIC se estima a través de estadísticas empíricas basadas en matrices de kernel construidas para una muestra de datos:

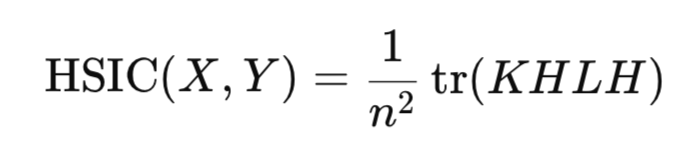
donde:

• K,L – matrices de kernel n*n,
• H – matriz de centrado n*n (I -1/n11^T),
• tr() – traza de la matriz,
• n – número de observaciones.

De forma similar al coeficiente de correlación, el HSIC estima la presencia de una relación entre las variables aleatorias X e Y utilizando estadísticas de muestra, sin la necesidad de construir distribuciones de estas variables.

La estadística HSIC siempre es no negativa:

• Un valor de HSIC > 0 indica la presencia de dependencia,
• mientras que HSIC = 0 indica independencia de los datos.

Prueba de significancia de HSIC

Sin embargo, para sacar conclusiones fiables no basta con calcular estadísticas; debemos confirmar su significancia estadística para excluir un resultado aleatorio. Para la estadística del HSIC, no existe una forma analítica exacta de la distribución bajo la hipótesis nula. Es decir, no podemos simplemente usar, por ejemplo, una distribución normal y obtener rápida y fácilmente un valor crítico o valor p sin costos computacionales. Existen dos enfoques principales para resolver este problema:

• la prueba de permutación,
• la aproximación gamma.

La prueba de permutación es el método básico y más preciso para estimar la distribución HSIC bajo H0. Su propósito consiste en romper cualquier dependencia entre X e Y permutando aleatoriamente los índices de una de las variables o mezclando la matriz de kernel resultante de esta variable. Para obtener un resultado preciso, debemos realizar un gran número de permutaciones (unas 1000). Por consiguiente, la prueba de permutación es bastante costosa, ya que requiere calcular el HSIC para cada una de esas permutaciones.

La principal ventaja de la prueba de permutación consiste en que no requiere ninguna suposición sobre la forma de la distribución de datos; en cambio, se basa en la distribución empírica de la estadística obtenida a través de permutaciones. Luego se usa la distribución empírica HSIC para obtener una estimación del valor p. 

Para acelerar los cálculos estadísticos, se utiliza la aproximación gamma. En este enfoque, la estadística HSIC se escala según el tamaño de la muestra (n*HSIC) y los parámetros de distribución gamma se estiman partiendo de los momentos de muestra HSIC (media y varianza). Este método resulta significativamente más rápido que la prueba de permutación, pero su precisión puede ser menor para muestras pequeñas. Existen otros métodos para estimar la distribución HSIC bajo la hipótesis nula de independencia, pero son complejos de implementar y rara vez se usan en la práctica, por lo que no se analizan en este artículo.

Implementación de la permutación HSIC en MQL5

La prueba de permutación se implementa en la función hsic_test.

//+------------------------------------------------------------------+
//| Функция для перестановочного теста                               |
//+------------------------------------------------------------------+
vector hsic_test(matrix &X,matrix &Y,const double alpha,bool Bootstrap = false,int n_permutations=1000)
{
vector ret = vector::Zeros(3);
int n = (int)X.Rows(); 

matrix K =  RBF_kernel(X); // матрица ядра для X
matrix L =  RBF_kernel(Y); // матрица ядра для Y
matrix H = matrix::Eye(n, n) - matrix::Ones(n, n)/n; // Центрирующая матрица
//--------------------------------------

// Kc центрированная ядерная матрица К
   matrix Kc(n, n);
   if(!Kc.GeMM(H, K, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Kc = H * K");
      return ret;
   }
   if(!Kc.GeMM(Kc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Kc * H");
      return ret;
   }
   Kc = Kc.Transpose();
   double coef = 1/pow(n,2);

// Вычисляем наблюдаемое значение статистики HSIC
   double  hsic_obs = compute_hsic(L,Kc,coef);
   ret[0]= hsic_obs;

  //------------ Перестановочный тест ------------------------------------
  if (Bootstrap == true){ 
    vector hsic_perms = vector::Zeros(n_permutations);   
    for ( int i = 0; i<n_permutations; i++)
    {        
        ShuffleMatrix(L); // Перемешиваем матрицу
        hsic_perms[i] = compute_hsic(L,Kc,coef);
    }
    
    int count = 0;
for(int i = 0; i < n_permutations; i++)
{
   if(hsic_perms[i] >= hsic_obs)
      count++;
}
   // Вычисляем p-value
double p_value = (n_permutations > 0) ? (double)count / n_permutations : 0.0;
    ret[1] = p_value; 
  
  // Вычисляем критическое значение
  double hsic_sort[];
  VectortoArray(hsic_perms,hsic_sort);
  ArraySort(hsic_sort);
  double CV = hsic_sort[(int)round((1-alpha)*n_permutations)];
    ret[2] = CV; 
    }
 //----------------------------------------------------------------------------------   
  return ret;  
}

• La función toma dos conjuntos de datos X e Y (estas son matrices de tamaño n*d, donde n es el número de observaciones y d es la dimensión de los datos),

• el parámetro alfa establece el nivel de significancia (este es un error Tipo I, es decir, la probabilidad de rechazar la hipótesis nula cuando en realidad es verdadera),

• el parámetro Bootstrap (si es verdadero, realiza una prueba de permutación para obtener un valor p, de lo contrario, solo calcula las estadísticas),

• n_permutations – número de permutaciones aleatorias,

• La función retorna un vector que contiene el valor HSIC observado, el valor p y la estadística de valor crítico para el nivel alfa seleccionado.

El cálculo de la matriz de kernel gaussiana se realiza en la función RBF_kernel.

//+------------------------------------------------------------------+
//| Гауссовское ядро                                                 |
//+------------------------------------------------------------------+ 
matrix RBF_kernel(const matrix &X) {
   int n = (int)X.Rows();
   
   // Вычисляем матрицу расстояний через скалярное произведение
   matrix XX(n, n); 
   if(!XX.GeMM(X, X.Transpose(), 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить XX = X * X^T");    
   }
   
 matrix diag(n,1);
 diag.Col(XX.Diag(),0);  // вектор диагональных элементов
 //  квадраты расстояний
 matrix D_sq = matrix::Ones(n, 1).MatMul(diag.Transpose()) + diag.MatMul(matrix::Ones(1, n)) - 2*XX;
   
   // Вычисляем sigma на первых n_sigma строках
   int n_sigma = MathMin(n, 100);
   int num_elements = (n_sigma * (n_sigma - 1)) / 2;
   vector upper_tri(num_elements);
   int idx = 0;
   for(int i = 0; i < n_sigma; i++) {
      for(int j = i + 1; j < n_sigma; j++) {
         upper_tri[idx] = D_sq[i, j]; 
         idx++;
      }
   }
  double sigma = MathSqrt(0.5 * upper_tri.Median());
   
   return MathExp((-1* D_sq) / (2 * sigma*sigma)); 
}

La función calcula el cuadrado de las distancias entre los puntos de datos, la anchura del kernel sigma y devuelve la matriz de kernel n*n deseada.

Para calcular eficientemente las distancias al cuadrado, se usa una forma matricial en lugar de un ciclo regular:

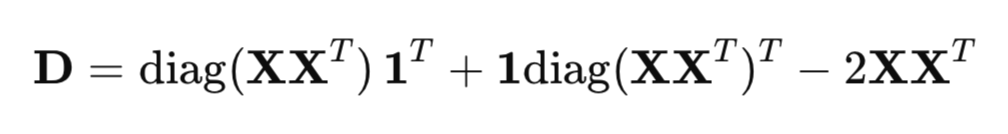
donde:

• XX^T - matriz de Gram (matriz del producto escalar),
• diag(XX^T ) - vector de elementos diagonales,
• 1 - vector de unidades.

El parámetro sigma en el kernel gaussiano determina la anchura del kernel y afecta significativamente la sensibilidad de HSIC para detectar dependencias en los datos. El parámetro sigma determina la escala de similitud: valores grandes de sigma hacen que el kernel sea más ancho (los puntos que están más separados todavía se consideran similares), mientras que valores pequeños lo hacen más estrecho (solo los puntos muy cercanos se consideran similares).

Un método común para seleccionar sigma es usar la siguiente heurística mediana:

Se toma el factor 0,5 para garantizar que el denominador del kernel RBF sea igual a la mediana de las distancias euclidianas al cuadrado entre los puntos de datos, lo que garantiza una estimación adaptativa que considera la escala de los datos. 

La variable n_sigma = MathMin(n, 100) limita la cantidad de datos para calcular sigma a 100. Esto se hace para reducir los costos computacionales para muestras grandes y mantener la representatividad de la estimación de sigma.  Los cuadrados de las distancias euclidianas se copian en el vector upper_tri, usando solo el triángulo superior de la matriz de distancias (sin la diagonal, i=j) para evitar la duplicación y las distancias cero.

Función para calcular estadística HSIC compute_hsic.

//+------------------------------------------------------------------+
//| Функция для вычисления HSIC                                      |
//+------------------------------------------------------------------+
double compute_hsic(const matrix &L, const matrix& Kc, const double coef){
matrix KcL= Kc*L;               
return coef*KcL.Sum();
}

Después de calcular la estadística HSIC observada, se realiza una prueba de permutación para probar su significancia estadística. La función ShuffleMatrix(matrix &m) implementa esta permutación para la matriz de kernel L correspondiente a la variable Y. Estadísticamente, no hay diferencia si se mezcla L o K, ya que HSIC es simétrico con respecto a X e Y, lo cual da resultados equivalentes en la prueba de permutación para HSIC. Mezclar la propia variable Y y luego recalcular la matriz L para cada permutación resulta ineficaz.

//+------------------------------------------------------------------+
//| Функция для перемешивания данных матрицы                         |
//+------------------------------------------------------------------+
void ShuffleMatrix(matrix &m)
{
   int rows = (int)m.Rows();
   int cols = (int)m.Cols();
   
   if (rows != cols) {
   Print("Ошибка: Матрица должна быть квадратной");
}  
   int perm[];
   GeneratePermutation(rows, perm);  // Генерация случайной перестановки индексов
   matrix temp = m;  
   // Перестановка строк и столбцов
   for(int i = 0; i < rows; i++)
   {
      for(int j = 0; j < cols; j++)
      {
         m[i,j] = temp[perm[i], perm[j]];
      }
   }
}

La generación de índices aleatorios se realiza usando la función GeneratePermutation.

//+------------------------------------------------------------------+
//| Функция для создания случайной перестановки индексов             |
//+------------------------------------------------------------------+ 
void GeneratePermutation(int size, int &perm[])
{
   MathSequence(0,size,1,perm);
   
   // Алгоритм Фишера-Йетса для перестановки
   for(int i = size - 1; i > 0; i--)
   {
      // Генерация случайного индекса от 0 до i
      int j = (int)(MathRand() / 32768.0 * (i + 1)); 
      int temp = perm[i];
      perm[i] = perm[j];
      perm[j] = temp;
   }
}

Después de múltiples permutaciones de la matriz de kernel L, se forma la distribución empírica de la estadística HSIC bajo la hipótesis nula de independencia utilizando la función ShuffleMatrix. El valor p se define como la proporción de valores de permutación HSIC mayores o iguales a la estadística observada. Si el valor p es menor que el nivel de significancia alfa, se rechaza la hipótesis nula de independencia.

El valor crítico se selecciona como el cuartil de la distribución empírica en el nivel 1−alfa, es decir, el valor por encima del cual se encuentran alfa⋅100% de los cálculos de permutación HSIC.

Implementación de HSIC Gamma

La función hsic_Gamma_test es responsable de calcular la aproximación Gamma.

//+------------------------------------------------------------------+
//| Функция для Гамма-аппроксимации HSIC                             |
//+------------------------------------------------------------------+
double hsic_Gamma_test(matrix &X, matrix &Y, double &CV, double & pvalue)
{
int n = (int)X.Rows(); 

matrix K =  RBF_kernel(X); // матрица ядра для X
matrix L =  RBF_kernel(Y); // матрица ядра для Y
matrix H = matrix::Eye(n, n) - matrix::Ones(n, n)/n; // Центрирующая матрица

   matrix Kc(n, n); // Вычисляем центрированную матрицу ядра X  
   if(!Kc.GeMM(H, K, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Kc = H * K");
      return 0;
   }
   if(!Kc.GeMM(Kc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Kc * H");
      return 0;
   }   
   matrix KcT = Kc.Transpose();
     
   matrix Lc(n, n);  // Вычисляем центрированную матрицу ядра Y 
   if(!Lc.GeMM(H, L, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить Lc = H * L");
      return 0;
   }
   
   if(!Lc.GeMM(Lc, H, 1.0, 0.0)) {
      Print("Ошибка: Не удалось вычислить temp = Lc * H");
      return 0;
      }
              
   double m = (double)n; 
   double coef = 1/m;
   
// Вычисляем наблюдаемое значение HSIC
matrix KcLc;
double  hsic_obs = compute_hsic_Gamma(Lc,KcT,coef,KcLc); // n*HSIC

   matrix varHSIC_m = KcLc*KcLc;
   varHSIC_m = (1.0/36.0)*varHSIC_m;  
   double  varHSIC = 1/(m)/(m-1) * (varHSIC_m.Sum() - varHSIC_m.Trace() );
   varHSIC = 72*(m-4)*(m-5)/m/(m-1)/(m-2)/(m-3)  *  varHSIC; // Дисперсия HSIC
   
   matrix KD;
   KD.Diag(K.Diag(),0);
   matrix LD;
   LD.Diag(L.Diag(),0);
   K = K-KD;   
   L = L-LD;  
   matrix one = matrix::Ones(n,1);
   matrix a = 1/m/(m-1)*one.Transpose();
   matrix muX;
   muX.GeMM(a,K.MatMul(one),1,0);
   matrix  muY;
   muY.GeMM(a,L.MatMul(one),1,0);
   double mHSIC  = 1/m * ( 1 +muX[0,0]*muY[0,0]  - muX[0,0] - muY[0,0] ) ; // математическое ожидание HSIC

//параметры Гамма распределения
 double alphaG = mHSIC*mHSIC / varHSIC;
 double beta = varHSIC*m / mHSIC;   
 
 int err;
 CV = MathQuantileGamma(1-alpha_,alphaG,beta,err);  // Critical value
 pvalue = 1 - MathCumulativeDistributionGamma(hsic_obs,alphaG,beta,err); // p-value 
 //----------------------------------------------------------------------------------   
  return hsic_obs;  
}

Aquí calculamos la estadística HSIC escalada por el tamaño de muestra n (n*HSIC), que se aproxima usando una distribución gamma con parámetros de forma (alfa) y escala (beta). Estos parámetros se determinan según la esperanza matemática y la varianza de las estadísticas del HSIC.

Pruebas con datos sintéticos

Para evaluar la capacidad de HSIC a la hora de detectar dependencias no lineales, vamos a simular un experimento típico de problemas comerciales. Así, podemos considerar dos características X={X 1 ,X 2 } relacionadas no linealmente con la variable objetivo escalar Y, pero no tienen una correlación lineal con ella (fig. 2). Esta situación refleja un desafío del mundo real que enfrenta un tráder: probar si las características seleccionadas influyen en la variable prevista antes de usarlas en un sistema comercial.

Vamos a generar los datos de la siguiente manera:

Y = X1^2 * cos(pi * X2) + Noise

donde:

• X1 y X2 - variables uniformes independientes y distribuidas de forma idéntica [-5,5],
• Noise – ruido gaussiano,
• Y - variable objetivo, relacionada con X1 y X2 por una relación no lineal.

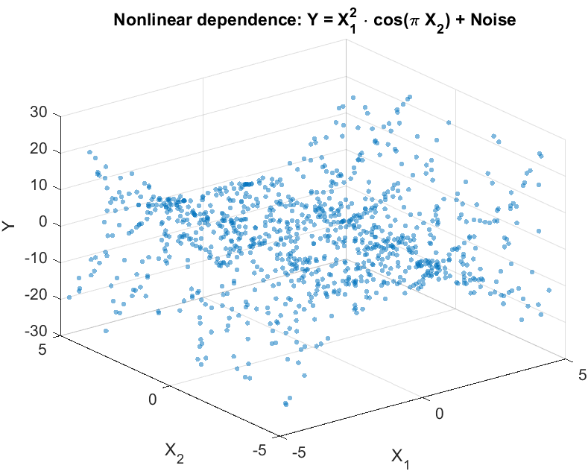
Fig. 2 Histograma de dispersión para la variable objetivo Y y las características X

El propósito del experimento es probar la hipótesis de independencia en la forma:

P(X1,X2,Y) = P(X1,X2)P(Y),

es decir, determinar si ambas características influyen conjuntamente en la variable objetivo o si no existe relación entre ambas.

En problemas del mundo real donde el número de características puede ser elevado, HSIC permite realizar pruebas flexibles de dependencias: tanto para características individuales (por ejemplo, X1 o X2 con Y) como para subgrupos aleatorios de datos. Esto hace que el método resulte útil para seleccionar características informativas, por ejemplo, clasificándolas según el valor p para seleccionar las más significativas para construir un sistema comercial.

La figura 3 muestra los resultados de la prueba HSIC usando la aproximación Gamma. El valor HSIC resultante, junto con su valor p y el valor crítico correspondiente, confirman una relación no lineal estadísticamente significativa entre X e Y. Esto demuestra la capacidad del HSIC para identificar eficazmente relaciones complejas en los datos, lo que resulta particularmente importante para el análisis del mercado de valores, donde las características a menudo tienen un efecto no lineal en la variable prevista. En comparación, el coeficiente de correlación calculado para X1, X2 e Y ha resultado cercano a cero, lo que no revela ninguna relación lineal.

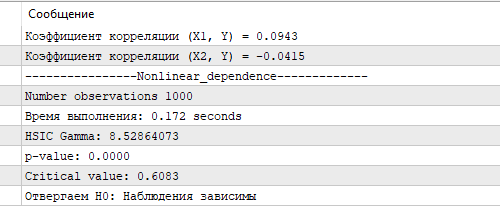
Fig.3 Resultados de la prueba HSIC, aproximación gamma

La prueba de permutación HSIC exacta, ejecutada en el mismo tamaño de muestra, ha tomado 8,5 segundos en la computadora del autor, bastante modesta para los estándares actuales (un Ryzen 3 de 4 núcleos). Sin embargo, el tiempo de cálculo de la aproximación gamma es significativamente más rápido, lo cual la convierte en la opción preferida para tareas donde la velocidad de cálculo es importante, como al analizar grandes volúmenes de datos financieros en tiempo real. La aproximación gamma, a pesar de las posibles imprecisiones con muestras pequeñas, ofrece un equilibrio entre velocidad y precisión, lo que la convierte en una herramienta valiosa para implementar HSIC en algoritmos comerciales MQL5.

Conclusión

En este artículo, hemos analizado el HSIC (Hilbert-Schmidt Independence Criterion), un poderoso método no paramétrico para evaluar la relación entre variables aleatorias. El HSIC utiliza un enfoque de kernel que le permite identificar dependencias no lineales complejas sin la necesidad de un modelado explícito de distribuciones conjuntas.

Beneficios clave del HSIC:

• trabaja con datos escalares y vectoriales de cualquier dimensionalidad,
• captura dependencias no lineales complejas,
• es relativamente fácil de implementar

No obstante, el método también tiene limitaciones:

• sensibilidad a la elección del parámetro de anchura del kernel σ,
• Dependencia del tamaño de la muestra: en muestras pequeñas, la prueba de permutación puede resultar menos potente y, en muestras grandes, el cálculo de las matrices de kernel K y L requiere bastante tiempo.
• El HSIC solo indica la presencia de una relación, pero no caracteriza su intensidad, a diferencia del coeficiente de correlación.

En este artículo, hemos demostrado la aplicación del HSIC a datos sintéticos con dependencia no lineal, confirmando su capacidad para detectar relaciones inaccesibles a los métodos tradicionales como la correlación de Pearson. La implementación del HSIC en MQL5 ha demostrado su aplicabilidad práctica para seleccionar características informativas en el desarrollo de sistemas comerciales.

Asimismo, hemos analizado la versión básica del método con un kernel gaussiano, pero el HSIC tiene capacidades más avanzadas, incluido el manejo de datos categóricos y la prueba de independencia condicional. Estas líneas potenciales descubren posibilidades para futuras investigaciones y aplicaciones del método en problemas de trading, aprendizaje automático y análisis de datos.