Прогнозирование условного распределения с помощью MLP

Введение

В условиях высокой волатильности и неопределенности финансовых рынков, таких как Forex, точное прогнозирование ценовых движений остается одной из ключевых задач для трейдеров и аналитиков. Традиционные подходы к регрессии, основанные на стандартных функциях потерь, таких как среднеквадратичная ошибка (MSE) или сумма квадратов ошибок (SSE), часто оказываются недостаточно эффективными. Эти функции предполагают гомоскедастичность, то есть постоянство дисперсии целевой переменной, что редко соответствует реальной динамике финансовых временных рядов. Для адекватного моделирования таких данных необходим подход, учитывающий гетероскедастичность — переменную дисперсию приращений цен, зависящую от входных признаков.

В данной статье представлен вероятностный подход к задаче регрессии с использованием многослойного перцептрона (MLP), позволяющий прогнозировать условное гауссовское распределение приращений цен. Для этого мы напишем пользовательскую функцию потерь, основанную на гауссовском отрицательном логарифме правдоподобия (GaussianNLLLoss).

Для реализации этого подхода создан класс MLPRegressor, интегрированный с библиотекой ALGLIB, предоставляющей алгоритм оптимизации L-BFGS. В статье подробно описаны ключевые методы класса — прямое и обратное распространение, интеграция с L-BFGS, а также индикатор, демонстрирующий применение модели для прогнозирования приращения цен на валютных парах с оценкой их неопределённости. В конечном итоге наша модель предоставляет трейдеру не просто точечный прогноз, а полное условное распределение целевой переменной.

Функция потерь MSE и ее связь с гауссовским правдоподобием с постоянной дисперсией

Для начала вспомним, что такое функция потерь и почему она играет ключевую роль в задачах машинного обучения. Функция потерь — это мера, которая количественно оценивает, насколько предсказания модели отклоняются от фактических данных. Одной из наиболее распространенных функций потерь для задач регрессии является среднеквадратичная ошибка (Mean Squared Error, MSE), которая вычисляется как:

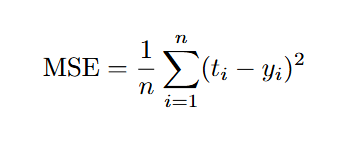
где:

• t — истинное значение целевой переменной (target), 
• y — предсказанное моделью значение, 
• n  — количество наблюдений.

Среднеквадратичная ошибка (MSE), часто используемая в задачах регрессии, предполагает, что целевая переменная подчиняется модели нормального распределения с постоянной дисперсией σ2:

t  ~ N (y, σ2)

Тогда функция правдоподобия для выборки из n  наблюдений для этой модели выражается как произведение плотностей нормального распределения:

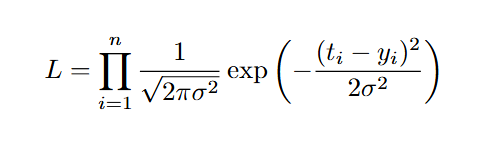
Для удобства оптимизации обычно минимизируют отрицательный логарифм  правдоподобия:

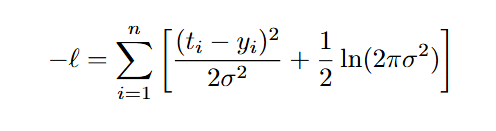
Поскольку дисперсия σ2 является константой, то второе слагаемое в формуле не зависит от параметров модели и не влияет на оптимизацию. Таким образом, минимизация функции правдоподобия становится эквивалентной минимизации MSE. Это показывает, что использование MSE в качестве функции потерь неявно предполагает, что приращения цен подчиняются нормальному распределению с постоянной дисперсией, не зависящей от входных признаков.

Однако в контексте финансовых данных, таких как приращения цен на валютных парах Forex, это предположение редко соответствует реальности. В таких условиях, использование MSE в качестве функции потерь является слишком упрощенным и может привести к недостаточно точным моделям, которые не учитывают изменяющуюся волатильность. Для преодоления этого ограничения мы построим пользовательскую функцию потерь, основанную на гауссовском отрицательном логарифме правдоподобия, которая моделирует условную дисперсию, зависящую от входных признаков.

Гауссовское правдоподобие с изменяющейся дисперсией GaussianNLLLoss

В этом случае мы предполагаем, что целевая переменная t  подчиняется нормальному распределению с условной дисперсией σi2, которая зависит от входных данных xi.

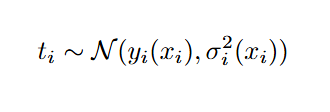
Тогда отрицательный логарифм правдоподобия с усреднением по n  наблюдениям  выражается как:

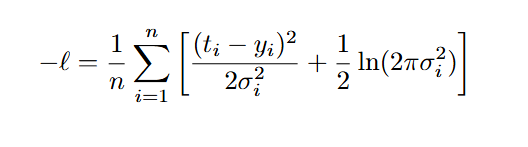
Эта функция потерь состоит из двух слагаемых. Первое слагаемое — это, по сути, взвешенная среднеквадратичная ошибка. Вес каждого члена обратно пропорционален предсказанной дисперсии. Это означает, что чем выше предсказанная неопределённость (σ2), тем меньше влияние соответствующей ошибки на общую функцию потерь.

Второе слагаемое учитывает сложность модели, предотвращая тривиальное увеличение дисперсии σi2 для минимизации первого слагаемого. Оно поощряет модель предсказывать дисперсию, которая соответствует реальной неопределенности данных.

Таким образом, функция GaussianNLLLoss позволяет одновременно прогнозировать две величины — условное математическое ожидание μi и дисперсию σi2. Это эквивалентно моделированию полного нормального распределения для каждой точки данных.

//+------------------------------------------------------------------+
//| GaussianNLLLoss (Negative Log-Likelihood)                        |
//+------------------------------------------------------------------+
double GaussianNLLLoss(const matrix &output, const matrix &target, int sample)
  {
   if(output.Rows() != 2 || output.Cols() != sample || target.Rows() != sample || target.Cols() != 1)
     {
      Print("GaussianNLLLoss: Invalid matrix dimensions");
      return DBL_MAX;
     }

   vector mu = output.Row(0);
   vector sigma2 = output.Row(1); // после softplus

// Ограничиваем дисперсию снизу значением eps
   for(int i = 0; i < sample; i++)
     {
      sigma2[i] = MathMax(sigma2[i], 1e-6); // max(sigma_i^2, eps)
     }

//  target - mu
   vector diff = target.Col(0) - mu;
//  (t - mu)^2 / (2 * sigma^2)
   vector term1 = diff * diff / (2.0 * sigma2);
//  0.5 * log(2 * PI * sigma^2)
   vector term2 = 0.5 * (MathLog(2.0 * M_PI * sigma2));
// Суммируем оба слагаемых и усредняем
   double sum = (term1 + term2).Sum();
   return sum / sample;
  }

Понятие правдоподобия

Правдоподобие — фундаментальное понятие в статистике, используемое как в частотном, так и в байесовском подходах. Оно характеризует вероятность наблюдаемых данных при заданных параметрах модели. В контексте машинного обучения правдоподобие позволяет оценить, насколько хорошо модель описывает данные.

Рассмотрим для примера набор данных, который, предположительно, подчиняется нормальному распределению со средним значением μ и дисперсией σ2. Функция правдоподобия показывает, насколько вероятно, что наблюдаемые данные были сгенерированы нормальным распределением с конкретными значениями этих параметров. Иными словами, она помогает ответить на вопрос: «Насколько выбранные параметры соответствуют наблюдаемым данным?».

Чтобы проиллюстрировать принцип максимального правдоподобия, можно запустить скрипт, который строит график логарифма правдоподобия для выборки из нормального распределения N(0,1) в зависимости от среднего. При фиксированной дисперсии σ2=1 перебираются значения μ в диапазоне [−3,3], а правдоподобие вычисляется с помощью функции MathProbabilityDensityNormal. Полученный график показывает, что максимум правдоподобия достигается при значении μ≈0, соответствующем истинному среднему выборки. Все остальные значения μ имеют меньшее правдоподобие, что указывает на их меньшее соответствие данным.

#include <Math\Stat\Normal.mqh>
#include <Graphics\Graphic.mqh>

//+----------------------------------------------------+
//| Log-Likelihood                             |
//+----------------------------------------------------+
double LogLikelihood(const double &t[], double mu, double sigma)
{
   int n = ArraySize(t);
   double result[];
   ArrayResize(result, n);
   // Вычисляем логарифм плотности вероятности
   MathProbabilityDensityNormal(t, mu, sigma, true, result);

   // Суммируем ln(p(x_i)) для получения логарифма правдоподобия
   double ll = 0.0;
   for(int i = 0; i < n; i++)
      ll += result[i]; 
  
   return ll;
} 

//+--------------------------------------------+
//| Plot Log-Likelihood                        |
//+--------------------------------------------+
void PlotLL(const double &mu_values[], const double &ll_values[], int sec)
{
   ChartSetInteger(0, CHART_SHOW, false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0, CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0, CHART_HEIGHT_IN_PIXELS);
   graphic.Create(0, "LL_Graphic", 0, 0, 0, int(width), int(height));
   graphic.CurveAdd(mu_values,ll_values, ColorToARGB(clrBlue, 255), CURVE_LINES, "Log-Likelihood");
   graphic.XAxis().Name("Mu");
   graphic.YAxis().Name("Log-Likelihood");
   graphic.BackgroundMain("Log-Likelihood");
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack, 255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec * 1000);
   ChartSetInteger(0, CHART_SHOW, true);
   graphic.Destroy();
   ChartRedraw(0);
}

//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
{
   // Генерируем синтетическую выборку
   MathSrand(55); 
   int n = 100; // Количество наблюдений
   double true_mu = 0.0; // Истинное среднее
   double true_sigma = 1.0; // Фиксированное стандартное отклонение
   double t[]; // Выборка
   ArrayResize(t, n);
   MathRandomNormal(true_mu, true_sigma, n, t);

   // Диапазон для mu
   double mu_min = -3.0;
   double mu_max = 3.0;
   double mu_step = 0.1;
   int steps = (int)((mu_max - mu_min) / mu_step) + 1;

   double mu_values[];
   double ll_values[];
   ArrayResize(mu_values, steps);
   ArrayResize(ll_values, steps);

   // Вычисляем log-likelihood для каждого mu
   double max_ll = -DBL_MAX;
   double best_mu = 0.0;
   for(int i = 0; i < steps; i++)
   {
      mu_values[i] = mu_min + i * mu_step;
      ll_values[i] = LogLikelihood(t, mu_values[i], true_sigma);
      if(ll_values[i] > max_ll)
      {
         max_ll = ll_values[i];
         best_mu = mu_values[i];
      }
   }

   PlotLL(mu_values, ll_values, 10); 

   // Вывод результатов
   Print("Истинное среднее: mu = ", true_mu);
   Print("Найденное среднее: mu = ", best_mu);
   Print("Максимальное значение Log-Likelihood: ", max_ll);
}

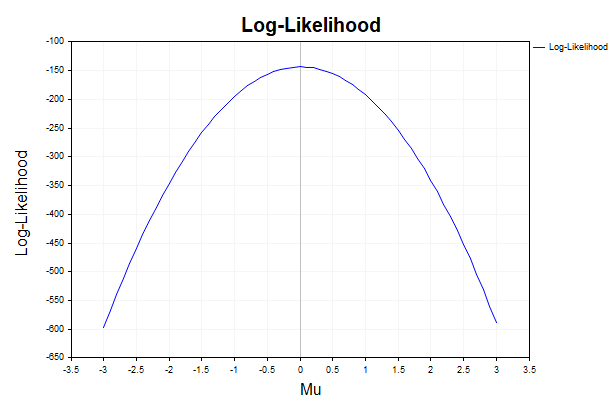
Рис.1. График логарифмической функции правдоподобия для среднего N(0,1)

Реализация модели MLP для задачи регрессии с функцией потерь GaussianNLLLoss

Для реализации предложенного подхода к прогнозированию условного гауссовского распределения, будем использовать модель многослойного перцептрона (класс MLPRegressor). Архитектура сети очень простая, модель состоит всего из одного скрытого слоя и имеет фиксированное количество выходов, равное двум, где первый выход соответствует условному математическому ожиданию приращений цен, а второй — условной дисперсии. 

Для обеспечения корректного моделирования этих параметров, мы используем фиксированные функции активации на выходном слое: линейную активацию для среднего и функцию Softplus для дисперсии, которая гарантирует положительность предсказанных значений. Функция активации скрытого слоя  может быть выбрана пользователем по своему усмотрению. Список всех доступных функций активации смотрите  в справке MQL5 раздел «Машинное обучение /Activation». 

Ключевую роль в работе модели играют два метода: прямое распространение (FeedForward) и обратное распространение (Backprop). Первый вычисляет предсказания μi и σi2 на основе входных данных, второй находит градиенты функции потерь GaussianNLLLoss, чтобы алгоритм L-BFGS мог обновить параметры модели.

Прямой проход (FeedForward)

Метод FeedForward реализует прямое распространение сигнала через нейронную сеть, вычисляя предсказания на основе входных данных:

//+------------------------------------------------------------------+
//| Прямой проход                                                    |
//+------------------------------------------------------------------+
bool MLPRegressor::FeedForward(const matrix &data)
  {
   ones_ = matrix::Ones(1, data.Rows());
   n1 = weights1.MatMul(data.Transpose()) + bias1.MatMul(ones_);
   n1.Activation(act1, ac_func);
   n2 = weights2.MatMul(act1) + bias2.MatMul(ones_);
   act2.Init(n2.Rows(), n2.Cols());
   act2.Row(n2.Row(0), 0); // Первый выход: линейная активация (копируем напрямую)
// Второй выход: softplus
   vector z = n2.Row(1);
   vector sigma2;
   z.Activation(sigma2, AF_SOFTPLUS);
   act2.Row(sigma2, 1);

   return true;
  }

В последнем слое сеть выдаёт два значения: 

• μi — среднее, получаемое напрямую с линейной активацией, 
• σi2 — дисперсия, которая проходит через softplus, чтобы всегда оставаться положительной. 

Обратный проход (Backprop)

Метод Backprop реализует обратное распространение ошибки, вычисляя градиенты функции потерь по всем параметрам модели — весам и смещениям. Эти градиенты необходимы для обучения модели с использованием алгоритма L-BFGS:

//+--------------------------------------------------------+
//| Обратный проход                                        |
//+--------------------------------------------------------+
bool MLPRegressor::Backprop(const matrix &data, const matrix &target)
  {
   const double eps = 1e-6;     // Параметр для численной стабильности оптимизации
   vector mu = act2.Row(0);     // mu_i (выход сети для среднего)
   vector sigma2 = act2.Row(1); // sigma_i^2 (выход сети для дисперсии)
// Ограничиваем sigma2 снизу значением eps
   for(int i = 0; i < Sample_; i++)
     {
      sigma2[i] = MathMax(sigma2[i], eps); // max(sigma_i^2, eps)
     }
   vector t = target.Col(0);    // t_i (целевая переменная)
   vector diff = t - mu;        // t_i - mu_i

// 1. Градиенты функции потерь по выходам сети (mu_i, sigma_i^2)
   matrix DerivLoss_wrt_Output(layer2, Sample_);
   DerivLoss_wrt_Output.Row(-1*diff / sigma2 /Sample_, 0);  // dL/d(mu_i) = -(t_i - mu_i) / sigma^2_i
   vector term = 0.5 / sigma2 - 0.5 * (diff * diff / (sigma2 * sigma2)); // dL/d(sigma_i^2)
   DerivLoss_wrt_Output.Row(term/Sample_, 1); // dL/d(sigma_i^2) = (1/(2*sigma_i^2) - (t_i - mu_i)^2 / (2*sigma_i^2)^2)

// 2. Производные активаций выходного слоя
   matrix deriv_act2(layer2, Sample_);
   deriv_act2.Row(vector::Ones(Sample_), 0);
   vector z = n2.Row(1);
   vector sigmoid_z;
   z.Derivative(sigmoid_z, AF_SOFTPLUS);
   deriv_act2.Row(sigmoid_z, 1);

// 3. Ошибка выходного слоя D2
   matrix D2 = deriv_act2 * DerivLoss_wrt_Output; // [layer2, Sample_]

// 4. Производные активаций скрытого слоя
   matrix deriv_act1;
   n1.Derivative(deriv_act1, ac_func); // [layer1, Sample_]

// 5. Ошибка скрытого слоя D1
   matrix D1 = weights2.Transpose().MatMul(D2); // [layer1, Sample_]
   D1 = D1 * deriv_act1;

// 6. Вычисление градиентов
   matrix ones = matrix::Ones(Sample_, 1);
   gW1 = D1.MatMul(data);             // Градиенты для weights1
   gb1 = D1.MatMul(ones);             // Градиенты для bias1
   gW2 = D2.MatMul(act1.Transpose()); // Градиенты для weights2
   gb2 = D2.MatMul(ones);             // Градиенты для bias2

   return true;
  }

Метод Backprop начинается с вычисления градиентов функции потерь по выходам сети — среднего μi и дисперсии σi2. К сожалению, мы не сможем воспользоваться уже готовой функцией LossGradient из раздела по машинному обучению, потому что она рассчитана на встроенные функции потерь. Поэтому мы должны вычислить эти градиенты самостоятельно по следующим формулам.

Градиент функции потерь по выходу среднего вычисляется как:

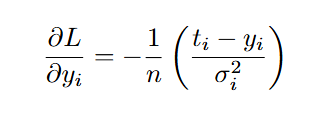
Градиент функции потерь по выходу дисперсии :

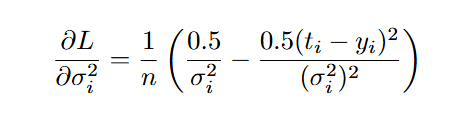
Метод Backprop адаптирован для функции потерь GaussianNLLLoss, но его структура универсальна. Если вы хотите использовать другую нестандартную функцию потерь, ключевым шагом будет вычисление градиентов по выходам сети. Остальные этапы — производные активаций и распространение ошибки — следуют стандартным правилам обратного распространения.

Метод Fit: обучение модели с помощью L-BFGS

Метод Fit отвечает за обучение нейронной сети, объединяя прямое распространение, обратное распространение и оптимизацию параметров с помощью алгоритма L-BFGS.

//+-------------------------------------------------+
//| Метод Fit с использованием L-BFGS               |
//+-------------------------------------------------+
bool MLPRegressor::Fit(const matrix &data, const matrix &target)
  {
   Sample_ = (int)data.Rows();
   Features = (int)data.Cols();
   ones_ = matrix::Ones(1, Sample_);

   ArrayResize(target_Plot, Sample_);
   for(int i = 0; i < Sample_; i++)
      target_Plot[i] = target[i, 0];

   if(!CreateNet())
      return false;

// Создаем объект для оптимизации
   MLPOptimizationObjective objective(GetPointer(this), data, target);
   MLPReportCallback frep(GetPointer(this)); // Создаем объект для отслеживания функции потерь
   CObject obj;

// Подготавливаем параметры
   CRowDouble params;
   objective.PackParameters(params);
   double theta[];
   ArrayResize(theta, params.Size());
   for(int i = 0; i < params.Size(); i++)
      theta[i] = params[i];

// Настраиваем параметры оптимизации
   double epsg = 0.0001;     // Точность по градиенту
   double epsf = 0.00001;     // Точность по значению функции
   double epsw = 0.0000;   // Точность по параметрам
   int maxits = Epochs;       // Максимальное число итераций

// Инициализация и запуск L-BFGS
   CMinLBFGSStateShell state;
   CMinLBFGSReportShell rep;
   CAlglib::MinLBFGSCreate(params.Size(), theta, state);
   CAlglib::MinLBFGSSetCond(state, epsg, epsf, epsw, maxits);
   CAlglib::MinLBFGSSetXRep(state, true); // Включаем отчеты о прогрессе оптимизации
   CAlglib::MinLBFGSOptimize(state, objective, frep, true, obj);
   CAlglib::MinLBFGSResults(state, theta, rep);

//----------TerminationType field contains completion code, which can be:
//  -8    internal integrity control detected  infinite  or  NAN  values  in
//        function/gradient. Abnormal termination signalled.
//   1    relative function improvement is no more than EpsF.
//   2    relative step is no more than EpsX.
//   4    gradient norm is no more than EpsG
//   5    MaxIts steps was taken
//   7    stopping conditions are too stringent,
//        further improvement is impossible,
//        X contains best point found so far.
//   8    terminated    by  user  who  called  minlbfgsrequesttermination().
//        X contains point which was   "current accepted"  when  termination
//        request was submitted.
//--------------------------------------------------------------------------
// Получаем финальный массив параметров
   for(int i = 0; i < (int)params.Size(); i++)
     {
      params.Set(i, theta[i]);
     }
   objective.UnpackParameters(params);

// Финальный прямой проход с оптимизированными параметрами
   if(!FeedForward(data))
      return false;

// Сохраняем все выходы сети в одномерном виде для последующего использования в методе PlotGraphic
// для визуализации.Массив содержит параметры нормального распределения для каждого наблюдения.
   ArrayResize(NetOutput, Sample_ * layer2);
   for(int i = 0; i < Sample_; i++)
      for(int j = 0; j < layer2; j++)
         NetOutput[i * layer2 + j] = act2.Transpose()[i, j];

   PrintFormat("L-BFGS Optimization completed. Iterations: %d, Termination type: %d, Final loss: %.5f",
               rep.GetIterationsCount(), rep.GetTerminationType(), objective.GetLoss());

   for(int i = 0; i < LossCount; i++)
      PrintFormat("Iteration %d, Loss: %.5f", i, LossPlot[i]);

   return true;
  }

Процесс обучения организован как последовательность следующих этапов. Сначала вызывается метод CreateNet, который инициализирует матрицы весов (weights1, weights2) и смещений (bias1, bias2) случайными значениями, подготавливая модель к обучению. Затем создаётся объект класса MLPOptimizationObjective, который связывает модель с оптимизатором L-BFGS, предоставляя функцию потерь и её градиенты.

Параметры модели преобразуются в одномерный массив params с помощью метода PackParameters, чтобы соответствовать формату, требуемому L-BFGS. Для мониторинга сходимости создаётся объект класса MLPReportCallback, который фиксирует значения функции потерь в массив LossPlot после каждой итерации оптимизации.

Далее настраивается алгоритм L-BFGS с использованием параметров оптимизации:

• epsg — точность по норме градиента, определяющая критерий остановки по малости градиентов,
• epsf — точность по значению функции потерь,
• epsw — точность по изменению параметров,
• maxits — максимальное число итераций, соответствующее заданному пользователем числу эпох.

Оптимизация запускается с начальным вектором параметров через функции MinLBFGSCreate и MinLBFGSOptimize. Активация функции MinLBFGSSetXRep(state, true) обеспечивает вызов виртуального метода Rep класса MLPReportCallback для сохранения истории значений функции потерь. По завершении оптимизации финальные параметры извлекаются в массив theta с помощью MinLBFGSResults и распаковываются обратно в матрицы весов и смещений. После этого, выполняется финальный прямой проход через метод FeedForward, чтобы получить предсказания модели. Эти результаты сохраняются в массив NetOutput для последующего анализа или визуализации.

Почему выбран L-BFGS

Для обучения модели MLPRegressor я остановился на алгоритме L-BFGS, так как он без проблем работает с пользовательскими функциями потерь, в отличие от алгоритма Левенберга-Марквардта, ограниченного только квадратичными функциями, такими как MSE.

Стохастические градиентные методы, такие как Adam, являются оптимальным и, зачастую, единственным выбором для обучения нейронных сетей с множеством скрытых слоёв на больших массивах данных, где требуется обработка огромных объёмов информации. Однако в контексте анализа котировок, где используются относительно небольшие наборы данных, из-за быстрого затухания памяти прошлых событий, эти методы значительно уступают в скорости сходимости методам второго порядка, таким как L-BFGS.

Классы для интеграции с оптимизатором L-BFGS

Для того чтобы связать наш класс с методом оптимизации, реализовано два вспомогательных класса: MLPOptimizationObjective и MLPReportCallback. С их помощью мы передаем в оптимизатор  функции потерь и градиенты, а также отслеживаем прогресс оптимизации. 

Класс MLPOptimizationObjective

Класс MLPOptimizationObjective связывает нейронную сеть MLPRegressor с алгоритмом оптимизации L-BFGS из библиотеки ALGLIB. Наследуясь от CNDimensional_Grad, он переопределяет виртуальную функцию Grad, чтобы предоставлять L-BFGS значение функции потерь GaussianNLLLoss и её градиенты, необходимые для обучения.

//+------------------------------------------------------------------+
//| Класс для целевой функции оптимизатора L-BFGS                    |
//+------------------------------------------------------------------+
class MLPOptimizationObjective : public CNDimensional_Grad
  {
private:
   MLPRegressor*     m_mlp;  // Указатель на объект нейронной сети
   matrix            m_data;        // Входные данные
   matrix            m_target;      // Целевые значения
   double            m_loss;        // Текущие потери

public:
                     MLPOptimizationObjective(MLPRegressor* mlpLBFGS, const matrix &data, const matrix &target)
      :              m_mlp(mlpLBFGS), m_data(data), m_target(target), m_loss(0.0) {}

   double            GetLoss() { return m_loss; }

   // Метод для преобразования параметров в одномерный массив
   void              PackParameters(CRowDouble &params)
     {
      int total_params = (int)(m_mlp.GetNumNeuronsLayer1() * m_data.Cols() +     // weights1
                               m_mlp.GetNumNeuronsLayer1() +                     // bias1
                               m_mlp.GetNumNeuronsLayer2() * m_mlp.GetNumNeuronsLayer1() + // weights2
                               m_mlp.GetNumNeuronsLayer2()) ;                     // bias2
      params.Resize(total_params);

      int idx = 0;
      //  weights1
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer1(); i++)
         for(int j = 0; j < (int)m_data.Cols(); j++)
            params.Set(idx++, m_mlp.weights1[i,j]);

      //  bias1
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer1(); i++)
         params.Set(idx++, m_mlp.bias1[i,0]);

      //  weights2
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer2(); i++)
         for(int j = 0; j < m_mlp.GetNumNeuronsLayer1(); j++)
            params.Set(idx++,m_mlp.weights2[i,j]);

      //  bias2
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer2(); i++)
         params.Set(idx++,m_mlp.bias2[i,0]);
     }

   // Метод для распаковки параметров из одномерного массива
   void              UnpackParameters(const CRowDouble &params)
     {
      int idx = 0;
      //  weights1
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer1(); i++)
         for(int j = 0; j <(int) m_data.Cols(); j++)
            m_mlp.weights1[i,j] = params[idx++];

      //  bias1
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer1(); i++)
         m_mlp.bias1[i,0] = params[idx++];

      //  weights2
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer2(); i++)
         for(int j = 0; j < m_mlp.GetNumNeuronsLayer1(); j++)
            m_mlp.weights2[i,j] = params[idx++];

      //  bias2
      for(int i = 0; i < m_mlp.GetNumNeuronsLayer2(); i++)
         m_mlp.bias2[i,0] = params[idx++];
     }

   virtual void      Grad(CRowDouble &params, double &func, CRowDouble &grad, CObject &obj) override
     {
      UnpackParameters(params);

      // Прямой проход
      if(!m_mlp.FeedForward(m_data))
        {
         func = DBL_MAX;
         for(int i = 0; i < params.Size(); i++)
            grad.Set(i, DBL_MAX);
         return;
        }

      // Вычисляем функцию потерь
      func = GaussianNLLLoss(m_mlp.act2, m_target,(int) m_data.Rows());
      m_loss = func;

      // Выполняем обратное распространение для получения градиентов
      if(!m_mlp.Backprop(m_data, m_target))
        {
         func = DBL_MAX;
         for(int i = 0; i < params.Size(); i++)
            grad.Set(i, DBL_MAX);
         return;
        }

      // Формируем вектор градиентов
      int idx = 0;

      for(int i = 0; i < m_mlp.GetNumNeuronsLayer1(); i++)
         for(int j = 0; j <(int) m_data.Cols(); j++)
            grad.Set(idx++, m_mlp.gW1[i,j]);

      for(int i = 0; i < m_mlp.GetNumNeuronsLayer1(); i++)
         grad.Set(idx++, m_mlp.gb1[i,0]);

      for(int i = 0; i < m_mlp.GetNumNeuronsLayer2(); i++)
         for(int j = 0; j < m_mlp.GetNumNeuronsLayer1(); j++)
            grad.Set(idx++, m_mlp.gW2[i,j]);

      for(int i = 0; i < m_mlp.GetNumNeuronsLayer2(); i++)
         grad.Set(idx++, m_mlp.gb2[i,0]);
     }
  };

L-BFGS работает с одномерным массивом параметров, но наша сеть хранит параметры в виде матриц весов и векторов смещений. Поэтому мы векторизуем параметры с помощью функции PackParameters и раскладываем их обратно в матрицы с помощью функции UnpackParameters. 

Метод Grad — это основной метод, вызываемый L-BFGS на каждой итерации. Он вызывается многократно, иногда десятки или сотни раз за итерацию, чтобы оценить функцию потерь и градиенты для разных наборов параметров. Поэтому мы не можем сохранять значение функции потерь в этом методе, иначе мы бы получили кучу промежуточных значений, которые не отражают реальный прогресс обучения, а только пробы L-BFGS.

Для мониторинга сходимости используется отдельный класс MLPReportCallback, который фиксирует потери только после завершения итерации.

Класс MLPReportCallback

Наследуясь от CNDimensional_Rep из библиотеки ALGLIB, наш класс  переопределяет виртуальную функцию Rep, чтобы сохранять значения функции потерь в массив LossPlot для последующего анализа сходимости модели.

//+------------------------------------------------------------------+
//| Класс для отслеживания прогресса обучения сети                   |
//+------------------------------------------------------------------+
class MLPReportCallback : public CNDimensional_Rep
  {
private:
   MLPRegressor      *mlp;

public:
                     MLPReportCallback(MLPRegressor *mlp_instance) : mlp(mlp_instance) {}
                    ~MLPReportCallback() {}

   virtual void      Rep(CRowDouble &arg, double func, CObject &obj) override
     {
      if(mlp != NULL)
        {
         ArrayResize(mlp.LossPlot, mlp.LossCount + 1, 10000);
         mlp.LossPlot[mlp.LossCount] = func;
         mlp.LossCount++;
        }
      else
        {
         Print("MLPReportCallback: Invalid pointer to MLPRegressor");
        }

     }
  };

Алгоритм L-BFGS вызывает метод Rep, передавая текущие параметры модели (arg) и значение функции потерь (func). Важно, что вызов Rep происходит только после завершения полноценной итерации L-BFGS, а не во время промежуточных вычислений в методе Grad класса MLPOptimizationObjective. Нам остается только сложить в массив необходимую нам информацию, например, значение функции потерь.

Индикатор для прогнозирования условного распределения

Для тестирования модели MLPRegressor напишем индикатор, который будет прогнозировать условное математическое ожидание приращения цены и условную дисперсию.

Входные параметры индикатора:

• InpPeriodWindow — размер окна для вычисления приращений цен,
• InpSamples — количество обучающих примеров,
• InpShift — количество баров для тестирования,
• InpLayer1 — количество нейронов в скрытом слое сети,
• InpEpochs — максимальное количество эпох для обучения модели.

Обучающий и тестовый наборы данных формируются с помощью функций CollectData и CollectTestData. Для обучения используются исторические цены закрытия. Признаки представляют собой матрицу размером nsamples×(window−1), где каждая строка содержит приращения цен за window−1 предыдущих баров. Целевая переменная — вектор размером nsamples×1, содержащий приращения цен (close_i − close_i+1).

Данные нормализуются с использованием среднего (train_data_mean) и стандартного отклонения (train_data_std), вычисленных на обучающем наборе. Нормализация стабилизирует обучение, улучшая сходимость модели за счёт приведения входных признаков и целевой переменной к единому масштабу. Функция CollectTestData формирует тестовый набор для последних InpShift баров, применяя те же параметры нормализации.

В функции OnInit создаётся экземпляр класса MLPRegressor с заданной функцией активации скрытого слоя. После обучения выводится время, затраченное на обучение, и общее количество параметров модели.

В функции OnCalculate прогноз выполняется с помощью метода Predict, вычисления проводятся только при появлении нового бара.

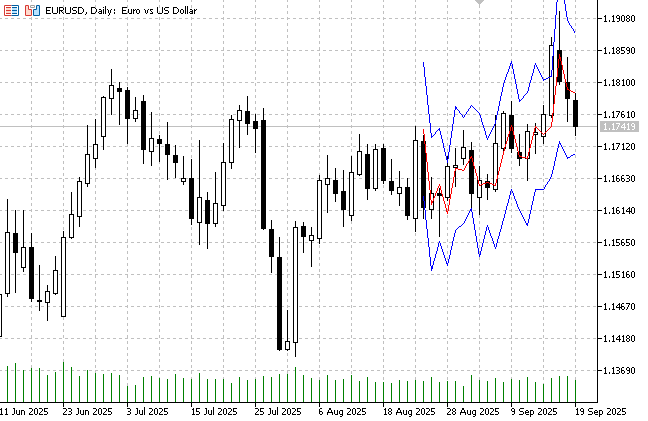
Рис.2. Прогноз среднего для пары EURUSD и 95% доверительные интервалы

Заключение

В данной статье мы использовали модель многослойного перцептрона, которая прогнозирует параметры условного гауссовского распределения. Для этого мы применили пользовательскую функцию потерь на основе гауссовского отрицательного логарифма правдоподобия. Эта функция позволяет эффективно моделировать гетероскедастичность приращений цен, что является ключевым преимуществом по сравнению с традиционными подходами к обучению нейронных сетей, основанными на среднеквадратичной ошибке (MSE), которая неявно предполагает постоянство дисперсии целевой переменной. 

Мы подробно описали архитектуру класса MLPRegressor, включая методы прямого и обратного распространения, а также интеграцию с алгоритмом оптимизации L-BFGS из библиотеки ALGLIB через классы MLPOptimizationObjective и MLPReportCallback. 

Индикатор, построенный на основе  класса MLPRegressor, демонстрирует практическую применимость модели, позволяя трейдерам получать помимо прогноза среднего также и  доверительные интервалы. Это позволяет принимать более обоснованные решения, учитывая не только ожидаемые ценовые движения, но и их неопределённость, что особенно ценно на волатильных рынках.

Важно подчеркнуть, что обучение нейронных сетей не должно ограничиваться стандартными функциями потерь, такими как MSE. Эксперименты с различными вероятностными моделями и функциями правдоподобия открывают новые возможности для анализа данных. Исследователи и практики могут адаптировать модели машинного обучения к уникальным особенностям финансовых рынков, что способствует повышению точности прогнозов и более глубокому пониманию рыночной динамики.