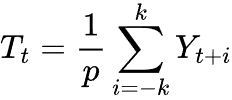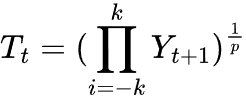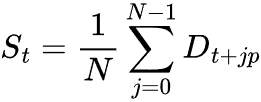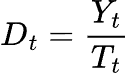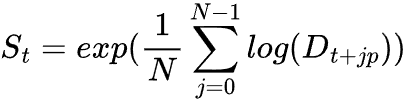
Машинное обучение и Data Science (Часть 34): Разложение временных рядов, раскрываем саму суть фондового рынка

Введение

Прогнозирование на основе данных временных рядов никогда не было простым делом. Часто закономерности скрыты за шумом и неопределенностью, а графики вводят в заблуждение, поскольку содержат общий обзор рыночной динамики, который не дает глубокого понимания происходящего.

В статистическом прогнозировании и машинном обучении мы стремимся разложить данные временного ряда, представляющие собой значения цен на рынке (цены открытия, максимума, минимума и закрытия), на несколько компонентов, которые могут быть более информативными, чем один массив временных рядов.

В этой статье мы рассмотрим статистический метод, известный как сезонное разложение (seasonal decomposition). Наша цель — использовать его для анализа фондовых рынков с целью выявления трендов, сезонных закономерностей и многого другого.

Что такое сезонное разложение?

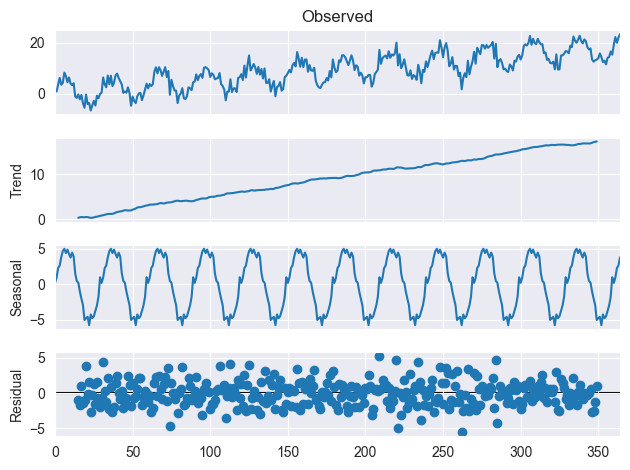
Сезонное разложение — это статистический метод, используемый для разложения данных временных рядов на несколько компонентов: тренд (trend), сезонность (seasonality) и остаток (residual).

Тренд

Трендовая составляющая временных рядов относится к долгосрочным изменениям или закономерностям, наблюдаемым с течением времени.

Она отражает общее направление движения данных. Например, если данные со временем растут, то трендовая составляющая будет иметь восходящий наклон, а если снижаются, то нисходящий.

Это знакомо практически всем трейдерам: чтобы определить тренд, достаточно просто взглянуть на график.

Сезонность

Сезонная составляющая временного ряда данных относится к циклическим закономерностям, наблюдаемым в течение определенного периода времени. Например, если мы анализируем ежемесячные данные о продажах розничного продавца, специализирующегося на товарах для дома и подарках, то сезонный компонент будет отражать тот факт, что продажи, как правило, достигают пика в декабре из-за рождественских покупок, а затем стабилизируются после окончания праздничного сезона в январе, феврале и т. д.

Остаток

Остаточная составляющая данных временного ряда представляет собой случайную вариацию, остающуюся после учета тренда и сезонной составляющей. Она представляет собой шум или ошибку в данных, которые нельзя объяснить трендом или сезонными закономерностями.

Чтобы лучше это понять, взглянем на изображение ниже.

Чем нам может помочь сезонное разложение?

Прежде чем углубляться в математические детали и реализовывать сезонное разложение в MQL5, давайте сначала разберемся, чем нам может помочь сезонное разложение данных временных рядов.

1. Выявление скрытых закономерностей и трендов в данных
   
   Сезонный анализ может помочь нам выявить тренды и закономерности в данных, которые могут быть неочевидны при изучении исходных данных. Разложив данные на составляющие компоненты (тренд, сезонность и остаток), мы получаем лучшее понимание того, как эти компоненты влияют на общее поведение данных.
   
   
2. Устранение влияния сезонности
   
   Сезонное разложение может использоваться для устранения влияния сезонности на данные, позволяя нам сосредоточиться на главном тренде или, наоборот, на сезонных колебаниях, например при работе с данными о погоде, которые демонстрируют выраженную сезонность.
   
   
3. Составление точных прогнозов
   
   Когда данные разбиты на компоненты, это помогает отсортировать ненужную информацию, которая может быть менее нужна в зависимости от задачи. Например, при попытке прогнозирования тренда целесообразнее иметь только информацию о тренде, а не сезонные данные.
   
   
4. Сравнение трендов за разные периоды времени или в разных регионах
   
   Сезонный анализ можно использовать для сравнения трендов в разные периоды времени или в разных регионах, что позволяет понять, как различные факторы могут влиять на данные. Например, при сравнении данных о розничных продажах в разных регионах, сезонный анализ может помочь выявить региональные различия в сезонных закономерностях и соответствующим образом скорректировать наш анализ.

Внедрение сезонного разложения в MQL5

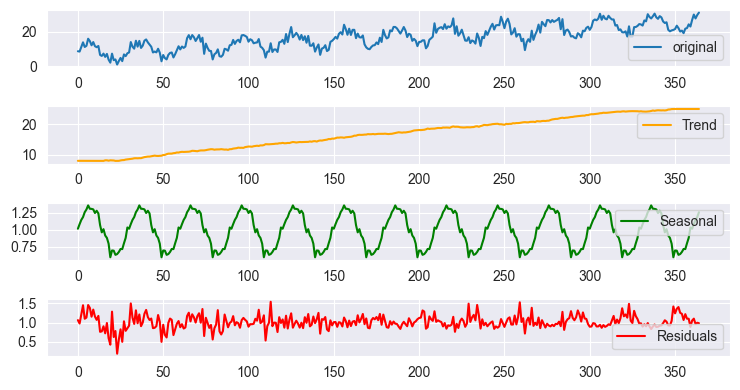
Для реализации этого аналитического алгоритма давайте сначала сгенерируем простые случайные данные с признаками тренда, сезонными закономерностями и некоторым шумом. Это то, что можно увидеть в реальных сценариях обработки данных, особенно на валютном и фондовом рынках, где данные не всегда однородны и понятны.

Для решения этой задачи мы будем использовать язык программирования Python.

Файл: seasonal_decomposition_visualization.ipynb

import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt
import os

sns.set_style("darkgrid")

# Create synthetic time-series data
np.random.seed(42)
time = np.arange(0, 365)  # 1 year (daily data)
trend = 0.05 * time  # Linear upward trend
seasonality = 5 * np.sin(2 * np.pi * time / 30)  # 30-day periodic seasonality
noise = np.random.normal(scale=2, size=len(time))  # Random noise

# Combine components to form the time-series
time_series = trend + seasonality + noise

# Plot the original time-series
plt.figure(figsize=(10, 4))
plt.plot(time, time_series, label="Original Time-Series", color="blue")
plt.xlabel("Time (Days)")
plt.ylabel("Value")
plt.title("Synthetic Time-Series with Trend and Seasonality")
plt.legend()
plt.show()

Результат

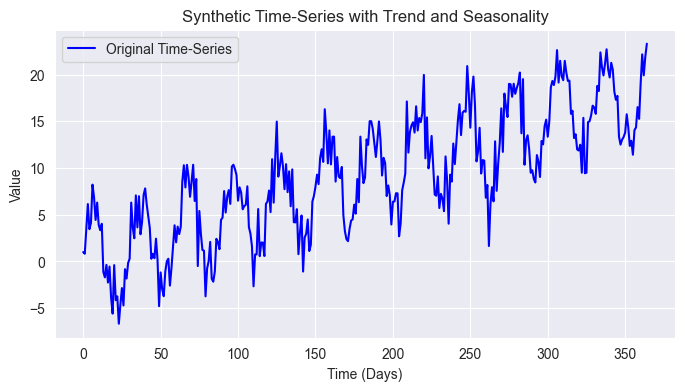
Разумеется, фондовый рынок гораздо сложнее, но давайте используем эти простые данные и попробуем выявить сезонные закономерности за 30 дней, которые мы добавили к временному ряду, общий тренд и отфильтровать некоторый шум из данных.

Извлечение тренда

Для выявления тренда можно использовать скользящую среднюю (MA), поскольку она сглаживает временной ряд, усредняя значения по фиксированному окну. Это помогает отфильтровать краткосрочные колебания и выявить лежащий в их основе тренд.

При аддитивном разложении тренд оценивается с помощью скользящего среднего по окну, равному сезонному периоду p.

где:

 = компонент тренда в момент времени t.

 = размер окна или сезонный период.

 = половина сезонного периода.

 = наблюдаемые значения временного ряда.

При мультипликативном разложении мы используем геометрическое среднее.

где:

 = оператор произведения, где вместо сложения мы умножаем все значения в пределах окна, поскольку мультипликативное разложение предполагает, что сезонные эффекты масштабируют данные, а не добавляют к ним.

Расчеты могут показаться математически сложными, но их можно разложить на несколько строк MQL5-кода.

vector moving_average(const vector &v, uint k, ENUM_VECTOR_CONVOLVE mode=VECTOR_CONVOLVE_VALID)
 {
   vector kernel = vector::Ones(k) /  k;
   vector ma = v.Convolve(kernel, mode);
    
   return ma;  
 }

Мы рассчитываем скользящую среднюю на основе метода свертки, потому что он гибок, эффективен и обрабатывает пропущенные значения на краях массива, в отличие от вычисления скользящего среднего с использованием метода скользящего окна (rolling window).

Формулу можно завершить следующим образом.

//--- compute the trend

   int n = (int)timeseries.Size();  
   res.trend = moving_average(timeseries, period);
   
   // We align trend array with the original series length
   
   int pad = (int)MathFloor((n - res.trend.Size()) / 2.0);
   int pad_array[] = {pad, n-(int)res.trend.Size()-pad};
   
   res.trend = Pad(res.trend, pad_array, edge);

Извлечение сезонного компонента

Извлечение сезонного компонента подразумевает изолирование повторяющихся закономерностей во временном ряду, которые встречаются с заданным интервалом, например, ежедневно, ежемесячно, ежегодно и т. д.

Этот компонент вычисляется после удаления тренда из исходных данных временного ряда; его можно извлечь по-разному в зависимости от того, является ли модель аддитивной или мультипликативной.

Аддитивная модель

После оценки и удаления тренда  , ряд рассчитывается так:

где:

 = значение без тренда в момент времени t.

 =  значение временного ряда в момент времени t.

 = трендовая составляющая в момент времени t.

Для вычисления сезонной составляющей мы берем среднее значений после удаления тренда за все полные циклы сезонного периода p.

где:

 = количество полных сезонных циклов в наборе данных.

 = сезонный период (например, 30 для ежедневных данных в месячном цикле).

 = выделенная сезонная составляющая.

Мультипликативная модель

В мультипликативной модели для удаления тренда из временного ряда мы используем деление, а не вычитание.

Сезонная составляющая извлекается путем вычисления геометрического среднего вместо арифметического.

Это помогает предотвратить предвзятость, обусловленную мультипликативным характером модели.

Реализуем эту функцию в MQL5 следующим образом.

//--- compute the seasonal component
   
   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }
   
   vector detrended = {};
   vector seasonal = {};
   
   switch(model)
     {
      case  additive:
        {
          detrended = timeseries - res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = SliceStep(detrended, i, period).Mean(); //Arithmetic mean over cycles
        }    
        break;
      case  multiplicative:
        {
          detrended = timeseries / res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = MathExp(MathLog(SliceStep(detrended, i, period)).Mean()); //Geometric mean
        }    
        break;
      default:
        printf("Unknown model for seasonal component calculations");
        break;
     }

    
    vector seasonal_repeated = Tile(seasonal, (int)MathFloor(n/period)+1);
    res.seasonal = Slice(seasonal_repeated, 0, n);

Функция Pad добавляет заполнение (дополнительные значения) вокруг вектора. Аналогично функции Numpy.pad в этом сценарии это помогает обеспечить центрирование значений скользящего среднего.

Благодаря функции логарифмического преобразования MathLog, которая не может использоваться для нулевых и отрицательных значений, мультипликативная модель должна быть ограничена только положительными временными рядами; это условие необходимо проверить и усилить.

   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }

Функция Tile создает большой вектор, повторяя сезонный вектор несколько раз. Этот процесс имеет решающее значение для выявления повторяющихся сезонных закономерностей во временном ряду.

Расчет остатка

Наконец, мы вычисляем остаток, вычитая тренд и сезонность.

Для аддитивной модели:

Для мультипликативной модели:

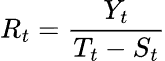
где:

 = исходное значение временного ряда в момент времени t.

 = значение тренда в момент времени t.

 = сезонное значение в момент времени t.

Объединяем компоненты в одной функции

Аналогично функции seasonal_decompose, которая послужила отправной точкой в моей работе, я объединил все расчеты в одну функцию seasonal_decompose, которая возвращает структуру, содержащую векторы тренда, сезонности и остатка.

enum seasonal_model
 {
   additive,
   multiplicative
 };

struct seasonal_decompose_results
 {
   vector trend;
   vector seasonal;
   vector residuals;
 };
 
seasonal_decompose_results seasonal_decompose(const vector &timeseries, uint period, seasonal_model model=additive)
 {
   seasonal_decompose_results res;
   
   if (timeseries.Size() < period)
    {
      printf("%s Error: Time series length is smaller than the period. Cannot compute seasonal decomposition.",__FUNCTION__);
      return res;
    }
   
//--- compute the trend

   int n = (int)timeseries.Size();  
   res.trend = moving_average(timeseries, period);
   
   // We align trend array with the original series length
   
   int pad = (int)MathFloor((n - res.trend.Size()) / 2.0);
   int pad_array[] = {pad, n-(int)res.trend.Size()-pad};
   
   res.trend = Pad(res.trend, pad_array, edge);

//--- compute the seasonal component
   
   if (model == multiplicative)
     {
       for (ulong i=0; i<timeseries.Size(); i++)
         if (timeseries[i]<=0)
            {
               printf("Error, Multiplicative seasonality is not appropriate for zero and negative values");
               return res;
            }
     }
   
   vector detrended = {};
   vector seasonal = {};
   
   switch(model)
     {
      case  additive:
        {
          detrended = timeseries - res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = SliceStep(detrended, i, period).Mean(); //Arithmetic mean over cycles
        }    
        break;
      case  multiplicative:
        {
          detrended = timeseries / res.trend;
          seasonal = vector::Zeros(period);
         
          for (uint i = 0; i < period; i++)
            seasonal[i] = MathExp(MathLog(SliceStep(detrended, i, period)).Mean()); //Geometric mean
        }    
        break;
      default:
        printf("Unknown model for seasonal component calculations");
        break;
     }


    
    vector seasonal_repeated = Tile(seasonal, (int)MathFloor(n/period)+1);
    res.seasonal = Slice(seasonal_repeated, 0, n);

//--- Compute Residuals

    if (model == additive)
        res.residuals = timeseries - res.trend - res.seasonal;
    else  // Multiplicative
        res.residuals = timeseries / (res.trend * res.seasonal);
        
   return res;
 }

Наконец-то мы можем протестировать эту функцию.

Мне также пришлось сгенерировать положительные значения и сохранить их в CSV-файле для тестирования сезонного разложения с использованием мультипликативной модели.

Файл: seasonal_decomposition_visualization.ipynb

# Create synthetic time-series data
np.random.seed(42)
time = np.arange(0, 365)  # 1 year (daily data)
trend = 0.05 * time  # Linear upward trend
seasonality = 5 * np.sin(2 * np.pi * time / 30)  # 30-day periodic seasonality
noise = np.random.normal(scale=2, size=len(time))  # Random noise

# Combine components to form the time-series
time_series = trend + seasonality + noise

# Fix for multiplicative decomposition: Shift the series to make all values positive
min_value = np.min(time_series)
if min_value <= 0:
    shift_value = abs(min_value) + 1  # Ensure strictly positive values
    time_series_shifted = time_series + shift_value
else:
    time_series_shifted = time_series

ts_pos_df = pd.DataFrame({
    "timeseries": time_series_shifted
})

ts_pos_df.to_csv(os.path.join(files_path,"pos_ts_df.csv"), index=False)

Внутри нашего MQL5-скрипта мы загружаем оба набора данных временных рядов, используя библиотеку для работы с фреймами данных, которую мы обсуждали в статье. После загрузки данных мы запускаем алгоритмы сезонного разложения.

Файл: seasonal_decompose test.mq5

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//--- Additive model
   
   CDataFrame df;
   df.FromCSV("ts_df.csv");
   
   vector time_series = df["timeseries"];
   
//---
    
    seasonal_decompose_results res_ad = seasonal_decompose(time_series, 30, additive);
    
    df.Insert("original", time_series);
    df.Insert("trend",res_ad.trend);
    df.Insert("seasonal",res_ad.seasonal);
    df.Insert("residuals",res_ad.residuals);
    
    df.ToCSV("seasonal_decomposed_additive.csv");

//--- Multiplicative model

   CDataFrame pos_df;
   pos_df.FromCSV("pos_ts_df.csv");
   
   time_series = pos_df["timeseries"];
   
//---
    
    seasonal_decompose_results res_mp = seasonal_decompose(time_series, 30, multiplicative);
    
    pos_df.Insert("original", time_series);
    pos_df.Insert("trend",res_mp.trend);
    pos_df.Insert("seasonal",res_mp.seasonal);
    pos_df.Insert("residuals",res_mp.residuals);
    
    pos_df.ToCSV("seasonal_decomposed_multiplicative.csv");
  }

Мне пришлось сохранить результаты в новые CSV-файлы для визуализации с помощью Python.

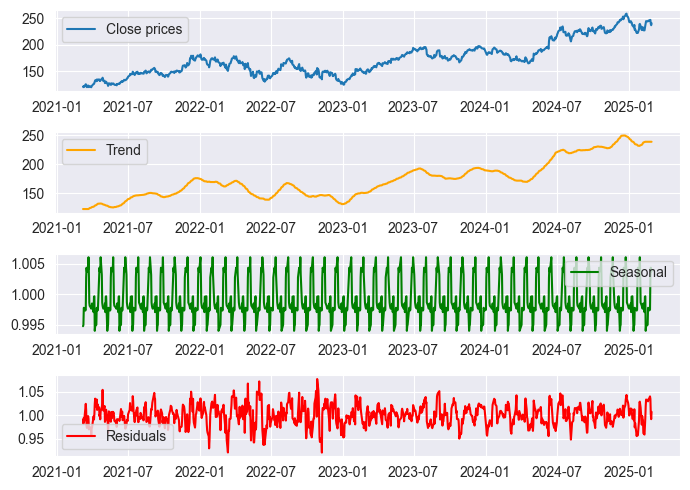
Сезонное разложение с использованием графика результатов аддитивной модели

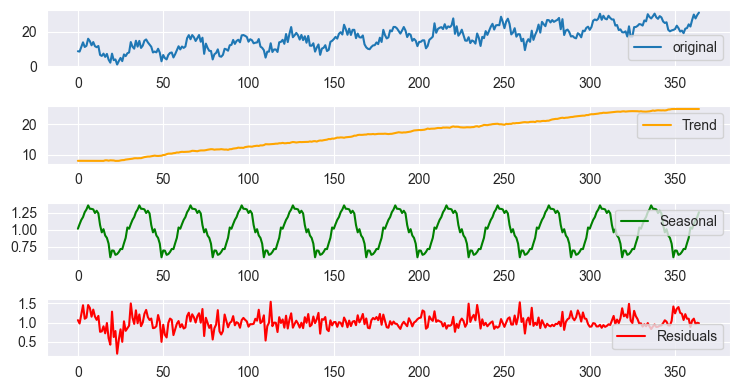
Сезонное разложение с использованием графика результатов мультипликативной модели

Из-за масштаба графики выглядят почти одинаково, но результаты различаются при анализе данных. Результат будет таким же, как и при использовании tsa.seasonal.seasonal_decompose от stats models в Python.

Теперь, когда у нас есть функция сезонного разложения, давайте используем ее для анализа фондовых рынков.

Наблюдение за закономерностями на фондовом рынке

При анализе фондового рынка выявление тренда часто оказывается несложной задачей, особенно для устоявшихся и фундаментально сильных компаний. Многие крупные, финансово стабильные корпорации, как правило, демонстрируют восходящую траекторию развития в долгосрочной перспективе благодаря стабильному росту, инновациям и рыночному спросу.

Однако выявление сезонных закономерностей в ценах на акции может быть гораздо более сложной задачей. В отличие от трендов, сезонность относится к повторяющимся движениям цен через фиксированные интервалы, которые не всегда очевидны; эти закономерности могут проявляться в разные временные рамки.

Внутридневная сезонность

В определенные часы торгового дня может наблюдаться повторяющееся поведение цен (например, повышенная волатильность при открытии или закрытии рынка).

Сезонность в течение месяца или квартала

Цены на акции могут следовать циклам, основанным на отчетах о прибыли, экономических условиях или настроениях инвесторов.

Долгосрочная сезонность

Некоторые акции демонстрируют повторяющиеся тенденции на протяжении многих лет из-за экономических циклов или факторов, специфичных для конкретной компании.

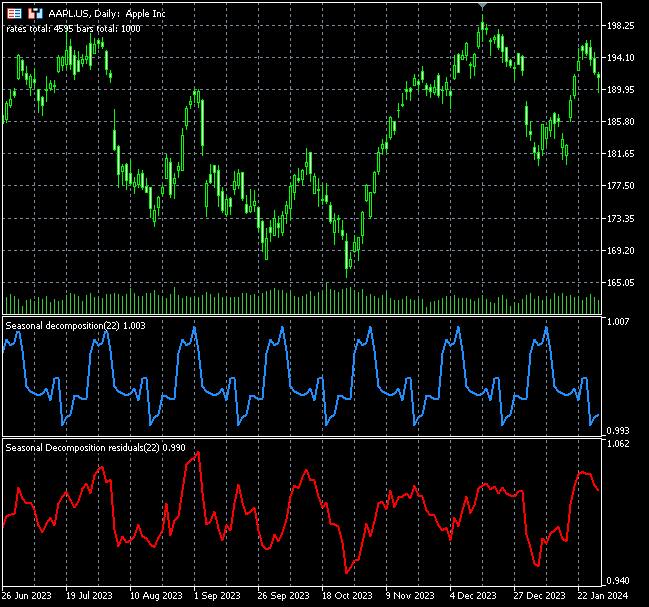
Пример из практики: акции компании Apple (AAPL)

На примере акций Apple можно предположить, что сезонные закономерности проявляются каждые 22 торговых дня, что примерно соответствует одному торговому месяцу в годовом массиве данных. Это предположение основано на том факте, что в месяце примерно 22 торговых дня (исключая выходные и праздничные дни).

Применяя методы сезонного анализа, мы можем проанализировать, демонстрируют ли акции Apple повторяющиеся ценовые движения каждые 22 дня. Наличие выраженной сезонности указывает на то, что колебания цен могут следовать предсказуемым циклам, что может быть полезно для трейдеров и аналитиков. Однако, если значительная сезонность не обнаружена, движение цен может быть в значительной степени обусловлено внешними факторами, шумом или доминирующим трендом.

Соберем ежедневные цены закрытия для 1000 баров и выполним мультипликативное сезонное разложение за период в 22 дня.

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>

input uint bars_total = 1000;
input uint period_ = 22;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   
    vector close, time;
    close.CopyRates(Symbol(), PERIOD_D1, COPY_RATES_CLOSE, 1, bars_total); //closing prices
    time.CopyRates(Symbol(), PERIOD_D1, COPY_RATES_TIME, 1, bars_total); //time
   
    seasonal_decompose_results res_ad = seasonal_decompose(close, period_, multiplicative);
    
    CDataFrame df; //A dataframe object for storing the seasonal decomposition outcome
    
    df.Insert("time", time);
    df.Insert("close", close);
    df.Insert("trend",res_ad.trend);
    df.Insert("seasonal",res_ad.seasonal);
    df.Insert("residuals",res_ad.residuals);
    
    df.ToCSV(StringFormat("%s.%s.period=%d.seasonal_dec.csv",Symbol(), EnumToString(PERIOD_D1), period_));
  }

Затем результат был визуализирован в Jupyter Notebook под названием stock_market seasonal dec.ipynb. Результат показан ниже.

На приведенном выше графике мы видим некоторые сезонные закономерности, но мы не можем быть на 100% уверены в них, поскольку всегда существуют определенные погрешности. Задача состоит в том, чтобы интерпретировать значения погрешностей и провести соответствующий анализ.

На основе графика остатков мы видим всплески значений остатков в период с 2020 по 2022 год. Всем известно, что это был период глобальной пандемии, поэтому, возможно, сезонные закономерности были нарушены и непоследовательны, что указывает на то, что мы не можем доверять сезонным закономерностям, наблюдаемым в тот период.

Общее правило.

Правильное разложение: остатки должны выглядеть как случайный (белый) шум.

Неправильное разложение: остатки по-прежнему демонстрируют видимую структуру (тренды или сезонные эффекты, которые не были удалены).

Для визуализации остатков можно использовать различные математические методы, такие как:

График распределения

У нас есть график остатков с нормальным распределением, это может быть хорошим признаком того, что в акциях Apple могут наблюдаться определенные ежемесячные закономерности.

Среднее значение и стандартное отклонение

В аддитивной модели среднее значение остатков должно быть близко к 0, что означает, что большая часть вариаций объясняется трендом и сезонностью.

В мультипликативной модели среднее значение остатков в идеале близко к 1, что означает, что исходный ряд хорошо объясняется трендом и сезонностью.

Значение стандартного отклонения должно быть небольшим

print("Residual Mean:", residuals.mean())  # Should be close to 0
print("Residual Std Dev:", residuals.std())  # Should be small

Выходные параметры

Residual Mean: 1.0002367590572043
Residual Std Dev: 0.021749969975933727

Наконец, мы можем поместить всё это в индикатор.

#property indicator_separate_window
#property indicator_buffers 2
#property indicator_plots 1

#property indicator_color1 clrDodgerBlue
#property indicator_style1 STYLE_SOLID
#property indicator_type1 DRAW_LINE
#property indicator_width1 2

//+------------------------------------------------------------------+

double trend_buff[];
double seasonal_buff[];

#include <MALE5\Stats Models\Tsa\Seasonal Decompose.mqh>
#include <MALE5\pandas.mqh>

input uint bars_total = 10000;
input uint period_ = 22;
input ENUM_COPY_RATES price = COPY_RATES_CLOSE;

//+------------------------------------------------------------------+
//| Custom indicator initialization function                         |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- indicator buffers mapping
   
   SetIndexBuffer(0, seasonal_buff, INDICATOR_DATA);
   SetIndexBuffer(1, trend_buff, INDICATOR_CALCULATIONS);
   
//---
   
   IndicatorSetString(INDICATOR_SHORTNAME, "Seasonal decomposition("+string(period_)+")");
   PlotIndexSetString(1, PLOT_LABEL, "seasonal ("+string(period_)+")");
   
   PlotIndexSetDouble(0, PLOT_EMPTY_VALUE, 0.0);
   
   ArrayInitialize(seasonal_buff, EMPTY_VALUE);
   ArrayInitialize(trend_buff, EMPTY_VALUE);
    
   return(INIT_SUCCEEDED);
  }

//+------------------------------------------------------------------+
//| Custom indicator iteration function                              |
//+------------------------------------------------------------------+
int OnCalculate(const int rates_total,
                const int prev_calculated,
                const datetime &time[],
                const double &open[],
                const double &high[],
                const double &low[],
                const double &close[],
                const long &tick_volume[],
                const long &volume[],
                const int &spread[])
  {
//---
    
    if (prev_calculated==rates_total) //not on a new bar, calculate the indicator on the opening of a new bar  
      return rates_total;
    
    ArrayInitialize(seasonal_buff, EMPTY_VALUE);
    ArrayInitialize(trend_buff, EMPTY_VALUE);

//---

    Comment("rates total: ",rates_total," bars total: ",bars_total);
    
    //if (rates_total<(int)bars_total)
    //  return rates_total;
          
    vector close_v;
    close_v.CopyRates(Symbol(), Period(), price, 0, bars_total); //closing prices
      
    seasonal_decompose_results res = seasonal_decompose(close_v, period_, multiplicative);
    
    for (int i=MathAbs(rates_total-(int)bars_total), count=0; i<rates_total; i++, count++) //calculate only the chosen number of bars
      {
         trend_buff[i] = res.trend[count];
         seasonal_buff[i] = res.seasonal[count];
      }
    
//--- return value of prev_calculated for next call
   return(rates_total);
  }

В силу особенностей расчета сезонного разложения, вычисление новых значений по мере их появления на графике может быть вычислительно затратным, поскольку мы используем все доступные на графике значения. В этом случае нам приходится ограничивать количество столбцов, используемых для расчета и построения графика.

Мне пришлось создать два отдельных индикатора: один для построения сезонных закономерностей, а другой для построения графиков остатков, используя ту же логику.

Ниже представлены графики индикаторов для Apple. 

Сезонные закономерности индикатора также можно интерпретировать как торговые сигналы или как условия перепроданности и перекупленности, как это видно на графике выше. На данный момент сложно сказать наверняка, поскольку я еще не изучал его в действии. Я рекомендую вам сделать это в качестве домашнего задания.

Заключительные мысли

Сезонное разложение — полезный метод, который стоит иметь в арсенале алгоритмической торговли. Некоторые специалисты по анализу данных используют его для создания новых признаков на основе имеющихся временных рядов, в то время как другие применяют его в анализе характера данных и последующего выбора подходящих методов машинного обучения для решения конкретной задачи. Это поднимает важный вопрос о том, когда следует использовать сезонное разложение.

Некоторые специалисты по анализу данных начинают с выполнения сезонного разложения, чтобы разделить временной ряд на его составляющие: тренд, сезонность и остаток. Если в данных наблюдается четкая сезонная закономерность, то для прогнозирования используется сезонное экспоненциальное сглаживание (также известное как сезонный метод Хольта-Винтерса). Однако, если четкой сезонной закономерности нет, или если она слабая или нерегулярная, то для выявления закономерностей во временных рядах и прогнозирования используются модели ARIMA и другие стандартные модели машинного обучения.

Приложения

Имя файла и путь	Описание и использование
Include\pandas.mqh	Состоит из класса Dataframe для хранения и обработки данных в формате, аналогичном Pandas.
Include\Seasonal Decompose.mqh	Содержит все функции и строки кода, которые позволяют реализовать сезонное разложение в MQL5.
Indicators\Seasonal Decomposition.mq5	Индикатор отображает сезонную составляющую.
Indicators\Seasonal Decomposition residuals.mq5	Индикатор отображает остаточную составляющую.
Scripts\seasonal_decompose test.mq5	Простой скрипт, используемый для реализации и отладки функции сезонного разложения и ее составляющих.
Scripts\stock market seasonal dec.mq5	Скрипт для анализа цены закрытия символа и сохранения результатов в CSV-файл для аналитических целей.
Python\seasonal_decomposition_visualization.ipynb	Jupyter Notebook для визуализации результатов сезонного разложения в CSV-файлах.
Python\stock_market seasonal dec.ipynb	Jupyter Notebook для визуализации результатов сезонного разложения акций.
Files\*.csv	CSV-файлы, содержащие результаты сезонного разложения и данные, полученные как из кода Python, так и из MQL5.