
Ensemble methods to enhance classification tasks in MQL5
Introduction
In a previous article, we explored model combination methods for numeric predictions. This article extends that exploration by focusing on ensemble techniques tailored specifically for classification tasks. Along the way we also examine strategies for utilizing component classifiers that generate class ranks on an ordinal scale. Even though numeric combination techniques can sometimes be applied to classification tasks where models rely on numeric outputs, many classifiers adopt a more rigid approach, producing only discrete class decisions. Additionally, numeric-based classifiers often exhibit prediction instability, underscoring the need for specialized combination methods.
The classification ensembles discussed in this article operate under specific assumptions about their component models. First, it is assumed that these models are trained on data with mutually exclusive and exhaustive class targets, ensuring that each instance belongs to exactly one class. When a "none of the above" option is required, it should either be treated as a separate class or managed using a numerical combination method with a defined membership threshold. Furthermore, when given an input vector of predictors, component models are expected to produce N outputs, where N represents the number of classes. These outputs may be probabilities or confidence scores that indicate the likelihood of membership for each of the classes. They could also be binary decisions, where one output is 1.0 (true) and the others are 0.0 (false), or the model outputs could be integer rankings from 1 to N, reflecting the relative likelihood of class membership.
Some of the ensemble methods we will look at benefit greatly from component classifiers that produce ranked outputs. Models capable of accurately estimating class membership probabilities are usually highly valuable, it's just that there are significant risks to treating outputs as probabilities when they are not. When there is doubt about what model outputs represent, converting them to ranks provides may be beneficial. The utility of rank information increases with the number of classes. For binary classification, ranks offer no additional insight, and their value for three-class problems remains modest. However, in scenarios involving numerous classes, the ability to interpret a model's runner-up choices becomes highly beneficial, particularly when individual predictions are fraught with uncertainty. For example, support vector machines (SVMs) could be enhanced to produce not only binary classifications but also decision boundary distances for each class, thereby offering greater insight into prediction confidence.
Ranks also address a key challenge in ensemble methods: normalizing the outputs from diverse classification models. Consider two models analyzing market movements: one specializes in short-term price fluctuations in highly liquid markets, while the other focuses on long-term trends over weeks or months. The broader focus of the second model might introduce noise into short-term predictions. Converting class decision confidences into ranks mitigates this issue, ensuring that valuable short-term insights are not overshadowed by broader trend signals. This approach leads to more balanced and effective ensemble predictions.
Alternative objectives for classifier combination
The primary goal of applying ensemble classifiers is usually to improve classification accuracy. This need not be always the case, some classification tasks can also benefit from looking beyond this specific goal. Besides basic classification accuracy, more sophisticated success measures can be implemented to address scenarios where the initial decision may be incorrect. Taking this into consideration, classification can be approached through two distinct yet complementary objectives, either of which can serve as a performance metric for class combination strategies:
- Class Set Reduction: This approach aims to identify the smallest subset of the original classes that retains a high probability of including the true class. Here, the internal ranking within the subset is secondary to ensuring that the subset is both compact and likely to contain the correct classification.
- Class Ordering: This method focuses on ranking class membership likelihoods to position the true class as close to the top as possible. Instead of using fixed rank thresholds, performance is assessed by measuring the average distance between the true class and the top-ranked position.
In certain applications, emphasizing one of these schemes over the other can provide significant advantages. Even when such a preference is not explicitly required. Selecting the most relevant objective and implementing its corresponding error measure often yields more reliable performance metrics than relying solely on classification accuracy. Also, these two objectives need not be mutually exclusive. A hybrid approach can be particularly effective: first, apply a combination method centered on class set reduction to identify a small, highly probable subset of classes. Then, use a secondary method to rank the classes within this refined subset. The highest-ranked class from this two-step process becomes the final decision, benefiting from both the efficiency of set reduction and the precision of ordered ranking. This dual-objective strategy could offer a more robust classification framework than traditional single-class prediction methods, particularly in complex scenarios where classification certainty varies widely. With that in mind we begin our exploration of ensemble classifiers.
Ensembles based on the Majority Rule
The majority rule is a simple and intuitive approach to ensemble classification, derived from the familiar concept of voting. The method involves selecting the class that receives the most votes from component models. This straightforward method offers particular value in scenarios where models can only provide discrete class selections, making it an excellent choice for systems with limited model sophistication. The formal mathematical representation of the majority rule is depicted in the equation below.
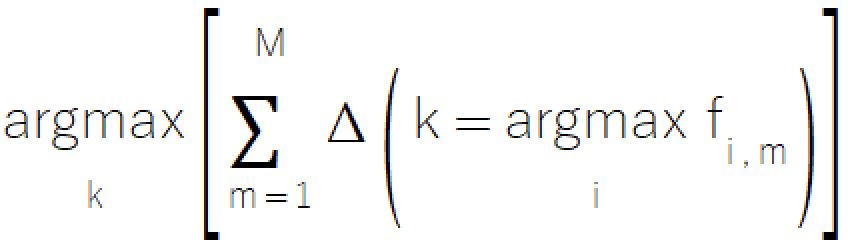
The implementation of the majority rule resides in the ensemble.mqh file, where the CMajority class manages its core functionality via the classify() method.
//+------------------------------------------------------------------+ //| Compute the winner via simple majority | //+------------------------------------------------------------------+ class CMajority { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMajority(void); ~CMajority(void); ulong classify(vector &inputs, IClassify* &models[]); };
This method takes as input a vector of predictors and an array of component models provided as IClassify pointers. The IClassify interface standardizes model manipulation in much the same way as the IModel interface described in the previous article.
//+------------------------------------------------------------------+ //| IClassify interface defining methods for manipulation of | //|classification algorithms | //+------------------------------------------------------------------+ interface IClassify { //train a model bool train(matrix &predictors,matrix&targets); //make a prediction with a trained model vector classify(vector &predictors); //get number of inputs for a model ulong getNumInputs(void); //get number of class outputs for a model ulong getNumOutputs(void); };
The classify() function returns an integer representing the selected class, ranging from zero to one less than the total number of possible classes. The returned class corresponds to the one receiving the highest number of "votes" from the component models. Implementation of the majority rule may at first seem simple enough, but there is a significant problem with its practical application. What happens when two or more classes receive an equal number of votes? In democratic settings, such a situation leads to another round of voting, but that will not work in this context. To resolve ties fairly, the method introduces small random perturbations to each class's vote count during the comparison process. This technique ensures that tied classes are given equal probabilities of selection, thus maintaining the method's integrity and avoiding bias.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMajority::classify(vector &inputs,IClassify *&models[]) { double best, sum, temp; ulong ibest; best =0; ibest = 0; CHighQualityRandStateShell state; CHighQualityRand::HQRndRandomize(state.GetInnerObj()); m_output = vector::Zeros(models[0].getNumOutputs()); for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); m_output[classification.ArgMax()] += 1.0; } sum = 0.0; for(ulong i=0 ; i<m_output.Size() ; i++) { temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state); if((i == 0) || (temp > best)) { best = temp ; ibest = i ; } sum += m_output[i] ; } if(sum>0.0) m_output/=sum; return ibest; }
Despite its utility, the majority rule presents several limitations that warrant consideration:
- The method only considers the top choice from each model, potentially discarding valuable information contained in lower rankings. While using a simple arithmetic average of class outputs might seem like a solution, this approach can introduce additional complications related to noise and scaling.
- In scenarios involving multiple classes, the simple voting mechanism may not capture the subtle relationships between different class options.
- The approach treats all component models equally, regardless of their individual performance characteristics or reliability in different contexts.
The next method we will discuss is another "vote" based system, which looks to overcome some of the drawbacks of the majority rule by employing a little more sophistication.
The Borda count method
The Borda count method calculates a score for each class by aggregating, across all models, the number of classes ranked below it in each model's assessment. This method achieves an optimal balance between utilizing and moderating the influence of lower-ranked choices, providing a more refined alternative to simpler voting mechanisms. In a system with 'm' models and 'k' classes, the scoring range is well-defined: a class consistently ranked last across all models receives a Borda count of zero, while one ranked first by all models achieves a maximum score of m(k-1).

This method represents a significant advancement over simpler voting methods, offering enhanced capability to capture and utilize the full spectrum of model predictions while maintaining computational efficiency. Although the method effectively handles ties within individual model rankings, ties in the final Borda counts across models require careful consideration. For binary classification tasks, the Borda count method is functionally equivalent to the majority rule. Therefore, its distinct advantages emerge primarily in scenarios involving three or more classes. The method's efficiency stems from its sorting-based approach, which enables streamlined processing of class outputs while maintaining accurate index associations.
Implementation of the Borda count shares structural similarities with the majority rule methodology, but incorporates additional computational efficiencies. The process is managed through the CBorda class within ensemble.mqh and operates without requiring a preliminary training phase.
//+------------------------------------------------------------------+ //| Compute the winner via Borda count | //+------------------------------------------------------------------+ class CBorda { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; long m_indices[]; public: CBorda(void); ~CBorda(void); ulong classify(vector& inputs, IClassify* &models[]); };
The classification procedure starts with the initialization of the output vector, designated to store cumulative Borda counts. Followed by the evaluation of all component models given the input vector. An array of indices is established to keep track of class relationships. The classification outputs from each model are sorted in ascending order. And finally, the Borda counts are systematically accumulated based on the sorted rankings.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CBorda::classify(vector &inputs,IClassify *&models[]) { double best=0, sum, temp; ulong ibest=0; CHighQualityRandStateShell state; CHighQualityRand::HQRndRandomize(state.GetInnerObj()); if(m_indices.Size()) ArrayFree(m_indices); m_output = vector::Zeros(models[0].getNumOutputs()); if(ArrayResize(m_indices, int(m_output.Size()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return ULONG_MAX; } for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j = 0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong k =0; k<classification.Size(); k++) m_output[m_indices[k]] += double(k); } sum = 0.0; for(ulong i=0 ; i<m_output.Size() ; i++) { temp = m_output[i] + 0.999 * CAlglib::HQRndUniformR(state); if((i == 0) || (temp > best)) { best = temp ; ibest = i ; } sum += m_output[i] ; } if(sum>0.0) m_output/=sum; return ibest; }
In the sections that follow we consider ensembles that incorporate most, if not all, the information generated by component models in making the final class decision.
Averaging Component Model Outputs
When component models generate outputs with meaningful and comparable relative values across models, incorporating these numeric measurements significantly enhances ensemble performance. While the majority rule and Borda count methods disregard substantial portions of available information, averaging component outputs provides a more comprehensive approach to data utilization. The method computes the mean output for each class across all component models. Given that the number of models remains constant, this approach is mathematically equivalent to output summation. This technique effectively treats each classification model as a numeric predictor, combining them through simple averaging methods. The final classification decision is determined by identifying the class with the highest aggregated output.
A significant distinction exists between averaging in numeric prediction tasks versus classification tasks. In numeric prediction, component models typically share a common training objective, ensuring output consistency. However, classification tasks, where only output rankings hold significance for individual models, can inadvertently produce incomparable outputs. Sometimes, this incoherence can result in the combination effectively becoming an implicit weighted average rather than a true arithmetic mean. Alternatively, individual models can have a disproportionate effect on the final sum, compromising the ensemble's effectiveness. Therefore, to maintain the integrity of the metamodel, verification of output coherence across all component models is critical.
Under the assumption that component model outputs are in fact probabilities, has led to the development of alternative combination methods, conceptually similar to averaging. One of these is the Product rule. Which swaps addition for the multiplication of model outputs. The problem is that this approach demonstrates extreme sensitivity to even minor violations of probability assumptions. A single model's significant underestimation of class probability can irreversibly penalize that class, as multiplication by near-zero values produces negligible results regardless of other factors. This heightened sensitivity renders the product rule impractical for most applications, despite its theoretical elegance. It serves primarily as a cautionary example of how mathematically sound approaches may prove problematic in practical implementations.
The Average rule implementation resides in the CAvgClass class, structurally mirroring the CMajority class framework.
//+------------------------------------------------------------------+ //| full resolution' version of majority rule. | //+------------------------------------------------------------------+ class CAvgClass { private: ulong m_outputs; ulong m_inputs; vector m_output; public: CAvgClass(void); ~CAvgClass(void); ulong classify(vector &inputs, IClassify* &models[]); };
During classification, the classify() method collects predictions from all component models and cumulates their respective outputs. The final class is based on the maximum cumulative score.
//+------------------------------------------------------------------+ //| make classification with consensus model | //+------------------------------------------------------------------+ ulong CAvgClass::classify(vector &inputs, IClassify* &models[]) { m_output=vector::Zeros(models[0].getNumOutputs()); vector model_classification; for(uint i =0 ; i<models.Size(); i++) { model_classification = models[i].classify(inputs); m_output+=model_classification; } double sum = m_output.Sum(); ulong min = m_output.ArgMax(); m_output/=sum; return min; }
The Median
Mean aggregation has the advantage of comprehensive data utilization, but that comes at the cost of sensitivity to outliers, which can compromise ensemble performance. The median presents a robust alternative that, despite a marginal reduction in information utilization, provides reliable central tendency measurements while maintaining resistance to extreme values. The median ensemble method, implemented through the CMedian class in ensemble.mqh, offers a straightforward yet effective approach to ensemble classification. This implementation addresses the challenges of managing outlier predictions and the preservation of meaningful relative ordering among classes. Outliers are dealt with, by implementing a rank-based transformation. The outputs from each component model are independently ranked, and then the mean of these ranks for each class are calculated. This approach effectively reduces the influence of extreme predictions while preserving the essential hierarchical relationship among class predictions.
The median approach enhances stability in the presence of occasional extreme predictions. It remains effective even when dealing with asymmetric or skewed prediction distributions, and strikes a balanced compromise between utilizing complete information and managing outliers robustly. When applying the median rule, practitioners should evaluate their specific use case requirements. In scenarios where occasional extreme predictions are likely or where prediction stability is paramount, the median method often provides an optimal balance between reliability and performance.
//+------------------------------------------------------------------+ //| median of predications | //+------------------------------------------------------------------+ class CMedian { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMedian(void); ~CMedian(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMedian::CMedian(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMedian::~CMedian(void) { } //+------------------------------------------------------------------+ //| consensus classification | //+------------------------------------------------------------------+ ulong CMedian::classify(vector &inputs,IClassify *&models[]) { m_out = matrix::Zeros(models[0].getNumOutputs(),models.Size()); vector model_classification; for(uint i = 0; i<models.Size(); i++) { model_classification = models[i].classify(inputs); if(!m_out.Col(model_classification,i)) { Print(__FUNCTION__, " ", __LINE__, " failed row insertion ", GetLastError()); return ULONG_MAX; } } m_output = vector::Zeros(models[0].getNumOutputs()); for(ulong i = 0; i<m_output.Size(); i++) { vector row = m_out.Row(i); if(!row.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortd(0,row.Size()-1,row); m_output[i] = row.Median(); } double sum = m_output.Sum(); ulong mx = m_output.ArgMax(); if(sum>0.0) m_output/=sum; return mx; }
MaxMax and MaxMin ensemble classifiers
Sometimes, within an ensemble of component models, individual models may have been designed to have expertise in specific subsets of the class set. When operating within their specialized domains, these models generate high-confidence outputs, while producing less meaningful moderate values for classes outside their expertise. The MaxMax rule addresses this scenario by evaluating each class based on its maximum output across all models. This approach prioritizes high-confidence predictions while disregarding potentially less informative moderate outputs. However, practitioners should note that this method proves unsuitable for scenarios where secondary outputs carry significant analytical value.
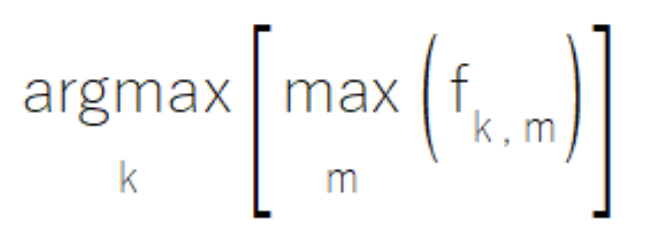
The implementation of the MaxMax rule resides in the CMaxmax class within ensemble.mqh, providing a structured framework for leveraging model specialization patterns.
//+------------------------------------------------------------------+ //|Compute the maximum of the predictions | //+------------------------------------------------------------------+ class CMaxMax { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMaxMax(void); ~CMaxMax(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMaxMax::CMaxMax(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMaxMax::~CMaxMax(void) { } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMaxMax::classify(vector &inputs,IClassify *&models[]) { double sum; ulong ibest; m_output = vector::Zeros(models[0].getNumOutputs()); for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(ulong j = 0; j<classification.Size(); j++) { if(classification[j] > m_output[j]) m_output[j] = classification[j]; } } ibest = m_output.ArgMax(); sum = m_output.Sum(); if(sum>0.0) m_output/=sum; return ibest; }
Conversely, some ensemble systems feature models that excel at excluding specific classes rather than identifying them. In these cases, when an instance belongs to a particular class, at least one model in the ensemble will generate a distinctly low output for each incorrect class, effectively eliminating them from consideration.
The MaxMin rule capitalizes on this characteristic by evaluating class membership based on the minimum output across all models for each class.
This approach, implemented in the CMaxmin class within ensemble.mqh, provides a mechanism for leveraging the exclusionary strengths of specific models.
//+------------------------------------------------------------------+ //| Compute the minimum of the predictions | //+------------------------------------------------------------------+ class CMaxMin { private: ulong m_outputs; ulong m_inputs; vector m_output; matrix m_out; public: CMaxMin(void); ~CMaxMin(void); ulong classify(vector &inputs, IClassify* &models[]); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMaxMin::CMaxMin(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMaxMin::~CMaxMin(void) { } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CMaxMin::classify(vector &inputs,IClassify *&models[]) { double sum; ulong ibest; for(uint i = 0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); if(i == 0) m_output = classification; else { for(ulong j = 0; j<classification.Size(); j++) if(classification[j] < m_output[j]) m_output[j] = classification[j]; } } ibest = m_output.ArgMax(); sum = m_output.Sum(); if(sum>0.0) m_output/=sum; return ibest; }
When implementing either the MaxMax or MaxMin approach, practitioners should carefully assess the characteristics of their model ensemble. For the MaxMax approach, it is essential to confirm that the models exhibit clear specialization patterns. It is especially important to ensure that moderate outputs represent noise rather than valuable secondary information, and lastly, ensure the ensemble provides comprehensive coverage across all relevant classes. When applying the MaxMin approach, practitioners should ensure that the ensemble collectively addresses all potential misclassification scenarios and look out for any gaps in exclusion coverage.
The Intersection Method
The intersection method represents a specialized approach to classifier combination, primarily designed for class set reduction rather than general-purpose classification. Admittedly, its direct application may be limited, it is included in this text to serve as a foundational precursor for more robust methods, particularly the union method. This approach requires component models to generate complete class rankings for each input case, from most to least likely. Many classifiers can fulfill this requirement, and the process of ranking real-valued outputs often enhances performance by effectively filtering noise while preserving valuable information. The method's training phase identifies the minimum number of top-ranked outputs each component model must retain to ensure consistent inclusion of the true class across the training set. For new cases, the combined decision comprises a minimal subset containing the true class, determined by intersecting the minimal subsets from all component models.
Consider a practical example with multiple classes and four models. Examining the five sample in the training set reveals varying rank patterns for the true class across models.
| Sample | Model 1 | Model 2 | Model 3 | Model 4 |
|---|---|---|---|---|
| 1 | 3 | 21 | 4 | 5 |
| 2 | 8 | 4 | 8 | 9 |
| 3 | 1 | 17 | 12 | 3 |
| 4 | 7 | 16 | 2 | 8 |
| 5 | 7 | 8 | 6 | 1 |
| Max | 8 | 21 | 12 | 9 |
The table shows that the true class of the second sample was ranked eighth best by the first model, fourth best by the second model, and ninth by the fourth model. The last row in the table shows the maximum ranks column-wise, which are 8, 21, 12, and 9 respectively. When evaluating unknown cases, the ensemble selects and intersects the top-ranked classes from each model according to these thresholds, producing a final subset of classes common to all sets.
The CIntersection class manages the intersection method's implementation, featuring a distinct training procedure through its fit() function. This function analyzes training data to determine worst-case rankings for each model, tracking the minimum number of top-ranked classes needed to consistently include correct classifications.
//+------------------------------------------------------------------+ //| Use intersection rule to compute minimal class set | //+------------------------------------------------------------------+ class CIntersection { private: ulong m_nout; long m_indices[]; vector m_ranks; vector m_output; public: CIntersection(void); ~CIntersection(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
Invoking the classify() method of the CIntersection class evaluates all component models sequentially on the input data. For each model, its output vector is sorted, and the indices of the sorted vector are used to compute the intersection of the classes that belong to the highest-ranked subset for each model.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool CIntersection::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Ones(m_nout); m_ranks = vector::Zeros(models.Size()); double best = 0.0; ulong nbad; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k; for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); best = classification[k]; nbad = 1; for(ulong ii = 0; ii<m_nout; ii++) { if(ii == k) continue; if(classification[ii] >= best) ++nbad; } if(nbad > ulong(m_ranks[j])) m_ranks[j] = double(nbad); } } return true; } //+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CIntersection::classify(vector &inputs,IClassify *&models[]) { for(long j =0; j<long(m_nout); j++) m_indices[j] = j; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); ArraySort(m_indices); qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j = 0; j<m_nout-ulong(m_ranks[i]); j++) { m_output[m_indices[j]] = 0.0; } } ulong n=0; double cut = 0.5; for(ulong i = 0; i<m_nout; i++) { if(m_output[i] > cut) ++n; } return n; }
Despite its theoretical elegance, the intersection method has several significant limitations. While it guarantees the inclusion of true classes from the training set, this advantage is tempered by its inherent constraints. The method may also produce empty class subsets for cases outside the training set, particularly when the top-ranked subsets lack common elements across models. Most critically, the method's reliance on worst-case performance often results in overly large class subsets, which diminishes both its effectiveness and efficiency.
The intersection method may be valuable in specific contexts where all component models perform consistently across the entire class set. However, its sensitivity to poor model performance in non-specialized areas often limits its practical utility, especially in applications that rely on specialist models for different class subsets. Ultimately, the primary value of this method lies in its conceptual contribution to more robust approaches, such as the union method, rather than its direct application in most classification tasks.
The Union Rule
The union rule represents a strategic enhancement to the intersection method, addressing its primary limitation of over-reliance on worst-case performances. This modification proves particularly valuable when combining specialist models with varying areas of expertise, shifting focus from worst-case to best-case performance scenarios. The initial process mirrors the intersection method's approach: analyzing training set cases to determine true class rankings across component models. However, the union rule diverges by identifying and tracking the best-performing model for each case, rather than monitoring worst-case performances. The method then evaluates the least favorable of these best-case performances across the training dataset. For classification of unknown cases, the system constructs a combined class subset by unifying the optimal subsets from each component model. Consider our previous dataset example, now enhanced with performance tracking columns prefixed with "Perf".
| Sample | Model 1 | Model 2 | Model 3 | Model 4 | Perf_Model 1 | Perf_Model 2 | Perf_Model 3 | Perf_Model 4 |
|---|---|---|---|---|---|---|---|---|
| 1 | 3 | 21 | 4 | 5 | 3 | 0 | 0 | 0 |
| 2 | 8 | 4 | 8 | 9 | 0 | 4 | 0 | 0 |
| 3 | 1 | 17 | 12 | 3 | 1 | 0 | 0 | 0 |
| 4 | 7 | 16 | 2 | 8 | 0 | 0 | 2 | 0 |
| 5 | 7 | 8 | 6 | 1 | 0 | 0 | 0 | 1 |
| Max | 3 | 4 | 2 | 1 |
The extra columns track instances where each model demonstrates superior performance, with the bottom row indicating the maximum values of these best-case scenarios.
The union rule offers several distinct advantages over the intersection method. It eliminates the possibility of empty subsets, as at least one model will consistently perform optimally for any given case. The method, also effectively manages specialist models by disregarding poor performance outside their areas of expertise during training, allowing the appropriate specialists to take control. Lastly, it provides a natural mechanism for identifying and potentially excluding consistently underperforming models, as indicated by columns of zeros in the tracking matrix.
The implementation of the Union method maintains significant structural similarity with the intersection method, utilizing the m_ranks container to monitor maximum values from the performance tracking columns.
//+------------------------------------------------------------------+ //| Use union rule to compute minimal class set | //+------------------------------------------------------------------+ class CUnion { private: ulong m_nout; long m_indices[]; vector m_ranks; vector m_output; public: CUnion(void); ~CUnion(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
However, key distinctions emerge in the handling of class rankings and flag initialization. During training, the system tracks minimum ranks across models for each case, updating maximum values in m_ranks when necessary.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool CUnion::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Zeros(m_nout); m_ranks = vector::Zeros(models.Size()); double best = 0.0; ulong nbad; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k, ibestrank=0, bestrank=0; for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); best = classification[k]; nbad = 1; for(ulong ii = 0; ii<m_nout; ii++) { if(ii == k) continue; if(classification[ii] >= best) ++nbad; } if(j == 0 || nbad < bestrank) { bestrank = nbad; ibestrank = j; } } if(bestrank > ulong(m_ranks[ibestrank])) m_ranks[ibestrank] = double(bestrank); } return true; }
The classification phase progressively includes classes that meet specific performance criteria.
//+------------------------------------------------------------------+ //| ensemble classification | //+------------------------------------------------------------------+ ulong CUnion::classify(vector &inputs,IClassify *&models[]) { for(long j =0; j<long(m_nout); j++) m_indices[j] = j; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); ArraySort(m_indices); qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j =(m_nout-ulong(m_ranks[i])); j<m_nout; j++) { m_output[m_indices[j]] = 1.0; } } ulong n=0; double cut = 0.5; for(ulong i = 0; i<m_nout; i++) { if(m_output[i] > cut) ++n; } return n; }
Despite the union rule's ability to effectively address many limitations of the intersection method, it retains vulnerability to outlier cases where all component models generate poor rankings. This scenario, while challenging, should remain rare in well-designed applications and can often be mitigated through proper system design and model selection. The method's effectiveness particularly shines in environments with specialist models, where each component excels in specific domains while potentially performing poorly in others. This characteristic makes it especially valuable for complex classification tasks requiring diverse expertise.
Classifier combinations based on Logistic regression
Out of all the ensemble classifiers discussed so far, the Borda count method serves as universally effective solution for combining classifiers with similar performance, it assumes uniform predictive power across all models. When performance varies significantly between models, implementing differential weights based on individual model performance may be desirable. Logistic regression provides a sophisticated framework for this weighted combination approach.
The implementation of logistic regression for classifier combination builds upon ordinary linear regression principles but addresses the specific challenges of classification. Instead of directly predicting continuous values, logistic regression calculates class membership probabilities, offering a refined approach to classification tasks. The process begins by transforming the original training data into a regression-compatible format. Consider a system with three classes and four models generating the following outputs.
| Model 1 | Model 2 | Model 3 | Model 4 | |
|---|---|---|---|---|
| 1 | 0.7 | 0.1 | 0.8 | 0.4 |
| 2 | 0.8 | 0.3 | 0.9 | 0.3 |
| 3 | 0.2 | 0.2 | 0.7 | 0.2 |
This data generates three new regression training cases for each original case, with the target variable set to 1.0 for the correct class and 0.0 for incorrect classes. The predictors utilize proportional rankings rather than raw outputs, improving numerical stability.
The CLogitReg class in ensemble.mqh manages the implementation of a weighted combination approach for classifier ensembles.
//+------------------------------------------------------------------+ //| Use logistic regression to find best class | //| This uses one common weight vector for all classes. | //+------------------------------------------------------------------+ class ClogitReg { private: ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs; matrix m_input; logistic::Clogit *m_logit; public: ClogitReg(void); ~ClogitReg(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
The fit() method constructs the regression training set by systematically processing individual cases. First, the true class membership of each training sample is determined. Then, the results from evaluating each component model are organized into the matrix m_ranks. This matrix is processed to generate the dependent and independent variables for the regression problem, which is subsequently solved using the m_logit object.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool ClogitReg::fit(matrix &inputs,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_input = matrix::Zeros(inputs.Rows(),models.Size()); m_targs = vector::Zeros(inputs.Rows()); m_output = vector::Zeros(m_nout); m_ranks = matrix::Zeros(models.Size(),m_nout); double best = 0.0; ulong nbelow; if(ArrayResize(m_indices,int(m_nout))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k; if(CheckPointer(m_logit) == POINTER_DYNAMIC) delete m_logit; m_logit = new logistic::Clogit(); for(ulong i = 0; i<inputs.Rows(); i++) { vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint j = 0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); if(!m_ranks.Row(classification,j)) { Print(__FUNCTION__, " ", __LINE__, " failed row insertion ", GetLastError()); return false; } } for(ulong j = 0; j<m_nout; j++) { for(uint jj =0; jj<models.Size(); jj++) { nbelow = 0; best = m_ranks[jj][j]; for(ulong ii =0; ii<m_nout; ii++) { if(m_ranks[jj][ii]<best) ++nbelow; } m_input[i][jj] = double(nbelow)/double(m_nout); } m_targs[i] = (j == k)? 1.0:0.0; } } return m_logit.fit(m_input,m_targs); }
This implementation represents a sophisticated approach to classifier combination, offering particular value in scenarios where component models exhibit varying levels of effectiveness across different classification tasks.
The weighted classification process builds on the Borda count methodology by integrating model-specific weights. The algorithm begins by initializing accumulation vectors and processing unknown cases through each component model. The optimal weights, computed by the m_logit object, are applied to adjust the contributions from the component classifiers. The final class is determined as the index corresponding to the largest value in m_output.
//+------------------------------------------------------------------+ //| classify with ensemble model | //+------------------------------------------------------------------+ ulong ClogitReg::classify(vector &inputs,IClassify *&models[]) { double temp; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j =0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); temp = m_logit.coeffAt(i); for(ulong j = 0 ; j<m_nout; j++) { m_output[m_indices[j]] += j * temp; } } double sum = m_output.Sum(); ulong ibest = m_output.ArgMax(); double best = m_output[ibest]; if(sum>0.0) m_output/=sum; return ibest; }
The implementation emphasizes universal weights due to their greater stability and lower risk of overfitting. However, class-specific weights remain a viable option for applications with extensive training data. A method that employs class-specific weights is discussed in a following section. For now, we divert attention to how the optimal weights are derived, specifically the logistic regression model.
Central to logistic regression is the logistic or logit transformation shown below.
This function maps an unlimited domain to the interval [0, 1]. When, x in the equation above, is extremely negative the result approaches zero. Conversely, as x becomes larger, the value of the function approaches unity. If x=0, the function returns a value exactly halfway between the two extremes. Allowing x to represent the predicted variable in the regression model, means that when x is zero, there is a 50% chance that a sample belongs to a particular class. As x increases in value from 0, the percentage of chance increases accordingly. On the other hand, as x decreases in value from 0, the percentage decreases.
An alternate way of conveying probability, are odds. This is formally referred to as the odds ratio, which is the probability of an event occurring divided by the probability of it not occurring. Expressing e^x in the logit transform, in terms of f(x) yields the following equation.
Removing the exponents in this equation by applying logs to both sides and letting x be the predicted variable of the regression problem, results in the equation depicted below.
This expression, stated in the context of classifier ensembles, stipulates that for each sample in the training set, a linear combination of predictors from component classifiers provides the log of the odds for the corresponding class label. The optimal weights, w, can be obtained using maximum likelihood estimation or by minimizing an objective function. Details of which are beyond the scope of this article.
A comprehensive implementation of logistic regression in MQL5 proved difficult to find at first. The MQL5 port of the Alglib library has dedicated tools for logistic regression but, this author has never been able to get them to compile successfully. Neither are there any examples of their use in the demo programs showcasing Alglib tools. Alas, the Alglib library was useful in the implementing the Clogit class defined in the logistic.mqh file. The file includes the definition of the CFg class which implements the CNDimensional_Grad interface.
//+------------------------------------------------------------------+ //| function and gradient calculation object | //+------------------------------------------------------------------+ class CFg:public CNDimensional_Grad { private: matrix m_preds; vector m_targs; ulong m_nclasses,m_samples,m_features; double loss_gradient(matrix &coef,double &gradients[]); void weight_intercept_raw(matrix &coef,matrix &x, matrix &wghts,vector &intcept,matrix &rpreds); void weight_intercept(matrix &coef,matrix &wghts,vector &intcept); double l2_penalty(matrix &wghts,double strenth); void sum_exp_minus_max(ulong index,matrix &rp,vector &pr); void closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &intout_2); public: //--- constructor, destructor CFg(matrix &predictors,vector &targets, ulong num_classes) { m_preds = predictors; vector classes = np::unique(targets); np::sort(classes); vector checkclasses = np::arange(classes.Size()); if(checkclasses.Compare(classes,1.e-1)) { double classv[]; np::vecAsArray(classes,classv); m_targs = targets; for(ulong i = 0; i<targets.Size(); i++) m_targs[i] = double(ArrayBsearch(classv,m_targs[i])); } else m_targs = targets; m_nclasses = num_classes; m_features = m_preds.Cols(); m_samples = m_preds.Rows(); } ~CFg(void) {} virtual void Grad(double &x[],double &func,double &grad[],CObject &obj); virtual void Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj); }; //+------------------------------------------------------------------+ //| this function is not used | //+------------------------------------------------------------------+ void CFg::Grad(double &x[],double &func,double &grad[],CObject &obj) { matrix coefficients; arrayToMatrix(x,coefficients,m_nclasses>2?m_nclasses:m_nclasses-1,m_features+1); func=loss_gradient(coefficients,grad); return; } //+------------------------------------------------------------------+ //| get function value and gradients | //+------------------------------------------------------------------+ void CFg::Grad(CRowDouble &x,double &func,CRowDouble &grad,CObject &obj) { double xarray[],garray[]; x.ToArray(xarray); Grad(xarray,func,garray,obj); grad = garray; return; } //+------------------------------------------------------------------+ //| loss gradient | //+------------------------------------------------------------------+ double CFg::loss_gradient(matrix &coef,double &gradients[]) { matrix weights; vector intercept; vector losses; matrix gradpointwise; matrix rawpredictions; matrix gradient; double loss; double l2reg; //calculate weights intercept and raw predictions weight_intercept_raw(coef,m_preds,weights,intercept,rawpredictions); gradpointwise = matrix::Zeros(m_samples,rawpredictions.Cols()); losses = vector::Zeros(m_samples); double sw_sum = double(m_samples); //loss gradient calculations if(m_nclasses>2) { double max_value, sum_exps; vector p(rawpredictions.Cols()+2); //--- for(ulong i = 0; i< m_samples; i++) { sum_exp_minus_max(i,rawpredictions,p); max_value = p[rawpredictions.Cols()]; sum_exps = p[rawpredictions.Cols()+1]; losses[i] = log(sum_exps) + max_value; //--- for(ulong k = 0; k<rawpredictions.Cols(); k++) { if(ulong(m_targs[i]) == k) losses[i] -= rawpredictions[i][k]; p[k]/=sum_exps; gradpointwise[i][k] = p[k] - double(int(ulong(m_targs[i])==k)); } } } else { for(ulong i = 0; i<m_samples; i++) { closs_grad_halfbinmial(m_targs[i],rawpredictions[i][0],losses[i],gradpointwise[i][0]); } } //--- loss = losses.Sum()/sw_sum; l2reg = 1.0 / (1.0 * sw_sum); loss += l2_penalty(weights,l2reg); gradpointwise/=sw_sum; //--- if(m_nclasses>2) { gradient = gradpointwise.Transpose().MatMul(m_preds) + l2reg*weights; gradient.Resize(gradient.Rows(),gradient.Cols()+1); vector gpsum = gradpointwise.Sum(0); gradient.Col(gpsum,m_features); } else { gradient = m_preds.Transpose().MatMul(gradpointwise) + l2reg*weights.Transpose(); gradient.Resize(gradient.Rows()+1,gradient.Cols()); vector gpsum = gradpointwise.Sum(0); gradient.Row(gpsum,m_features); } //--- matrixToArray(gradient,gradients); //--- return loss; } //+------------------------------------------------------------------+ //| weight intercept raw preds | //+------------------------------------------------------------------+ void CFg::weight_intercept_raw(matrix &coef,matrix &x,matrix &wghts,vector &intcept,matrix &rpreds) { weight_intercept(coef,wghts,intcept); matrix intceptmat = np::vectorAsRowMatrix(intcept,x.Rows()); rpreds = (x.MatMul(wghts.Transpose()))+intceptmat; } //+------------------------------------------------------------------+ //| weight intercept | //+------------------------------------------------------------------+ void CFg::weight_intercept(matrix &coef,matrix &wghts,vector &intcept) { intcept = coef.Col(m_features); wghts = np::sliceMatrixCols(coef,0,m_features); } //+------------------------------------------------------------------+ //| sum exp minus max | //+------------------------------------------------------------------+ void CFg::sum_exp_minus_max(ulong index,matrix &rp,vector &pr) { double mv = rp[index][0]; double s_exps = 0.0; for(ulong k = 1; k<rp.Cols(); k++) { if(mv<rp[index][k]) mv=rp[index][k]; } for(ulong k = 0; k<rp.Cols(); k++) { pr[k] = exp(rp[index][k] - mv); s_exps += pr[k]; } pr[rp.Cols()] = mv; pr[rp.Cols()+1] = s_exps; } //+------------------------------------------------------------------+ //| l2 penalty | //+------------------------------------------------------------------+ double CFg::l2_penalty(matrix &wghts,double strenth) { double norm2_v; if(wghts.Rows()==1) { matrix nmat = (wghts).MatMul(wghts.Transpose()); norm2_v = nmat[0][0]; } else norm2_v = wghts.Norm(MATRIX_NORM_FROBENIUS); return 0.5*strenth*norm2_v; } //+------------------------------------------------------------------+ //| closs_grad_half_binomial | //+------------------------------------------------------------------+ void CFg::closs_grad_halfbinmial(double y_true,double raw, double &inout_1,double &inout_2) { if(raw <= -37.0) { inout_2 = exp(raw); inout_1 = inout_2 - y_true * raw; inout_2 -= y_true; } else if(raw <= -2.0) { inout_2 = exp(raw); inout_1 = log1p(inout_2) - y_true * raw; inout_2 = ((1.0 - y_true) * inout_2 - y_true) / (1.0 + inout_2); } else if(raw <= 18.0) { inout_2 = exp(-raw); // log1p(exp(x)) = log(1 + exp(x)) = x + log1p(exp(-x)) inout_1 = log1p(inout_2) + (1.0 - y_true) * raw; inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2); } else { inout_2 = exp(-raw); inout_1 = inout_2 + (1.0 - y_true) * raw; inout_2 = ((1.0 - y_true) - y_true * inout_2) / (1.0 + inout_2); } }
This is needed by the LBFGS function minimization procedure. Clogit has familiar methods for training and inference.
//+------------------------------------------------------------------+ //| logistic regression implementation | //+------------------------------------------------------------------+ class Clogit { public: Clogit(void); ~Clogit(void); bool fit(matrix &predictors, vector &targets); double predict(vector &preds); vector proba(vector &preds); matrix probas(matrix &preds); double coeffAt(ulong index); private: ulong m_nsamples; ulong m_nfeatures; bool m_trained; matrix m_train_preds; vector m_train_targs; matrix m_coefs; vector m_bias; vector m_classes; double m_xin[]; CFg *m_gradfunc; CObject m_dummy; vector predictProba(double &in); }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ Clogit::Clogit(void) { } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ Clogit::~Clogit(void) { if(CheckPointer(m_gradfunc) == POINTER_DYNAMIC) delete m_gradfunc; } //+------------------------------------------------------------------+ //| fit a model to a dataset | //+------------------------------------------------------------------+ bool Clogit::fit(matrix &predictors, vector &targets) { m_trained = false; m_classes = np::unique(targets); np::sort(m_classes); if(predictors.Rows()!=targets.Size() || m_classes.Size()<2) { Print(__FUNCTION__," ",__LINE__," invalid inputs "); return m_trained; } m_train_preds = predictors; m_train_targs = targets; m_nfeatures = m_train_preds.Cols(); m_nsamples = m_train_preds.Rows(); m_coefs = matrix::Zeros(m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1); matrixToArray(m_coefs,m_xin); m_gradfunc = new CFg(m_train_preds,m_train_targs,m_classes.Size()); //--- CMinLBFGSStateShell state; CMinLBFGSReportShell rep; CNDimensional_Rep frep; //--- CAlglib::MinLBFGSCreate(m_xin.Size(),m_xin.Size()>=5?5:m_xin.Size(),m_xin,state); //--- CAlglib::MinLBFGSOptimize(state,m_gradfunc,frep,true,m_dummy); //--- CAlglib::MinLBFGSResults(state,m_xin,rep); //--- if(rep.GetTerminationType()>0) { m_trained = true; arrayToMatrix(m_xin,m_coefs,m_classes.Size()>2?m_classes.Size():m_classes.Size()-1,m_nfeatures+1); m_bias = m_coefs.Col(m_nfeatures); m_coefs = np::sliceMatrixCols(m_coefs,0,m_nfeatures); } else Print(__FUNCTION__," ", __LINE__, " failed to train the model ", rep.GetTerminationType()); delete m_gradfunc; return m_trained; } //+------------------------------------------------------------------+ //| get probability for single sample | //+------------------------------------------------------------------+ vector Clogit::proba(vector &preds) { vector predicted; if(!m_trained) { Print(__FUNCTION__," ", __LINE__," no trained model available "); predicted.Fill(EMPTY_VALUE); return predicted; } predicted = ((preds.MatMul(m_coefs.Transpose()))); predicted += m_bias; if(predicted.Size()>1) { if(!predicted.Activation(predicted,AF_SOFTMAX)) { Print(__FUNCTION__," ", __LINE__," errror ", GetLastError()); predicted.Fill(EMPTY_VALUE); return predicted; } } else { predicted = predictProba(predicted[0]); } return predicted; } //+------------------------------------------------------------------+ //| get probability for binary classification | //+------------------------------------------------------------------+ vector Clogit::predictProba(double &in) { vector out(2); double n = 1.0/(1.0+exp(-1.0*in)); out[0] = 1.0 - n; out[1] = n; return out; } //+------------------------------------------------------------------+ //| get probabilities for multiple samples | //+------------------------------------------------------------------+ matrix Clogit::probas(matrix &preds) { matrix output(preds.Rows(),m_classes.Size()); vector rowin,rowout; for(ulong i = 0; i<preds.Rows(); i++) { rowin = preds.Row(i); rowout = proba(rowin); if(rowout.Max() == EMPTY_VALUE || !output.Row(rowout,i)) { Print(__LINE__," probas error ", GetLastError()); output.Fill(EMPTY_VALUE); break; } } return output; } //+------------------------------------------------------------------+ //| get probability for single sample | //+------------------------------------------------------------------+ double Clogit::predict(vector &preds) { vector prob = proba(preds); if(prob.Max() == EMPTY_VALUE) { Print(__LINE__," predict error "); return EMPTY_VALUE; } return m_classes[prob.ArgMax()]; } //+------------------------------------------------------------------+ //| get model coefficient at specific index | //+------------------------------------------------------------------+ double Clogit::coeffAt(ulong index) { if(index<(m_coefs.Rows())) { return (m_coefs.Row(index)).Sum(); } else { return 0.0; } } } //+------------------------------------------------------------------+
Ensemble combinations based on Logistic regression with class-specific weights
The single-weight-set approach described in the previous section offers stability and effectiveness, but it is limited in that it may not fully capitalize on model specialization. If individual models demonstrate superior performance for specific classes, whether by design or natural development, implementing separate weight sets for each class can leverage these specialized capabilities more effectively. The transition to class-specific weight sets introduces significant complexity to the optimization process. Rather than optimizing a single set of weights, the ensemble must manage K sets (one per class), each containing M parameters, yielding a total of K*M parameters. This increase in parameters demands careful consideration of data requirements and implementation risks.
A robust application of separate weight sets requires substantial training data to maintain statistical validity. As a general guideline, each class should have at least ten times as many training cases as there are models. Even with sufficient data, this approach should be implemented cautiously and only when clear evidence suggests significant model specialization across classes.
The CLogitRegSep class manages the implementation of separate weight sets, differing from CLogitReg in its allocation of individual Clogit objects for each class. The training process distributes regression cases across class-specific training sets instead of consolidating them into a single set.
//+------------------------------------------------------------------+ //| Use logistic regression to find best class. | //| This uses separate weight vectors for each class. | //+------------------------------------------------------------------+ class ClogitRegSep { private: ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs[]; matrix m_input[]; logistic::Clogit *m_logit[]; public: ClogitRegSep(void); ~ClogitRegSep(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[]); vector proba(void) { return m_output;} };
The classification of unknown cases follows a similar process to the single-weight approach, with one key difference: class-specific weights are applied during the Borda count computation. This specialization enables the system to leverage class-specific model expertise more effectively.
//+------------------------------------------------------------------+ //| classify with ensemble model | //+------------------------------------------------------------------+ ulong ClogitRegSep::classify(vector &inputs,IClassify *&models[]) { double temp; for(uint i =0; i<models.Size(); i++) { vector classification = models[i].classify(inputs); for(long j =0; j<long(classification.Size()); j++) m_indices[j] = j; if(!classification.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,classification.Size()-1,classification,m_indices); for(ulong j = 0 ; j<m_nout; j++) { temp = m_logit[j].coeffAt(i); m_output[m_indices[j]] += j * temp; } } double sum = m_output.Sum(); ulong ibest = m_output.ArgMax(); double best = m_output[ibest]; if(sum>0.0) m_output/=sum; return ibest; }
The implementation of separate weight sets necessitates rigorous validation procedures. Practitioners should monitor weight distributions for unexplained extreme values, ensuring that weight disparities align with known model characteristics. Safeguards must be implemented to prevent regression process instabilities. All of which can be effectively applied by maintaining comprehensive testing protocols.
The successful implementation of class-specific weight sets relies on careful attention to several critical factors: ensuring sufficient training data for each class, verifying that specialization patterns justify separate weights, monitoring weight stability, and confirming improved classification accuracy over single-weight approaches. While this advanced implementation of logistic regression offers enhanced classification capabilities, it requires careful management to address the increased complexity and potential risks.
Ensembles leveraging local accuracy
To further leverage the strengths of individual models, we can consider their local accuracy within the predictor space. Sometimes component classifiers demonstrate superior performance within specific regions of the predictor space. This specialization manifests when models excel under particular predictor variable conditions - for example, one model might perform optimally with lower variable values while another excels with higher values. Such specialization patterns, whether intentionally designed or naturally emerging, can significantly enhance classification accuracy when properly utilized.
The implementation follows a straightforward yet effective approach. When evaluating an unknown case, the system collects classifications from all component models and selects the model deemed most reliable for that specific case. The ensemble evaluates a model's reliability, by employing a method proposed in the paper, "Combination of multiple classifiers using local accuracy estimates", authored by Woods, Kegelmeyer, and Bowyer. This approach operates through several defined steps:
- Calculate the Euclidean distances between the unknown case and all training cases.
- Identify a predefined number of nearest training cases for comparative analysis.
- Evaluate each model's performance specifically on these nearby cases, focusing on instances where the model assigns the same classification as it did for the unknown case.
- Compute a performance criterion based on the proportion of correct classifications among the cases where the model predicted the same class for the unknown case and its neighbors.
Consider a scenario analyzing ten nearest neighbors. Upon identifying these neighbors through Euclidean distance calculations, the ensemble presents an unknown case to a model, which assigns it to class 3. The system then evaluates this model's performance on the ten nearby training cases. If the model classifies six of these cases as class 3, with four of these classifications being correct, the model achieves a performance criterion of 0.67 (4/6). This evaluation process continues across all component models, with the highest-scoring model ultimately determining the final classification. This approach ensures that classification decisions leverage the most reliable model for each specific case context.
To address ties, we select the model with the highest certainty, calculated as the ratio of its maximum output to the sum of all outputs. Determining the size of this local subset is necessary, since smaller subsets are more sensitive to local variations, while larger subsets are more robust but may reduce the "local" nature of the evaluation. Cross-validation can help determine the optimal subset size, with smaller sizes typically prioritized for efficiency in case of ties. By applying this approach, the ensemble effectively utilizes domain-specific model expertise, whilst maintaining computational efficiency. The method allows the ensemble to adapt dynamically to varying regions of the predictor space, and the reliability measure can be leveraged to provide a transparent metric for model selection.
The ClocalAcc class in ensemble.mqh is designed to determine the most likely class from an ensemble of classifiers based on local accuracy.
//+------------------------------------------------------------------+ //| Use local accuracy to choose the best model | //+------------------------------------------------------------------+ class ClocalAcc { private: ulong m_knn; ulong m_nout; long m_indices[]; matrix m_ranks; vector m_output; vector m_targs; matrix m_input; vector m_dist; matrix m_trnx; matrix m_trncls; vector m_trntrue; ulong m_classprep; bool m_crossvalidate; public: ClocalAcc(void); ~ClocalAcc(void); ulong classify(vector &inputs, IClassify* &models[]); bool fit(matrix &inputs, matrix &targets, IClassify* &models[], bool crossvalidate = false); vector proba(void) { return m_output;} };
The fit() method trains the ClocalAcc object. It takes the input data (inputs), target values (targets), an array of classifier models (models), and an optional flag for cross-validation (crossvalidate). During training, fit() calculates the distance between each input data point and all other data points. It then determines the k nearest neighbors for each point, where k is determined through cross-validation if crossvalidate is set to true. For each neighbor, the method evaluates the performance of each classifier in the ensemble.
//+------------------------------------------------------------------+ //| fit an ensemble model | //+------------------------------------------------------------------+ bool ClocalAcc::fit(matrix &inputs,matrix &targets,IClassify *&models[], bool crossvalidate = false) { m_crossvalidate = crossvalidate; m_nout = targets.Cols(); m_input = matrix::Zeros(inputs.Rows(),models.Size()); m_targs = vector::Zeros(inputs.Rows()); m_output = vector::Zeros(m_nout); m_ranks = matrix::Zeros(models.Size(),m_nout); m_dist = vector::Zeros(inputs.Rows()); m_trnx = matrix::Zeros(inputs.Rows(),inputs.Cols()); m_trncls = matrix::Zeros(inputs.Rows(),models.Size()); m_trntrue = vector::Zeros(inputs.Rows()); double best = 0.0; if(ArrayResize(m_indices,int(inputs.Rows()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k, knn_min,knn_max,knn_best=0,true_class, ibest=0; for(ulong i = 0; i<inputs.Rows(); i++) { np::matrixCopyRows(m_trnx,inputs,i,i+1,1); vector trow = targets.Row(i); vector inrow = inputs.Row(i); k = trow.ArgMax(); best = trow[k]; m_trntrue[i] = double(k); for(uint j=0; j<models.Size(); j++) { vector classification = models[j].classify(inrow); ibest = classification.ArgMax(); best = classification[ibest]; m_trncls[i][j] = double(ibest); } } m_classprep = 1; if(!m_crossvalidate) { m_knn=3; return true; } else { ulong ncases = inputs.Rows(); if(inputs.Rows()<20) { m_knn=3; return true; } knn_min = 3; knn_max = 10; vector testcase(inputs.Cols()) ; vector clswork(m_nout) ; vector knn_counts(knn_max - knn_min + 1) ; for(ulong i = knn_min; i<=knn_max; i++) knn_counts[i-knn_min] = 0; --ncases; for(ulong i = 0; i<=ncases; i++) { testcase = m_trnx.Row(i); true_class = ulong(m_trntrue[i]); if(i<ncases) { if(!m_trnx.SwapRows(ncases,i)) { Print(__FUNCTION__, " ", __LINE__, " failed row swap ", GetLastError()); return false; } m_trntrue[i] = m_trntrue[ncases]; double temp; for(uint j = 0; j<models.Size(); j++) { temp = m_trncls[i][j]; m_trncls[i][j] = m_trncls[ncases][j]; m_trncls[ncases][j] = temp; } } m_classprep = 1; for(ulong knn = knn_min; knn<knn_max; knn++) { ulong iclass = classify(testcase,models); if(iclass == true_class) { ++knn_counts[knn-knn_min]; } m_classprep=0; } if(i<ncases) { if(!m_trnx.SwapRows(i,ncases) || !m_trnx.Row(testcase,i)) { Print(__FUNCTION__, " ", __LINE__, " error ", GetLastError()); return false; } m_trntrue[ncases] = m_trntrue[i]; m_trntrue[i] = double(true_class); double temp; for(uint j = 0; j<models.Size(); j++) { temp = m_trncls[i][j]; m_trncls[i][j] = m_trncls[ncases][j]; m_trncls[ncases][j] = temp; } } } ++ncases; for(ulong knn = knn_min; knn<=knn_max; knn++) { if((knn==knn_min) || (ulong(knn_counts[knn-knn_min])>ibest)) { ibest = ulong(knn_counts[knn-knn_min]); knn_best = knn; } } m_knn = knn_best; m_classprep = 1; } return true; }
The classify() method predicts the class label for a given input vector. It calculates the distances between the input vector and all training data points and identifies the k nearest neighbors. For each classifier in the ensemble, it determines the accuracy of the classifier on these neighbors. The classifier with the highest accuracy on the nearest neighbors is selected, and its predicted class label is returned.
//+------------------------------------------------------------------+ //| classify with an ensemble model | //+------------------------------------------------------------------+ ulong ClocalAcc::classify(vector &inputs,IClassify *&models[]) { double dist=0, diff=0, best=0, crit=0, bestcrit=0, conf=0, bestconf=0, sum ; ulong k, ibest, numer, denom, bestmodel=0, bestchoice=0 ; if(m_classprep) { for(ulong i = 0; i<m_input.Rows(); i++) { m_indices[i] = long(i); dist = 0.0; for(ulong j = 0; j<m_trnx.Cols(); j++) { diff = inputs[j] - m_trnx[i][j]; dist+= diff*diff; } m_dist[i] = dist; } if(!m_dist.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0, m_dist.Size()-1, m_dist,m_indices); } for(uint i = 0; i<models.Size(); i++) { vector vec = models[i].classify(inputs); sum = vec.Sum(); ibest = vec.ArgMax(); best = vec[ibest]; conf = best/sum; denom = numer = 0; for(ulong ii = 0; ii<m_knn; ii++) { k = m_indices[ii]; if(ulong(m_trncls[k][i]) == ibest) { ++denom; if(ibest == ulong(m_trntrue[k])) ++numer; } } if(denom > 0) crit = double(numer)/double(denom); else crit = 0.0; if((i == 0) || (crit > bestcrit)) { bestcrit = crit; bestmodel = ulong(i); bestchoice = ibest; bestconf = conf; m_output = vec; } else if(fabs(crit-bestcrit)<1.e-10) { if(conf > bestconf) { bestcrit= crit; bestmodel = ulong(i); bestchoice = ibest; bestconf = conf; m_output = vec; } } } sum = m_output.Sum(); if(sum>0) m_output/=sum; return bestchoice; }
Ensembles combined using the Fuzzy integral
Fuzzy logic is a mathematical framework that deals with degrees of truth rather than absolute true or false values. In the context of classifier combination, fuzzy logic can be used to integrate the outputs of multiple models, considering the reliability of each model. The fuzzy integral, originally proposed by Sugeno (1977), involves a fuzzy measure that assigns values to subsets of a universe. This measure satisfies certain properties, including boundary conditions, monotonicity, and continuity. Sugeno extended this concept with the λ fuzzy measure, which incorporates an additional factor for combining the measures of disjoint sets.
The fuzzy integral itself is calculated using a specific formula involving the membership function and the fuzzy measure. While a brute-force computation is possible, a more efficient method exists for finite sets, involving a recursive calculation. The value of λ is determined by ensuring that the final measure equals one. In the context of classifier combination, the fuzzy integral can be applied by treating each classifier as an element of the universe, with its reliability as its membership value. The fuzzy integral is then calculated for each class, and the class with the highest integral is selected. This method effectively combines the outputs of multiple classifiers, considering their individual reliabilities.
The CFuzzyInt class implements the fuzzy integral method for combining classifiers.
//+------------------------------------------------------------------+ //| Use fuzzy integral to combine decisions | //+------------------------------------------------------------------+ class CFuzzyInt { private: ulong m_nout; vector m_output; long m_indices[]; matrix m_sort; vector m_g; double m_lambda; double recurse(double x); public: CFuzzyInt(void); ~CFuzzyInt(void); bool fit(matrix &predictors, matrix &targets, IClassify* &models[]); ulong classify(vector &inputs, IClassify* &models[]); vector proba(void) { return m_output;} };
The core of this method lies in the recurse() function, which iteratively calculates the fuzzy measure. The key parameter, λ, is determined by finding the value that ensures the fuzzy measure of all models converges to one. We start with an initial value and gradually adjust it until the fuzzy measure of all models converges to one. This typically involves bracketing the correct λ value and then refining the search using a bisection method.
//+------------------------------------------------------------------+ //| recurse | //+------------------------------------------------------------------+ double CFuzzyInt::recurse(double x) { double val ; val = m_g[0] ; for(ulong i=1 ; i<m_g.Size() ; i++) val += m_g[i] + x * m_g[i] * val ; return val - 1.0 ; }
To estimate the reliability of each model, we evaluate its accuracy on the training set. We then adjust this accuracy by subtracting the expected accuracy from random guessing and rescaling the result to a value between zero and one. There are more sophisticated ways to estimate model reliability, this approach is preferred because of its simplicity.
//+------------------------------------------------------------------+ //| fit ensemble model | //+------------------------------------------------------------------+ bool CFuzzyInt::fit(matrix &predictors,matrix &targets,IClassify *&models[]) { m_nout = targets.Cols(); m_output = vector::Zeros(m_nout); m_sort = matrix::Zeros(models.Size(), m_nout); m_g = vector::Zeros(models.Size()); if(ArrayResize(m_indices,int(models.Size()))<0) { Print(__FUNCTION__, " ", __LINE__, " array resize error ", GetLastError()); return false; } ulong k=0, iclass =0 ; double best=0, xlo=0, xhi=0, y=0, ylo=0, yhi=0, step=0 ; for(ulong i = 0; i<predictors.Rows(); i++) { vector trow = targets.Row(i); vector inrow = predictors.Row(i); k = trow.ArgMax(); best = trow[k]; for(uint ii = 0; ii< models.Size(); ii++) { vector vec = models[ii].classify(inrow); iclass = vec.ArgMax(); best = vec[iclass]; if(iclass == k) m_g[ii] += 1.0; } } for(uint i = 0; i<models.Size(); i++) { m_g[i] /= double(predictors.Rows()) ; m_g[i] = (m_g[i] - 1.0 / m_nout) / (1.0 - 1.0 / m_nout) ; if(m_g[i] > 1.0) m_g[i] = 1.0 ; if(m_g[i] < 0.0) m_g[i] = 0.0 ; } xlo = m_lambda = -1.0 ; ylo = recurse(xlo) ; if(ylo >= 0.0) // Theoretically should never exceed zero return true; // But allow for pathological numerical problems step = 1.0 ; for(;;) { xhi = xlo + step ; yhi = recurse(xhi) ; if(yhi >= 0.0) // If we have just bracketed the root break ; // We can quit the search if(xhi > 1.e5) // In the unlikely case of extremely poor models { m_lambda = xhi ; // Fudge a value return true ; // And quit } step *= 2.0 ; // Keep increasing the step size to avoid many tries xlo = xhi ; // Move onward ylo = yhi ; } for(;;) { m_lambda = 0.5 * (xlo + xhi) ; y = recurse(m_lambda) ; // Evaluate the function here if(fabs(y) < 1.e-8) // Primary convergence criterion break ; if(xhi - xlo < 1.e-10 * (m_lambda + 1.1)) // Backup criterion break ; if(y > 0.0) { xhi = m_lambda ; yhi = y ; } else { xlo = m_lambda ; ylo = y ; } } return true; }
During classification, the class with the highest fuzzy integral is selected. The fuzzy integral for each class is computed by iteratively comparing the model's output with the recursively calculated fuzzy measure and selecting the minimum value at each step. The final fuzzy integral for a class represents the combined confidence of the models in that class.
//+------------------------------------------------------------------+ //| classify with ensemble | //+------------------------------------------------------------------+ ulong CFuzzyInt::classify(vector &inputs,IClassify *&models[]) { ulong k, iclass; double sum, gsum, minval, maxmin, best ; for(uint i = 0; i<models.Size(); i++) { vector vec = models[i].classify(inputs); sum = vec.Sum(); vec/=sum; if(!m_sort.Row(vec,i)) { Print(__FUNCTION__, " ", __LINE__, " row insertion error ", GetLastError()); return false; } } for(ulong i = 0; i<m_nout; i++) { for(uint ii =0; ii<models.Size(); ii++) m_indices[ii] = long(ii); vector vec = m_sort.Col(i); if(!vec.Size()) { Print(__FUNCTION__," ", __LINE__," empty vector "); return ULONG_MAX; } qsortdsi(0,long(vec.Size()-1), vec, m_indices); maxmin = gsum = 0.0; for(int j = int(models.Size()-1); j>=0; j--) { k = m_indices[j]; if(k>=vec.Size()) { Print(__FUNCTION__," ",__LINE__, " out of range ", k); } gsum += m_g[k] + m_lambda * m_g[k] * gsum; if(gsum<vec[k]) minval = gsum; else minval = vec[k]; if(minval > maxmin) maxmin = minval; } m_output[i] = maxmin; } iclass = m_output.ArgMax(); best = m_output[iclass]; return iclass; }
Pairwise Coupling
Pairwise coupling is a unique approach to multi-class classification that leverages the power of specialized binary classifiers. It combines a set of K(K−1)/2 binary classifiers (where, K is the number of classes), each designed to distinguish between a specific pair of classes. Imagine we have a dataset consisting of targets with 3 classes. To compare them, we create a set of 3*(3-1)/2 = 3 models. Each model is designed to decide between only two classes. If the classes were designated, the identifiers (A, B, and C). The 3 models would be configured as follows:
- Model 1: Decides between Class A and Class B.
- Model 2: Decides between Class A and Class C.
- Model 3: Decides between Class B and Class C.
The training data would have to be partitioned to include the samples relevant to each model's classification task. Evaluation of these models would result in a set of probabilities that could be arranged in a K by K matrix. Below is a hypothetical example of such a matrix.
| A | B | C | |
| A | ---- | 0.2 | 0.7 |
| B | 0.8 | ---- | 0.4 |
| C | 0.3 | 0.6 | ---- |
In this matrix, the model that discriminates between Classes A and B assigns a probability of 0.2 that the sample belongs to Class A. The upper-right diagonal elements of the matrix depict the complete set of probabilities calculated to decide between the paired classes, as the matrix is symmetric. Given the model outputs, the goal is to calculate an estimation of the probability that an out-of-sample case belongs to a particular class. This means we need to find a set of probabilities whose distribution corresponds with that of the observed pairwise probabilities or at the very least, matches them as closely as possible. An iterative approach is employed to refine these initial probability estimates, without having to use a function minimization procedure.
This iterative process gradually refines the initial class probability estimates, ensuring that they align better with the pairwise predictions from the individual classifiers. In essence, it is like gradually refining a map until it accurately reflects the real world. We start with a rough sketch and then make small adjustments based on new information until we have a highly accurate map. This iterative approach is efficient and generally converges quickly to a solution.
The CPairWise class implements the pairwise coupling algorithm.
//+------------------------------------------------------------------+ //| Use pairwise coupling to combine decisions | //+------------------------------------------------------------------+ class CPairWise { private: ulong m_nout; ulong m_npairs; vector m_output; vector m_rij; vector m_uij; public: CPairWise(void); ~CPairWise(void); ulong classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]); vector proba(void) { return m_output;} };
The core computation is done within the classify() method, which follows a structured process for computing the class probabilities from the outputs of the pairwise classifiers. The method begins by evaluating all pairwise models for a given test case. Each model corresponds to a specific pair of classes and generates an output that represents the likelihood that the test case belongs to one of the two classes in the pair.
//+------------------------------------------------------------------+ //| classify using ensemble model | //+------------------------------------------------------------------+ ulong CPairWise::classify(ulong numclasses,vector &inputs,IClassify *&models[],ulong &samplesPerModel[]) { m_nout=numclasses; m_npairs = m_nout*(m_nout-1)/2; m_output = vector::Zeros(m_nout); m_rij = vector::Zeros(m_npairs); m_uij = vector::Zeros(m_npairs); long k; ulong iclass=0 ; double rr, best=0, numer, denom, sum, delta, oldval ; for(ulong i = 0; i<m_npairs; i++) { vector vec = models[i].classify(inputs); rr = vec[0]; if(vec[0]> 0.999999) vec[0] = 0.999999 ; if(vec[0] < 0.000001) vec[0] = 0.000001 ; m_rij[i] = vec[0] ; } k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) { rr = m_rij[k++] ; m_output[i] += rr ; m_output[j] += 1.0 - rr ; } } for(ulong i=0 ; i<m_nout ; i++) m_output[i] /= double(m_npairs) ; k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ; } for(int iter=0 ; iter<10000 ; iter++) { delta = 0.0 ; for(ulong i=0 ; i<m_nout ; i++) { numer = denom = 0.0 ; for(ulong j=0 ; j<m_nout ; j++) { if(i < j) { k = (long(i) * (2 * long(m_nout) - long(i) - 3) - 2) / 2 + long(j) ; numer += samplesPerModel[k] * m_rij[k] ; denom += samplesPerModel[k] * m_uij[k] ; } else if(i > j) { k = (long(j) * (2 * long(m_nout) - long(j) - 3) - 2) / 2 + long(i) ; //Print(__FUNCTION__," ",__LINE__," k ", k); numer += samplesPerModel[k] * (1.0 - m_rij[k]) ; denom += samplesPerModel[k] * (1.0 - m_uij[k]) ; } } oldval = m_output[i] ; m_output[i] *= numer / denom ; sum = 0.0 ; for(ulong j=0 ; j<m_nout ; j++) sum += m_output[j] ; for(ulong j=0 ; j<m_nout ; j++) m_output[j] /= sum ; if(fabs(m_output[i]-oldval) > delta) delta = fabs(m_output[i]-oldval) ; k = 0 ; for(ulong i=0 ; i<m_nout-1 ; i++) { for(ulong j=i+1 ; j<m_nout ; j++) m_uij[k++] = m_output[i] / (m_output[i] + m_output[j]) ; } } if(delta < 1.e-6) break ; } return m_output.ArgMax() ; }
Once the initial outputs (probabilities) are obtained, they are used as starting estimates for the class probabilities. The method then iteratively refines these estimates to improve accuracy. After refining the class probabilities, the final step is to identify the class with the greatest probability. The class with the highest probability is considered the most likely class for the given test case, and its index is returned as the output of the classify() method.
Conclusion: Comparing Combination Methods
The ClassificationEnsemble_Demo.mq5 script is designed to compare the performance of the ensemble algorithms discussed in this article across various scenarios. By running multiple Monte Carlo replications, the script enables the evaluation of each ensemble method's performance under different conditions. The script allows users to specify the number of training samples used in each run, enabling testing across datasets of varying sizes, from small to large. The number of classes can be adjusted to test the scalability of the ensemble methods as the problem's complexity increases. The number of base classifiers (models) used in the ensemble can be varied to evaluate how the algorithms perform with different levels of complexity.
Users can specify the number of Monte Carlo replications for each scenario to assess the stability and consistency of the ensemble algorithms. The out-of-sample probability of misclassification is used as the performance metric, ensuring that the models are evaluated on unseen data to simulate real-world classification tasks. If four or more models are employed, one model is deliberately made useless (e.g., by having it make random predictions or produce constant outputs). This tests the robustness of the ensemble algorithms, evaluating how well they handle the inclusion of irrelevant or non-informative models.
If five or more models are used, the fifth model is set up to occasionally produce extreme or erratic predictions, simulating a real-world scenario where a model might be unstable or noisy. This feature evaluates how the ensemble methods handle unreliable models and whether they can maintain good classification performance by properly weighting or down-weighting problematic models. The classification difficulty factor defines the spread between classes, which controls the difficulty of the problem for the component models. A larger spread makes classes easier to distinguish, while a smaller spread increases the difficulty. This allows testing how well the ensemble methods perform under varying levels of difficulty, assessing their ability to maintain accuracy in challenging scenarios.
//+------------------------------------------------------------------+ //| ClassificationEnsemble_Demo.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<ensemble.mqh> #include<multilayerperceptron.mqh> //--- input parameters input int NumSamples=10; input int NumClasses=3; input int NumModels=3; input int NumReplications=1000; input double ClassificationDifficultyFactor=0.0; //+------------------------------------------------------------------+ //| normal(rngstate) | //+------------------------------------------------------------------+ double normal(CHighQualityRandStateShell &state) { return CAlglib::HQRndNormal(state); } //+------------------------------------------------------------------+ //| unifrand(rngstate) | //+------------------------------------------------------------------+ double unifrand(CHighQualityRandStateShell &state) { return CAlglib::HQRndUniformR(state); } //+------------------------------------------------------------------+ //|Multilayer perceptron | //+------------------------------------------------------------------+ class CMLPC:public ensemble::IClassify { private: CMlp *m_mlfn; double m_learningrate; double m_tolerance; double m_alfa; double m_beyta; uint m_epochs; ulong m_in,m_out; ulong m_hl1,m_hl2; public: CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2); ~CMLPC(void); void setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs); bool train(matrix &predictors,matrix&targets); vector classify(vector &predictors); ulong getNumInputs(void) { return m_in;} ulong getNumOutputs(void) { return m_out;} }; //+------------------------------------------------------------------+ //| constructor | //+------------------------------------------------------------------+ CMLPC::CMLPC(ulong ins, ulong outs,ulong numhl1,ulong numhl2) { m_in = ins; m_out = outs; m_alfa = 0.3; m_beyta = 0.01; m_learningrate=0.001; m_tolerance=1.e-8; m_epochs= 1000; m_hl1 = numhl1; m_hl2 = numhl2; m_mlfn = new CMlp(); } //+------------------------------------------------------------------+ //| destructor | //+------------------------------------------------------------------+ CMLPC::~CMLPC(void) { if(CheckPointer(m_mlfn) == POINTER_DYNAMIC) delete m_mlfn; } //+------------------------------------------------------------------+ //| set other hyperparameters of the i_model | //+------------------------------------------------------------------+ void CMLPC::setParams(double alpha_, double beta_,double learning_rate, double tolerance, uint num_epochs) { m_alfa = alpha_; m_beyta = beta_; m_learningrate=learning_rate; m_tolerance=tolerance; m_epochs= num_epochs; } //+------------------------------------------------------------------+ //| fit a i_model to the data | //+------------------------------------------------------------------+ bool CMLPC::train(matrix &predictors,matrix &targets) { if(m_in != predictors.Cols() || m_out != targets.Cols()) { Print(__FUNCTION__, " failed training due to invalid training data"); return false; } return m_mlfn.fit(predictors,targets,m_alfa,m_beyta,m_hl1,m_hl2,m_epochs,m_learningrate,m_tolerance); } //+------------------------------------------------------------------+ //| make a prediction with the trained i_model | //+------------------------------------------------------------------+ vector CMLPC::classify(vector &predictors) { return m_mlfn.predict(predictors); } //+------------------------------------------------------------------+ //| clean up dynamic array pointers | //+------------------------------------------------------------------+ void cleanup(ensemble::IClassify* &array[]) { for(uint i = 0; i<array.Size(); i++) if(CheckPointer(array[i])==POINTER_DYNAMIC) delete array[i]; } //+------------------------------------------------------------------+ //| global variables | //+------------------------------------------------------------------+ int nreplications, nsamps,nmodels, divisor, nreps_done ; int n_classes, nnn, n_pairs, nh_g ; ulong ntrain_pair[]; matrix xdata, xbad_data, xtainted_data, test[],x_targ,xbad_targ,xwild_targ; vector inputdata; double cd_factor, err_score, err_score_1, err_score_2, err_score_3 ; vector classification_err_raw, output_vector; double classification_err_average ; double classification_err_median ; double classification_err_maxmax ; double classification_err_maxmin ; double classification_err_intersection_1 ; double classification_err_intersection_2 ; double classification_err_intersection_3 ; double classification_err_union_1 ; double classification_err_union_2 ; double classification_err_union_3 ; double classification_err_majority ; double classification_err_borda ; double classification_err_logit ; double classification_err_logitsep ; double classification_err_localacc ; double classification_err_fuzzyint ; double classification_err_pairwise ; //+------------------------------------------------------------------+ //| ensemble i_model objects | //+------------------------------------------------------------------+ ensemble::CAvgClass average_ensemble ; ensemble::CMedian median_ensemble ; ensemble::CMaxMax maxmax_ensemble ; ensemble::CMaxMin maxmin_ensemble ; ensemble::CIntersection intersection_ensemble ; ensemble::CUnion union_rule ; ensemble::CMajority majority_ensemble ; ensemble::CBorda borda_ensemble ; ensemble::ClogitReg logit_ensemble ; ensemble::ClogitRegSep logitsep_ensemble ; ensemble::ClocalAcc localacc_ensemble ; ensemble::CFuzzyInt fuzzyint_ensemble ; ensemble::CPairWise pairwise_ensemble ; int n_hid = 4 ; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CHighQualityRandStateShell rngstate; CHighQualityRand::HQRndRandomize(rngstate.GetInnerObj()); //--- nsamps = NumSamples ; n_classes = NumClasses ; nmodels = NumModels ; nreplications = NumReplications ; cd_factor = ClassificationDifficultyFactor ; if((nsamps <= 3) || (n_classes <= 1) || (nmodels <= 0) || (nreplications <= 0) || (cd_factor < 0.0)) { Alert(" Invalid inputs "); return; } divisor = 1 ; ensemble::IClassify* models[]; ensemble::IClassify* model_pairs[]; /* Allocate memory and initialize */ n_pairs = n_classes * (n_classes-1) / 2 ; if(ArrayResize(models,nmodels)<0 || ArrayResize(model_pairs,n_pairs)<0 || ArrayResize(test,10)<0 || ArrayResize(ntrain_pair,n_pairs)<0) { Print(" Array resize errors ", GetLastError()); cleanup(models); cleanup(model_pairs); return; } ArrayInitialize(ntrain_pair,0); for(int i=0 ; i<nmodels ; i++) models[i] = new CMLPC(2,ulong(n_classes),4,0) ; xdata = matrix::Zeros(nsamps,(2+n_classes)); xbad_data = matrix::Zeros(nsamps,(2+n_classes)); xtainted_data = matrix::Zeros(nsamps,(2+n_classes)); inputdata = vector::Zeros(3); for(uint i = 0; i<test.Size(); i++) test[i] = matrix::Zeros(nsamps,(2+n_classes)); classification_err_raw = vector::Zeros(nmodels); classification_err_average = 0.0 ; classification_err_median = 0.0 ; classification_err_maxmax = 0.0 ; classification_err_maxmin = 0.0 ; classification_err_intersection_1 = 0.0 ; classification_err_intersection_2 = 0.0 ; classification_err_intersection_3 = 0.0 ; classification_err_union_1 = 0.0 ; classification_err_union_2 = 0.0 ; classification_err_union_3 = 0.0 ; classification_err_majority = 0.0 ; classification_err_borda = 0.0 ; classification_err_logit = 0.0 ; classification_err_logitsep = 0.0 ; classification_err_localacc = 0.0 ; classification_err_fuzzyint = 0.0 ; classification_err_pairwise = 0.0 ; for(int i_rep=0 ; i_rep<nreplications ; i_rep++) { nreps_done = i_rep + 1 ; if(i_rep>0) xdata.Fill(0.0); //--- for(int i=0, z=0; i<nsamps ; i++) { xdata[i][0] = normal(rngstate) ; xdata[i][1] = normal(rngstate) ; if(i < n_classes) z = i ; else z = (int)(unifrand(rngstate) * n_classes) ; if(z >= n_classes) z = n_classes - 1 ; xdata[i][2+z] = 1.0 ; xdata[i][0] += double(z) * cd_factor ; xdata[i][1] -= double(z) * cd_factor ; } if(nmodels >= 4) { xbad_data = xdata; matrix arm = np::sliceMatrixCols(xbad_data,2); for(int i = 0; i<nsamps; i++) for(int z = 0; z<n_classes; z++) arm[i][z] = (unifrand(rngstate)<(1.0/double(n_classes)))?1.0:0.0; np::matrixCopy(xbad_data,arm,0,xbad_data.Rows(),1,2); } if(nmodels >= 5) { xtainted_data = xdata; matrix arm = np::sliceMatrixCols(xtainted_data,2); for(int i = 0; i<nsamps; i++) for(int z = 0; z<n_classes; z++) if(unifrand(rngstate)<0.1) arm[i][z] = xdata[i][2+z] * 1000.0 - 500.0 ; np::matrixCopy(xtainted_data,arm,0,xtainted_data.Rows(),1,2); } for(int i=0 ; i<10 ; i++) // Build a test dataset { if(i_rep>0) test[i].Fill(0.0); for(int j=0,z=0; j<nsamps; j++) { test[i][j][0] = normal(rngstate) ; test[i][j][1] = normal(rngstate) ; z = (int)(unifrand(rngstate) * n_classes) ; if(z >= n_classes) z = n_classes - 1 ; test[i][j][2+z] = 1.0 ; test[i][j][0] += double(z) * cd_factor ; test[i][j][1] -= double(z) * cd_factor ; } } for(int i_model=0 ; i_model<nmodels ; i_model++) { matrix preds,targs; if(i_model == 3) { targs = np::sliceMatrixCols(xbad_data,2); preds = np::sliceMatrixCols(xbad_data,0,2); } else if(i_model == 4) { targs = np::sliceMatrixCols(xtainted_data,2); preds = np::sliceMatrixCols(xtainted_data,0,2); } else { targs = np::sliceMatrixCols(xdata,2); preds = np::sliceMatrixCols(xdata,0,2); } if(!models[i_model].train(preds,targs)) { Print(" failed to train i_model at shift ", i_model); cleanup(model_pairs); cleanup(models); return; } err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { vector testvec,testin,testtarg; for(int j=0; j<nsamps; j++) { testvec = test[i].Row(j); testtarg = np::sliceVector(testvec,2); testin = np::sliceVector(testvec,0,2); output_vector = models[i_model].classify(testin) ; if(output_vector.ArgMax() != testtarg.ArgMax()) err_score += 1.0 ; } } classification_err_raw[i_model] += err_score / (10 * nsamps) ; } int i_model = 0; for(int i=0 ; i<n_classes-1 ; i++) { for(int j=i+1 ; j<n_classes ; j++) { ntrain_pair[i_model] = 0 ; for(int z=0 ; z<nsamps ; z++) { if((xdata[z][2+i]> 0.5) || (xdata[z][2+j] > 0.5)) ++ntrain_pair[i_model] ; } nh_g = (n_hid < int(ntrain_pair[i_model]) - 1) ? n_hid : int(ntrain_pair[i_model]) - 1; model_pairs[i_model] = new CMLPC(2, 1, ulong(nh_g+1),0) ; matrix training; matrix preds,targs; ulong msize=0; for(int z=0 ; z<nsamps ; z++) { inputdata[0] = xdata[z][0] ; inputdata[1] = xdata[z][1] ; if(xdata[z][2+i]> 0.5) inputdata[2] = 1.0 ; else if(xdata[z][2+j] > 0.5) inputdata[2] = 0.0 ; else continue ; training.Resize(msize+1,inputdata.Size()); training.Row(inputdata,msize++); } preds = np::sliceMatrixCols(training,0,2); targs = np::sliceMatrixCols(training,2); model_pairs[i_model].train(preds,targs); ++i_model ; } } err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(average_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_average += err_score / (10 * nsamps) ; /* median_ensemble */ err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(median_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_median += err_score / (10 * nsamps) ; /* maxmax_ensemble */ err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(maxmax_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_maxmax += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(maxmin_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) // If predicted class not true class err_score += 1.0 ; // Count this misclassification } } classification_err_maxmin += err_score / (10 * nsamps) ; matrix preds,targs; err_score_1 = err_score_2 = err_score_3 = 0.0 ; preds = np::sliceMatrixCols(xdata,0,2); targs = np::sliceMatrixCols(xdata,2); intersection_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); ulong class_ = intersection_ensemble.classify(rowtest,models) ; output_vector = intersection_ensemble.proba(); if(output_vector[rowtarg.ArgMax()] < 0.5) { err_score_1 += 1.0 ; err_score_2 += 1.0 ; err_score_3 += 1.0 ; } else { if(class_ > 3) err_score_3 += 1.0 ; if(class_ > 2) err_score_2 += 1.0 ; if(class_ > 1) err_score_1 += 1.0 ; } } } classification_err_intersection_1 += err_score_1 / (10 * nsamps) ; classification_err_intersection_2 += err_score_2 / (10 * nsamps) ; classification_err_intersection_3 += err_score_3 / (10 * nsamps) ; union_rule.fit(preds,targs,models); err_score_1 = err_score_2 = err_score_3 = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); ulong clss = union_rule.classify(rowtest,models) ; output_vector = union_rule.proba(); if(output_vector[rowtarg.ArgMax()] < 0.5) { err_score_1 += 1.0 ; err_score_2 += 1.0 ; err_score_3 += 1.0 ; } else { if(clss > 3) err_score_3 += 1.0 ; if(clss > 2) err_score_2 += 1.0 ; if(clss > 1) err_score_1 += 1.0 ; } } } classification_err_union_1 += err_score_1 / (10 * nsamps) ; classification_err_union_2 += err_score_2 / (10 * nsamps) ; classification_err_union_3 += err_score_3 / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(majority_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_majority += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(borda_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_borda += err_score / (10 * nsamps) ; err_score = 0.0 ; logit_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(logit_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_logit += err_score / (10 * nsamps) ; err_score = 0.0 ; logitsep_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(logitsep_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_logitsep += err_score / (10 * nsamps) ; err_score = 0.0 ; localacc_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(localacc_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_localacc += err_score / (10 * nsamps) ; err_score = 0.0 ; fuzzyint_ensemble.fit(preds,targs,models); for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(fuzzyint_ensemble.classify(rowtest,models) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_fuzzyint += err_score / (10 * nsamps) ; err_score = 0.0 ; for(int i=0 ; i<10 ; i++) { for(int z=0;z<nsamps;z++) { vector row = test[i].Row(z); vector rowtest = np::sliceVector(row,0,2); vector rowtarg = np::sliceVector(row,2); if(pairwise_ensemble.classify(ulong(n_classes),rowtest,model_pairs,ntrain_pair) != rowtarg.ArgMax()) err_score += 1.0 ; } } classification_err_pairwise += err_score / (10 * nsamps) ; cleanup(model_pairs); } err_score = 0.0 ; PrintFormat("Test Config: Classification Difficulty - %8.8lf\nNumber of classes - %5d\nNumber of component models - %5d\n Sample Size - %5d", ClassificationDifficultyFactor,NumClasses,NumModels,NumSamples); PrintFormat("%5d Replications:", nreps_done) ; for(int i_model=0 ; i_model<nmodels ; i_model++) { PrintFormat(" %.8lf", classification_err_raw[i_model] / nreps_done) ; err_score += classification_err_raw[i_model] / nreps_done ; } PrintFormat(" Mean raw error = %8.8lf", err_score / nmodels) ; PrintFormat(" average_ensemble error = %8.8lf", classification_err_average / nreps_done) ; PrintFormat(" median_ensemble error = %8.8lf", classification_err_median / nreps_done) ; PrintFormat(" maxmax_ensemble error = %8.8lf", classification_err_maxmax / nreps_done) ; PrintFormat(" maxmin_ensemble error = %8.8lf", classification_err_maxmin / nreps_done) ; PrintFormat(" majority_ensemble error = %8.8lf", classification_err_majority / nreps_done) ; PrintFormat(" borda_ensemble error = %8.8lf", classification_err_borda / nreps_done) ; PrintFormat(" logit_ensemble error = %8.8lf", classification_err_logit / nreps_done) ; PrintFormat(" logitsep_ensemble error = %8.8lf", classification_err_logitsep / nreps_done) ; PrintFormat(" localacc_ensemble error = %8.8lf", classification_err_localacc / nreps_done) ; PrintFormat(" fuzzyint_ensemble error = %8.8lf", classification_err_fuzzyint / nreps_done) ; PrintFormat(" pairwise_ensemble error = %8.8lf", classification_err_pairwise / nreps_done) ; PrintFormat(" intersection_ensemble error 1 = %8.8lf", classification_err_intersection_1 / nreps_done) ; PrintFormat(" intersection_ensemble error 2 = %8.8lf", classification_err_intersection_2 / nreps_done) ; PrintFormat(" intersection_ensemble error 3 = %8.8lf", classification_err_intersection_3 / nreps_done) ; PrintFormat(" Union error 1 = %8.8lf", classification_err_union_1 / nreps_done) ; PrintFormat(" Union error 2 = %8.8lf", classification_err_union_2 / nreps_done) ; PrintFormat(" Union error 3 = %8.8lf", classification_err_union_3 / nreps_done) ; cleanup(models); } //+------------------------------------------------------------------+
Examples of results obtained from running script are shown below. These are results where classification task was set to the highest difficulty.
ClassificationDifficultyFactor=0.0 DM 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 0.00000000 RP 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 QI 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 EK 0 05:40:06.441 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 MN 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: CF 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66554000 HI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66706000 DP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) 0.66849000 II 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.66703000 JS 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.66612000 HR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.66837000 QF 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.66704000 MD 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.66586000 GI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.66772000 HR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.66747000 MO 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.66556000 MP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.66570000 JD 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.66578000 OJ 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.66503000 KO 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.66799000 GS 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.96686000 DP 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.95847000 QE 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.95447000 OI 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.99852000 DM 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.97931000 JR 0 05:40:06.442 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.01186000
Next are the results for test where classification difficulty was moderate.
LF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 1.00000000 IG 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 JP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 FQ 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 KH 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: NO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.46236000 QF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.45818000 II 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) 0.45779000 FR 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.45944333 DI 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.44881000 PH 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.45564000 JO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.46763000 GS 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.44935000 GP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.45573000 PI 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.45593000 DF 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.46353000 FO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.46726000 ER 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.46096000 KP 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.45098000 OD 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.66485000 IJ 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.93533000 RO 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.92527000 OL 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.92527000 OR 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.99674000 KG 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.97231000 NK 0 05:42:00.329 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.00877000
The last set of results illustrate results from a test conducted where the classification difficulty was configured to be relatively easy.
PL 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Test Config: Classification Difficulty - 10.00000000 CN 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Number of classes - 3 PK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Number of component models - 3 LH 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Sample Size - 10 EQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 1000 Replications: MD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02905000 LO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02861000 CF 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) 0.02879000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Mean raw error = 0.02881667 RN 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) average_ensemble error = 0.02263000 PQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) median_ensemble error = 0.02956000 QD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) maxmax_ensemble error = 0.03426000 KJ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) maxmin_ensemble error = 0.02263000 IO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) majority_ensemble error = 0.02956000 HP 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) borda_ensemble error = 0.02956000 KM 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) logit_ensemble error = 0.03171000 OE 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) logitsep_ensemble error = 0.04840000 GK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) localacc_ensemble error = 0.03398000 FO 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) fuzzyint_ensemble error = 0.02263000 QM 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) pairwise_ensemble error = 0.65277000 CQ 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 1 = 0.96303000 DF 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 2 = 0.96167000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) intersection_ensemble error 3 = 0.96167000 IK 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 1 = 0.98620000 CP 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 2 = 0.95624000 LD 0 05:45:11.711 ClassificationEnsemble_Demo (BTCUSD,D1) Union error 3 = 0.00000000
All the code featured in the text attached with the article. And a description of each source file is given in the table below.
| FileName | File Description |
|---|---|
| MQL5/include/np.mqh | This is a collection of utility functions for manipulating vectors and matrices |
| MQL5/include/nom2ord.mqh | This file contains classes for encoding categorical data |
| MQL5/include/multilayerperceptron.mqh | Provides the definition of the CMlp class representing a Feed forward neural network |
| MQL5/include/logistic.mqh | Contains the definition of the Clogit class that implements logistic regression |
| MQL5/include/ensemble.mqh | Contains definitions for various implementations of metamodels |
| MQL5/scripts/ClassificationEnsemble_Demo.mq5 | This is a script that compares the performance of ensemble classifiers defined in ensemble.mqh |
| MQL5/scripts/PairWise_Ensemble_Demo.mq5 | This is a demo script showing how to apply the CPairWise class for pairwise coupling |
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.
This article was written by a user of the site and reflects their personal views. MetaQuotes Ltd is not responsible for the accuracy of the information presented, nor for any consequences resulting from the use of the solutions, strategies or recommendations described.
 MQL5 Wizard Techniques you should know (Part 52): Accelerator Oscillator
MQL5 Wizard Techniques you should know (Part 52): Accelerator Oscillator
 Reimagining Classic Strategies (Part 13): Minimizing The Lag in Moving Average Cross-Overs
Reimagining Classic Strategies (Part 13): Minimizing The Lag in Moving Average Cross-Overs
 Neural Networks Made Easy (Part 97): Training Models With MSFformer
Neural Networks Made Easy (Part 97): Training Models With MSFformer
 Artificial Electric Field Algorithm (AEFA)
Artificial Electric Field Algorithm (AEFA)
- Free trading apps
- Over 8,000 signals for copying
- Economic news for exploring financial markets
You agree to website policy and terms of use