Прогнозирование в трейдинге и Grey-модели

Введение

Современные финансовые рынки отличаются высокой волатильностью и динамичностью, поэтому точное и своевременное прогнозирование играет очень важную роль при принятии торговых решений. Любой трейдер стремится к разработке и применению методов прогнозирования, позволяющих предвидеть будущие колебания цен и максимизировать прибыль.

Технический анализ предлагает самые разные способы прогнозирования. Но многие методы прогнозирования имеют свои ограничения. Например, статистический подход к прогнозированию требует большого объема исторических данных. Другие подходы хорошо работают только на стационарных временных рядах, и т.д.

В связи с этим, растет интерес к методам прогнозирования, способным работать с ограниченной и неполной информацией.  Одним из таких подходов являются Grey-модели (GM), которые могут оказаться очень полезны в ситуациях, когда данные ограничены, ненадежны или содержат много шума. А такие ситуации довольно часто встречается на финансовых рынках. В этой статье мы рассмотрим основы GM, и возможности их применения для прогнозирования финансовых временных рядов.

Классическая модель GM(1,1)

Grey-модели можно применять для решения самых разных задач. С помощью GM мы можем анализировать временной ряд, сглаживать его или выявлять основные тенденции в движении цены. Но эту модель можно использовать и для прогнозирования. Основное преимущество применения GM заключается в том, что эта модель не накладывает никаких ограничений на стационарность временного ряда. Например, SMA проявит все свои лучшие качества, если временной ряд стационарен и его значения нормально распределены. Если же временной ряд нестационарен (попросту говоря, есть тренд), то SMA будет безнадежно запаздывать. Для GM эти требования не важны, и она может справиться с любым временным рядом. Ну или должна справляться. Требования к GM просты и легко выполнимы:

• длина временного ряда должна быть не меньше 4;
• значения временного ряда должны быть строго положительны и следовать через равный временной интервал, без пропусков.

Построение любой GM начинается с применения Accumulated Generating Operating (AGO). Суть этой операции очень проста — нужно суммировать текущее значение временного ряда со всеми ему предшествующими. В дальнейшем такой временной ряд я буду называть Grey-рядом (GS). Возьмем, для примера, 5 цен. Тогда операция AGO, примененная к ним, будет выглядеть так:

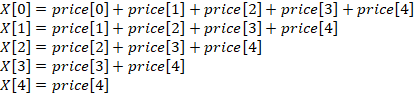
Эта операция выполняет две основные цели. Во-первых, мы снижаем влияние шумов. Во-вторых, новый временной ряд становится более предсказуемым — он строго растет и может выглядеть, например, так:

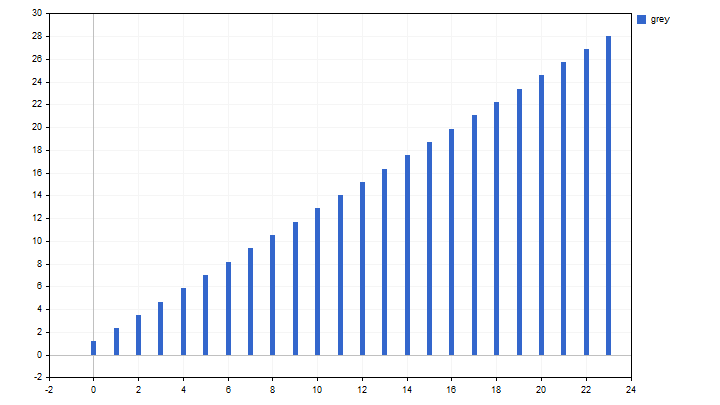
После того, как мы получили значения нового временного ряда, можно приступать к построению GM(1,1). В этом обозначении первое число указывает на порядок дифференциального уравнения, а второе — на количество обрабатываемых GS. Модель GM(1,1) описывается линейным дифференциальным уравнением.

Чтобы решить это уравнение, нам потребуется какая-нибудь система символьной математики. Я использую Maple. Сначала записываем исходное уравнение, потом задаем начальное условие, относительно которого будет происходить поиск решения, и получаем результат. В Maple все эти операции будут выглядеть так:

de:=diff(x(t),t)+a*x(t)=b; #исходное уравнение
cond:=x(1)=X[1];           #начальное условие
dsolve({de,cond},x(t));    #решение уравнения

Так мы получили зависимость изменения GS от времени. Обратите внимание, что индекс t носит характер времени и увеличивается от прошлого к будущему, начиная с 1. Из этого уравнения мы можем получить такую же зависимость для изменения цены:

В Maple решение этого уравнения будет выглядеть так:

eq:=price[t]=(b+(a*X[1]-b)*exp(-a*t))/a-(b+(a*X[1]-b)*exp(-a*(t-1)))/a;#разность 2 последовательных значений GS
simplify(eq);#упрощаем результат

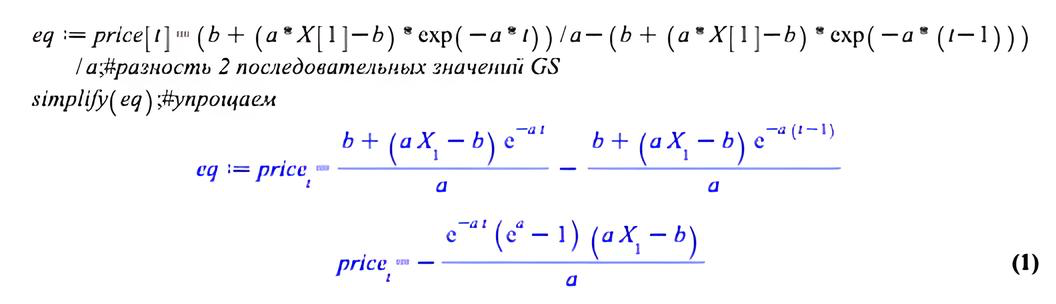
Немного упростим результат вручную, и формула примет окончательный вид.

Из этой формулы становится ясно, что зная параметры a и b, мы можем произвести оценку значений цены. Говоря иначе, сгладить исходный временной ряд. Для того, чтобы оценить эти параметры, нам нужно взять дифференциальное уравнение и привести к дискретному виду. Для этого воспользуемся таким переходом:

После этого перехода, мы получим дискретный вариант.

Коэффициенты такого уравнения можно легко оценить с помощью метода наименьших квадратов (МНК). И вот тут начинается самое интересное. Мы можем получить сглаженную оценку значений GS. Такое сглаживание представляет чисто академический интерес, на практике от него толку нет.

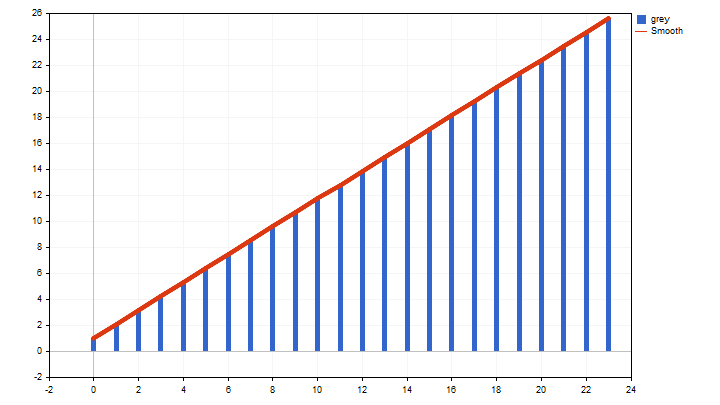
А можем и сразу сгладить исходный временной ряд.

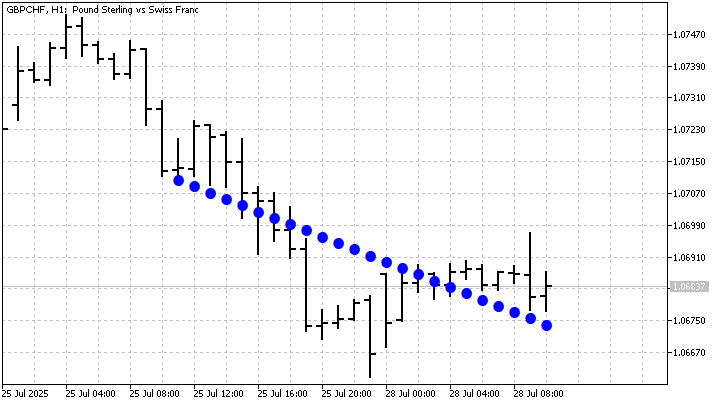
Теперь мы готовы сделать следующий шаг. Вспомните, что формула для расчета значений цены не накладывает никаких ограничений на увеличение времени. То есть, мы можем продолжать строить новый временной ряд сколь угодно долго вперед. В этом случае, у нас получится прогноз движения цены. Конечно же, этот прогноз построен на предположении о том, что характеристики исходного временного ряда останутся неизменными. Я сделаю прогноз на 5 отсчетов вперед.

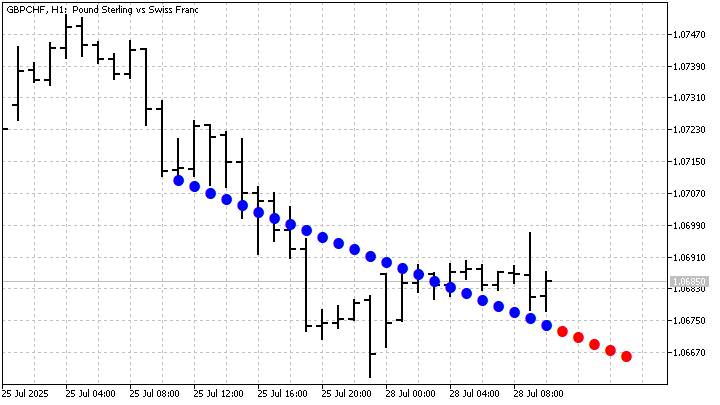
Как вы можете видеть, эта модель хорошо справляется с линейными трендами. Но из-за этого она может пропускать другие важные движения цены. Давайте попробуем применить более сложные GM модели и посмотрим, как ведут себя они.

Модификации GM(1,1)

Самое простое усложнение классической GM(1,1) носит название Rolling GM (RGM). Суть этого усложнения очень проста. Нам нужно взять значения нескольких GM с разными периодами и найти их среднее. Благодаря такому подходу, мы можем получить более гладкую оценку значений цены. Прогноз также окажется более гладким. Сделаем RGM, собранную из нескольких GM(1,1) с периодами 4 — 24. Вот так она выглядит на графике:

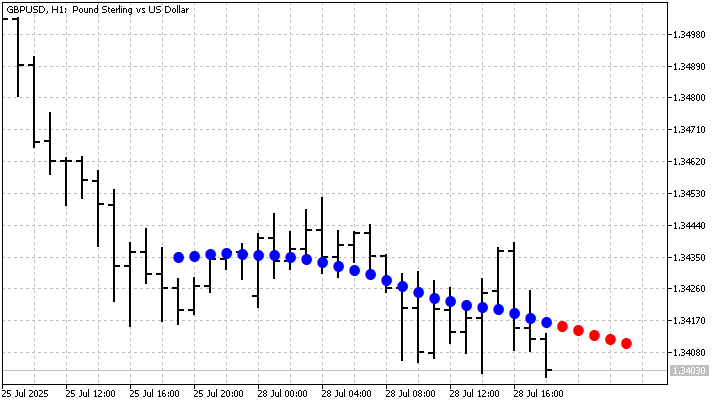
Модель RGM тоже можно модифицировать. Основная идея такой модификации — придать каждой GM свой вес. Причем эти веса могут быть как фиксированными, так и зависеть от ошибки прогноза. Первый случай довольно тривиальный. Вы можете назначить веса, исходя из каких-либо собственных соображений. А потом получить взвешенную сумму.

Если веса будут зависеть от ошибки прогноза, то вы получите адаптивный вариант RGM. В этом случае, вес каждой GM можно определить следующим образом. Сначала считаем ошибку прогноза для каждой GM отдельно:

Весовой коэффициент GM будет зависеть от этой ошибки — чем больше ошибка, тем ниже вес:

Таким образом, RGM станет предпочитать только те тренды, которые наиболее точно соответствуют движению цены. Соответственно, может повыситься и качество прогноза.

Еще одно усложнение сводится к предварительной обработке исходного временного ряда. Например, вместо цен мы можем использовать значения SMA. Тогда, GM(1,1) даcт более сглаженные результаты. На практике такой подход можно использовать для определения границ тренда.

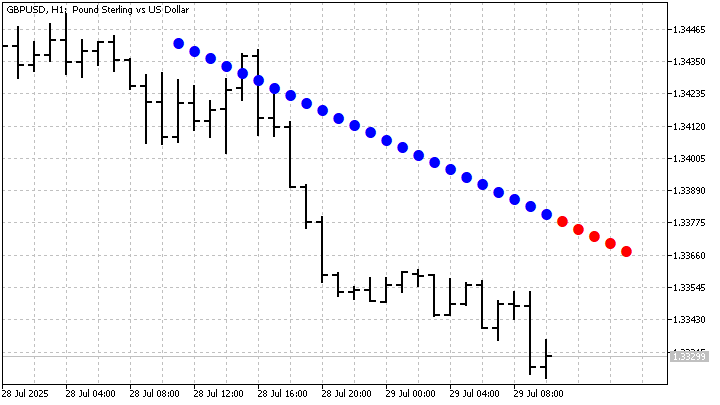
Но канал можно построить и по-другому. Сначала нам нужно рассчитать параметры GM(1,1). Точнее, сейчас нам нужен только параметр роста a. Теперь для каждого реального значения цены рассчитаем ее параметр b.

Из всех возможных вариантов, нас интересуют максимальное и минимальное значения этого параметра. С их помощью мы можем получить верхнюю и нижнюю границы трендового канала.

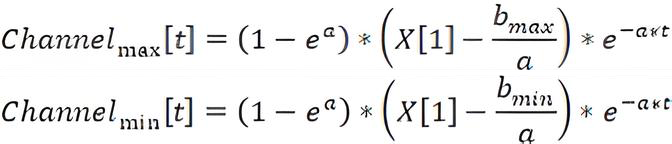
А вот так выглядит такой канал на графике:

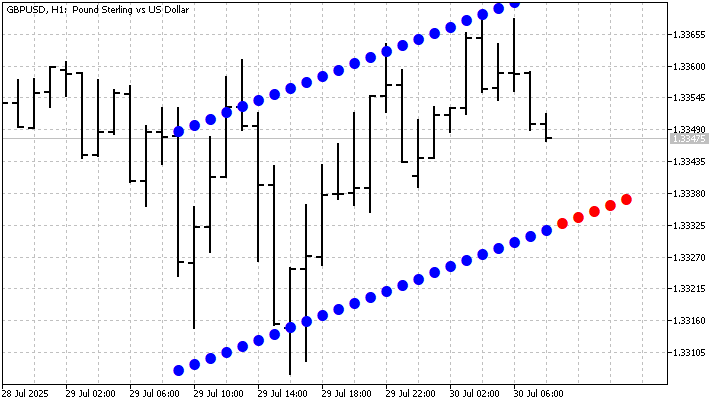
Существует большое количество различных модификаций Grey-моделей. Некоторые из этих модификаций применимы только к специфическим временным рядам. Другие, как GM(1,1) носят универсальный характер. Все эти модификации имеют одну цель —повышение точности прогнозов и выявление особенностей временных рядов.

Дискретные модели GM

Решение дифференциальных уравнений выглядит конечно красиво, но даже небольшое усложнение моделей приводит к очень непростым решениям. К тому же, оценка параметров модели может оказаться численно неустойчивой. Одна ошибка неизвестно в каком знаке после запятой приведет к тому, что на графике нам смотреть будет не на что.

От этих недостатков свободны дискретные варианты GM. Давайте попробуем построить такой вариант для GM(1,1). Такая модель может быть выражена таким линейным рекуррентным уравнением:

То есть, мы строим линейную зависимость текущего значения GS от предыдущего. Оценить параметры этого уравнения не составит большого труда. Теперь нам нужно найти параметры уравнения.

re:=x(n+1)=a*x(n)+b;              #исходное уравнение
cond:=x(1)=X[1];                  #начальное условие
simplify(rsolve({re,cond},x(t))); #решение уравнения

В итоге у нас получится уравнение с явно заданными значениями GS.

Из этого уравнения мы можем получить оценку цены.

А так выглядит индикатор, построенный на основе этой модели:

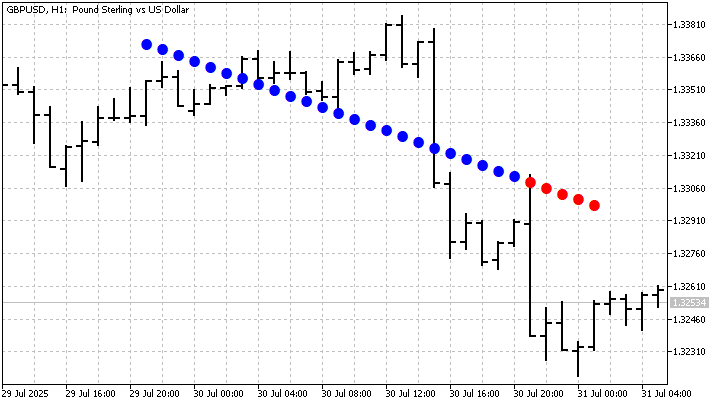
Опыт получился удачным. Теперь давайте попробуем построить модель GM(0,2). Из обозначения нам ясно, что в этой модели производные не используются, а количество учитываемых факторов возрастает. И кстати, эта модель может существовать только в дискретном виде.

В этой модели используется 2 GS. Предположим, что период модели равен N. Первый GS мы строим как обычно, начиная с цены с индексом N-1. А для построения второго (я буду обозначать его Y) мы используем цены со сдвигом на 1 отсчет назад, начав с цены с индексом N. Уравнение этой модели выглядит так:

Конечно же, мы можем построить рекуррентное уравнение и найти его решение. Но эта модель станет особенно простой, если мы ограничимся прогнозом на 1 шаг вперед. Итак, сначала с помощью МНК оценим параметры модели. Ряд X мы продолжить не можем — новая цена еще неизвестна. А вот для ряда Y следующая цена уже известна, и мы можем получить его новое значение.

Получив новое значение ряда Y, мы также можем оценить будущее значение ряда X.

После этого сделать прогноз цены не составит никакого труда. А так выглядит индикатор, построенный на этой модели:

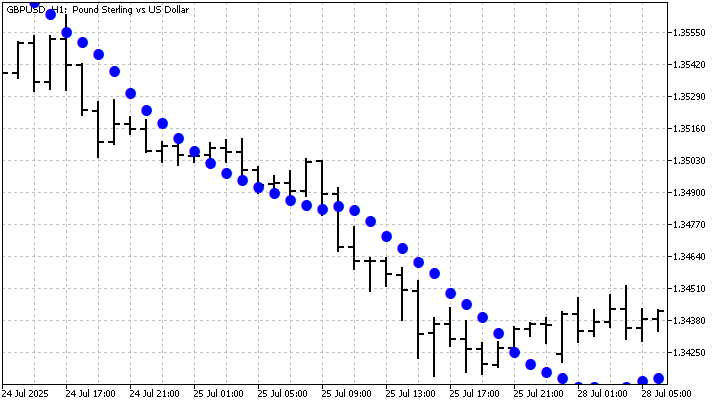
Модель GM(0,2) является аналогом линейной регрессии. Увеличение количества учитываемых GS может сделать модель более гибкой и улучшить качество прогноза. Это улучшение будет особенно заметным при небольшом периоде индикатора.

Сейчас мы готовы перейти к построению дискретной модели GM(1,2). Она объединяет подходы двух предыдущих моделей, и может быть описана формулой:

То есть, мы строим все ту же линейную регрессию по двум GS. С найденными параметрами этой регрессии, мы можем оценить будущее значение цены. Так выглядит индикатор, построенный на основе этой модели:

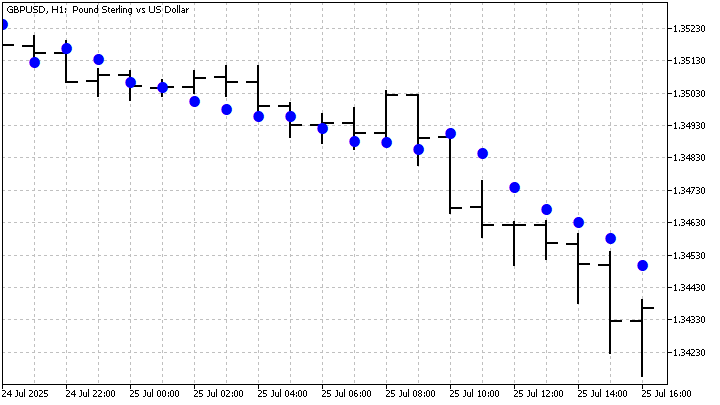
Дискретный подход позволяет достаточно легко построить модели более высоких порядков. Для примера я возьму модель GM(2,1). Решать ее традиционным способом, находить значения ее параметров — занятие на любителя. Но давайте переведем эту модель в дискретный вид, тогда ее уравнение будет выглядеть так:

Рассчитать параметры этой модели не составит большого труда. Для упрощения мы также ограничимся прогнозом на один отсчет вперед. На графике индикатор выглядит так:

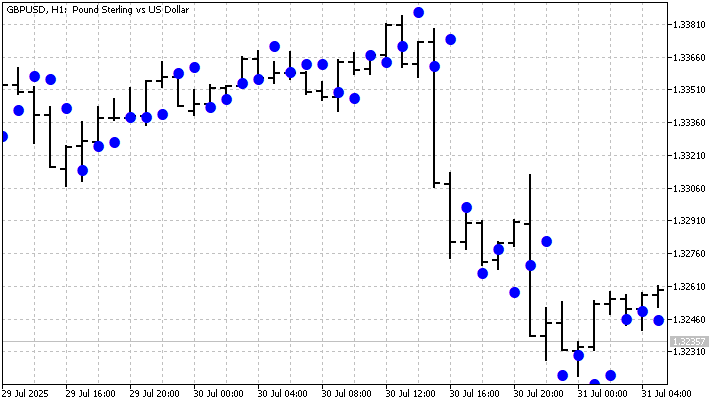
Назвать такой индикатор сглаживающим нельзя. Зато он довольно быстро реагирует на изменение рыночной ситуации. Это делает его заслуживающим внимания. Если же вы хотите получить более плавный вариант, то вспомните о RGM.

Подводя краткие итоги, я могу сказать, что дискретные модели проще в своих расчетах. Это их несомненное достоинство. Но эта простота накладывает ограничения на горизонт прогноза. Чаще всего дискретные модели хорошо работают только на 1 шаг вперед. Попытки увеличения горизонта прогнозирования ведут к излишним усложнениям, и вряд ли они пригодятся на практике.

Заключение

Grey-модели представляют собой перспективный инструмент для моделирования и описания финансовых временных рядов. GM можно применять для сглаживания, выявления трендов и прогнозирования будущих значений цен, а также для построения трендовых каналов.

Несомненное достоинство GM — возможность их модификаций почти под любые внешние условия. Серьезный недостаток — математическая сложность некоторых подходов. В любом случае, GM требуют дальнейшего изучения и выявления наиболее подходящих для трейдера вариантов.

К статье прилагаются программы:

Название	Тип	Описание
sGM	скрипт	Скрипт демонстрирует построение GS и сглаживание по модели GM(1,1). Если ScreenShot включен, то картинка сохраняется в папке Files
GM11	индикатор	Индикатор демонстрирует работу классического варианта GM(1,1) iPeriod - период индикатора; Forecast - горизонт прогноза Shift - сдвиг индикатора
RGM11	индикатор	Индикатор показывает среднюю между несколькими вариантами GM(1,1)
GM11sma	индикатор	В качестве входных значений, вместо цен, используются значения SMA
GM11Ch	индикатор	Индикатор строит трендовый канал на основе GM(1,1)
DGM11	индикатор	Дискретный вариант GM(1,1)
DGM02	индикатор	Аналог парной линейной регрессии
DGM12	индикатор	Дискретная модель GM(1,1) с двумя управляющими параметрами
DGM21	индикатор	Дискретный аналог модели 2-го порядка