Нейросети в трейдинге: Устойчивые торговые сигналы в любых режимах рынка (ST-Expert)

Введение

Современные финансовые рынки — это динамичная экосистема, в которой миллионы сделок, решения регуляторов, корпоративные отчёты и макроэкономические сигналы складываются в сложный узор. Для трейдера или аналитика ключевая задача заключается в том, чтобы распознать закономерности в этом узоре и на их основе построить прогноз. Но именно здесь возникает основное противоречие: рынок меняется быстрее, чем успевают адаптироваться привычные модели. То, что работало вчера, завтра может оказаться не просто бесполезным, но и опасным.

Мы привыкли мыслить в терминах корреляций. Есть устойчивая связь между ценой нефти и курсом канадского доллара, между процентными ставками ФРС и технологическим сектором, между спросом на золото и динамикой доллара. Но стоит измениться внешним условиям, как эти зависимости рушатся. В ковидном обвале 2020 года за считанные недели привычные зависимости между акциями, облигациями и сырьём перестали отражать реальность. Даже более мягкие режимные сдвиги, например, циклы повышения и снижения ставок ФРС, способны резко изменить корреляции и разрушить модели, которые казались надёжными.

Суть проблемы в том, что современные алгоритмы обучаются на относительно коротких и однородных интервалах данных. В этих лабораторных условиях они показывают впечатляющие результаты, улавливая тонкие взаимосвязи между активами. Но как только рынок выходит за пределы привычного распределения, точность прогнозов резко падает. По сути, модели прекрасно работают в спокойное время, но не умеют справляться с фазовыми переходами рынка.

Эта ситуация во многом напоминает городские транспортные сети, на примере которых авторы работы "Robust Traffic Forecasting against Spatial Shift over Years" предложили новый фреймворк ST-Expert. Пока город остаётся неизменным, прогнозы движения транспорта работают отлично. Но стоит построить новую развязку или открыть крупный торговый центр, и прежние маршруты перестают быть актуальными. В финансовой среде такими драйверами становятся решения регуляторов, санкции, геополитические конфликты или появление новых технологий. Карта взаимосвязей меняется, и старые модели оказываются бессильными.

Чтобы справиться с этой задачей, авторы ST-Expert предлагают оригинальное решение на основе Mixture of Experts. Его ключевая идея заключается в том, что модель учится не на единой жёсткой структуре зависимостей, а на множестве генераторов графов, так называемых графонов. Каждый из них отражает определённый тип рыночного поведения. Один фиксирует закономерности в условиях устойчивого тренда, другой описывает фазу высокой волатильности, третий выявляет локальные корреляции внутри отраслей. Когда рынок меняется, система не рушится, а адаптивно комбинирует уже выученные сценарии, создавая новые связи между инструментами и сохраняя точность прогноза.

Именно здесь проявляется первое и, пожалуй, главное достоинство подхода — способность адаптироваться к изменившимся рыночным условиям. Если стандартные модели оказываются пленниками конкретного периода истории, то новый фреймворк рассматривает рынок как мозаику, где каждый режим — лишь временный фрагмент целого. Благодаря этому, алгоритм способен из уже изученных элементов собрать новую комбинацию и дать точный прогноз там, где другие системы теряют устойчивость. Для трейдера это означает меньше ложных сигналов в периоды турбулентности и больше надёжности при построении долгосрочных стратегий.

Но адаптивность — лишь одна грань. Не менее важным достоинством является универсальность архитектуры. Слой экспертных графонов легко встраивается в существующие решения. Его можно добавить как в графовые нейросети, анализирующие сетевые взаимосвязи активов, так и в трансформеры, работающие с временными рядами котировок. Это делает подход особенно ценным для практиков. Он не требует радикального пересмотра инфраструктуры и может усиливать уже отлаженные системы.

Ещё одно преимущество заключается в устойчивости к так называемым режимным сдвигам. История финансовых рынков убедительно показывает: постоянство — редкость, а перемены — правило. Каждое десятилетие приносит новый кризис, и каждая эпоха внутри кризиса сопровождается каскадом непредсказуемых потрясений. Попытка найти вечные инварианты оказывается иллюзией. Новый фреймворк честно признаёт изменчивость рынков и строит свою силу именно на умении переключаться между сценариями. Это особенно важно для стресс-тестирования и долгосрочного прогнозирования, где цена ошибки крайне высока.

При этом подход остаётся компактным и эффективным. В финансовых приложениях критически важно время. Решение о сделке должно приниматься в миллисекунды. Поэтому модели, какими бы точными они ни были, не могут позволить себе быть чрезмерно тяжёлыми. Предложенный фреймворк учитывает этот фактор. Он добавляет гибкость и устойчивость без резкого роста вычислительных затрат. Благодаря этому, его можно применять в системах реального времени — от алгоритмической торговли до управления рисками.

Наконец, стоит отметить и гибкость в расширении. Экспертные графоны не ограничены каким-то одним рынком или классом активов. Их можно использовать в акциях, облигациях, валютах и криптовалютных рынках. Более того, они способны интегрировать данные разных типов — от котировок и новостных потоков до макроэкономических индикаторов. Это открывает путь к построению по-настоящему комплексных моделей, которые учитывают всю многослойную природу финансовых систем.

Это принципиально новый взгляд на саму природу моделирования в условиях неопределённости. Если традиционные модели упорно ищут некие вечные закономерности, то ST-Expert учит систему жить в изменчивом мире. Он превращает прогнозирование в динамический процесс, который способен учитывать неожиданные перемены и перестраиваться в режиме реального времени.

Алгоритм ST-Expert

Построение надёжной прогностической модели для финансовых рынков требует умения различать и учитывать разнообразные рыночные режимы. В реальности структура корреляций между активами далеко не статична. То, что вчера казалось устойчивым правилом, завтра может оказаться случайным совпадением. В периоды роста технологического сектора связи между акциями IT-компаний и ставками рефинансирования могут быть минимальными, но при первых признаках перегрева они выходят на первый план. На сырьевых рынках корреляция между ценой нефти и валютами экспортёров проявляется особенно ярко в кризисные периоды, а затем может практически исчезнуть. Очевидно, что модель, которая пытается свести всё это многообразие к одной фиксированной матрице связей, обречена терять точность.

Именно поэтому авторы предлагают подход, основанный на выделении характерных временных сегментов, внутри которых рынок ведёт себя относительно однородно. Идея проста. Если рассматривать всю историю как единый массив данных, то важные режимы размоются, и ни один эксперт не сможет выучить их правильно. Но если разделить историю на периоды, каждый из которых обладает собственным устойчивым типом корреляций, то для каждого такого периода можно построить специализированного эксперта. В дальнейшем модель будет комбинировать этих экспертов, создавая гибкое представление рыночной среды.

Формально это приводит к задаче максимального пространственно-временного разбиения (Maximum Spatiotemporal Graph Division, MSGD). Весь временной ряд (обозначим T) делится на K непересекающихся интервалов. Каждый интервал Tk включает пары (Xt, Yt) для t ∈ [tk, tk+1). Важно, что внутри такого интервала рыночные связи описываются одной и той же структурой Rk, тогда как для разных интервалов эти структуры различны.

По сути, это означает, что утренние сессии фондового рынка могут быть похожи друг на друга, даже если берутся в разные дни. Активность розничных инвесторов создаёт один тип корреляций, а вечерние часы, когда на рынок выходят институциональные участники, образуют совершенно другую картину связей. Идея MSGD состоит в разделении данных именно так, чтобы различие между выделенными интервалами было максимальным.

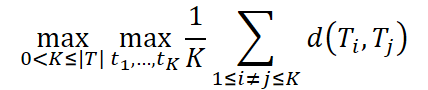
При условиях

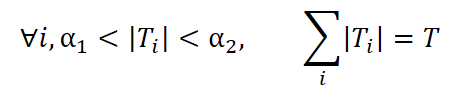
Здесь в качестве меры различия d(•,•) авторы фреймворка предлагают использовать коэффициент Кендалла τ, который отражает, насколько отличаются структуры корреляций в разные периоды. Ограничения α1, α2 задают минимальную и максимальную допустимую длину интервала, а T — полную продолжительность ряда.

Таким образом, задача сводится к тому, чтобы разрезать историю на такие части, которые наиболее сильно отличаются друг от друга по типу зависимостей. Иными словами, мы ищем чистые рыночные режимы: фазу роста, фазу боковика, фазу высокой волатильности. Такой подход напоминает создание тематических индексов. Каждый индекс собирает бумаги одного типа и показывает их поведение, не смешивая его с другими сегментами рынка.

Решение этой задачи, конечно, непросто. В аналитическом виде оно не выражается, поэтому авторы фреймворка прибегают к динамическому программированию. Это позволяет эффективно подобрать как число интервалов K, так и их границы, даже при больших объёмах данных.

После того как периоды определены, возникает вопрос: как именно задать структуру связей внутри каждого из них? Для этого вводится понятие графона — вероятностного генератора графа. В отличие от фиксированной матрицы смежности, здесь графон задаётся вероятностной матрицей P, где элемент P(i,j) отражает вероятность связи между активами i и j. Таким образом, графон не жёстко фиксирует наличие рёбер, а описывает их вероятностное распределение. Это гораздо ближе к реальности финансового рынка, где связи носят стохастический характер.

Чтобы построить графон для каждого эксперта, используются обучаемые матрицы эмбеддингов Eg^k ∈ R^|V|*d и динамический слой эмбеддинга Et ∈ R^|V|*d, зависящий от текущих рыночных данных. Тогда вероятностная матрица для k-го эксперта вычисляется по формуле:

где σ — сигмоида, которая переводит все значения в диапазон (0,1).

Чтобы из этой вероятностной матрицы получить конкретный граф, применяется репараметризация через Gumbel-SoftMax.

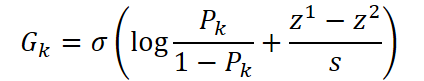
где z¹, z² сэмплируются из распределения Gumbel(0,1), а s — температурный параметр.

По сути, этот приём позволяет сэмплировать конкретные связи, избегая жёсткой бинаризации и одновременно минимизируя влияние слабых шумовых корреляций, которые в изобилии встречаются на финансовых рынках.

В результате, каждый эксперт получает собственный генератор графов, отражающий уникальный тип рыночного поведения. Одни графоны будут тяготеть к формированию плотных кластеров — например, внутри отраслей. Другие будут строить более разреженные связи, характерные для глобальных корреляций между классами активов. А вместе они формируют целый ансамбль экспертов, готовых описывать и комбинировать новые рыночные режимы, даже если те ранее не встречались.

Однако, построение экспертов — лишь первый шаг. Ключевым является их обучение в условиях изменчивости. В реальном мире рыночные зависимости подвержены постоянным изменениям. Структуры корреляций между активами формируются и разрушаются под влиянием целого спектра факторов. Решения центральных банков меняют поведение валют и облигаций. Изменения в налоговой политике или регулировании перестраивают секторальные связи. Кризисы или технологические сдвиги вносят собственные резкие коррективы. Для модели, которая обучалась на относительно стабильном наборе данных, подобные изменения представляют собой серьёзную проблему. Её карта рынка внезапно перестаёт совпадать с реальностью.

Чтобы подготовить систему к такому типу неопределённости, авторы фреймворка предлагают использовать эпизодическое обучение. Суть этого подхода заключается в разделении функций экспертов. Когда на вход поступает наблюдение xi ∈ Ti, только графон Pi, закреплённый за данным временным интервалом, выполняет основную задачу прогнозирования. Он используется для построения графа Gi ⁓ Pi, который в дальнейшем подаётся в модуль ST-GNN для генерации прогноза.

Таким образом, именно свой эксперт обучается через основную функцию потерь, которая отвечает за точность прогнозирования.

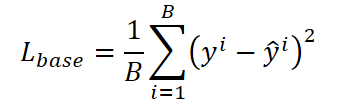
Но на этом процесс обучения не заканчивается. Остальные эксперты {Pk}^Kk=1,k≠i, хотя и не используются для прямого прогноза в данном случае, выполняют важную вспомогательную роль. С их помощью формируется смесь графонов Pⁱmix(x), которая должна максимально точно воспроизводить структуру эталонного Pi.

Для этого вводится гейтинг-сеть, которая по исходному сигналу xi вычисляет вектор весов.

Эти веса определяют, в какой пропорции комбинируются остальные эксперты.

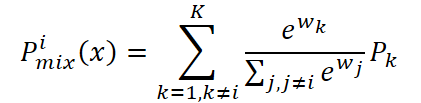
Затем она сравнивается с эталонным графоном Pi.

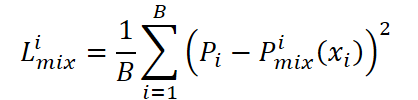
Важно отметить, что Lmix обновляет исключительно веса смешивания w, не затрагивая параметры самих графонов. Благодаря этому, эксперты сохраняют независимость и продолжают специализироваться на своих рыночных режимах, тогда как вектор весов учится правильно комбинировать их, чтобы воспроизвести свойства эталонного графона.

Таким образом, обучение разделяется на два параллельных процесса. Каждый эксперт совершенствует умение прогнозировать именно в своём рыночном режиме, не вмешиваясь в чужие, а гейтинг-сеть тренируется на задаче имитации. Она должна научиться собирать воедино знания остальных экспертов так, чтобы они воспроизводили структуру текущего эталона. Такое разделение ролей делает модель одновременно глубоко специализированной и гибкой, способной адаптироваться к новым рыночным ситуациям.

Это можно сравнить с работой команды аналитиков. У каждого из них есть собственная область экспертизы. Один лучше понимает сырьевые активы, другой специализируется на валютных рынках, третий — на облигациях. Когда возникает новая ситуация, прогноз делает именно тот аналитик, чья область знаний максимально релевантна. Остальные в этот момент выполняют вспомогательную роль. Они помогают команде лучше оценить, насколько их комбинированные взгляды могут воспроизвести ключевое понимание ведущего эксперта.

После обучения, когда модель сталкивается с реальными рыночными данными, она впервые оказывается в условиях полной неопределённости. Если в процессе обучения у неё всегда был доступ к правильному графону Pi, закреплённому за соответствующим временным интервалом, то теперь такой подсказки больше нет. Это соответствует естественной ситуации в торговле. Трейдер может опираться на исторические закономерности, но никогда не знает заранее, в какой именно фазе цикла находится рынок сегодня.

Первым шагом в фазе эксплуатации является генерация набора вероятностных графонов всеми экспертами одновременно. Каждый из них создаёт свою интерпретацию структуры связей между активами. По сути, каждый эксперт выдвигает собственную гипотезу рынка. Кто-то видит чётко очерченные кластеры по секторам, другой — глобальные корреляции между валютами и товарными активами, третий — нестабильные, но значимые локальные взаимосвязи.

Следующий шаг заключается в том, чтобы на основе текущего рыночного сигнала xtest вычислить вектор весов.

Эти веса отражают значимость каждого из экспертов в данный момент времени. Можно сказать, гейтинг-сеть играет роль арбитра, который определяет важность мнения каждого эксперта именно в данный момент. Если, например, рынок переживает всплеск волатильности в сырьевых активах, больший вес получат эксперты, обученные на соответствующих сценариях.

После вычисления весов, формируется итоговый смешанный графон, представляющий собой агрегированную картину рыночных связей.

Ключевое отличие фазы эксплуатации от тренировочной заключается в том, что теперь в процесс вовлечены все эксперты одновременно. Если раньше система знала правильного эксперта и использовала остальных лишь для имитации, то теперь приходится доверять коллективной оценке. Этот момент принципиально важен. Реальный рынок не предоставляет готовых эталонов, и модель должна уметь синтезировать новое представление из накопленных знаний.

На заключительном этапе из полученной вероятностной матрицы сэмплируется конкретный граф, отражающий текущее распределение связей между активами. Именно он используется в модуле ST-GNN для построения прогноза. Здесь система фактически строит прогноз динамики рынка, опираясь не на жёстко зафиксированную структуру, а на гибко формируемое представление, созданное всеми экспертами совместно.

В результате получается модель, которая во время эксплуатации ведёт себя как опытный портфельный менеджер. Она не полагается на один источник информации, а сопоставляет и комбинирует разные точки зрения, создавая динамическую карту рынка. Такой подход делает её устойчивой, гибкой и способной сохранять точность прогноза даже тогда, когда привычные рыночные закономерности ломаются под давлением новых событий.

Ещё одно принципиальное достоинство предложенного подхода заключается в универсальности обучаемых графонов. Хотя в представленном выше описании они используются в связке с пространственно-временными графовыми сетями (ST-GNNs), их потенциал значительно шире. Сами по себе графоны являются гибким инструментом описания вероятностных зависимостей и могут служить связующим звеном для целого ряда архитектур.

В частности, в трансформерных моделях графон может выполнять роль динамической маски или формируемой матрицы внимания, где связи между элементами последовательности определяются не заранее заданными правилами, а обученной вероятностной структурой. Это открывает путь к созданию более адаптивных трансформеров, которые способны лучше улавливать меняющиеся рыночные закономерности. Более того, графоны могут использоваться и в гибридных системах, где комбинируются CNN, RNN и механизмы внимания, повышая эффективность любого из этих блоков.

Авторская визуализация фреймворка ST-Expert представлена ниже.

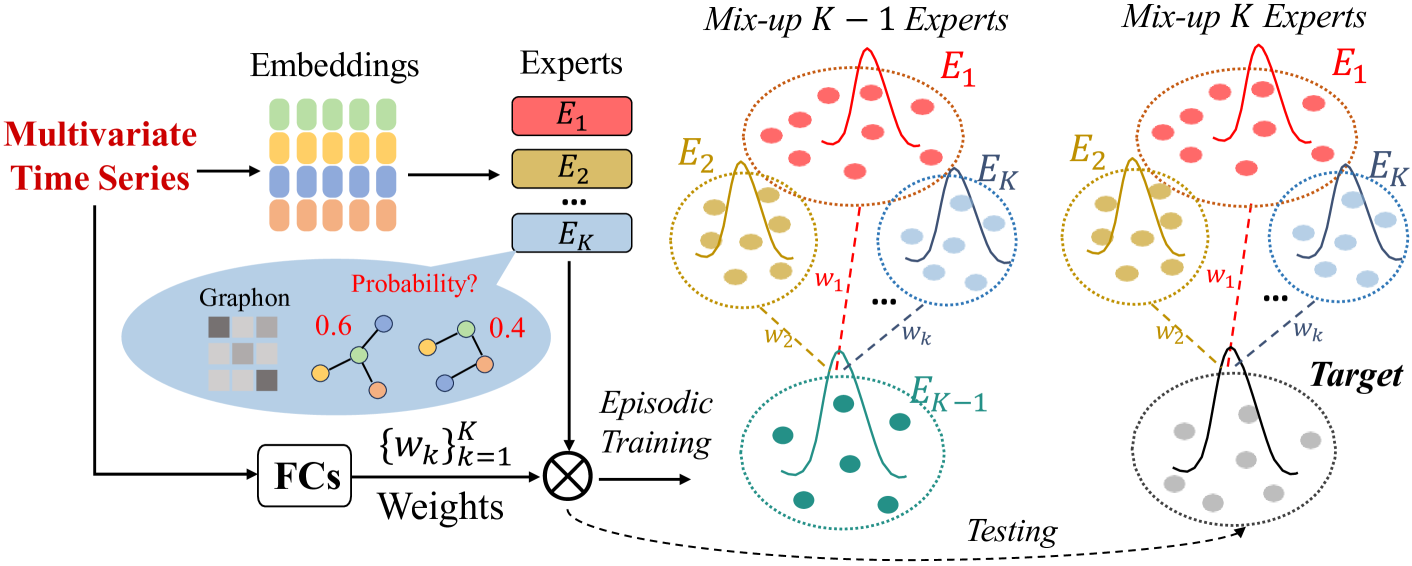
Реализация средствами MQL5

После рассмотрения теоретических аспектов фреймворка ST-Expert, мы переходим к практической реализации его подходов средствами MQL5. И начнём мы свою работу, разумеется, с построения графонов. Но прежде давайте обсудим подходы нашей реализации.

Лично меня в предложенном авторами фреймворка процессе обучения смущают два момента. Первое — это необходимость предварительной обработки обучающей выборки для выделения конкретных рыночных режимов. Процесс этот довольно трудоёмкий, требует дополнительной оптимизационной процедуры и нередко опирается на эвристику. В условиях реального рынка подобная жёсткая сегментация может оказаться не только ресурсоёмкой, но и не вполне надёжной. Границы между режимами часто размыты, а сами режимы могут быстро сменять друг друга. Если мы излишне жёстко разрежем историю, то рискуем потерять важные переходные фазы, которые как раз и формируют основу многих рыночных движений.

Второй момент связан с самой логикой обучения графонов и весов. В оригинальной постановке предполагается, что при подаче наблюдения из интервала Ti именно соответствующий эксперт Pi выполняет прогноз, а оставшиеся комбинируются в смесь, которая должна воспроизвести его структуру. Формально такая схема выглядит элегантно. Каждый графон учится прогнозировать свой режим, а гейтинг-сеть учится собирать остальные так, чтобы они могли имитировать эталон. Однако на практике здесь возникает тонкая проблема. Мы фактически, жёстко закрепляем роли экспертов и исключаем их перекрёстное обучение. Это приводит к риску избыточной специализации, когда эксперт действительно хорошо работает лишь в своей узкой зоне, но абсолютно теряется при малейшем сдвиге рыночного контекста.

Более того, подобная схема делает обучение весов зависимым от корректности эталонного графона. Если Pi в какой-то момент оказался испорчен шумом или зафиксировал нетипичное рыночное состояние, то гейтинг-сеть будет вынуждена учиться воспроизводить именно его, вместо того чтобы выделять более общую закономерность. В условиях финансовых данных, насыщенных случайными выбросами и ложными корреляциями, это может оказаться серьёзным источником ошибок.

В нашей реализации мы попробуем смягчить эту жёсткую иерархию. Вместо того, чтобы навсегда закреплять за каждым экспертом его режим, позволим каждому графону вносить вклад в прогноз с вероятностью, зависящей от текущего состояния рынка. Формально в системе N экспертов, и каждый эксперт даёт свой прогноз. Гейтинг — лёгкая сеть, которая по признакам рынка возвращает логиты. Чтобы добавить эпизодичность и не дать одному эксперту монополизировать внимание, мы используем случайную маску Dropout и пропускаем через SoftMax. В результате получаем веса и итоговый прогноз ансамбля. Такая схема позволяет весам учиться не только на задаче имитации эталона, но и на коллективном улучшении прогноза — когда важность эксперта определяется тем, насколько его вклад улучшает ансамбль в данном состоянии рынка.

Функция потерь строится как смесь задач. В её основе должна лежать мера качества ансамбля, но к ней добавляется взвешенная сумма индивидуальных потерь экспертов. Это стимулирует экспертов улучшать прогнозы именно там, где они важны.

Dropout в гейтинге превращает обучение в эпизодическое испытание. В каждом батче активный набор экспертов немного меняется, и модель учится не полагаться постоянно на одного везучего эксперта. В процессе обучения Dropout включён, а при инференсе отключается, что позволяет использовать знания всех экспертов.

Новый класс CNeuronGraphons служит предметной оболочкой для нашей реализации гибкого ансамбля графонов. Он инкапсулирует состояние гейта, эмбеддинги входных данных, параметры экспертов и сам набор графонов — всё, что нужно генерации взвешенно графона из множества экспертных голосов на каждом шаге.

class CNeuronGraphons   :  public CNeuronBaseOCL
  {
protected:
   CLayer            acProbability;
   CLayer            acDataEmb;
   CParams           cExpertsEmb;
   CNeuronBaseOCL    cGraphs;
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL) override;
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL) override;

public:
                     CNeuronGraphons(void) {};
                    ~CNeuronGraphons(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint units, uint window, uint emb_dimension,
                          uint experts, float dropout,
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void) override const   {  return defNeuronGraphons;   }
   //--- methods for working with files
   virtual bool      Save(int const file_handle) override;
   virtual bool      Load(int const file_handle) override;
   //---
   virtual bool      WeightsUpdate(CNeuronBaseOCL *source, float tau) override;
   virtual void      SetOpenCL(COpenCLMy *obj) override;
   virtual void      SetActivationFunction(ENUM_ACTIVATION value) override { };
   virtual void      TrainMode(bool flag) override;
  };

Внутри класса объявлены четыре внутренних объекта, и каждый из них выполняет свою отдельную функцию — о подробностях мы поговорим при реализации методов. Все они объявлены статично, а значит, жизненный цикл этих компонентов управляется на уровне класса. Благодаря этому, конструктор и деструктор могут оставаться пустыми. Никакой дополнительной инициализации или очистки на каждое создание объекта не требуется. Такое решение упрощает управление ресурсами, уменьшает накладные расходы при множественном создании экземпляров и делает поведение класса более предсказуемым.

Инициализация через `Init` даёт полный контроль над конфигурацией: количество выходов, индекс нейрона в сети, указатель на OpenCL-контекст, число внутренние юнитов и окно агрегирования, размер эмбеддинга, число экспертов, величина dropout, тип оптимизации и размер батча. Это позволяет, с одной стороны, задать лёгкую MLP-реализацию гейта для быстрых тестов, а с другой — при необходимости переключиться на высокопроизводительный OpenCL-путь. Метод `TrainMode(bool)` управляет режимом работы: в тренировке включается inverted Dropout и возможны дополнительные стохастические приёмы; в инференсе отключение Dropout делает поведение детерминированным, что важно для продакшна и стабильных торговых решений.

Весь процесс создания архитектуры объекта и наполнения внутренних компонентов вынесен в метод Init, который выполняет роль дирижёра всего процесса. Он поднимает базовую иерархию нейронов, связывает внутренние компоненты с OpenCL-контектсом и аккуратно проверяет каждый шаг, чтобы на выходе получить полностью готовый к работе модуль.

bool CNeuronGraphons::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                           uint units, uint window, uint emb_dimension,
                           uint experts, float dropout,
                           ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, units * units, optimization_type, batch))
      return false;
   activation = None;

Сначала вызывается одноименный метод родительского класса — это обязательная предварительная инициализация базового объекта. Если она возвращает false, значит базовая инфраструктура не готова и дальнейшая сборка бессмысленна, поэтому метод сразу завершает работу с результатом false. После успешного возврата, мы явно снимаем активацию, ведь конкретные функции активации для подкомпонентов мы зададим ниже индивидуально.

Следующим шагом инициализируется буфер cGraphs — здесь мы подготавливаем контейнер для записи индивидуальных графонов наших экспертов. После этого, явно задаётся функция активация SIGMOID, чтобы их внутренняя логика работала в нужном диапазоне.

   int index = 0;
   if(!cGraphs.Init(0, index, OpenCL, Neurons()*experts, optimization, iBatch))
      return false;
   cGraphs.SetActivationFunction(SIGMOID);

Затем объявляется набор локальных переменных для временного хранения указателей на подкомпоненты, которыми мы будем манипулировать при пошаговой сборке модели.

   CNeuronBaseOCL       *neuron  = NULL;
   CNeuronConvOCL       *conv    = NULL;
   CNeuronTransposeOCL  *transp  = NULL;
   CNeuronDropoutOCL    *dout    = NULL;
   CNeuronSoftMaxOCL    *softmax = NULL;

Переходим к формированию модели генерации вероятностей использования экспертов. Вначале мы очищаем соответствующий динамический массив и привязываем к контексту OpenCL.

//--- Probability
   acProbability.Clear();
   acProbability.SetOpenCL(OpenCL);
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(experts, index, OpenCL, window, window, experts, units, 1, optimization, iBatch) ||
      !acProbability.Add(conv))
     {
      DeleteObj(conv);
      return false;
     }
   conv.SetActivationFunction(SoftPlus);

И начинаем поочерёдную сборку. Первым создаём свёрточный слой с нелинейностью SoftPlus, что даёт мягкую, монотонно возрастающую трансформацию логитов перед следующим слоем. А за ним создаём полносвязный слой, возвращающий experts чисел — это тот самый вектор логитов до Dropout.

   index++;
   neuron = new CNeuronBaseOCL();
   if(!neuron ||
      !neuron.Init(0, index, OpenCL, experts, optimization, iBatch) ||
      !acProbability.Add(neuron))
     {
      DeleteObj(neuron);
      return false;
     }

Как и прежде, при ошибке выделения или инициализации мы корректно удаляем объект и завершаем инициализацию с false.

Далее создаём слой Dropout — именно этот объект реализует случайное исключение экспертов, о котором говорили ранее.

   index++;
   dout = new CNeuronDropoutOCL();
   if(!dout ||
      !dout.Init(0, index, OpenCL, experts, dropout, optimization, iBatch) ||
      !acProbability.Add(dout))
     {
      DeleteObj(dout);
      return false;
     }

Ещё один шаг — создание слоя SoftMax, который переводит полученные ранее логиты в вектор вероятностей важности экспертов.

   index++;
   softmax = new CNeuronSoftMaxOCL();
   if(!softmax ||
      !softmax.Init(0, index, OpenCL, experts, optimization, iBatch) ||
      !acProbability.Add(softmax))
     {
      DeleteObj(softmax);
      return false;
     }
   softmax.SetHeads(1);

Далее начинается подготовка блока эмбеддингов исходных данных acDataEmb. Очищаем его, привязываем к OpenCL и начинаем по аналогии сборку из свёрточных слоёв. Здесь мы используем небольшую MLP из двух последовательных сверточных слоев с нелинейностью SoftPlus между ними.

//--- Data Embedding
   acDataEmb.Clear();
   acDataEmb.SetOpenCL(OpenCL);
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, window, window, 2 * emb_dimension, units, 1, optimization,
                                                                                   iBatch) ||
      !acDataEmb.Add(conv))
     {
      DeleteObj(conv);
      return false;
     }
   conv.SetActivationFunction(SoftPlus);
   index++;
   conv = new CNeuronConvOCL();
   if(!conv ||
      !conv.Init(0, index, OpenCL, 2 * emb_dimension, 2 * emb_dimension, emb_dimension, units,
                                                                   1, optimization, iBatch) ||
      !acDataEmb.Add(conv))
     {
      DeleteObj(conv);
      return false;
     }
   conv.SetActivationFunction(None);

На выходе этой MLP мы ожидаем получить эмбеддинги каждого временного шага анализируемой мультимодальной последовательности. Однако для генерации графонов нам потребуется транспонированная копия данного представления. Поэтому следом добавляется слой транспонирования данных.

   index++;
   transp = new CNeuronTransposeOCL();
   if(!transp ||
      !transp.Init(0, index, OpenCL, units, emb_dimension, optimization, iBatch) ||
      !acDataEmb.Add(transp))
     {
      DeleteObj(transp);
      return false;
     }
   transp.SetActivationFunction((ENUM_ACTIVATION)conv.Activation());

Далее нам остается инициализировать лишь объект генерации эмбедингов наших экспертов cExpertsEmb. Здесь  готовится пространство для их индивидуальных представлений.

   index++;
   if(!cExpertsEmb.Init(0, index, OpenCL, units * emb_dimension * experts, optimization, iBatch))
      return false;
//---
   return true;
  }

И наконец, при отсутствии ошибок метод возвращает true, сигнализируя, что объект полностью инициализирован и готов к обучению.

В поведении метода мы видим чёткую идеологию: сначала готовится контейнер графонов, затем строится пайплайн генерации вероятностей, формируется эмбеддинг исходных данных и в конце выделяется пространство параметров для экспертов. Такая последовательность обеспечивает логичную сборку, удобную для отладки и последующей интеграции с OpenCL.

Метод feedForward строит прямой проход как аккуратно прописанную фабрику сигналов. Вначале мы сохраняем указатель на текущий источник сигнала локальную переменную и заводим дополнительную для временного хранения ссылки на обрабатываемый слой.

bool CNeuronGraphons::feedForward(CNeuronBaseOCL *NeuronOCL)
  {
   CNeuronBaseOCL* prev = NeuronOCL;
   CNeuronBaseOCL* current = NULL;

Дальше идёт проход по блоку прогнозирования вероятностей использования экспертов. Мы в цикле перебирает все подкомпоненты, отвечающие за генерацию логитов.

//--- Probability
   for(int i = 0; i < acProbability.Total(); i++)
     {
      current = acProbability[i];
      if(!current ||
         !current.FeedForward(prev))
         return false;
      prev = current;
     }

На каждой итерации мы берём очередной компонент и просим его выполнить свой прямой проход. Если компонент отсутствует, или его FeedForward вернул false, мы немедленно завершаем работу метода с результатом false. Это строгая и надёжная политика fail-fast, которая защищает от некорректной сборки пайплайна.

После успешного выполнения слоя, мы сдвигаем указатель на объект исходных данных. Следующий слой получит на вход выход текущего. В результате этого цикла получаем готовый вектор нормированных вероятностей.

Далее мы заново инициализируем указатель источника исходных данных и точно тем же шаблоном обходим блок acDataEmb. Этот вторичный линейный проход формирует эмбеддинги исходных данных.

//--- Data Embedding
   prev = NeuronOCL;
   for(int i = 0; i < acDataEmb.Total(); i++)
     {
      current = acDataEmb[i];
      if(!current ||
         !current.FeedForward(prev))
         return false;
      prev = current;
     }

Затем идёт маленькая, но важная ветка: если мы в режиме обучения, то вызываем метод генерации эмбедингов экспертов. Это означает, что параметры или представления экспертов обновляются только в тренировочном прогоне. В режиме инференса мы ожидаем, что cExpertsEmb уже содержит готовые веса, и пропускаем этот шаг, экономя время.

//--- Experts
   if(bTrain)
      if(!cExpertsEmb.FeedForward())
         return false;

Далее начинается ключевая алгебра. Мы вычисляем вспомогательные размеры архитектуры объекта.

//--- Graphs
   uint units = (uint)MathSqrt((double)Neurons());
   uint emb_dim = acDataEmb[-1].Neurons() / units;
   uint experts = cExpertsEmb.Neurons() / acDataEmb[-1].Neurons();

Эти простые выкладки гарантируют согласование форматов перед матричными умножениями. Первое матричное умножение строит для каждого эксперта его собственную матрицу графа. Результирующий буфер cGraphs аккуратно содержит последовательность таких матриц для всех экспертов.

   if(!MatMul(cExpertsEmb.getOutput(), current.getOutput(), cGraphs.getOutput(),
              units, emb_dim, units, experts, false))
      return false;
   if(cGraphs.Activation() != None)
      if(!Activation(cGraphs.getOutput(), cGraphs.getOutput(), cGraphs.Activation()))
         return false;

После получения сырых матриц графонов, выполняется контрольная нелинейность. Здесь мы применяем выбранную функцию активации ко всем элементам выходного буфера. Это важный шаг для приведения значений в требуемый диапазон и добавления желаемой нелинейности.

Финальная редукция превращает набор экспертных матриц и вектор вероятностей в единственный итоговый тензор взвешенного графа. Иными словами, мы берём вектор нормированных весов от последнего слоя acProbability и склеиваем матрицы всех экспертов в один взвешенный результат.

//--- Result
   if(!MatMul(acProbability[-1].getOutput(), cGraphs.getOutput(), Output, 1, experts, units * units, 1, false))
      return false;
//---
   return true;
  }

Если все шаги выполнены успешно, метод возвращает true, подтверждая корректное завершение прямого прохода.

Алгоритм методов обратного прохода следует той же логике, что и прямой проход, но движется в обратном направлении. Сигналы ошибки проходят через все слои в обратном порядке, градиенты аккуратно накапливаются и передаются от выходов к входам, обеспечивая корректное обучение всех компонентов. Поскольку структура полностью зеркальна методу feedForward и все шаги легко прослеживаются по уже разобранной последовательности, детально останавливаться на каждом этапе сейчас не имеет смысла. Для полного понимания и практической работы со всеми методами класса, весь код, включая обратный проход, представлен во вложении.

Сегодня мы хорошо поработали, и пришло время немного передохнуть, дать информации осесть и структурироваться в голове. В следующей статье мы продолжим начатую работу и подробно рассмотрим практическое применение графонов.

Заключение

В данной статье мы подробно познакомились с теоретическими аспектами фреймворка ST-Expert, который сочетает в себе принципы гибкого гейтинга, коллективного обучения и адаптивной агрегации. Мы рассмотрели, как комбинация блоков генерации вероятностей, эмбеддингов исходных данных и экспертных представлений позволяет создавать устойчивые к шуму и неопределённости модели.

В практической части представлена архитектура класса CNeuronGraphons, позволяющую реализовать построение и обучение графонов. Описанные методы формируют прочную основу для последующего практического использования.

Ссылки

• Robust Traffic Forecasting against Spatial Shift over Years
• Другие статьи серии

Программы, используемые в статье

#	Имя	Тип	Описание
1	Study.mq5	Советник	Советник офлайн обучения моделей
2	StudyOnline.mq5	Советник	Советник онлайн обучения моделей
3	Test.mq5	Советник	Советник для тестирования модели
4	Trajectory.mqh	Библиотека класса	Структура описания состояния системы и архитектуры моделей
5	NeuroNet.mqh	Библиотека класса	Библиотека классов для создания нейронной сети
6	NeuroNet.cl	Библиотека	Библиотека кода OpenCL-программы