MetaTrader 5 / Statistics and analysis
Русский 中文 Español Deutsch 日本語
preview
Stepwise feature selection in MQL5

Stepwise feature selection in MQL5

MetaTrader 5 — Statistics and analysis |
953 0
Francis Dube
Francis Dube

Introduction

Traditional stepwise feature selection is a technique used to identify an optimal subset of variables from a larger pool of candidate features for a machine learning task. This process begins by evaluating each candidate feature individually to select the most promising variable for inclusion in the final model. Subsequently, additional candidates are tested for their contribution in combination with those already chosen, continuing until a target level of predictive or classification performance is achieved.

In this article, we examine the limitations of conventional stepwise feature selection, such as its potential for overfitting and its challenges in capturing interactions between features. We then introduce an enhanced algorithm designed to address these issues, implemented in MQL5, which provides flexible integration with various supervised learning methods.

This improved approach, was developed by Timothy Masters and described in his book Modern Data Mining Algorithms in C++ and CUDA C. Finally, we showcase the algorithm’s practical application by using it to select optimal variables for a sample regression task, illustrating its effectiveness.


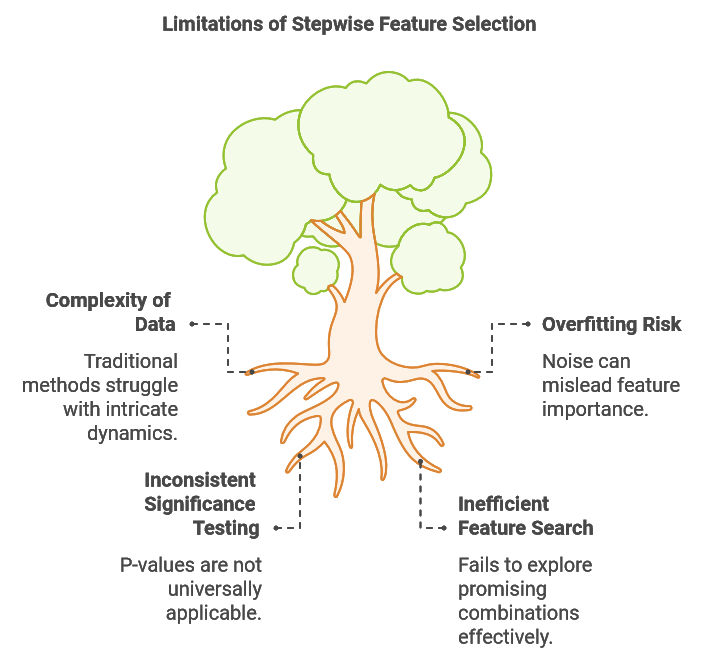
Limitations of Stepwise Feature Selection

Data sets used in machine learning tasks are often inherently complex, sometimes, featuring non-linear relationships, time-varying patterns, and numerous interconnected factors. This complexity poses significant challenges for feature selection, as traditional methods like stepwise selection may struggle to capture these intricate dynamics. One key limitation of stepwise selection is its inability to evaluate the impact of diverse feature combinations. Frequently, a feature that appears uninformative on its own or when paired with certain other variables may become highly predictive when combined with specific complementary features.

Consider the task of building a predictive model for foreign exchange rates. In this scenario, we might gather various technical and fundamental indicators. Some fundamental indicators may seem to offer little predictive value individually or when paired with non-complementary technical data. However, combining indicators such as upcoming election outcomes with the current market trend might yield a more robust prediction than relying on market trends alone. Furthermore, understanding the overall economic climate and anticipating how incoming leadership might respond to macroeconomic conditions could significantly enhance the model’s predictive accuracy. These challenges highlight the need for an enhanced stepwise selection method that can test promising feature combinations without resorting to a computationally prohibitive exhaustive search.

A second challenge with stepwise selection is its susceptibility to overfitting due to noise. Each time a new variable is added, the algorithm risks mistaking random fluctuations for valuable information, which can lead it to learn patterns that fail to generalize. For example, adding multiple technical indicators may increase in-sample performance if the model starts fitting to market noise rather than meaningful trends, thereby compromising its robustness on out-of-sample data. This issue often arises when model performance is judged solely by in-sample fit, resulting in the inclusion of more variables than necessary and ultimately degrading out-of-sample performance.

The statistical significance of feature selection is often evaluated using p-values. In traditional regression-based stepwise selection, p-values assess the likelihood that a feature’s coefficient is zero, reflecting its predictive power. Confidence intervals further provide a range for the true population coefficient, accounting for sampling uncertainty. A low p-value indicates strong evidence against the null hypothesis (that the coefficient is zero), supporting the feature’s significance. These p-values are derived from hypothesis testing, where the null hypothesis assumes a zero coefficient and the alternative hypothesis assumes a non-zero coefficient. To obtain the p-value, we calculate a t-score based on the coefficient estimate and its standard error.

However, this approach is specific to regression models. For other machine learning techniques, obtaining comparable p-values would require a customized hypothesis test, adding complexity to the practical application of the algorithm. Ideally, a more universally applicable technique would provide a relevant measure of significance, producing a p-value or equivalent metric that remains consistent across different types of machine learning methods.

Limitations of conventional stepwise feature selection

Considering the limitations of conventional stepwise feature selection, the modified algorithm presented here offers three key improvements over the traditional method. The first enhancement addresses the challenge of efficiently searching for promising feature subsets. By maintaining multiple high-potential subsets and evaluating new candidates in combination with these subsets, the modified algorithm achieves a balance between comprehensive exploration and computational efficiency. This approach allows it to uncover synergistic relationships among features that traditional stepwise selection may overlook.

To reduce the risk of overfitting, the algorithm uses cross-validation performance as the basis for assessing feature sets. This rigorous evaluation method minimizes the chances of mistaking random noise for meaningful predictive information and provides a straightforward mechanism for automatically halting the inclusion of additional features when diminishing returns are detected.

Additionally, for each new feature added, the algorithm calculates two probabilities:

  • Probability of chance occurrence: This probability measures the likelihood that the observed performance of the current feature set could be attributed to chance, assuming all selected features are irrelevant.
  • Probability of spurious improvement: This probability assesses the chance that the performance gain from the latest feature addition is due to chance rather than genuine predictive value.

These probabilities offer insights into the statistical significance of the feature selection process, helping to distinguish genuine predictive power from statistical noise. Notably, these calculated probabilities are model-agnostic, allowing the algorithm to integrate seamlessly with a wide range of machine learning models. In the following sections, we will examine key parts of the code that implement this algorithm. The code snippets provided are extracted from the CStepwisebase class, defined in stepwise.mqh. This class is abstract, requiring users to create a derived class that implements certain virtual members, enabling the integration of any type of model.


The Stepwise Procedure

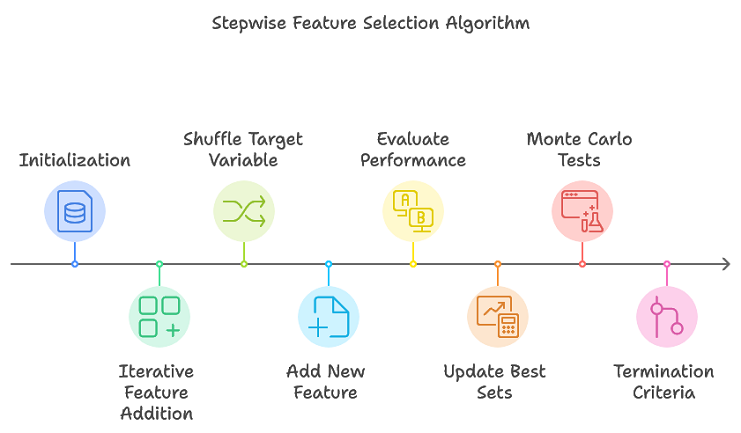
The proposed algorithm enhances traditional stepwise selection by tracking multiple promising feature subsets, avoiding the need for an exhaustive search. This approach efficiently narrows down feature subsets likely to form the final optimal set. An overview of the procedure is as follows:

  1. Initialization: Data structures used throughout the process to store information about feature set trials are initialized.
  2. Iterative feature addition: For each iteration, perform multiple permutation replications. Shuffle the target variable to create a new permutation. Add a new feature to the current feature set. Evaluate the performance of the updated feature set using cross-validation. Update the best-performing feature sets and their corresponding performance metrics. 
  3. Termination criteria: The algorithm terminates when either the maximum number of features (as defined by max_num_predictors) is reached or when the performance improvement falls below a predefined threshold.

    Enhanced Stepwise Feature Selection Algorithm

The main steps are implemented in stepwiseSearch(), with the process governed by several hyperparameters that control different aspects of the search. These hyperparameters are:

  • num_kept: The number of candidate feature subsets with the best performance, based on the criterion, to retain at each iteration. These candidates are considered likely to form the optimal feature set,
  • num_folds: The number of folds used in cross-validation. While larger values improve the accuracy of performance estimates, they also increase the computational cost,
  • min_num_predictors: The minimum number of predictors the final feature set can contain, allowing users to define a lower limit for model complexity,
  • max_num_predictors: The maximum number of predictors allowed in the final feature set, providing an upper bound for model complexity,
  • num_replications: The number of iterations for the Monte Carlo permutation test, which helps assess the statistical significance of feature performance,
  • verbose_output: Determines whether the results of each step in the feature selection process are displayed in MetaTrader 5’s Experts tab.

These parameters provide flexibility, allowing users to fine-tune the feature selection process to match their needs. They can be specified by invoking setParams().

//+------------------------------------------------------------------+
//|   set the stepwise selection parameters                          |
//+------------------------------------------------------------------+
void              setParams(ulong num_kept, ulong num_folds, ulong min_num_predictors, ulong max_num_predictors,long num_replications,bool verbose_output)
  {
   m_keptvars = num_kept>0?num_kept:1;
   m_folds = num_folds>0?num_folds:ULONG_MAX;
   m_min_num_preds = min_num_predictors;
   m_max_num_preds = max_num_predictors;
   m_reps = num_replications>0?num_replications:1;
   m_verbose = verbose_output;
   return;
  }

The stepwiseSearch() method begins by initializing internal data structures to keep track of the various trials of feature sets. It then enters a main loop that continues until the maximum number of predictors is reached. During each iteration of the loop, the target variable is randomly shuffled for multiple repetitions, and a new variable is added to the model by calling addFeature(). The algorithm stores the best-performing model features, and if adding a new variable results in performance degradation, it may terminate early. If the performance continues to improve, the process persists until the maximum number of predictors is achieved. Finally, the indices of the selected variables are saved in the m_var_indices array.

//+------------------------------------------------------------------+
//|  coordinates main stepwise search operation                      |
//+------------------------------------------------------------------+
int               stepwiseSearch(void)
  {
   int done = 1;
   int btrials;
   m_trial_length = m_max_num_preds*m_vars*m_keptvars;

   reset();

   if(!m_prior_best_crits.Resize(m_keptvars) || !m_all_best_crits.Resize(m_reps,m_keptvars))
     {
      Print(__FUNCTION__," data structure resizing error ", GetLastError());
      return done;
     }

   if(ArrayResize(m_all_best_trials,int(m_reps*m_max_num_preds*m_keptvars))<0  ||
      ArrayResize(m_already_tried,int(m_trial_length))<0 ||
      ArrayResize(m_trial_vars,int(m_max_num_preds))<0 ||
      ArrayResize(m_prior_best_trials,int(m_max_num_preds*m_keptvars))<0)
     {
      Print(__FUNCTION__,"  error resizing array ", GetLastError());
      return done;
     }


   ArrayInitialize(m_all_best_trials,-1);
   ArrayInitialize(m_already_tried,-1);
   ArrayInitialize(m_trial_vars,-1);
   ArrayInitialize(m_prior_best_trials,-1);

   vector target;
   int n_so_far =0;
   int rval, rem, j,n_this_rep = 0;
   int mcpt_mod_count, mcpt_change_count;
   mcpt_mod_count = mcpt_mod_count = mcpt_change_count = -1;
   double temp,prior_crit;
   double original_crit, original_change, new_crit;
   original_crit = original_change = new_crit = -DBL_MIN;

   if(m_verbose)
     {
      if(m_reps>1)
         Print("Criterion  || New pval  || Diff pval  || Column Indices");
      else
         Print("Criterion  || Column Indices");
     }
   while(true)
     {

      target = m_target;

      for(ulong rep=0; rep<m_reps; rep++)
        {


         if(rep)
           {
            rval = 17*int(rep) + 11;
            unif(rval);
            unif(rval);
            rem = int(m_samples);
            while(rem>1)
              {
               j = (int)(unif(rval))*rem;
               if(j>=rem)
                  j = rem-1;
               temp = target[--rem];
               target[rem] = target[j];
               target[j] = temp;
              }
           }

         btrials = int(rep*m_max_num_preds*m_keptvars);
         if(n_so_far == 0)
            prior_crit = -1.e60;
         else
            prior_crit = m_all_best_crits[rep][0];
         n_this_rep = n_so_far;

         done = addFeature(target,n_this_rep,btrials,rep);

         if(done || n_this_rep!=(n_so_far+1))
           {
            Print(__FUNCTION__, " internal error ");
            return 1;
           }

         if(m_all_best_crits[rep][0]<=prior_crit && n_so_far>=int(m_min_num_preds) && !rep)
           {
            for(ulong i = 0 ; i<m_keptvars; i++)
              {
               m_all_best_crits[rep][i] = m_prior_best_crits[i];
               if(ArrayCopy(m_all_best_trials,m_prior_best_trials,btrials+int(i*n_so_far),int(i*n_so_far),n_so_far)<0)
                 {
                  Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
                  return 1;
                 }
              }
            if(m_verbose)
               Print(__FUNCTION__, " procedure terminated early because adding a new variable caused performance degradation");
            return 0;
           }

         if(prior_crit < 0.0)
            prior_crit = 0.0;

         new_crit = m_all_best_crits[rep][0];

         if(new_crit<0.0)
            new_crit = 0.0;

         if(rep == 0)
           {
            original_crit = new_crit;
            original_change = new_crit - prior_crit;
            mcpt_mod_count = mcpt_change_count = 1;
           }
         else
           {
            if(new_crit >= original_crit)
               ++mcpt_mod_count;
            if(new_crit - prior_crit >= original_change)
               ++mcpt_change_count;
           }

        }

      if(n_so_far == 0)
         mcpt_change_count = mcpt_mod_count;

      if(!m_decision_matrix.Resize(n_so_far+1,m_reps>1?3:1,100) || ArrayResize(m_var_indices,int(m_var_indices.Size())+n_this_rep,100)<0)
        {
         Print(__FUNCTION__, " container resize error ", GetLastError());
         return 1;
        }

      string msg;
      if(m_reps>1)
        {
         double mod_pval = (double) mcpt_mod_count / (double) m_reps;
         double change_pval = (double) mcpt_change_count / (double) m_reps;

         if(m_verbose)
            msg = StringFormat("%10.8lf %10.8lf %10.8lf  ", original_crit,mod_pval,change_pval);

         m_decision_matrix[n_so_far][0] = original_crit;
         m_decision_matrix[n_so_far][1] = mod_pval;
         m_decision_matrix[n_so_far][2] = change_pval;
        }
      else
        {
         msg = m_verbose?StringFormat("%10.8lf", original_crit):NULL;
         m_decision_matrix[n_so_far][0] = original_crit;
        }
      if(m_verbose)
        {
         for(int i = 0; i<n_this_rep; i++)
           {
            msg += StringFormat(" %s",IntegerToString(m_all_best_trials[i]));
           }
        }
      if(ArrayCopy(m_var_indices,m_all_best_trials,(n_so_far*(n_so_far+1))/2,0,n_this_rep)<0)
        {
         Print(__FUNCTION__, " array copy error ", GetLastError());
         return 1;
        }

      if(m_verbose)
         Print(msg);

      ++n_so_far;
      if(n_so_far == int(m_max_num_preds))
        {
         if(m_verbose)
            Print(" Stepwise selection successfully completed ");
         break;
        }
     }

   return 0;

  }


Calculating the Cross-Validated Criterion

Relying on a single training dataset for feature selection often yields suboptimal results due to the risk of overfitting. To mitigate this risk, cross-validation is used. Cross-validation involves splitting the dataset into multiple training and validation sets, allowing for a more comprehensive evaluation of model performance and feature importance. By iteratively training and testing on different data subsets, cross-validation reduces overfitting and improves generalization.

While cross-validation is highly effective, it does present a trade-off between computational efficiency and statistical reliability. A larger number of folds generally provides a more accurate estimate of model performance but increases computational demands. The ideal number of folds depends on both the dataset characteristics and the available computational resources. In practice, determining the appropriate number of folds requires careful consideration of dataset size and the desired level of statistical confidence. By understanding both the principles and limitations of cross-validation, practitioners can apply this technique to enhance the reliability and robustness of their feature selection and model-building processes.

The cross-validation procedure is implemented by the crossEval() method. 

//+------------------------------------------------------------------+
//|  evaluates a predictor set using cross validation                |
//+------------------------------------------------------------------+
int               crossEval(ulong num_vars,vector &target,double &criterion)
  {
   ulong ifold, n_remaining, test_start, test_stop ;
   double error, evalresult ;

   n_remaining = m_samples;
   test_start = 0;

   error = 0.0;

   for(ifold = 0; ifold<m_folds; ifold++)
     {
      test_stop = test_start + (n_remaining/(m_folds-ifold));
      if(!fitModel(num_vars,test_start,test_stop,target))
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " fit() failed ");
         return 1;
        }
      evalresult = evalModel(num_vars,test_start,test_stop,target);
      if(evalresult==EMPTY_VALUE)
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " evalModel() failed ");
         return 1;
        }
      error+=evalresult;
      n_remaining -= test_stop - test_start;
      test_start = test_stop;
     }

   criterion = 1.0 - error/double(m_samples);
   return 0;
  }

This function takes as input the number of predictors to be assessed, a vector of shuffled target values, and a reference to a variable that will return the value of a criterion—used as one of the decision variables for identifying the most suitable feature subset. The function returns 0 upon successful execution. It operates by first fitting a model and then evaluating its performance across all folds of the sample data.

The fitModel() method is responsible for training a model on a candidate feature subset. It takes the following inputs:

  • num_preds: The number of predictors,
  • row_start: The index of the first sample,
  • row_stop: The index one past the last sample to exclude from the training set, and,
  • targets: The vector of shuffled target values.

This function returns a boolean value indicating whether the model was successfully trained.

The evalModel() function has the same inputs as fitModel(), but this time, the specified partition of rows represents the samples used to evaluate the trained model. This function returns a value that provides an indication of the model's performance. Both fitModel() and evalModel() are virtual members, requiring implementation in a derived class to integrate the specific model type being used.

//+------------------------------------------------------------------+
//| fit a model                                                      |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return false;}
//+------------------------------------------------------------------+
//| evaluate a model                                                 |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return EMPTY_VALUE;}


Finding the First Feature

The addFirstFeature() method is invoked by addFeature() to identify the first predictor in a given set.

//+------------------------------------------------------------------+
//|     finds the first predictor in the set                         |
//+------------------------------------------------------------------+
int               addFirstFeature(vector &targ, int bindex,ulong rep_index)
  {
   double crit;

   for(ulong i = 0; i<m_keptvars; i++)
     {
      m_all_best_crits[rep_index][i] = -1.e60;
      m_all_best_trials[bindex+i] = -1;
     }

   for(int i = 0; i<int(m_vars); i++)
     {
      m_trial_vars[0] = i;
      if(crossEval(1,targ,crit))
        {
         Print(__FUNCTION__, " xval error ");
         return 1;
        }
      ulong j;
      for(j = 0; j<m_keptvars; j++)
        {
         if(crit > m_all_best_crits[rep_index][j])
            break;
        }
      if(j<m_keptvars)
        {
         for(long k = long(m_keptvars-2); k>=long(j); k--)
           {
            m_all_best_trials[bindex+k+1] = m_all_best_trials[bindex+k];
            m_all_best_crits[rep_index][k+1] = m_all_best_crits[rep_index][k];
           }
         m_all_best_trials[bindex+j] = i;
         m_all_best_crits[rep_index][j] = crit;
        }
     }

   return 0;
  }

It iterates over each variable, evaluating its performance using cross-validation. The performance is assessed based on a criterion defined in a derived class, which, in turn, informs the learning technique that determines the model.

During this evaluation, the method maintains a list of the best-performing variables along with their corresponding criterion values. As each variable is assessed, its performance is compared to that of the current best variables. If a new variable outperforms one of the existing top-performing variables, it is inserted into the list, causing the lower-performing variables to shift down.

This process continues until all variables have been evaluated, culminating in the identification of the first predictor. For subsequent calls to addFeature(), a new variable is introduced by invoking addNewFeature(), ensuring a systematic approach to feature addition.


Adding to the Feature Set

The addNewFeature() method identifies the next predictor to include in the model's feature set. 

//+------------------------------------------------------------------+
//|  looks for next predictor to include                             |
//+------------------------------------------------------------------+
int               addNewFeature(vector& target,int &ind, int bindex,ulong rep_index)
  {
   int i, j, k, ivar, ir ;
   int npred, n_already_tried,nbest, rootvars;
   nbest  = -1;
   double crit;

   ind = npred = ind+1;

   for(i = 0; i<int(m_keptvars); i++)
     {
      m_prior_best_crits[i] = m_all_best_crits[rep_index][i];
      if(ArrayCopy(m_prior_best_trials,m_all_best_trials,int(i*(npred-1)),bindex+int(i*(npred-1)),npred-1)<0)
        {
         Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
         return 1;
        }
      m_all_best_crits[rep_index][i] = -1.e60;
     }
   n_already_tried = 0;
   for(ir = 0; ir<int(m_keptvars); ir++)
     {
      if(m_prior_best_crits[ir] < -1.e59)
         break;
     }
   nbest = ir;

   for(ir = 0; ir<nbest; ir++)
     {
      rootvars = ir*(npred-1);
      for(ivar=0; ivar<int(m_vars); ivar++)
        {
         for(i = 0; i<npred-1; i++)
           {
            if(m_prior_best_trials[rootvars+i] == ivar)
               break;
           }
         if(i < npred-1)
            continue;
         k = 0;

         for(i = 0; i<int(m_vars); i++)
           {
            for(j=0; j<npred-1; j++)
              {
               if(m_prior_best_trials[rootvars+j] == i)
                 {
                  m_trial_vars[k++] = i;
                  break;
                 }
              }
            if(ivar == i)
               m_trial_vars[k++] = i;
           }
         for(i = 0; i<n_already_tried; i++)
           {
            for(j = 0; j<npred; j++)
              {
               if(m_trial_vars[j] != m_already_tried[i*npred+j])
                  break;
              }
            if(j == npred)
               break;
           }
         if(i < n_already_tried)
            continue;

         for(i =0; i<npred; i++)
            m_already_tried[n_already_tried*npred+i]=m_trial_vars[i];
         ++n_already_tried;

         if(crossEval(ulong(npred),target,crit))
           {
            Print(__FUNCTION__, " xval error ");
            return 1;
           }

         for(i = 0; i< int(m_keptvars); i++)
           {
            if(crit > m_all_best_crits[rep_index][i])
               break;
           }

         if(i<int(m_keptvars))
           {
            for(j = int(m_keptvars-2); j>=i; j--)
              {
               m_all_best_crits[rep_index][j+1] = m_all_best_crits[rep_index][j];
               if(ArrayCopy(m_all_best_trials,m_all_best_trials,bindex+int((j+1)*npred),bindex+int(j*npred),npred)<0)
                 {
                  Print(__FUNCTION__, " array copy error ", GetLastError());
                  return 1;
                 }
              }
            m_all_best_crits[rep_index][i] = crit;
            if(ArrayCopy(m_all_best_trials,m_trial_vars,bindex+int(i*npred),0,npred)<0)
              {
               Print(__FUNCTION__, " array copy error ", GetLastError());
               return 1;
              }
           }
        }
     }
   return 0;
  }

It builds upon the existing set of predictors by examining all possible combinations of the current best predictors with additional variables. For each combination, the method performs cross-validation to evaluate its performance, which is measured using a specified criterion. Having examined the core elements of the stepwise feature selection code, we will now explore how these snippets integrate to form the complete implementation.


The CStepwisebase Class

The CStepwisebase class serves as a foundational implementation for stepwise feature selection, designed to select predictive features iteratively from a set of candidates. This selection process systematically adds variables based on their contributions to a predictive model's performance. As an abstract class, it allows for the integration of any type of learning technique and its corresponding criterion within a derived class by implementing the methods fitModel() and evalModel(). An example of this implementation will be provided in the next section.

The method stepwiseSelection() acts as the main publicly accessible entry point, initiating the process by preparing the data and executing stepwiseSearch(). 

//+------------------------------------------------------------------+
//|  main method to execute stepwise feature selection               |
//+------------------------------------------------------------------+
bool              stepwiseSelection(matrix& predictors, vector& targets)
  {

   if(targets.Size()!=predictors.Rows() || !targets.Size())
     {
      Print(__FUNCTION__, " invalid inputs ");
      return false;
     }

   m_data = stdmat(predictors);

   m_target = (targets-targets.Mean())/(targets.Std()+1e-10);

   m_vars = predictors.Cols();
   m_samples = predictors.Rows();

   if(m_keptvars>m_vars || m_keptvars<1)
      m_keptvars = m_vars;

   if(m_folds<1)
      m_folds = 1;

   if(m_folds>m_samples)
      m_folds = m_samples;

   if(m_min_num_preds==0 || m_min_num_preds>m_vars || m_min_num_preds>m_max_num_preds)
      m_min_num_preds = m_vars;

   if(m_max_num_preds==0 || m_max_num_preds>m_vars || m_max_num_preds<m_min_num_preds)
      m_max_num_preds = m_vars;

   if(m_reps<1)
      m_reps = 1;

   if(m_verbose)
     {
      Print(" STEPWISE SELECTION PARAMETERS ");
      Print(" Number of retained candidate variables for each iteration ", m_keptvars);
      Print(" Number of folds in cross validation procedure ", m_folds);
      Print(" Final minimum number of selected predictors ", m_min_num_preds);
      Print(" Final maximum number of selected predictors ", m_max_num_preds);
      Print(" Number of replications for MCP test ", m_reps);
     }

   return (stepwiseSearch()==0);
  }

To configure the parameters for the feature selection process beforehand, the setParams() method is available. The output from the feature selection process can be displayed in MetaTrader 5's Experts tab by setting the last parameter of setParams() to true. Furthermore, results from the selection procedure can be retrieved using the following methods:

  •  Calling getCriticalVals() returns a matrix with a varying number of columns depending on whether a Monte Carlo permutation (MCP) test is specified as part of the stepwise search. This is achieved by setting num_replications in setParams() to any value greater than 1. In this case, getCriticalVals() returns a matrix with three columns, where each row contains values quantifying the addition of an extra feature. The number of rows in this matrix corresponds to the number of iterations through the outermost loop of the stepwise algorithm. The three values in each row consist of the criterion, a p-value indicating the probability that the observed performance is attributable to chance (assuming the selected features are irrelevant), and another p-value reflecting the probability that the performance improvement resulting from the iteration's feature addition is due to chance.
    //+------------------------------------------------------------------+
//| get all crit values and corresponding p-values                   |
//+------------------------------------------------------------------+
matrix            getCriticalVals(void)
  {
   return m_decision_matrix;
  }
  • When no MCP test is specified, the function returns a single column containing the respective criterion values for each iteration of the algorithm's run. The number of best feature subsets found can be queried using getNumFeatureSets(), while the feature sets themselves can be retrieved by calling getFeatureSetAt(), which accepts an index corresponding to the desired iteration and a reference to an array where the indices of the columns representing the feature subset will be copied.
    //+------------------------------------------------------------------+
//|  get the selected features at a specific iteration of the process|
//|  iterations denoted as zero based indices                        |
//|  eg, first selected feature located at iteration index 0         |
//+------------------------------------------------------------------+
bool              getFeatureSetAt(ulong iteration_index,ulong &selectedvars[])
  {
   if(ArrayCopy(selectedvars,m_var_indices,0,int((iteration_index*(iteration_index+1))/2),int(iteration_index+1))>0)
      return true;
   else
     {
      Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
      return false;
     }
  }
//+---------------------------------------------------------------------+
//| get maximum number of iterations cycled through in selection process|
//+---------------------------------------------------------------------+
ulong             getNumFeatureSets(void)
  {
   return m_decision_matrix.Rows();
  }

This concludes our discussion of the base class. In the next section, we will explore how to apply this code by integrating a model and running tests.


An Example Using a Linear-Quadratic Regression Model

To illustrate the enhanced stepwise selection algorithm, we will demonstrate its application in evaluating a dataset of candidate predictors for fitting a linear-quadratic regression model. This implementation is provided in the MetaTrader 5 script, StepWiseFeatureSelection_Demo.mq5. In this script, we will outline the process of selecting the most predictive features through the enhanced stepwise selection method, showcasing how the algorithm identifies optimal predictors for the linear-quadratic regression model. The practical demonstration will include setting up the dataset, configuring the model parameters, and executing the feature selection process within the MetaTrader 5 environment.

Linear-quadratic regression is an extension of linear regression that incorporates both linear and quadratic (squared) terms of the predictor variable(s). This approach enables the model to capture non-linear relationships by fitting a curve to the data instead of a straight line. The general form of a linear-quadratic regression equation for a single predictor variable X is given by the general formula below.

Linear Quadratic Regression Formula

Where:

  • y is the dependent variable,
  • x is the independent variable,
  • β0, β1​, and β2​ are coefficients to be estimated,
  • x-squared is the quadratic term, which allows the model to account for curvature,
  • ϵ is the error term.

In this equation, the term βx models the linear relationship, while β(x-squared) captures the curvature, making the model useful for data that displays a parabolic or curved trend. The coefficient β0​ represents the intercept, β1​ controls the slope of the linear portion, and β2​ affects the curvature, determining whether the parabola opens upward (β2>0) or downward (β2<0).

In practice, linear-quadratic regression is applied in situations where the relationship between the dependent and independent variables is not strictly linear. The implementation of linear-quadratic regression in our script is enabled by leveraging the Ordinary Least Squares (OLS) class defined in OLS.mqh.

Next, we will walk through how this regression model is integrated into the stepwise selection process, allowing for the identification of optimal predictors from our dataset.

The StepWiseFeatureSelection_Demo.mq5 script effectively implements the enhanced stepwise feature selection algorithm tailored for linear-quadratic regression models. What follows is a breakdown of the components and functionalities of the script. The CStepwise class inherits from CStepwisebase, providing a concrete implementation of the abstract methods defined in the base class. This design allows for the integration of specific model logic for linear-quadratic regression. The core logic for fitting and evaluating the linear-quadratic model is encapsulated within the CStepwise class. This includes the necessary adjustments to accommodate both linear and quadratic terms of the predictor variables.

The method, fitModel(), is responsible for constructing the design matrix based on the training samples. It excludes the specified range of data meant for validation during cross-validation. An instance of the OLS class is created (denoted as m_ols), which manages the ordinary least squares regression operations. 

//+------------------------------------------------------------------+
//|    fit the OLS model                                             |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   ulong ntrain = m_samples - (row_stop - row_start);

   vector dependent(ntrain);
   matrix independent(ntrain,nvars+1);
   ntrain = 0;

   for(ulong sample=0; sample<m_samples; sample++)
     {
      if(sample>=row_start && sample<row_stop)
         continue;
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            independent[ntrain][var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               independent[ntrain][var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               independent[ntrain][var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }
      independent[ntrain][nvars] = 1.0;
      dependent[ntrain++] = targets[sample];
     }

   return m_ols.Fit(dependent,independent);
  }

In evalModel(), the method evaluates the performance of the trained linear-quadratic model using the data that was left out during the training phase. The criterion for assessing model performance is specified here, which, in this case, is the summation of squared errors (SSE). This criterion measures how well the model's predictions align with the actual outcomes.

//+------------------------------------------------------------------+
//|      evaluate the model                                          |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   if(m_ols.Loglikelihood()==EMPTY_VALUE)
     {
      Print(__FUNCTION__, " OLS error ");
      return EMPTY_VALUE;
     }

   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   double prediction;
   vector row(nvars);
   double error = 0.0;
   for(ulong sample=row_start; sample<row_stop; sample++)
     {
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            row[var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               row[var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               row[var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }

      prediction = m_ols.Predict(row);
      if(prediction == EMPTY_VALUE)
        {
         Print(__FUNCTION__, " OLS predict() error ");
         return EMPTY_VALUE;
        }
      error+=pow(prediction-targets[sample],2.0);
     }

   return error;
  }

Following the definition of the derived CStepwise class, the script generates a random 100 by 10 matrix, denoted as mat, is generated with values ranging between 0 and 1. This matrix serves as the dataset containing the predictor variables.

//---
   MathSrand(120);
//---
   matrix mat(100,10);
//---
   mat.Random(0.0,1.0);
//---

A target vector is created by summing specific columns. The target variable is defined as the sum of values from columns 0, 5, 4, and 6 of the matrix. This defines the dependent variable (or output) that the model aims to predict based on the independent variables (the remaining columns).

//---
   vector target = mat.Col(0) + mat.Col(5) + mat.Col(4) + mat.Col(6);
//---

An instance of the CStepwise class is created, referred to as stepwise. This instance will manage the stepwise feature selection process tailored for the linear-quadratic regression model. The setParams() method is invoked on the stepwise instance to configure the parameters for the stepwise selection process.

//---
   CStepwise stepwise;
   stepwise.setParams(NumKeptVars,NumFolds,MinNumVars,MaxNumVars,NumReplications,true);
   if(!stepwise.stepwiseSelection(mat,target))
      return;

The parameters, which can be adjusted by the user, include:

input ulong NumKeptVars = 1;
input ulong NumFolds = 10;
input ulong MinNumVars = 3;
input ulong MaxNumVars = 5;
input long NumReplications = 1;
  • NumKeptVars: Specifies the desired number of features to retain in each iteration of the selection process.
  • NumFolds: Determines the number of folds to be used for cross-validation, facilitating robust evaluation of the model's performance.
  • MinNumVars: Sets the minimum number of features that the final selected feature set can contain, ensuring that the model remains adequately equipped for prediction.
  • MaxNumVars: Establishes the maximum number of features allowed in the final feature set, preventing overfitting by controlling model complexity.
  • NumReplications: Indicates the number of iterations for the Monte-Carlo permutation test, enhancing the reliability of the significance tests performed during feature selection.

Once the stepwiseSelection() method is invoked, the stepwise feature selection process begins. This method orchestrates the entire selection algorithm, implementing the strategies discussed earlier to identify the most relevant predictors for the linear-quadratic regression model. The output generated from the StepWiseFeatureSelection_Demo.mq5 script can provide valuable insights into how different hyperparameters influence the feature selection process. Let's delve into the various aspects of the output and how they relate to the specified input parameters.

The key output components of the algorithm are:

  1. Selected Feature Sets: The primary output is the set of features selected by the algorithm after running the stepwise selection. Each feature set represents a combination of predictors deemed most relevant based on their contribution to model performance.
  2. Performance Metrics:For each iteration of the selection process, the script will typically output performance metrics such as:
    •  Criterion Value: The summation of squared errors or another chosen criterion, providing a quantifiable measure of the model's fit.
    •  P-Values: If Monte-Carlo permutation testing is employed, the output will include p-values indicating the probability that the observed performance improvements are due to chance.

In the initial run of the StepWiseFeatureSelection_Demo.mq5 script with default parameters, we set the stage for observing how the stepwise selection process functions under a constrained setup. Here’s a breakdown of what to expect from the output, the rationale behind these expectations, and how the results align with our observations.

Since no MCP test is specified, the output will indeed only a single column with the criterion values corresponding to each iteration. This will reflect the performance of the model as predictors are added. The criterion values are expected to increase at each iteration. This indicates that the model’s performance is improving as relevant predictors are added. The algorithm strategically selects features that enhance predictive accuracy, thereby driving the criterion upward. Eventually, as the relevant predictors are identified, the criterion will reach an optimal value (in this case, 1). This suggests that the model has successfully incorporated the most informative predictors and is performing as best as it can, given the constraints of the model.

MM      0       20:20:28.754    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 
QM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
KG      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
QH      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
FI      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
FM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
PM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 1
KR      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || Column Indices
ED      0       21:05:21.067    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 6
NO      0       21:05:21.089    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 4 6
RG      0       21:05:21.122    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 4 5 6
HH      0       21:05:21.170    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0 4 5 6
GL      0       21:05:21.240    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

In the output log, each iteration will display the current criterion value after evaluating the selected predictors. The increasing trend will provide a clear picture of how each feature addition contributes to model performance. The output should also indicate the reason for termination, which will likely mention that additional features did not lead to improved performance, affirming the algorithm’s decision-making process in real time. This is enabled by the parameter that specifies the minimum number of predictors allowed in a feature set.

In a subsequent run of the StepWiseFeatureSelection_Demo.mq5 script, we introduce a Monte-Carlo permutation (MCP) test with 100 permutations while maintaining the default values for the other parameters. This adjustment significantly enriches the output, providing more profound insights into the feature selection process.

With the MCP test enabled, the output will now consist of multiple columns. Each row will correspond to an iteration, displaying the criterion value and the probability of chance occurrence and the probability of spurious improvement. A low p-value (typically ≤ 0.05) indicates that the observed performance is likely not due to chance, supporting the inclusion of the corresponding feature.

The two p-values presented will guide users in evaluating the reliability of the selected predictors.

RI      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
LK      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
RD      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
EM      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
EQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
OQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
PI      0       21:10:57.101    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
RD      0       21:10:58.851    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 0.01000000 0.01000000   6
EI      0       21:11:01.243    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 0.01000000 0.01000000   4 6
KM      0       21:11:04.482    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 0.01000000 0.01000000   4 5 6
FP      0       21:11:09.151    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
CI      0       21:11:09.214    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

This run, enhanced by the inclusion of a Monte-Carlo permutation test, provides a richer and more informative output. The multiple columns allow users to make more informed decisions about the optimal feature set based on both performance criteria and statistical significance. As a result, users can confidently identify which predictors should be retained in the final model, guided by high criterion values and low p-values.

LL      0       07:22:46.657    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
GH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
ID      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 5
FH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 10
JO      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 10
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
LG      0       07:22:47.303    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26726680 0.01000000 0.01000000   6
LJ      0       07:22:48.153    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.56836766 0.01000000 0.01000000   4 6
FH      0       07:22:49.518    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.74542884 0.01000000 0.01000000   4 5 6
NM      0       07:22:51.488    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
KQ      0       07:22:54.163    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.71000000   0 1 4 5 6
JF      0       07:22:57.793    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.85000000   0 1 2 4 5 6
DD      0       07:23:02.436    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.94000000   0 1 2 3 4 5 6
MK      0       07:23:08.007    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7
DH      0       07:23:13.842    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8
HO      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8 9
PL      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed

In the final run of the StepWiseFeatureSelection_Demo.mq5 script, the focus is on expanding the scope of the feature selection process by increasing the MinNumVars parameter to allow for a minimum of 10 predictors. Allowing for more predictors in the final subset will enable the algorithm to evaluate larger combinations of features, potentially uncovering interactions or nonlinear relationships that a smaller subset might miss. While increasing the minimum number of predictors allows for a more extensive search, it is essential to note that this will also lead to longer runtime for the algorithm. The added complexity of evaluating larger feature sets necessitates more computational resources and time.

The algorithm's built-in checks ensure that if MinNumVars or MaxNumVars are set to values exceeding the total number of candidate predictors (in this case, 10), they will be automatically adjusted to match the available number of predictors in the dataset. This safeguard prevents configuration errors that could lead to runtime issues or improper feature selection behaviour. By modifying the MinNumVars parameter, users can tailor the stepwise feature selection process to explore a broader range of features, potentially leading to the discovery of more informative predictor sets. This flexibility enhances the algorithm's usability, allowing practitioners to adapt the selection process to the specific characteristics of their datasets and analysis goals.

The runtime of the algorithm depends on the selected hyperparameters. The Monte-Carlo permutation test can significantly slow down the process, especially as the number of permutations increases. Each permutation requires a full evaluation of the model, which adds to the total number of computations performed. Thus, while more permutations can enhance the robustness of the statistical significance results, they also demand more processing time.

Outside the MCP test, the next parameter that can impact the runtime of the algorithm is the number of folds specified for cross-validation. Cross-validation involves partitioning the dataset into several subsets and repeatedly training and testing the model across these different subsets. As the number of folds increases, the algorithm must perform more training and evaluation iterations. This is particularly time-consuming, especially with larger datasets, as each fold requires a complete model fit and evaluation.

Lastly, careful consideration should be given when selecting the appropriate minimum and maximum number of predictors allowed in the final model. With more predictors being considered for inclusion, the algorithm has to assess more combinations during the feature selection process, leading to an increase in the number of search cycles needed to uncover the optimal feature subsets. Given the trade-offs involved in these parameters, it is important for practitioners to thoughtfully select hyperparameters based on their specific use case.


Conclusion

In this article, we explored an enhanced stepwise feature selection algorithm designed to optimize the identification of predictive features from a larger set of variables. Augmented by cross-validation and optional Monte-Carlo permutation tests, the algorithm provides a framework that addresses the limitations of traditional stepwise methods, enabling the selection of feature subsets that maximize predictive performance while minimizing the risk of overfitting.

We examined the importance of hyperparameter tuning in balancing computational efficiency and statistical reliability, highlighting how parameters such as the number of folds for cross-validation, the number of permutations for significance testing, and constraints on the minimum and maximum number of predictors can significantly impact the algorithm's runtime.

The practical demonstration using the StepWiseFeatureSelection_Demo.mq5 script illustrated how the algorithm can be effectively applied to real datasets, yielding insights into the significance of selected feature subsets. In conclusion, the proposed method not only enhances the feature selection process but also could empower practitioners to make informed decisions about model building. All code referenced in the text is attached in the files below.

File
Description
MQL5/include/np.mqh
 Contains definition of utility functions for manipulating matrices and vectors.
MQL5/include/OLS.mqh
 Header file for OLS class that implements Ordinary least squares regression.
MQL5/include/stepwise.mqh
 Header file for CStepwisebase class that implements an enchanced stepwise feature selection method.
MQL5/scripts/StepWiseFeatureSelection_Demo.mq5
 A script that applies the CStepwisebase class to perform stepwise feature selection on an arbitrary dataset.
Attached files |
Download ZIP
np.mqh (74.16 KB)
OLS.mqh (13.32 KB)
stepwise.mqh (21.13 KB)
StepWiseFeatureSelection_Demo.mq5 (5.37 KB)
MQL5.zip (19.51 KB)
Warning: All rights to these materials are reserved by MetaQuotes Ltd. Copying or reprinting of these materials in whole or in part is prohibited.

Other articles by this author

Go to discussion
MQL5 Wizard Techniques you should know (Part 46): Ichimoku MQL5 Wizard Techniques you should know (Part 46): Ichimoku
The Ichimuko Kinko Hyo is a renown Japanese indicator that serves as a trend identification system. We examine this, on a pattern by pattern basis, as has been the case in previous similar articles, and also assess its strategies & test reports with the help of the MQL5 wizard library classes and assembly.
Multiple Symbol Analysis With Python And MQL5 (Part II): Principal Components Analysis For Portfolio Optimization Multiple Symbol Analysis With Python And MQL5 (Part II): Principal Components Analysis For Portfolio Optimization
Managing trading account risk is a challenge for all traders. How can we develop trading applications that dynamically learn high, medium, and low-risk modes for various symbols in MetaTrader 5? By using PCA, we gain better control over portfolio variance. I’ll demonstrate how to create applications that learn these three risk modes from market data fetched from MetaTrader 5.
Feature Engineering With Python And MQL5 (Part II): Angle Of Price Feature Engineering With Python And MQL5 (Part II): Angle Of Price
There are many posts in the MQL5 Forum asking for help calculating the slope of price changes. This article will demonstrate one possible way of calculating the angle formed by the changes in price in any market you wish to trade. Additionally, we will answer if engineering this new feature is worth the extra effort and time invested. We will explore if the slope of the price can improve any of our AI model's accuracy when forecasting the USDZAR pair on the M1.
News Trading Made Easy (Part 5): Performing Trades (II) News Trading Made Easy (Part 5): Performing Trades (II)
This article will expand on the trade management class to include buy-stop and sell-stop orders to trade news events and implement an expiration constraint on these orders to prevent any overnight trading. A slippage function will be embedded into the expert to try and prevent or minimize possible slippage that may occur when using stop orders in trading, especially during news events.