MQL5中的逐步特征选择

MetaTrader 5 — 统计分析 | 29 七月 2025, 14:44

105

Francis Dube

概述

传统的逐步特征选择是一种用于从较大的候选特征池中识别出最优变量子集的技术，用于机器学习任务。这一过程从单独评估每个候选特征开始，以选择最有希望被纳入最终模型的变量。随后，会测试其他候选特征与已选定特征的组合贡献，直到达到目标水平的预测或分类性能为止。

在本文中，我们探讨了传统逐步特征选择的局限性，例如其过拟合的潜在风险以及在捕捉特征之间相互作用方面的挑战。然后，我们介绍了一种增强型算法，该算法旨在解决这些问题，并在MQL5中实现，它能够灵活地与各种监督学习方法集成。

这种改进方法由Timothy Masters开发，并在其著作《C++和CUDA C中的现代数据挖掘算法》中进行了阐述。最后，我们通过使用该算法为样本回归任务选择最优变量，展示其实际应用，证明其有效性。

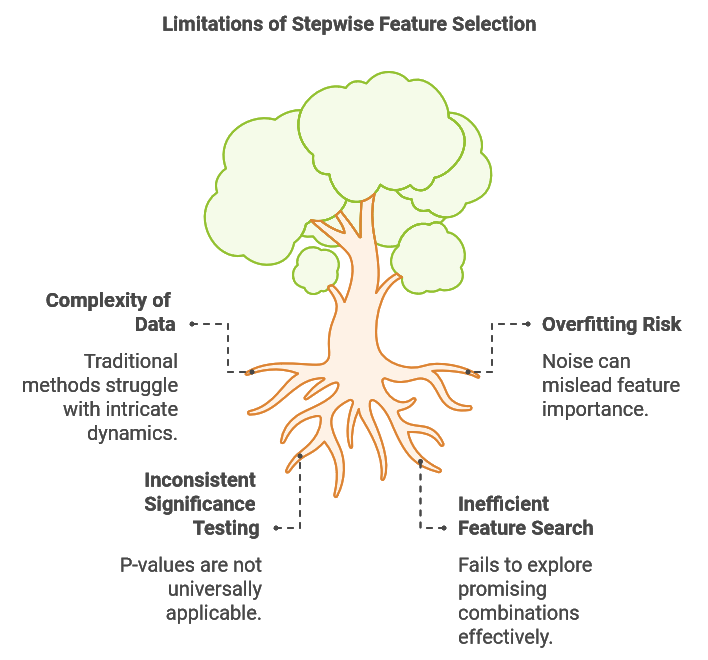
逐步特征选择的局限性

机器学习任务中使用的数据集通常具有内在的复杂性，有时会呈现非线性关系、时变模式以及众多相互关联的因素。这种复杂性给特征选择带来了重大挑战，因为传统的逐步选择方法可能难以捕捉这些复杂动态。逐步选择的一个关键局限性是其无法评估多样化特征组合的影响。通常，一个单独看起来没有信息量的特征，或者与某些其他变量配对时，当与特定的互补特征组合时，可能会变得具有高度预测性。

考虑构建外汇汇率预测模型的任务。在这种情况下，我们可能会收集各种技术和基本面指标。一些基本面指标单独或与非互补技术数据配对时，似乎只提供很少的预测价值。然而，将即将举行的选举结果与当前市场趋势相结合，与单独依赖市场趋势相比，可能会产生更稳健的预测。此外，了解整体经济环境并预测新领导层可能如何应对宏观经济条件，可以显著提高模型的预测准确性。这些挑战突显了需要一种增强的逐步选择方法，该方法能够在不诉诸计算成本高昂的穷尽搜索的情况下，对有潜力的特征组合进行测试。

逐步选择的第二个挑战是其由于噪声而容易过拟合。每添加一个新变量时，算法都有可能将随机波动误认为有价值的信息，这可能导致它学习到无法泛化的模式。例如，如果模型开始拟合市场噪声而不是有意义的趋势，添加多个技术指标可能会增加样本内性能，从而损害其在样本外数据上的稳健性。当仅根据样本内拟合来判断模型性能时，通常会出现这个问题，结果是包含的变量比必要的多，最终降低了样本外性能。

特征选择的统计显著性通常使用p值来评估。在传统的基于回归的逐步选择中，p值评估特征系数为0的可能性，反映其预测能力。置信区间进一步为真实总体系数提供了一个范围，考虑了抽样不确定性。低p值表明对零假设（系数为0）有强有力的证据，支持特征的显著性。这些p值是通过假设检验得出的，其中零假设假设系数为0，备择假设假设系数不为0。为了获得p值，我们根据系数估计值及其标准误差计算t分数。

然而，这种方法特别针对于回归模型。对于其他机器学习技术而言，要获得可比较的p值则需要进行定制化的假设检验，这增加了算法在实际应用中的复杂性。理想情况下，一种更普遍适用的技术将提供一个相关的显著性度量，产生一个在不同类型的机器学习方法中保持一致的p值或等效指标。

传统逐步特征选择的局限性

考虑传统逐步特征选择的局限性，这里提出的改进算法基于传统方法上有三个关键改进。第一个增强解决了高效搜索有希望的特征子集的挑战。通过维护多个高潜力子集，并评估这些子集与新候选特征的组合，改进后的算法在全面探索和计算效率之间取得了平衡。这种方法使它能够发现传统逐步选择可能忽视的特征之间的协同关系。

为了减少过拟合的风险，该算法使用交叉验证性能作为评估特征集的基础。这种严格的评估方法最小化了将随机噪声误认为有意义的预测信息的可能性，并提供了一个简单的机制，当检测到收益递减时自动停止添加更多特征。

此外，对于每个新添加的特征，算法计算两个概率：

偶然发生的概率：这个概率衡量当前特征集的表现可以归因于偶然的可能性，假设所有选定的特征都是无关的。
虚假改进的概率：这个概率评估最新特征添加带来的性能提升是由于偶然而不是真正的预测价值的可能性。

这些概率为特征选择过程的统计显著性提供了见解，帮助区分真正的预测能力与统计噪声。值得注意的是，这些计算出的概率是模型不可知的，允许该算法无缝地与各种机器学习模型集成。在接下来的部分中，我们将检查实现该算法的关键代码部分。提供的代码段是从stepwise.mqh中定义的CStepwisebase类中提取的。这个类是抽象的，需要用户创建一个派生类来实现某些虚拟成员，从而实现任何类型的模型的集成。

逐步过程

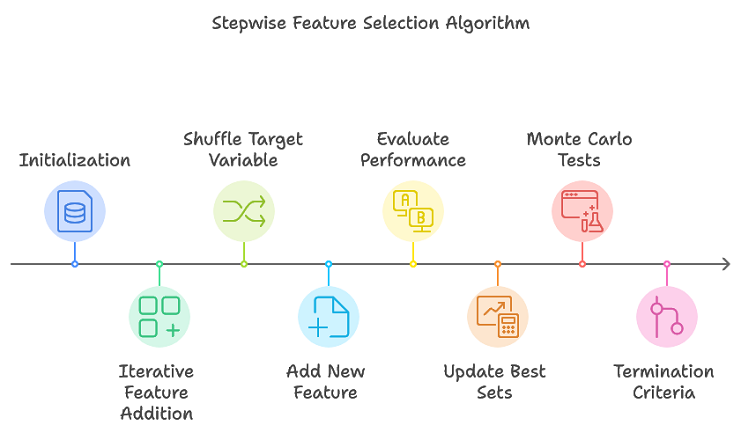
提出的算法通过跟踪多个有希望的特征子集来增强传统的逐步选择，避免了穷尽搜索的必要性。这种方法有效地缩小了可能形成最终最优集的特征子集。该过程的概述如下：

初始化：用于存储特征集试验信息的数据结构在整个过程中被初始化。
迭代特征添加：对于每次迭代，执行多次排列复制。打乱目标变量以创建一个新的排列。将一个新特征添加到当前特征集中。使用交叉验证评估更新后的特征集的性能。更新表现最优的特征集及其对应的性能指标。
终止条件：当达到最大特征数量（由max_num_predictors定义）或者性能提升低于预定义阈值时，算法终止。

主要步骤在stepwiseSearch()函数中实现，整个过程由几个超参数控制，这些超参数负责搜索的不同方面。这些超参数包括：

num_kept：在每次迭代中，根据标准保留表现最佳的候选特征子集的数量。这些候选特征被认为可能形成最优特征集。
num_folds：在交叉验证中使用的折数。虽然较大的值可以提高性能估计的准确性，但它们也会增加计算成本。
min_num_predictors：最终特征集可以包含的最小预测器数量，允许用户定义模型复杂度的下限。
max_num_predictors：最终特征集允许的最大预测器数量，为模型复杂度提供上限。
num_replications：蒙特卡洛排列测试的迭代次数，这有助于评估特征表现的统计显著性。
verbose_output：决定是否在MetaTrader 5的“专家”标签中显示特征选择过程每一步的结果。

这些参数提供了灵活性，允许用户根据自己的需求微调特征选择过程。它们可以通过调用setParams()来指定。

//+------------------------------------------------------------------+
//|   set the stepwise selection parameters                          |
//+------------------------------------------------------------------+
void              setParams(ulong num_kept, ulong num_folds, ulong min_num_predictors, ulong max_num_predictors,long num_replications,bool verbose_output)
  {
   m_keptvars = num_kept>0?num_kept:1;
   m_folds = num_folds>0?num_folds:ULONG_MAX;
   m_min_num_preds = min_num_predictors;
   m_max_num_preds = max_num_predictors;
   m_reps = num_replications>0?num_replications:1;
   m_verbose = verbose_output;
   return;
  }

stepwiseSearch()方法首先初始化内部数据结构，用于跟踪各种特征集的试验情况。随后，它进入一个主循环，该循环会一直持续，直到达到最大预测器数量。在循环的每次迭代中，目标变量会被多次随机打乱，并通过调用addFeature()方法向模型中添加一个新的变量。算法会存储表现最优的模型特征，如果添加一个新变量导致性能下降，它可能会提前终止。如果性能持续改善，该过程会一直持续，直到达到最大预测器数量。最后，所选变量的索引被保存在m_var_indices数组中。

//+------------------------------------------------------------------+
//|  coordinates main stepwise search operation                      |
//+------------------------------------------------------------------+
int               stepwiseSearch(void)
  {
   int done = 1;
   int btrials;
   m_trial_length = m_max_num_preds*m_vars*m_keptvars;

   reset();

   if(!m_prior_best_crits.Resize(m_keptvars) || !m_all_best_crits.Resize(m_reps,m_keptvars))
     {
      Print(__FUNCTION__," data structure resizing error ", GetLastError());
      return done;
     }

   if(ArrayResize(m_all_best_trials,int(m_reps*m_max_num_preds*m_keptvars))<0  ||
      ArrayResize(m_already_tried,int(m_trial_length))<0 ||
      ArrayResize(m_trial_vars,int(m_max_num_preds))<0 ||
      ArrayResize(m_prior_best_trials,int(m_max_num_preds*m_keptvars))<0)
     {
      Print(__FUNCTION__,"  error resizing array ", GetLastError());
      return done;
     }


   ArrayInitialize(m_all_best_trials,-1);
   ArrayInitialize(m_already_tried,-1);
   ArrayInitialize(m_trial_vars,-1);
   ArrayInitialize(m_prior_best_trials,-1);

   vector target;
   int n_so_far =0;
   int rval, rem, j,n_this_rep = 0;
   int mcpt_mod_count, mcpt_change_count;
   mcpt_mod_count = mcpt_mod_count = mcpt_change_count = -1;
   double temp,prior_crit;
   double original_crit, original_change, new_crit;
   original_crit = original_change = new_crit = -DBL_MIN;

   if(m_verbose)
     {
      if(m_reps>1)
         Print("Criterion  || New pval  || Diff pval  || Column Indices");
      else
         Print("Criterion  || Column Indices");
     }
   while(true)
     {

      target = m_target;

      for(ulong rep=0; rep<m_reps; rep++)
        {


         if(rep)
           {
            rval = 17*int(rep) + 11;
            unif(rval);
            unif(rval);
            rem = int(m_samples);
            while(rem>1)
              {
               j = (int)(unif(rval))*rem;
               if(j>=rem)
                  j = rem-1;
               temp = target[--rem];
               target[rem] = target[j];
               target[j] = temp;
              }
           }

         btrials = int(rep*m_max_num_preds*m_keptvars);
         if(n_so_far == 0)
            prior_crit = -1.e60;
         else
            prior_crit = m_all_best_crits[rep][0];
         n_this_rep = n_so_far;

         done = addFeature(target,n_this_rep,btrials,rep);

         if(done || n_this_rep!=(n_so_far+1))
           {
            Print(__FUNCTION__, " internal error ");
            return 1;
           }

         if(m_all_best_crits[rep][0]<=prior_crit && n_so_far>=int(m_min_num_preds) && !rep)
           {
            for(ulong i = 0 ; i<m_keptvars; i++)
              {
               m_all_best_crits[rep][i] = m_prior_best_crits[i];
               if(ArrayCopy(m_all_best_trials,m_prior_best_trials,btrials+int(i*n_so_far),int(i*n_so_far),n_so_far)<0)
                 {
                  Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
                  return 1;
                 }
              }
            if(m_verbose)
               Print(__FUNCTION__, " procedure terminated early because adding a new variable caused performance degradation");
            return 0;
           }

         if(prior_crit < 0.0)
            prior_crit = 0.0;

         new_crit = m_all_best_crits[rep][0];

         if(new_crit<0.0)
            new_crit = 0.0;

         if(rep == 0)
           {
            original_crit = new_crit;
            original_change = new_crit - prior_crit;
            mcpt_mod_count = mcpt_change_count = 1;
           }
         else
           {
            if(new_crit >= original_crit)
               ++mcpt_mod_count;
            if(new_crit - prior_crit >= original_change)
               ++mcpt_change_count;
           }

        }

      if(n_so_far == 0)
         mcpt_change_count = mcpt_mod_count;

      if(!m_decision_matrix.Resize(n_so_far+1,m_reps>1?3:1,100) || ArrayResize(m_var_indices,int(m_var_indices.Size())+n_this_rep,100)<0)
        {
         Print(__FUNCTION__, " container resize error ", GetLastError());
         return 1;
        }

      string msg;
      if(m_reps>1)
        {
         double mod_pval = (double) mcpt_mod_count / (double) m_reps;
         double change_pval = (double) mcpt_change_count / (double) m_reps;

         if(m_verbose)
            msg = StringFormat("%10.8lf %10.8lf %10.8lf  ", original_crit,mod_pval,change_pval);

         m_decision_matrix[n_so_far][0] = original_crit;
         m_decision_matrix[n_so_far][1] = mod_pval;
         m_decision_matrix[n_so_far][2] = change_pval;
        }
      else
        {
         msg = m_verbose?StringFormat("%10.8lf", original_crit):NULL;
         m_decision_matrix[n_so_far][0] = original_crit;
        }
      if(m_verbose)
        {
         for(int i = 0; i<n_this_rep; i++)
           {
            msg += StringFormat(" %s",IntegerToString(m_all_best_trials[i]));
           }
        }
      if(ArrayCopy(m_var_indices,m_all_best_trials,(n_so_far*(n_so_far+1))/2,0,n_this_rep)<0)
        {
         Print(__FUNCTION__, " array copy error ", GetLastError());
         return 1;
        }

      if(m_verbose)
         Print(msg);

      ++n_so_far;
      if(n_so_far == int(m_max_num_preds))
        {
         if(m_verbose)
            Print(" Stepwise selection successfully completed ");
         break;
        }
     }

   return 0;

  }

计算交叉验证标准

仅依赖单一训练数据集进行特征选择，往往会因过拟合风险而导致结果次优。为了降低这种风险，通常会使用交叉验证。交叉验证涉及将数据集划分为多个训练集和验证集，从而能够更全面地评估模型性能和特征的重要性。通过在不同的数据子集上迭代地进行训练和测试，交叉验证可以减少过拟合并提高模型的泛化能力。

尽管交叉验证非常有效，但它确实存在计算效率与统计可靠性之间的权衡。更多的折数通常可以更准确地估计模型性能，但会增加计算需求。理想的折数取决于数据集的特性和可用的计算资源。在实践中，确定合适的折数需要审慎考虑数据集的大小以及所需的统计置信水平。通过理解交叉验证的原理和局限性，使用者可以将这一技术应用于增强特征选择和模型构建过程的可靠性和稳健性。

交叉验证过程通过crossEval()方法实现。

//+------------------------------------------------------------------+
//|  evaluates a predictor set using cross validation                |
//+------------------------------------------------------------------+
int               crossEval(ulong num_vars,vector &target,double &criterion)
  {
   ulong ifold, n_remaining, test_start, test_stop ;
   double error, evalresult ;

   n_remaining = m_samples;
   test_start = 0;

   error = 0.0;

   for(ifold = 0; ifold<m_folds; ifold++)
     {
      test_stop = test_start + (n_remaining/(m_folds-ifold));
      if(!fitModel(num_vars,test_start,test_stop,target))
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " fit() failed ");
         return 1;
        }
      evalresult = evalModel(num_vars,test_start,test_stop,target);
      if(evalresult==EMPTY_VALUE)
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " evalModel() failed ");
         return 1;
        }
      error+=evalresult;
      n_remaining -= test_stop - test_start;
      test_start = test_stop;
     }

   criterion = 1.0 - error/double(m_samples);
   return 0;
  }

这个函数的输入包括要评估的预测器数量、一个打乱的目标值向量，以及一个将返回标准值的变量的引用——该标准值被用作识别最合适的特征子集的决策变量之一。函数成功执行后返回0。其工作原理是首先拟合一个模型，然后在样本数据的所有折上评估其性能。

fitModel()方法负责在候选特征子集上训练模型。其输入包括：

num_preds：预测器的数量
row_start：第一个样本的索引
row_stop：训练集中最后一个样本之后的索引（用于排除最后一个样本）
targets：打乱的目标值向量

该函数返回一个布尔值，指示模型是否成功训练。

evalModel()函数的输入与fitModel()相同，但这次指定的行分区代表用于评估训练模型的样本。这个函数返回一个值，提供模型性能的指示。fitModel()和evalModel()都是虚拟成员，需要在派生类中实现，以便集成正在使用的特定模型类型。

//+------------------------------------------------------------------+
//| fit a model                                                      |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return false;}
//+------------------------------------------------------------------+
//| evaluate a model                                                 |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return EMPTY_VALUE;}

寻找第一个特征

addFirstFeature()方法由addFeature()调用，用于识别给定集合中的第一个预测器。

//+------------------------------------------------------------------+
//|     finds the first predictor in the set                         |
//+------------------------------------------------------------------+
int               addFirstFeature(vector &targ, int bindex,ulong rep_index)
  {
   double crit;

   for(ulong i = 0; i<m_keptvars; i++)
     {
      m_all_best_crits[rep_index][i] = -1.e60;
      m_all_best_trials[bindex+i] = -1;
     }

   for(int i = 0; i<int(m_vars); i++)
     {
      m_trial_vars[0] = i;
      if(crossEval(1,targ,crit))
        {
         Print(__FUNCTION__, " xval error ");
         return 1;
        }
      ulong j;
      for(j = 0; j<m_keptvars; j++)
        {
         if(crit > m_all_best_crits[rep_index][j])
            break;
        }
      if(j<m_keptvars)
        {
         for(long k = long(m_keptvars-2); k>=long(j); k--)
           {
            m_all_best_trials[bindex+k+1] = m_all_best_trials[bindex+k];
            m_all_best_crits[rep_index][k+1] = m_all_best_crits[rep_index][k];
           }
         m_all_best_trials[bindex+j] = i;
         m_all_best_crits[rep_index][j] = crit;
        }
     }

   return 0;
  }

它会遍历每个变量，使用交叉验证来评估其性能。性能是基于在派生类中定义的标准进行评估的，而这个标准反过来又决定了用于确定模型的学习技术。

在评估过程中，该方法会维护一个表现最优的变量列表及其对应的标准值。随着每个变量被评估，其性能会与当前表现最优的变量进行比较。如果一个新变量的表现超过了现有的表现最优的变量之一，那么将其插入到列表中，导致表现较差的变量向下移动。

这个过程会一直持续，直到所有变量都被评估完毕，最终确定第一个预测器。对于后续对addFeature()的调用，通过调用addNewFeature()引入一个新变量，确保了特征添加的系统化方法。

添加到特征集

addNewFeature()方法用于识别要包含在模型特征集中的下一个预测器。

//+------------------------------------------------------------------+
//|  looks for next predictor to include                             |
//+------------------------------------------------------------------+
int               addNewFeature(vector& target,int &ind, int bindex,ulong rep_index)
  {
   int i, j, k, ivar, ir ;
   int npred, n_already_tried,nbest, rootvars;
   nbest  = -1;
   double crit;

   ind = npred = ind+1;

   for(i = 0; i<int(m_keptvars); i++)
     {
      m_prior_best_crits[i] = m_all_best_crits[rep_index][i];
      if(ArrayCopy(m_prior_best_trials,m_all_best_trials,int(i*(npred-1)),bindex+int(i*(npred-1)),npred-1)<0)
        {
         Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
         return 1;
        }
      m_all_best_crits[rep_index][i] = -1.e60;
     }
   n_already_tried = 0;
   for(ir = 0; ir<int(m_keptvars); ir++)
     {
      if(m_prior_best_crits[ir] < -1.e59)
         break;
     }
   nbest = ir;

   for(ir = 0; ir<nbest; ir++)
     {
      rootvars = ir*(npred-1);
      for(ivar=0; ivar<int(m_vars); ivar++)
        {
         for(i = 0; i<npred-1; i++)
           {
            if(m_prior_best_trials[rootvars+i] == ivar)
               break;
           }
         if(i < npred-1)
            continue;
         k = 0;

         for(i = 0; i<int(m_vars); i++)
           {
            for(j=0; j<npred-1; j++)
              {
               if(m_prior_best_trials[rootvars+j] == i)
                 {
                  m_trial_vars[k++] = i;
                  break;
                 }
              }
            if(ivar == i)
               m_trial_vars[k++] = i;
           }
         for(i = 0; i<n_already_tried; i++)
           {
            for(j = 0; j<npred; j++)
              {
               if(m_trial_vars[j] != m_already_tried[i*npred+j])
                  break;
              }
            if(j == npred)
               break;
           }
         if(i < n_already_tried)
            continue;

         for(i =0; i<npred; i++)
            m_already_tried[n_already_tried*npred+i]=m_trial_vars[i];
         ++n_already_tried;

         if(crossEval(ulong(npred),target,crit))
           {
            Print(__FUNCTION__, " xval error ");
            return 1;
           }

         for(i = 0; i< int(m_keptvars); i++)
           {
            if(crit > m_all_best_crits[rep_index][i])
               break;
           }

         if(i<int(m_keptvars))
           {
            for(j = int(m_keptvars-2); j>=i; j--)
              {
               m_all_best_crits[rep_index][j+1] = m_all_best_crits[rep_index][j];
               if(ArrayCopy(m_all_best_trials,m_all_best_trials,bindex+int((j+1)*npred),bindex+int(j*npred),npred)<0)
                 {
                  Print(__FUNCTION__, " array copy error ", GetLastError());
                  return 1;
                 }
              }
            m_all_best_crits[rep_index][i] = crit;
            if(ArrayCopy(m_all_best_trials,m_trial_vars,bindex+int(i*npred),0,npred)<0)
              {
               Print(__FUNCTION__, " array copy error ", GetLastError());
               return 1;
              }
           }
        }
     }
   return 0;
  }

通过检查当前最优预测器与附加变量的所有可能组合来扩展现有的预测器集合。对于每一种组合，该方法都会执行交叉验证以评估其性能，而性能是通过指定的标准来衡量的。在探讨了逐步特征选择代码的核心要素之后，我们现在将探究如何将这些代码段进行整合，以构成完整的实现。

CStepwisebase类

CStepwisebase类是逐步特征选择的基础实现，旨在从一组候选特征中迭代地选择预测性特征。这一选择过程会根据变量对预测模型性能的贡献系统地添加变量。作为一个抽象类，它允许在派生类中通过实现fitModel()和evalModel()方法，整合任何类型的学习技术及其对应的标准。在下一节中将提供这一实现的示例。

stepwiseSelection()方法作为主要的公开可访问的入口点，通过准备数据并执行stepwiseSearch()来启动整个过程。

//+------------------------------------------------------------------+
//|  main method to execute stepwise feature selection               |
//+------------------------------------------------------------------+
bool              stepwiseSelection(matrix& predictors, vector& targets)
  {

   if(targets.Size()!=predictors.Rows() || !targets.Size())
     {
      Print(__FUNCTION__, " invalid inputs ");
      return false;
     }

   m_data = stdmat(predictors);

   m_target = (targets-targets.Mean())/(targets.Std()+1e-10);

   m_vars = predictors.Cols();
   m_samples = predictors.Rows();

   if(m_keptvars>m_vars || m_keptvars<1)
      m_keptvars = m_vars;

   if(m_folds<1)
      m_folds = 1;

   if(m_folds>m_samples)
      m_folds = m_samples;

   if(m_min_num_preds==0 || m_min_num_preds>m_vars || m_min_num_preds>m_max_num_preds)
      m_min_num_preds = m_vars;

   if(m_max_num_preds==0 || m_max_num_preds>m_vars || m_max_num_preds<m_min_num_preds)
      m_max_num_preds = m_vars;

   if(m_reps<1)
      m_reps = 1;

   if(m_verbose)
     {
      Print(" STEPWISE SELECTION PARAMETERS ");
      Print(" Number of retained candidate variables for each iteration ", m_keptvars);
      Print(" Number of folds in cross validation procedure ", m_folds);
      Print(" Final minimum number of selected predictors ", m_min_num_preds);
      Print(" Final maximum number of selected predictors ", m_max_num_preds);
      Print(" Number of replications for MCP test ", m_reps);
     }

   return (stepwiseSearch()==0);
  }

为了提前配置特征选择过程的参数，可以使用setParams()方法。通过将setParams()的最后一个参数设置为true，可以在MetaTrader 5的“Experts”标签中显示特征选择过程的输出。此外，可以使用以下方法获取选择过程的结果：

调用getCriticalVals()会返回一个矩阵，其列数根据是否在逐步搜索中指定了蒙特卡洛排列测试（MCP）而有所不同。这可以通过在setParams()中将num_replications设置为大于1的值来实现。在这种情况下，getCriticalVals()返回一个包含三列的矩阵，每一行包含量化新增特征的值。该矩阵的行数对应于逐步算法最外层循环的迭代次数。每一行中的三个值分别是：标准值、一个表示观察到的性能可归因于偶然的概率的p值（假设所选特征无关紧要），以及另一个表示迭代中新增特征带来的性能提升是由于偶然的概率的p值。
```
//+------------------------------------------------------------------+
//| get all crit values and corresponding p-values                   |
//+------------------------------------------------------------------+
matrix            getCriticalVals(void)
  {
   return m_decision_matrix;
  }
```

当未指定蒙特卡洛排列（MCP）测试时，该函数返回一个单一列，包含算法每次运行迭代对应的标准值。可以通过getNumFeatureSets()查询找到的最佳特征子集的数量，而特征子集本身可以通过调用getFeatureSetAt()获取，该函数接受一个与所需迭代对应的索引以及一个引用，将代表特征子集的列索引复制到该数组中。

//+------------------------------------------------------------------+
//|  get the selected features at a specific iteration of the process|
//|  iterations denoted as zero based indices                        |
//|  eg, first selected feature located at iteration index 0         |
//+------------------------------------------------------------------+
bool              getFeatureSetAt(ulong iteration_index,ulong &selectedvars[])
  {
   if(ArrayCopy(selectedvars,m_var_indices,0,int((iteration_index*(iteration_index+1))/2),int(iteration_index+1))>0)
      return true;
   else
     {
      Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
      return false;
     }
  }
//+---------------------------------------------------------------------+
//| get maximum number of iterations cycled through in selection process|
//+---------------------------------------------------------------------+
ulong             getNumFeatureSets(void)
  {
   return m_decision_matrix.Rows();
  }

我们对基础类的讨论将告一段落。在下一部分中，我们将探讨如何通过整合模型并运行测试来应用这段代码。

一个使用线性-二次回归模型的示例

为了展示增强型逐步选择算法，我们将通过一个示例来说明其在评估候选预测器数据集以拟合线性-二次回归模型中的应用。这一实现收录在MetaTrader 5脚本StepWiseFeatureSelection_Demo.mq5中。在这个脚本中，我们将简述通过增强型逐步选择方法选择最具预测性的特征的过程，展示算法如何为线性-二次回归模型识别最优预测器。实际演示将包括设置数据集、配置模型参数，并在MetaTrader 5环境中执行特征选择过程。

线性-二次回归是线性回归的扩展，它同时包含了预测变量的线性和二次（平方）项。这种方法通过拟合一条曲线而不是一条直线来捕捉非线性关系，从而使模型能够更好地拟合数据。单个预测变量X的线性-二次回归方程的一般形式由以下通用公式给出：

其中：

y是因变量
x是自变量
β0、β1和β2是需要估计的系数
x²是二次项，它允许模型考虑曲线的变化
ϵ是误差项

在该方程中，βx项模拟线性关系，而 βx²捕捉曲线的变化，使模型适用于显示抛物线或曲线趋势的数据。系数β0 表示截距，β1控制线性部分的斜率，而β2影响曲线的变化，决定抛物线是向上开口 (β >0) 还是向下开口 (β<0)。

在实践中，线性-二次回归应用于因变量和自变量之间的关系不是严格线性的情况。我们脚本中的线性-二次回归实现是通过利用在OLS.mqh中定义的普通最小二乘法（OLS）类来实现的。

接下来，我们将介绍如何将这种回归模型整合到逐步选择过程中，从而从我们的数据集中识别出最优的预测器。

StepWiseFeatureSelection_Demo.mq5脚本有效地实现了针对线性-二次回归模型的增强型逐步特征选择算法。以下是该脚本的组件和功能的分解。CStepwise类继承自CStepwisebase，提供了对基类中定义的抽象方法的具体实现。这种设计允许将线性-二次回归的具体模型逻辑整合进去。线性-二次模型的拟合和评估核心逻辑被封装在CStepwise类中。这包括对预测变量的线性和二次项的必要调整。

fitModel() 方法负责根据训练样本构建设计矩阵。其排除了在交叉验证中用于验证的指定范围的数据。创建一个OLS类的实例（记作m_ols），用于管理普通最小二乘回归操作。

//+------------------------------------------------------------------+
//|    fit the OLS model                                             |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   ulong ntrain = m_samples - (row_stop - row_start);

   vector dependent(ntrain);
   matrix independent(ntrain,nvars+1);
   ntrain = 0;

   for(ulong sample=0; sample<m_samples; sample++)
     {
      if(sample>=row_start && sample<row_stop)
         continue;
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            independent[ntrain][var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               independent[ntrain][var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               independent[ntrain][var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }
      independent[ntrain][nvars] = 1.0;
      dependent[ntrain++] = targets[sample];
     }

   return m_ols.Fit(dependent,independent);
  }

在evalModel()中，该方法使用在训练阶段留出的数据来评估训练好的线性-二次回归模型的性能。这里指定评估模型性能的标准，而在此情况下，它是平方误差之和（SSE）。这一标准衡量了模型的预测结果与实际结果的契合程度。

//+------------------------------------------------------------------+
//|      evaluate the model                                          |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   if(m_ols.Loglikelihood()==EMPTY_VALUE)
     {
      Print(__FUNCTION__, " OLS error ");
      return EMPTY_VALUE;
     }

   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   double prediction;
   vector row(nvars);
   double error = 0.0;
   for(ulong sample=row_start; sample<row_stop; sample++)
     {
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            row[var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               row[var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               row[var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }

      prediction = m_ols.Predict(row);
      if(prediction == EMPTY_VALUE)
        {
         Print(__FUNCTION__, " OLS predict() error ");
         return EMPTY_VALUE;
        }
      error+=pow(prediction-targets[sample],2.0);
     }

   return error;
  }

在定义了派生的CStepwise类之后，脚本生成了一个随机的100×10矩阵，记作mat，其值介于0和1之间。该矩阵作为包含预测变量的数据集。

//---
   MathSrand(120);
//---
   matrix mat(100,10);
//---
   mat.Random(0.0,1.0);
//---

通过将特定列的值相加来创建目标向量。目标变量被定义为矩阵中第0、5、4和6列的值之和。这样就定义了模型旨在基于自变量（剩余列）预测的因变量（或输出）。

//---
   vector target = mat.Col(0) + mat.Col(5) + mat.Col(4) + mat.Col(6);
//---

创建了一个CStepwise类的实例，称为stepwise。这个实例将管理针对线性-二次回归模型的逐步特征选择过程。调用stepwise实例的setParams()方法来配置逐步选择过程的参数。

//---
   CStepwise stepwise;
   stepwise.setParams(NumKeptVars,NumFolds,MinNumVars,MaxNumVars,NumReplications,true);
   if(!stepwise.stepwiseSelection(mat,target))
      return;

用户可以调整的参数包括：

input ulong NumKeptVars = 1;
input ulong NumFolds = 10;
input ulong MinNumVars = 3;
input ulong MaxNumVars = 5;
input long NumReplications = 1;

NumKeptVars：指定在选择过程的每次迭代中保留的特征数量。

NumFolds：确定用于交叉验证的折数，以便对模型性能进行稳健评估。

MinNumVars：设置最终选定的特征集可以包含的最小特征数量，确保模型具备足够的预测能力。

MaxNumVars：设定最终特征集允许的最大特征数量，通过控制模型复杂度来防止过拟合。

NumReplications：表示蒙特卡洛排列测试的迭代次数，通过增强特征选择过程中执行的显著性测试的可靠性。

一旦调用了stepwiseSelection()方法，逐步特征选择过程就开始了。该方法协调整个选择算法，实施前面讨论的策略，以识别对线性-二次回归模型最相关的预测器。由StepWiseFeatureSelection_Demo.mq5脚本生成的输出可以为不同超参数如何影响特征选择过程提供宝贵的见解。让我们深入探讨输出的各个方面以及它们与指定输入参数的关系。

算法的关键输出组件包括：

选定的特征集：主要输出是算法在运行逐步选择后选定的特征集。每个特征集代表了一组被认为最相关的预测器组合，这是基于它们对模型性能的贡献得出的。
性能指标：对于选择过程的每次迭代，脚本通常会输出性能指标，例如：
- 标准值：平方误差之和或另一个选定的标准，提供了一个可量化的模型拟合度量。
- p值：如果使用了蒙特卡洛排列（MCP）测试，输出将包括p值，这些p值表明观察到的性能提升是由于偶然的概率。

在使用默认参数首次运行StepWiseFeatureSelection_Demo.mq5脚本时，我们为观察逐步选择过程在受限设置下的功能奠定了基础。以下是关于输出的预期内容、这些预期背后的逻辑以及与我们的观察一致的结果分析。

由于未指定MCP测试，输出确实将只有一列，对应于每次迭代的标准值。这反映随着预测器的添加，模型的性能如何变化。预期每次迭代的标准值都会增加。这表明随着相关预测器的添加，模型的性能正在改善。算法策略性地选择能够增强预测准确性的特征，从而推动标准值上升。最终，当识别出相关的预测器后，标准值将达到最优值（在这种情况下为1）。这表明模型已成功纳入最具信息量的预测器，并且在模型约束条件下表现得尽可能好。

MM      0       20:20:28.754    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 
QM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
KG      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
QH      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
FI      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
FM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
PM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 1
KR      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || Column Indices
ED      0       21:05:21.067    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 6
NO      0       21:05:21.089    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 4 6
RG      0       21:05:21.122    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 4 5 6
HH      0       21:05:21.170    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0 4 5 6
GL      0       21:05:21.240    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

在输出日志中，每次迭代都会显示在评估选定的预测器后当前的标准值。这种上升趋势将清晰地展示每个特征的添加如何对模型性能做出贡献。输出还应该指出终止的原因，这很可能会提到附加的特征并没有导致性能的提升，从而证实算法在实时中的决策过程。可以通过指定特征集中允许的最小预测器数量的参数来实现。

在后续运行StepWiseFeatureSelection_Demo.mq5脚本时，我们在保持其他参数默认值的同时，引入了一个包含100次排列的MCP测试。这一调整极大地丰富了输出内容，为特征选择过程提供了更深入的见解。

启用MCP测试后，输出将现在包含多列。每一行将对应一次迭代，显示标准值以及偶然发生概率和虚假改进概率。较低的p值（通常≤0.05）表明观察到的性能不太可能是由于偶然因素导致的，从而支持包含相应的特征。

呈现的两个p值将指导用户评估所选预测器的可靠性。

RI      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
LK      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
RD      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
EM      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
EQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
OQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
PI      0       21:10:57.101    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
RD      0       21:10:58.851    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 0.01000000 0.01000000   6
EI      0       21:11:01.243    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 0.01000000 0.01000000   4 6
KM      0       21:11:04.482    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 0.01000000 0.01000000   4 5 6
FP      0       21:11:09.151    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
CI      0       21:11:09.214    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

此次运行通过引入MCP测试，提供了更丰富且更具信息量的输出。多列数据使用户能够根据性能标准和统计显著性，更明智地决定最优特征集。因此，用户可以在高标准值和低p值的指导下，成功地识别哪些预测器应保留在最终模型中。

LL      0       07:22:46.657    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
GH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
ID      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 5
FH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 10
JO      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 10
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
LG      0       07:22:47.303    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26726680 0.01000000 0.01000000   6
LJ      0       07:22:48.153    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.56836766 0.01000000 0.01000000   4 6
FH      0       07:22:49.518    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.74542884 0.01000000 0.01000000   4 5 6
NM      0       07:22:51.488    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
KQ      0       07:22:54.163    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.71000000   0 1 4 5 6
JF      0       07:22:57.793    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.85000000   0 1 2 4 5 6
DD      0       07:23:02.436    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.94000000   0 1 2 3 4 5 6
MK      0       07:23:08.007    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7
DH      0       07:23:13.842    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8
HO      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8 9
PL      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed

在StepWiseFeatureSelection_Demo.mq5脚本的最后一次运行中，重点是通过增加MinNumVars参数来扩大特征选择过程的范围，允许最少有10个预测器。允许最终子集中有更多的预测器，将使算法能够评估更大范围的特征组合，这样一来，可能会发现较小子集遗漏的交互作用或非线性关系。尽管增加最小预测器数量可以进行更广泛的搜索，但需要注意的是，这也会导致算法运行时间变长。评估更大特征集的复杂性需要更多的计算资源和时间。

算法内置的检查确保，如果MinNumVars或MaxNumVars设置的值超过了候选预测器的总数（在本例中为10），它们将自动调整为与数据集中可用的预测器数量相匹配。这一保护措施可以防止可能导致运行时问题或不当特征选择行为的配置错误。通过修改MinNumVars参数，用户可以根据数据集的特定特征和分析目标，调整逐步特征选择过程以探索更广泛的特征，可能会发现更具信息量的预测器集合。这种灵活性增强了算法的可用性，以便使用者能够根据其特定用例审慎选择超参数。

算法的运行时间取决于选定的超参数。MCP测试可能会显著减慢进程，尤其是随着排列次数的增加。每次排列都需要对模型进行全面评估，这增加了执行的总计算量。因此，尽管更多的排列可以增强统计显著性结果的稳健性，但它们也需要更多的处理时间。

除MCP测试外，影响算法运行时间的下一个参数是为交叉验证指定的折数。交叉验证涉及将数据集划分为若干子集，并在这些不同的子集上反复训练和测试模型。随着折数的增加，算法必须执行更多的训练和评估迭代。这就会特别耗时，尤其是在处理较大的数据集时，因为每个折都需要对模型进行全面拟合和评估。

最后，在选择最终模型允许的最小和最大预测器数量时，需要谨慎考虑。随着更多预测器被考虑纳入，算法在特征选择过程中需要评估更多的组合，从而导致发现最优特征子集所需的搜索周期数量增加。鉴于这些参数所涉及的权衡，使用者根据其特定用例审慎选择超参数至关重要。

结论

在本文中，我们探讨了一种增强型逐步特征选择算法，该算法旨在从一组较大的变量中优化预测性特征的识别。通过交叉验证和可选的蒙特卡洛排列（MCP）测试增强，该算法提供了一个框架，解决了传统逐步方法的局限性，使得所选择的特征子集能够在最小化过拟合风险的同时最大化预测性能。

我们考察了超参数调整在平衡计算效率和统计可靠性方面的重要性，强调了交叉验证的折数、显著性检验的排列数以及对最小和最大预测器数量的限制等参数如何显著影响算法的运行时间。

使用StepWiseFeatureSelection_Demo.mq5脚本进行的实际演示说明了该算法如何有效地应用于真实数据集，为所选特征子集的重要性提供了见解。总之，所提出的方法不仅增强了特征选择过程，还能够赋予使用者在模型构建方面做出明智决策的能力。文中引用的所有代码都附在以下文件中。

文件	描述
MQL5/include/np.mqh	包含用于操作矩阵和向量的工具函数的定义。
MQL5/include/OLS.mqh	实现普通最小二乘回归的OLS类的头文件。
MQL5/include/stepwise.mqh	实现增强型逐步特征选择方法的CStepwisebase类的头文件。
MQL5/scripts/StepWiseFeatureSelection_Demo.mq5	一个脚本，它应用CStepwisebase类在任意数据集上执行逐步特征选择。