MQL5における段階的特徴量選択

はじめに

従来の段階的特徴量選択は、機械学習タスクにおいて、候補となる特徴量の大きなプールから最適な変数のサブセットを選択する手法です。このプロセスは、各特徴量を個別に評価し、最も有望な変数を最終モデルに含めることから始まります。その後、追加の特徴量が選ばれた特徴量と組み合わせて評価され、目標となる予測精度または分類性能が達成されるまで続けられます。

しかし、従来の段階的特徴量選択には、過剰適合のリスクや特徴量間の相互作用を適切に捉えるのが難しいといった課題があります。この記事では、これらの問題に対処するために設計されたアルゴリズムを紹介します。このアルゴリズムは、MQL5に実装されており、さまざまな教師あり学習手法との柔軟な統合が可能です。

この改良されたアプローチは、Timothy Mastersによって開発され、彼の著書「Modern Data Mining Algorithms in C++ and CUDA C」で詳述されています。最後に、このアルゴリズムを使用してサンプルの回帰タスクにおける最適な特徴量選択をおこない、その有効性を実際の応用例を通じて示します。

段階的特徴量選択の限界

機械学習タスクで使用されるデータセットは、本質的に複雑であり、非線形関係、時間とともに変化するパターン、または相互に関連する多数の要因を特徴量とすることがよくあります。この複雑さは特徴量選択における大きな課題となり、従来の方法、例えば段階的選択ではこれらの複雑なダイナミクスを捉えることが難しい場合があります。段階的選択の主要な制限の1つは、多様な特徴量の組み合わせの影響を評価できないことです。しばしば、単独では、または特定の他の変数と組み合わせた場合に有益ではないと思われる特徴量が、特定の補完的な特徴量と組み合わせることで非常に予測的になることがあります。

たとえば、外国為替レートの予測モデルを構築するタスクを考えてみましょう。このシナリオでは、さまざまなテクニカル指標とファンダメンタル指標を収集することになるでしょう。いくつかのファンダメンタル指標は、単独で、または補完的でないテクニカルデータと組み合わせても予測価値がほとんどないように見えるかもしれません。しかし、選挙結果などの指標と現在の市場動向を組み合わせると、市場動向のみを頼りにするよりも、より堅牢な予測が得られる可能性があります。さらに、全体的な経済情勢を理解し、新しい指導者がマクロ経済状況にどう反応するかを予測することで、モデルの予測精度が大きく向上する可能性もあります。これらの課題は、計算負荷が非常に高い徹底的な探索を避けつつ、有望な特徴量の組み合わせをテストできる強化された段階的選択方法の必要性を浮き彫りにしています。

段階的選択における2番目の課題は、ノイズによる過剰適合の影響を受けやすいことです。新しい変数を追加するたびに、アルゴリズムはランダムな変動を貴重な情報として誤認するリスクがあり、これが一般化できないパターンを学習させることにつながります。例えば、複数のテクニカル指標を追加することで、モデルが市場のノイズに適合し、意味のあるトレンドに基づくものではなくなり、その結果、サンプル内でのパフォーマンスが向上しても、サンプル外のデータに対しては堅牢性が損なわれる可能性があります。この問題は、モデルのパフォーマンスがサンプル内での適合度だけで判断される場合にしばしば発生し、その結果、必要以上に多くの変数が含まれ、最終的にサンプル外でのパフォーマンスが低下することになります。

特徴量選択の統計的有意性は、一般的にp値を使用して評価されます。従来の回帰ベースの段階的選択では、p値が特徴量の係数がゼロである可能性を評価し、その予測力を反映します。信頼区間は、サンプリングの不確実性を考慮して、真の母集団係数の範囲を提供します。低いp値は、帰無仮説（係数がゼロである）に対して強力な証拠があることを示し、特徴量の重要性を支持します。これらのp値は仮説検定から導かれ、帰無仮説では係数がゼロであると仮定し、対立仮説では係数がゼロではないと仮定します。p値を求めるためには、係数推定値とその標準誤差に基づいてtスコアを計算します。

しかし、このアプローチは回帰モデルに特有のものです。他の機械学習技術では、同等のp値を取得するためにカスタマイズされた仮説検定が必要となり、アルゴリズムの実際の適用が複雑になります。理想的には、より普遍的に適用可能な手法が、さまざまな種類の機械学習手法において一貫性を持つp値または同等の指標を生成することで、関連性のある有意性の尺度を提供することです。

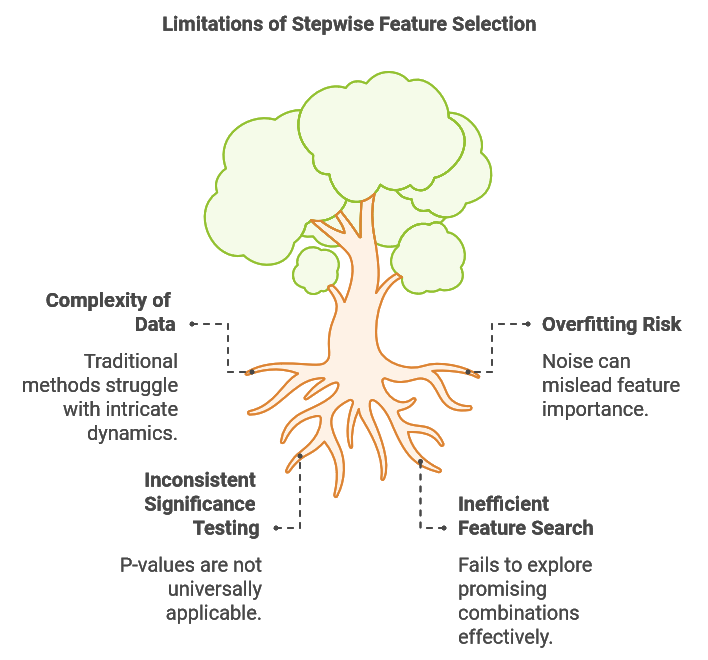
従来の段階的特徴量選択の限界を考慮して、ここで紹介する修正アルゴリズムは、従来の方法に対して3つの重要な改善点を提供します。最初の改善点は、有望な特徴量サブセットを効率的に検索するという課題に対処することです。複数の高い潜在能力を持つサブセットを維持し、それらのサブセットと新たな候補を組み合わせて評価することで、修正アルゴリズムは包括的な探索と計算効率のバランスを実現します。このアプローチにより、従来の段階的選択では見逃される可能性のある特徴量間の相乗関係を明らかにできます。

過剰適合のリスクを軽減するために、アルゴリズムは特徴量セットの評価基準として交差検証のパフォーマンスを使用します。この厳密な評価方法により、ランダムノイズを意味のある予測情報と誤認するリスクが最小限に抑えられ、収穫逓減が検出された場合には追加特徴量の追加を自動的に停止するシンプルで効果的なメカニズムが提供されます。

さらに、各新しい特徴量が追加されるごとに、アルゴリズムは次の2つの確率を計算します。

• 偶然発生の確率：この確率は、選択された特徴量が全て無関係であると仮定した場合、現在の特徴量セットの観測されたパフォーマンスが偶然によるものである可能性を測定します。
• 偽の改善の確率：この確率は、最新の特徴量追加によるパフォーマンス向上が偶然によるもので、真の予測力に基づいたものではない可能性を評価します。
  

これらの確率は、特徴量選択プロセスにおける統計的有意性に関する洞察を提供し、真の予測力と統計的ノイズを区別するために役立ちます。特筆すべきは、これらの計算された確率がモデルに依存しないため、アルゴリズムはさまざまな機械学習モデルとシームレスに統合できることです。次のセクションでは、このアルゴリズムを実装するコードの主要な部分を紹介します。提供するコードスニペットは、stepwise.mqhに定義されているCStepwisebaseクラスから抽出されたものです。このクラスは抽象クラスであり、ユーザーは特定の仮想メンバーを実装する派生クラスを作成する必要があり、これによって任意のモデルの統合が可能になります。

段階的な手順

提案されたアルゴリズムは、従来の段階的選択を強化し、複数の有望な特徴量サブセットを追跡することで、徹底的な検索の必要性を回避します。このアプローチにより、最終的な最適セットを形成する可能性のある特徴量サブセットを効率的に絞り込むことができます。手順の概要は次の通りです。

1. 初期化：特徴量セットの試行に関する情報を保存するために、プロセス全体で使用されるデータ構造が初期化されます。
2. 反復的な特徴量追加：各反復ごとに、複数の順列レプリケーションを実行します。目的変数をシャッフルして新しい順列を作成し、現在の特徴量セットに新しい特徴量を追加します。その後、交差検証を使用して更新された特徴量セットのパフォーマンスを評価します。最も優れたパフォーマンスを示す特徴量セットとそのパフォーマンスメトリックを更新します。 
   
3. 終了基準：アルゴリズムは、特徴量の最大数（max_num_predictorsで定義）に達した場合、またはパフォーマンスの改善が事前に設定された閾値を下回った場合に終了します。

   

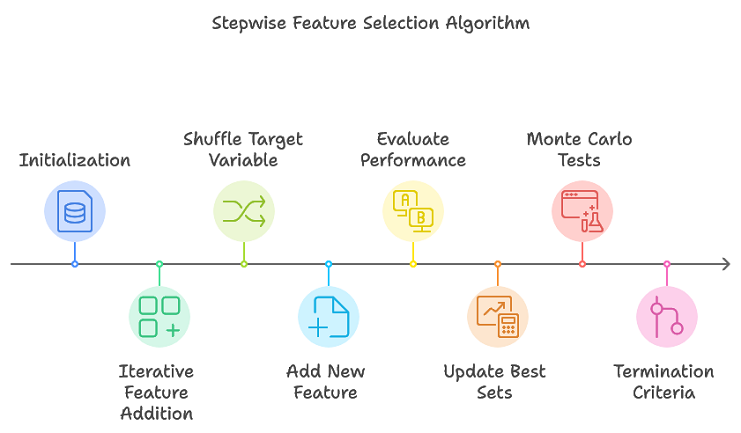
主な手順はstepwiseSearch()で実装され、プロセスは検索のさまざまな側面を制御するいくつかのハイパーパラメータによって制御されます。これらのハイパーパラメータは次のとおりです。

• num_kept：各反復で保持する、基準に基づいてパフォーマンスが最も優れている候補特徴量サブセットの数。これらの候補は最適な特徴量セットを形成する可能性が高いと考えられています。
• num_folds：交差検証で使用されるフォールドの数。値が大きいほどパフォーマンス推定の精度は向上しますが、計算コストも増加します。
• min_num_predictors：最終的な特徴量セットに含まれる予測変数の最小数。これにより、ユーザーはモデルの複雑さの下限を定義できます。
• max_num_predictors：最終的な特徴量セットで許容される予測変数の最大数。モデルの複雑さの上限を提供します。
• num_replications：モンテカルロ順列検定の反復回数は、特徴量のパフォーマンスの統計的有意性を評価するのに役立ちます。
• verbose_output：特徴量選択プロセスの各手順の結果をMetaTrader 5のエキスパートタブに表示するかどうかを決定します。
  

これらのパラメータは柔軟性を提供し、ユーザーはニーズに合わせて特徴量選択プロセスを微調整できます。これらは、setParams()を呼び出すことによって指定できます。

//+------------------------------------------------------------------+
//|   set the stepwise selection parameters                          |
//+------------------------------------------------------------------+
void              setParams(ulong num_kept, ulong num_folds, ulong min_num_predictors, ulong max_num_predictors,long num_replications,bool verbose_output)
  {
   m_keptvars = num_kept>0?num_kept:1;
   m_folds = num_folds>0?num_folds:ULONG_MAX;
   m_min_num_preds = min_num_predictors;
   m_max_num_preds = max_num_predictors;
   m_reps = num_replications>0?num_replications:1;
   m_verbose = verbose_output;
   return;
  }

stepwiseSearch()メソッドは、特徴量セットのさまざまな試行を追跡するために内部データ構造を初期化することから始まります。次に、予測子の最大数に達するまで継続するメインループに入ります。ループの各反復中に、目的変数は複数の繰り返しに対してランダムにシャッフルされ、addFeature()を呼び出すことによって新しい変数がモデルに追加されます。アルゴリズムは、最もパフォーマンスの高いモデル特徴量を保存し、新しい変数を追加することでパフォーマンスが低下する場合は、早期に終了する可能性があります。パフォーマンスが引き続き向上する場合、予測子の最大数が達成されるまでプロセスは継続されます。最後に、選択した変数のインデックスがm_var_indices配列に保存されます。

//+------------------------------------------------------------------+
//|  coordinates main stepwise search operation                      |
//+------------------------------------------------------------------+
int               stepwiseSearch(void)
  {
   int done = 1;
   int btrials;
   m_trial_length = m_max_num_preds*m_vars*m_keptvars;

   reset();

   if(!m_prior_best_crits.Resize(m_keptvars) || !m_all_best_crits.Resize(m_reps,m_keptvars))
     {
      Print(__FUNCTION__," data structure resizing error ", GetLastError());
      return done;
     }

   if(ArrayResize(m_all_best_trials,int(m_reps*m_max_num_preds*m_keptvars))<0  ||
      ArrayResize(m_already_tried,int(m_trial_length))<0 ||
      ArrayResize(m_trial_vars,int(m_max_num_preds))<0 ||
      ArrayResize(m_prior_best_trials,int(m_max_num_preds*m_keptvars))<0)
     {
      Print(__FUNCTION__,"  error resizing array ", GetLastError());
      return done;
     }


   ArrayInitialize(m_all_best_trials,-1);
   ArrayInitialize(m_already_tried,-1);
   ArrayInitialize(m_trial_vars,-1);
   ArrayInitialize(m_prior_best_trials,-1);

   vector target;
   int n_so_far =0;
   int rval, rem, j,n_this_rep = 0;
   int mcpt_mod_count, mcpt_change_count;
   mcpt_mod_count = mcpt_mod_count = mcpt_change_count = -1;
   double temp,prior_crit;
   double original_crit, original_change, new_crit;
   original_crit = original_change = new_crit = -DBL_MIN;

   if(m_verbose)
     {
      if(m_reps>1)
         Print("Criterion  || New pval  || Diff pval  || Column Indices");
      else
         Print("Criterion  || Column Indices");
     }
   while(true)
     {

      target = m_target;

      for(ulong rep=0; rep<m_reps; rep++)
        {


         if(rep)
           {
            rval = 17*int(rep) + 11;
            unif(rval);
            unif(rval);
            rem = int(m_samples);
            while(rem>1)
              {
               j = (int)(unif(rval))*rem;
               if(j>=rem)
                  j = rem-1;
               temp = target[--rem];
               target[rem] = target[j];
               target[j] = temp;
              }
           }

         btrials = int(rep*m_max_num_preds*m_keptvars);
         if(n_so_far == 0)
            prior_crit = -1.e60;
         else
            prior_crit = m_all_best_crits[rep][0];
         n_this_rep = n_so_far;

         done = addFeature(target,n_this_rep,btrials,rep);

         if(done || n_this_rep!=(n_so_far+1))
           {
            Print(__FUNCTION__, " internal error ");
            return 1;
           }

         if(m_all_best_crits[rep][0]<=prior_crit && n_so_far>=int(m_min_num_preds) && !rep)
           {
            for(ulong i = 0 ; i<m_keptvars; i++)
              {
               m_all_best_crits[rep][i] = m_prior_best_crits[i];
               if(ArrayCopy(m_all_best_trials,m_prior_best_trials,btrials+int(i*n_so_far),int(i*n_so_far),n_so_far)<0)
                 {
                  Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
                  return 1;
                 }
              }
            if(m_verbose)
               Print(__FUNCTION__, " procedure terminated early because adding a new variable caused performance degradation");
            return 0;
           }

         if(prior_crit < 0.0)
            prior_crit = 0.0;

         new_crit = m_all_best_crits[rep][0];

         if(new_crit<0.0)
            new_crit = 0.0;

         if(rep == 0)
           {
            original_crit = new_crit;
            original_change = new_crit - prior_crit;
            mcpt_mod_count = mcpt_change_count = 1;
           }
         else
           {
            if(new_crit >= original_crit)
               ++mcpt_mod_count;
            if(new_crit - prior_crit >= original_change)
               ++mcpt_change_count;
           }

        }

      if(n_so_far == 0)
         mcpt_change_count = mcpt_mod_count;

      if(!m_decision_matrix.Resize(n_so_far+1,m_reps>1?3:1,100) || ArrayResize(m_var_indices,int(m_var_indices.Size())+n_this_rep,100)<0)
        {
         Print(__FUNCTION__, " container resize error ", GetLastError());
         return 1;
        }

      string msg;
      if(m_reps>1)
        {
         double mod_pval = (double) mcpt_mod_count / (double) m_reps;
         double change_pval = (double) mcpt_change_count / (double) m_reps;

         if(m_verbose)
            msg = StringFormat("%10.8lf %10.8lf %10.8lf  ", original_crit,mod_pval,change_pval);

         m_decision_matrix[n_so_far][0] = original_crit;
         m_decision_matrix[n_so_far][1] = mod_pval;
         m_decision_matrix[n_so_far][2] = change_pval;
        }
      else
        {
         msg = m_verbose?StringFormat("%10.8lf", original_crit):NULL;
         m_decision_matrix[n_so_far][0] = original_crit;
        }
      if(m_verbose)
        {
         for(int i = 0; i<n_this_rep; i++)
           {
            msg += StringFormat(" %s",IntegerToString(m_all_best_trials[i]));
           }
        }
      if(ArrayCopy(m_var_indices,m_all_best_trials,(n_so_far*(n_so_far+1))/2,0,n_this_rep)<0)
        {
         Print(__FUNCTION__, " array copy error ", GetLastError());
         return 1;
        }

      if(m_verbose)
         Print(msg);

      ++n_so_far;
      if(n_so_far == int(m_max_num_preds))
        {
         if(m_verbose)
            Print(" Stepwise selection successfully completed ");
         break;
        }
     }

   return 0;

  }

交差検証基準の計算

特徴量選択において単一の訓練データセットに依存すると、過剰適合のリスクがあるため、最適ではない結果が得られることがよくあります。このリスクを軽減するために、交差検証が使用されます。交差検証では、データセットを複数の訓練セットと検証セットに分割し、モデルのパフォーマンスと特徴量の重要性をより包括的に評価できます。異なるデータサブセットで反復的に訓練とテストをおこなうことにより、交差検証によって過剰適合が軽減され、一般化が向上します。

交差検証は非常に効果的ですが、計算効率と統計的信頼性の間でトレードオフが発生します。通常、フォールドの数が多いほど、モデルのパフォーマンスの推定値はより正確になりますが、計算要件も増加します。理想的な折り畳みの数は、データセットの特性と利用可能な計算リソースの両方によって異なります。実際には、適切な折り畳み数を決定するには、データセットのサイズと必要な統計的信頼性のレベルを慎重に考慮する必要があります。交差検証の原理と限界の両方を理解することで、実践者はこの手法を適用して、特徴量選択とモデル構築プロセスの信頼性と堅牢性を高めることができます。

交差検証手順は、crossEval()メソッドによって実装されます。

//+------------------------------------------------------------------+
//|  evaluates a predictor set using cross validation                |
//+------------------------------------------------------------------+
int               crossEval(ulong num_vars,vector &target,double &criterion)
  {
   ulong ifold, n_remaining, test_start, test_stop ;
   double error, evalresult ;

   n_remaining = m_samples;
   test_start = 0;

   error = 0.0;

   for(ifold = 0; ifold<m_folds; ifold++)
     {
      test_stop = test_start + (n_remaining/(m_folds-ifold));
      if(!fitModel(num_vars,test_start,test_stop,target))
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " fit() failed ");
         return 1;
        }
      evalresult = evalModel(num_vars,test_start,test_stop,target);
      if(evalresult==EMPTY_VALUE)
        {
         criterion = -DBL_MIN;
         Print(__FUNCTION__, " evalModel() failed ");
         return 1;
        }
      error+=evalresult;
      n_remaining -= test_stop - test_start;
      test_start = test_stop;
     }

   criterion = 1.0 - error/double(m_samples);
   return 0;
  }

この関数は、評価する予測子の数、シャッフルされた目的値のベクトル、および基準の値を返す変数への参照を入力として受け取ります。基準値は、最も適切な特徴量サブセットを識別するための決定変数の1つとして使用されます。関数は正常に実行されると0を返します。これは、最初にモデルを適合させ、次にサンプルデータのすべてのフォールドにわたってそのパフォーマンスを評価することによって動作します。

fitModel()メソッドは、候補となる特徴量サブセットでモデルを訓練する役割を担います。以下の入力が必要です。

• num_preds：予測因子の数
• row_start：最初のサンプルのインデックス
• row_stop：訓練セットから除外する最後のサンプルの1つ後のインデックス
• targets：シャッフルされた目的値のベクトル
  

この関数は、モデルが正常に訓練されたかどうかを示すブール値を返します。

evalModel()関数にはfitModel()と同じ入力がありますが、今回は、指定された行のパーティションが訓練済みモデルの評価に使用されるサンプルを表します。この関数は、モデルのパフォーマンスを示す値を返します。fitModel()とevalModel()はどちらも仮想メンバーであり、使用されている特定のモデルタイプを統合するには派生クラスでの実装が必要です。

//+------------------------------------------------------------------+
//| fit a model                                                      |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return false;}
//+------------------------------------------------------------------+
//| evaluate a model                                                 |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop, vector& targets) { return EMPTY_VALUE;}

最初の特徴量を見つける

addFirstFeature()メソッドは、指定されたセット内の最初の予測子を識別するためにaddFeature()によって呼び出されます。

//+------------------------------------------------------------------+
//|     finds the first predictor in the set                         |
//+------------------------------------------------------------------+
int               addFirstFeature(vector &targ, int bindex,ulong rep_index)
  {
   double crit;

   for(ulong i = 0; i<m_keptvars; i++)
     {
      m_all_best_crits[rep_index][i] = -1.e60;
      m_all_best_trials[bindex+i] = -1;
     }

   for(int i = 0; i<int(m_vars); i++)
     {
      m_trial_vars[0] = i;
      if(crossEval(1,targ,crit))
        {
         Print(__FUNCTION__, " xval error ");
         return 1;
        }
      ulong j;
      for(j = 0; j<m_keptvars; j++)
        {
         if(crit > m_all_best_crits[rep_index][j])
            break;
        }
      if(j<m_keptvars)
        {
         for(long k = long(m_keptvars-2); k>=long(j); k--)
           {
            m_all_best_trials[bindex+k+1] = m_all_best_trials[bindex+k];
            m_all_best_crits[rep_index][k+1] = m_all_best_crits[rep_index][k];
           }
         m_all_best_trials[bindex+j] = i;
         m_all_best_crits[rep_index][j] = crit;
        }
     }

   return 0;
  }

各変数を反復処理し、交差検証を使用してそのパフォーマンスを評価します。パフォーマンスは派生クラスで定義された基準に基づいて評価され、その基準に基づいてモデルを決定する学習手法が決定されます。

この評価中、この方法では、最もパフォーマンスの高い変数とそれに対応する基準値のリストが維持されます。各変数が評価されると、そのパフォーマンスが現在の最良の変数のパフォーマンスと比較されます。新しい変数が既存のトップパフォーマンス変数の1つを上回る場合、その変数はリストに挿入され、パフォーマンスの低い変数は下位に移動します。

このプロセスは、すべての変数が評価され、最初の予測子が特定されるまで継続されます。後続のaddFeature()の呼び出しでは、addNewFeature()を呼び出すことによって新しい変数が導入され、特徴量追加に対する体系的なアプローチが保証されます。

特徴量セットの追加

addNewFeature()メソッドは、モデルの特徴量セットに含める次の予測子を識別します。

//+------------------------------------------------------------------+
//|  looks for next predictor to include                             |
//+------------------------------------------------------------------+
int               addNewFeature(vector& target,int &ind, int bindex,ulong rep_index)
  {
   int i, j, k, ivar, ir ;
   int npred, n_already_tried,nbest, rootvars;
   nbest  = -1;
   double crit;

   ind = npred = ind+1;

   for(i = 0; i<int(m_keptvars); i++)
     {
      m_prior_best_crits[i] = m_all_best_crits[rep_index][i];
      if(ArrayCopy(m_prior_best_trials,m_all_best_trials,int(i*(npred-1)),bindex+int(i*(npred-1)),npred-1)<0)
        {
         Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
         return 1;
        }
      m_all_best_crits[rep_index][i] = -1.e60;
     }
   n_already_tried = 0;
   for(ir = 0; ir<int(m_keptvars); ir++)
     {
      if(m_prior_best_crits[ir] < -1.e59)
         break;
     }
   nbest = ir;

   for(ir = 0; ir<nbest; ir++)
     {
      rootvars = ir*(npred-1);
      for(ivar=0; ivar<int(m_vars); ivar++)
        {
         for(i = 0; i<npred-1; i++)
           {
            if(m_prior_best_trials[rootvars+i] == ivar)
               break;
           }
         if(i < npred-1)
            continue;
         k = 0;

         for(i = 0; i<int(m_vars); i++)
           {
            for(j=0; j<npred-1; j++)
              {
               if(m_prior_best_trials[rootvars+j] == i)
                 {
                  m_trial_vars[k++] = i;
                  break;
                 }
              }
            if(ivar == i)
               m_trial_vars[k++] = i;
           }
         for(i = 0; i<n_already_tried; i++)
           {
            for(j = 0; j<npred; j++)
              {
               if(m_trial_vars[j] != m_already_tried[i*npred+j])
                  break;
              }
            if(j == npred)
               break;
           }
         if(i < n_already_tried)
            continue;

         for(i =0; i<npred; i++)
            m_already_tried[n_already_tried*npred+i]=m_trial_vars[i];
         ++n_already_tried;

         if(crossEval(ulong(npred),target,crit))
           {
            Print(__FUNCTION__, " xval error ");
            return 1;
           }

         for(i = 0; i< int(m_keptvars); i++)
           {
            if(crit > m_all_best_crits[rep_index][i])
               break;
           }

         if(i<int(m_keptvars))
           {
            for(j = int(m_keptvars-2); j>=i; j--)
              {
               m_all_best_crits[rep_index][j+1] = m_all_best_crits[rep_index][j];
               if(ArrayCopy(m_all_best_trials,m_all_best_trials,bindex+int((j+1)*npred),bindex+int(j*npred),npred)<0)
                 {
                  Print(__FUNCTION__, " array copy error ", GetLastError());
                  return 1;
                 }
              }
            m_all_best_crits[rep_index][i] = crit;
            if(ArrayCopy(m_all_best_trials,m_trial_vars,bindex+int(i*npred),0,npred)<0)
              {
               Print(__FUNCTION__, " array copy error ", GetLastError());
               return 1;
              }
           }
        }
     }
   return 0;
  }

これは、現在の最良の予測子と追加の変数のすべての可能な組み合わせを調べることにより、既存の予測子のセットを基に構築されます。この方法では、組み合わせごとに交差検証を実行してパフォーマンスを評価します。パフォーマンスは指定された基準を使用して測定されます。段階的特徴量選択コードの主要要素を調べたので、次にこれらのスニペットがどのように統合されて完全な実装が形成されるかを検討します。

CStepwisebaseクラス

CStepwisebaseクラスは、候補のセットから予測特徴量を反復的に選択するように設計された段階的特徴量選択の基盤となる実装です。この選択プロセスでは、予測モデルのパフォーマンスへの貢献度に基づいて変数が体系的に追加されます。抽象クラスとして、fitModel()メソッドとevalModel()メソッドを実装することにより、派生クラス内であらゆる種類の学習手法とそれに対応する基準を統合できます。この実装の例は次のセクションで示します。

メソッドstepwiseSelection()は、パブリックにアクセス可能なメインのエントリポイントとして機能し、データを準備してstepwiseSearch()を実行することでプロセスを開始します。

//+------------------------------------------------------------------+
//|  main method to execute stepwise feature selection               |
//+------------------------------------------------------------------+
bool              stepwiseSelection(matrix& predictors, vector& targets)
  {

   if(targets.Size()!=predictors.Rows() || !targets.Size())
     {
      Print(__FUNCTION__, " invalid inputs ");
      return false;
     }

   m_data = stdmat(predictors);

   m_target = (targets-targets.Mean())/(targets.Std()+1e-10);

   m_vars = predictors.Cols();
   m_samples = predictors.Rows();

   if(m_keptvars>m_vars || m_keptvars<1)
      m_keptvars = m_vars;

   if(m_folds<1)
      m_folds = 1;

   if(m_folds>m_samples)
      m_folds = m_samples;

   if(m_min_num_preds==0 || m_min_num_preds>m_vars || m_min_num_preds>m_max_num_preds)
      m_min_num_preds = m_vars;

   if(m_max_num_preds==0 || m_max_num_preds>m_vars || m_max_num_preds<m_min_num_preds)
      m_max_num_preds = m_vars;

   if(m_reps<1)
      m_reps = 1;

   if(m_verbose)
     {
      Print(" STEPWISE SELECTION PARAMETERS ");
      Print(" Number of retained candidate variables for each iteration ", m_keptvars);
      Print(" Number of folds in cross validation procedure ", m_folds);
      Print(" Final minimum number of selected predictors ", m_min_num_preds);
      Print(" Final maximum number of selected predictors ", m_max_num_preds);
      Print(" Number of replications for MCP test ", m_reps);
     }

   return (stepwiseSearch()==0);
  }

特徴量選択プロセスのパラメータを事前に設定するには、setParams()メソッドを使用します。特徴量選択プロセスからの出力は、setParams()の最後のパラメータをtrueに設定することで、MetaTrader 5の[エキスパート]タブに表示できます。さらに、選択手順の結果は次の方法で取得できます。

•  getCriticalVals()を呼び出すと、段階的検索の一部としてモンテカルロ順列(MCP)テストが指定されているかどうかに応じて、列数が変化する行列が返されます。これは、setParams()のnum_replicationsを1より大きい値に設定することで実現されます。この場合、getCriticalVals()は3つの列を持つ行列を返します。各行には、追加特徴量の追加を定量化する値が含まれます。この行列の行数は、段階的アルゴリズムの最も外側のループを繰り返す回数に対応します。各行の3つの値は、基準、観測されたパフォーマンスが偶然によるものである確率を示すp値（選択された特徴量が無関係であると仮定）、および反復の特徴量の追加によって生じるパフォーマンスの向上が偶然によるものである確率を反映する別のp値で構成されます。
  

  //+------------------------------------------------------------------+
  //| get all crit values and corresponding p-values                   |
  //+------------------------------------------------------------------+
  matrix            getCriticalVals(void)
    {
     return m_decision_matrix;
    }

• MCPテストが指定されていない場合、関数はアルゴリズムの実行の各反復のそれぞれの基準値を含む単一の列を返します。見つかった最適な特徴量サブセットの数はgetNumFeatureSets()を使用して照会できますが、特徴量セット自体はgetFeatureSetAt()を呼び出すことによって取得できます。getFeatureSetAt()は、目的の反復に対応するインデックスと、特徴量サブセットを表す列のインデックスがコピーされる配列への参照を受け入れます。
  

  //+------------------------------------------------------------------+
  //|  get the selected features at a specific iteration of the process|
  //|  iterations denoted as zero based indices                        |
  //|  eg, first selected feature located at iteration index 0         |
  //+------------------------------------------------------------------+
  bool              getFeatureSetAt(ulong iteration_index,ulong &selectedvars[])
    {
     if(ArrayCopy(selectedvars,m_var_indices,0,int((iteration_index*(iteration_index+1))/2),int(iteration_index+1))>0)
        return true;
     else
       {
        Print(__FUNCTION__, " ArrayCopy error ", GetLastError());
        return false;
       }
    }
  //+---------------------------------------------------------------------+
  //| get maximum number of iterations cycled through in selection process|
  //+---------------------------------------------------------------------+
  ulong             getNumFeatureSets(void)
    {
     return m_decision_matrix.Rows();
    }

これで基本クラスについての説明は終了です。次のセクションでは、モデルを統合してテストを実行することでこのコードを適用する方法について説明します。

線形二次回帰モデルを使用した例

強化された段階的選択アルゴリズムを説明するために、線形二次回帰モデルを適合するための候補予測子のデータセットを評価する際のそのアプリケーションを示します。この実装は、MetaTrader5スクリプトStepWiseFeatureSelection_Demo.mq5で提供されています。このスクリプトでは、強化された段階的選択方法を通じて最も予測力の高い特徴量を選択するプロセスの概要を示し、アルゴリズムが線形二次回帰モデルの最適な予測子を識別する方法を紹介します。実践的なデモンストレーションには、データセットの設定、モデルパラメータの構成、MetaTrader5環境内での特徴量選択プロセスの実行が含まれます。

線形二次回帰は、予測変数の線形項と二次項（2乗項）の両方を組み込んだ線形回帰の拡張です。このアプローチにより、モデルは直線ではなく曲線をデータに当てはめることで非線形関係を捉えることができます。単一の予測変数Xに対する線形二次回帰方程式の一般的な形式は、以下の一般的な式で与えられます。

ここで

• yは従属変数
  
• xは独立変数
  
• β0、β1​、β2​は推定される係数
  
• xの2乗は2次項であり、モデルが曲率を考慮することを可能にする
  
• ϵは誤差項
  

この式では、βxという項が線形関係をモデル化し、β(xの2乗)が曲率を捉えているため、このモデルは放物線または曲線の傾向を示すデータに役立ちます。係数β0​切片βを表す1​線形部分の傾きを制御し、β2​ 曲率に影響し、放物線が上向きに開くか(β2>0)、下向きに開くか(β2<0)を決定します。

実際には、従属変数と独立変数の関係が厳密に線形ではない状況で線形二次回帰が適用されます。私たちのスクリプトでの線形二次回帰の実装は、OLS.mqhで定義されている通常の最小二乗法(OLS)クラスを活用することで可能になります。

次に、この回帰モデルを段階的選択プロセスに統合して、データセットから最適な予測子を特定できるようにする方法について説明します。

StepWiseFeatureSelection_Demo.mq5スクリプトは、線形二次回帰モデル向けに調整された、強化された段階的特徴量選択アルゴリズムを効果的に実装します。以下は、スクリプトのコンポーネントと機能の詳細です。CStepwiseクラスはCStepwisebaseから継承され、基本クラスで定義された抽象メソッドの具体的な実装を提供します。この設計により、線形二次回帰の特定のモデルロジックを統合できるようになります。線形二次モデルを適合および評価するためのコアロジックは、CStepwiseクラス内にカプセル化されています。これには、予測変数の線形項と二次項の両方に対応するために必要な調整が含まれます。

メソッドfitModel()は、訓練サンプルに基づいて設計行列を構築する役割を担います。交差検証中に検証を目的とした指定された範囲のデータを除外します。OLSクラスのインスタンス（m_olsと表記）が作成され、通常の最小二乗回帰演算が管理されます。

//+------------------------------------------------------------------+
//|    fit the OLS model                                             |
//+------------------------------------------------------------------+
virtual bool      fitModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   ulong ntrain = m_samples - (row_stop - row_start);

   vector dependent(ntrain);
   matrix independent(ntrain,nvars+1);
   ntrain = 0;

   for(ulong sample=0; sample<m_samples; sample++)
     {
      if(sample>=row_start && sample<row_stop)
         continue;
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            independent[ntrain][var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               independent[ntrain][var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               independent[ntrain][var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }
      independent[ntrain][nvars] = 1.0;
      dependent[ntrain++] = targets[sample];
     }

   return m_ols.Fit(dependent,independent);
  }

evalModel()メソッドでは、訓練フェーズで使用されなかったデータを使って、訓練された線形二次モデルのパフォーマンスが評価されます。ここで使用される評価基準は、平方誤差の合計(SSE)であり、これはモデルの予測が実際の結果とどれだけ一致しているかを測定します。

//+------------------------------------------------------------------+
//|      evaluate the model                                          |
//+------------------------------------------------------------------+
virtual double    evalModel(ulong num_preds,ulong row_start,ulong row_stop,vector& targets)
  {
   if(m_ols.Loglikelihood()==EMPTY_VALUE)
     {
      Print(__FUNCTION__, " OLS error ");
      return EMPTY_VALUE;
     }

   int k1,k2;

   ulong nvars = num_preds + num_preds * (num_preds+1)/2;
   double prediction;
   vector row(nvars);
   double error = 0.0;
   for(ulong sample=row_start; sample<row_stop; sample++)
     {
      k1=0;
      k2=1;
      for(ulong var=0; var<nvars; var++)
        {
         if(var<num_preds)
            row[var]=m_data[sample][m_trial_vars[var]];
         else
           {
            if(var<(num_preds*2))
              {
               row[var]=pow(m_data[sample][m_trial_vars[var-num_preds]],2.0);
              }
            else
              {
               row[var]=m_data[sample][m_trial_vars[k1]]*m_data[sample][m_trial_vars[k2]];
               ++k2;
               if(ulong(k2)==num_preds)
                 {
                  ++k1;
                  k2 = k1 + 1;
                 }
              }
           }
        }

      prediction = m_ols.Predict(row);
      if(prediction == EMPTY_VALUE)
        {
         Print(__FUNCTION__, " OLS predict() error ");
         return EMPTY_VALUE;
        }
      error+=pow(prediction-targets[sample],2.0);
     }

   return error;
  }

派生したCStepwiseクラスの定義に従い、スクリプトは0と1の間の値を持つ100行10列のランダムな行列(mat)を生成します。この行列は、予測変数を含むデータセットとして使用されます。

//---
   MathSrand(120);
//---
   matrix mat(100,10);
//---
   mat.Random(0.0,1.0);
//---

特定の列を合計することによって目的ベクトルが作成されます。目的変数は、行列の列0、5、4、6の値の合計として定義されます。これは、モデルが独立変数（残りの列）に基づいて予測しようとする従属変数（または出力）を定義します。

//---
   vector target = mat.Col(0) + mat.Col(5) + mat.Col(4) + mat.Col(6);
//---

CStepwiseクラスのインスタンスが作成され、stepwiseと呼ばれます。このインスタンスは、線形二次回帰モデルに合わせて調整された段階的な特徴量選択プロセスを管理します。段階的インスタンスでsetParams()メソッドが呼び出され、段階的選択プロセスのパラメータが構成されます。

//---
   CStepwise stepwise;
   stepwise.setParams(NumKeptVars,NumFolds,MinNumVars,MaxNumVars,NumReplications,true);
   if(!stepwise.stepwiseSelection(mat,target))
      return;

ユーザーが調整できるパラメータは次のとおりです。

input ulong NumKeptVars = 1;
input ulong NumFolds = 10;
input ulong MinNumVars = 3;
input ulong MaxNumVars = 5;
input long NumReplications = 1;

• NumKeptVars：選択プロセスの各反復で保持する特徴量の希望数を指定します。

• NumFolds：交差検証に使用するフォールドの数を決定し、モデルのパフォーマンスの堅牢な評価を容易にします。

• MinNumVars：最終的に選択された特徴量セットに含めることができる特徴量の最小数を設定し、モデルが予測に適切に備えられた状態を保つようにします。

• MaxNumVars：最終的な特徴量セットで許可される特徴量の最大数を確立し、モデルの複雑さを制御することで過剰適合を防止します。

• NumReplications：モンテカルロ順列検定の反復回数を示し、特徴量選択中に実行される有意性検定の信頼性を高めます。

stepwiseSelection()メソッドが呼び出されると、段階的特徴量選択プロセスが開始されます。この方法は、選択アルゴリズム全体を調整し、前述の戦略を実装して、線形二次回帰モデルに最も関連性の高い予測子を識別します。StepWiseFeatureSelection_Demo.mq5スクリプトから生成された出力は、さまざまなハイパーパラメータが特徴量選択プロセスにどのように影響するかについての貴重な洞察を提供します。出力のさまざまな側面と、それらが指定された入力パラメータとどのように関連しているかを詳しく見てみましょう。

アルゴリズムの主な出力コンポーネントは次のとおりです。

1. 選択された特徴量セット：主な出力は、段階的選択を実行した後にアルゴリズムによって選択された特徴量のセットです。各特徴量セットは、モデルのパフォーマンスへの貢献度に基づいて最も関連性が高いと判断された予測子の組み合わせを表します。
2. パフォーマンスメトリック：選択プロセスの各反復ごとに、スクリプトは通常次のようなパフォーマンスメトリックを出力します。
   
   •  基準値：二乗誤差または別の選択された基準の合計。モデルの適合性を定量化できる尺度を提供します。
   •  P値：モンテカルロ順列検定を採用した場合、出力には、観測されたパフォーマンスの向上が偶然によるものである確率を示すp値が含まれます。

デフォルトパラメータを使用したStepWiseFeatureSelection_Demo.mq5スクリプトの最初の実行では、制約付き設定で段階的選択プロセスがどのように機能するかを観察するための準備が整いました。ここでは、出力から何が期待できるか、これらの期待の根拠、そして結果が私たちの観察とどのように一致するかについて詳しく説明します。

MCPテストが指定されていないため、出力には各反復に対応する基準値を含む単一の列のみが表示されます。これは、予測子が追加されるにつれてモデルのパフォーマンスを反映します。基準値は反復ごとに増加すると予想されます。これは、関連する予測変数が追加されるにつれてモデルのパフォーマンスが向上していることを示しています。アルゴリズムは、予測精度を高める特徴量を戦略的に選択し、それによって基準を高めます。最終的に、関連する予測子が特定されると、基準は最適な値(この場合は1)に到達します。これは、モデルが最も有益な予測子をうまく組み込み、モデルの制約を考慮して可能な限り最高のパフォーマンスを発揮していることを示しています。

MM      0       20:20:28.754    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 
QM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
KG      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
QH      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
FI      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
FM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
PM      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 1
KR      0       21:05:21.050    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || Column Indices
ED      0       21:05:21.067    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 6
NO      0       21:05:21.089    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 4 6
RG      0       21:05:21.122    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 4 5 6
HH      0       21:05:21.170    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0 4 5 6
GL      0       21:05:21.240    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

出力ログでは、各反復で選択した予測子を評価した後の基準値が表示されます。基準値の増加傾向により、各特徴量の追加がモデルのパフォーマンスにどのように貢献したかが明確に示されます。出力には終了の理由も記載されるはずで、これは追加特徴量がパフォーマンス向上に寄与しなかったことを示し、アルゴリズムの意思決定プロセスがリアルタイムで確認できます。これは、特徴量セットで許可される予測子の最小数を指定するパラメータによって有効になります。

StepWiseFeatureSelection_Demo.mq5スクリプトのその後の実行では、他のパラメータのデフォルト値を維持しながら、100個の順列を持つモンテカルロ順列(MCP)テストを導入します。この調整により出力が大幅に充実し、特徴量選択プロセスに関するより深い洞察が得られます。

MCPテストを有効にすると、出力は複数の列で構成されるようになります。各行は反復に対応し、基準値、偶然の発生確率、および偽の改善の確率が表示されます。p値が低い（通常は0.05以下）ということは、観測されたパフォーマンスが偶然によるものではない可能性が高く、対応する特徴量が含まれていることを支持することになります。

提示された2つのp値は、ユーザーが選択した予測子の信頼性を評価する際に役立ちます。

RI      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
LK      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
RD      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 10
EM      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 3
EQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 5
OQ      0       21:10:57.100    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
PI      0       21:10:57.101    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
RD      0       21:10:58.851    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26300861 0.01000000 0.01000000   6
EI      0       21:11:01.243    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.57220902 0.01000000 0.01000000   4 6
KM      0       21:11:04.482    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.75419718 0.01000000 0.01000000   4 5 6
FP      0       21:11:09.151    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
CI      0       21:11:09.214    StepWiseFeatureSelection_Demo (BTCUSD,D1)       CStepwisebase::stepwise_search procedure terminated early because adding a new variable caused performance degradation

この実行は、モンテカルロ順列テストを組み込むことで強化され、より豊富で有益な出力を提供します。複数の列を使用することで、ユーザーはパフォーマンス基準と統計的有意性の両方に基づいて、最適な特徴量セットについてより情報に基づいた決定を下すことができます。その結果、ユーザーは、高い基準値と低いp値に基づいて、どの予測子を最終モデルに保持する必要があるかを自信を持って識別できます。

LL      0       07:22:46.657    StepWiseFeatureSelection_Demo (BTCUSD,D1)        STEPWISE SELECTION PARAMETERS 
GH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of retained candidate variables for each iteration 1
ID      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of folds in cross validation procedure 5
FH      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final minimum number of selected predictors 10
JO      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Final maximum number of selected predictors 10
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Number of replications for MCP test 100
FL      0       07:22:46.658    StepWiseFeatureSelection_Demo (BTCUSD,D1)       Criterion  || New pval  || Diff pval  || Column Indices
LG      0       07:22:47.303    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.26726680 0.01000000 0.01000000   6
LJ      0       07:22:48.153    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.56836766 0.01000000 0.01000000   4 6
FH      0       07:22:49.518    StepWiseFeatureSelection_Demo (BTCUSD,D1)       0.74542884 0.01000000 0.01000000   4 5 6
NM      0       07:22:51.488    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.01000000   0 4 5 6
KQ      0       07:22:54.163    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.71000000   0 1 4 5 6
JF      0       07:22:57.793    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.85000000   0 1 2 4 5 6
DD      0       07:23:02.436    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 0.94000000   0 1 2 3 4 5 6
MK      0       07:23:08.007    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7
DH      0       07:23:13.842    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8
HO      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)       1.00000000 0.01000000 1.00000000   0 1 2 3 4 5 6 7 8 9
PL      0       07:23:18.949    StepWiseFeatureSelection_Demo (BTCUSD,D1)        Stepwise selection successfully completed 

StepWiseFeatureSelection_Demo.mq5スクリプトの最終実行では、MinNumVarsパラメータを増やして最小10個の予測子を許可することにより、特徴量選択プロセスの範囲を拡大することに重点が置かれています。最終的なサブセットでより多くの予測子を考慮すると、アルゴリズムはより大きな特徴量の組み合わせを評価できるようになり、より小さなサブセットでは見逃される可能性のある相互作用や非線形関係を発見できる可能性があります。予測子の最小数を増やすと、より広範囲な検索が可能になりますが、これによりアルゴリズムの実行時間が長くなることにも注意することが重要です。より大きな特徴量セットを評価する複雑さが増すため、より多くの計算リソースと時間が必要になります。

アルゴリズムの組み込みチェックにより、MinNumVarsまたはMaxNumVarsが候補予測子の総数（この場合は10）を超える値に設定されている場合、データセット内の使用可能な予測子の数に合わせて自動的に調整されます。この安全策により、実行時の問題や不適切な特徴量選択動作につながる可能性のある構成エラーが防止されます。MinNumVarsパラメータを変更することで、ユーザーは段階的特徴量選択プロセスをカスタマイズして、より広範囲の特徴量を探索することができるので、より有益な予測子セットを発見できる可能性があります。この柔軟性によりアルゴリズムの使いやすさが向上し、選択プロセスを実践者はデータセットや分析目標の特定の特性に適応させることができます。

アルゴリズムの実行時間は、選択されたハイパーパラメータによって異なります。モンテカルロ順列検定では、順列の数が増えると特に、プロセスが大幅に遅くなる可能性があります。各順列にはモデルの完全な評価が必要であり、実行される計算の合計数が増加します。したがって、順列を増やすと統計的有意性の結果の堅牢性は高まりますが、処理時間も長くなります。

MCPテスト以外で、アルゴリズムの実行時間に影響を与える可能性がある次のパラメータは、交差検証に指定されたフォールドの数です。交差検証では、データセットを複数のサブセットに分割し、これらの異なるサブセットにわたってモデルを繰り返し訓練およびテストします。折り畳みの数が増えると、アルゴリズムはより多くの訓練と評価の反復を実行する必要があります。これは、特に大規模なデータセットの場合、各フォールドで完全なモデルの適合と評価が必要になるため、特に時間がかかります。

最後に、最終モデルで許可される予測変数の適切な最小数と最大数を選択する際には、慎重に検討する必要があります。含める対象として考慮される予測子が増えると、アルゴリズムは特徴量選択プロセス中にさらに多くの組み合わせを評価する必要があり、最適な特徴量サブセットを見つけるために必要な検索サイクルの数が増加します。これらのパラメータにはトレードオフが伴うため、実践者は特定のユースケースに基づいてハイパーパラメータを慎重に選択することが重要です。

結論

この記事では、より大きな変数セットから予測特徴量を識別する最適化された強化段階的特徴量選択アルゴリズムを検討しました。交差検証とオプションのモンテカルロ順列テストによって強化されたこのアルゴリズムは、従来の段階的手法の限界に対処し、過剰適合のリスクを最小限に抑えながら、予測パフォーマンスを最大化する特徴量サブセットの選択を可能にします。

計算効率と統計的信頼性のバランスをとるためのハイパーパラメータ調整の重要性を調査し、交差検証のフォールド数、有意性検定の順列数、予測子の最小数と最大数の制約などのパラメータが、アルゴリズムの実行時間に大きな影響を与えることを強調しました。

StepWiseFeatureSelection_Demo.mq5スクリプトを使用した実践的なデモンストレーションでは、アルゴリズムが実際のデータセットにどのように効果的に適用され、選択された特徴量サブセットの重要性に関する洞察を提供できるかが示されました。結論として、提案された手法は特徴量選択プロセスを強化するだけでなく、実務者がモデル構築に関して情報に基づいた意思決定をおこなうための支援にもなります。本文中で参照されたすべてのコードは、以下のファイルに添付されています。

ファイル	詳細
MQL5/include/np.mqh	行列とベクトルを操作するためのユーティリティ関数の定義が含まれています
MQL5/include/OLS.mqh	通常最小二乗回帰を実装するOLSクラスのヘッダーファイル
MQL5/include/stepwise.mqh	強化された段階的特徴量選択メソッドを実装するCStepwisebaseクラスのヘッダーファイル
MQL5/scripts/StepWiseFeatureSelection_Demo.mq5	CStepwisebaseクラスを適用して、任意のデータセットに対して段階的な特徴量選択を実行するスクリプト