Как опередить любой рынок (Часть IV): Индексы волатильности евро и золота CBOE

MetaTrader 5 — Примеры | 16 апреля 2025, 14:17

916

В эпоху больших данных существуют сотни миллионов наборов данных, каждый из которых обладает потенциалом обеспечения высокой точности при прогнозировании финансовых рынков. К сожалению, маловероятно, что все существующие наборы данных будут соответствовать этому потенциалу. В этой серии статей наша цель — помочь вам сориентироваться в обширном спектре возможных наборов данных. В конце вы сможете прийти к обоснованному решению о том, следует ли включать предлагаемые альтернативные данные в вашу торговую стратегию или лучше обойтись без них.

Обзор торговой стратегии

Мы проанализируем рынок XAUEUR. Символ отслеживает цену золота в EUR. Золото добывают на всех континентах Земли, за исключением Антарктиды. Значительная часть мирового золота торгуется Лондонской ассоциацией участников рынка драгоценных металлов (London Bullion Market Association, LBMA), которая устанавливает общепризнанный эталон цены на золото. Чикагская опционная биржа (Chicago Board of Options Exchange, CBOE) — американская компания, обеспечивающая международную рыночную инфраструктуру. CBOE использует свои сети для создания индексов волатильности, отслеживающих основные рынки по всему миру. Мы проанализируем два индекса волатильности CBOE, которые отслеживают рынки евро и золота соответственно.

За прошедшие годы трейдеры реализовали различные стратегии успешной торговли на волатильных рынках, минимизируя при этом риск. Как правило, когда рынки нестабильны, трейдеры имеют возможность достичь целевых показателей прибыли за относительно короткие периоды времени. С другой стороны, также можно быстро потерять значительную сумму капитала из-за больших разрывов в уровнях цен, которые могут не привести к своевременному срабатыванию стоп-ордеров.

Некоторые трейдеры предпочитают открывать меньше позиций или рисковать меньшим капиталом, чем обычно, при большем количестве позиций, чтобы потенциально выиграть от прибыльных ценовых движений, минимизируя при этом свои риски. Как правило, опытные трейдеры на волатильных рынках фиксируют прибыль гораздо быстрее, чем при торговле на более спокойных рынках. Другие трейдеры ждут, когда уровни цен впервые попадут в диапазон между уровнями поддержки и сопротивления. Когда уровни цен наконец выходят за пределы диапазона, трейдеры могут открывать позиции, ожидая более сильных движений за пределы идентифицируемого диапазона.

В нормальных рыночных условиях прорыв зоны поддержки и сопротивления может быстро потерять импульс и начать пробуксовывать. Однако на волатильном рынке за прорывами могут следовать резкие изменения цен в том же направлении, что обеспечивает трейдерам, следующим таким стратегиям, доходность выше среднего. К сожалению, такие стратегии подвержены ложным прорывам, которые заканчиваются резкими разворотами, приводя к большим убыткам.

Обзор методологии

Мы использовали API Python Экономической базы данных Федеральной резервной системы (Federal Reserve Economic Database, FRED) Федерального резервного банка Сент-Луиса для извлечения экономических временных рядов волатильности евро и золота на CBOE. Данные предоставляются в ежедневном формате и содержат пропущенные значения.

К сожалению, ни одно из описаний, предоставленных вместе с наборами данных, не объясняет ни одно из отсутствующих значений.
В терминале MetaTrader 5 мы извлекли около 4000 строк ежедневных рыночных котировок по цене открытия, максимума, минимума и закрытия (OHLC) символа XAUEUR, используя специальный скрипт, написанный нами на языке MQL5.

При анализе корреляции между альтернативными данными CBOE и рыночными данными MetaTrader 5 мы наблюдали уровни корреляции, не сильно отличающиеся от 0. Примечательно, что уровень корреляции между двумя альтернативными наборами данных составил 0,4. Положительный уровень корреляции может указывать на наличие взаимодействий или общих участников, влияющих на оба рынка.

Когда мы построили диаграммы рассеяния данных, используя любой из альтернативных наборов данных по оси X и цену закрытия XAUEUR по оси Y, оказалось, что существует порог высоких уровней волатильности, который последовательно приводит к повышению уровней цен. К сожалению, наш небольшой набор данных (в общей сложности около 3000 строк после слияния с альтернативными наборами данных) требует осторожности, чтобы не поддаться заблуждению и не увидеть в данных закономерности, которых на самом деле нет.

Эффективный просмотр многомерных данных может оказаться сложной задачей. Поэтому мы применили двойную процедуру для просмотра наших данных. Первоначально мы создали трехмерные диаграммы рассеяния, используя два набора данных CBOE по осям X и Y соответственно, а также данные по закрытию XAUEUR по оси Z. Группа бычьих свечей, которую мы наблюдали на наших двухмерных диаграммах рассеяния, по-прежнему была отчетливо видна.

Наконец, мы всегда можем воспользоваться алгоритмами, предназначенными для преобразования многомерных данных в подпространство меньшей размерности. Известным алгоритмом снижения размерности является метод главных компонент (Principal Components Analysis). Мы решили использовать реализацию scikit-learn для t-распределенного стохастического встраивания соседей (t-SNE) для создания двухмерного представления нашего шестимерного набора данных. Полученный график показал, что в нашем наборе данных могут быть 4 отдельных кластера. Более того, мы, по-видимому, наблюдали эффект последовательной зависимости в нашем наборе данных, что позволяет предположить, что между нашими наборами данных CBOE и MetaTrader 5 может развиваться связь.

Последним методом визуализации, который мы использовали, были графики автокорреляции. Все созданные нами графики автокорреляции показали сильные хвосты, что может указывать на наличие долгосрочных данных, сохраняющихся в наших временных рядах. Это может быть вызвано сильными трендами или сезонными эффектами. Наши графики частичной автокорреляции показали, что большая часть наблюдаемой нами автокорреляции объясняется лишь несколькими задержками. Это говорит о том, что данные временного ряда можно успешно смоделировать как модель скользящего среднего.

После визуализации наших данных мы создали 3 набора предикторов:

Рыночные данные OHLC MetaTrader 5
Альтернативные наборы данных FRED CBOE
Расширенный набор из двух предыдущих наборов

Для сравнения трех наборов предикторов использовались три идентичные глубокие нейронные сети с использованием 5-кратной перекрестной проверки временных рядов без случайного перемешивания. Последний набор предикторов дал самый низкий уровень ошибок при прогнозировании будущей цены закрытия символа XAUEUR. Это может указывать на то, что между двумя наборами данных существуют взаимосвязи, которые помогают нашей модели.

Опираясь на уверенность, полученную в ходе нашего первого теста, мы попытались оценить глобальную важность признаков нашей глубокой нейронной сети. Мы выбрали методы накопленных локальных эффектов (Accumulated Local Effects, ALE) и аддитивного объяснения Шепли (Shapley Additive Explanations, SHAP), чтобы получить представление о том, от каких моделей больше всего зависит наша модель. Ни один из использованных нами методов не отверг выбранные нами альтернативные наборы данных.

Мы настроили гиперпараметры нашей модели на обучающем наборе в ходе двухэтапного процесса, в результате которого было создано две модели. Первоначально мы выполнили 500 итераций случайного поиска по выборке параметров нашей модели. На втором этапе мы оптимизировали наилучшие значения непрерывных параметров нашей модели из случайного поиска, используя алгоритм ограниченной памяти Бройдена - Флетчера - Гольдфарба - Шанно (Limited Memory Broyden Fletcher Goldfarb Shanno algorithm, L-BFGS-B). Все остальные параметры модели, которые не были непрерывными, были зафиксированы на втором этапе.

Обе настроенные модели превзошли стандартную нейронную сеть на проверочных данных. Однако модель, полученная с помощью случайного поиска, показала наилучшие результаты на тестовом наборе. Это говорит о том, что мы, возможно, успешно оптимизировали нашу модель под обучающие данные, не переобучая наши параметры.

После этого мы подготовили нашу лучшую модель для экспорта в формат ONNX для интеграции в настраиваемую программу MetaTrader 5 и, наконец, написали скрипт Python для передачи последних данных FRED в наш терминал через общий CSV-файл.

Извлечение данных

Я добавил удобный скрипт, написанный на MQL5, который извлекает наши рыночные данные и записывает их в формат CSV. Скрипт имеет один входной параметр, который указывает, сколько баров данных необходимо извлечь. Просто перетащите скрипт на свой график.

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/en/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- Load indicator
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE);
   CopyBuffer(rsi_handler,0,0,size,rsi_buffer);
   ArraySetAsSeries(rsi_buffer,true);

//--- File name
   string file_name = "Market Data " + Symbol() + ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);

  }
//+------------------------------------------------------------------+

Подготовка данных

После получения рыночных данных OHLC для MetaTrader 5 мы начали процесс очистки и форматирования данных. Нашим первым шагом был импорт стандартных библиотек Python для машинного обучения.

#Import the libraries we need
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
from fredapi import Fred
from datetime import datetime
import time

Вот версии библиотек, которые мы используем.

#Display library versions
print(f"Pandas version {pd.__version__}")
print(f"Numpy version {np.__version__}")
print(f"Seaborn version {sns.__version__}")
print(f"Statsmodels version {statsmodels.__version__}")

Pandas version 2.1.4
Numpy version 1.26.4
Seaborn version 0.13.1
Statsmodels version 0.14.

Теперь мы можем прочитать CSV-файл, который мы только что создали, и установить столбец времени в качестве нашего индекса. Это позволит нам объединить данные MetaTrader 5 и CBOE в хронологическом порядке.

#Read in the data
xau_eur = pd.read_csv("Market Data XAUEUR.csv")
xau_eur = xau_eur.loc[96911:,:]
xau_eur.set_index("Time",inplace=True)
xau_eur.index = pd.to_datetime(xau_eur.index)

Давайте теперь получим альтернативные рыночные данные CBOE из FRED. Прежде всего вам необходимо создать бесплатную учетную запись на сайте FRED, чтобы получить закрытый ключ API. Здесь всё просто, никаких скрытых платежей.

#Fetch FRED data
fred = Fred(api_key='ENTER YOUR API KEY HERE')
fred_euro_data = pd.DataFrame(fred.get_series('EVZCLS'),columns=["EVZCLS"])
fred_gold_data = pd.DataFrame(fred.get_series('GVZCLS'),columns=["GVZCLS"])
#Fill in any missing values with the column mean
fred_euro_data = fred_euro_data.fillna(fred_euro_data.mean())
fred_gold_data = fred_gold_data.fillna(fred_gold_data.mean())

В Pandas есть команды, похожие на SQL, для объединения фреймов данных. Мы объединили только данные по датам, которые являются общими для обоих временных рядов.

#Merge the data
merged_data = pd.merge(xau_eur,fred_euro_data,left_index=True,right_index=True)
merged_data = pd.merge(merged_data,fred_gold_data,left_index=True,right_index=True)
merged_data

Рис. 1. Наш объединенный набор данных

Маркировка данных — важный шаг в любом проекте контролируемого машинного обучения. Сначала мы определили горизонт нашего прогноза, который в данном случае составляет 20 дней в будущем. Затем мы определили цель как будущую цену закрытия XAUEUR. Мы также создали бинарные целевые показатели, позволяющие оценить, выросли или упали уровни цен. Бинарные цели будут использоваться исключительно в целях визуализации.

#Let us label the data
look_ahead = 20

#Define the labels
merged_data["Target"] = merged_data["Close"].shift(-look_ahead)
merged_data["Binary Target"] = np.nan

merged_data.loc[merged_data["Target"] > merged_data["Close"],"Binary Target"] = 1
merged_data.loc[merged_data["Target"] <= merged_data["Close"],"Binary Target"] = 0

merged_data.dropna(inplace=True)
merged_data

Рис. 2. Наш набор данных с включенной целью

Наконец, мы определили три набора предикторов, которые мы собираемся эмпирически сравнить.

#Let us define the predictors and target
ohlc_predictors = ["Open","High","Low","Close"]
fred_predictors = ["EVZCLS","GVZCLS"]
predictors = ohlc_predictors + fred_predictors
target = "Target"
binary_target = "Binary Target"

Разведочный анализ данных

Наличие или отсутствие сильных уровней корреляции не обязательно означает наличие или отсутствие связи между анализируемыми данными. Наши альтернативные данные, по-видимому, имеют непостоянные уровни корреляции с набором данных XAUEUR. Однако, по-видимому, наблюдаются сильные уровни корреляции непосредственно между двумя альтернативными наборами данных.

#Exploratory Data Analysis
#Analyzing correlation levels
sns.heatmap(merged_data[predictors].corr(),annot=True)

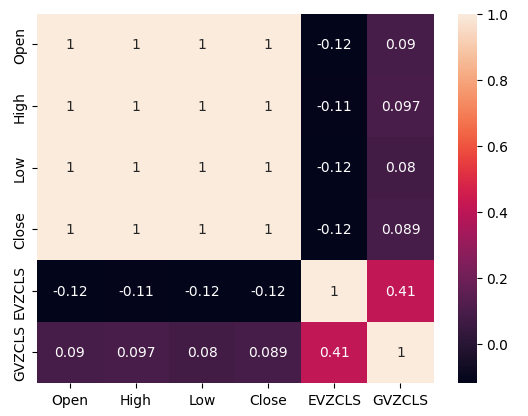
Рис. 3. Тепловая карта корреляций

Мы создали 3 диаграммы рассеяния имеющихся у нас данных. На первых двух диаграммах рассеяния по оси X откладывался индекс волатильности золота и евро, а по оси Y — цена закрытия XAUEUR. На нашей первой диаграмме рассеяния видно, что когда уровень волатильности золота поднимается выше уровня 30–35, мы постоянно наблюдаем бычье ценовое движение.

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="GVZCLS",y="Close",hue="Binary Target")

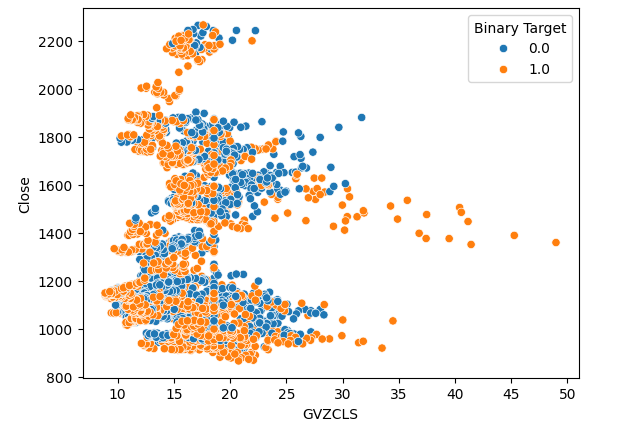
Рис. 4. Наша первая диаграмма рассеяния

Такое же явление наблюдается и на второй диаграмме рассеяния. Похоже, что когда уровень волатильности евро превышает уровень 14–16, уровень цен последовательно растет. Однако наш набор данных ограничен и может не в полной мере отражать истинную взаимосвязь между двумя рынками.

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="EVZCLS",y="Close",hue="Binary Target")

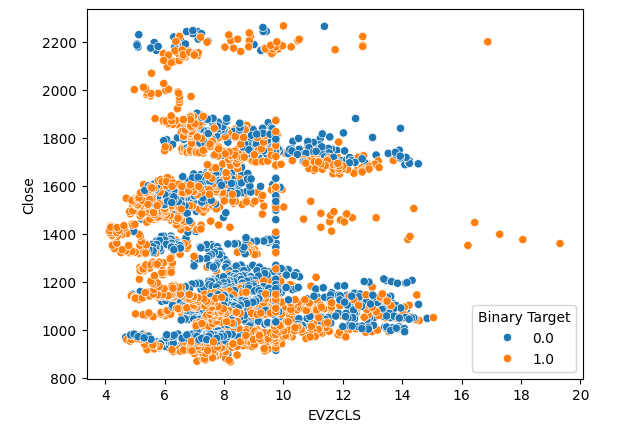
Рис. 5. Наша вторая диаграмма рассеяния

Наконец, мы создали диаграмму рассеяния, используя два наших альтернативных набора данных по обеим осям. Наши данные создали конусообразную структуру, в которой кластер бычьих свечей по-прежнему отчетливо виден и хорошо разделен.

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="GVZCLS",y="EVZCLS",hue="Binary Target")

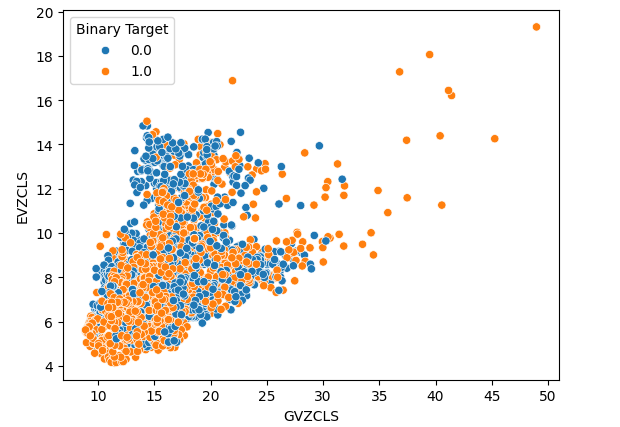
Рис. 6. Наша окончательная диаграмма рассеяния

В наших данных могут быть скрытые структуры, которые невозможно визуализировать в двух измерениях. Поэтому мы создали трехмерную диаграмму рассеяния, чтобы визуализировать влияние обоих наших альтернативных наборов данных на XAUEUR. Группа бычьих свечей по-прежнему отчетливо видна на трехмерном графике. Это может указывать на то, что наши альтернативные данные хорошо разделяют данные в определенных точках.

#Define the 3D Plot
fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection="3d")
ax.scatter(merged_data["GVZCLS"],merged_data["EVZCLS"],merged_data["Close"],c=merged_data["Binary Target"],cmap="plasma")
ax.set_xlabel("GVZCLS")
ax.set_ylabel("EVZCLS")
ax.set_zlabel("Close")

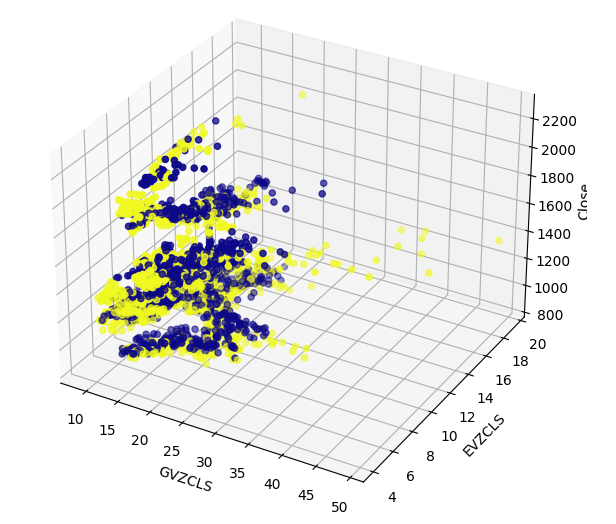
Рис. 7: Трехмерная диаграмма рассеяния наших рыночных данных

Мы также можем использовать методы снижения размерности, чтобы создать двухмерное представление наших шестимерных рыночных данных. Для выполнения этой задачи мы воспользуемся алгоритмом t-SNE. Алгоритм был впервые предложен в статье 2002 года, опубликованной Джеффри Хинтоном и его коллегами С оригинальной статьей (на английском) можно ознакомиться здесь. Хинтон считается пионером в области машинного обучения, во многом благодаря своей статье 1986 года, демонстрирующей, как алгоритм обратного распространения (back-propagation algorithm) может быть использован для обучения нейронной сети прогнозированию следующего слова в векторном представлении предложения. Его вклад способствовал популяризации и широкому внедрению алгоритма обратного распространения.

Хинтон

Рис. 8. Джеффри Хинтон

Алгоритм t-SNE предназначен для создания компактного представления многомерных данных, в котором близость между всеми точками данных в многомерном пространстве сохраняется в новом маломерном представлении. Для достижения этой цели алгоритм минимизирует специализированную функцию стоимости, которая измеряет разницу между двумя распределениями. Обычно эта процедура оптимизации достигается с помощью градиентного спуска. Сначала алгоритм создает матрицу более низкого ранга из исходных многомерных данных. Затем он итеративно перемещает точки данных, чтобы минимизировать стоимость. Напомним, что стоимость — это разница между распределениями данных в матрице нижнего ранга и исходным распределением данных. Алгоритм t-SNE полезен для визуализации кластеров данных, скрытых в многомерном пространстве.

Импортируем необходимые нам библиотеки.

#Let's create a TSNE Plot
from sklearn.manifold import TS

Затем мы создадим объект t-SNE и дадим ему команду создать двухмерное представление наших данных.

#Create a TSNE object which will reduce the data to 2 dimensions
tsne = TSNE(n_components=2,perplexity=30)

Подгоним объект t-SNE к имеющимся у нас данным.

#Apply TSNE to the data
tsne_data = tsne.fit_transform(merged_data[predictors])

Создадим новое представление данных.

#Create a scatter plot
plt.scatter(tsne_data[:,0],tsne_data[:,1])

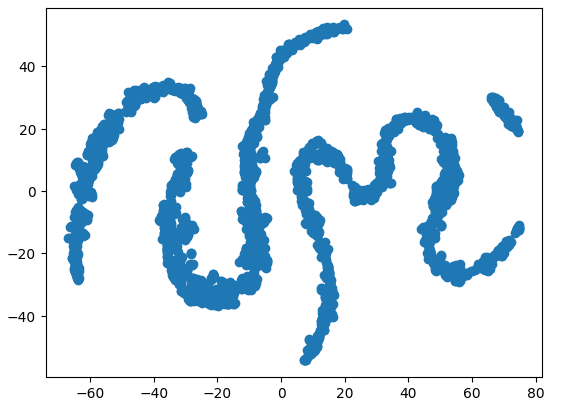
Рис. 9. График t-SNE рыночных данных

Из-за стохастического характера процедуры итеративной оптимизации может оказаться сложным воспроизвести график, полученный нами в ходе этого обсуждения. Более того, если бы мы выполнили процедуру второй раз, мы бы не были встревожены, получив другую диаграмму рассеяния. Нас особенно интересует количество кластеров, которые алгоритм пытается сохранить. Похоже, что наш набор данных содержит 4 отдельных кластера, более того, криволинейный характер графиков может указывать на зависимость, разделяемую во времени внутри кластеров.

Графики автокорреляции (ACF) широко используются в анализе временных рядов для проверки того, являются ли данные стационарными, содержат ли они сезонные колебания и так далее. Графики ACF показывают нам уровень корреляции между текущим значением временного ряда и его предыдущими значениями. Мы построили 3 графика ACF по закрытию XAUEUR и 2 альтернативным наборам данных CBOE. Все три графика предполагают, что данные имеют постоянные компоненты, это же подтверждается и тепловой картой, которую мы визуализировали ранее. Когда графики ACF имеют длинные хвосты, которые медленно спадают до 0, мы, естественно, рассматриваем возможность наличия в данных сильных трендовых или сезонных компонентов.

#Let's look at an autocorrelation plot of the data
close_acf = plot_acf(merged_data["Close"])

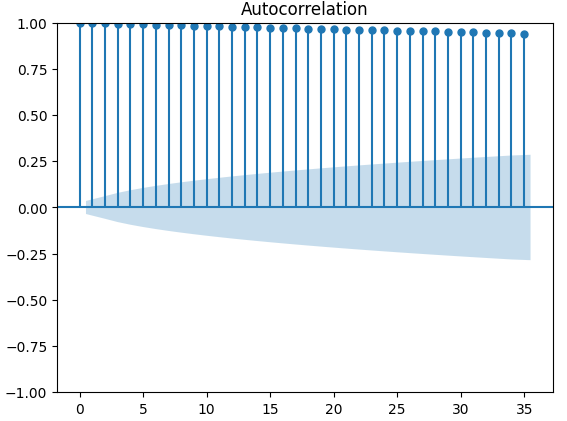
Рис. 10. График ACF цены закрытия XAUEUR

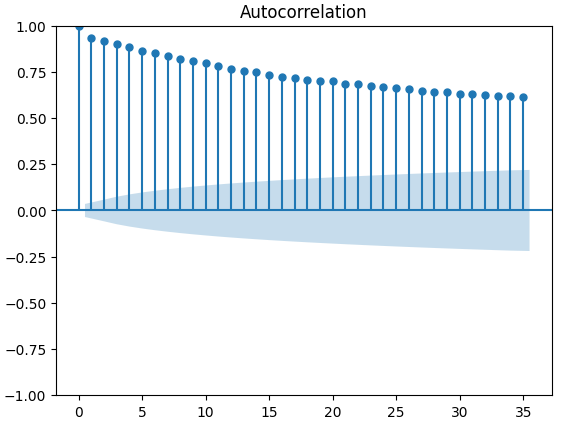
Рис. 11. График ACF индекса волатильности евро CBOE

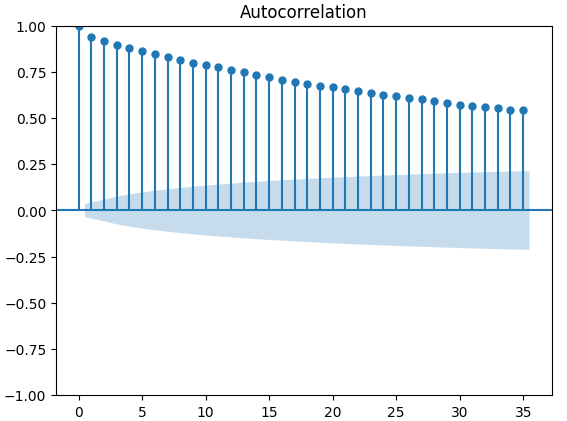
Рис. 12. График ACF индекса волатильности золота CBOE

Графики частичной автокорреляции (PACF) дают нам информацию о том, насколько далеко в прошлое следует заглянуть, чтобы объяснить большую часть корреляции, наблюдаемой между временным рядом и его задержками. Другими словами, они отвечают на вопрос: "Какая часть корреляции, наблюдаемой в задержке 3, не была перенесена из задержки 2"? Все три наших графика PACF показали, что не более 4 задержек объясняют большую часть автокорреляции в данных временного ряда.

#Let's look at an partial autocorrelation plot of the close data
close_pacf = plot_pacf(merged_data["Close"])

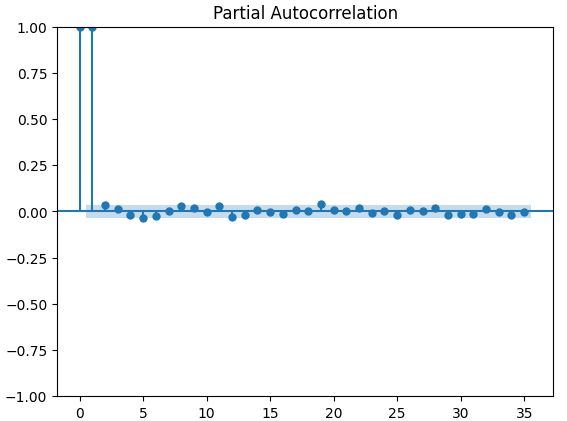
Рис. 13. Графики PACF закрытия XAUEUR

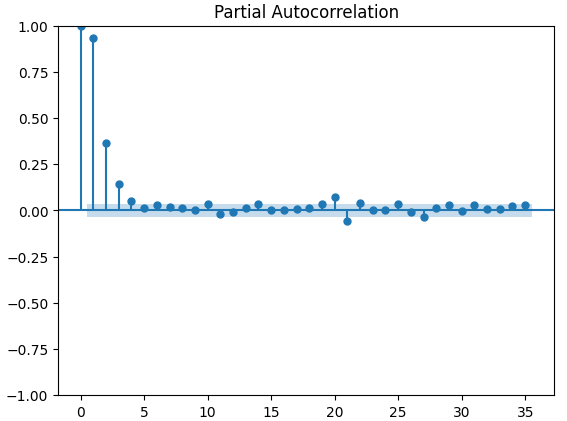
Рис. 14. Графики PACF индекса волатильности евро CBOE

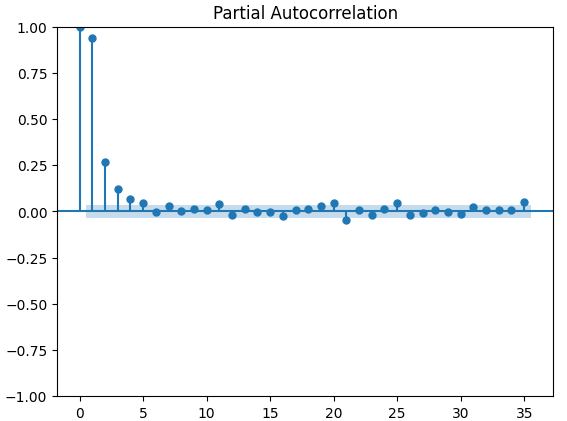
Рис. 15. Графики PACF индекса волатильности золота CBOE

Подготовка к моделированию данных

Прежде чем приступить к моделированию данных с помощью нашей глубокой нейронной сети, нам необходимо выполнить некоторые приготовления.

#Preparing to model the data
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import TimeSeriesSplit,train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.neural_network import MLPRegressor

Первый шаг — стандартизировать и масштабировать входные данные, чтобы наша модель могла эффективно обучаться.

#Reset the index of our data
merged_data.reset_index(inplace=True)

X = merged_data.loc[:,predictors]
y = merged_data.loc[:,target]

#Scale our data
scaler = RobustScaler()
X = pd.DataFrame(scaler.fit_transform(merged_data[predictors]),columns=predictors)

Теперь нам нужно создать разделение данных на обучающие и тестовые данные для трех имеющихся у нас наборов предикторов. Будьте осторожны, чтобы случайно не перемешать данные на этом этапе. В противном случае будет поставлена под угрозу целостность анализа.

#Perform train test splits
ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,shuffle=False,train_size=0.5)
fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,shuffle=False,train_size=0.5)
train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,shuffle=False,train_size=0.5)

Наконец, нам необходимо создать объект временного ряда, а затем создать фрейм данных для хранения уровней ошибок проверки.

#Let's now cross-validate each of the predictors
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

validation_error = pd.DataFrame(columns=["OHLC Predictors","FRED Predictors","All Predictors"],index=np.arange(0,5))

Моделирование данных

Мы готовы приступить к моделированию наших данных и перекрестной проверке наших моделей.

#Performing cross validation
model = MLPRegressor(hidden_layer_sizes=(20,5))
for i,(train,test) in enumerate(tscv.split(train_X)):
  model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
  validation_error.iloc[i,2] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))

Наши уровни ошибок проверки.

#Our validation error
validation_error

Данные MetaTrader 5 OHLC	Альтернативные данные FRED CBOE	Все данные
875423.637167	881892.498319	857846.11554
794999.120981	831138.370726	946193.178747
1058884.292095	474744.732539	631259.842972
419566.842693	882615.372658	483408.373559
96693.318078	618647.934237	237935.04009

Нам может быть не сразу очевидно, какая модель работает лучше всего, однако, когда мы анализируем средние значения столбцов, мы ясно видим, что последняя модель работает исключительно хорошо. На графике ниже мы вычли среднее значение первого столбца из оставшихся столбцов. При этом значение первого столбца будет равно 0, а все неудовлетворительные модели будут иметь значения столбцов больше 0. Таким образом, мы ясно видим, что наша последняя модель работает достаточно хорошо.

#Our mean error levels
val_err = validation_error.mean()
val_err = val_err.iloc[:] - val_err.iloc[0]
val_err.plot(kind="bar")

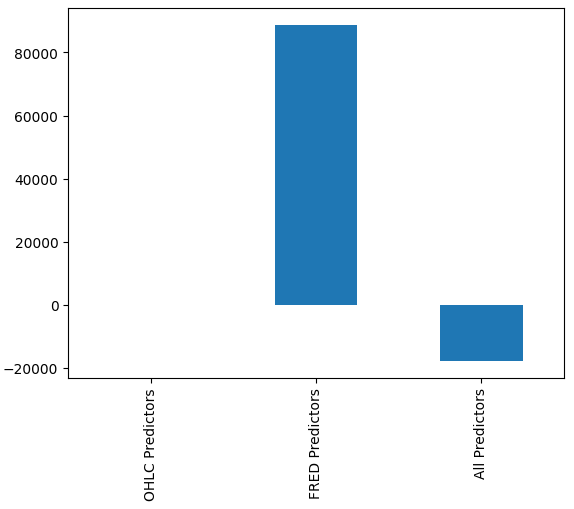
Рис. 16. Эффективность нашей модели при использовании трех различных наборов данных

Построение диаграмм производительности модели дополнительно показывает, что последний набор предикторов представляется оптимальным, средняя частота ошибок самая низкая, а дисперсия не такая большая, как при использовании только данных OHCL.

#Let's perform boxplots of our validation error
sns.boxplot(validation_error)

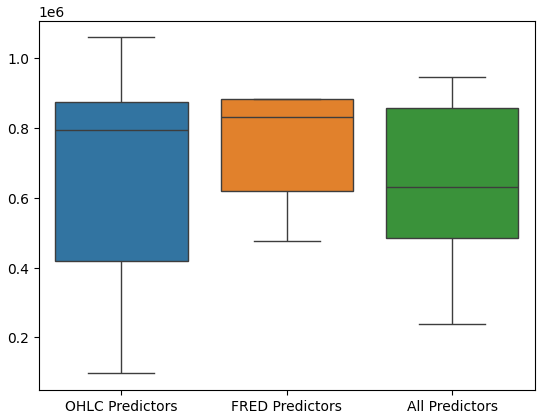
Рис. 17: Эффективность модели в виде блочной диаграммы

Значимость признаков

Мы никогда не должны слепо доверять какой-либо модели и внедрять ее только из-за низких показателей ошибок. Давайте рассмотрим взаимосвязи, изученные моделью. Мы хотели бы получить представление о глобальной значимости признаков нашей модели. Начнем с создания графиков накопленного локального эффекта (ALE). ALE разработан для предоставления надежных объяснений для моделей машинного обучения, обученных на данных с высоким уровнем корреляции. ALE пытается изолировать влияние каждого входного параметра на результат модели.

#Feature importance
from alibi.explainers import ALE , plot_ale

Теперь мы создадим наш объект ALE и выведем пояснения по глобальной важности признаков для нашей глубокой нейронной сети. Это поможет нам понять, какое влияние каждый из наших входных параметров оказывает на прогноз модели.

#Explaining our deep neural network
model = MLPRegressor(hidden_layer_sizes=(20,5))
model.fit(train_X,train_y)
dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["XAUEUR Close"])

Давайте теперь вычислим и построим график значений ALE для каждого из входных параметров модели.

#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)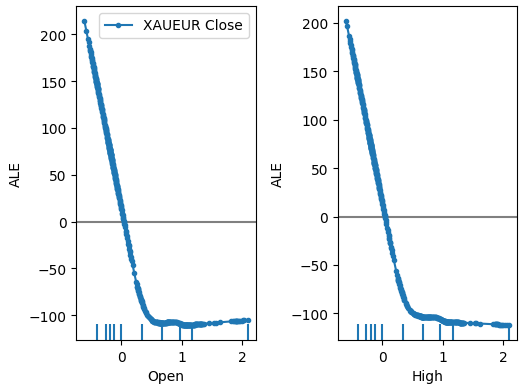

Рис. 18. Наши графики ALE для некоторых предикторов XAUEUR Open и High

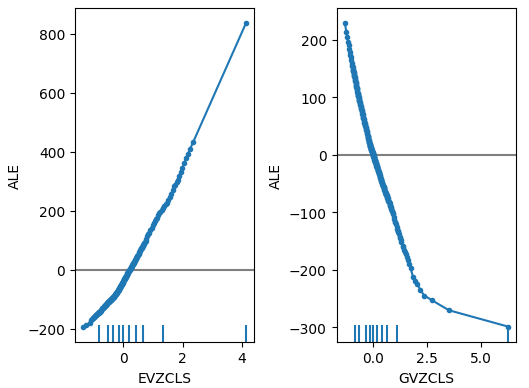
Рис. 19. Наши графики ALE для индексов волатильности FRED CBOE

Интерпретация графиков ALE вполне интуитивна: график иллюстрирует, как прогноз модели изменяется по мере изменения значения каждого предиктора. Как мы видим, по мере роста цен открытия и максимума прогноз модели изначально падает. Однако он становится менее чувствительным по мере дальнейшего роста цен. Хотя мы их здесь не включили, графики ALE для минимальной цены и цены закрытия выглядят идентично двум показанным графикам.

Если теперь обратиться к графикам ALE альтернативных данных, то можно заметить, что индекс волатильности евро создал график ALE, который охватывает часть графика, которую не смогли охватить другие переменные. Другими словами, предиктор, по-видимому, объясняет дисперсию в цели, которую мы не смогли объяснить без него. Более того, восходящий наклон графика ALE свидетельствует о том, что по мере увеличения значения предиктора увеличивается и прогноз модели.

Далее выведем объяснения SHAP относительно эффективности нашей модели. Значения SHAP помогают нам количественно оценить, какой вклад каждый из входных параметров модели внес в конкретный прогноз по сравнению со средним прогнозом модели. Значения SHAP берут свое начало в математической области теории игр. Алгоритм рассматривает каждый возможный набор предикторов, а затем вычисляет средний эффект входных данных по всем возможным наборам.

Сначала импортируем библиотеку SHAP.

#SHAP Values
import shap

Рассчитаем значения SHAP.

#Calculating SHAP values
explainer = shap.Explainer(model.predict,train_X)
shap_values = explainer(test_X)#Calculating SHAP values

Постройте график значений SHAP.

#Plot the beeswarm plot
shap.plots.beeswarm(shap_values)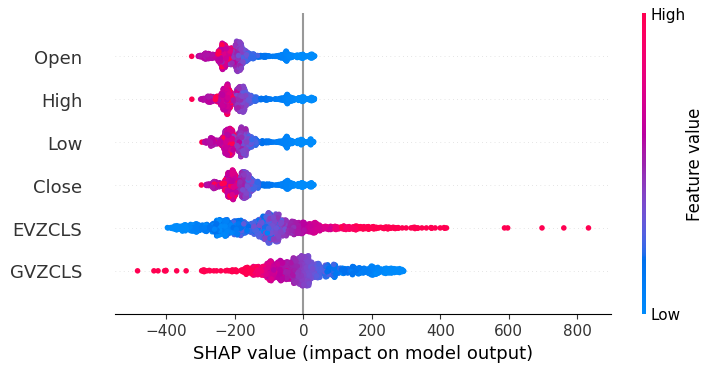

Рис. 20. Наши объяснения SHAP

Согласно нашим пояснениям SHAP, рыночные данные, полученные непосредственно с рынка XAUEUR, являются наиболее важными данными, которые у нас есть. Более того, график SHAP также показывает нам, что по мере роста текущей рыночной цены целевое значение имеет тенденцию к снижению.

Настройка параметров

Давайте попробуем повысить производительность нашей модели. Начнем с импорта необходимых нам библиотек.

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

Инициализируем модель.

#Reinitialize the model
model = MLPRegressor(hidden_layer_sizes=(20,5))

Определим объект тюнера.

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "shuffle": [True,False]
        },
        n_iter=500,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

Устанавливаем тюнер.

#Fit the tuner
tuner_results = tuner.fit(train_X,train_y)

Лучшие параметры, которые мы нашли.

#The best parameters we found
tuner_results.best_params_

{'tol': 1e-07,
'solver': 'lbfgs',
'shuffle': True,
'learning_rate': 'adaptive',
'alpha': 0.1,
'activation': 'identity'}

В модуль минимизации Scipy включены процедуры оптимизации. Эти процедуры требуют отправной точки для процесса оптимизации. В качестве отправной точки на втором этапе оптимизации мы будем использовать наилучшие значения параметров, найденные с помощью случайного поиска.

#Deeper optimization
from scipy.optimize import minimize

Теперь создадим объект фрейма данных для хранения наших уровней ошибок при проверке.

#Create a dataframe to store our accuracy
current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])

Каждому алгоритму оптимизации необходима целевая функция для работы. В нашем случае целевой функцией является средняя перекрестно проверенная ошибка модели на обучающем наборе. Наша процедура оптимизации будет искать параметры модели, которые минимизируют нашу среднюю ошибку.

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1])
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(train_X)):
        #Train the model
        model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
        #Measure the RMSE
        current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

Определим отправную точку для процедуры оптимизации, а также границы допустимых входных значений.

#Define the starting point
pt = [0.1,0.00000001]
bnds = ((0.0000000000000000001,10000000000),(0.0000000000000000001,10000000000))

Оптимизируем модель.

#Searchin deeper for parameters
result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)

Проверка на переобучение

Переобучение — проблема любого проекта машинного обучения. Это происходит, когда наша модель не может создать осмысленные обобщения данных, а вместо этого начинает изучать шум и другие бессмысленные ассоциации в данных. Для проверки на переобучение мы сравним точность наших двух настроенных моделей с моделью по умолчанию.

#Testing for overfitting
default_model          = MLPRegressor(hidden_layer_sizes=(20,5))
customized_model       = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=0.1,tol=0.0000001)
customized_lbfgs_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=result.x[0],tol=result.x[1])

Давайте теперь подготовимся к перекрестной проверке каждой модели.

#Preparing to cross validate the models
models = [
    default_model,
    customized_model,
    customized_lbfgs_model
]

#We will store our validation error here
validation_error = pd.DataFrame(columns=["Default Model","Customized Model","L-BFGS Model"],index=np.arange(0,5))

#We will now reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()

Нам необходимо подогнать каждую из моделей под обучающий набор.

#Fit each of the models
for m in models:
  m.fit(train_X,train_y)

Теперь давайте проверим эффективность нашей модели на ранее неизвестных данных — тестовом наборе, который мы использовали до сих пор.

#Cross validating each model
for j in np.arange(0,len(models)):
  model = models[j]
  for i,(train,test) in enumerate(tscv.split(test_X)):
    model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1],"Target"])
    validation_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"Target"],model.predict(test_X.loc[test[0]:test[-1],:]))

Наши уровни ошибок проверки.

#Our validation error
validation_error

Модель по умолчанию	Модель рандомизированного поиска	Модель L-BFGS-B
22360.060721	5917.062055	3734.212826
17385.289026	36726.684574	35886.972729
13782.649037	5128.022626	20886.845316
3082484.290698	6950.786438	5789.948045
4076009.132941	27729.589769	22931.572161

Наиболее эффективной моделью является модель рандомизированного поиска.

#Plotting the difference in our performance levels
mean = validation_error.mean()
mean = mean.iloc[:] - mean.iloc[0]
mean.plot(kind="bar")

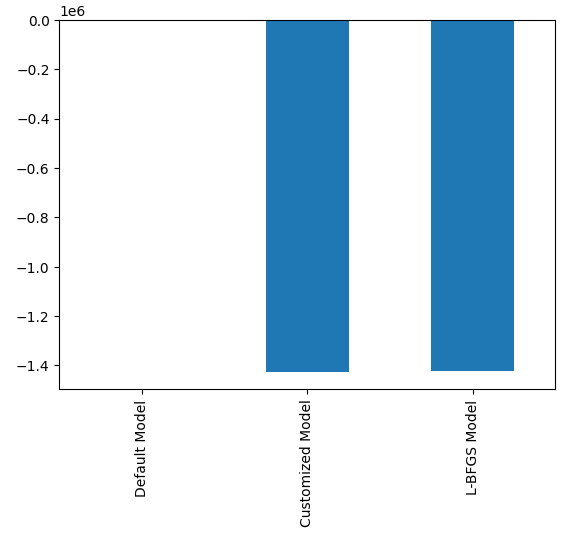
Рис. 21: Уровни ошибок проверки

Визуализация производительности нашей модели наглядно демонстрирует, насколько плохо модель по умолчанию обрабатывает данные.

#Visualizing the results
validation_error.plot()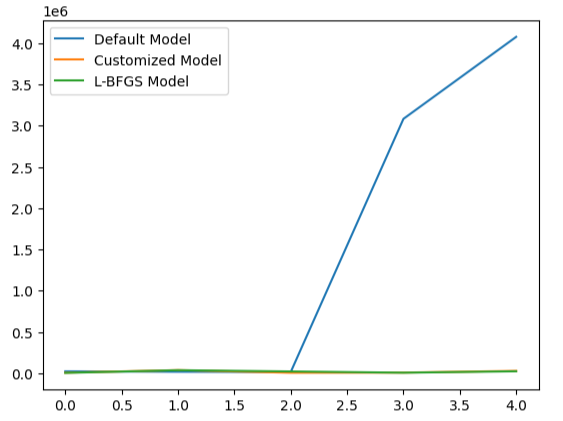

Рис. 22. Проверка на переобучение

Эту точку зрения еще больше подтверждают наши блочные диаграммы. Мы значительно превзошли модель по умолчанию.

#Visualizing our results
sns.boxplot(validation_error)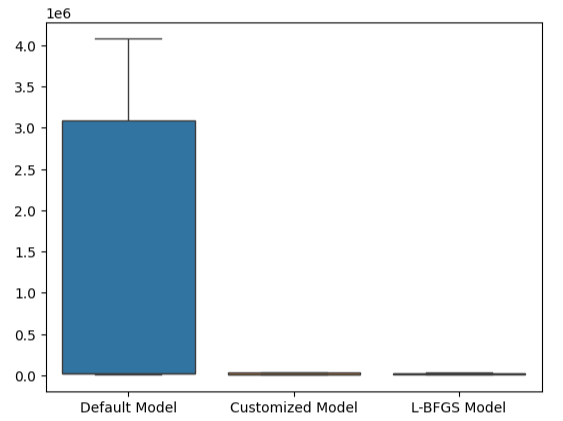

Рис. 23. Мы значительно превосходим модель по умолчанию.

Подготовка к экспорту в формат ONNX

Прежде чем экспортировать нашу модель в формат ONNX, нам необходимо стандартизировать и масштабировать наши данные таким образом, чтобы их можно было воспроизвести в нашем терминале MetaTrader 5. Для этого мы вычтем среднее значение из каждого столбца, а затем разделим каждый столбец на его стандартное отклонение. Мы запишем наши коэффициенты масштабирования в формате CSV, чтобы иметь возможность извлечь их в нашем терминале MetaTrader 5 для масштабирования входных данных нашей модели.

#Let us now prepare to export our model to onnx format
scale_factors = pd.DataFrame(columns=predictors,index=["mean","standard deviation"])

for i in np.arange(0,len(predictors)):
  scale_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
  scale_factors.iloc[1,i] =  merged_data.loc[:,predictors[i]].std()
  merged_data.loc[:,predictors[i]] = (merged_data.loc[:,predictors[i]] - merged_data.loc[:,predictors[i]].mean())/merged_data.loc[:,predictors[i]].std()

scale_factors

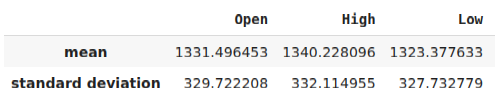
Рис. 24. Некоторые из наших коэффициентов масштабирования

Теперь запишем данные в формате CSV.

#Save the scale factors to CSV
scale_factors.to_csv("scale_factors.csv")

Экспорт в формат ONNX

Open Neural Network Exchange (ONNX) — это протокол для создания и совместного использования моделей машинного обучения на разных языках программирования. Протокол ONNX позволяет нам легко встроить нашу глубокую нейронную сеть в нашего советника с помощью API MQL5 ONNX.

Давайте сначала загрузим необходимые библиотеки.

#Exporting to ONNX format
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

Обучим модель на всех имеющихся у нас данных.

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])

При экспорте моделей ONNX форма входных данных может быть потеряна. Поэтому давайте укажем ее явно.

# Define the input type
initial_types = [("float_input",FloatTensorType([1,6]))]

Создадим ONNX-представление модели.

# Create the ONNX representation
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

Сохраним ONNX-представление в файле с расширением ".onnx".

# Save the ONNX model
onnx_name = "XAUEUR FRED D1.onnx"
onnx.save_model(onnx_model,onnx_name)

Получение актуальных данных FRED

Прежде чем приступить к созданию нашего советника, нам необходимо создать скрипт Python, который будет постоянно обмениваться актуальными данными FRED с нашим терминалом. Мы создадим скрипт, который будет извлекать последние доступные данные один раз в день и записывать их в CSV в папке "Файлы", чтобы мы могли получить доступ к данным с помощью нашего торгового приложения.

#A function to write out our alternative data to CSV
def write_out_alternative_data():
        euro = fred.get_series("EVZCLS")
        euro = euro.iloc[-1]
        gold = fred.get_series("GVZCLS")
        gold = gold.iloc[-1]
        data = pd.DataFrame(np.array([euro,gold]),columns=["Data"],index=["Fred Euro","Fred Gold"])
        data.to_csv("C:\\ENTER\\YOUR\\PATH\\HERE\\MetaQuotes\\Terminal\\D0E8209F77C8CF37AD8BF550E51FF075\\MQL5\\Files\\fred_xau_eur.csv")

Теперь мы напишем бесконечный цикл, чтобы записать данные, а затем встать на паузу на один день.

while True:
        #Update the fred data for our MT5 EA
        write_out_alternative_data()
        #If we have finished all checks then we can wait for one day before checking for new data
        time.sleep(24 * 60 * 60)

Создание советника

Теперь мы готовы приступить к созданию нашего советника. Начнем с того, что потребуем файл ONNX, который мы только что создали.

//+------------------------------------------------------------------+
//|                                               EURXAU Fred AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/en/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Volatility Doctor"
#property link      "https://www.mql5.com/en/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Require the ONNX file                                            |
//+------------------------------------------------------------------+
#resource "\\Files\\XAUEUR FRED D1.onnx" as const uchar onnx_buffer[];

Загрузим торговую библиотеку для управления позициями.

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

Эти глобальные переменные будут использоваться совместно во многих различных частях нашего приложения.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long    onnx_model;
vector  mean_values  = vector::Zeros(6);
vector  std_values   = vector::Zeros(6);
vectorf model_inputs = vectorf::Zeros(6);
vectorf model_output = vectorf::Zeros(1);
double  bid,ask;
int     system_state,model_sate;

Теперь нам нужна функция, которая создаст нашу ONNX-модель из ONNX-буфера, который мы создали в начале нашего приложения. Наша функция сначала создаст и проверит ONNX-модель, а затем установит и проверит формы входных и выходных данных модели. Если в какой-либо момент произойдет сбой, функция вернет false, что, в свою очередь, остановит процедуру инициализации.

//+------------------------------------------------------------------+
//| Load the ONNX file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the ONNX model from the buffer we loaded earlier
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Validate the model we just created
   if(onnx_model == INVALID_HANDLE)
     {
      //--- Give the user feedback on the error
      Comment("Failed to create the ONNX model: ",GetLastError());
      //--- Break initialization
      return(false);
     }

//--- Define the I/O shape
   ulong input_shape [] = {1,6};

//--- Validate the input shape
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      //--- Give the user feedback
      Comment("Failed to define the ONNX input shape: ",GetLastError());
      //--- Break initialization
      return(false);
     }

   ulong output_shape [] = {1,1};

//--- Validate the output shape
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      //--- Give the user feedback
      Comment("Failed to define the ONNX output shape: ",GetLastError());
      //--- Break initialization
      return(false);
     }

//--- We've finished
   return(true);
  }
//+------------------------------------------------------------------+

Теперь мы определим коэффициенты масштабирования, которые нам понадобятся для нормализации входных данных нашей модели.

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
bool load_scaling_factors(void)
  {
//--- Load the scaling values
   mean_values[0] = 1331.4964525595044;
   mean_values[1] = 1340.2280958591457;
   mean_values[2] = 1323.3776328659928;
   mean_values[3] = 1331.706768829475;
   mean_values[4] = 8.258127607767035;
   mean_values[5] = 16.35582438284101;
   std_values[0] = 329.7222075527991;
   std_values[1] = 332.11495530642173;
   std_values[2] = 327.732778866831;
   std_values[3] = 330.1146052811378;
   std_values[4] = 2.199782202942867;
   std_values[5] = 4.241112965400358;

//--- Validate the values loaded correctly
   if((mean_values.Sum() > 0) && (std_values.Sum() > 0))
     {
      return(true);
     }

//--- We failed to load the scaling values
   return(false);
  }

Когда наше приложение перестанет использоваться, мы освободим ресурсы, которые больше не используем.

//+------------------------------------------------------------------+
//| Free up the resources we no longer need                          |
//+------------------------------------------------------------------+
void release_resources(void)
  {
//--- Free up all the resources we have used so far
   OnnxRelease(onnx_model);
   ExpertRemove();
   Print("Thank you for choosing Volatility Doctor");
  }

Эта функция будет отвечать за обновление наших данных о рыночных ценах.

//+------------------------------------------------------------------+
//| Fetch market data                                                |
//+------------------------------------------------------------------+
void fetch_market_data(void)
  {
//--- Update the market data
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

Следующая функция отвечает за получение прогноза от нашей модели. Сначала мы получим текущие данные OHLC по символу XAUEUR, используя матричную функцию MQL5 CopyRates(). После извлечения данных мы нормализуем их и сохраним во входном векторе, который мы определили ранее. Отсюда мы вызовем другую функцию для считывания последних данных FRED, имеющихся в файле.

//+------------------------------------------------------------------+
//| This function will fetch a prediction from our model             |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Get the input data ready
   for(int i =0; i < 6; i++)
     {
      //--- The first 4 inputs will be fetched from the market
      matrix xau_eur_ohlc = matrix::Zeros(1,4);
      xau_eur_ohlc.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OHLC,0,1);
      //--- Fill in the data
      if(i<4)
        {
         model_inputs[i] = (float)((xau_eur_ohlc[i,0] - mean_values[i])/ std_values[i]);
        }
      //--- We have to read in the fred alternative data
      else
        {
         read_fred_data();
        }
     }
  }

Функция, определенная ниже, прочитает CSV-файл с последними данными FRED и нормализует данные перед их сохранением во входном векторе и извлечением прогноза из нашей модели. Мы представим прогноз модели с помощью целого числа. Это поможет нам быстро обнаружить потенциальные развороты и закрыть наши позиции, надеемся, на правильной стороне рынка.

//+-------------------------------------------------------------------+
//| Read in the FRED data                                             |
//+-------------------------------------------------------------------+
void read_fred_data(void)
  {
//--- Read in the file
   string file_name = "fred_xau_eur.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file

      int counter = 0;
      string value = "";
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {
         if(counter > 10)  //if you aim to read 10 values set a break point after 10 elements have been read
            break;          //stop the reading progress

         value = FileReadString(result);
         Print("Counter: ");
         Print(counter);
         Print("Trying to read string: ",value);

         if(counter == 3)
           {
            Print("Fred Euro data: ",value);
            model_inputs[4] = (float)((((float) value) - mean_values[4])/std_values[4]);
           }

         if(counter == 5)
           {
            Print("Fred Gold data: ",value);
            model_inputs[5] = (float)((((float) value) - mean_values[5])/std_values[5]);
           }

         if(FileIsLineEnding(result))
           {
            Print("row++");
           }

         counter++;
        }

      //--- Show the input and Fred data
      Print("Input Data: ");
      Print(model_inputs);

      //---Close the file
      FileClose(result);

      //--- Store the model prediction
      OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
      Comment("Model Forecast",model_output[0]);
      if(model_output[0] > iClose(Symbol(),PERIOD_D1,0))
        {
         model_sate = 1;
        }

      else
        {
         model_sate = -1;
        }
     }

//--- We failed to find the file
   else
     {
      //--- Give the user feedback
      Print("We failed to find the file with the FRED data");
     }
  }

Давайте теперь определим, как должно запускаться наше приложение. Наше приложение должно сначала создать ONNX-модель, а затем загрузить необходимые нам коэффициенты масштабирования. Если хотя бы один из этих шагов не будет выполнен, мы прерываем процедуру инициализации.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX model
   if(!load_onnx_file())
     {
      //--- We failed to load our ONNX model
      return(INIT_FAILED);
     }

//--- Load the scaling factors
   if(!load_scaling_factors())
     {
      //--- We failed to read in the scaling factors
      return(INIT_FAILED);
     }

//--- We mamnaged to load our model
   return(INIT_SUCCEEDED);
  }

Когда наше приложение будет удалено с графика, освободим ресурсы, которые нам больше не нужны.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we no longer need
   release_resources();
  }

Наконец, всякий раз, когда мы получаем обновленные рыночные котировки, мы сначала сохраняем обновленные рыночные цены в памяти. Впоследствии, если у нас нет открытых позиций, мы будем следовать прогнозу нашей модели только в том случае, если он будет подкреплен ценовым действием на более крупных таймфреймах. Если у нас уже есть открытые позиции, мы закроем их, если наша модель предвидит развороты ценовых уровней.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market data
   fetch_market_data();

//--- Fetch a prediction from our model
   model_predict();

//--- If we have no positions follow the model's lead
   if(PositionsTotal() == 0)
     {
      //--- Buy position
      if(model_sate == 1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Buy(0.3,Symbol(),ask,0,0,"XAUEUR Fred AI");
            system_state = 1;
           }
        };

      //--- Sell position
      if(model_sate == -1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Sell(0.3,Symbol(),bid,0,0,"XAUEUR Fred AI");
            system_state = -1;
           }
        };
     }

//--- If we allready have positions open, let's manage them
   if(model_sate != system_state)
     {
      Trade.PositionClose(Symbol());
     }

  }
//+------------------------------------------------------------------+

Наша система в действии

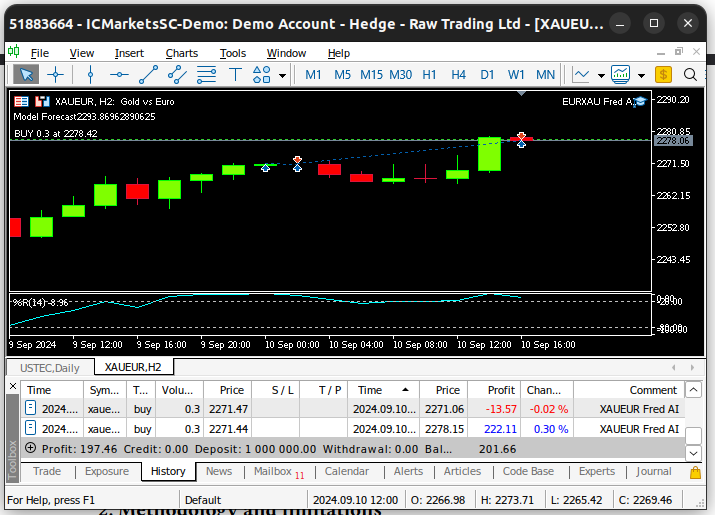
Рис. 25. Наш советник в действии

Заключение

В этой статье мы продемонстрировали, что включение индексов волатильности FRED CBOE может быть полезным для повышения точности моделей машинного обучения. Хотя мы не можем гарантировать, что информация, представленная в этой статье, будет постоянно приносить пользу, ее, безусловно, стоит рассмотреть, если вы готовы начать использовать альтернативные данные в своих торговых стратегиях.

Перевод с английского произведен MetaQuotes Ltd.
Оригинальная статья: https://www.mql5.com/en/articles/15841

Прикрепленные файлы |

Загрузить ZIP

FetchData21s.mq5 (2.05 KB)

EURXAU_Fred_AI.mq5 (9.9 KB)

fred_xau_eur.csv (0.04 KB)

xau_eur_scale_factors.csv (0.27 KB)

XAUEUR_FRED_D1.onnx (1.72 KB)

Gain_an_Edge_XAUEUR.ipynb (1456.96 KB)

Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.

Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.

Другие статьи автора

Перейти к обсуждению на форуме трейдеров

Создание торговой панели администратора на MQL5 (Часть III): Улучшение графического интерфейса пользователя (GUI) с помощью визуального оформления (I)

В настоящей статье мы сосредоточимся на визуальном оформлении графического интерфейса пользователя (GUI) нашей торговой панели администратора с использованием MQL5. Мы рассмотрим различные методы и функции, доступные в MQL5, которые позволяют настраивать и оптимизировать интерфейс, обеспечивая его соответствие потребностям трейдеров при сохранении привлекательной эстетики.

Оптимизация коралловых рифов — Coral Reefs Optimization (CRO)

В данной статье представлен комплексный анализ алгоритма оптимизации коралловых рифов (CRO) — метаэвристического метода, вдохновленного биологическими процессами формирования и развития коралловых рифов. Алгоритм моделирует ключевые аспекты эволюции кораллов: внешнее и внутреннее размножение, оседание личинок, бесполое размножение и конкуренцию за ограниченное пространство в рифе. Особое внимание в работе уделяется усовершенствованной версии алгоритма.

Угловой анализ ценовых движений: гибридная модель прогнозирования финансовых рынков

Что такое угловой анализ финансовых рынков? Как использовать углы движения цен и машинное обучение для точного прогнозирования с точностью 67? Как совместить регрессионную и классификационную модель с угловыми признаками и получить работающий алгоритм? Причем тут Ганн? Почему углы движения цен являются хорошим признаком для машинного обучения?

Торговля по алгоритму: ИИ и его путь к золотым вершинам

В данной статье продемонстрирован подход к созданию торговых стратегий для золота с помощью машинного обучения. Рассматривая предложенный подход к анализу и прогнозированию временных рядов с разных ракурсов, можно определить его преимущества и недостатки по сравнению с другими способами создания торговых систем, основанных исключительно на анализе и прогнозировании финансовых временных рядов.