どんな市場でも優位性を得る方法（第4回）：CBOEのユーロおよびゴールドボラティリティインデックス

MetaTrader 5 — 例 | 22 11月 2024, 10:09

277

ビッグデータの時代では、金融市場を予測する際に、それぞれが未開拓レベルの精度をもたらす可能性を秘めた何億ものデータセットがあります。残念ながら、既存のデータセットすべてがこの可能性に応えることはまずありません。本連載の目標は、考えられるデータセットの広大な範囲を網羅できるように支援し、議論の最後には、提案された代替データを取引戦略に含めるべきか、それとも使用しない方がよいかを十分な情報に基づいて判断できるようにすることです。

取引戦略の概要

XAUEUR銘柄を分析します。この銘柄はユーロ建ての金の価格を追跡します。金は南極を除く地球上のすべての大陸で採掘されており、世界の金のかなりの部分はロンドン貴金属市場協会(LBMA)によって取引され、金の価格の世界的なベンチマークとして認められています。シカゴオプション取引所(CBOE)は、世界的な市場インフラを提供するアメリカの企業で、世界中の主要市場を追跡するボラティリティインデックスを作成するために、自社のネットワークを活用しています。ユーロ市場と金市場を追跡するCBOEのボラティリティインデックス2つを分析します。

トレーダーは長年にわたり、リスクを最小限に抑えながら不安定な市場での取引を成功させるためのさまざまな戦略を編み出してきました。一般的に、市場が不安定な場合、トレーダーは比較的短期間で利益目標を達成できる可能性があります。一方で、価格レベルに大きなギャップがあると、ストップロス注文がタイムリーにトリガーされない可能性があり、その結果、多額の資本を急速に失うことがあります。

大まかに言えば、一部のトレーダーは、市場へのエクスポージャーを最小限に抑えながら、利益を生む価格変動から利益を得るために、通常よりも少ないポジションを建てたり、より多くのポジションで通常よりも少ない資本をリスクにさらしたりすることを好みます。一般的に、経験豊富なトレーダーは、不安定な市場では、より静かな市場で取引する場合よりもずっと早く利益を得る傾向があります。逆に、他のトレーダーは、価格レベルが支持レベルと抵抗レベルの間の範囲にとらわれるのを待ち、価格レベルが最終的にその範囲を抜け出すと、強い動きが出ることを予想してポジションを建てる場合があります。

通常の市場状況では、支持と抵抗のゾーンからのブレイクアウトはすぐに勢いを失い、漂い始めることがよくあります。しかし、市場状況が不安定な場合、ブレイクアウト後に同じ方向への激しい価格変動が続く可能性があり、そのような戦略に従うトレーダーは平均以上の利益を得ることができます。残念ながら、そのような戦略は偽のブレイクアウトを引き起こしやすく、激しく反転する可能性があり、一部のトレーダーは不利なポジションに陥り、大きな損失を抱えることになります。

方法論の概要

セントルイス連邦準備銀行が管理する連邦準備銀行経済データベース(FRED)のPython APIを利用して、CBOEユーロおよび金のボラティリティ経済時系列データを取得しました。データは日次形式で提供されており、欠損値が含まれています。

残念ながら、データセットに提供されている説明のいずれも、欠損値について説明していません。したがって、両方のデータセットのすべての欠損値を平均値代入によって補完しました。

MetaTrader 5端末では、MQL5で作成したカスタマイズされたスクリプトを使用して、XAUEUR銘柄の始値、高値、安値、終値(OHLC)の毎日の市場相場を約4000行取得しました。

CBOE代替データとMetaTrader 5市場データの相関を分析したところ、相関レベルは0からそれほど離れていないことがわかりました。特に、2つの代替データセット間の相関レベルは0.4でした。相関レベルが正であることは、2つの市場に影響を与える相互作用または共通の市場参加者の存在を示唆している可能性があります。

X軸に代替データセットのいずれか、Y軸にXAUEURの終値を使用してデータの散布図を作成したところ、一貫して価格レベルの上昇につながる高ボラティリティレベルの閾値があることがわかりました。残念ながら、私たちのデータセットは小さく、代替データセットとマージした後の合計行数は約3000行であるため、実際には存在しないデータパターンを誤って認識しないように注意する必要があります。

高次元データを効果的に表示するのは難しい場合があります。そのため、2段階の手順でデータを表示しました。最初に、2つのCBOEデータセットをそれぞれx軸とy軸に、XAUEUR終値をz軸に使用して3D散布図を作成しました。2D散布図で確認した強気ローソク足のクラスタは、依然としてはっきりと見えています。

最後に、高次元データを低次元のサブスペースにマッピングするように設計されたアルゴリズムをいつでも利用できます。よく知られている次元削減アルゴリズムは、主成分分析です。6次元データセットの2次元表現を作成するために、t分布確率的近傍埋め込み(t-SNE)のscikit-learn実装を使用することにしました。結果のプロットは、データセットに4つの異なるクラスターがある可能性があることを示唆しています。さらに、データセットにはシリアル依存性の影響と思われるものが見られ、CBOEとMetaTrader 5データセットの間に関係が発展している可能性があることを示唆しています。

使用した最終的な視覚化手法は、自己相関プロットです。作成したすべての自己相関プロットは強いテールを示しており、これは時系列に長期データが残っていることを示唆している可能性があります。これは、強いトレンドまたは季節的影響によって作成された可能性があります。部分的な自己相関プロットは、観察された自己相関の大部分が少数のラグによって説明されていることを示唆しています。これは、時系列データを移動平均モデルとしてうまくモデル化できることを示しています。

データを視覚化した後、3セットの予測変数を作成しました。

OHLC MetaTrader 5市場データ
FRED CBOE代替データセット
1と2の上位集合

3つの同一のディープニューラルネットワークを使用して、ランダムシャッフルなしで5倍の時系列交差検証をおこない、3セットの予測変数を比較しました。最後の予測変数セットは、XAUEUR銘柄の将来の終値を予測する際に最も低い誤差率を生成しました。これは、2つのデータセット間にモデルに役立つ関係があることを示唆している可能性があります。

最初のテストの信頼性に基づいて、ディープニューラルネットワークの全体的な特徴の重要性を評価しようとしました。モデルが最も依存している特徴を把握するために、Accumulated Local Effects (ALE)法とShapley Additive Explanations (SHAP)法を選択しました。採用したどちらの方法でも、選択した代替データセットは拒否されませんでした。

取引セットでモデルのハイパーパラメータを調整し、2つのモデルを作成する2段階のプロセスを実行しました。最初に、選択したモデルパラメータに対してランダムサーチを500回繰り返しました。2番目のステップでは、Limited Memory Broyden Fletcher Goldfarb Shano (L-BFGS-B)アルゴリズムを使用して、ランダム検索からモデルの連続パラメータの最適値を最適化しました。連続していない残りのモデルパラメータはすべて、2番目のフェーズで修正されました。

カスタマイズされたモデルは両方とも、検証データでデフォルトのニューラルネットワークよりも優れたパフォーマンスを発揮しました。ただし、ランダム検索で取得したモデルは、テストセットで最適なパフォーマンスを発揮しました。これは、パラメータを過剰適合させることなく、モデルをトレーニングデータに最適化できたことを示しています。

そこから、カスタマイズされたMetaTrader 5プログラムに統合するためにONNX形式にエクスポートするための最適なモデルを準備し、最後に、共有CSVファイルを通じて最新のFREDデータを端末に共有するためのPythonスクリプトを作成しました。

データの取得

市場データを取得してCSV形式で書き出すための、MQL5で書かれた便利なスクリプトを用意しました。スクリプトには1つの入力パラメータがあり、取得するデータのバー数を指定します。スクリプトをチャートにドラッグ＆ドロップするだけで、すぐに実行できます。

//+------------------------------------------------------------------+
//|                                                      ProjectName |
//|                                      Copyright 2020, CompanyName |
//|                                       http://www.companyname.net |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com/ja/users/gamuchiraindawa"
#property version   "1.00"
#property script_show_inputs

//+------------------------------------------------------------------+
//| Script Inputs                                                    |
//+------------------------------------------------------------------+
input int size = 100000; //How much data should we fetch?

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
int rsi_handler;
double rsi_buffer[];

//+------------------------------------------------------------------+
//| On start function                                                |
//+------------------------------------------------------------------+
void OnStart()
  {

//--- Load indicator
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE);
   CopyBuffer(rsi_handler,0,0,size,rsi_buffer);
   ArraySetAsSeries(rsi_buffer,true);

//--- File name
   string file_name = "Market Data " + Symbol() + ".csv";

//--- Write to file
   int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,",");

   for(int i= size;i>=0;i--)
     {
      if(i == size)
        {
         FileWrite(file_handle,"Time","Open","High","Low","Close");
        }

      else
        {
         FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i),
                   iOpen(Symbol(),PERIOD_CURRENT,i),
                   iHigh(Symbol(),PERIOD_CURRENT,i),
                   iLow(Symbol(),PERIOD_CURRENT,i),
                   iClose(Symbol(),PERIOD_CURRENT,i)
                  );
        }
     }
//--- Close the file
   FileClose(file_handle);

  }
//+------------------------------------------------------------------+

データの準備

OHLC MetaTrader 5市場データを取得した後、データのクリーニングとフォーマットのプロセスを開始しました。最初のステップは、機械学習用の標準Pythonライブラリをインポートすることでした。

#Import the libraries we need
import pandas as pd
import numpy as np
import matplotlib.pyplot as plt
import seaborn as sns
import statsmodels
from statsmodels.graphics.tsaplots import plot_acf,plot_pacf
from fredapi import Fred
from datetime import datetime
import time

これらは私たちが使用しているライブラリのバージョンです。

#Display library versions
print(f"Pandas version {pd.__version__}")
print(f"Numpy version {np.__version__}")
print(f"Seaborn version {sns.__version__}")
print(f"Statsmodels version {statsmodels.__version__}")

Pandas version 2.1.4
Numpy version 1.26.4
Seaborn version 0.13.1
Statsmodels version 0.14.

これで、作成したCSVファイルを読み込み、時間列をインデックスとして設定できます。これにより、MetaTrader 5とCBOEのデータを時系列で結合できるようになります。

#Read in the data
xau_eur = pd.read_csv("Market Data XAUEUR.csv")
xau_eur = xau_eur.loc[96911:,:]
xau_eur.set_index("Time",inplace=True)
xau_eur.index = pd.to_datetime(xau_eur.index)

それでは、FREDから代替CBOE市場データを取得してみましょう。続行する前に、まず FRED Webサイトで無料アカウントを作成し、プライベートAPIキーを取得する必要があります。これは簡単に完了できるプロセスで、隠れ料金はありません。

#Fetch FRED data
fred = Fred(api_key='ENTER YOUR API KEY HERE')
fred_euro_data = pd.DataFrame(fred.get_series('EVZCLS'),columns=["EVZCLS"])
fred_gold_data = pd.DataFrame(fred.get_series('GVZCLS'),columns=["GVZCLS"])
#Fill in any missing values with the column mean
fred_euro_data = fred_euro_data.fillna(fred_euro_data.mean())
fred_gold_data = fred_gold_data.fillna(fred_gold_data.mean())

Pandasには、データフレームを統合するためのSQLのようなコマンドがあります。両方の時系列に共通する日付のデータのみを統合しました。

#Merge the data
merged_data = pd.merge(xau_eur,fred_euro_data,left_index=True,right_index=True)
merged_data = pd.merge(merged_data,fred_gold_data,left_index=True,right_index=True)
merged_data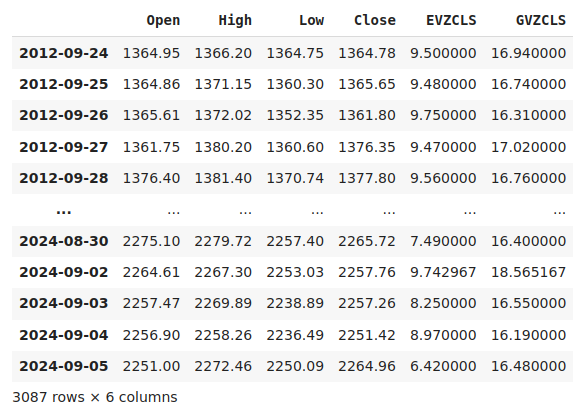

図1：結合されたデータセット

データのラベル付けは、あらゆる教師あり機械学習プロジェクトにおいて重要なステップです。まず、予測期間を定義しました。この場合は、20日後です。次に、ターゲットをXAUEUR銘柄の将来の終値として定義しました。また、価格レベルが上昇したか下落したかをまとめるバイナリターゲットも作成しました。バイナリターゲットは、視覚化の目的でのみ使用されます。

#Let us label the data
look_ahead = 20

#Define the labels
merged_data["Target"] = merged_data["Close"].shift(-look_ahead)
merged_data["Binary Target"] = np.nan

merged_data.loc[merged_data["Target"] > merged_data["Close"],"Binary Target"] = 1
merged_data.loc[merged_data["Target"] <= merged_data["Close"],"Binary Target"] = 0

merged_data.dropna(inplace=True)
merged_data

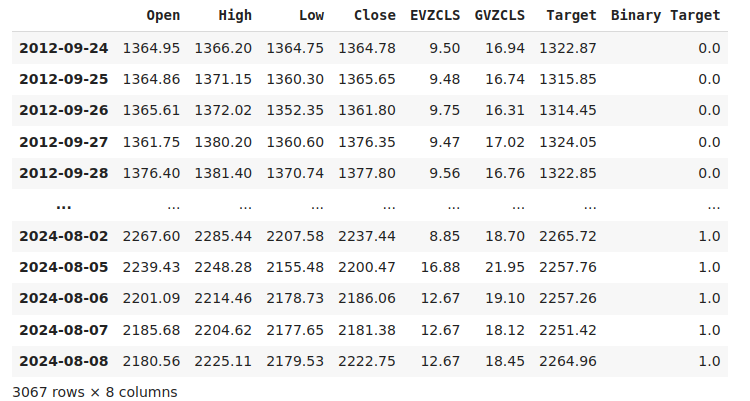
図2：ターゲットを含むデータセット

最後に、経験的に比較する 3 つの予測変数セットを定義しました。

#Let us define the predictors and target
ohlc_predictors = ["Open","High","Low","Close"]
fred_predictors = ["EVZCLS","GVZCLS"]
predictors = ohlc_predictors + fred_predictors
target = "Target"
binary_target = "Binary Target"

探索的データ分析

強い相関水準の有無は、必ずしも分析対象データ間の関係の有無を意味するものではありません。私たちの代替データは、XAUEURデータセットとの相関レベルが断続的であるように見えます。ただし、2 つの代替データセット間に直接的に強い相関レベルがあるように見えます。

#Exploratory Data Analysis
#Analyzing correlation levels
sns.heatmap(merged_data[predictors].corr(),annot=True)

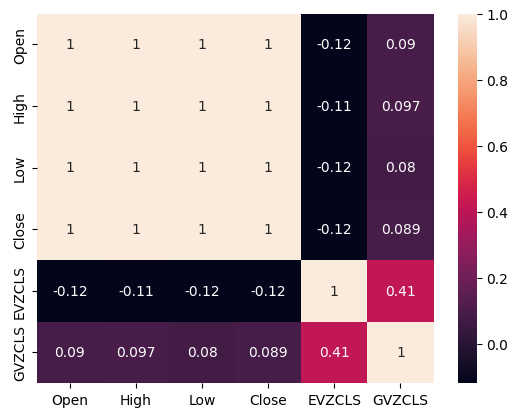
図3：相関ヒートマップ

保有するデータから3つの散布図を作成しました。最初の2つの散布図では、両方のプロットで、x軸にゴールドとユーロのボラティリティインデックス、y軸にXAUEUR終値を使用しました。最初の散布図では、ゴールドのボラティリティレベルが30 ～ 35レベルを超えると、一貫して強気の価格変動が見られることがわかります。

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="GVZCLS",y="Close",hue="Binary Target")

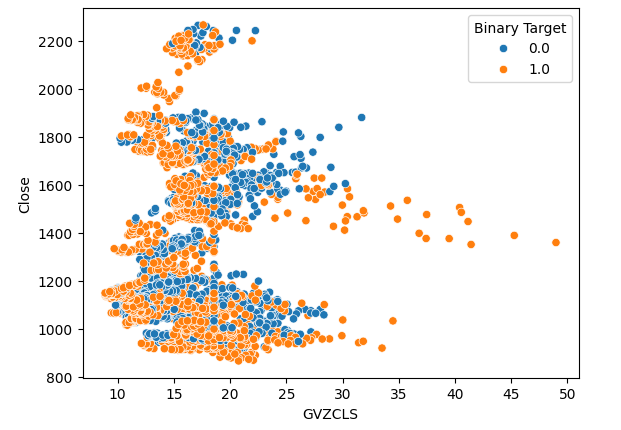
図4：最初の散布図

同じ現象が2番目の散布図でも見られます。ユーロのボラティリティレベルが14 ～ 16レベルを超えると、価格レベルが一貫して上昇するようです。ただし、データセットは限られているため、2つの市場の真の関係を完全には表していない可能性があります。

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="EVZCLS",y="Close",hue="Binary Target")

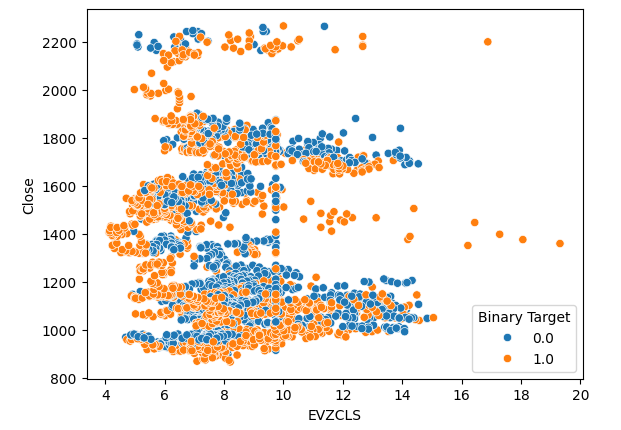
図5：2つ目の散布図

最後に、2つの代替データセットを両軸に用いて散布図を作成しました。データは円錐状の構造を作成し、強気のローソク足のクラスタがはっきりと見え、十分に分離されています。

#Let's create scatter plots
sns.scatterplot(data=merged_data,x="GVZCLS",y="EVZCLS",hue="Binary Target")

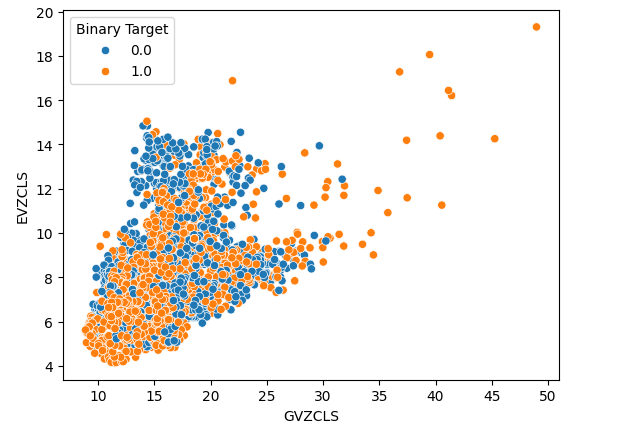
図6：最終的な散布図

データには、2次元では視覚化できない隠れた構造がある可能性があります。そこで、3D散布図を作成し、両方の代替データセットがXAUEURに与える影響を視覚化しました。3Dプロットでは、強気ローソク足のクラスタがまだはっきりと確認できます。これは、代替データが特定のポイントでデータをうまく分離していることを示している可能性があります。

#Define the 3D Plot
fig = plt.figure(figsize=(7,7))
ax = plt.axes(projection="3d")
ax.scatter(merged_data["GVZCLS"],merged_data["EVZCLS"],merged_data["Close"],c=merged_data["Binary Target"],cmap="plasma")
ax.set_xlabel("GVZCLS")
ax.set_ylabel("EVZCLS")
ax.set_zlabel("Close")

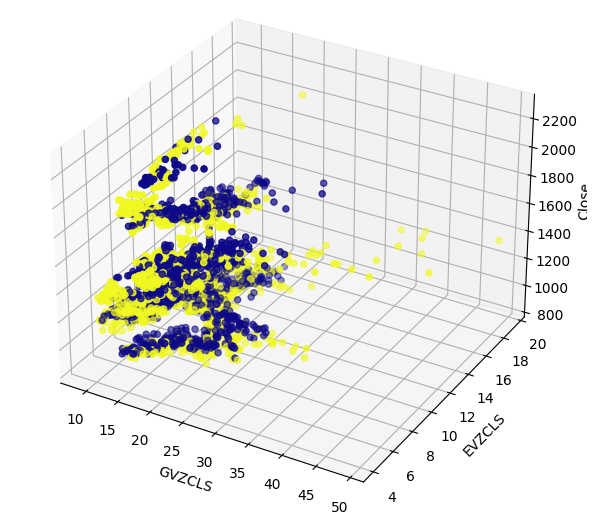
図7：市場データの3D散布図

次元削減技術を使用して、6次元の市場データを2次元で表現することも可能です。このタスクを実行するには、t-SNEアルゴリズムを使用します。このアルゴリズムは、2002年にジェフリー・ヒントンらが発表した論文で初めて提案されました。原著論文はこちらから参照できます。ヒントンは、主に1986年の論文で、バックプロパゲーションアルゴリズムを使用してニューラルネットワークを訓練し、文のベクトル表現の次の単語を予測する方法を示したことにより、機械学習の分野の先駆者と見なされています。彼の貢献により、バックプロパゲーションアルゴリズムが広く採用されるようになりました。

ヒントン

図8：ジェフリー・ヒントン博士

t-SNEアルゴリズムは、高次元空間内のすべてのデータポイント間の近接性を新しい低次元空間に保持するように設計されており、高次元データのコンパクトな表現を作成します。この目標を達成するために、アルゴリズムは2つの確率分布の差を測定する特別なコスト関数を最小化します。この最適化手順は、通常、勾配降下法を使用して実行されます。最初に、アルゴリズムは元の高次元データに基づいて、下位ランク行列を生成します。次に、データポイントを繰り返し移動させながらコストを最小化していきます。コスト関数は、下位ランク行列内でのデータの分布と、元の高次元データの分布との差を示します。t-SNEアルゴリズムは、高次元空間に隠れているデータクラスタを視覚化するのに非常に有用です。

必要なライブラリをインポートします。

#Let's create a TSNE Plot
from sklearn.manifold import TS

次にt-SNEオブジェクトをインスタンス化し、データの2次元表現を作成するよう指示します。

#Create a TSNE object which will reduce the data to 2 dimensions
tsne = TSNE(n_components=2,perplexity=30)

私たちが持っているデータにt-SNEオブジェクトを適合させます。

#Apply TSNE to the data
tsne_data = tsne.fit_transform(merged_data[predictors])

データの新しい表現をプロットします。

#Create a scatter plot
plt.scatter(tsne_data[:,0],tsne_data[:,1])

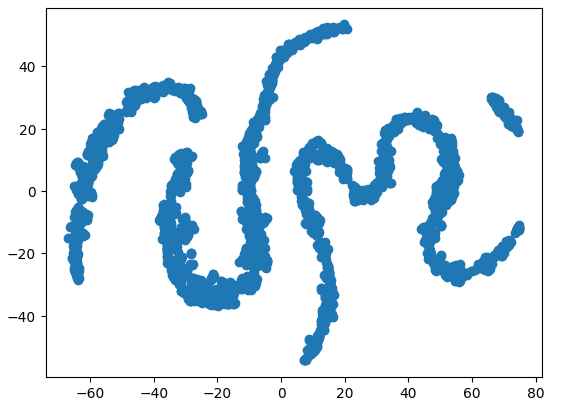
図9：市場データのt-SNEプロット

反復最適化手順の確率的性質により、この説明で得られたプロットを再現することは難しい場合があります。さらに、手順を2回実行した場合、異なる散布図が得られることは通常の結果であり、心配する必要はありません。特に注目すべき点は、アルゴリズムが保持しようとしているクラスタの数です。データセットには4つの異なるクラスタが存在しているようです。さらに、プロットに現れる曲線の性質は、クラスタ内で時間を通じて共有される依存関係を示唆している可能性があります。

自己相関(ACF)プロットは、時系列分析で広く使用され、データが定常であるか、季節変動が含まれているかなどを調べる際に有効です。 ACFプロットは、時系列データの現在の値とその前の値との相関関係を示します。XAUEURの終値と2つのCBOE代替データセットを使用して3つのACFプロットを実行した結果、いずれのプロットもデータに永続的なコンポーネントが存在することを示唆しています。これは、先に視覚化されたヒートマップでも確認できました。もしACFプロットにおいて、ゆっくりと0に減少する長いテールが現れる場合、データには強いトレンドや季節的なコンポーネントが存在する可能性が高いと考えられます。

#Let's look at an autocorrelation plot of the data
close_acf = plot_acf(merged_data["Close"])

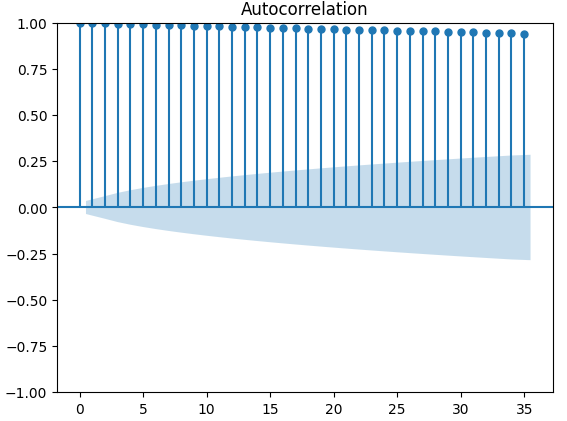
図10：XAUEUR終値のACFプロット

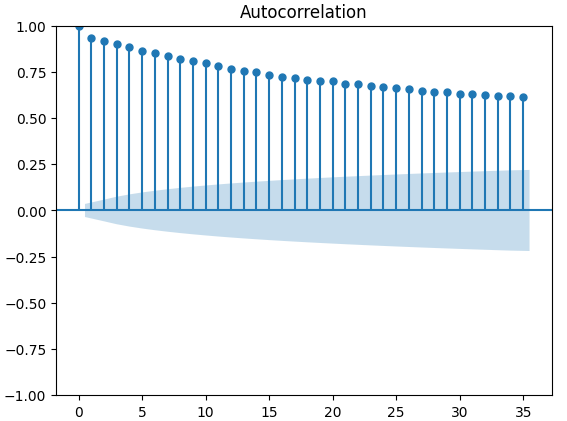
図11：CBOEユーロボラティリティインデックスのACFプロット

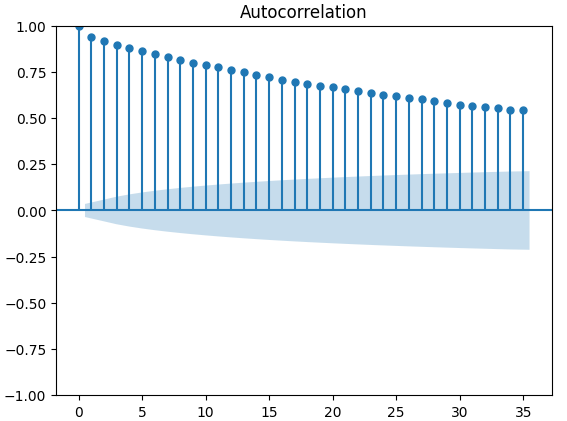
図12：CBOEゴールドボラティリティインデックスのACFプロット

偏自己相関(PACF)プロットは、時系列とそのラグの間で観察される相関の大部分を説明するために、どのくらい過去に遡って調べればよいかを示します。言い換えると、ラグ3で観察される相関のうち、ラグ2から持ち越されなかったものはどれくらいあるかということです。3つのPACFプロットはすべて、最大4つのラグが時系列データの自己相関の大部分を説明することを示唆しています。

#Let's look at an partial autocorrelation plot of the close data
close_pacf = plot_pacf(merged_data["Close"])

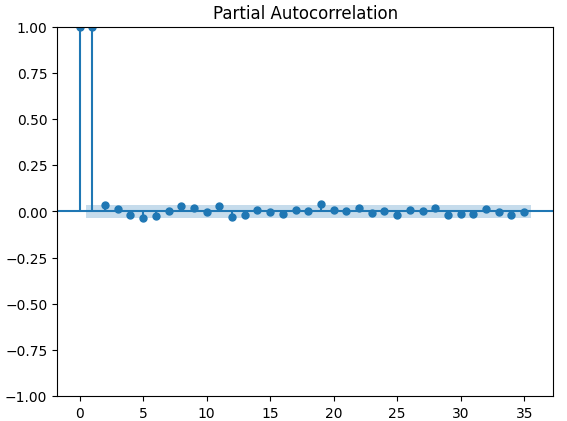
図13：XAUEURクローズのPACFプロット

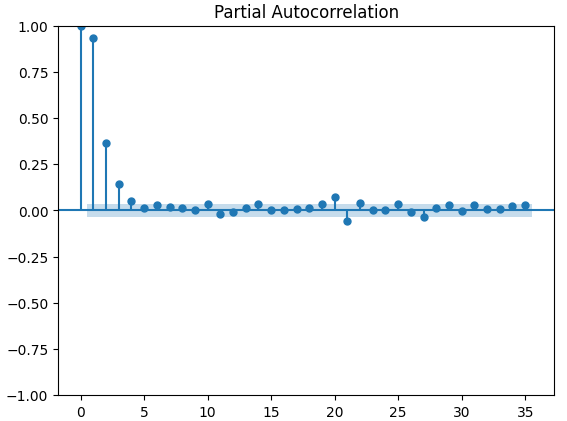
図14：CBOEユーロボラティリティインデックスのPACFプロット

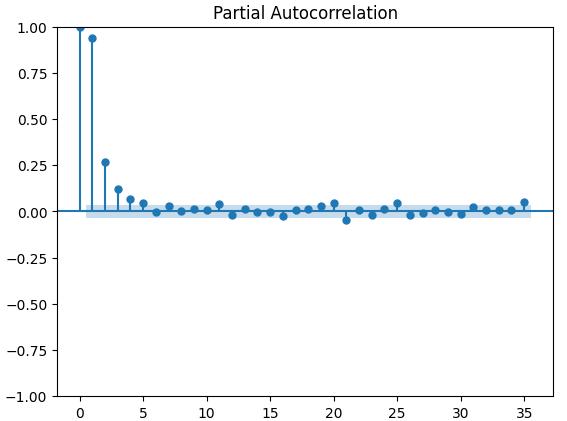
図15：CBOEゴールドボラティリティインデックスのPACFプロット

データモデル化の準備

ディープニューラルネットワークでデータのモデリングを始める前に、まずいくつかの準備をしなければなりません。

#Preparing to model the data
from sklearn.preprocessing import RobustScaler
from sklearn.model_selection import TimeSeriesSplit,train_test_split
from sklearn.metrics import mean_squared_error
from sklearn.neural_network import MLPRegressor

最初のステップは、モデルが効果的に学習できるように、入力データを標準化し、スケーリングすることです。

#Reset the index of our data
merged_data.reset_index(inplace=True)

X = merged_data.loc[:,predictors]
y = merged_data.loc[:,target]

#Scale our data
scaler = RobustScaler()
X = pd.DataFrame(scaler.fit_transform(merged_data[predictors]),columns=predictors)

ここにある3つの予測変数のセットについて、訓練とテストの分割を作成する必要があります。このステップでは、データをランダムにシャッフルしないように注意してください。データをランダムにシャッフルすると、分析の整合性が損なわれてしまう可能性があります。

#Perform train test splits
ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,shuffle=False,train_size=0.5)
fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,shuffle=False,train_size=0.5)
train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,shuffle=False,train_size=0.5)

最後に、時系列オブジェクトを作成し、検証誤差レベルを格納するデータフレームを作成します。

#Let's now cross-validate each of the predictors
#Create the time-series split object
tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead)

validation_error = pd.DataFrame(columns=["OHLC Predictors","FRED Predictors","All Predictors"],index=np.arange(0,5))

データのモデリング

これでデータのモデリングとモデルの相互検証を始める準備が整いました。

#Performing cross validation
model = MLPRegressor(hidden_layer_sizes=(20,5))
for i,(train,test) in enumerate(tscv.split(train_X)):
  model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
  validation_error.iloc[i,2] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))

検証誤差レベル。

#Our validation error
validation_error

MetaTrader 5 OHLCデータ	FRED CBOE代替データ	すべてのデータ
875423.637167	881892.498319	857846.11554
794999.120981	831138.370726	946193.178747
1058884.292095	474744.732539	631259.842972
419566.842693	882615.372658	483408.373559
96693.318078	618647.934237	237935.04009

どのモデルが最もパフォーマンスが良いかはすぐには分からないかもしれませんが、列の平均を分析すると、最後のモデルのパフォーマンスが並外れていることがはっきりと分かります。下のグラフでは、最初の列の平均値を残りの列から減算しています。そうすることで、最初の列の値は 0 になり、不満足なモデルはすべて列の値が 0 より大きくなります。結果として、最後のモデルのパフォーマンスが非常に良いことが明確に示されます。

#Our mean error levels
val_err = validation_error.mean()
val_err = val_err.iloc[:] - val_err.iloc[0]
val_err.plot(kind="bar")

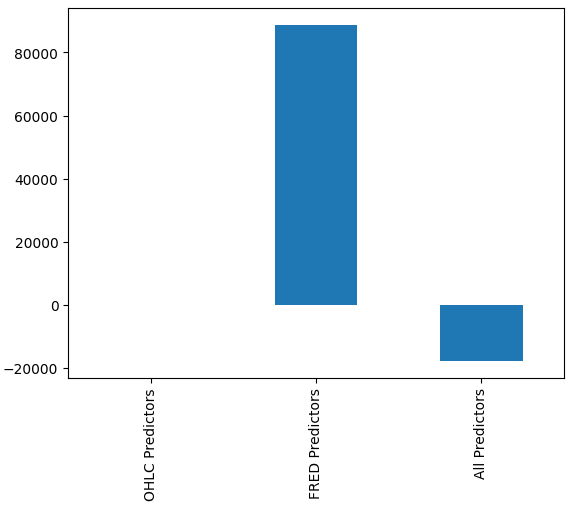
図16：3つの異なるデータセットを使ったモデルのパフォーマンス

モデルのパフォーマンスを箱髭図にすると、最後の予測変数のセットが最適な選択であるように思われ、平均誤差率が最も低く、分散がOHCLデータのみを使用した場合ほど大きくないことがさらに示されます。

#Let's perform boxplots of our validation error
sns.boxplot(validation_error)

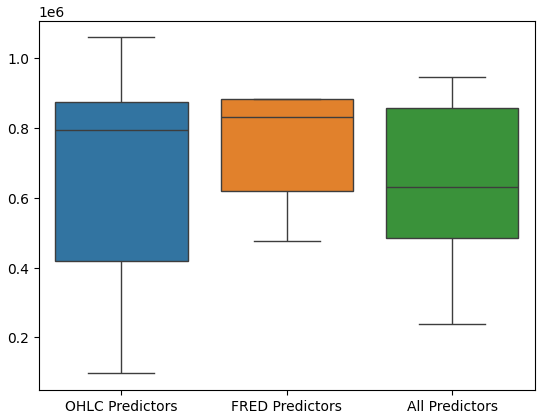
図17：箱ひげ図として可視化されたモデルのパフォーマンス

特徴量の重要性

誤差メトリクスが低かったからと言って、どんなモデルでも盲目的に信頼して本番環境に導入すべきではありません。モデルが学習した関係を検証してみましょう。モデルにとっての大域的な特徴量の重要性を理解したいと思います。最初に、 Accumulated Local Effect (ALE)プロットを作成します。ALEは、高い相関性を持つデータで訓練された機械学習モデルに対して、堅牢な説明を提供するように設計されています。ALEは、各入力がモデルの出力に与える影響を分離しようとします。

#Feature importance
from alibi.explainers import ALE , plot_ale

次に、ALEオブジェクトをインスタンス化し、ディープニューラルネットワークのグローバルな特徴の重要性に関する説明を取得します。これにより、各入力がモデルの予測に与える影響を理解することができます。

#Explaining our deep neural network
model = MLPRegressor(hidden_layer_sizes=(20,5))
model.fit(train_X,train_y)
dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["XAUEUR Close"])

次に、モデルの各入力についてALE値を計算し、プロットしてみましょう。

#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None)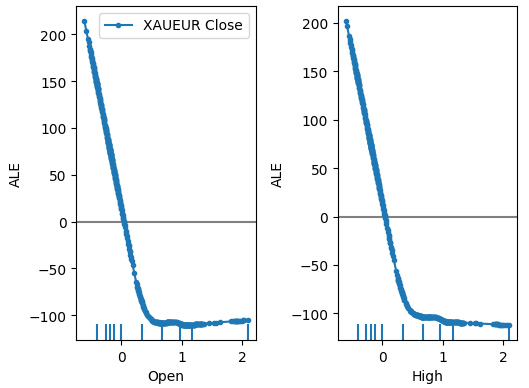

図18：XAUEUR始値および高値予測変数のいくつかのALEプロット

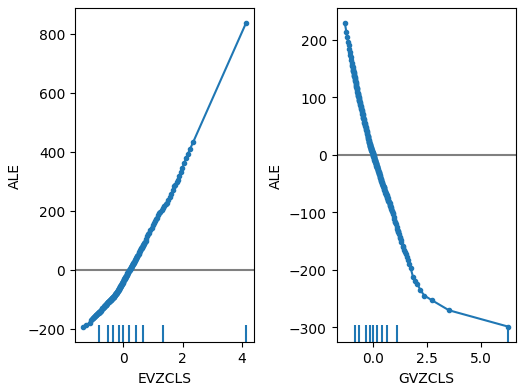
図19：FRED CBOEボラティリティインデックスのALEプロット

ALEプロットの解釈は非常に直感的であり、各予測変数の値が変化することでモデルの予測がどのように変動するかを示しています。ご覧の通り、始値と高値が上昇すると、モデルの予測は最初は下がります。しかし、価格レベルがさらに上昇すると、予測の感度は低下します。ここでは示していませんが、安値と終値のALEプロットは、示した2つのプロットと同様の傾向を示しています。

代替データのALEプロットに注目すると、ユーロボラティリティインデックスによって、他の変数では説明できなかったグラフの一部を補完するALEプロットが作成されたことがわかります。言い換えれば、予測変数は他の予測変数では説明できなかったターゲットの分散を説明しているように見えます。さらに、ALEプロットの上向きの傾斜は、予測変数の値が増加すると、モデルの予測も増加することを示唆しています。

次に、モデルのパフォーマンスに関するSHAPの説明を見ていきます。SHAP値は、モデルの平均予測と比較した場合、各入力が特定の予測にどのように貢献しているかを定量化するのに役立ちます。SHAP値は、ゲーム理論という数学的なアプローチに基づいており、アルゴリズムは予測子の可能なセットをそれぞれ検討し、すべての可能なセットにわたる入力の平均的な効果を計算します。

まず、SHAPライブラリをインポートします。

#SHAP Values
import shap

SHAP値を計算します。

#Calculating SHAP values
explainer = shap.Explainer(model.predict,train_X)
shap_values = explainer(test_X)#Calculating SHAP values

SHAP値をプロットします。

#Plot the beeswarm plot
shap.plots.beeswarm(shap_values)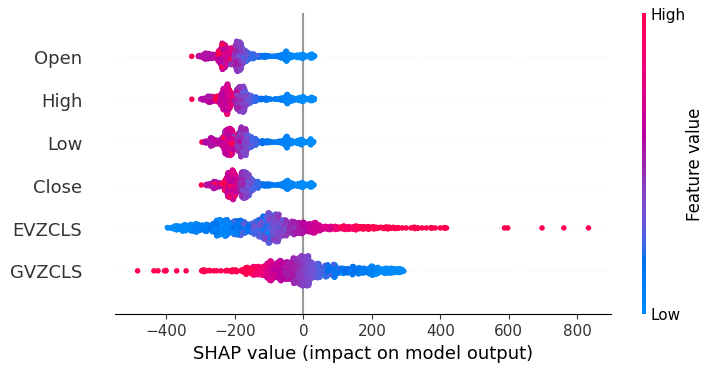

図20：SHAPの説明

SHAPの説明によると、XAUEUR市場自体から取得した市場データは、私たちが持っている最も重要なデータです。さらに、SHAPプロットは、現在の市場価格が上昇するにつれて、ターゲットが下落する傾向があることも示唆しています。

パラメータチューニング

まず、必要なライブラリをインポートすることから始めます。

#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV

モデルを初期化します。

#Reinitialize the model
model = MLPRegressor(hidden_layer_sizes=(20,5))

チューナーオブジェクトを定義します。

#Define the tuner
tuner = RandomizedSearchCV(
        model,
        {
        "activation" : ["relu","logistic","tanh","identity"],
        "solver":["adam","sgd","lbfgs"],
        "alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
        "tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
        "learning_rate":['constant','adaptive','invscaling'],
        "shuffle": [True,False]
        },
        n_iter=500,
        cv=5,
        n_jobs=-1,
        scoring="neg_mean_squared_error"
)

チューナーを適合させます。

#Fit the tuner
tuner_results = tuner.fit(train_X,train_y)

以下が、見つかった最高のパラメータです。

#The best parameters we found
tuner_results.best_params_

{'tol':1e-07,
'solver': 'lbfgs',
'shuffle':True,
'learning_rate': 'adaptive',
'alpha':0.1,
'activation': 'identity'}

Scipyのminimizeモジュールには最適化処理が含まれています。これらの手順は、最適化プロセスの出発点を必要とします。ランダムサーチによって見つかった最適なパラメータ値を、2回目の最適化フェーズの出発点として使用します。

#Deeper optimization
from scipy.optimize import minimize

次に、検証のエラーレベルを格納するデータフレームオブジェクトを作成します。

#Create a dataframe to store our accuracy
current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])

あらゆる最適化アルゴリズムには、取り組むべき目的関数が必要です。ここでの場合、目的関数は訓練セットにおけるモデルの平均交差検証誤差です。最適化手順では、平均誤差を最小化するモデルパラメータを探します。

#Define the objective function
def objective(x):
    #The parameter x represents a new value for our neural network's settings
    #In order to find optimal settings, we will perform 10 fold cross validation using the new setting
    #And return the average RMSE from all 10 tests
    #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization
    model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1])
    #Now we will cross validate the model
    for i,(train,test) in enumerate(tscv.split(train_X)):
        #Train the model
        model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]])
        #Measure the RMSE
        current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
    #Return the Mean CV RMSE
    return(current_error_rate.iloc[:,0].mean())

最適化手順の開始点を定義し、許容される入力値の境界も定義しておきましょう。

#Define the starting point
pt = [0.1,0.00000001]
bnds = ((0.0000000000000000001,10000000000),(0.0000000000000000001,10000000000))

モデルを最適化します。

#Searchin deeper for parameters
result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)

過剰適合のテスト

過剰適合は、あらゆる機械学習プロジェクトで問題となります。これは、モデルがデータの意味のある一般化を作成できず、むしろデータ内のノイズやその他の意味のない関連性を学習し始めるときに発生します。過剰適合をテストするには、2 つのカスタマイズされたモデルの精度をデフォルトモデルと比較します。

#Testing for overfitting
default_model          = MLPRegressor(hidden_layer_sizes=(20,5))
customized_model       = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=0.1,tol=0.0000001)
customized_lbfgs_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=result.x[0],tol=result.x[1])

それでは、各モデルを交差検証する準備をしましょう。

#Preparing to cross validate the models
models = [
    default_model,
    customized_model,
    customized_lbfgs_model
]

#We will store our validation error here
validation_error = pd.DataFrame(columns=["Default Model","Customized Model","L-BFGS Model"],index=np.arange(0,5))

#We will now reset the indexes
test_y = test_y.reset_index()
test_X = test_X.reset_index()

各モデルを訓練セットに適合させる必要があります。

#Fit each of the models
for m in models:
  m.fit(train_X,train_y)

では、今まで保持してきたテストセット、つまり未経験のデータでモデルの性能を交差検証してみましょう。

#Cross validating each model
for j in np.arange(0,len(models)):
  model = models[j]
  for i,(train,test) in enumerate(tscv.split(test_X)):
    model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1],"Target"])
    validation_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"Target"],model.predict(test_X.loc[test[0]:test[-1],:]))

検証誤差レベル。

#Our validation error
validation_error

デフォルトモデル	ランダムサーチモデル	L-BFGS-Bモデル
22360.060721	5917.062055	3734.212826
17385.289026	36726.684574	35886.972729
13782.649037	5128.022626	20886.845316
3082484.290698	6950.786438	5789.948045
4076009.132941	27729.589769	22931.572161

最も性能が良いのはランダムサーチモデルです。

#Plotting the difference in our performance levels
mean = validation_error.mean()
mean = mean.iloc[:] - mean.iloc[0]
mean.plot(kind="bar")

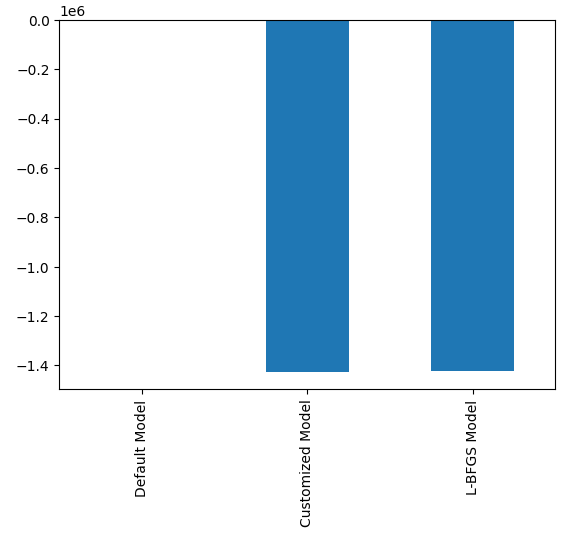
図21：検証エラーレベル

モデルのパフォーマンスを可視化することで、デフォルトモデルがいかにデータをうまく扱っていないかが明らかになります。

#Visualizing the results
validation_error.plot()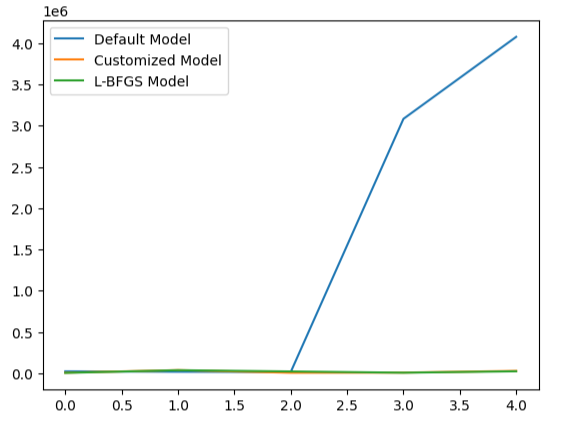

図22：過剰適合のテスト

この点は、箱ひげ図によってさらに補強されています。デフォルトモデルをかなりの差で上回っていることがわかります。

#Visualizing our results
sns.boxplot(validation_error)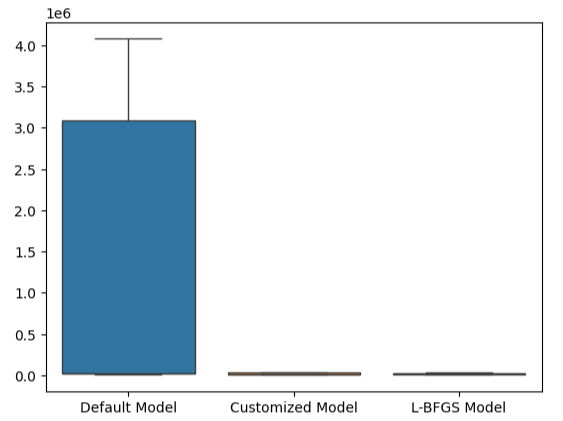

図23：デフォルトモデルを大きく上回っている

ONNX形式へのエクスポートの準備

モデルをONNX形式にエクスポートする前に、まずデータを標準化し、MetaTrader 5端末で再現できる方法でスケーリングする必要があります。これを実現するには、各列から列の平均を減算してから、最後に各列をその標準偏差で割ります。スケーリング係数をCSV形式で書き出し、MetaTrader 5端末でそれを取得してモデル入力をスケーリングできるようにします。

#Let us now prepare to export our model to onnx format
scale_factors = pd.DataFrame(columns=predictors,index=["mean","standard deviation"])

for i in np.arange(0,len(predictors)):
  scale_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean()
  scale_factors.iloc[1,i] =  merged_data.loc[:,predictors[i]].std()
  merged_data.loc[:,predictors[i]] = (merged_data.loc[:,predictors[i]] - merged_data.loc[:,predictors[i]].mean())/merged_data.loc[:,predictors[i]].std()

scale_factors

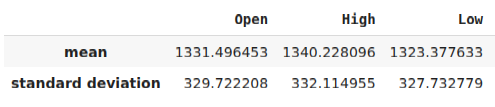
図24：スケーリング係数の一部

次にCSV形式でデータを書き出します。

#Save the scale factors to CSV
scale_factors.to_csv("scale_factors.csv")

ONNX形式へのエクスポート

Open Neural Network Exchange (ONNX)は、異なるプログラミング言語間で機械学習モデルを構築・共有するためのプロトコルです。ONNXプロトコルは、MQL5 ONNX APIを使用して、エキスパートアドバイザー(EA)にディープニューラルネットワークをシームレスに組み込むことを可能にします。

まず、必要なライブラリをロードしてみましょう。

#Exporting to ONNX format
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType

保有するすべてのデータでモデルを訓練します。

#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target])

ONNXモデルをエクスポートする際、入力形状が失われる場合があります。そこで、入力形状を明示的に指定してみます。

# Define the input type
initial_types = [("float_input",FloatTensorType([1,6]))]

モデルのONNX表現を作成します。

# Create the ONNX representation
onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)

ONNX表現を拡張子「.onnx」のファイルに保存します。

# Save the ONNX model
onnx_name = "XAUEUR FRED D1.onnx"
onnx.save_model(onnx_model,onnx_name)

EAの構築

これでEAの構築を開始する準備が整いました。まず最初に、先ほど作成したONNXファイルを必要とすることから始めます。

//+------------------------------------------------------------------+
//|                                               EURXAU Fred AI.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                          https://www.mql5.com/ja/gamuchiraindawa |
//+------------------------------------------------------------------+
#property copyright "Volatility Doctor"
#property link      "https://www.mql5.com/ja/gamuchiraindawa"
#property version   "1.00"

//+------------------------------------------------------------------+
//| Require the ONNX file                                            |
//+------------------------------------------------------------------+
#resource "\\Files\\XAUEUR FRED D1.onnx" as const uchar onnx_buffer[];

ポジションの管理に役立つ取引ライブラリをインポートします。

//+------------------------------------------------------------------+
//| Libraries                                                        |
//+------------------------------------------------------------------+
#include  <Trade/Trade.mqh>
CTrade Trade;

これらのグローバル変数は、アプリケーションのさまざまな部分で共有されます。

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
long    onnx_model;
vector  mean_values  = vector::Zeros(6);
vector  std_values   = vector::Zeros(6);
vectorf model_inputs = vectorf::Zeros(6);
vectorf model_output = vectorf::Zeros(1);
double  bid,ask;
int     system_state,model_sate;

次に、アプリケーションの最初に作成したONNXバッファから、ONNXモデルを作成する関数が必要です。この関数は最初にONNXモデルを作成して検証し、最後にモデルの入力と出力の形状を設定して検証します。いずれかの時点で失敗すると、関数はfalseを返し、初期化手順を停止します。

//+------------------------------------------------------------------+
//| Load the ONNX file                                               |
//+------------------------------------------------------------------+
bool load_onnx_file(void)
  {
//--- Create the ONNX model from the buffer we loaded earlier
   onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT);

//--- Validate the model we just created
   if(onnx_model == INVALID_HANDLE)
     {
      //--- Give the user feedback on the error
      Comment("Failed to create the ONNX model: ",GetLastError());
      //--- Break initialization
      return(false);
     }

//--- Define the I/O shape
   ulong input_shape [] = {1,6};

//--- Validate the input shape
   if(!OnnxSetInputShape(onnx_model,0,input_shape))
     {
      //--- Give the user feedback
      Comment("Failed to define the ONNX input shape: ",GetLastError());
      //--- Break initialization
      return(false);
     }

   ulong output_shape [] = {1,1};

//--- Validate the output shape
   if(!OnnxSetOutputShape(onnx_model,0,output_shape))
     {
      //--- Give the user feedback
      Comment("Failed to define the ONNX output shape: ",GetLastError());
      //--- Break initialization
      return(false);
     }

//--- We've finished
   return(true);
  }
//+------------------------------------------------------------------+

ここから、モデル入力を正規化するために必要なスケーリング係数を定義します。

//+------------------------------------------------------------------+
//| Load our scaling factors                                         |
//+------------------------------------------------------------------+
bool load_scaling_factors(void)
  {
//--- Load the scaling values
   mean_values[0] = 1331.4964525595044;
   mean_values[1] = 1340.2280958591457;
   mean_values[2] = 1323.3776328659928;
   mean_values[3] = 1331.706768829475;
   mean_values[4] = 8.258127607767035;
   mean_values[5] = 16.35582438284101;
   std_values[0] = 329.7222075527991;
   std_values[1] = 332.11495530642173;
   std_values[2] = 327.732778866831;
   std_values[3] = 330.1146052811378;
   std_values[4] = 2.199782202942867;
   std_values[5] = 4.241112965400358;

//--- Validate the values loaded correctly
   if((mean_values.Sum() > 0) && (std_values.Sum() > 0))
     {
      return(true);
     }

//--- We failed to load the scaling values
   return(false);
  }

アプリケーションが使われなくなったら、いつでも、使わなくなったリソースを解放する。

//+------------------------------------------------------------------+
//| Free up the resources we no longer need                          |
//+------------------------------------------------------------------+
void release_resources(void)
  {
//--- Free up all the resources we have used so far
   OnnxRelease(onnx_model);
   ExpertRemove();
   Print("Thank you for choosing Volatility Doctor");
  }

この関数は、市場価格情報の更新を担当します。

//+------------------------------------------------------------------+
//| Fetch market data                                                |
//+------------------------------------------------------------------+
void fetch_market_data(void)
  {
//--- Update the market data
   bid = SymbolInfoDouble(Symbol(),SYMBOL_BID);
   ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK);
  }

次の関数は、モデルから予測を取得する役割を担っています。まず、MQL5行列関数CopyRates()を使用して、XAUEUR銘柄の現在のOHLCデータを取得します。データを取得した後、正規化し、先ほど定義した入力ベクトルに格納します。ここから別の関数を呼び出して、ファイルにある最新のFREDデータを読み込みます。

//+------------------------------------------------------------------+
//| This function will fetch a prediction from our model             |
//+------------------------------------------------------------------+
void model_predict(void)
  {
//--- Get the input data ready
   for(int i =0; i < 6; i++)
     {
      //--- The first 4 inputs will be fetched from the market
      matrix xau_eur_ohlc = matrix::Zeros(1,4);
      xau_eur_ohlc.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OHLC,0,1);
      //--- Fill in the data
      if(i<4)
        {
         model_inputs[i] = (float)((xau_eur_ohlc[i,0] - mean_values[i])/ std_values[i]);
        }
      //--- We have to read in the fred alternative data
      else
        {
         read_fred_data();
        }
     }
  }

以下に定義する関数は、最新のFREDデータのCSVファイルを読み込み、入力ベクトルに格納する前にデータを正規化し、モデルから予測を取得します。モデルの予測を整数で表します。こうすることで、反転の可能性を素早く察知し、できれば相場の右側でポジションを閉じることができます。

//+-------------------------------------------------------------------+
//| Read in the FRED data                                             |
//+-------------------------------------------------------------------+
void read_fred_data(void)
  {
//--- Read in the file
   string file_name = "fred_xau_eur.csv";

//--- Try open the file
   int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols).

//--- Check the result
   if(result != INVALID_HANDLE)
     {
      Print("Opened the file");
      //--- Store the values of the file

      int counter = 0;
      string value = "";
      while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end
        {
         if(counter > 10)  //if you aim to read 10 values set a break point after 10 elements have been read
            break;          //stop the reading progress

         value = FileReadString(result);
         Print("Counter: ");
         Print(counter);
         Print("Trying to read string: ",value);

         if(counter == 3)
           {
            Print("Fred Euro data: ",value);
            model_inputs[4] = (float)((((float) value) - mean_values[4])/std_values[4]);
           }

         if(counter == 5)
           {
            Print("Fred Gold data: ",value);
            model_inputs[5] = (float)((((float) value) - mean_values[5])/std_values[5]);
           }

         if(FileIsLineEnding(result))
           {
            Print("row++");
           }

         counter++;
        }

      //--- Show the input and Fred data
      Print("Input Data: ");
      Print(model_inputs);

      //---Close the file
      FileClose(result);

      //--- Store the model prediction
      OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output);
      Comment("Model Forecast",model_output[0]);
      if(model_output[0] > iClose(Symbol(),PERIOD_D1,0))
        {
         model_sate = 1;
        }

      else
        {
         model_sate = -1;
        }
     }

//--- We failed to find the file
   else
     {
      //--- Give the user feedback
      Print("We failed to find the file with the FRED data");
     }
  }

次に、アプリケーションの起動方法を定義します。アプリケーションはまずONNXモデルを作成し、必要なスケーリング係数をロードします。これらのステップのいずれかが失敗した場合は、初期化手順を完全に中止します。

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Load the ONNX model
   if(!load_onnx_file())
     {
      //--- We failed to load our ONNX model
      return(INIT_FAILED);
     }

//--- Load the scaling factors
   if(!load_scaling_factors())
     {
      //--- We failed to read in the scaling factors
      return(INIT_FAILED);
     }

//--- We mamnaged to load our model
   return(INIT_SUCCEEDED);
  }

アプリケーションがチャートから削除されたら、不要になったリソースを解放します。

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Free up the resources we no longer need
   release_resources();
  }

最後に、更新された市場価格を受け取るたびに、まず更新された市場価格をメモリに保存します。その後、未決済のポジションがない場合は、より高い時間枠のプライスアクションによって裏付けられる場合にのみ、モデルの予測に従います。あるいは、すでにポジションがある場合、モデルが価格水準の反転を予測していれば、ポジションをクローズします。

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- Update market data
   fetch_market_data();

//--- Fetch a prediction from our model
   model_predict();

//--- If we have no positions follow the model's lead
   if(PositionsTotal() == 0)
     {
      //--- Buy position
      if(model_sate == 1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Buy(0.3,Symbol(),ask,0,0,"XAUEUR Fred AI");
            system_state = 1;
           }
        };

      //--- Sell position
      if(model_sate == -1)
        {
         if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12))
           {
            Trade.Sell(0.3,Symbol(),bid,0,0,"XAUEUR Fred AI");
            system_state = -1;
           }
        };
     }

//--- If we allready have positions open, let's manage them
   if(model_sate != system_state)
     {
      Trade.PositionClose(Symbol());
     }

  }
//+------------------------------------------------------------------+

システムの動作

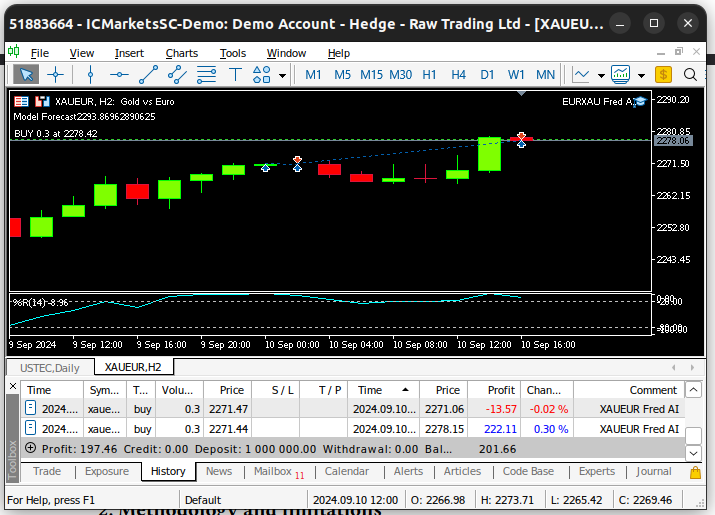
図25：EAの動作

結論

この記事では、機械学習モデルの精度を向上させるために、FRED CBOEボラティリティインデックスを組み込むことが有益である可能性があることを示しました。提供された情報が必ずしも成功を保証するものではありませんが、代替データを取引戦略に取り入れる準備が整っている場合は、検討する価値が十分にあると言えます。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/15841

添付されたファイル |

ZIPをダウンロード

FetchData21s.mq5 (2.05 KB)

EURXAU_Fred_AI.mq5 (9.9 KB)

fred_xau_eur.csv (0.04 KB)

xau_eur_scale_factors.csv (0.27 KB)

XAUEUR_FRED_D1.onnx (1.72 KB)

Gain_an_Edge_XAUEUR.ipynb (1456.96 KB)

警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動

知っておくべきMQL5ウィザードのテクニック（第39回）：RSI (Relative Strength Index)

RSIは、モメンタムオシレーターとして人気があり、最近の価格変動のペースと大きさを測定し、証券価格の過大評価と過小評価の状況を評価します。スピードと大きさに関するこれらの洞察は、反転ポイントを定義する上で鍵となります。このオシレーターを別のカスタムシグナルクラスで動作させ、そのシグナルの特徴を調べてみましょう。まず、ボリンジャーバンドについてのまとめから始めます。

MQL5で古典的な戦略を再構築する（第3回）：FTSE100予想

この連載では、よく知られた取引戦略を再検討し、AIを使って改善できるかどうかを検証します。本日の記事では、FTSE100について調べ、指数を構成する個別銘柄の一部を使って指数の予測を試みます。

MacOSでのMetaTrader 4

macOS上のMetaTrader 4取引プラットフォーム用の特別なインストーラーを提供します。これは、アプリケーションをネイティブにインストールできる本格的なウィザードです。インストーラーは、システムの識別、最新のWineバージョンのダウンロードとインストール、設定の適用、その後のMetaTraderのインストールまで、すべての手順を自動で実行します。インストールが完了すると、すぐにプラットフォームを使用できます。

多通貨エキスパートアドバイザーの開発（第13回）：第2段階の自動化 - グループへの選択

自動最適化の第１段階はすでに実装されています。いくつかの基準に従ってさまざま銘柄と時間枠の最適化を実行し、各パスの結果に関する情報をデータベースに保存します。ここで、最初の段階で見つかったものから最適なパラメータセットのグループを選択します。