
Verschaffen Sie sich einen Vorteil auf jedem Markt (Teil IV): CBOE: Volatilitätsindizes von Euro und Gold
Im Zeitalter von Big Data gibt es Hunderte von Millionen von Datensätzen, die alle das Potenzial haben, bei der Vorhersage von Finanzmärkten ein bisher unerreichtes Maß an Genauigkeit zu bieten. Leider ist es unwahrscheinlich, dass alle vorhandenen Datensätze diesem Potenzial gerecht werden. In dieser Artikelserie möchten wir Ihnen dabei helfen, die riesige Landschaft möglicher Datensätze zu durchqueren. Am Ende der Diskussion werden Sie in der Lage sein, eine fundierte Entscheidung darüber zu treffen, ob die vorgeschlagenen alternativen Daten in Ihre Handelsstrategie einbezogen werden sollten oder ob Sie vielleicht besser ohne sie auskommen.
Überblick über die Handelsstrategie
Wir werden den XAUEUR-Markt analysieren. Das Symbol zeigt den Goldpreis in Euro an. Gold wird auf allen Kontinenten der Erde abgebaut, mit Ausnahme der Antarktis. Ein großer Teil des weltweiten Goldes wird von der London Bullion Market Association (LBMA) gehandelt, die einen weltweit anerkannten Maßstab für den Goldpreis setzt. Die Chicago Board of Options Exchange (CBOE) ist ein amerikanisches Unternehmen, das eine globale Marktinfrastruktur bereitstellt. Die CBOE nutzt ihre Netzwerke, um Volatilitätsindizes zu erstellen, die die wichtigsten Märkte der Welt abbilden. Wir werden 2 Volatilitätsindizes der CBOE analysieren, die den Euro- bzw. den Goldmarkt abbilden.
Im Laufe der Jahre haben Händler verschiedene Strategien entwickelt, um erfolgreich mit volatilen Märkten zu handeln und gleichzeitig das Risiko zu minimieren. Wenn die Märkte volatil sind, können die Händler im Allgemeinen ihre Gewinnziele in relativ kurzen Zeiträumen erreichen. Andererseits ist es auch möglich, schnell erhebliche Kapitalbeträge zu verlieren, wenn große Kurslücken entstehen und Stop-Loss-Aufträge nicht rechtzeitig ausgelöst werden.
Grob gesagt, ziehen es einige Händler vor, weniger Positionen zu eröffnen oder weniger Kapital zu riskieren, als sie es normalerweise bei einer größeren Anzahl von Positionen tun würden, um potenziell von profitablen Kursbewegungen zu profitieren und gleichzeitig ihr Marktengagement klein zu halten. Im Allgemeinen neigen erfahrene Händler auf volatilen Märkten dazu, ihre Gewinne viel schneller mitzunehmen, als sie es auf ruhigeren Märkten tun würden. Andere Händler warten darauf, dass sich die Kurse zunächst in einer Spanne zwischen Unterstützungs- und Widerstandsniveaus bewegen. Wenn die Kurse schließlich aus der Spanne ausbrechen, können Händler ihre Positionen in Erwartung stärkerer Bewegungen aus der identifizierbaren Spanne eröffnen.
Unter normalen Marktbedingungen kann ein Ausbruch aus einer Unterstützungs- und Widerstandszone schnell an Schwung verlieren und ins Trudeln geraten. Wenn die Marktbedingungen jedoch unbeständig sind, können auf Ausbrüche heftige Kursänderungen in dieselbe Richtung folgen, was Händlern, die solche Strategien verfolgen, überdurchschnittliche Renditen beschert. Bedauerlicherweise sind solche Strategien anfällig für falsche Ausbrüche, die sich heftig umkehren können, sodass einige Händler in ungünstigen Positionen mit erheblichen Verlusten bleiben.
Überblick über die Methodik
Wir nutzten die Python-API der Federal Reserve Economic Database (FRED), die von der St. Louis Federal Reserve verwaltet wird, um die wirtschaftlichen Zeitreihen der CBOE Euro- und Goldvolatilität abzurufen. Die Daten werden im Tagesformat geliefert und enthalten fehlende Werte.
Leider erklärt keine der mit den Datensätzen gelieferten Beschreibungen einen der fehlenden Werte. Daher haben wir alle fehlenden Werte in beiden Datensätzen unterstellt.
In unserem MetaTrader 5-Terminal haben wir mit Hilfe eines von uns in MQL5 geschriebenen angepassten Skripts ca. 4000 Zeilen täglicher Marktnotierungen für den Eröffnungs-, Höchst-, Tiefst- und Schlusskurs (OHLC) des Symbols XAUEUR abgerufen.
Als wir die Korrelation zwischen den alternativen Daten der CBOE und den Marktdaten des MetaTrader 5 analysierten, stellten wir Korrelationswerte fest, die nicht signifikant weit von 0 entfernt waren. Der Korrelationsgrad zwischen den beiden alternativen Datensätzen betrug 0,4. Ein positives Korrelationsniveau kann auf das Vorhandensein von Wechselwirkungen oder gemeinsamen Marktteilnehmern hinweisen, die die beiden Märkte beeinflussen.
Bei der Erstellung von Streudiagrammen der Daten unter Verwendung der beiden alternativen Datensätze auf der x-Achse und des Schlusskurses der XAUEUR auf der y-Achse schien es einen Schwellenwert für hohe Volatilitätsniveaus zu geben, der durchweg zu höheren Kursniveaus führte. Bedauerlicherweise ist unser kleiner Datensatz, der nach der Zusammenführung mit den alternativen Datensätzen insgesamt etwa 3000 Zeilen umfasst, ein guter Grund, vorsichtig zu sein und sich nicht dazu verleiten zu lassen, Muster in den Daten zu erkennen, die einfach nicht vorhanden sind.
Die effektive Anzeige hochdimensionaler Daten kann eine Herausforderung sein. Daher haben wir unsere Daten in einem 2-fachen Verfahren gesichtet. Zunächst erstellten wir 3D-Streudiagramme mit den beiden CBOE-Datensätzen auf der x- bzw. y-Achse und dem XAUEUR-Schluss auf der z-Achse. Die Gruppe von Bullenkerzen, die wir in unseren 2D-Streudiagrammen beobachtet hatten, war immer noch deutlich sichtbar.
Schließlich können wir jederzeit Algorithmen nutzen, die darauf ausgelegt sind, hochdimensionale Daten auf einen niedrigdimensionalen Unterraum abzubilden. Ein bekannter Algorithmus zur Dimensionenreduktion ist die Hauptkomponentenanalyse. Wir haben uns für die Scikit-Learn-Implementierung von t-verteilte stochastische Nachbarschaftseinbettung (t-distributed stochastic neighbor embedding, t-SNE) entschieden, um eine 2-dimensionale Darstellung unseres 6-dimensionalen Datensatzes zu erstellen. Die daraus resultierende Darstellung deutet darauf hin, dass es in unserem Datensatz möglicherweise 4 verschiedene Cluster gibt. Darüber hinaus beobachteten wir in unserem Datensatz den Effekt der seriellen Abhängigkeit, was darauf hindeutet, dass sich möglicherweise eine Beziehung zwischen unseren CBOE- und MetaTrader 5-Datensätzen entwickelt.
Die letzte von uns verwendete Visualisierungstechnik waren Autokorrelationsdiagramme. Alle von uns erstellten Autokorrelationsdiagramme wiesen starke Ausläufer auf, was darauf hindeuten könnte, dass in unseren Zeitreihen langfristige Daten vorhanden sind. Dies kann auf starke Trends oder saisonale Effekte zurückzuführen sein. Unsere partiellen Autokorrelationsdiagramme deuten darauf hin, dass der Großteil der beobachteten Autokorrelation auf eine geringe Anzahl von berücksichtigten Balken zurückzuführen ist. Dies deutet darauf hin, dass die Zeitreihendaten erfolgreich als Modell des gleitenden Durchschnitts modelliert werden können.
Nachdem wir unsere Daten visualisiert hatten, erstellten wir 3 Sätze von Prädiktoren:
- OHLC MetaTrader 5 Marktdaten
- FRED CBOE alternative Datensätze
- Eine Übermenge der beiden vorherigen Sätze
Drei identische tiefe neuronale Netze wurden zum Vergleich der drei Prädiktoren eingesetzt, wobei eine 5-fache Zeitreihen-Kreuzvalidierung ohne zufälliges Mischen durchgeführt wurde. Der letzte Satz von Prädiktoren ergab die geringste Fehlerquote bei der Vorhersage des zukünftigen Schlusskurses des XAUEUR-Symbols. Dies könnte darauf hindeuten, dass es Beziehungen zwischen den beiden Datensätzen gibt, die unser Modell unterstützen.
Aufbauend auf der Zuversicht unseres ersten Tests haben wir versucht, die globale Merkmalsbedeutung unseres tiefen neuronalen Netzes zu bewerten. Wir haben die Methoden Accumulated Local Effects (ALE) und Shapley Additive Explanations (SHAP) ausgewählt, um herauszufinden, von welchen Modellen unser Modell am stärksten abhängt. Keine der von uns verwendeten Methoden lehnte die von uns ausgewählten alternativen Datensätze ab.
Wir haben die Hyperparameter unseres Modells auf der Trainingsmenge in einem zweistufigen Prozess abgestimmt, bei dem 2 Modelle erstellt wurden. Zu Beginn führten wir 500 Iterationen einer zufälligen Suche über eine Auswahl unserer Modellparameter durch. Im zweiten Schritt optimierten wir die besten Werte der kontinuierlichen Parameter unseres Modells aus der Zufallssuche mit Hilfe des Algorithmus Limited Memory Broyden Fletcher Goldfarb Shano (L-BFGS-B). Alle übrigen Modellparameter, die nicht kontinuierlich waren, wurden in der zweiten Phase festgelegt.
Beide angepassten Modelle übertrafen das standardmäßige neuronale Netz bei den Validierungsdaten. Das durch zufällige Suche erhaltene Modell schnitt jedoch in der Testmenge am besten ab. Dies deutet darauf hin, dass wir unser Modell erfolgreich auf die Trainingsdaten hin optimiert haben, ohne dass unsere Parameter zu stark angepasst wurden.
Anschließend bereiteten wir unser bestes Modell für den Export in das ONNX-Format vor, um es in ein individuelles MetaTrader 5-Programm zu integrieren. Schließlich schrieben wir ein Python-Skript, um die neuesten FRED-Daten über eine gemeinsame CSV-Datei an unser Terminal weiterzugeben.
Abrufen der Daten
Ich habe ein praktisches, in MQL5 geschriebenes Skript beigefügt, das unsere Marktdaten für uns abruft und sie im CSV-Format ausgibt. Das Skript hat 1 Eingabeparameter, der angibt, wie viele Balken der Daten abgerufen werden sollen. Ziehen Sie das Skript einfach per Drag & Drop auf Ihr Chart, und schon können Sie mitlesen.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script Inputs | //+------------------------------------------------------------------+ input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int rsi_handler; double rsi_buffer[]; //+------------------------------------------------------------------+ //| On start function | //+------------------------------------------------------------------+ void OnStart() { //--- Load indicator rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE); CopyBuffer(rsi_handler,0,0,size,rsi_buffer); ArraySetAsSeries(rsi_buffer,true); //--- File name string file_name = "Market Data " + Symbol() + ".csv"; //--- Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Vorbereitung der Daten
Nachdem wir unsere OHLC MetaTrader 5 die Marktdaten abgerufen hatten, begannen wir mit der Bereinigung und Formatierung der Daten. Unser erster Schritt bestand darin, Standard-Python-Bibliotheken für maschinelles Lernen zu importieren.#Import the libraries we need import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import statsmodels from statsmodels.graphics.tsaplots import plot_acf,plot_pacf from fredapi import Fred from datetime import datetime import time
Dies sind die Versionen der Bibliotheken, die wir verwenden.
#Display library versions print(f"Pandas version {pd.__version__}") print(f"Numpy version {np.__version__}") print(f"Seaborn version {sns.__version__}") print(f"Statsmodels version {statsmodels.__version__}")
Numpy version 1.26.4
Seaborn version 0.13.1
Statsmodels version 0.14.
Jetzt können wir die soeben erstellte CSV-Datei einlesen und die Zeitspalte als unseren Index festlegen. Auf diese Weise können wir die Daten des MetaTrader 5 und der CBOE in chronologischer Reihenfolge zusammenführen.
#Read in the data xau_eur = pd.read_csv("Market Data XAUEUR.csv") xau_eur = xau_eur.loc[96911:,:] xau_eur.set_index("Time",inplace=True) xau_eur.index = pd.to_datetime(xau_eur.index)
Lassen Sie uns nun die alternativen CBOE-Marktdaten von FRED abrufen. Bevor Sie fortfahren können, müssen Sie zunächst ein kostenloses Konto auf der FRED-Website erstellen, um einen privaten API-Schlüssel zu erhalten. Es ist ein einfaches Verfahren ohne versteckte Kosten.
#Fetch FRED data
fred = Fred(api_key='ENTER YOUR API KEY HERE')
fred_euro_data = pd.DataFrame(fred.get_series('EVZCLS'),columns=["EVZCLS"])
fred_gold_data = pd.DataFrame(fred.get_series('GVZCLS'),columns=["GVZCLS"])
#Fill in any missing values with the column mean
fred_euro_data = fred_euro_data.fillna(fred_euro_data.mean())
fred_gold_data = fred_gold_data.fillna(fred_gold_data.mean()) Pandas verfügt über SQL-ähnliche Befehle zum Zusammenführen von Datenrahmen. Wir haben nur die Daten zu den Daten zusammengeführt, die in beiden Zeitreihen enthalten sind.
#Merge the data
merged_data = pd.merge(xau_eur,fred_euro_data,left_index=True,right_index=True)
merged_data = pd.merge(merged_data,fred_gold_data,left_index=True,right_index=True)
merged_data 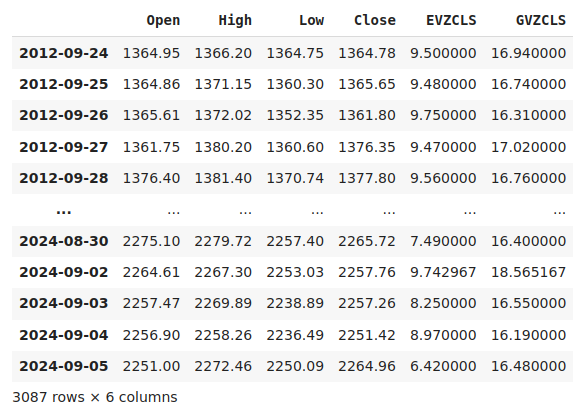
Abb. 1: Unser zusammengefasster Datensatz
Die Kennzeichnung der Daten ist ein wichtiger Schritt in jedem überwachten maschinellen Lernprojekt. Zunächst haben wir unseren Prognosehorizont festgelegt, der in diesem Fall 20 Tage in die Zukunft reicht. Dann haben wir das Ziel als den zukünftigen Schlusskurs des Symbols XAUEUR definiert. Wir haben auch binäre Ziele erstellt, um zusammenzufassen, ob das Preisniveau gestiegen oder gesunken ist. Die binären Ziele werden ausschließlich zu Visualisierungszwecken verwendet.
#Let us label the data look_ahead = 20 #Define the labels merged_data["Target"] = merged_data["Close"].shift(-look_ahead) merged_data["Binary Target"] = np.nan merged_data.loc[merged_data["Target"] > merged_data["Close"],"Binary Target"] = 1 merged_data.loc[merged_data["Target"] <= merged_data["Close"],"Binary Target"] = 0 merged_data.dropna(inplace=True) merged_data
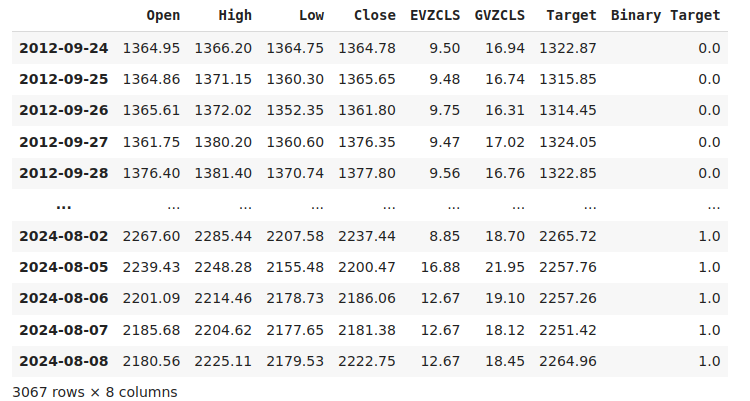
Abb. 2: Unser Datensatz mit dem Ziel umfasst
Schließlich haben wir die 3 Prädiktoren definiert, die wir empirisch vergleichen wollen.
#Let us define the predictors and target ohlc_predictors = ["Open","High","Low","Close"] fred_predictors = ["EVZCLS","GVZCLS"] predictors = ohlc_predictors + fred_predictors target = "Target" binary_target = "Binary Target"
Explorative Datenanalyse
Das Vorhandensein oder Nichtvorhandensein starker Korrelationsniveaus bedeutet nicht unbedingt das Vorhandensein oder Nichtvorhandensein einer Beziehung zwischen den analysierten Daten. Unsere alternativen Daten scheinen eine unregelmäßige Korrelation mit dem XAUEUR-Datensatz aufzuweisen. Es schien jedoch eine starke Korrelation direkt zwischen den beiden alternativen Datensätzen zu bestehen.
#Exploratory Data Analysis #Analyzing correlation levels sns.heatmap(merged_data[predictors].corr(),annot=True)
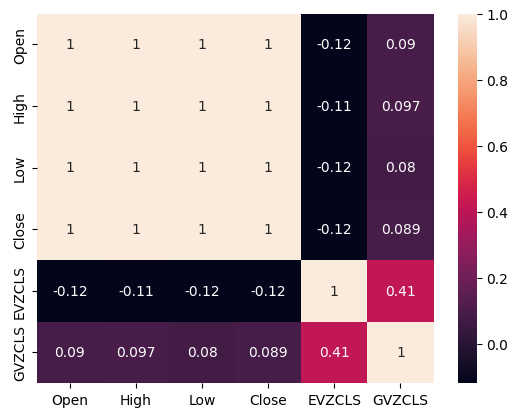
Abb. 3: Unsere Heatmap der Korrelation
Wir haben 3 Streudiagramme der Daten erstellt, die wir haben. In den ersten beiden Streudiagrammen wurden der Gold- und der Euro-Volatilitätsindex auf der x-Achse und der XAUEUR-Schlusskurs auf der y-Achse dargestellt. In unserem ersten Streudiagramm zeigt sich, dass die Preise durchweg nach oben tendieren, wenn die Volatilität bei Gold über die Marke von 30-35 steigt.
#Let's create scatter plots sns.scatterplot(data=merged_data,x="GVZCLS",y="Close",hue="Binary Target")
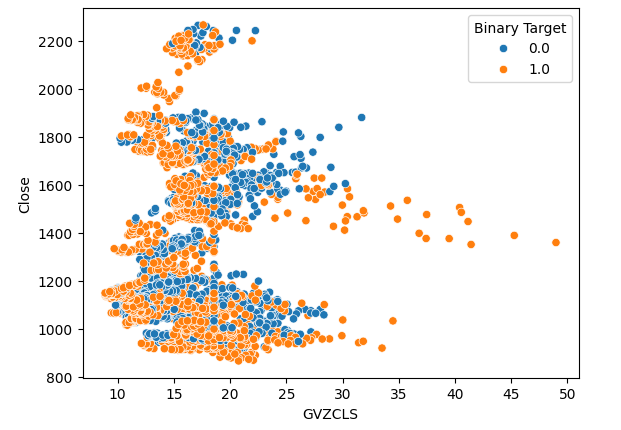
Abb. 4: Unser erstes Streudiagramm
Das gleiche Phänomen ist im zweiten Streudiagramm zu beobachten. Wenn die Euro-Volatilität über die Schwelle von 14 bis 16 ansteigt, scheinen die Kurse durchweg zu steigen. Unser Datensatz ist jedoch begrenzt und repräsentiert möglicherweise nicht vollständig die tatsächliche Beziehung zwischen den beiden Märkten.
#Let's create scatter plots sns.scatterplot(data=merged_data,x="EVZCLS",y="Close",hue="Binary Target")
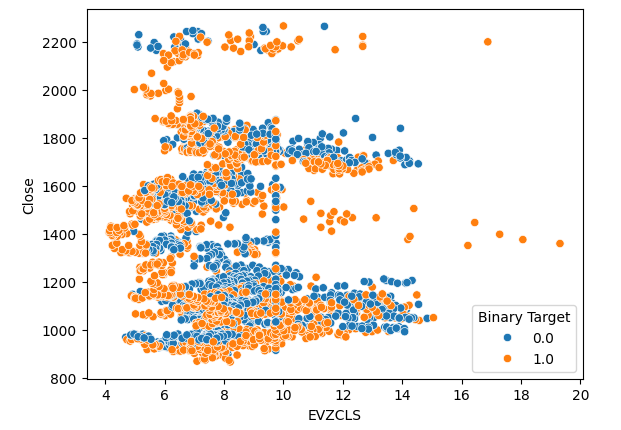
Abb. 5: Unser zweites Streudiagramm
Schließlich erstellten wir ein Streudiagramm mit unseren beiden alternativen Datensätzen auf beiden Achsen. Unsere Daten ergaben eine kegelförmige Struktur, wobei die Gruppe der Aufwärtskerzen noch deutlich sichtbar und gut voneinander getrennt war.
#Let's create scatter plots sns.scatterplot(data=merged_data,x="GVZCLS",y="EVZCLS",hue="Binary Target")
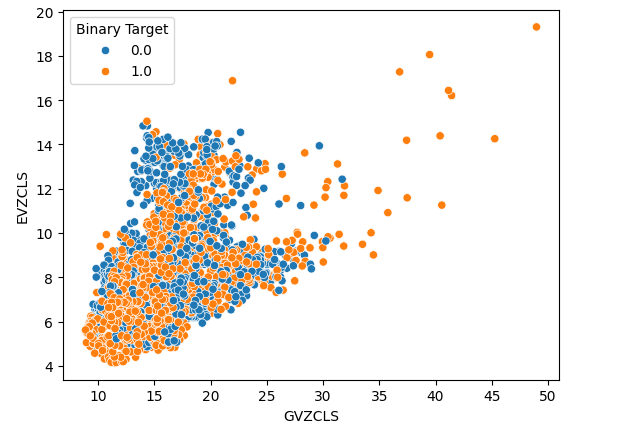
Abb. 6: Unser endgültiges Streudiagramm
Möglicherweise gibt es in unseren Daten verborgene Strukturen, die nicht in 2 Dimensionen visualisiert werden können. Daher haben wir ein 3D-Streudiagramm erstellt, um die Auswirkungen unserer beiden alternativen Datensätze auf den XAUEUR zu veranschaulichen. Die Gruppe der Aufwärtskerzen ist im 3D-Diagramm immer noch deutlich zu erkennen. Dies könnte darauf hindeuten, dass unsere alternativen Daten die Daten an bestimmten Punkten gut trennen.
#Define the 3D Plot fig = plt.figure(figsize=(7,7)) ax = plt.axes(projection="3d") ax.scatter(merged_data["GVZCLS"],merged_data["EVZCLS"],merged_data["Close"],c=merged_data["Binary Target"],cmap="plasma") ax.set_xlabel("GVZCLS") ax.set_ylabel("EVZCLS") ax.set_zlabel("Close")
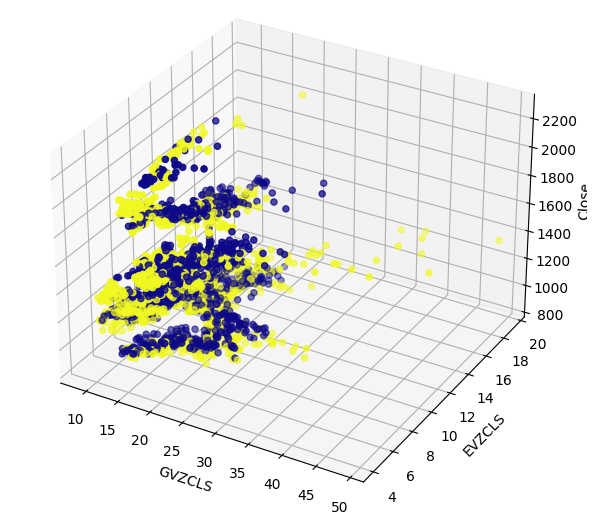
Abb. 7: Ein 3D-Streudiagramm unserer Marktdaten
Wir können auch Techniken zur Dimensionenreduktion anwenden, um eine 2-dimensionale Darstellung unserer 6-dimensionalen Marktdaten zu erstellen. Wir werden den t-SNE-Algorithmus verwenden, um diese Aufgabe zu erfüllen. Der Algorithmus wurde erstmals in einem 2002 von Geoffrey Hinton et al. veröffentlichten Papier vorgeschlagen. Das Originalpapier kann über diesen Link abgerufen werden. Hinton gilt als Pionier auf dem Gebiet des maschinellen Lernens, vor allem wegen seiner Arbeit aus dem Jahr 1986, in der er zeigte, wie der Back-Propagation-Algorithmus verwendet werden kann, um ein neuronales Netzwerk zu trainieren, das das nächste Wort in einer Vektordarstellung eines Satzes vorhersagt. Seine Beiträge trugen zur Verbreitung des Backpropagation-Algorithmus bei.

Abb. 8: Dr. Geoffrey Hinton
Der t-SNE-Algorithmus wurde entwickelt, um eine kompakte Darstellung von hochdimensionalen Daten zu erstellen, bei der die Nähe zwischen allen Datenpunkten im hochdimensionalen Raum in der neuen niedrigdimensionalen Darstellung erhalten bleibt. Um dieses Ziel zu erreichen, minimiert der Algorithmus eine spezielle Kostenfunktion, die die Differenz zwischen zwei Verteilungen misst. Normalerweise wird dieses Optimierungsverfahren durch Gradientenabstieg erreicht. Zunächst erstellt der Algorithmus eine Matrix niedrigeren Ranges aus den ursprünglichen hochdimensionalen Daten. Dann werden die Datenpunkte iterativ verschoben, um die Kosten zu minimieren. Die Kosten sind die Differenz zwischen den Verteilungen der Daten in der Matrix mit niedrigerem Rang und der ursprünglichen Verteilung der Daten. Der t-SNE-Algorithmus ist hilfreich für die Visualisierung von Datenclustern, die im höherdimensionalen Raum verborgen sind.
Wir werden die benötigten Bibliotheken importieren.
#Let's create a TSNE Plot from sklearn.manifold import TS
Dann werden wir das t-SNE-Objekt instanziieren und es anweisen, eine 2-dimensionale Darstellung unserer Daten zu erstellen.
#Create a TSNE object which will reduce the data to 2 dimensions tsne = TSNE(n_components=2,perplexity=30)
Passen wir das t-SNE-Objekt an die Daten an, die wir haben.
#Apply TSNE to the data
tsne_data = tsne.fit_transform(merged_data[predictors]) Zeichnen der neuen Darstellung der Daten.
#Create a scatter plot plt.scatter(tsne_data[:,0],tsne_data[:,1])
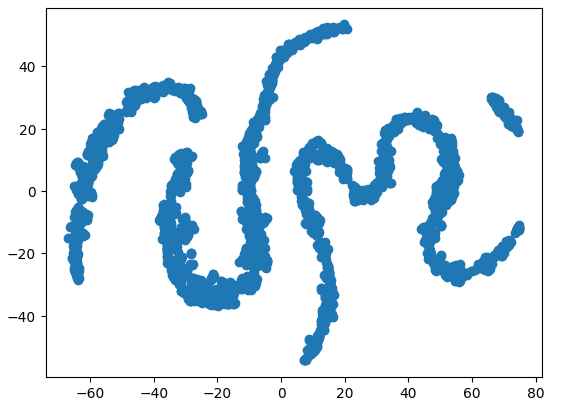
Abb. 9: Unser t-SNE-Diagramm der Marktdaten
Aufgrund des stochastischen Charakters des iterativen Optimierungsverfahrens kann es eine Herausforderung sein, die in dieser Diskussion erhaltene Darstellung zu reproduzieren. Wenn wir die Prozedur ein zweites Mal durchführen würden, wären wir nicht beunruhigt, wenn wir ein anderes Streudiagramm erhalten würden. Was uns besonders interessiert, ist die Anzahl der Cluster, die der Algorithmus zu erhalten versucht. Es hat den Anschein, dass unser Datensatz 4 verschiedene Cluster aufweist, außerdem könnte die gekrümmte Natur der Diagramme auf eine Abhängigkeit hinweisen, die innerhalb der Cluster über die Zeit verteilt ist.
Autokorrelationsdiagramme (ACF) werden in der Zeitreihenanalyse häufig verwendet, um zu prüfen, ob die Daten stationär sind, saisonale Schwankungen enthalten und vieles mehr. ACF-Diagramme zeigen uns den Grad der Korrelation zwischen dem aktuellen Wert einer Zeitreihe und ihren früheren Werten. Wir haben 3 ACF-Diagramme für den XAUEUR-Schlusskurs und die 2 alternativen Datensätze der CBOE erstellt. Alle 3 Diagramme deuten darauf hin, dass die Daten persistente Komponenten haben, was uns auch durch die zuvor visualisierte Heatmap suggeriert wurde. Wenn ACF-Diagramme lange Ausläufer haben, die langsam auf 0 abklingen, werden wir natürlich überlegen, ob es starke Trend- oder Saisonkomponenten in den Daten geben könnte.
#Let's look at an autocorrelation plot of the data close_acf = plot_acf(merged_data["Close"])
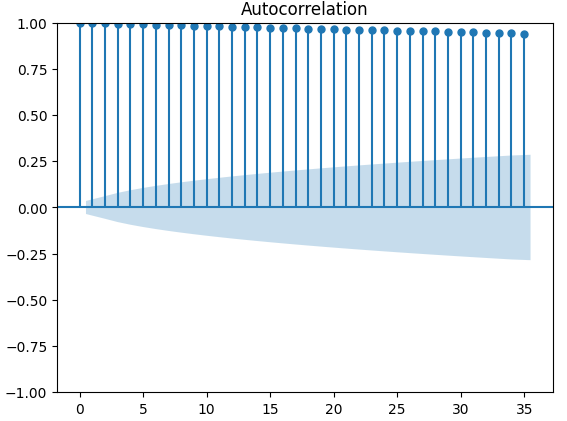
Abb. 10: ACF-Diagramm des XAUEUR Schlusskurses
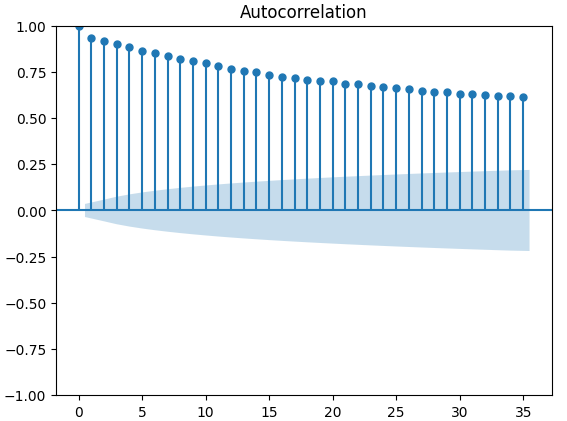
Abb. 11: ACF-Diagramm des CBOE Euro-Volatilitätsindex
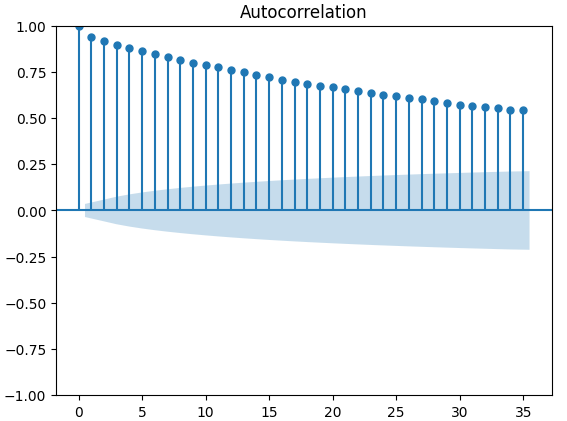
Abb. 12: ACF-Diagramm des CBOE Gold Volatilitätsindex
Partielle Autokorrelationsdiagramme (PACF) geben Aufschluss darüber, wie weit man in die Vergangenheit zurückblicken sollte, um den größten Teil der beobachteten Korrelation zwischen der Zeitreihe und ihren berücksichtigten Balken zu erklären. Mit anderen Worten: Wie viel von der in 3 Balken beobachteten Korrelation wurde nicht von 2 Balken übernommen? Alle drei PACF-Diagramme deuten darauf hin, dass der größte Teil der Autokorrelation in den Zeitreihendaten auf höchstens 4 Balken zurückzuführen ist.
#Let's look at an partial autocorrelation plot of the close data close_pacf = plot_pacf(merged_data["Close"])
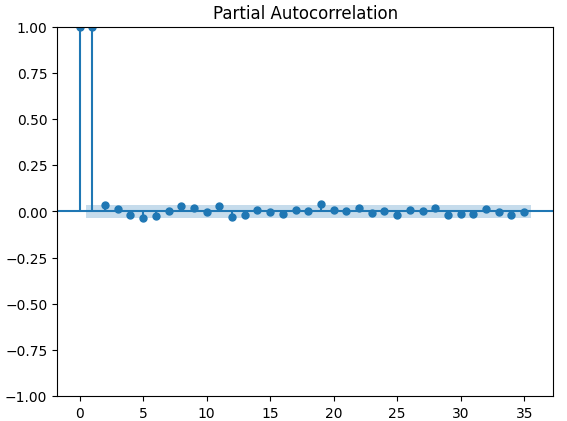
Abb. 13: PACF-Diagramme für den XAUEUR-Abschluss
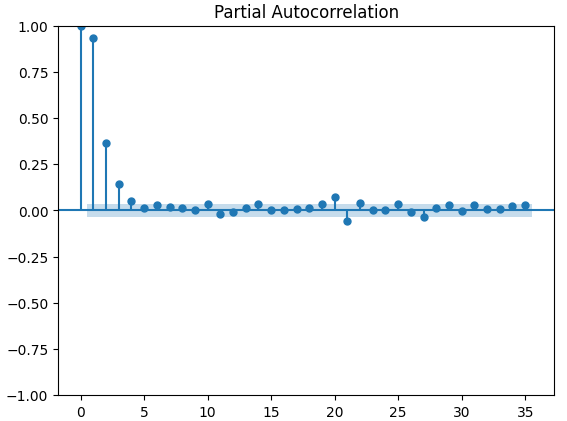
Abb. 14: PACF-Diagramme des CBOE Euro-Volatilitätsindex
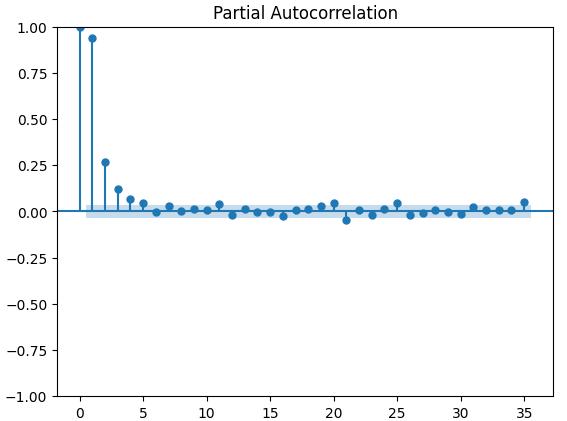
Abb. 15: PACF-Diagramme des CBOE Gold Volatilitätsindex
Vorbereiten der Datenmodellierung
Bevor wir mit der Modellierung unserer Daten mit unserem tiefen neuronalen Netz beginnen können, müssen wir zunächst einige Vorbereitungen treffen.
#Preparing to model the data from sklearn.preprocessing import RobustScaler from sklearn.model_selection import TimeSeriesSplit,train_test_split from sklearn.metrics import mean_squared_error from sklearn.neural_network import MLPRegressor
Der erste Schritt besteht darin, die Eingabedaten zu standardisieren und zu skalieren, damit unser Modell effektiv lernen kann.
#Reset the index of our data merged_data.reset_index(inplace=True) X = merged_data.loc[:,predictors] y = merged_data.loc[:,target] #Scale our data scaler = RobustScaler() X = pd.DataFrame(scaler.fit_transform(merged_data[predictors]),columns=predictors)
Nun müssen wir für die 3 Prädiktoren, die wir haben, die Aufteilung in Trainings- und Testteil erstellen. Achten Sie darauf, dass Ihre Daten in diesem Schritt nicht zufällig gemischt werden. Andernfalls würden wir die Integrität unserer Analyse gefährden.
#Perform train test splits ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,shuffle=False,train_size=0.5) fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,shuffle=False,train_size=0.5) train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,shuffle=False,train_size=0.5)
Schließlich müssen wir unser Zeitreihenobjekt erstellen und anschließend einen Datenrahmen erstellen, um unsere Validierungsfehlerniveaus zu speichern.
#Let's now cross-validate each of the predictors #Create the time-series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead) validation_error = pd.DataFrame(columns=["OHLC Predictors","FRED Predictors","All Predictors"],index=np.arange(0,5))
Modellierung der Daten
Wir sind nun bereit, mit der Modellierung unserer Daten und der Kreuzvalidierung unserer Modelle zu beginnen.
#Performing cross validation model = MLPRegressor(hidden_layer_sizes=(20,5)) for i,(train,test) in enumerate(tscv.split(train_X)): model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) validation_error.iloc[i,2] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
Unsere Fehlerquote bei der Validierung.
#Our validation error
validation_error | MetaTrader 5 OHLC-Daten | FRED CBOE Alternative Daten | Alle Daten |
|---|---|---|
| 875423.637167 | 881892.498319 | 857846.11554 |
| 794999.120981 | 831138.370726 | 946193.178747 |
| 1058884.292095 | 474744.732539 | 631259.842972 |
| 419566.842693 | 882615.372658 | 483408.373559 |
| 96693.318078 | 618647.934237 | 237935.04009 |
Es mag für uns nicht sofort ersichtlich sein, welches Modell am besten abschneidet, aber wenn wir die Spaltenmittelwerte analysieren, können wir deutlich sehen, dass das letzte Modell außergewöhnlich gut abschneidet. In der folgenden Grafik wurde der Mittelwert der ersten Spalte von den übrigen Spalten abgezogen. Dabei ist der erste Spaltenwert 0 und alle nicht zufriedenstellenden Modelle haben Spaltenwerte größer als 0. Wir können also deutlich sehen, dass unser letztes Modell recht gut funktioniert.
#Our mean error levels val_err = validation_error.mean() val_err = val_err.iloc[:] - val_err.iloc[0] val_err.plot(kind="bar")
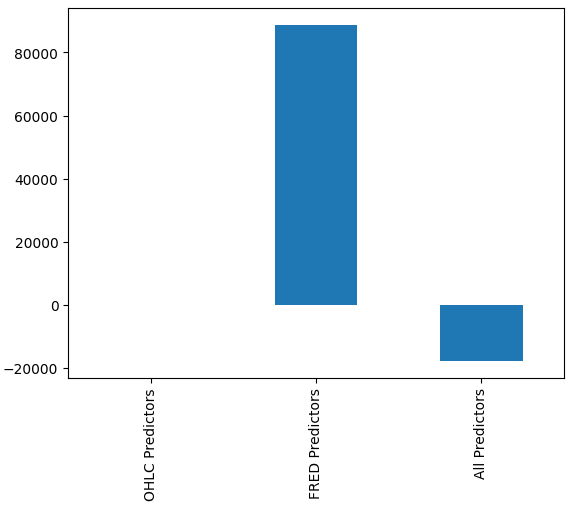
Abb. 16: Die Leistung unseres Modells mit 3 verschiedenen Datensätzen
Boxplots der Modellleistung zeigen außerdem, dass die letzte Gruppe von Prädiktoren für uns die optimale Wahl zu sein scheint, die mittlere Fehlerquote ist die niedrigste und die Varianz ist nicht so groß wie bei der Verwendung von OHCL-Daten.
#Let's perform boxplots of our validation error sns.boxplot(validation_error)
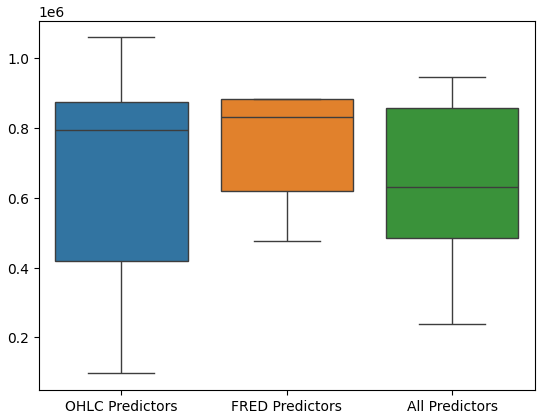
Abb. 17: Die Leistung unseres Modells als Boxplots visualisiert
Die Bedeutung der Merkmale
Wir sollten niemals einem Modell blind vertrauen und es in der Produktion einsetzen, nur weil es niedrige Fehlermetriken aufweist. Sehen wir uns die Beziehungen an, die das Modell gelernt hat. Wir möchten ein Verständnis für die Bedeutung globaler Merkmale für unser Modell gewinnen. Wir beginnen mit der Erstellung von ALE-Plots (Accumulated Local Effect). ALE wurde entwickelt, um robuste Erklärungen für Modelle des maschinellen Lernens zu liefern, die auf Daten mit hohem Korrelationsgrad trainiert werden. ALE versucht, die Auswirkungen jedes Inputs auf den Output des Modells zu isolieren.
#Feature importance
from alibi.explainers import ALE , plot_ale Wir werden nun unser ALE-Objekt instanziieren und Erklärungen zur globalen Merkmalsbedeutung für unser tiefes neuronales Netz abrufen. Dies wird uns helfen zu verstehen, wie sich die einzelnen Eingaben auf die Modellvorhersage auswirken.
#Explaining our deep neural network model = MLPRegressor(hidden_layer_sizes=(20,5)) model.fit(train_X,train_y) dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["XAUEUR Close"])
Berechnen wir nun unsere ALE-Werte für jeden Input des Modells und stellen sie dar.
#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None) 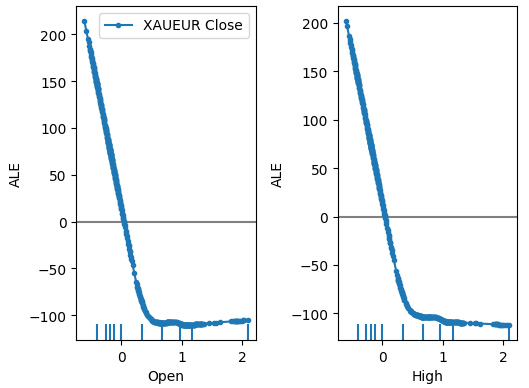
Abb. 18: Unsere ALE-Diagramme für einige der XAUEUR Open und High Prädiktoren
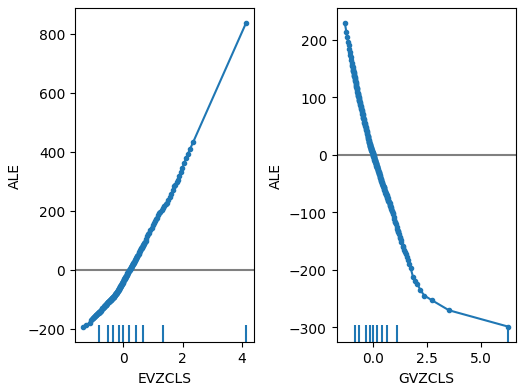
Abb. 19: Unsere ALE-Diagramme für die FRED-CBOE-Volatilitätsindizes
Die Interpretation von ALE-Diagrammen ist recht intuitiv, denn das Diagramm veranschaulicht, wie sich die Vorhersage des Modells ändert, wenn sich der Wert der einzelnen Prädiktoren ändert. Wie wir sehen können, sinkt die Vorhersage des Modells zunächst, wenn der Eröffnungs- und der Höchstkurs steigen. Sie wird jedoch weniger empfindlich, wenn das Preisniveau weiter steigt. Obwohl wir sie hier nicht aufgeführt haben, sehen die ALE-Diagramme des Tiefstkurses und des Schlusskurses identisch aus wie die beiden von uns gezeigten Diagramme.
Wenn wir uns nun den ALE-Diagrammen der alternativen Daten zuwenden, stellen wir fest, dass der Euro-Volatilitätsindex ein ALE-Diagramm erzeugt, das einen Teil des Diagramms abdeckt, der von den anderen Variablen nicht erfasst wird. Mit anderen Worten: Der Prädiktor scheint die Varianz im Ziel zu erklären, die wir ohne ihn nicht erklären konnten. Außerdem deutet die steigende Neigung des ALE-Diagramms darauf hin, dass die Vorhersage des Modells mit zunehmendem Wert des Prädiktors ansteigt.
Als Nächstes werden wir SHAP-Erklärungen für die Leistung unseres Modells abrufen. Mithilfe der SHAP-Werte lässt sich quantifizieren, wie die einzelnen Eingaben des Modells im Vergleich zur durchschnittlichen Vorhersage des Modells zu einer bestimmten Vorhersage beitragen. Die SHAP-Werte sind im mathematischen Bereich der Spieltheorie verwurzelt. Der Algorithmus berücksichtigt jeden möglichen Satz von Prädiktoren und berechnet dann die durchschnittliche Wirkung der Eingaben über alle möglichen Sätze hinweg.
Zunächst importieren wir die SHAP-Bibliothek.
#SHAP Values
import shap Dann berechnen wir die SHAP-Werte
#Calculating SHAP values explainer = shap.Explainer(model.predict,train_X) shap_values = explainer(test_X)#Calculating SHAP values
und zeichnen die SHAP-Werte auf.
#Plot the beeswarm plot
shap.plots.beeswarm(shap_values) 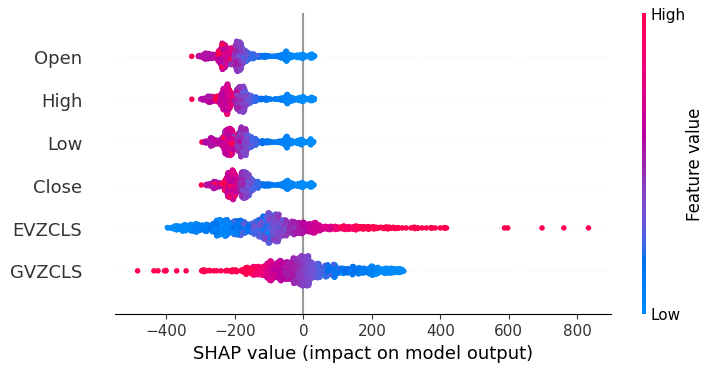
Abb. 20: Unsere SHAP-Erklärungen
Nach unseren SHAP-Erklärungen sind die Marktdaten, die vom XAUEUR-Markt selbst stammen, die wichtigsten Daten, über die wir verfügen. Das SHAP-Diagramm deutet außerdem darauf hin, dass bei einem Anstieg des aktuellen Marktpreises das Ziel tendenziell sinkt.
Einstellung der Parameter
Um die Leistung unseres Modells zu verbessern, importieren wir zunächst die benötigten Bibliotheken.
#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV Initialisieren wir das Modell,
#Reinitialize the model model = MLPRegressor(hidden_layer_sizes=(20,5))
definieren das Tuner-Objekt
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"shuffle": [True,False]
},
n_iter=500,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
) und passen den Tuner an:
#Fit the tuner
tuner_results = tuner.fit(train_X,train_y) Die besten Parameter, die wir gefunden haben.
#The best parameters we found
tuner_results.best_params_ 'solver': 'lbfgs',
'shuffle': True,
'learning_rate': 'adaptive',
'alpha': 0.1,
'activation': 'identity'}
Scipy verfügt über Optimierungsverfahren, die in seinem Minimieren-Modul enthalten sind. Diese Verfahren erfordern eine Ausgangsbasis für den Optimierungsprozess. Wir werden die besten Parameterwerte, die durch die Zufallssuche gefunden wurden, als Ausgangspunkt für unsere zweite Optimierungsphase verwenden.
#Deeper optimization
from scipy.optimize import minimize Nun werden wir ein Datenrahmenobjekt erstellen, um unsere Fehlerstufen in der Validierung zu speichern.
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
Jeder Optimierungsalgorithmus benötigt eine Zielfunktion, mit der er arbeiten kann. In unserem Fall ist die Zielfunktion der durchschnittliche kreuzvalidierte Fehler des Modells in der Trainingsmenge. Unser Optimierungsverfahren sucht nach Modellparametern, die unseren durchschnittlichen Fehler minimieren.
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1]) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(train_X)): #Train the model model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:])) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
Legen wir den Ausgangspunkt für das Optimierungsverfahren fest, und wir sollten auch Grenzen für die zulässigen Eingabewerte definieren.
#Define the starting point pt = [0.1,0.00000001] bnds = ((0.0000000000000000001,10000000000),(0.0000000000000000001,10000000000))
Optimierung des Modells.
#Searchin deeper for parameters result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)
Testen auf Überanpassung
Die Überanpassung ist ein Problem bei jedem maschinellen Lernprojekt. Sie tritt auf, wenn unser Modell keine sinnvollen Verallgemeinerungen der Daten erstellen kann und stattdessen beginnt, Rauschen und andere bedeutungslose Assoziationen in den Daten zu lernen. Um zu prüfen, ob eine Überanpassung vorliegt, vergleichen wir die Genauigkeit unserer beiden angepassten Modelle mit der des Standardmodells.
#Testing for overfitting default_model = MLPRegressor(hidden_layer_sizes=(20,5)) customized_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=0.1,tol=0.0000001) customized_lbfgs_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=result.x[0],tol=result.x[1])
Bereiten wir uns nun auf die Kreuzvalidierung der einzelnen Modelle vor.
#Preparing to cross validate the models models = [ default_model, customized_model, customized_lbfgs_model ] #We will store our validation error here validation_error = pd.DataFrame(columns=["Default Model","Customized Model","L-BFGS Model"],index=np.arange(0,5)) #We will now reset the indexes test_y = test_y.reset_index() test_X = test_X.reset_index()
Wir sollten jedes der Modelle an die Trainingsmenge anpassen.
#Fit each of the models for m in models: m.fit(train_X,train_y)
Lassen Sie uns nun die Leistung unseres Modells an ungesehenen Daten, dem Testsatz, den wir bis jetzt zurückgehalten haben, kreuzvalidieren.
#Cross validating each model for j in np.arange(0,len(models)): model = models[j] for i,(train,test) in enumerate(tscv.split(test_X)): model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1],"Target"]) validation_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"Target"],model.predict(test_X.loc[test[0]:test[-1],:]))
Unsere Fehlerquote bei der Validierung.
#Our validation error
validation_error | Standardmodell | Randomisiertes Suchmodell | L-BFGS-B Modell |
|---|---|---|
| 22360.060721 | 5917.062055 | 3734.212826 |
| 17385.289026 | 36726.684574 | 35886.972729 |
| 13782.649037 | 5128.022626 | 20886.845316 |
| 3082484.290698 | 6950.786438 | 5789.948045 |
| 4076009.132941 | 27729.589769 | 22931.572161 |
Das Modell mit der besten Leistung ist das Modell der zufälligen Suche.
#Plotting the difference in our performance levels mean = validation_error.mean() mean = mean.iloc[:] - mean.iloc[0] mean.plot(kind="bar")
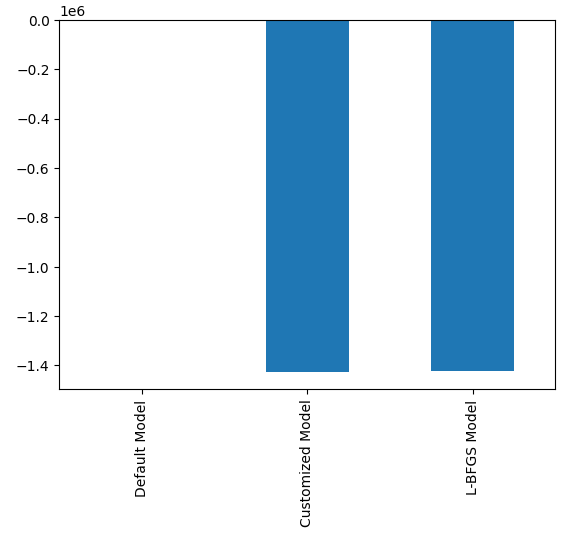
Abb. 21: Unsere Validierungsfehler
Die Visualisierung der Leistung unseres Modells macht deutlich, wie schlecht das Standardmodell die Daten verarbeitet.
#Visualizing the results
validation_error.plot() 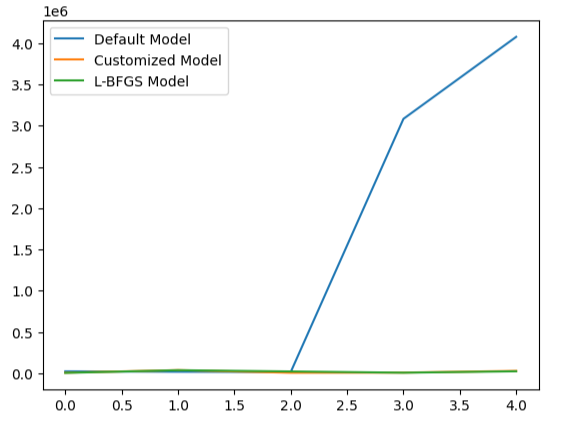
Abb. 22: Prüfung auf Überanpassung
Dieser Punkt wird durch unsere Boxplots noch verstärkt. Wir können feststellen, dass wir das Standardmodell bei weitem übertroffen haben.
#Visualizing our results
sns.boxplot(validation_error) 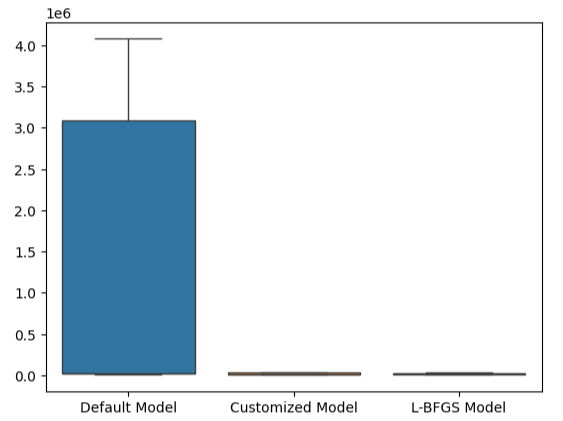
Abb. 23: Wir übertreffen das Standardmodell um ein Vielfaches
Vorbereiten des Exports in das ONNX-Format
Bevor wir unser Modell in das ONNX-Format exportieren können, müssen wir unsere Daten zunächst so standardisieren und skalieren, dass wir sie in unserem MetaTrader 5 Terminal reproduzieren können. Zu diesem Zweck ziehen wir von jeder Spalte den Mittelwert ab, bevor wir schließlich jede Spalte durch ihre Standardabweichung dividieren. Wir werden unsere Skalierungsfaktoren im CSV-Format ausgeben, damit wir sie in unserem MetaTrader 5-Terminal abrufen können, um unsere Modelleingaben zu skalieren.
#Let us now prepare to export our model to onnx format scale_factors = pd.DataFrame(columns=predictors,index=["mean","standard deviation"]) for i in np.arange(0,len(predictors)): scale_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean() scale_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std() merged_data.loc[:,predictors[i]] = (merged_data.loc[:,predictors[i]] - merged_data.loc[:,predictors[i]].mean())/merged_data.loc[:,predictors[i]].std() scale_factors
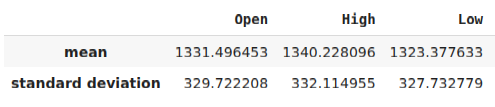
Abb. 24: Einige unserer Skalierungsfaktoren
Jetzt werden wir die Daten im CSV-Format ausgeben.
#Save the scale factors to CSV scale_factors.to_csv("scale_factors.csv")
Exportieren ins ONNX-Format
Open Neural Network Exchange (ONNX) ist ein Protokoll zur Erstellung und gemeinsamen Nutzung von Modellen für maschinelles Lernen in verschiedenen Programmiersprachen. Das ONNX-Protokoll ermöglicht es uns, unser tiefes neuronales Netzwerk nahtlos in unseren Expert Advisor einzubetten, indem wir die MQL5 ONNX API verwenden.
Laden wir zunächst die benötigten Bibliotheken.
#Exporting to ONNX format
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType Trainieren wir das Modell mit allen Daten, die wir haben.
#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target]) Beim Export von ONNX-Modellen kann die Eingabeform verloren gehen. Daher sollten wir die Eingabeform explizit angeben.
# Define the input type initial_types = [("float_input",FloatTensorType([1,6]))]
Erstellen der ONNX-Darstellung des Modells.
# Create the ONNX representation onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)
Speichern der ONNX-Darstellung in einer Datei mit der Erweiterung „.onnx“.
# Save the ONNX model onnx_name = "XAUEUR FRED D1.onnx" onnx.save_model(onnx_model,onnx_name)
Aktuelle FRED-Daten erhalten
Bevor wir mit dem Aufbau unseres Expert Advisors beginnen können, müssen wir ein Python-Skript erstellen, das ständig aktuelle FRED-Daten mit unserem Terminal austauscht. Wir werden ein Skript erstellen, das einmal am Tag die neuesten verfügbaren Daten abruft und sie als CSV-Datei in den Ordner „Files“ schreibt, damit wir mit unserer Handelsanwendung auf die Daten zugreifen können.
#A function to write out our alternative data to CSV def write_out_alternative_data(): euro = fred.get_series("EVZCLS") euro = euro.iloc[-1] gold = fred.get_series("GVZCLS") gold = gold.iloc[-1] data = pd.DataFrame(np.array([euro,gold]),columns=["Data"],index=["Fred Euro","Fred Gold"]) data.to_csv("C:\\ENTER\\YOUR\\PATH\\HERE\\MetaQuotes\\Terminal\\D0E8209F77C8CF37AD8BF550E51FF075\\MQL5\\Files\\fred_xau_eur.csv")
Jetzt werden wir eine Endlosschleife schreiben, um die Daten zu schreiben und dann einen Tag lang zu „schlafen“.
while True: #Update the fred data for our MT5 EA write_out_alternative_data() #If we have finished all checks then we can wait for one day before checking for new data time.sleep(24 * 60 * 60)
Aufbau unseres Expert Advisors
Wir sind nun bereit, mit dem Aufbau unseres Expert Advisors zu beginnen. Wir beginnen damit, dass wir zunächst die soeben erstellte ONNX-Datei benötigen.
//+------------------------------------------------------------------+ //| EURXAU Fred AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Volatility Doctor" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\XAUEUR FRED D1.onnx" as const uchar onnx_buffer[];
Laden wir die Handelsbibliothek, um uns bei der Verwaltung unserer Positionen zu helfen.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Diese globalen Variablen werden in vielen verschiedenen Teilen unserer Anwendung gemeinsam genutzt werden.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; vector mean_values = vector::Zeros(6); vector std_values = vector::Zeros(6); vectorf model_inputs = vectorf::Zeros(6); vectorf model_output = vectorf::Zeros(1); double bid,ask; int system_state,model_sate;
Jetzt brauchen wir eine Funktion, die unser ONNX-Modell aus dem ONNX-Puffer erstellt, den wir zu Beginn unserer Anwendung angelegt haben. Unsere Funktion wird zunächst das ONNX-Modell erstellen und validieren und schließlich die Eingabe- und Ausgabeformen des Modells festlegen und validieren. Wenn wir an irgendeinem Punkt scheitern, wird die Funktion false zurückgeben, was wiederum die Initialisierungsprozedur stoppt.
//+------------------------------------------------------------------+ //| Load the ONNX file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the ONNX model from the buffer we loaded earlier onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model we just created if(onnx_model == INVALID_HANDLE) { //--- Give the user feedback on the error Comment("Failed to create the ONNX model: ",GetLastError()); //--- Break initialization return(false); } //--- Define the I/O shape ulong input_shape [] = {1,6}; //--- Validate the input shape if(!OnnxSetInputShape(onnx_model,0,input_shape)) { //--- Give the user feedback Comment("Failed to define the ONNX input shape: ",GetLastError()); //--- Break initialization return(false); } ulong output_shape [] = {1,1}; //--- Validate the output shape if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { //--- Give the user feedback Comment("Failed to define the ONNX output shape: ",GetLastError()); //--- Break initialization return(false); } //--- We've finished return(true); } //+------------------------------------------------------------------+
Von dort aus werden wir nun die Skalierungsfaktoren festlegen, die wir zur Normalisierung unserer Modelleingaben benötigen.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ bool load_scaling_factors(void) { //--- Load the scaling values mean_values[0] = 1331.4964525595044; mean_values[1] = 1340.2280958591457; mean_values[2] = 1323.3776328659928; mean_values[3] = 1331.706768829475; mean_values[4] = 8.258127607767035; mean_values[5] = 16.35582438284101; std_values[0] = 329.7222075527991; std_values[1] = 332.11495530642173; std_values[2] = 327.732778866831; std_values[3] = 330.1146052811378; std_values[4] = 2.199782202942867; std_values[5] = 4.241112965400358; //--- Validate the values loaded correctly if((mean_values.Sum() > 0) && (std_values.Sum() > 0)) { return(true); } //--- We failed to load the scaling values return(false); }
Wenn unsere Anwendung nicht mehr genutzt wird, geben wir die nicht mehr benötigten Ressourcen frei.
//+------------------------------------------------------------------+ //| Free up the resources we no longer need | //+------------------------------------------------------------------+ void release_resources(void) { //--- Free up all the resources we have used so far OnnxRelease(onnx_model); ExpertRemove(); Print("Thank you for choosing Volatility Doctor"); }
Diese Funktion wird für die Aktualisierung unserer Marktpreisinformationen zuständig sein.
//+------------------------------------------------------------------+ //| Fetch market data | //+------------------------------------------------------------------+ void fetch_market_data(void) { //--- Update the market data bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
Die folgende Funktion ist für das Abrufen einer Vorhersage aus unserem Modell verantwortlich. Zunächst holen wir die aktuellen OHLC-Daten des XAUEUR-Symbols mit Hilfe der MQL5-Matrixfunktion CopyRates(). Nach dem Abrufen der Daten werden diese normalisiert und in dem zuvor definierten Eingabevektor gespeichert. Von hier aus rufen wir eine weitere Funktion auf, um die neuesten FRED-Daten zu lesen, die wir in der Datei haben.
//+------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get the input data ready for(int i =0; i < 6; i++) { //--- The first 4 inputs will be fetched from the market matrix xau_eur_ohlc = matrix::Zeros(1,4); xau_eur_ohlc.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OHLC,0,1); //--- Fill in the data if(i<4) { model_inputs[i] = (float)((xau_eur_ohlc[i,0] - mean_values[i])/ std_values[i]); } //--- We have to read in the fred alternative data else { read_fred_data(); } } }
Die unten definierte Funktion liest die CSV-Datei mit den neuesten FRED-Daten ein und normalisiert die Daten, bevor sie im Eingabevektor gespeichert und eine Vorhersage von unserem Modell abgerufen wird. Wir werden die Vorhersage des Modells durch eine ganze Zahl darstellen. Auf diese Weise können wir potenzielle Umkehrungen schnell erkennen und unsere Positionen schließen, hoffentlich auf der richtigen Seite des Marktes.
//+-------------------------------------------------------------------+ //| Read in the FRED data | //+-------------------------------------------------------------------+ void read_fred_data(void) { //--- Read in the file string file_name = "fred_xau_eur.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 10) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Counter: "); Print(counter); Print("Trying to read string: ",value); if(counter == 3) { Print("Fred Euro data: ",value); model_inputs[4] = (float)((((float) value) - mean_values[4])/std_values[4]); } if(counter == 5) { Print("Fred Gold data: ",value); model_inputs[5] = (float)((((float) value) - mean_values[5])/std_values[5]); } if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //--- Show the input and Fred data Print("Input Data: "); Print(model_inputs); //---Close the file FileClose(result); //--- Store the model prediction OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output); Comment("Model Forecast",model_output[0]); if(model_output[0] > iClose(Symbol(),PERIOD_D1,0)) { model_sate = 1; } else { model_sate = -1; } } //--- We failed to find the file else { //--- Give the user feedback Print("We failed to find the file with the FRED data"); } }
Lassen Sie uns nun festlegen, wie unsere Anwendung gestartet werden soll. Unsere Anwendung sollte zunächst das ONNX-Modell erstellen und dann die benötigten Skalierungsfaktoren laden. Sollte einer dieser Schritte fehlschlagen, brechen wir die Initialisierungsprozedur komplett ab.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX model if(!load_onnx_file()) { //--- We failed to load our ONNX model return(INIT_FAILED); } //--- Load the scaling factors if(!load_scaling_factors()) { //--- We failed to read in the scaling factors return(INIT_FAILED); } //--- We mamnaged to load our model return(INIT_SUCCEEDED); }
Wenn unsere Anwendung aus dem Chart entfernt wurde, geben wir die nicht mehr benötigten Ressourcen frei.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we no longer need release_resources(); }
Schließlich werden wir, sobald wir aktualisierte Marktkurse erhalten, diese zunächst im Speicher ablegen. Wenn wir keine offenen Positionen haben, folgen wir der Vorhersage unseres Modells nur dann, wenn sie durch die Preisentwicklung auf höheren Zeitebenen bestätigt wird. Wenn wir jedoch bereits offene Positionen haben, schließen wir diese, wenn unser Modell eine Umkehrung der Preisniveaus vorhersagt.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market data fetch_market_data(); //--- Fetch a prediction from our model model_predict(); //--- If we have no positions follow the model's lead if(PositionsTotal() == 0) { //--- Buy position if(model_sate == 1) { if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12)) { Trade.Buy(0.3,Symbol(),ask,0,0,"XAUEUR Fred AI"); system_state = 1; } }; //--- Sell position if(model_sate == -1) { if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12)) { Trade.Sell(0.3,Symbol(),bid,0,0,"XAUEUR Fred AI"); system_state = -1; } }; } //--- If we allready have positions open, let's manage them if(model_sate != system_state) { Trade.PositionClose(Symbol()); } } //+------------------------------------------------------------------+
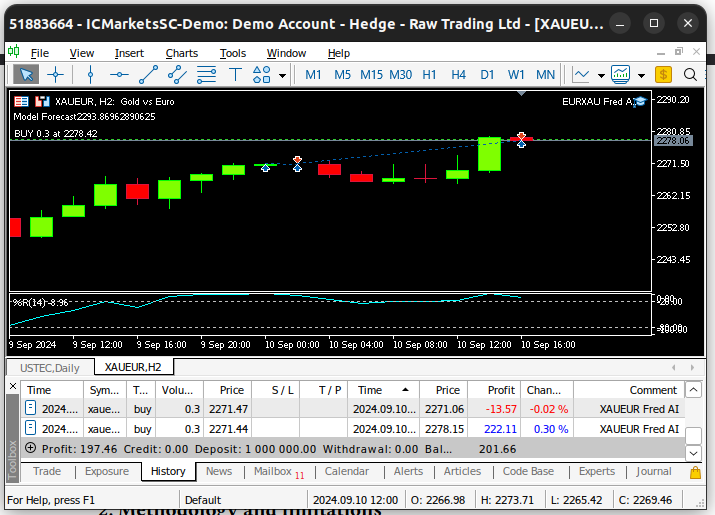
Abb. 25: Unser Expert Advisor in Aktion
Schlussfolgerung
In diesem Artikel haben wir gezeigt, dass es sinnvoll sein kann, die FRED CBOE Volatilitätsindizes einzubeziehen, um die Genauigkeit maschineller Lernmodelle zu verbessern. Wir können zwar nicht garantieren, dass die in diesem Artikel enthaltenen Informationen durchgängig zum Erfolg führen, aber sie sind sicherlich eine Überlegung wert, wenn Sie bereit sind, alternative Daten in Ihre Handelsstrategien einzubeziehen.
Übersetzt aus dem Englischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/en/articles/15841
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 40): Parabolic SAR
MQL5-Assistenten-Techniken, die Sie kennen sollten (Teil 40): Parabolic SAR
 Selbstoptimierender Expert Advisor mit MQL5 und Python (Teil IV): Stacking-Modelle
Selbstoptimierender Expert Advisor mit MQL5 und Python (Teil IV): Stacking-Modelle
 HTTP und Connexus (Teil 2): Verstehen der HTTP-Architektur und des Bibliotheksdesigns
HTTP und Connexus (Teil 2): Verstehen der HTTP-Architektur und des Bibliotheksdesigns
 MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 39): RSI (Relative Strength Index)
MQL5-Assistent-Techniken, die Sie kennen sollten (Teil 39): RSI (Relative Strength Index)
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.