
Obtenga una ventaja sobre cualquier mercado (Parte IV): Índices CBOE de volatilidad del euro y el oro
En la era de los macrodatos, hay cientos de millones de conjuntos de datos que tienen el potencial de ofrecer niveles de precisión sin explotar a la hora de predecir los mercados financieros. Lamentablemente, es poco probable que todos los conjuntos de datos existentes estén a la altura de este potencial. En esta serie de artículos, nuestro objetivo es ayudarlo a recorrer el vasto panorama de posibles conjuntos de datos y, al final de la discusión, estará bien posicionado para llegar a una decisión informada sobre si los datos alternativos sugeridos deben incluirse en su estrategia comercial o si puede ser mejor para usted sin ellos.
Descripción general de la estrategia comercial
Analizaremos el mercado XAUEUR. El símbolo rastrea el precio del oro en euros. Se extrae oro en todos los continentes de la Tierra, excepto en la Antártida. Una proporción significativa del oro del mundo se comercializa a través de la 'London Bullion Market Association' (LBMA) para establecer un punto de referencia reconocido mundialmente para el precio del oro. El 'Chicago Board of Options Exchange' (CBOE) es una empresa estadounidense que proporciona infraestructura de mercado global. CBOE utiliza sus redes para crear índices de volatilidad que rastrean los principales mercados alrededor del mundo. Analizaremos dos de los índices de volatilidad del CBOE que siguen los mercados del euro y del oro, respectivamente.
A lo largo de los años, los traders han implementado diversas estrategias para operar con éxito en mercados volátiles, minimizando al mismo tiempo el riesgo. Generalmente, cuando los mercados son volátiles, los traders pueden alcanzar sus objetivos de ganancias posiblemente en períodos de tiempo relativamente cortos. Por otro lado, también es posible perder cantidades significativas de capital rápidamente, debido a grandes brechas en los niveles de precios que pueden no activar órdenes de stop loss de manera oportuna.
En términos generales, algunos traders prefieren abrir menos posiciones o arriesgar menos capital del que normalmente abrirían en un mayor número de posiciones para obtener ganancias potenciales de movimientos de precios rentables y, al mismo tiempo, minimizar su exposición al mercado. En general, los traders experimentados en mercados volátiles tienden a obtener ganancias mucho más rápido que si operaran en mercados más tranquilos. Otros traders esperan que los niveles de precios queden atrapados en un rango entre los niveles de soporte y resistencia. Cuando los niveles de precios finalmente rompen el rango, los operadores pueden abrir sus posiciones anticipando movimientos más fuertes fuera del rango identificable.
En condiciones normales de mercado, una ruptura de una zona de soporte y resistencia puede perder impulso rápidamente y comenzar a desviarse. Sin embargo, cuando las condiciones del mercado son volátiles, las rupturas pueden ser seguidas por cambios violentos de precios en la misma dirección, dando a los operadores que siguen tales estrategias retornos superiores al promedio. Lamentablemente, estas estrategias son propensas a falsas rupturas que pueden revertirse violentamente, dejando a algunos operadores en posiciones desfavorables con pérdidas materiales.
Descripción general de la metodología
Utilizamos la API de Python de la base de datos económica de la Reserva Federal (Federal Reserve Economic Database, FRED), mantenida por la Reserva Federal de San Luis, para recuperar las series temporales económicas de volatilidad del oro y el euro del CBOE. Los datos se proporcionan en formato diario y contienen valores faltantes.
Lamentablemente, ninguna de las descripciones proporcionadas con los conjuntos de datos explica ninguno de los valores faltantes. Por lo tanto, queremos decir que imputamos todos los valores faltantes en ambos conjuntos de datos.
En nuestro terminal MetaTrader 5, obtuvimos aproximadamente 4000 filas de cotizaciones diarias del mercado sobre el precio de apertura, máximo, mínimo y cierre (OHLC) del símbolo XAUEUR, utilizando un script personalizado que escribimos en MQL5.
Cuando analizamos la correlación entre los datos alternativos de CBOE y los datos del mercado de MetaTrader 5, observamos niveles de correlación no significativamente alejados de 0. En particular, los niveles de correlación entre los dos conjuntos de datos alternativos fueron de 0,4. Un nivel de correlación positivo puede sugerir la presencia de interacciones o participantes de mercado comunes que afectan a los dos mercados.
Cuando realizamos gráficos de dispersión de los datos, utilizando cualquiera de los conjuntos de datos alternativos en el eje x y el precio de cierre del XAUEUR en el eje y, pareció haber un umbral de altos niveles de volatilidad que constantemente resultaron en niveles de precios mayores. Lamentablemente, nuestro pequeño conjunto de datos, un total de aproximadamente 3000 filas después de fusionarlo con los conjuntos de datos alternativos, puede ser un buen motivo para tener cuidado de no ser engañados y ver patrones en los datos que simplemente no están presentes.
Visualizar datos de alta dimensión de manera efectiva puede ser un desafío. Por lo tanto, empleamos un procedimiento doble para ver nuestros datos. Inicialmente, creamos gráficos de dispersión 3D utilizando los 2 conjuntos de datos CBOE en los ejes x e y respectivamente, y el cierre XAUEUR en el eje z. El grupo de velas alcistas que observamos en nuestros gráficos de dispersión 2D todavía era claramente visible.
Por último, siempre podemos aprovechar los algoritmos que están diseñados para mapear datos de alta dimensión a un subespacio de menor dimensión. Un algoritmo de reducción de dimensionalidad bien conocido es el análisis de componentes principales. Elegimos utilizar la implementación de scikit-learn de incrustación de vecinos estocásticos distribuidos en t (t-SNE) para crear una representación bidimensional de nuestro conjunto de datos de 6 dimensiones. El gráfico resultante sugirió que podría haber cuatro grupos distintos en nuestro conjunto de datos. Además, observamos lo que parece ser el efecto de la dependencia serial en nuestro conjunto de datos, lo que sugiere que puede haber una relación en evolución entre nuestros conjuntos de datos CBOE y MetaTrader 5.
La técnica de visualización final que utilizamos fueron gráficos de autocorrelación. Todos los gráficos de autocorrelación que creamos exhibieron colas fuertes, esto puede sugerir que hay datos de largo plazo que persisten en nuestra serie temporal. Esto puede deberse a tendencias fuertes o efectos estacionales. Nuestros gráficos de autocorrelación parcial sugirieron que solo unos pocos rezagos explicaron la mayor parte de la autocorrelación que observamos. Esto sugiere que los datos de la serie temporal pueden modelarse con éxito como un modelo de media móvil.
Después de visualizar nuestros datos, creamos 3 conjuntos de predictores:
- Datos de mercado OHLC en MetaTrader 5
- Conjuntos de datos alternativos de FRED-CBOE
- Un superconjunto de los dos conjuntos anteriores
Se emplearon tres redes neuronales profundas idénticas para comparar los tres conjuntos de predictores utilizando una validación cruzada de series de tiempo de cinco veces sin mezcla aleatoria. El último conjunto de predictores generó la tasa de error más baja al pronosticar el precio de cierre futuro del símbolo XAUEUR. Esto puede sugerirnos que existen relaciones entre los dos conjuntos de datos que ayudan a nuestro modelo.
Con la confianza de nuestra primera prueba, intentamos evaluar la importancia de las características globales de nuestra red neuronal profunda. Seleccionamos los métodos de efectos locales acumulados (ALE) y explicaciones aditivas de Shapley (SHAP) para obtener más información sobre qué modelos dependen más de nuestro modelo. Ninguno de los métodos que empleamos rechazó los conjuntos de datos alternativos que hemos seleccionado.
Ajustamos los hiperparámetros de nuestro modelo en el conjunto de entrenamiento, en un proceso de 2 pasos que creó 2 modelos. Inicialmente, realizamos 500 iteraciones de una búsqueda aleatoria sobre una selección de los parámetros de nuestro modelo. En el segundo paso, optimizamos los mejores valores de los parámetros continuos de nuestro modelo a partir de la búsqueda aleatoria, utilizando el algoritmo 'Limited Memory Broyden Fletcher Goldfarb Shano' (L-BFGS-B). Todos los parámetros restantes del modelo, que no eran continuos, se fijaron en la segunda fase.
Ambos modelos personalizados superaron a la red neuronal predeterminada en los datos de validación. Sin embargo, el modelo obtenido mediante búsqueda aleatoria tuvo el mejor rendimiento en el conjunto de prueba. Esto indica que es posible que hayamos optimizado con éxito nuestro modelo para los datos de entrenamiento, sin sobreajustar nuestros parámetros.
A partir de ahí, preparamos nuestro mejor modelo para exportar al formato ONNX para integrarlo en un programa MetaTrader 5 personalizado y, por último, escribimos un script en Python para compartir los últimos datos de FRED en nuestra Terminal a través de un archivo CSV compartido.
Obteniendo los datos
He incluido un script útil escrito en MQL5 para obtener nuestros datos de mercado y escribirlos en formato CSV. El script tiene un parámetro de entrada, que especifica cuántas barras de datos se deben obtener. Simplemente arrastre y suelte el script en su gráfico y estará listo para seguirlo.
//+------------------------------------------------------------------+ //| ProjectName | //| Copyright 2020, CompanyName | //| http://www.companyname.net | //+------------------------------------------------------------------+ #property copyright "Gamuchirai Zororo Ndawana" #property link "https://www.mql5.com/en/users/gamuchiraindawa" #property version "1.00" #property script_show_inputs //+------------------------------------------------------------------+ //| Script Inputs | //+------------------------------------------------------------------+ input int size = 100000; //How much data should we fetch? //+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ int rsi_handler; double rsi_buffer[]; //+------------------------------------------------------------------+ //| On start function | //+------------------------------------------------------------------+ void OnStart() { //--- Load indicator rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,20,PRICE_CLOSE); CopyBuffer(rsi_handler,0,0,size,rsi_buffer); ArraySetAsSeries(rsi_buffer,true); //--- File name string file_name = "Market Data " + Symbol() + ".csv"; //--- Write to file int file_handle=FileOpen(file_name,FILE_WRITE|FILE_ANSI|FILE_CSV,","); for(int i= size;i>=0;i--) { if(i == size) { FileWrite(file_handle,"Time","Open","High","Low","Close"); } else { FileWrite(file_handle,iTime(Symbol(),PERIOD_CURRENT,i), iOpen(Symbol(),PERIOD_CURRENT,i), iHigh(Symbol(),PERIOD_CURRENT,i), iLow(Symbol(),PERIOD_CURRENT,i), iClose(Symbol(),PERIOD_CURRENT,i) ); } } //--- Close the file FileClose(file_handle); } //+------------------------------------------------------------------+
Preparación de datos
Después de obtener nuestros datos de mercado OHLC en MetaTrader 5, comenzamos el proceso de limpieza y formato de los datos. Nuestro primer paso fue importar bibliotecas estándar de Python para el aprendizaje automático.#Import the libraries we need import pandas as pd import numpy as np import matplotlib.pyplot as plt import seaborn as sns import statsmodels from statsmodels.graphics.tsaplots import plot_acf,plot_pacf from fredapi import Fred from datetime import datetime import time
Éstas son las versiones de las bibliotecas que estamos usando.
#Display library versions print(f"Pandas version {pd.__version__}") print(f"Numpy version {np.__version__}") print(f"Seaborn version {sns.__version__}") print(f"Statsmodels version {statsmodels.__version__}")
Numpy versión 1.26.4
Seaborn versión 0.13.1
Statsmodels versión 0.14.
Ahora podemos leer el archivo CSV que acabamos de crear y establecer la columna de tiempo como nuestro índice. Al hacerlo podremos fusionar los datos de MetaTrader 5 y CBOE de forma cronológica.
#Read in the data xau_eur = pd.read_csv("Market Data XAUEUR.csv") xau_eur = xau_eur.loc[96911:,:] xau_eur.set_index("Time",inplace=True) xau_eur.index = pd.to_datetime(xau_eur.index)
Ahora busquemos los datos alternativos del mercado CBOE de FRED. Tenga en cuenta que antes de continuar, primero debe crear una cuenta gratuita en el sitio web de FRED para obtener una clave API privada. Es un proceso fácil de completar, sin cargos ocultos.
#Fetch FRED data
fred = Fred(api_key='ENTER YOUR API KEY HERE')
fred_euro_data = pd.DataFrame(fred.get_series('EVZCLS'),columns=["EVZCLS"])
fred_gold_data = pd.DataFrame(fred.get_series('GVZCLS'),columns=["GVZCLS"])
#Fill in any missing values with the column mean
fred_euro_data = fred_euro_data.fillna(fred_euro_data.mean())
fred_gold_data = fred_gold_data.fillna(fred_gold_data.mean()) Pandas tiene comandos similares a SQL para fusionar marcos de datos. Solo fusionamos los datos de las fechas que comparten ambas series de tiempo.
#Merge the data
merged_data = pd.merge(xau_eur,fred_euro_data,left_index=True,right_index=True)
merged_data = pd.merge(merged_data,fred_gold_data,left_index=True,right_index=True)
merged_data 
Figura 1: Nuestro conjunto de datos fusionados.
Etiquetar los datos es un paso importante en cualquier proyecto de aprendizaje automático supervisado. En primer lugar, definimos nuestro horizonte de pronóstico, que en este caso son 20 días en el futuro. Luego, definimos el objetivo como el precio de cierre futuro del símbolo XAUEUR. También creamos objetivos binarios para resumir si los niveles de precios se apreciaron o depreciaron. Los objetivos binarios se utilizarán exclusivamente para fines de visualización.
#Let us label the data look_ahead = 20 #Define the labels merged_data["Target"] = merged_data["Close"].shift(-look_ahead) merged_data["Binary Target"] = np.nan merged_data.loc[merged_data["Target"] > merged_data["Close"],"Binary Target"] = 1 merged_data.loc[merged_data["Target"] <= merged_data["Close"],"Binary Target"] = 0 merged_data.dropna(inplace=True) merged_data
Figura 2: Nuestro conjunto de datos con el objetivo incluido.
Finalmente, definimos los 3 conjuntos de predictores que vamos a comparar empíricamente.
#Let us define the predictors and target ohlc_predictors = ["Open","High","Low","Close"] fred_predictors = ["EVZCLS","GVZCLS"] predictors = ohlc_predictors + fred_predictors target = "Target" binary_target = "Binary Target"
Análisis exploratorio de datos
La presencia o ausencia de fuertes niveles de correlación no implica necesariamente la presencia o ausencia de una relación entre los datos analizados. Nuestros datos alternativos parecen tener niveles de correlación intermitentes con el conjunto de datos XAUEUR. Sin embargo, parecía haber fuertes niveles de correlación directamente entre los dos conjuntos de datos alternativos.
#Exploratory Data Analysis #Analyzing correlation levels sns.heatmap(merged_data[predictors].corr(),annot=True)
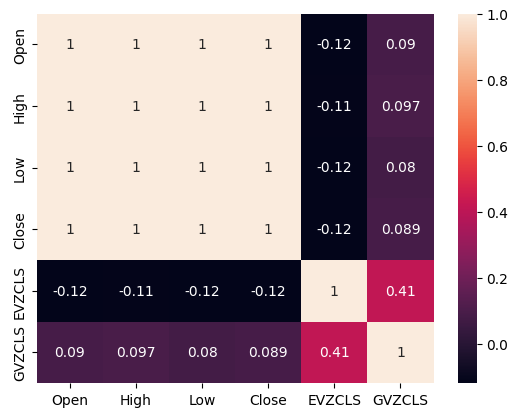
Figura 3: Nuestro mapa de calor de correlación.
Creamos 3 gráficos de dispersión de los datos que tenemos. Los primeros 2 gráficos de dispersión utilizaron el índice de volatilidad del oro y del euro en el eje x, y el precio de cierre del XAUEUR en el eje y en ambos gráficos. En nuestro primer gráfico de dispersión, parece que cuando los niveles de volatilidad del oro superan el nivel 30-35, observamos constantemente una acción alcista del precio.
#Let's create scatter plots sns.scatterplot(data=merged_data,x="GVZCLS",y="Close",hue="Binary Target")
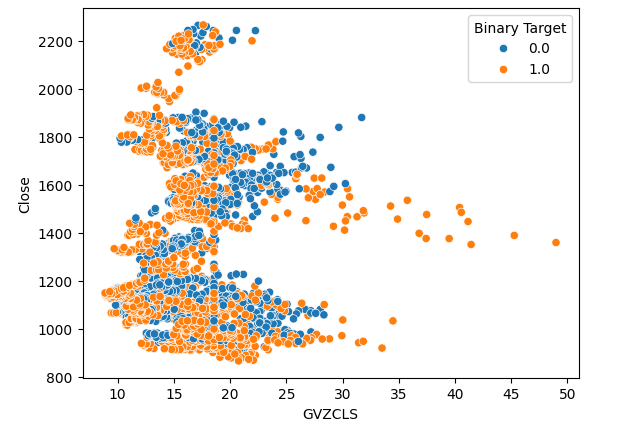
Figura 4: Nuestro primer diagrama de dispersión.
El mismo fenómeno se observa en el segundo diagrama de dispersión. Parece que cuando los niveles de volatilidad del euro superan el nivel 14-16, los niveles de precios se aprecian consistentemente. Sin embargo, nuestro conjunto de datos es limitado y puede que no represente totalmente la verdadera relación entre los dos mercados.
#Let's create scatter plots sns.scatterplot(data=merged_data,x="EVZCLS",y="Close",hue="Binary Target")
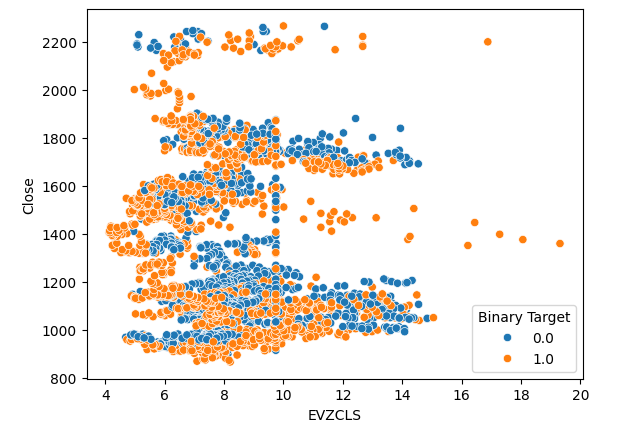
Figura 5: Nuestro segundo diagrama de dispersión.
Por último, creamos un gráfico de dispersión utilizando nuestros 2 conjuntos de datos alternativos en ambos ejes. Nuestros datos crearon una estructura similar a un cono, con el grupo de velas alcistas aún claramente visibles y bien separados.
#Let's create scatter plots sns.scatterplot(data=merged_data,x="GVZCLS",y="EVZCLS",hue="Binary Target")
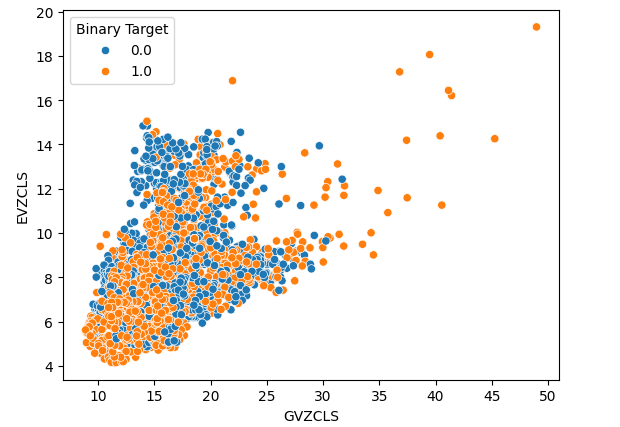
Figura 6: Nuestro diagrama de dispersión final.
Puede haber estructuras ocultas en nuestros datos que no se puedan visualizar en dos dimensiones. Por lo tanto, creamos un gráfico de dispersión 3D para visualizar el efecto de ambos conjuntos de datos alternativos en el XAUEUR. El conjunto de velas alcistas todavía se puede ver claramente en el gráfico 3D. Esto puede indicar que nuestros datos alternativos separan bien los datos en ciertos puntos.
#Define the 3D Plot fig = plt.figure(figsize=(7,7)) ax = plt.axes(projection="3d") ax.scatter(merged_data["GVZCLS"],merged_data["EVZCLS"],merged_data["Close"],c=merged_data["Binary Target"],cmap="plasma") ax.set_xlabel("GVZCLS") ax.set_ylabel("EVZCLS") ax.set_zlabel("Close")
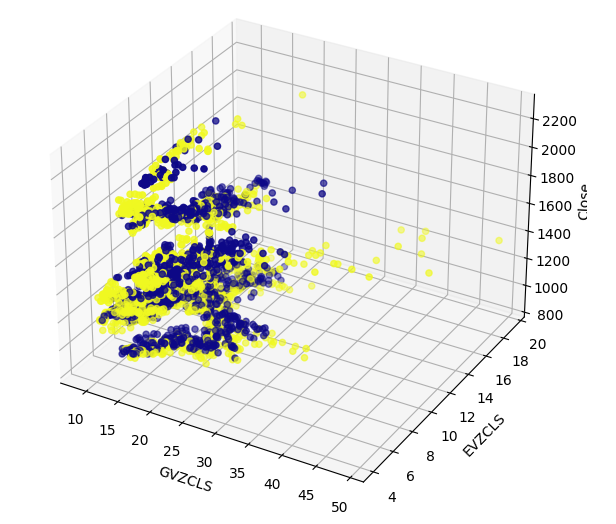
Figura 7: Un diagrama de dispersión 3D de nuestros datos de mercado.
También podemos emplear técnicas de reducción de dimensionalidad para crear una representación bidimensional de nuestros datos de mercado de 6 dimensiones. Utilizaremos el algoritmo t-SNE para realizar esta tarea. El algoritmo fue propuesto por primera vez en un artículo publicado en 2002 por Geoffrey Hinton y otros. El artículo original se puede encontrar en este enlace, aquí. Hinton es considerado un pionero en el campo del aprendizaje automático, en gran parte por su artículo de 1986 que demuestra cómo se puede utilizar el algoritmo de retropropagación para entrenar una red neuronal para predecir la siguiente palabra en una representación vectorial de una oración. Sus contribuciones ayudaron a popularizar la adopción generalizada del algoritmo de retropropagación.

Figura 8: Dr. Geoffrey Hinton.
El algoritmo t-SNE está diseñado para crear una representación compacta de datos de alta dimensión en la que la proximidad entre todos los puntos de datos en el espacio de alta dimensión se conserva en la nueva representación de menor dimensión. Para lograr este objetivo, el algoritmo minimiza una función de costo especializada que mide la diferencia entre dos distribuciones. Normalmente, este procedimiento de optimización se logra mediante descenso de gradiente. En primer lugar, el algoritmo crea una matriz de rango inferior de los datos originales de alta dimensión. Luego, mueve iterativamente los puntos de datos para minimizar el costo; recuerde que el costo es la diferencia entre las distribuciones de los datos en la matriz de rango inferior y la distribución original de los datos. El algoritmo t-SNE es útil para visualizar grupos de datos que están ocultos en un espacio de mayor dimensión.
Importaremos las librerías que necesitemos.
#Let's create a TSNE Plot from sklearn.manifold import TS
Luego instanciaremos el objeto t-SNE y le indicaremos que cree una representación bidimensional de nuestros datos.
#Create a TSNE object which will reduce the data to 2 dimensions tsne = TSNE(n_components=2,perplexity=30)
Ajustar el objeto t-SNE a los datos que tenemos.
#Apply TSNE to the data
tsne_data = tsne.fit_transform(merged_data[predictors]) Trazando la nueva representación de los datos.
#Create a scatter plot plt.scatter(tsne_data[:,0],tsne_data[:,1])
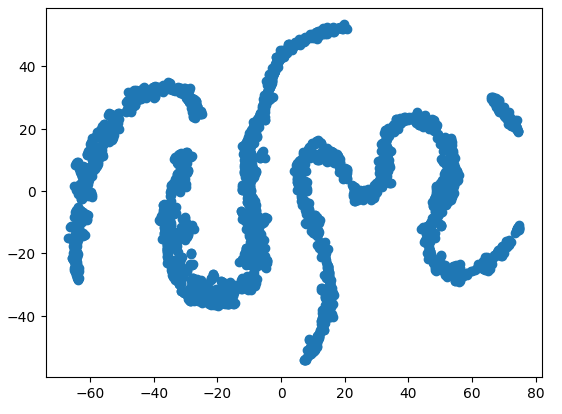
Figura 9: Nuestro gráfico t-SNE de los datos del mercado.
Debido a la naturaleza estocástica del procedimiento de optimización iterativa, puede resultar difícil reproducir la gráfica que hemos obtenido en esta discusión. Además, si realizáramos el procedimiento una segunda vez, no nos alarmaríamos si obtuviéramos un diagrama de dispersión diferente. Lo que nos interesa especialmente es el número de clústeres que el algoritmo intenta preservar. Parece que nuestro conjunto de datos tiene cuatro grupos distintos, además, la naturaleza curva de los gráficos puede sugerir una dependencia compartida a través del tiempo dentro de los grupos.
Los gráficos de autocorrelación (ACF) se utilizan ampliamente en el análisis de series temporales para comprobar si los datos son estacionarios, si presentan fluctuaciones estacionales, etc. Los gráficos ACF muestran el nivel de correlación entre el valor actual de una serie temporal y sus valores anteriores. Realizamos 3 gráficos ACF en el cierre de XAUEUR y los 2 conjuntos de datos alternativos de CBOE. Los tres gráficos sugirieron que los datos tienen componentes persistentes; esto también nos lo sugirió el mapa de calor que visualizamos anteriormente. Cuando los gráficos ACF tienen colas largas que decaen lentamente hasta 0, naturalmente consideraremos si podría haber una tendencia fuerte o componentes estacionales en los datos.
#Let's look at an autocorrelation plot of the data close_acf = plot_acf(merged_data["Close"])
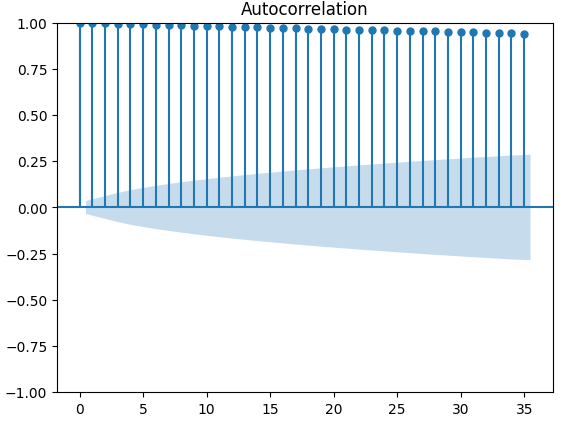
Figura 10: Gráfico ACF del precio de cierre del XAUEUR.
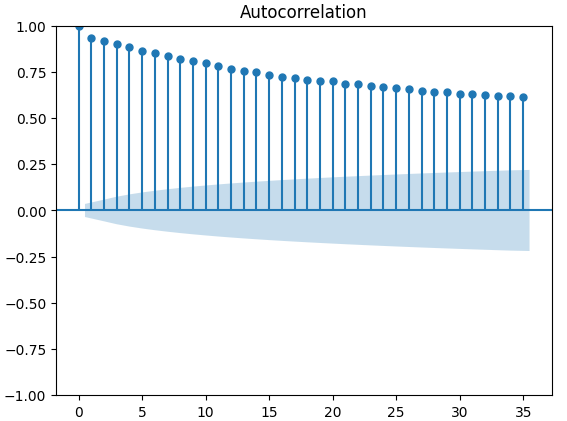
Figura 11: Gráfico ACF del índice de volatilidad del euro CBOE.
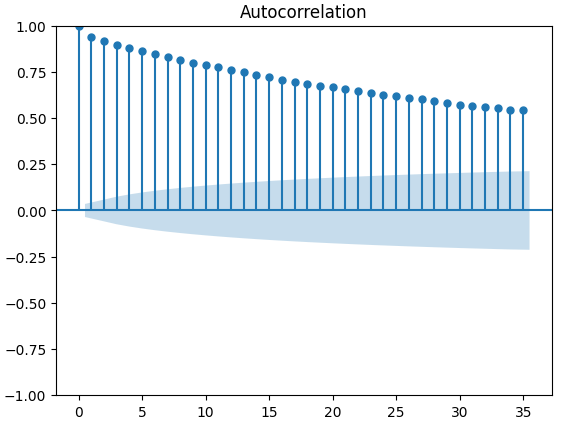
Figura 12: Gráfico ACF del índice de volatilidad del oro CBOE.
Los gráficos de autocorrelación parcial (PACF) nos informan de cuánto tiempo atrás debemos mirar para explicar la mayor parte de la correlación observada entre la serie temporal y sus retardos. En otras palabras, ¿qué parte de la correlación observada en el retraso 3 no se estaba arrastrando desde el retraso 2? Los tres gráficos PACF nos sugieren que la mayor parte de la autocorrelación de los datos de la serie temporal se debe a un máximo de 4 retardos.
#Let's look at an partial autocorrelation plot of the close data close_pacf = plot_pacf(merged_data["Close"])
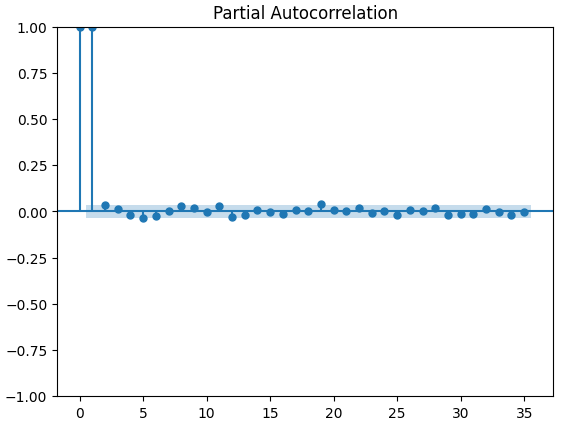
Figura 13: Gráficos PACF del cierre XAUEUR.
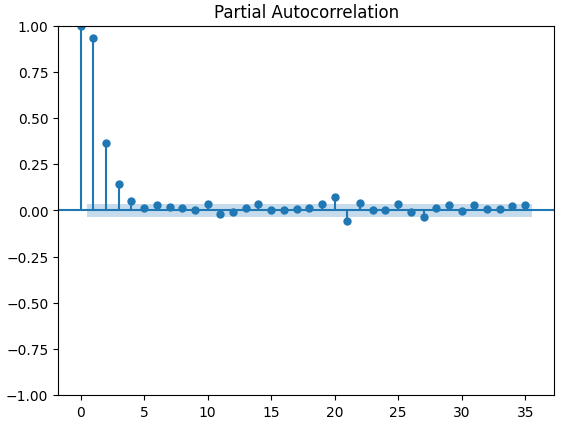
Figura 14: Gráficos PACF del índice de volatilidad del euro CBOE.
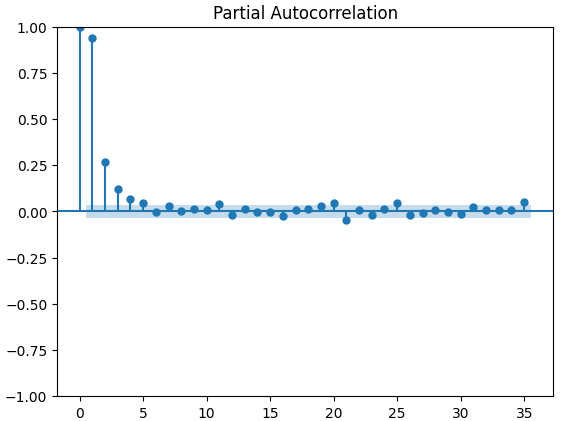
Figura 15: Gráficos PACF del índice de volatilidad del oro CBOE.
Preparación para modelar los datos
Antes de que podamos comenzar a modelar nuestros datos con nuestra red neuronal profunda, primero debemos hacer algunos preparativos.
#Preparing to model the data from sklearn.preprocessing import RobustScaler from sklearn.model_selection import TimeSeriesSplit,train_test_split from sklearn.metrics import mean_squared_error from sklearn.neural_network import MLPRegressor
El primer paso es estandarizar y escalar los datos de entrada, para que nuestro modelo aprenda de manera efectiva.
#Reset the index of our data merged_data.reset_index(inplace=True) X = merged_data.loc[:,predictors] y = merged_data.loc[:,target] #Scale our data scaler = RobustScaler() X = pd.DataFrame(scaler.fit_transform(merged_data[predictors]),columns=predictors)
Ahora necesitamos crear divisiones de entrenamiento y prueba para los tres conjuntos de predictores que tenemos. Tenga cuidado de no mezclar aleatoriamente sus datos en este paso. De lo contrario, comprometeríamos la integridad de nuestro análisis.
#Perform train test splits ohlc_train_X,ohlc_test_X,train_y,test_y = train_test_split(X.loc[:,ohlc_predictors],y,shuffle=False,train_size=0.5) fred_train_X,fred_test_X,_,_ = train_test_split(X.loc[:,fred_predictors],y,shuffle=False,train_size=0.5) train_X,test_X,_,_ = train_test_split(X.loc[:,predictors],y,shuffle=False,train_size=0.5)
Por último, necesitamos crear nuestro objeto de serie temporal y posteriormente crear un marco de datos para almacenar nuestros niveles de error de validación.
#Let's now cross-validate each of the predictors #Create the time-series split object tscv = TimeSeriesSplit(n_splits=5,gap=look_ahead) validation_error = pd.DataFrame(columns=["OHLC Predictors","FRED Predictors","All Predictors"],index=np.arange(0,5))
Modelado de datos
Ahora estamos listos para comenzar a modelar nuestros datos y validar nuestros modelos.
#Performing cross validation model = MLPRegressor(hidden_layer_sizes=(20,5)) for i,(train,test) in enumerate(tscv.split(train_X)): model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) validation_error.iloc[i,2] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:]))
Nuestros niveles de error de validación.
#Our validation error
validation_error | Datos OHLC de MetaTrader 5 | Datos alternativos de FRED-CBOE | Todos los datos |
|---|---|---|
| 875423.637167 | 881892.498319 | 857846.11554 |
| 794999.120981 | 831138.370726 | 946193.178747 |
| 1058884.292095 | 474744.732539 | 631259.842972 |
| 419566.842693 | 882615.372658 | 483408.373559 |
| 96693.318078 | 618647.934237 | 237935.04009 |
Puede que no nos resulte inmediatamente obvio qué modelo tiene el mejor rendimiento, pero cuando analizamos las medias de las columnas podemos ver claramente que el último modelo tiene un rendimiento excepcional. En la gráfica siguiente, restamos el valor medio de la primera columna de las columnas restantes. Al hacerlo, el valor de la primera columna será 0 y todos los modelos insatisfactorios tendrán valores de columna mayores que 0. Por lo tanto, podemos ver claramente que nuestro último modelo está funcionando bastante bien.
#Our mean error levels val_err = validation_error.mean() val_err = val_err.iloc[:] - val_err.iloc[0] val_err.plot(kind="bar")
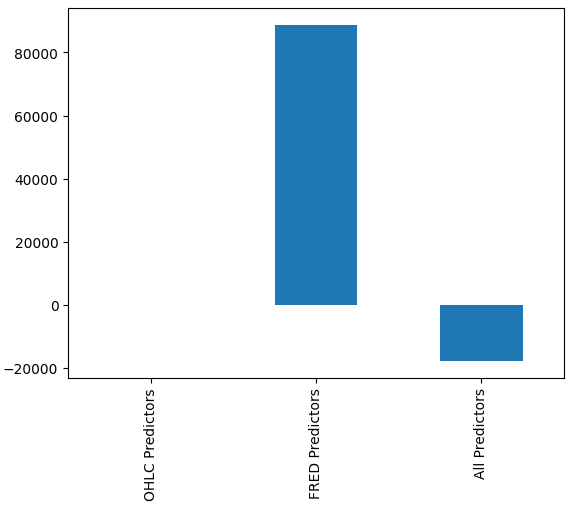
Figura 16: Rendimiento de nuestro modelo utilizando 3 conjuntos de datos diferentes.
La realización de diagramas de caja del rendimiento del modelo muestra además que el último conjunto de predictores parece ser la opción óptima para nosotros, la tasa de error media es la más baja y la varianza no es tan grande como cuando solo se utilizan datos OHCL.
#Let's perform boxplots of our validation error sns.boxplot(validation_error)
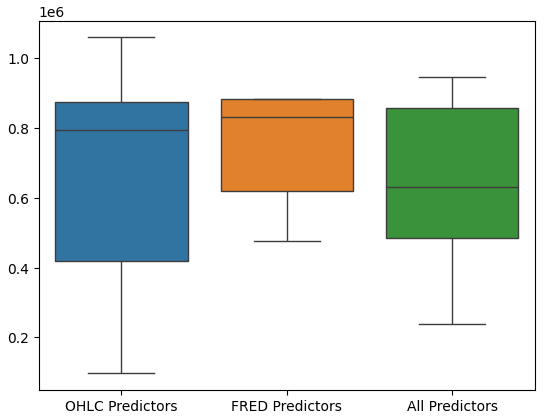
Figura 17: El rendimiento de nuestro modelo visualizado como diagramas de caja.
Importancia de las características
Nunca debemos confiar ciegamente en ningún modelo e implementarlo en producción simplemente porque produjo métricas de error bajas. Inspeccionemos las relaciones que ha aprendido el modelo. Nos gustaría comprender la importancia de las características globales para nuestro modelo. Comenzaremos creando gráficos de efectos locales acumulados (Accumulated Local Effect, ALE). ALE está diseñado para proporcionar explicaciones sólidas para los modelos de aprendizaje automático que se entrenan con datos con altos niveles de correlación. ALE intenta aislar el efecto que cada entrada tiene en la salida del modelo.
#Feature importance
from alibi.explainers import ALE , plot_ale Ahora instanciaremos nuestro objeto ALE y buscaremos explicaciones sobre la importancia de las características globales para nuestra red neuronal profunda. Esto nos ayudará a comprender el efecto que cada una de nuestras entradas parece tener en la predicción del modelo.
#Explaining our deep neural network model = MLPRegressor(hidden_layer_sizes=(20,5)) model.fit(train_X,train_y) dnn_ale = ALE(model.predict,feature_names=predictors,target_names=["XAUEUR Close"])
Ahora calculemos y grafiquemos nuestros valores ALE para cada una de las entradas del modelo.
#Obtaining the explanation
ale_X = X.to_numpy()
dnn_explanations = dnn_ale.explain(ale_X)
#Plotting feature importance
plot_ale(dnn_explanations,n_cols=3,fig_kw={'figwidth':8,'figheight':8},sharey=None) 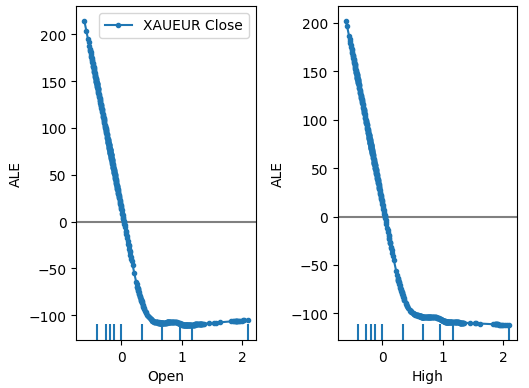
Figura 18: Nuestros gráficos ALE para algunos de los predictores abiertos y altos de XAUEUR.
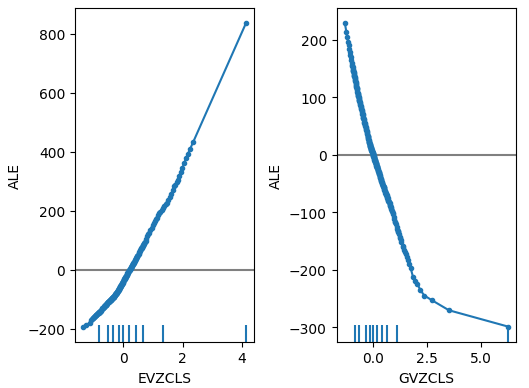
Figura 19: Nuestros gráficos ALE para los índices de volatilidad FRED-CBOE.
La interpretación de los gráficos ALE es bastante intuitiva; el gráfico ilustra cómo cambia la predicción del modelo a medida que cambia el valor de cada predictor. Como podemos ver, a medida que el precio de apertura y el precio máximo aumentan, la predicción del modelo cae inicialmente. Sin embargo, se vuelve menos sensible a medida que los niveles de precios continúan aumentando. Aunque no los incluimos aquí, los gráficos ALE del precio mínimo y de cierre parecen idénticos a los 2 gráficos que mostramos.
Cuando ahora dirigimos nuestra atención a los gráficos ALE de los datos alternativos, observamos que el índice de volatilidad del euro creó un gráfico ALE que cubre parte del gráfico que las otras variables no lograron cubrir. En otras palabras, el predictor parece estar explicando la variación en el objetivo que no podíamos explicar sin él. Además, la pendiente ascendente del gráfico ALE sugiere que a medida que aumenta el valor del predictor, también lo hace el pronóstico del modelo.
A continuación recuperaremos las expectativas de SHAP sobre el rendimiento de nuestro modelo. Los valores SHAP nos ayudan a cuantificar cómo cada una de las entradas del modelo contribuyó a una predicción específica en comparación con la predicción promedio del modelo. Los valores SHAP tienen sus raíces en el campo matemático de la teoría de juegos. El algoritmo consideró cada conjunto posible de predictores y luego calcula el efecto promedio de las entradas en todos los conjuntos posibles.
Primero, importaremos la biblioteca SHAP.
#SHAP Values
import shap Calcular los valores SHAP.
#Calculating SHAP values explainer = shap.Explainer(model.predict,train_X) shap_values = explainer(test_X)#Calculating SHAP values
Grafique los valores SHAP.
#Plot the beeswarm plot
shap.plots.beeswarm(shap_values) 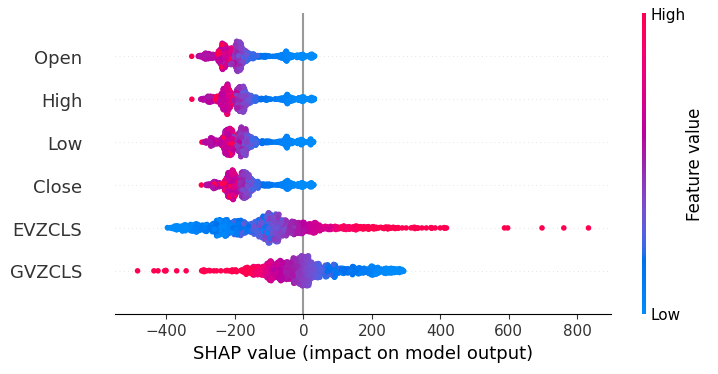
Figura 20: Nuestras expectativas de SHAP.
Según nuestras expectativas SHAP, los datos de mercado obtenidos del propio mercado XAUEUR son los datos más importantes que tenemos. Además, el gráfico SHAP también nos sugiere que, a medida que el precio actual del mercado aumenta, el objetivo tiende a caer.
Ajuste de parámetros
Intentemos obtener más rendimiento de nuestro modelo, comenzaremos importando las bibliotecas que necesitamos.
#Parameter tuning
from sklearn.model_selection import RandomizedSearchCV Inicializar el modelo.
#Reinitialize the model model = MLPRegressor(hidden_layer_sizes=(20,5))
Define el objeto afinador.
#Define the tuner
tuner = RandomizedSearchCV(
model,
{
"activation" : ["relu","logistic","tanh","identity"],
"solver":["adam","sgd","lbfgs"],
"alpha":[0.1,0.01,0.001,0.0001,0.00001,0.00001,0.0000001],
"tol":[0.1,0.01,0.001,0.0001,0.00001,0.000001,0.0000001],
"learning_rate":['constant','adaptive','invscaling'],
"shuffle": [True,False]
},
n_iter=500,
cv=5,
n_jobs=-1,
scoring="neg_mean_squared_error"
) Coloca el afinador.
#Fit the tuner
tuner_results = tuner.fit(train_X,train_y) Los mejores parámetros que hemos encontrado.
#The best parameters we found
tuner_results.best_params_ 'solver': 'lbfgs',
'shuffle': True,
'learning_rate': 'adaptive',
'alpha': 0.1,
'activation': 'identity'}
Scipy tiene procedimientos de optimización incluidos en su módulo de minimización. Estos procedimientos requieren un punto de partida para el proceso de optimización. Utilizaremos los mejores valores de parámetros encontrados mediante una búsqueda aleatoria como punto de partida en nuestra segunda fase de optimización.
#Deeper optimization
from scipy.optimize import minimize Ahora, crearemos un objeto de marco de datos para almacenar nuestros niveles de error en la validación.
#Create a dataframe to store our accuracy current_error_rate = pd.DataFrame(index = np.arange(0,5),columns=["Current Error"])
Todo algoritmo de optimización necesita una función objetivo sobre la cual trabajar. En nuestro caso, la función objetivo es el error cruzado promedio validado del modelo en el conjunto de entrenamiento. Nuestro procedimiento de optimización buscará parámetros del modelo que minimicen nuestro error promedio.
#Define the objective function def objective(x): #The parameter x represents a new value for our neural network's settings #In order to find optimal settings, we will perform 10 fold cross validation using the new setting #And return the average RMSE from all 10 tests #We will first turn the model's Alpha parameter, which controls the amount of L2 regularization model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=x[0],tol=x[1]) #Now we will cross validate the model for i,(train,test) in enumerate(tscv.split(train_X)): #Train the model model.fit(train_X.loc[train[0]:train[-1],:],train_y.loc[train[0]:train[-1]]) #Measure the RMSE current_error_rate.iloc[i,0] = mean_squared_error(train_y.loc[test[0]:test[-1]],model.predict(train_X.loc[test[0]:test[-1],:])) #Return the Mean CV RMSE return(current_error_rate.iloc[:,0].mean())
Definamos el punto de partida para el procedimiento de optimización y también deberíamos definir límites para los valores de entrada permitidos.
#Define the starting point pt = [0.1,0.00000001] bnds = ((0.0000000000000000001,10000000000),(0.0000000000000000001,10000000000))
Optimizando el modelo.
#Searchin deeper for parameters result = minimize(objective,pt,method="L-BFGS-B",bounds=bnds)
Prueba de sobreajuste
El sobreajuste es un problema en cualquier proyecto de aprendizaje automático. Se produce cuando nuestro modelo no logra crear generalizaciones significativas de los datos y, en cambio, comienza a aprender ruido y otras asociaciones sin sentido en los datos. Para probar el sobreajuste, compararemos la precisión de nuestros 2 modelos personalizados con el modelo predeterminado.
#Testing for overfitting default_model = MLPRegressor(hidden_layer_sizes=(20,5)) customized_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=0.1,tol=0.0000001) customized_lbfgs_model = MLPRegressor(hidden_layer_sizes=(20,5),activation='identity',learning_rate='adaptive',solver='lbfgs',shuffle=True,alpha=result.x[0],tol=result.x[1])
Preparémonos ahora para validar de forma cruzada cada modelo.
#Preparing to cross validate the models models = [ default_model, customized_model, customized_lbfgs_model ] #We will store our validation error here validation_error = pd.DataFrame(columns=["Default Model","Customized Model","L-BFGS Model"],index=np.arange(0,5)) #We will now reset the indexes test_y = test_y.reset_index() test_X = test_X.reset_index()
Deberíamos ajustar cada uno de los modelos al conjunto de entrenamiento.
#Fit each of the models for m in models: m.fit(train_X,train_y)
Ahora, vamos a validar de forma cruzada el rendimiento de nuestro modelo con datos no vistos, el conjunto de pruebas que hemos mantenido hasta ahora.
#Cross validating each model for j in np.arange(0,len(models)): model = models[j] for i,(train,test) in enumerate(tscv.split(test_X)): model.fit(test_X.loc[train[0]:train[-1],:],test_y.loc[train[0]:train[-1],"Target"]) validation_error.iloc[i,j] = mean_squared_error(test_y.loc[test[0]:test[-1],"Target"],model.predict(test_X.loc[test[0]:test[-1],:]))
Nuestros niveles de error de validación.
#Our validation error
validation_error | Modelo predeterminado | Modelo de búsqueda aleatoria | Modelo L-BFGS-B |
|---|---|---|
| 22360.060721 | 5917.062055 | 3734.212826 |
| 17385.289026 | 36726.684574 | 35886.972729 |
| 13782.649037 | 5128.022626 | 20886.845316 |
| 3082484.290698 | 6950.786438 | 5789.948045 |
| 4076009.132941 | 27729.589769 | 22931.572161 |
El modelo con mejor rendimiento es el modelo de búsqueda aleatoria.
#Plotting the difference in our performance levels mean = validation_error.mean() mean = mean.iloc[:] - mean.iloc[0] mean.plot(kind="bar")
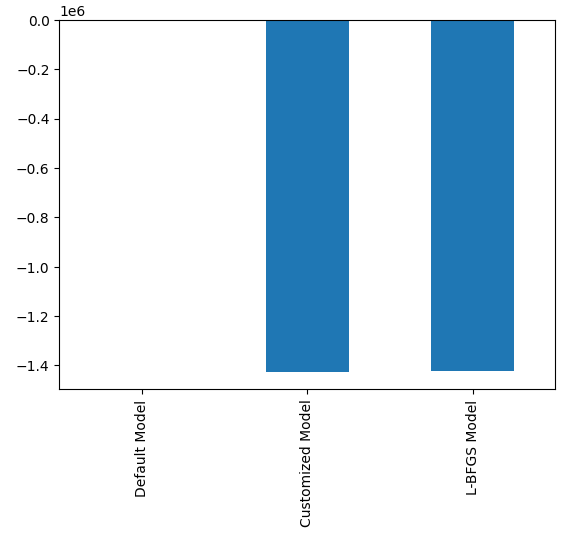
Figura 21: Nuestros niveles de error de validación.
Visualizar el rendimiento de nuestro modelo deja claro cuán mal el modelo predeterminado maneja los datos.
#Visualizing the results
validation_error.plot() 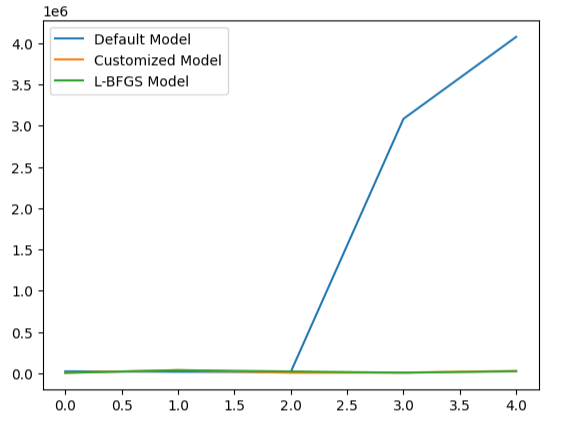
Figura 22: Prueba de sobreajuste.
Este punto se refuerza aún más con nuestros diagramas de caja. Podemos decir que hemos superado el modelo predeterminado por un margen considerable.
#Visualizing our results
sns.boxplot(validation_error) 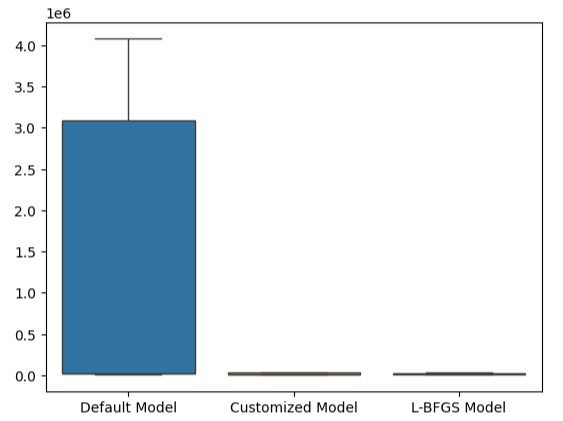
Figura 23: Estamos superando el modelo predeterminado por un amplio margen.
Preparación para exportar al formato ONNX
Antes de poder exportar nuestro modelo al formato ONNX, primero debemos estandarizar y escalar nuestros datos de una manera que podamos reproducir en nuestro terminal MetaTrader 5. Para lograr esto, restaremos la media de la columna de cada columna, antes de dividir finalmente cada columna por su desviación estándar. Escribiremos nuestros factores de escala en formato CSV para que podamos recuperarlos en nuestro terminal MetaTrader 5 para escalar las entradas de nuestro modelo.
#Let us now prepare to export our model to onnx format scale_factors = pd.DataFrame(columns=predictors,index=["mean","standard deviation"]) for i in np.arange(0,len(predictors)): scale_factors.iloc[0,i] = merged_data.loc[:,predictors[i]].mean() scale_factors.iloc[1,i] = merged_data.loc[:,predictors[i]].std() merged_data.loc[:,predictors[i]] = (merged_data.loc[:,predictors[i]] - merged_data.loc[:,predictors[i]].mean())/merged_data.loc[:,predictors[i]].std() scale_factors
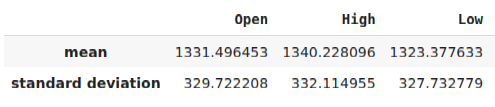
Figura 24: Algunos de nuestros factores de escala.
Ahora escribiremos los datos en formato CSV.
#Save the scale factors to CSV scale_factors.to_csv("scale_factors.csv")
Exportación al formato ONNX
Open Neural Network Exchange (ONNX) es un protocolo para crear y compartir modelos de aprendizaje automático en diferentes lenguajes de programación. El protocolo ONNX nos permite integrar sin problemas nuestra red neuronal profunda en nuestro Asesor Experto utilizando la API MQL5 ONNX.
Primero carguemos las bibliotecas que necesitamos.
#Exporting to ONNX format
import onnx
from skl2onnx import convert_sklearn
from skl2onnx.common.data_types import FloatTensorType Entrena el modelo con todos los datos que tenemos.
#Fit the model on all the data we have
customized_model.fit(merged_data.loc[:,predictors],merged_data.loc[:,target]) Al exportar modelos ONNX, es posible que se pierda la forma de entrada. Por lo tanto, especifiquemos explícitamente la forma de entrada.
# Define the input type initial_types = [("float_input",FloatTensorType([1,6]))]
Cree la representación ONNX del modelo.
# Create the ONNX representation onnx_model = convert_sklearn(customized_model,initial_types=initial_types,target_opset=12)
Guarde la representación ONNX en un archivo con la extensión ".onnx".
# Save the ONNX model onnx_name = "XAUEUR FRED D1.onnx" onnx.save_model(onnx_model,onnx_name)
Obtención de datos FRED actualizados
Antes de que podamos comenzar a construir nuestro Asesor Experto, necesitamos crear un script de Python que compartirá constantemente datos FRED actualizados con nuestra terminal. Crearemos un script que recuperará los últimos datos disponibles una vez al día y los escribirá en formato CSV en la carpeta "Archivos" para que podamos acceder a los datos con nuestra aplicación comercial.
#A function to write out our alternative data to CSV def write_out_alternative_data(): euro = fred.get_series("EVZCLS") euro = euro.iloc[-1] gold = fred.get_series("GVZCLS") gold = gold.iloc[-1] data = pd.DataFrame(np.array([euro,gold]),columns=["Data"],index=["Fred Euro","Fred Gold"]) data.to_csv("C:\\ENTER\\YOUR\\PATH\\HERE\\MetaQuotes\\Terminal\\D0E8209F77C8CF37AD8BF550E51FF075\\MQL5\\Files\\fred_xau_eur.csv")
Ahora escribiremos un bucle infinito para escribir los datos y luego dormiremos un día.
while True: #Update the fred data for our MT5 EA write_out_alternative_data() #If we have finished all checks then we can wait for one day before checking for new data time.sleep(24 * 60 * 60)
Construyendo nuestro Asesor Experto
Ahora estamos preparados para comenzar a construir nuestro Asesor Experto. Comenzaremos solicitando primero el archivo ONNX que acabamos de crear.
//+------------------------------------------------------------------+ //| EURXAU Fred AI.mq5 | //| Gamuchirai Zororo Ndawana | //| https://www.mql5.com/en/gamuchiraindawa | //+------------------------------------------------------------------+ #property copyright "Volatility Doctor" #property link "https://www.mql5.com/en/gamuchiraindawa" #property version "1.00" //+------------------------------------------------------------------+ //| Require the ONNX file | //+------------------------------------------------------------------+ #resource "\\Files\\XAUEUR FRED D1.onnx" as const uchar onnx_buffer[];
Cargue la biblioteca comercial para ayudarnos a administrar nuestras posiciones.
//+------------------------------------------------------------------+ //| Libraries | //+------------------------------------------------------------------+ #include <Trade/Trade.mqh> CTrade Trade;
Estas variables globales se compartirán en muchas partes diferentes de nuestra aplicación.
//+------------------------------------------------------------------+ //| Global variables | //+------------------------------------------------------------------+ long onnx_model; vector mean_values = vector::Zeros(6); vector std_values = vector::Zeros(6); vectorf model_inputs = vectorf::Zeros(6); vectorf model_output = vectorf::Zeros(1); double bid,ask; int system_state,model_sate;
Ahora, necesitamos una función que creará nuestro modelo ONNX, a partir del buffer ONNX que creamos al comienzo de nuestra aplicación. Nuestra función primero creará y validará el modelo ONNX y, por último, establecerá y validará las formas de entrada y salida del modelo. Si fallamos en cualquier punto, la función devolverá falso, lo que a su vez detendrá el procedimiento de inicialización.
//+------------------------------------------------------------------+ //| Load the ONNX file | //+------------------------------------------------------------------+ bool load_onnx_file(void) { //--- Create the ONNX model from the buffer we loaded earlier onnx_model = OnnxCreateFromBuffer(onnx_buffer,ONNX_DEFAULT); //--- Validate the model we just created if(onnx_model == INVALID_HANDLE) { //--- Give the user feedback on the error Comment("Failed to create the ONNX model: ",GetLastError()); //--- Break initialization return(false); } //--- Define the I/O shape ulong input_shape [] = {1,6}; //--- Validate the input shape if(!OnnxSetInputShape(onnx_model,0,input_shape)) { //--- Give the user feedback Comment("Failed to define the ONNX input shape: ",GetLastError()); //--- Break initialization return(false); } ulong output_shape [] = {1,1}; //--- Validate the output shape if(!OnnxSetOutputShape(onnx_model,0,output_shape)) { //--- Give the user feedback Comment("Failed to define the ONNX output shape: ",GetLastError()); //--- Break initialization return(false); } //--- We've finished return(true); } //+------------------------------------------------------------------+
A partir de ahí, definiremos ahora los factores de escala que necesitaremos para normalizar las entradas de nuestro modelo.
//+------------------------------------------------------------------+ //| Load our scaling factors | //+------------------------------------------------------------------+ bool load_scaling_factors(void) { //--- Load the scaling values mean_values[0] = 1331.4964525595044; mean_values[1] = 1340.2280958591457; mean_values[2] = 1323.3776328659928; mean_values[3] = 1331.706768829475; mean_values[4] = 8.258127607767035; mean_values[5] = 16.35582438284101; std_values[0] = 329.7222075527991; std_values[1] = 332.11495530642173; std_values[2] = 327.732778866831; std_values[3] = 330.1146052811378; std_values[4] = 2.199782202942867; std_values[5] = 4.241112965400358; //--- Validate the values loaded correctly if((mean_values.Sum() > 0) && (std_values.Sum() > 0)) { return(true); } //--- We failed to load the scaling values return(false); }
Cada vez que nuestra aplicación ya no esté en uso, liberaremos los recursos que ya no utilizamos.
//+------------------------------------------------------------------+ //| Free up the resources we no longer need | //+------------------------------------------------------------------+ void release_resources(void) { //--- Free up all the resources we have used so far OnnxRelease(onnx_model); ExpertRemove(); Print("Thank you for choosing Volatility Doctor"); }
Esta función será responsable de actualizar nuestra información de precios de mercado.
//+------------------------------------------------------------------+ //| Fetch market data | //+------------------------------------------------------------------+ void fetch_market_data(void) { //--- Update the market data bid = SymbolInfoDouble(Symbol(),SYMBOL_BID); ask = SymbolInfoDouble(Symbol(),SYMBOL_ASK); }
La siguiente función es responsable de obtener una predicción de nuestro modelo. Primero, obtendremos los datos OHLC actuales del símbolo XAUEUR usando la función de matriz MQL5 CopyRates(). Después de obtener los datos, los normalizaremos y los almacenaremos en el vector de entrada que definimos anteriormente. Desde aquí, llamaremos a otra función para leer los últimos datos FRED que tenemos archivados.
//+------------------------------------------------------------------+ //| This function will fetch a prediction from our model | //+------------------------------------------------------------------+ void model_predict(void) { //--- Get the input data ready for(int i =0; i < 6; i++) { //--- The first 4 inputs will be fetched from the market matrix xau_eur_ohlc = matrix::Zeros(1,4); xau_eur_ohlc.CopyRates(Symbol(),PERIOD_D1,COPY_RATES_OHLC,0,1); //--- Fill in the data if(i<4) { model_inputs[i] = (float)((xau_eur_ohlc[i,0] - mean_values[i])/ std_values[i]); } //--- We have to read in the fred alternative data else { read_fred_data(); } } }
La función, definida a continuación, leerá el archivo CSV con los últimos datos de FRED y normalizará los datos antes de almacenarlos en el vector de entrada y obtener una predicción de nuestro modelo. Representaremos la predicción del modelo utilizando un número entero. Esto nos ayudará a detectar rápidamente posibles reversiones y cerrar nuestras posiciones, con suerte en el lado correcto del mercado.
//+-------------------------------------------------------------------+ //| Read in the FRED data | //+-------------------------------------------------------------------+ void read_fred_data(void) { //--- Read in the file string file_name = "fred_xau_eur.csv"; //--- Try open the file int result = FileOpen(file_name,FILE_READ|FILE_CSV|FILE_ANSI,","); //Strings of ANSI type (one byte symbols). //--- Check the result if(result != INVALID_HANDLE) { Print("Opened the file"); //--- Store the values of the file int counter = 0; string value = ""; while(!FileIsEnding(result) && !IsStopped()) //read the entire csv file to the end { if(counter > 10) //if you aim to read 10 values set a break point after 10 elements have been read break; //stop the reading progress value = FileReadString(result); Print("Counter: "); Print(counter); Print("Trying to read string: ",value); if(counter == 3) { Print("Fred Euro data: ",value); model_inputs[4] = (float)((((float) value) - mean_values[4])/std_values[4]); } if(counter == 5) { Print("Fred Gold data: ",value); model_inputs[5] = (float)((((float) value) - mean_values[5])/std_values[5]); } if(FileIsLineEnding(result)) { Print("row++"); } counter++; } //--- Show the input and Fred data Print("Input Data: "); Print(model_inputs); //---Close the file FileClose(result); //--- Store the model prediction OnnxRun(onnx_model,ONNX_DEFAULT,model_inputs,model_output); Comment("Model Forecast",model_output[0]); if(model_output[0] > iClose(Symbol(),PERIOD_D1,0)) { model_sate = 1; } else { model_sate = -1; } } //--- We failed to find the file else { //--- Give the user feedback Print("We failed to find the file with the FRED data"); } }
Definamos ahora cómo debe iniciarse nuestra aplicación. Nuestra aplicación debe primero crear el modelo ONNX y luego cargar los factores de escala que necesitamos. Si alguno de estos pasos falla, cancelaremos por completo el procedimiento de inicialización.
//+------------------------------------------------------------------+ //| Expert initialization function | //+------------------------------------------------------------------+ int OnInit() { //--- Load the ONNX model if(!load_onnx_file()) { //--- We failed to load our ONNX model return(INIT_FAILED); } //--- Load the scaling factors if(!load_scaling_factors()) { //--- We failed to read in the scaling factors return(INIT_FAILED); } //--- We mamnaged to load our model return(INIT_SUCCEEDED); }
Cuando nuestra aplicación haya sido eliminada del gráfico, liberemos los recursos que ya no necesitamos.
//+------------------------------------------------------------------+ //| Expert deinitialization function | //+------------------------------------------------------------------+ void OnDeinit(const int reason) { //--- Free up the resources we no longer need release_resources(); }
Finalmente, cada vez que recibamos cotizaciones de mercado actualizadas, primero almacenaremos los precios de mercado actualizados en la memoria. Posteriormente, si no tenemos posiciones abiertas, seguiremos la predicción de nuestro modelo solo si está respaldada por la acción del precio en marcos temporales superiores. Alternativamente, si ya tenemos posiciones abiertas, cerraremos nuestras posiciones si nuestro modelo anticipa reversiones en los niveles de precios.
//+------------------------------------------------------------------+ //| Expert tick function | //+------------------------------------------------------------------+ void OnTick() { //--- Update market data fetch_market_data(); //--- Fetch a prediction from our model model_predict(); //--- If we have no positions follow the model's lead if(PositionsTotal() == 0) { //--- Buy position if(model_sate == 1) { if(iClose(Symbol(),PERIOD_W1,0) > iClose(Symbol(),PERIOD_W1,12)) { Trade.Buy(0.3,Symbol(),ask,0,0,"XAUEUR Fred AI"); system_state = 1; } }; //--- Sell position if(model_sate == -1) { if(iClose(Symbol(),PERIOD_W1,0) < iClose(Symbol(),PERIOD_W1,12)) { Trade.Sell(0.3,Symbol(),bid,0,0,"XAUEUR Fred AI"); system_state = -1; } }; } //--- If we allready have positions open, let's manage them if(model_sate != system_state) { Trade.PositionClose(Symbol()); } } //+------------------------------------------------------------------+
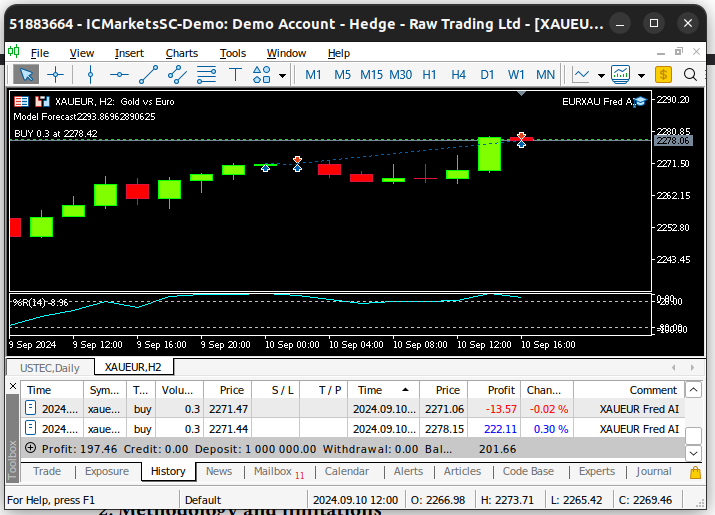
Figura 25: Nuestro Asesor Experto en acción.
Conclusión
En este artículo, hemos demostrado que puede ser ventajoso incluir los índices de volatilidad FRED-CBOE para ayudar a mejorar la precisión de sus modelos de aprendizaje automático. Si bien no podemos garantizar que la información proporcionada en este artículo genere éxito de manera constante, ciertamente vale la pena considerarla si está listo para comenzar a emplear datos alternativos en sus estrategias comerciales.
Traducción del inglés realizada por MetaQuotes Ltd.
Artículo original: https://www.mql5.com/en/articles/15841
Advertencia: todos los derechos de estos materiales pertenecen a MetaQuotes Ltd. Queda totalmente prohibido el copiado total o parcial.
Este artículo ha sido escrito por un usuario del sitio web y refleja su punto de vista personal. MetaQuotes Ltd. no se responsabiliza de la exactitud de la información ofrecida, ni de las posibles consecuencias del uso de las soluciones, estrategias o recomendaciones descritas.
 Del básico al intermedio: Definiciones (II)
Del básico al intermedio: Definiciones (II)
 Del básico al intermedio: Definiciones (I)
Del básico al intermedio: Definiciones (I)
 Desarrollo de un sistema de repetición (Parte 77): Un nuevo Chart Trade (IV)
Desarrollo de un sistema de repetición (Parte 77): Un nuevo Chart Trade (IV)
 Implementación de breakeven en MQL5 (Parte 1): Clase base y breakeven por puntos fijos
Implementación de breakeven en MQL5 (Parte 1): Clase base y breakeven por puntos fijos
- Aplicaciones de trading gratuitas
- 8 000+ señales para copiar
- Noticias económicas para analizar los mercados financieros
Usted acepta la política del sitio web y las condiciones de uso