
使用MQL5中的动态时间规整进行模式识别
概述
模式识别一直作为交易者的宝贵工具。无论是识别独特的K线图组合,还是在图表上绘制假想的线条,这些模式已经成为技术分析的组成部分。人类一直擅长发现和识别模式——以至于我们常常被认为有时会在不存在模式的地方看到模式。因此,当我们试图在金融时间序列中识别潜在的盈利模式时,应用更客观的技术将对我们有所帮助。在本文中,我们讨论了动态时间规整(Dynamic Time Warping,DTW)作为一种用于在价格数据中寻找独特模式的客观技术。我们将探讨它的起源、工作原理,以及它在金融时间序列分析中的应用。此外,我们将展示该算法在纯MQL5中的实现,并通过一个实际例子展示其用途。
动态时间规整
动态时间规整是一种复杂算法,旨在测量随时间演变的两个数据序列之间的相似性,即使它们的速度或节奏不同。与要求数据点严格对齐的传统方法不同,DTW通过允许时间的变形或拉伸,提供了一种更灵活的方法来找到序列之间的最佳匹配。想象两个人在森林中沿着不同的路径行走。他们从同一个地方出发,最终到达同一个地方,但其中一个人可能走得更快,或者出于某种原因随意停下。DTW能够帮助找出两者步伐的最佳匹配方式,即使他们走了不同的路径。DTW可以有效地考虑步行速度、加速度或减速度的差异,从而提供相似性的度量。这种多功能性使其适用于广泛的数据类型,包括音频、视频和图形。任何可以转换为序列格式的数据都是DTW分析的潜在对象。
DTW最初由Vintsyuk在1968年为语音识别开发,并在1978年由Sakoe和Chiba等研究人员进一步完善。由于其能够通过变形时间维度来对齐相似模式,从而能比较不同长度的序列,因此该方法在各个领域逐渐受到关注。DTW已经在生物信息学、步态分析等多样化领域得到应用。金融市场以非线性和非平稳的时间序列数据为特征。传统的距离度量方法(如欧几里得距离)可能无法捕捉此类数据中的复杂性和扭曲。然而,DTW在识别具有时间扭曲的时间序列之间的相似性方面表现出色,使其成为分析金融市场的合适工具。通过基于形状而非时间对齐来对齐序列,DTW可以揭示金融数据中的独特模式。
工作原理
在应用DTW算法时,目标是确定候选序列是否与预定义的参考序列相似。算法最终产生的度量值表示候选序列与参考序列之间的相似性——该值越低,序列越相似。如果序列完全相同,该值将为0。为了找到候选序列与参考数据集之间的最佳对齐方式,DTW算法遵循特定原则。候选序列中的每个点必须至少对应参考序列中的一个数据点,反之亦然。一个序列的起始点必须与另一个序列的起始点对齐,并且一个序列的终点也必须与另一个序列的终点对齐。此外,在遍历序列时,对应的点只能向前移动。这确保了一个序列中的点不能与另一个序列中之前的点对齐,从而防止了对齐到前一个点的可能性。
该过程首先通过构建一个距离矩阵开始,该矩阵捕捉两个序列元素之间的成对距离。该矩阵的每个元素表示第一个序列中的一个点与第二个序列中对应点之间的距离。在这个阶段,可以使用任何传统的空间距离度量方法。空间距离度量是用于量化给定空间内数据点之间的距离或不相似性的数学方法。距离度量的选择取决于数据的具体特征和任务需求。下表列出了最常见的空间距离度量及其简要描述。
| 距离度量 | 说明 |
|---|---|
| 欧几里德距离 | 欧几里得距离是欧几里得空间中两点之间的直线距离。它是最直观且广泛使用的距离度量方法。 |
| 曼哈顿距离 | 曼哈顿距离,也称为出租车距离或街区距离,通过计算两点坐标差的绝对值之和来衡量两点之间的距离。 |
| 闵可夫斯基距离 | 闵可夫斯基距离是欧几里得距离和曼哈顿距离的泛化形式。它包含一个可调节的参数,通过调整该参数可以在不同的距离度量之间切换。 |
| 切比雪夫距离 | 切比雪夫距离,也称为最大距离或棋盘距离,衡量的是一对点坐标之间的最大差异。 |
| 余弦相似度 | 余弦相似度衡量的是两个非零向量之间夹角的余弦值,反映的是它们的方向相似性而非大小。 |
空间距离度量的选择取决于数据的性质和任务的具体需求。理解这些度量之间的差异及其应用场景,有助于选择最适合的度量方法以进行有意义的分析。
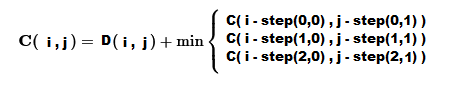
在下一步中,利用距离矩阵计算累积成本矩阵,其中每个元素表示对齐序列的最小代价。这一对齐过程涉及对候选序列进行变换,使其尽可能接近参考序列。累积成本矩阵量化了候选序列中的各个点需要进行多大的调整,才能与参考值形成最佳匹配。较高的成本表示需要进行更显著的变换,意味着序列之间的差异更大。这些累积成本矩阵的值被用来确定最优的变形路径,该路径表示将一个时间序列映射到另一个时间序列的对齐序列,同时使它们之间的距离最小化。本质上而言,变形路径展示了序列的各个部分是如何被拉伸或压缩,以尽可能紧密地与另一个序列对齐。
为了找到变形路径,我们想象将序列放置在一个网格上,一个序列沿x轴,另一个序列沿y轴。网格上的每个点代表第一个序列中的一个元素与第二个序列中的一个元素之间的可能匹配。变形路径是穿过这个网格的路径,它实现了两个序列之间的最佳对齐。路径从网格的左下角开始,对应于两个序列的第一个元素,并在右上角结束,对应于两个序列的最后一个元素。随着路径的推进,它可以沿三个方向移动:对角线方向,即匹配两个序列中的元素;水平方向,即重复第一个序列中的一个元素;或垂直方向,即重复第二个序列中的一个元素。这种移动方式确保了对齐过程始终按时间顺序向前推进,并且不会跳过序列中的任何元素。
变形路径的选择旨在最小化两个序列对齐元素之间的累积距离或成本。为了实现这一点,距离矩阵的值被覆盖在将用于对齐点的网格上。网格上每个点的成本是通过将相应的距离度量值加到之前点的相邻累积距离的最小值上计算得出的,这遵循在时间推进时可以采取的三个可能方向(对角线、水平或垂直)。由于每个网格点都与相应序列值的距离度量相关联,最小值表示将候选序列转换为匹配参考序列所需的运算。如果最小累积距离位于当前点的对角线方向,则表示匹配运算。如果从之前点到当前点的最小累积距离是水平方向的,则表示插入运算,即有效地将参考序列中的一个值插入到候选序列中。相反,如果最小累积距离位于当前点的垂直方向,则表示删除运算,即从候选序列中移除一个值。在寻找最小值时,所考虑的先前累积距离值的选择遵循特定的步长模式。
步进模式决定了在对齐过程中序列点之间允许的移动或转换方式。它们指定了在计算最小累积距离时考虑的任何有效方向(对角线、水平、垂直)中的点的数量。步进模式的选择对于对齐过程和整体距离计算产生显著影响。存在多种步进模式,每种模式都针对特定应用进行了优化。只要遵循前进运动和连续性的原则,从业者也可以创建自定义的步进模式。在本文中,我们将重点关注最常见且通用的步进模式,这些模式已在不同领域中证明是有效的。对于那些有兴趣探索其他步进模式的人,Sakoe-Chiba、Rabiner-Juang和Rabiner-Myers的论文提供了更深入的见解。
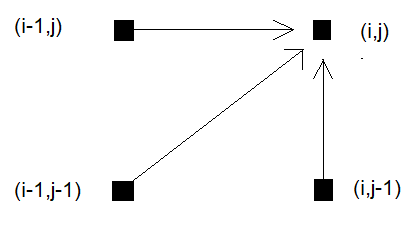
最常用的步进模式是标准步进模式,也称为对称步进模式或经典步进模式。它的主要优点是能够确保两个时间序列都被完整地遍历。这种模式仅考虑当前点上方、右侧和对角线方向的相邻值,允许在网格上进行对角线、水平和垂直的单步移动。
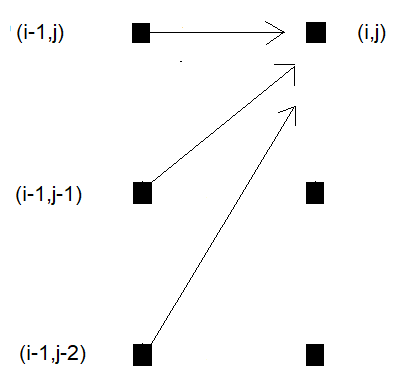
另一种流行的步进模式是经典非对称模式。与标准步进模式类似,它定义了三个方向的转换,但引入了对一个序列的偏好。这种模式允许算法沿对角线移动,但如果跳过一个点,则更倾向于在一个序列中向前推进,而不是另一个序列。它通常与额外的约束一起使用,这些约束限制了算法在网格上的移动。在非对称步进模式的情况下,还应用了一个额外的斜率约束,限制了变形路径的陡峭程度或平坦程度。当序列的长度和偏移量相似时,这种约束非常有用,因为它可以防止一个序列相对于另一个序列被过度拉伸或压缩。
额外的约束可以被应用以防止技术上完美但毫无意义的对齐,这可能导致数据过拟合。这些约束确保对齐在被分析数据的上下文中具有逻辑意义,防止序列被过度拉伸或压缩。这些约束被称为全局约束,它们增强了DTW算法在实际应用中的有效性和可解释性。两种常见的全局约束是Sakoe-Chiba带和Itakura平行四边形。
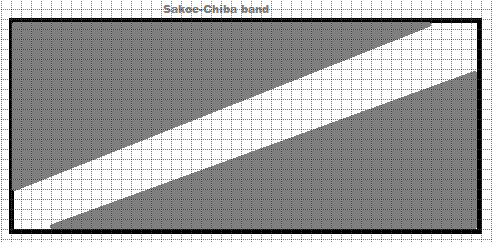
Sakoe-Chiba带将变形路径限制在对齐矩阵对角线周围的固定带内。这样能够防止对齐偏离原始时间或偏移量过远,在预期仅有轻微时间差异但不允许大幅偏离的任务中非常有用。
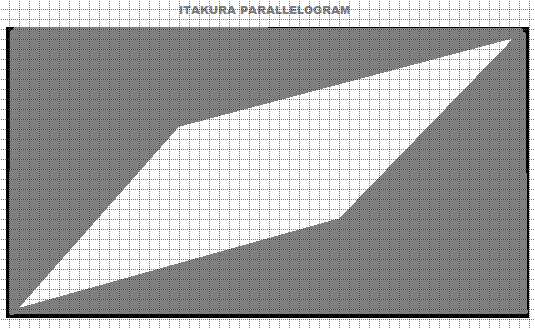
Itakura平行四边形约束定义了一个变形路径必须保持在内的平行四边形区域。它两端较窄,中间较宽,这在预期序列在开始和结束时更紧密对齐,但在中间允许一些灵活性时特别有用。全局约束对于DTW控制变形过程并确保结果对齐与特定任务相关至关重要。根据数据集的特性和分析目标选择最合适的约束非常重要。
完成累积成本矩阵后,将其用于确定最优变形路径。算法从累积成本矩阵的最后一个元素回溯到第一个元素,识别出最小化总对齐成本的路径。这条路径代表了序列之间的最佳对齐。累积成本矩阵中的最终值提供了整体距离分数,该分数还用于计算归一化的距离分数。变形路径将列出代表两个序列中对齐点的配对索引。为了评估对齐过程,通常会绘制最优变形路径。令人满意的结果是生成一个大致呈对角线的图。这个对角线图表明序列对齐得很好,一条完美的直线对应于两个相同的序列。在接下来的部分中,我们将讨论动态时间规整的MQL5原生实现。
MQL5实现
在文件dtw.mqh中,展示了DTW的MQL5实现。它并未涵盖动态时间规整的所有方面,也不提供完整的功能。稍后,我们将探讨一个功能更丰富的Python版本的DTW实现。创建这个库的目标是提供计算距离分数的基本功能。该库是dtw-python模块的部分分支。
代码首先定义了步进模式以及各种距离度量和全局约束的枚举类型。
//+------------------------------------------------------------------+ //| step patterns | //+------------------------------------------------------------------+ enum ENUM_STEP_PATTERN { STEP_SYMM1=0,//symmetric1 STEP_SYMM2,//symmetric2 STEP_ASYMM//asymmetric };
ENUM_STEP_PATTERN:定义了一组限制DTW算法路径搜索阶段允许的转换模式的枚举。这些模式指导变形过程,并影响时间序列之间允许的对齐方式。
//+------------------------------------------------------------------+ //| distance metric | //+------------------------------------------------------------------+ enum ENUM_DIST_METRIC { DIST_EUCLIDEAN=0,//euclidean DIST_CITYBLOCK,//city block DIST_COSINE,//cosine DIST_CORRELATION,//correlation DIST_CHEBYSHEV,//chebyshev DIST_SQEUCLIDEAN//squared euclidean };
ENUM_DIST_METRIC:提供了一组与支持的距离度量相对应的枚举集合。这些度量用于量化时间序列中数据点之间的不相似性,选项包括欧几里得距离、城市街区距离等。
//+------------------------------------------------------------------+ //| window function | //+------------------------------------------------------------------+ enum ENUM_GLOBAL_CONSTRAINT { CONSTRAINT_NONE=0,// no constrains applied CONSTRAINT_SAKOECHIBA,// sakoe chiba CONSTRAINT_SLATEDBAND,// slated band CONSTRAINT_ITAKURA// itakura };
ENUM_GLOBAL_CONSTRAINT:包含不同的全局约束,这些约束在路径搜索过程中施加限制。它们可以影响变形的灵活性,并有可能提高对齐的准确性。
//+------------------------------------------------------------------+ //| lists the transitions allowed while searching | //|for the minimum-distance path | //+------------------------------------------------------------------+ class CStepPattern { private: matrix m_mx,m_stepsMatrix; ENUM_HINT m_stephint; public: CStepPattern(matrix &mx, matrix &stepmatrix, ENUM_HINT hint=HINT_NA) { m_mx = mx; m_stepsMatrix = stepmatrix; m_stephint = hint; } ~CStepPattern(void) { } matrix getStepMatrix(void) { return m_stepsMatrix; } ulong getNRows(void) { return m_mx.Rows(); } int getNPatterns(void) { vector vec = m_mx.Col(0); return (int(vec.Max())); } CStepPattern* T(void) { ulong cols[] = {0, 2, 1, 3}; matrix cpy = np::selectMatrixCols(m_mx,cols); ENUM_HINT hint = m_stephint; if(m_stephint == HINT_N) hint = HINT_M; else if(m_stephint == HINT_M) hint = HINT_N; CStepPattern* out = new CStepPattern(cpy,m_stepsMatrix,hint); return out; } matrix extractPattern(vector &sn) { vector col = m_mx.Col(0); matrix out = matrix::Ones(1,1); for(ulong i = 0; i<m_mx.Rows(); i++) { for(ulong j = 0; j<col.Size(); j++) { if(col[j] == sn[j]) { if(!out.Resize(out.Rows()+1,m_mx.Cols()-1,100)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(1,1); } vector v = m_mx.Row(j); vector vv = np::sliceVector(v,1); if(!out.Row(vv,out.Rows()-1)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(1,1); } } } } if(!np::reverseMatrixRows(out)) { Print(__FUNCTION__, " Reverse Matrix failure "); return matrix::Zeros(1,1); } return out; } matrix mkDIrDeltas(void) { matrix out = matrix::Zeros(1,1); vector col = m_mx.Col(3); for(ulong i = 0; i<m_mx.Rows(); i++) { for(ulong j = 0; j<col.Size(); j++) { if(col[j] == -1.0) { if(!out.Resize(out.Rows()+1,m_mx.Cols(),100)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(1,1); } vector v = m_mx.Row(j); if(!out.Row(v,out.Rows()-1)) { Print(__FUNCTION__, " error ", GetLastError()); return matrix::Zeros(1,1); } } } } return np::sliceMatrixCols(out,1,3); } matrix getP(void) { ulong sel[] = {0, 2, 1, 3}; matrix s = np::selectMatrixCols(m_mx,sel); return s; } matrix getMx(void) { return m_mx; } };
CStepPattern是一个类,旨在通过管理定义允许的转换和操作的矩阵来处理不同的步进模式。它提供了基于特定序列提取模式的方法,以及用于方向差分的矩阵操作方法,这些对于DTW计算是必不可少的。
//+------------------------------------------------------------------+ //| Global constraints | //+------------------------------------------------------------------+ class CConstraint { public: CConstraint(void) { } ~CConstraint(void) { } static matrix noConstraint(ulong iw,ulong jw) { matrix mats[]; np::indices(iw,jw,mats); for(ulong i = 0; i<mats[0].Rows(); i++) { for(ulong j = 0; j<mats[0].Cols(); j++) { long value = long(mats[0][i][j]); mats[0][i][j] = (double)(value|1); if(mats[0][i][j]==0.0) mats[0][i][j] = double("inf"); } } return mats[0]; } static matrix sakoeChibaConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize, ulong winsize) { matrix mats[]; np::indices(iw,jw,mats); matrix abs = MathAbs(mats[1]-mats[0]); for(ulong i = 0; i<abs.Rows(); i++) { for(ulong j = 0; j<abs.Cols(); j++) { if(ulong(abs[i][j])<=winsize) abs[i][j] = (double)(1); else abs[i][j] = double("inf"); } } return abs; } static matrix itakuraConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize) { matrix mats[]; np::indices(iw,jw,mats); long a,b,c,d; for(ulong i = 0, k = 0; i<mats[0].Rows() && k<mats[1].Rows(); i++,k++) { for(ulong j = 0; j<mats[0].Cols(); j++) { a = long(mats[1][k][j]) < (2*long(mats[0][i][j]))?1:0; b = long(mats[0][i][j]) <=(2*long(mats[1][k][j]))?1:0; c = long(mats[0][i][j]) >=(long(qsize)-1-2*(long(refsize)-long(mats[1][k][j])))?1:0; d = long(mats[1][k][j]) > (long(refsize)-1-2*(long(qsize)-long(mats[0][i][j])))?1:0; mats[0][i][j] = double(ulong(a&b&c&d)); if(mats[0][i][j]==0.0) mats[0][i][j] = double("inf"); } } return mats[0]; } static matrix slantedBandConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize,ulong winsize) { matrix mats[]; np::indices(iw,jw,mats); matrix diagj = (mats[0]*refsize/qsize); matrix abs = MathAbs(mats[1]-diagj); for(ulong i = 0; i<abs.Rows(); i++) { for(ulong j = 0; j<abs.Cols(); j++) { if(ulong(abs[i][j])<=winsize) abs[i][j] = (double)(1); else abs[i][j] = double("inf"); } } return abs; } };
CConstraint类包含了用于实现不同类型约束的静态方法,例如Sakoe-Chiba、Itakura和倾斜带(Slanted Band)约束。这些方法通过基于预定义标准限制搜索空间,帮助约束DTW对齐,从而提高计算效率和相关性。
- noConstraint() 方法:生成一个全为1的矩阵,表示没有任何约束条件。
- sakoeChibaConstraint() 方法:根据指定的窗口大小和时间序列的长度,施加Sakoe-Chiba约束。
- itakuraWindow() 方法:使用时间序列的长度来强制实施Itakura约束。
- slantedBandConstraint() 方法:根据窗口大小和时间序列的长度,实现倾斜带约束。
Cdtw类是负责DTW(动态时间规整)计算的核心类。
//+------------------------------------------------------------------+ //| main interface method for dtw | //+------------------------------------------------------------------+ bool dtw(matrix&x, matrix&y, ENUM_DIST_METRIC dist_method,ENUM_STEP_PATTERN step_pattern=STEP_SYMM2, ENUM_GLOBAL_CONSTRAINT win_type=CONSTRAINT_NONE,ulong winsize=0) { if(y.Cols()!=x.Cols()) { Print(__FUNCTION__, " invalid input parameters, size containers donot match. "); return false; } if(CheckPointer(m_stepPattern)==POINTER_DYNAMIC) delete m_stepPattern; switch(step_pattern) { case STEP_SYMM1: m_stepPattern = new CStepPattern(_symmetric1,Symmetric); m_stephint = HINT_NA; break; case STEP_SYMM2: m_stepPattern = new CStepPattern(_symmetric2,Symmetric,HINT_NM); m_stephint = HINT_NM; break; case STEP_ASYMM: m_stepPattern = new CStepPattern(_asymmetric,Asymmetric,HINT_N); m_stephint = HINT_N; break; } if(CheckPointer(m_stepPattern)==POINTER_INVALID) { Print(__FUNCTION__," failed step pointer initialization ", GetLastError()); return false; } matrix stepsMatrix = m_stepPattern.getStepMatrix(); m_query = x; m_qlen = x.Rows(); m_ref = y; m_reflen = y.Rows(); m_distMetric = dist_method; m_winMethod = win_type; m_winsize = winsize; if(y.Rows()) { if(!m_distance.Resize(m_qlen,m_reflen)) { Print(__FUNCTION__," resize error ", GetLastError()); return false; } for(ulong i = 0; i<m_qlen; i++) for(ulong j =0; j<m_reflen; j++) m_distance[i][j]=dist(m_query.Row(i),m_ref.Row(j)); } else m_distance = m_query; ulong n,m; n=m_distance.Rows(); m=m_distance.Cols(); matrix wm; if(m_winMethod == CONSTRAINT_NONE) wm = matrix::Ones(m_distance.Rows(), m_distance.Cols()); else { switch(m_winMethod) { case CONSTRAINT_ITAKURA: wm = CConstraint::itakuraConstraint(n,m,m_qlen,m_reflen); break; case CONSTRAINT_SAKOECHIBA: wm = CConstraint::sakoeChibaConstraint(n,m,m_qlen,m_reflen,m_winsize); break; case CONSTRAINT_SLATEDBAND: wm = CConstraint::slantedBandConstraint(n,m,m_qlen,m_reflen,m_winsize); break; default: wm = CConstraint::noConstraint(n,m); break; } } if(m_winMethod!=CONSTRAINT_NONE) { for(ulong i = 0; i<wm.Rows(); i++) for(ulong j = 0; j<wm.Cols(); j++) if((i+j)>0 && wm[i][j] != 1.0) m_distance[i][j] = wm[i][j]; } m_costMatrix = matrix::Zeros(m_distance.Rows()+ulong(stepsMatrix.Col(0).Max()),m_distance.Cols()+ulong(stepsMatrix.Col(1).Max())); m_costMatrix.Fill(double("inf")); m_costMatrix[ulong(stepsMatrix.Col(0).Max())][ulong(stepsMatrix.Col(1).Max())] = m_distance[0][0]; m_dirMatrix = matrix::Zeros(m_costMatrix.Rows(),m_costMatrix.Cols()); m_dirMatrix.Fill(double(INT_MIN)); for(ulong i = 0; i<m_dirMatrix.Cols(); i++) m_dirMatrix[0][i] = double(1); for(ulong i = 0; i<m_dirMatrix.Rows(); i++) m_dirMatrix[i][0] = double(2); if(!calCM(m_distance,stepsMatrix,m_costMatrix,m_dirMatrix)) { Print(__FUNCTION__, " computeCM() failed "); return false; } m_jmin = m_costMatrix.Cols() - 1; return true; }
它提供了dtw()方法作为执行DTW的主要功能。需要注意的是,该方法被重载以适应单变量(向量)和多变量(矩阵)时间序列。它接受两个时间序列(以矩阵或向量形式表示)、距离度量、步进模式、全局约束和窗口大小作为输入参数。在调用时,该方法首先对输入数据的有效性和所选步进模式进行各种检查。随后,根据选定的距离度量计算距离矩阵。如果指定了全局约束,则在DTW算法中使用的代价矩阵和方向矩阵将相应地进行准备。然后调用calCM()函数来计算累积代价矩阵。最后,dtw()函数返回一个布尔值,指示成功或失败。
//+------------------------------------------------------------------+ //| Get the optimal path: corresponding points from both series | //+------------------------------------------------------------------+ matrix warpPath(bool openEnd=false) { matrix stmatrix = m_stepPattern.getStepMatrix(); return backtrack(m_dirMatrix,stmatrix,openEnd,openEnd?long(m_costMatrix.Row(m_costMatrix.Rows()-1).ArgMin()):-1); }
warpPath()方法根据可选的openEnd参数(用于控制路径的终止方式,即开放或封闭)检索两个时间序列中识别出的最优路径(对应点)。
//+------------------------------------------------------------------+ //| Get the accumulated cost matrix | //+------------------------------------------------------------------+ matrix costMatrix(void) { return m_costMatrix; }
costMatrix()方法提供了对累积成本矩阵的访问权限,这是DTW算法的关键输出之一。
//+------------------------------------------------------------------+ //| Get the cost matrix | //+------------------------------------------------------------------+ matrix localCostMatrix(void) { return m_distance; }
localCostMatrix()方法返回局部距离矩阵,该矩阵表示时间序列中数据点之间的成对距离。
//+------------------------------------------------------------------+ //| Get the direction matrix | //+------------------------------------------------------------------+ matrix directionMatrix(void) { return m_dirMatrix; }
directionMatrix()方法提供了对方向矩阵的访问权限,该矩阵在DTW算法的路径搜索过程中起到引导作用。
//+------------------------------------------------------------------+ //| private method implementing accumulated cost calculation | //+------------------------------------------------------------------+ bool calCM(matrix &distMatrix,matrix &stepMatrix,matrix &costMatrix,matrix &dirMatrix) { ulong max0,max1; max0 = ulong(stepMatrix.Col(0).Max()); max1 = ulong(stepMatrix.Col(1).Max()); double curCost,curd; for(ulong i = max0; i<costMatrix.Rows(); i++) { for(ulong j = max1; j<costMatrix.Cols(); j++) { for(ulong k = 0; k<stepMatrix.Rows(); k++) { curd = costMatrix[i-ulong(stepMatrix[k][0])][j-ulong(stepMatrix[k][1])]; curCost = curd + distMatrix[i-max0][j-max1]; if(curCost<costMatrix[i][j]) { costMatrix[i][j] = curCost; dirMatrix[i][j] = double(k); } } } } costMatrix = np::sliceMatrix(costMatrix,max0,END,1,max1); dirMatrix = np::sliceMatrix(dirMatrix,max0,END,1,max1); return true; }
calCM()私有方法计算累积成本矩阵,这是DTW算法的核心组成部分。它利用距离矩阵、步进模式、成本矩阵和方向矩阵作为输入。
//+------------------------------------------------------------------+ //| distance metric calculation | //+------------------------------------------------------------------+ double dist(vector &u,vector &v) { switch(m_distMetric) { case DIST_EUCLIDEAN: return euclidean(u,v); case DIST_CITYBLOCK: return cityblock(u,v); case DIST_CHEBYSHEV: return chebyshev(u,v); case DIST_CORRELATION: return correlation(u,v); case DIST_COSINE: return cosine(u,v); case DIST_SQEUCLIDEAN: return sqeuclidean(u,v); default: Print(__FUNCTION__, " invalid parameter "); return EMPTY_VALUE; } }
dist()私有函数根据选定的距离度量计算两个数据点之间的距离。
测试Cdtw类
在本节中,我们将通过将Cdtw类的输出与基于Python的DTW实现的输出进行比较,来展示Cdtw类的功能。dtw-python是Python中众多DTW实现之一。我们将运行一个简单的Python脚本,并查看我们的MQL5实现是否能够复现这些结果。我们首先列出Python脚本。
import numpy as np import matplotlib.pyplot as plt import dtw len = 10 add_noise = True noise = np.random.uniform(size=len)if add_noise else np.zeros((len,)) arx = np.linspace(start = 1, stop = 6.28,num = len) query = np.sin(arx) + noise ref = np.cos(arx) alignment = dtw.dtw(query,ref,dist_method='cosine',step_pattern='symmetric2', window_type=None,keep_internals=True) print( f'Accumulated Cost Matrix is {alignment.costMatrix}') print(f'Distance is {alignment.distance}, \n normalize distance is {alignment.normalizedDistance}') print(f'Warp Path is {alignment.index1[:]}:{alignment.index2[:]}') plt.plot(alignment.index1,alignment.index2) plt.show()
该脚本展示了如何使用DTW算法对齐两个时间序列,并且可视化对齐结果。运行代码首先导入必要的库:用于数值运算的numpy,用于绘图的matplotlib.pyplot,以及用于实现DTW算法的dtw。设置时间序列的长度为10,并创建了一个包含10个在1和6.28之间均匀分布的值的数组arx。通过取arx的正弦值并添加一些随机噪声,生成了一个时间序列query,而参考时间序列ref则是通过取arx的余弦值生成的。然后在query和ref序列之间执行DTW对齐。使用余弦距离方法测量时间序列之间的距离,并将对称步进模式应用于变形路径。不使用窗口约束,保留内部细节,如成本矩阵和变形路径。
运行代码随后打印累积成本矩阵、总对齐距离、归一化距离以及两个序列之间变形路径的索引。最后,通过绘制对齐索引的图来可视化变形路径,展示两个时间序列的索引如何对齐,并显示该图。这种方法允许对可能不同步或长度不同的两个时间序列进行详细的比较,使得可以观察到一个序列如何变形以与另一个序列对齐。
以下是上述Python代码的MQL5等效代码:
//+------------------------------------------------------------------+ //| dtwTest.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #property script_show_inputs #include<Math\Stat\Uniform.mqh> #include<dtw.mqh> //--- input ulong series_len = 10; input bool AddRandomNoise = false; input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN; input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2; input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE; input ulong GlobalConstraintWinSize = 0; input bool WarpPathConstraint = false; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { if(series_len<10) { Alert(" Invalid input for series_len parameter. Should be >=10 "); return; } //--- vector arg = np::linspace(1.0,6.28,series_len); vector noise = vector::Zeros(series_len); if(AddRandomNoise) { double array[]; if(!MathRandomUniform(0.0,1.0,int(series_len),array)) { Print(__LINE__, " MathRandomUniform() failed ", GetLastError()); return; } if(!noise.Assign(array)) { Print(__LINE__, " vector assignment failure ", GetLastError()); return; } } vector q = sin(arg) + noise; // candidate sequence vector rf = cos(arg); // reference sequence Cdtw cdtw; cdtw.dtw(q,rf,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize); Print(" local cm ", cdtw.localCostMatrix()); Print(" final cm ", cdtw.costMatrix()); Print(" direction matrix \n", cdtw.directionMatrix()); matrix path = cdtw.warpPath(); Print(" Warp path \n", cdtw.warpPath()); Print(" Distance metric ", cdtw.distance()); Print(" Normalized Distance metric ", cdtw.normalizedDistance()); vector xx = path.Col(0); vector yy = path.Col(1); CGraphic *g = np::plotXY(xx,yy,"Warp Plot", " Query ", " Reference "); Sleep(20000); g.Destroy(); ChartRedraw(); delete g; } //+------------------------------------------------------------------+
Python脚本输出:
KQ 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) Accumulated Cost Matrix is [[ 0. 2. 4. 6. 8. 10. 12. 12. 12. 12.] RD 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 0. 2. 4. 6. 8. 10. 12. 12. 12. 12.] FH 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 0. 2. 4. 6. 8. 10. 12. 12. 12. 12.] JL 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 0. 2. 4. 6. 8. 10. 12. 12. 12. 12.] NQ 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 0. 2. 4. 6. 8. 10. 12. 12. 12. 12.] GD 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 2. 0. 0. 0. 0. 0. 0. 2. 4. 6.] QH 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 4. 0. 0. 0. 0. 0. 0. 2. 4. 6.] KL 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 6. 0. 0. 0. 0. 0. 0. 2. 4. 6.] GS 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 6. 2. 2. 2. 2. 2. 2. 0. 0. 0.] PJ 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) [ 6. 4. 4. 4. 4. 4. 4. 0. 0. 0.]] LJ 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) Distance is 0.0, MM 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) normalize distance is 0.0 CH 0 20:52:53.954 DTW (EURUSD DFX 10 Index,Daily) Warp Path is [0 1 2 3 4 5 5 5 5 6 7 8 8 9]:[0 0 0 0 0 1 2 3 4 5 6 7 8 9]
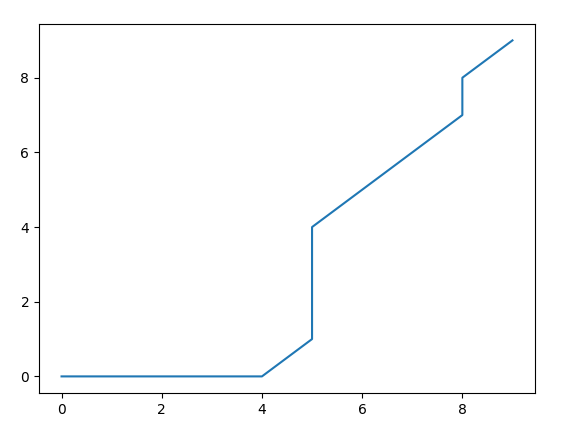
MQL5脚本输出:
NE 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) local cm [[0,2,2,2,2,2,2,0,0,0] LH 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [0,2,2,2,2,2,2,0,0,0] FR 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [0,2,2,2,2,2,2,0,0,0] HE 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [0,2,2,2,2,2,2,0,0,0] RL 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [0,2,2,2,2,2,2,0,0,0] DF 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [2,2.220446049250313e-16,0,0,2.220446049250313e-16,0,0,2,2,2] ND 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [2,0,0,0,0,0,0,2,2,2] FR 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [2,0,0,0,0,0,2.220446049250313e-16,2,2,2] RS 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [0,2,2,2,2,2,2,0,0,0] OH 0 20:56:48.971 dtwTest (EURUSD DFX 10 Index,D1) [0,2,2,2,2,2,2,0,0,0]] ML 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) final cm [[0,2,4,6,8,10,12,12,12,12] JR 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [0,2,4,6,8,10,12,12,12,12] JH 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [0,2,4,6,8,10,12,12,12,12] JN 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [0,2,4,6,8,10,12,12,12,12] JD 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [0,2,4,6,8,10,12,12,12,12] EI 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16,2,4,6] CP 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [4,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2,4,6] EH 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [6,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,2,4,6] IN 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [6,2,2,2,2,2,2,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16] HS 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [6,4,4,4,4,4,4,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]] MO 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) direction matrix QK 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [[-2147483648,1,1,1,1,1,1,1,1,1] GN 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,0,0,0,0,0,0,0,0,0] QQ 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,0,0,0,0,0,0,0,0,0] CK 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,0,0,0,0,0,0,0,0,0] MR 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,0,0,0,0,0,0,0,0,0] OE 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,0,1,1,1,1,1,1,1,1] HO 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,2,0,0,0,1,1,1,0,0] MF 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,2,0,0,0,0,0,0,0,0] CH 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,2,0,0,0,0,0,0,1,1] LN 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,2,0,0,0,0,0,2,0,0]] PK 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) Warp path HM 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [[9,9] GJ 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [8,8] HS 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [8,7] DK 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [7,6] HP 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [6,5] QI 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [6,4] GQ 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [5,3] RN 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [5,2] MG 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [5,1] CO 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [4,0] LD 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [3,0] EL 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [2,0] JE 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [1,0] DO 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) [0,0]] LD 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) Distance metric 4.440892098500626e-16 NR 0 20:56:48.972 dtwTest (EURUSD DFX 10 Index,D1) Normalized Distance metric 2.2204460492503132e-17
比较两个脚本的输出结果,确认代码似乎运行良好。可以用于更实际的用途。这使我们能够将动态时间规整(DTW)应用于策略开发。
应用动态时间规整(DTW)
DTW可以通过启用金融时间序列的灵活模式识别和比较技术,应用于自动化策略开发。例如,DTW能够识别重复出现的价格模式,即使这些模式在不同尺度或时间动态下出现。通过将这些模式与历史数据对齐,可以检测到可能预示重大市场变动的微妙变化和异常。
在回测中,DTW可以通过对齐各自的时间序列结果,比较不同策略在不同市场条件下的表现。这种方法有助于评估策略对市场行为变化的适应能力,提供对其稳健性的更深入理解。此外,DTW可以用于聚类相似的交易信号或市场状态,这些信号或状态随后可以被分析以识别高概率的交易机会。通过识别这些聚类,策略可以被微调,以更有效地利用重复出现的市场行为。
此外,在算法策略的优化中,DTW可以帮助将最有希望的参数集与历史市场条件匹配,这些条件与当前市场动态非常相似。这使得策略能够更动态地适应不断变化的市场条件。通过利用DTW,自动化策略可以变得更加适应性强、具有情境感知能力,并能够识别金融数据中复杂的时序关系。尽管DTW可能是一个有用的工具,但它并非万能的。尤其是对于没有经验的用户而言,它可能不容易使用。
DTW最大的难处之一与其操作参数的配置有关。全局和局部约束的正确组合对于充分发挥该方法的潜力至关重要。DTW容易产生虚假匹配,而获得最佳结果通常需要大量的尝试和错误。这一点体现在下面的MQL5脚本中。
//+------------------------------------------------------------------+ //| dtwPatternSearch.mq5 | //| Copyright 2024, MetaQuotes Ltd. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2024, MetaQuotes Ltd." #property link "https://www.mql5.com" #property version "1.00" #resource "\\Indicators\\LogReturns.ex5" #property script_show_inputs #include<dtw.mqh> #include<ErrorDescription.mqh> enum ENUM_PRICE { CLOSE=0,//close price MEDIAN,//median price TYPICAL//typical price }; enum ENUM_TRANSFORM_TYPE { PERCENT_DIFF=0,//percent difference LOG_DIFF//log difference }; //--- input parameters input string Pattern = "0.0469,0.0093,0.0697,-0.0699"; input string SymbolName="BTCUSD"; input datetime SearchStartDate=D'2024.06.01'; input datetime SearchStopDate=D'2018.04.22'; input double NormalizedDistanceThreshold=0.01; input ENUM_TIMEFRAMES TimeFrame=PERIOD_D1; input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN; input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2; input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE; input ulong GlobalConstraintWinSize = 0; input ENUM_PRICE AppliedPrice=CLOSE; input ENUM_TRANSFORM_TYPE AppliedTransform=LOG_DIFF; input int Lag = 1; //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { //--- string pattern_values[]; //--- int len = StringSplit(Pattern,StringGetCharacter(",",0),pattern_values); if(pattern_values[len-1]=="") len--; //--- if(len<3) { Alert("Pattern sequence is inadequately defined"); return; } //--- vector pattern(len); for(ulong i = 0; i<pattern.Size(); i++) pattern[i]=StringToDouble(pattern_values[i]); //---set prices handle int handle = INVALID_HANDLE; handle=iCustom(SymbolName!=""?SymbolName:NULL,TimeFrame,"::Indicators\\LogReturns.ex5",AppliedPrice,AppliedTransform,1); if(handle==INVALID_HANDLE) { Print("invalid handle ",ErrorDescription(GetLastError())); return; } //--- vector searchBuffer; if(!searchBuffer.CopyIndicatorBuffer(handle,0,SearchStartDate,SearchStopDate)) { Print("History loading error ",ErrorDescription(GetLastError())); return; } //--- ulong stop = searchBuffer.Size()-pattern.Size(); vector subv; Cdtw cdtw; ulong counter=0; for(ulong i = 0; i<stop; i++) { subv = np::sliceVector(searchBuffer,i,i+pattern.Size()); if(!cdtw.dtw(subv,pattern,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize)) { Print(" dtw failed "); return; } if(cdtw.normalizedDistance()<NormalizedDistanceThreshold) { counter++; Print(" pattern found ", datetime(SearchStopDate+(PeriodSeconds(TimeFrame)*(i+pattern.Size()-1)))); } } //--- Print(" SearchBuffer size ", searchBuffer.Size()); Print(" Reference pattern found ", counter, " times."); } //+------------------------------------------------------------------+
该脚本允许用户定义一个由指标“LogReturns.ex5”计算得出的对数收益率序列组成的任意模式。脚本旨在使用动态时间规整(DTW)进行比较,以在金融工具的价格数据中搜索特定模式。它包含了必要的库,例如用于DTW算法的dtw.mqh和用于处理错误描述的ErrorDescription.mqh。脚本定义了两个枚举类型:ENUM_PRICE,指定要使用的价位类型(收盘价、中位价或典型价);ENUM_TRANSFORM_TYPE,决定价格数据将如何转换(百分比差异或对数差异)。
输入参数允许用户指定搜索的详细信息,包括要匹配的模式、交易品种名称(例如“BTCUSD”)、搜索的日期范围、归一化距离的阈值、数据的时间框架、距离度量、步进模式、全局约束、约束的窗口大小、要使用的价位类型、要应用的转换类型以及滞后值。当脚本启动时,它首先将输入模式字符串拆分为一个值数组,确保模式至少定义了三个值。如果模式有效,则将其转换为向量格式以供进一步处理。然后,脚本尝试通过使用iCustom函数调用自定义指标(LogReturns.ex5)来加载价格数据,该指标将所选价位类型和转换应用于数据。如果iCustom返回的句柄无效,则打印错误消息并退出脚本。
假设价格数据加载成功,其将被存储于searchBuffer向量中。然后,脚本遍历searchBuffer,将其切片为与模式大小相同的较小子向量,并使用DTW算法将每个子向量与模式进行比较。DTW比较使用指定的距离度量、步进模式和全局约束。对于每次比较,如果子向量与模式之间的归一化距离小于指定的阈值,则脚本认为在该点的价格数据中找到了模式。然后会打印一条消息,指示找到模式的时间戳,并增加一个计数器。最后,脚本打印searchBuffer的大小以及在指定日期范围内找到模式的总次数。该脚本允许自动检测历史价格数据中的特定模式,这在基于模式识别的交易策略开发中可能非常有用。
默认序列描述了以下所示的模式。
使用不同的约束运行脚本会产生不同数量的匹配结果。这是使用默认设置时的输出结果。
RN 0 22:00:09.210 dtwPatternSearch (BTCUSD,D1) Chosen Parameters IJ 0 22:00:09.210 dtwPatternSearch (BTCUSD,D1) Distance Threshold 0.01 CS 0 22:00:09.210 dtwPatternSearch (BTCUSD,D1) DIST_EUCLIDEAN ND 0 22:00:09.211 dtwPatternSearch (BTCUSD,D1) STEP_SYMM2 CN 0 22:00:09.211 dtwPatternSearch (BTCUSD,D1) CONSTRAINT_NONE HG 0 22:00:09.211 dtwPatternSearch (BTCUSD,D1) WinSize 0 OO 0 22:00:09.211 dtwPatternSearch (BTCUSD,D1) pattern found 2018.04.25 00:00:00 NJ 0 22:00:09.221 dtwPatternSearch (BTCUSD,D1) pattern found 2019.04.28 00:00:00 KD 0 22:00:09.222 dtwPatternSearch (BTCUSD,D1) pattern found 2019.07.01 00:00:00 QO 0 22:00:09.230 dtwPatternSearch (BTCUSD,D1) pattern found 2020.04.27 00:00:00 II 0 22:00:09.234 dtwPatternSearch (BTCUSD,D1) pattern found 2020.10.26 00:00:00 PD 0 22:00:09.237 dtwPatternSearch (BTCUSD,D1) pattern found 2021.02.06 00:00:00 RN 0 22:00:09.250 dtwPatternSearch (BTCUSD,D1) pattern found 2024.01.29 00:00:00 DH 0 22:00:09.250 dtwPatternSearch (BTCUSD,D1) SearchBuffer size 2197 PQ 0 22:00:09.250 dtwPatternSearch (BTCUSD,D1) Reference pattern found 7 times.
“归一化距离阈值”参数显然在确定是否存在匹配项方面起着重要作用。然而,不同的约束条件可能导致截然不同的结果。不仅仅是约束条件,用户还需要选择合适距离度量方法。显然,在使用DTW算法时,掌握深厚的领域知识是必不可少的。
结论
动态时间规整(DTW)为金融时间序列分析中的模式识别提供了一种复杂的方法,但它也存在一些缺点,需要加以考虑。首先,DTW计算量大,尤其是在处理长时间序列或大型数据集时。该算法涉及将一个时间序列中的每个点与另一个时间序列中的每个点进行比较,这可能导致显著的处理时间和内存使用。当尝试分析高频金融数据或进行实时分析时,这个问题尤为突出。其次,DTW对金融数据中的噪声和异常值很敏感。
金融时间序列通常由于市场波动而存在噪声,较小的波动或异常可能会导致DTW算法产生误导性的对齐结果。这种敏感性可能导致模式识别中的假阳性,即识别出的模式并不具备显著的预测能力。最后,DTW在可解释性方面存在挑战。尽管它提供了时间序列之间的相似性度量,但变形路径和结果距离度量可能难以以有意义的方式进行解释,尤其是在金融分析中,清晰且可操作的见解至关重要。这些挑战表明,尽管DTW可以作为金融时间序列模式识别的有用工具,但应谨慎使用,并且通常需要与其他能够弥补其不足的分析方法结合使用。
| 文件 | 说明 |
|---|---|
| Mql5\include\np.mqh | 各向量和矩阵实用函数的头文件 |
| Mql5\include\dtw.mqh | 包含MQL5实现的DTW算法的头文件 |
| Mql5\indicators\LogReturns.mq5 | 价格序列对数收益率指标 |
| Mql5\scripts\dwTest.mq5 | 用于测试和演示MQL5实现的DTW算法的脚本 |
| Mql5\scripts\dtwPatternSearch.mq5 | 在数据样本中用于搜索任意模式的脚本 |
| Mql5\scripts\DTW.py | 使用dtw-python模块通过DTW算法对齐两个序列的Python脚本 |
本文由MetaQuotes Ltd译自英文
原文地址: https://www.mql5.com/en/articles/15572
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 您应当知道的 MQL5 向导技术(第 26 部分):移动平均和赫斯特(Hurst)指数
您应当知道的 MQL5 向导技术(第 26 部分):移动平均和赫斯特(Hurst)指数
 MQL5集成:Python
MQL5集成:Python

