Mustererkennung mit dynamischer Zeitnormierung in MQL5

Einführung

Die Erkennung von Mustern war schon immer ein wertvolles Instrument für Trader. Ob es nun darum geht, einzigartige Kombinationen von Kerzen zu identifizieren oder imaginäre Linien auf einem Diagramm zu zeichnen, diese Muster sind zu einem festen Bestandteil der technischen Analyse geworden. Der Mensch hat sich schon immer durch das Finden und Erkennen von Mustern ausgezeichnet — so sehr, dass oft behauptet wird, wir sähen manchmal Muster, wo es keine gibt. Daher wäre es für uns von Vorteil, objektivere Techniken anzuwenden, um potenziell profitable Muster in Finanzzeitreihen zu erkennen. In diesem Artikel erörtern wir die Anwendung der dynamische Zeitnormierung (Dynamic Time Warping, DTW) als objektive Technik zum Auffinden einzigartiger Muster in Preisdaten. Wir werden seine Ursprünge, seine Funktionsweise und seine Anwendung auf die finanzielle Zeitreihenanalyse untersuchen. Darüber hinaus werden wir die Implementierung des Algorithmus in reinem MQL5 vorstellen und seine Anwendung anhand eines praktischen Beispiels demonstrieren.

Dynamische Zeitnormierung

Die dynamisches Zeitnormierung (Dynamic Time Warping) ist ein hochentwickelter Algorithmus zur Messung der Ähnlichkeit zwischen zwei Datenfolgen, die sich im Laufe der Zeit entwickeln, auch wenn ihre Geschwindigkeit oder ihr Rhythmus variieren. Im Gegensatz zu herkömmlichen Methoden, die eine strikte Ausrichtung zwischen den Datenpunkten erfordern, bietet DTW einen flexibleren Ansatz, indem es eine Verzerrung oder Dehnung der Zeit zulässt, um die optimale Übereinstimmung zwischen den Sequenzen zu finden. Stellen Sie sich zwei Personen vor, die auf unterschiedlichen Wegen durch einen Wald gehen. Sie beginnen beide am selben Ort und enden am selben Ort, aber der eine geht vielleicht schneller als der andere und macht aus irgendeinem Grund willkürlich Halt. DTW hilft dabei, den besten Weg zu finden, um die Schritte beider zu verbinden, auch wenn sie unterschiedliche Wege gegangen sind. DTW kann Unterschiede in der Gehgeschwindigkeit, der Beschleunigung oder der Verlangsamung effektiv berücksichtigen und liefert ein Maß für die Ähnlichkeit. Diese Vielseitigkeit macht es für eine breite Palette von Datentypen, einschließlich Audio, Video und Grafik, einsetzbar. Alle Daten, die in ein sequentielles Format umgewandelt werden können, sind potenzielle Kandidaten für eine DTW-Analyse.

DTW wurde ursprünglich von Taras Vintsyuk im Jahr 1968 für die Spracherkennung entwickelt und später von Forschern wie Sakoe und Chiba im Jahr 1978 verfeinert. Die Methode hat sich in verschiedenen Bereichen durchgesetzt, da sie es ermöglicht, Sequenzen unterschiedlicher Länge zu vergleichen, indem sie die zeitliche Dimension verzerrt, um ähnliche Muster anzugleichen. DTW hat seitdem Anwendungen in verschiedenen Bereichen wie der Bioinformatik und der Ganganalyse gefunden. Die Finanzmärkte sind durch nichtlineare und nichtstationäre Zeitreihendaten gekennzeichnet. Herkömmliche Abstandsmaße wie der euklidische Abstand können die Komplexität und Verzerrungen in solchen Daten nicht erfassen. DTW zeichnet sich jedoch durch die Identifizierung von Ähnlichkeiten zwischen Zeitreihen mit zeitlichen Verzerrungen aus, was es zu einem geeigneten Instrument für die Analyse von Finanzmärkten macht. Durch den Abgleich von Sequenzen auf der Grundlage ihrer Form und nicht ihrer zeitlichen Ausrichtung kann DTW einzigartige Muster in Finanzdaten aufdecken.

Wie es funktioniert.

Bei der Anwendung des DTW-Algorithmus besteht das Ziel darin, festzustellen, ob eine Kandidatensequenz einer vordefinierten Referenzsequenz ähnlich ist. Die endgültige Metrik, die der Algorithmus erzeugt, gibt die Ähnlichkeit zwischen der Kandidaten- und der Referenzsequenz an — je niedriger dieser Wert ist, desto ähnlicher sind die Sequenzen. Wenn die Sequenzen gleich sind, wäre dieser Wert 0. Um die optimale Anpassung zwischen einer Kandidatensequenz und einem Referenzdatensatz zu finden, hält sich der DTW-Algorithmus an bestimmte Prinzipien. Jeder Punkt in der Kandidatensequenz muss mindestens einem Datenpunkt in der Referenzsequenz entsprechen und vice versa. Der Anfang der einen Sequenz muss mit dem Anfang der anderen übereinstimmen, und das Ende der einen muss mit dem Ende der anderen übereinstimmen. Außerdem dürfen beim Durchlaufen der Sequenzen die entsprechenden Punkte nur vorwärts laufen. Dadurch wird sichergestellt, dass kein Punkt in einer Sequenz mit einem Punkt übereinstimmen kann, der in der anderen Sequenz vor ihm liegt, sodass eine Ausrichtung auf frühere Punkte nicht möglich ist.

Der Prozess beginnt mit der Erstellung einer Abstandsmatrix, die die paarweisen Abstände zwischen den Elementen der beiden Sequenzen erfasst. Jedes Element dieser Matrix stellt den Abstand zwischen einem Punkt in der ersten Sequenz und einem entsprechenden Punkt in der zweiten Sequenz dar. In diesem Stadium kann jedes der traditionellen räumlichen Abstandsmaße verwendet werden. Räumliche Abstandsmaße sind mathematische Methoden, die zur Quantifizierung des Abstands oder der Unähnlichkeit zwischen Datenpunkten in einem bestimmten Raum verwendet werden. Die Wahl des Abstandsmaßes hängt von den spezifischen Merkmalen der Daten und der jeweiligen Aufgabe ab. In der nachstehenden Tabelle sind die gebräuchlichsten räumlichen Abstandsmaße und kurze Beschreibungen der einzelnen Maße aufgeführt.

Entfernung Metrisch	Beschreibung
Euklidischer Abstand	Der euklidische Abstand ist der geradlinige Abstand zwischen zwei Punkten im euklidischen Raum. Es ist das intuitivste und am weitesten verbreitete Abstandsmaß.
Manhattan-Metrik	Die Manhattan-Metrik, auch bekannt als Taxi-Entfernung oder City-Block-Entfernung, misst die Entfernung zwischen zwei Punkten durch Summierung der absoluten Differenzen ihrer Koordinaten.
Minkowski-Abstand	Der Minkowski-Abstand ist eine verallgemeinerte Form des Euklidischen und des Manhattan-Abstands. Es enthält einen Parameter, mit dem zwischen verschiedenen Abstandsmaßen umgeschaltet werden kann.
Maximumsnorm	Der Maximumsnorm, auch Maximal- oder Schachbrettabstand genannt, misst den größten Unterschied zwischen den Koordinaten eines Punktpaares.
Kosinus-Ähnlichkeit	Die Kosinus-Ähnlichkeit misst den Kosinus des Winkels zwischen zwei Vektoren, die nicht Null sind, und stellt somit die Ähnlichkeit in der Richtung und nicht in der Größe dar.

Die Wahl des räumlichen Abstandsmaßes hängt von der Art der Daten und den spezifischen Anforderungen der Aufgabe ab. Das Verständnis der Unterschiede und Anwendungen dieser Maßnahmen hilft bei der Auswahl der am besten geeigneten Maßnahmen für eine aussagekräftige Analyse.

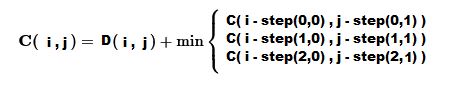
Im nächsten Schritt wird die Abstandsmatrix zur Berechnung der kumulativen Kostenmatrix verwendet, wobei jedes Element die minimalen Kosten für die Ausrichtung der Sequenzen darstellt. Bei diesem Anpassungsprozess wird die Kandidatensequenz so umgewandelt, dass sie der Referenzsequenz sehr ähnlich ist. Die kumulative Kostenmatrix gibt an, wie stark einzelne Punkte in der Kandidatensequenz verändert werden müssen, um den Referenzwerten bestmöglich zu entsprechen. Größere Kosten bedeuten eine stärkere Umwandlung, was auf eine größere Unähnlichkeit zwischen den Sequenzen hinweist. Diese kumulativen Kostenmatrixwerte werden verwendet, um den optimalen Normierungspfad zu bestimmen, der die Abfolge von Ausrichtungen darstellt, die eine Zeitreihe auf eine andere abbildet und dabei den Abstand zwischen ihnen minimiert. Im Wesentlichen veranschaulicht der Normierungspfad, wie Teile einer Sequenz gedehnt oder gestaucht werden, um sie so eng wie möglich an eine andere Sequenz anzupassen.

Um den Normierungspfad zu finden, stellen wir uns die Sequenzen auf einem Gitter vor, wobei eine Sequenz auf der x-Achse und die andere auf der y-Achse liegt. Jeder Punkt auf diesem Raster stellt eine mögliche Übereinstimmung zwischen einem Element aus der ersten Sequenz und einem Element aus der zweiten Sequenz dar. Der Normierungspfad ist der Weg durch dieses Gitter, der die beste Ausrichtung zwischen den beiden Sequenzen ergibt. Der Pfad beginnt in der linken unteren Ecke des Gitters, was den ersten Elementen der beiden Sequenzen entspricht, und endet in der rechten oberen Ecke, was den letzten Elementen der beiden Sequenzen entspricht. Im Verlauf des Pfades kann er sich in drei Richtungen bewegen: diagonal, wodurch Elemente aus beiden Sequenzen übereinstimmen; horizontal, wodurch ein Element aus der ersten Sequenz wiederholt wird; oder vertikal, wodurch ein Element aus der zweiten Sequenz wiederholt wird. Durch diese Bewegung wird sichergestellt, dass sich der Normierungsprozess immer vorwärts bewegt und keine Elemente in den Sequenzen überspringt.

Der Normierungspfad wird so gewählt, dass der kumulative Abstand oder die Kosten zwischen den ausgerichteten Elementen der beiden Sequenzen minimiert werden. Zu diesem Zweck werden die Werte der Abstandsmatrix über das Gitter gelegt, das zur Ausrichtung der Punkte verwendet wird. Die Kosten an jedem Punkt des Gitters werden berechnet, indem die entsprechende Entfernungsmetrik zum Minimalwert der benachbarten kumulativen Entfernungen von den vorhergehenden Punkten addiert wird, wobei die drei möglichen Richtungen (diagonal, horizontal oder vertikal) berücksichtigt werden, die bei einer Vorwärtsbewegung in der Zeit eingeschlagen werden können. Da jeder Rasterpunkt mit der Abstandsmetrik der entsprechenden Sequenzwerte verknüpft ist, stellt der Mindestwert die Operation dar, die erforderlich ist, um die Kandidatensequenz so umzuwandeln, dass sie der Referenzsequenz entspricht. Liegt der minimale kumulative Abstand diagonal zum aktuellen Punkt, handelt es sich um eine übereinstimmende Operation. Wenn der kleinste kumulative Abstand von den vorherigen Punkten horizontal zum aktuellen Punkt verläuft, deutet dies auf eine Einfügeoperation hin, bei der ein Wert aus der Referenzsequenz effektiv in die Kandidatensequenz eingefügt wird. Umgekehrt, wenn der minimale kumulative Abstand senkrecht zum aktuellen Punkt ist, bedeutet dies einen Löschvorgang, bei dem ein Wert aus der Kandidatenfolge entfernt wird. Die Wahl der vorherigen kumulativen Abstandswerte, die zur Ermittlung des Minimums berücksichtigt werden, wird durch ein bestimmtes Schrittmuster bestimmt.

Schrittmuster bestimmen die zulässigen Bewegungen oder Übergänge zwischen Punkten in den Sequenzen während der Ausrichtung. Sie geben die Anzahl der Punkte in jeder der gültigen Richtungen (diagonal, horizontal, vertikal) an, die bei der Berechnung des kumulativen Mindestabstands berücksichtigt werden. Die Wahl des Schrittmusters beeinflusst den Ausrichtungsprozess und die gesamte Abstandsberechnung erheblich. Es gibt verschiedene Stufenmuster, die jeweils auf bestimmte Anwendungen zugeschnitten sind. Die Übenden können auch eigene Schrittmuster erstellen, sofern sie die Prinzipien der Vorwärtsbewegung und Kontinuität einhalten. In diesem Text werden wir uns auf die gängigsten und allgemeinsten Schrittmuster konzentrieren, die sich in verschiedenen Bereichen bewährt haben. Für diejenigen, die an der Erforschung anderer Schrittmuster interessiert sind, bieten die Artikel von Sakoe-Chiba, Rabiner-Juang, und Rabiner-Myers tiefgreifende Einblicke.

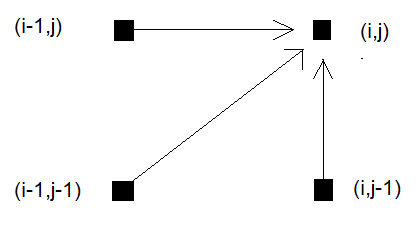
Das am häufigsten verwendete Schrittmuster ist das Standardschrittmuster, auch bekannt als symmetrisches oder klassisches Schrittmuster. Ihr Hauptvorteil besteht darin, dass sie sicherstellt, dass beide Zeitreihen vollständig durchlaufen werden. Dieses Muster berücksichtigt nur die unmittelbaren Werte oberhalb, rechts und diagonal zum aktuellen Punkt, sodass diagonale, horizontale und vertikale Einzelschrittbewegungen auf dem Gitter möglich sind.

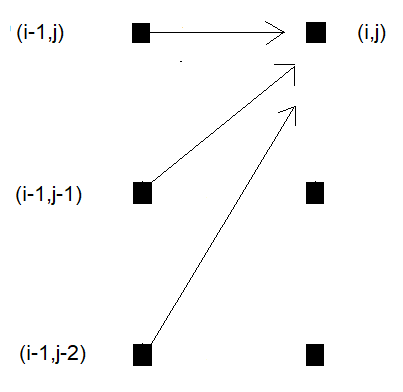
Ein weiteres beliebtes Schrittmuster ist das klassische asymmetrische Muster. Ähnlich wie das Standard-Schrittmuster definiert es Übergänge in drei Richtungen, führt aber eine Tendenz zu einer Sequenz ein. Dieses Muster ermöglicht es dem Algorithmus, sich diagonal zu bewegen, aber wenn ein Punkt übersprungen wird, bevorzugt er das Vorwärtskommen in einer Sequenz mehr als in der anderen. Sie wird häufig zusammen mit zusätzlichen Beschränkungen verwendet, die die Bewegungen des Algorithmus auf dem Gitter begrenzen. Im Falle des asymmetrischen Stufenmusters wird eine zusätzliche Neigungsbeschränkung angewandt, die die Steilheit oder Flachheit des Verformungspfads einschränkt. Diese Einschränkung ist nützlich, wenn die Sequenzen in Länge und Verschiebung ähnlich sein sollen, da sie verhindert, dass eine Sequenz im Vergleich zur anderen übermäßig gestreckt oder gestaucht wird.

Zusätzliche Beschränkungen können angewandt werden, um technisch perfekte, aber bedeutungslose Ausrichtungen zu verhindern, die zu einer Überanpassung der Daten führen könnten. Diese Einschränkungen stellen sicher, dass die Anpassung im Kontext der analysierten Daten logisch sinnvoll ist und eine übermäßige Dehnung oder Komprimierung der Sequenzen verhindert wird. Solche Beschränkungen werden als globale Beschränkungen bezeichnet und verbessern die Wirksamkeit und Interpretierbarkeit des DTW-Algorithmus in praktischen Anwendungen. Zwei gängige globale Beschränkungen sind das Sakoe-Chiba-Band und das Itakura-Parallelogramm.

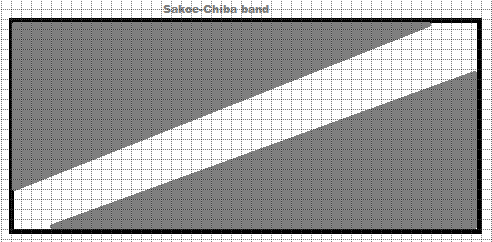
Das Sakoe-Chiba-Band schränkt den Normierungspfad so ein, dass er innerhalb eines festen Bandes um die Diagonale der Ausrichtungsmatrix bleibt. Dadurch wird verhindert, dass die Ausrichtung zu weit vom ursprünglichen Timing oder der ursprünglichen Verschiebung abweicht, was bei Aufgaben nützlich ist, bei denen leichte Timing-Abweichungen erwartet werden, große Abweichungen jedoch nicht.

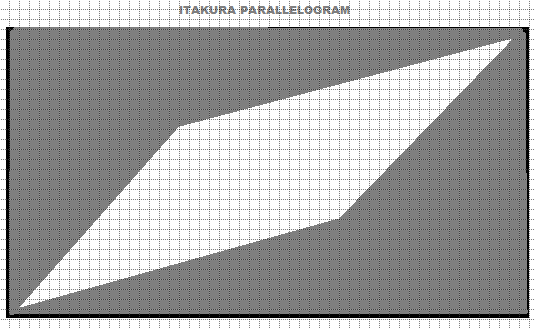
Die Itakura-Parallelogramm-Beschränkung definiert einen parallelogrammförmigen Bereich, innerhalb dessen der Verformungspfad bleiben muss. Sie ist an den Enden schmaler und in der Mitte breiter, was besonders nützlich ist, wenn die Sequenzen am Anfang und am Ende enger aufeinander abgestimmt sein sollen, in der Mitte aber eine gewisse Flexibilität zulassen. Globale Beschränkungen sind für das DTW unerlässlich, um den Normierungsprozess zu steuern und sicherzustellen, dass die resultierende Ausrichtung für die jeweilige Aufgabe relevant ist. Es ist wichtig, die am besten geeigneten Beschränkungen auf der Grundlage der Merkmale der Datensätze und der Ziele der Analyse auszuwählen.

Sobald die kumulative Kostenmatrix fertiggestellt ist, wird sie zur Bestimmung des optimalen Verzugswegs verwendet. Der Algorithmus geht vom letzten Element der kumulativen Kostenmatrix zum ersten zurück und ermittelt den Pfad, der die Gesamtkosten der Ausrichtung minimiert. Dieser Pfad stellt die beste Ausrichtung zwischen den Sequenzen dar. Der letzte Wert in der kumulativen Kostenmatrix ergibt die Gesamtentfernungsbewertung, die auch zur Berechnung der normalisierten Entfernungsbewertung verwendet wird. Der Normierungspfad listet die gepaarten Indizes auf, die in beiden Sequenzen aufeinander abgestimmte Punkte darstellen. Um das Ausrichtungsverfahren zu bewerten, wird üblicherweise der optimale Normierungspfad aufgezeichnet. Ein zufriedenstellendes Ergebnis sollte eine annähernd diagonale Darstellung ergeben. Diese diagonale Darstellung zeigt, dass die Sequenzen gut aufeinander abgestimmt sind, wobei eine vollkommen gerade diagonale Linie zwei identischen Sequenzen entspricht. Im folgenden Abschnitt wird eine native MQL5-Implementierung des dynamischen Time Warping diskutiert.

MQL5-Implementierung

Die DTW-MQL5-Implementierung ist in der Include-Datei dtw.mqh enthalten. Es werden nicht alle Aspekte des dynamischen Time Warping vollständig oder umfassend behandelt. Später werden wir uns eine Python-Implementierung der DTW ansehen, die viel mehr Funktionen bietet. Das Ziel bei der Erstellung dieser Bibliothek ist es, die grundlegenden Funktionen für die Berechnung der Abstandsbewertung bereitzustellen. Die Bibliothek ist ein partieller Fork des dtw-python-Moduls.

Der Code beginnt mit der Definition von Enumerationen für Schrittmuster und verschiedene Abstandsmaße und globale Beschränkungen.

//+------------------------------------------------------------------+
//|  step patterns                                                   |
//+------------------------------------------------------------------+
enum ENUM_STEP_PATTERN
  {
   STEP_SYMM1=0,//symmetric1
   STEP_SYMM2,//symmetric2
   STEP_ASYMM//asymmetric
  };

ENUM_STEP_PATTERN: Definiert eine Reihe von Enumerationen, die zulässige Übergangsmuster während der Pfadsuchphase des DTW-Algorithmus einschränken. Diese Muster leiten den Normierungsprozess und beeinflussen die zulässigen Angleichungen zwischen den Zeitreihen.

//+------------------------------------------------------------------+
//|  distance metric                                                 |
//+------------------------------------------------------------------+
enum ENUM_DIST_METRIC
  {
   DIST_EUCLIDEAN=0,//euclidean
   DIST_CITYBLOCK,//city block
   DIST_COSINE,//cosine
   DIST_CORRELATION,//correlation
   DIST_CHEBYSHEV,//chebyshev
   DIST_SQEUCLIDEAN//squared euclidean
  };

ENUM_DIST_METRIC: Stellt eine Sammlung von Enumerationen bereit, die den unterstützten Abstandsmetriken entsprechen. Diese Metriken quantifizieren die Unähnlichkeit zwischen Datenpunkten in der Zeitreihe, mit Optionen wie Euklidischer Abstand, City-Block-Abstand und mehr.

//+------------------------------------------------------------------+
//|   window function                                                |
//+------------------------------------------------------------------+
enum ENUM_GLOBAL_CONSTRAINT
  {
   CONSTRAINT_NONE=0,// no constrains applied
   CONSTRAINT_SAKOECHIBA,// sakoe chiba
   CONSTRAINT_SLATEDBAND,// slated band
   CONSTRAINT_ITAKURA// itakura
  };

ENUM_GLOBAL_CONSTRAINT: Umfasst verschiedene globale Restriktionen, die bei der Pfadsuche Beschränkungen auferlegen. Diese können die Verzugsflexibilität beeinflussen und möglicherweise die Ausrichtungsgenauigkeit verbessern.

//+------------------------------------------------------------------+
//| lists the transitions allowed while searching                    |
//|for the minimum-distance path                                     |
//+------------------------------------------------------------------+
class CStepPattern
  {
private:
   matrix            m_mx,m_stepsMatrix;
   ENUM_HINT         m_stephint;
public:
                     CStepPattern(matrix &mx, matrix &stepmatrix, ENUM_HINT hint=HINT_NA)
     {
      m_mx = mx;
      m_stepsMatrix = stepmatrix;
      m_stephint = hint;
     }
                    ~CStepPattern(void)
     {

     }
   matrix            getStepMatrix(void)
     {
      return m_stepsMatrix;
     }
   ulong             getNRows(void)
     {
      return m_mx.Rows();
     }
   int               getNPatterns(void)
     {
      vector vec = m_mx.Col(0);
      return (int(vec.Max()));
     }

   CStepPattern*     T(void)
     {
      ulong cols[] = {0, 2, 1, 3};

      matrix cpy = np::selectMatrixCols(m_mx,cols);
      ENUM_HINT hint = m_stephint;

      if(m_stephint == HINT_N)
         hint = HINT_M;
      else
         if(m_stephint == HINT_M)
            hint = HINT_N;

      CStepPattern* out = new CStepPattern(cpy,m_stepsMatrix,hint);

      return out;
     }

   matrix            extractPattern(vector &sn)
     {
      vector col  =  m_mx.Col(0);
      matrix out = matrix::Ones(1,1);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == sn[j])
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols()-1,100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               vector vv = np::sliceVector(v,1);
               if(!out.Row(vv,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      if(!np::reverseMatrixRows(out))
        {
         Print(__FUNCTION__, " Reverse Matrix failure ");
         return matrix::Zeros(1,1);
        }
      return out;
     }

   matrix            mkDIrDeltas(void)
     {
      matrix out = matrix::Zeros(1,1);
      vector col = m_mx.Col(3);
      for(ulong i = 0; i<m_mx.Rows(); i++)
        {
         for(ulong j = 0; j<col.Size(); j++)
           {
            if(col[j] == -1.0)
              {
               if(!out.Resize(out.Rows()+1,m_mx.Cols(),100))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
               vector v = m_mx.Row(j);
               if(!out.Row(v,out.Rows()-1))
                 {
                  Print(__FUNCTION__, " error ", GetLastError());
                  return matrix::Zeros(1,1);
                 }
              }
           }
        }

      return np::sliceMatrixCols(out,1,3);
     }

   matrix             getP(void)
     {
      ulong sel[] = {0, 2, 1, 3};
      matrix s = np::selectMatrixCols(m_mx,sel);
      return s;
     }

   matrix            getMx(void)
     {
      return m_mx;
     }
  };

CStepPattern ist eine Klasse, mit der verschiedene Schrittmuster durch die Verwaltung von Matrizen, die die zulässigen Übergänge und Operationen definieren, gehandhabt werden können. Es bietet Methoden zur Extraktion von Mustern auf der Grundlage bestimmter Sequenzen und zur Manipulation von Matrizen für Richtungsdeltas, die für DTW-Berechnungen unerlässlich sind.

//+------------------------------------------------------------------+
//| Global constraints                                               |
//+------------------------------------------------------------------+
class CConstraint
  {
public:
                     CConstraint(void)
     {

     }
                    ~CConstraint(void)
     {

     }

   static matrix       noConstraint(ulong iw,ulong jw)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      for(ulong i = 0; i<mats[0].Rows(); i++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            long value = long(mats[0][i][j]);
            mats[0][i][j] = (double)(value|1);
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       sakoeChibaConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize, ulong winsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      matrix abs = MathAbs(mats[1]-mats[0]);

      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;
     }

   static matrix       itakuraConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize)
     {
      matrix mats[];

      np::indices(iw,jw,mats);

      long a,b,c,d;

      for(ulong i = 0, k = 0; i<mats[0].Rows() && k<mats[1].Rows(); i++,k++)
        {
         for(ulong j = 0; j<mats[0].Cols(); j++)
           {
            a = long(mats[1][k][j]) < (2*long(mats[0][i][j]))?1:0;
            b = long(mats[0][i][j]) <=(2*long(mats[1][k][j]))?1:0;
            c = long(mats[0][i][j]) >=(long(qsize)-1-2*(long(refsize)-long(mats[1][k][j])))?1:0;
            d = long(mats[1][k][j]) > (long(refsize)-1-2*(long(qsize)-long(mats[0][i][j])))?1:0;
            mats[0][i][j] = double(ulong(a&b&c&d));
            if(mats[0][i][j]==0.0)
               mats[0][i][j] = double("inf");
           }
        }

      return mats[0];
     }

   static matrix       slantedBandConstraint(ulong iw,ulong jw, ulong qsize, ulong refsize,ulong winsize)
     {

      matrix mats[];

      np::indices(iw,jw,mats);

      matrix  diagj = (mats[0]*refsize/qsize);

      matrix abs = MathAbs(mats[1]-diagj);


      for(ulong i = 0; i<abs.Rows(); i++)
        {
         for(ulong j = 0; j<abs.Cols(); j++)
           {
            if(ulong(abs[i][j])<=winsize)
               abs[i][j] = (double)(1);
            else
               abs[i][j] = double("inf");
           }
        }

      return abs;

     }

  };

Die Klasse CConstraint enthält statische Methoden für verschiedene Arten von Nebenbedingungen, wie Sakoe-Chiba, Itakura und Slanted Band. Diese helfen, den DTW-Abgleich einzuschränken, um die Recheneffizienz und die Relevanz zu verbessern, indem sie den Suchraum auf der Grundlage vordefinierter Kriterien einschränken.

• Die Methode noConstraint(): Erzeugt eine Matrix, die mit Einsen gefüllt ist, was bedeutet, dass es keine Beschränkungen gibt.

• Die Methode sakoeChibaConstraint(): Erzwingt eine Sakoe-Chiba-Beschränkung auf der Grundlage der angegebenen Fenstergröße und der Längen der Zeitreihen.

• Die Methode itakuraWindow(): Erzwingt eine Itakura-Beschränkung anhand der Längen der Zeitreihen.

• Die Methode slantedBandConstraint(): Implementiert eine Schrägband-Beschränkung auf der Grundlage der Fenstergröße und der Längen der Zeitreihen.
  

Die Klasse Cdtw ist die Kernklasse, die für DTW-Berechnungen zuständig ist.

   //+------------------------------------------------------------------+
   //|     main interface method for dtw                                |
   //+------------------------------------------------------------------+

   bool              dtw(matrix&x, matrix&y, ENUM_DIST_METRIC dist_method,ENUM_STEP_PATTERN step_pattern=STEP_SYMM2, ENUM_GLOBAL_CONSTRAINT win_type=CONSTRAINT_NONE,ulong winsize=0)
     {
      if(y.Cols()!=x.Cols())
        {
         Print(__FUNCTION__, " invalid input parameters, size containers donot match. ");
         return false;
        }

      if(CheckPointer(m_stepPattern)==POINTER_DYNAMIC)
         delete m_stepPattern;

      switch(step_pattern)
        {
         case STEP_SYMM1:
            m_stepPattern = new CStepPattern(_symmetric1,Symmetric);
            m_stephint = HINT_NA;
            break;

         case STEP_SYMM2:
            m_stepPattern = new CStepPattern(_symmetric2,Symmetric,HINT_NM);
            m_stephint = HINT_NM;
            break;

         case STEP_ASYMM:
            m_stepPattern = new CStepPattern(_asymmetric,Asymmetric,HINT_N);
            m_stephint = HINT_N;
            break;
        }

      if(CheckPointer(m_stepPattern)==POINTER_INVALID)
        {
         Print(__FUNCTION__," failed step pointer initialization ", GetLastError());
         return false;
        }

      matrix stepsMatrix = m_stepPattern.getStepMatrix();
      m_query = x;
      m_qlen = x.Rows();
      m_ref = y;
      m_reflen = y.Rows();
      m_distMetric = dist_method;
      m_winMethod = win_type;
      m_winsize = winsize;

      if(y.Rows())
        {
         if(!m_distance.Resize(m_qlen,m_reflen))
           {
            Print(__FUNCTION__," resize error ", GetLastError());
            return false;
           }
         for(ulong i = 0; i<m_qlen; i++)
            for(ulong j =0; j<m_reflen; j++)
               m_distance[i][j]=dist(m_query.Row(i),m_ref.Row(j));
        }
      else
         m_distance = m_query;

      ulong n,m;
      n=m_distance.Rows();
      m=m_distance.Cols();
      matrix wm;
      if(m_winMethod == CONSTRAINT_NONE)
         wm = matrix::Ones(m_distance.Rows(), m_distance.Cols());
      else
        {
         switch(m_winMethod)
           {
            case CONSTRAINT_ITAKURA:
               wm = CConstraint::itakuraConstraint(n,m,m_qlen,m_reflen);
               break;
            case CONSTRAINT_SAKOECHIBA:
               wm = CConstraint::sakoeChibaConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            case CONSTRAINT_SLATEDBAND:
               wm = CConstraint::slantedBandConstraint(n,m,m_qlen,m_reflen,m_winsize);
               break;
            default:
               wm = CConstraint::noConstraint(n,m);
               break;
           }
        }

      if(m_winMethod!=CONSTRAINT_NONE)
        {
         for(ulong i = 0; i<wm.Rows(); i++)
            for(ulong j = 0; j<wm.Cols(); j++)
               if((i+j)>0 && wm[i][j] != 1.0)
                  m_distance[i][j] = wm[i][j];
        }


      m_costMatrix = matrix::Zeros(m_distance.Rows()+ulong(stepsMatrix.Col(0).Max()),m_distance.Cols()+ulong(stepsMatrix.Col(1).Max()));
      m_costMatrix.Fill(double("inf"));
      m_costMatrix[ulong(stepsMatrix.Col(0).Max())][ulong(stepsMatrix.Col(1).Max())] = m_distance[0][0];

      m_dirMatrix = matrix::Zeros(m_costMatrix.Rows(),m_costMatrix.Cols());
      m_dirMatrix.Fill(double(INT_MIN));
      for(ulong i = 0; i<m_dirMatrix.Cols(); i++)
         m_dirMatrix[0][i] = double(1);
      for(ulong i = 0; i<m_dirMatrix.Rows(); i++)
         m_dirMatrix[i][0] = double(2);

      if(!calCM(m_distance,stepsMatrix,m_costMatrix,m_dirMatrix))
        {
         Print(__FUNCTION__, " computeCM() failed ");
         return false;
        }

      m_jmin = m_costMatrix.Cols() - 1;

      return true;
     }

Sie hat die Methode dtw() als Hauptfunktion für die Durchführung von DTW. Beachten Sie, dass die Methode überladen ist, um univariaten (Vektoren) und multivariaten (Matrizen) Zeitreihen gerecht zu werden. Als Eingabeargumente dienen zwei Zeitreihen (dargestellt als Matrizen oder Vektoren), eine Abstandsmetrik, ein Schrittmuster, eine globale Beschränkung und die Fenstergröße. Beim Aufruf beginnt die Methode mit der Durchführung verschiedener Prüfungen der Gültigkeit der Eingabedaten und des gewählten Schrittmusters. Anschließend erfolgt die Berechnung der Abstandsmatrix auf der Grundlage der gewählten Abstandsmetrik. Wenn eine globale Einschränkung angegeben wird, werden die Kosten- und Richtungsmatrizen, die während des DTW-Algorithmus verwendet werden, entsprechend vorbereitet. Anschließend wird die Funktion calCM() aufgerufen, um die kumulierte Kostenmatrix zu berechnen. Schließlich gibt die Funktion dtw() einen booleschen Wert zurück, der Erfolg oder Misserfolg anzeigt. 

   //+------------------------------------------------------------------+
   //|    Get the optimal path: corresponding points from both series   |
   //+------------------------------------------------------------------+

   matrix            warpPath(bool openEnd=false)
     {
      matrix stmatrix = m_stepPattern.getStepMatrix();
      return backtrack(m_dirMatrix,stmatrix,openEnd,openEnd?long(m_costMatrix.Row(m_costMatrix.Rows()-1).ArgMin()):-1);
     }

Die Methode warpPath() ruft den optimalen Pfad (entsprechende Punkte) ab, der aus beiden Zeitreihen auf der Grundlage eines optionalen Arguments „openEnd“ ermittelt wurde, das die Beendigung des Pfades (offen oder geschlossen) steuert.

   //+------------------------------------------------------------------+
   //|     Get the accumulated cost matrix                              |
   //+------------------------------------------------------------------+

   matrix            costMatrix(void)
     {
      return m_costMatrix;
     }

Die Methode costMatrix() ermöglicht den Zugriff auf die akkumulierte Kostenmatrix, eine wichtige Ausgabe des DTW-Algorithmus.

   //+------------------------------------------------------------------+
   //|       Get the cost matrix                                        |
   //+------------------------------------------------------------------+

   matrix            localCostMatrix(void)
     {
      return m_distance;
     }

Die Methode localCostMatrix() gibt die lokale Abstandsmatrix zurück, die die paarweisen Abstände zwischen Datenpunkten in der Zeitreihe darstellt.

   //+------------------------------------------------------------------+
   //|        Get the direction matrix                                  |
   //+------------------------------------------------------------------+

   matrix            directionMatrix(void)
     {
      return m_dirMatrix;
     }

Die Methode directionMatrix() ermöglicht den Zugriff auf die Richtungsmatrix, die bei der Pfadsuche während des DTW-Prozesses eine Rolle spielt.

   //+------------------------------------------------------------------+
   //|  private method implementing accumulated cost calculation        |
   //+------------------------------------------------------------------+

   bool              calCM(matrix &distMatrix,matrix &stepMatrix,matrix &costMatrix,matrix &dirMatrix)
     {
      ulong max0,max1;
      max0 = ulong(stepMatrix.Col(0).Max());
      max1 = ulong(stepMatrix.Col(1).Max());
      double curCost,curd;

      for(ulong i = max0; i<costMatrix.Rows(); i++)
        {
         for(ulong j = max1; j<costMatrix.Cols(); j++)
           {
            for(ulong k = 0; k<stepMatrix.Rows(); k++)
              {
               curd = costMatrix[i-ulong(stepMatrix[k][0])][j-ulong(stepMatrix[k][1])];
               curCost = curd + distMatrix[i-max0][j-max1];
               if(curCost<costMatrix[i][j])
                 {
                  costMatrix[i][j] = curCost;
                  dirMatrix[i][j] = double(k);
                 }
              }
           }
        }
      costMatrix = np::sliceMatrix(costMatrix,max0,END,1,max1);
      dirMatrix  = np::sliceMatrix(dirMatrix,max0,END,1,max1);
      return true;

     }

Die private Methode calCM() berechnet die kumulierte Kostenmatrix, eine Kernkomponente des DTW-Algorithmus. Es verwendet die Distanzmatrix, das Schrittmuster, die Kostenmatrix und die Richtungsmatrix als Eingabe.

   //+------------------------------------------------------------------+
   //|  distance metric calculation                                     |
   //+------------------------------------------------------------------+


   double            dist(vector &u,vector &v)
     {
      switch(m_distMetric)
        {
         case DIST_EUCLIDEAN:
            return euclidean(u,v);
         case DIST_CITYBLOCK:
            return cityblock(u,v);
         case DIST_CHEBYSHEV:
            return chebyshev(u,v);
         case DIST_CORRELATION:
            return correlation(u,v);
         case DIST_COSINE:
            return cosine(u,v);
         case DIST_SQEUCLIDEAN:
            return sqeuclidean(u,v);
         default:
            Print(__FUNCTION__, " invalid parameter ");
            return EMPTY_VALUE;
        }
     }

Die private Funktion dist() berechnet den Abstand zwischen zwei Datenpunkten auf der Grundlage einer gewählten Abstandsmetrik.

Testen der Klasse Cdtw

In diesem Abschnitt werden wir die Fähigkeiten der Klasse Cdtw demonstrieren, indem wir ihre Ausgabe mit der einer Python-basierten Implementierung des DTW vergleichen. Das Modul dtw-python ist eine von mehreren DTW-Implementierungen in Python. Wir werden ein einfaches Skript in Python ausführen und sehen, ob die Ergebnisse von unserer MQL5-Implementierung reproduziert werden können. Wir beginnen mit dem Code des Python-Skripts.

import numpy as np
import matplotlib.pyplot as plt
import dtw

len = 10
add_noise = True
noise = np.random.uniform(size=len)if add_noise else np.zeros((len,))
arx = np.linspace(start = 1, stop = 6.28,num = len)
query = np.sin(arx) + noise
ref = np.cos(arx)

alignment =  dtw.dtw(query,ref,dist_method='cosine',step_pattern='symmetric2', window_type=None,keep_internals=True)
print( f'Accumulated Cost Matrix is {alignment.costMatrix}')
print(f'Distance is {alignment.distance}, \n normalize distance is {alignment.normalizedDistance}')
print(f'Warp Path is {alignment.index1[:]}:{alignment.index2[:]}')
plt.plot(alignment.index1,alignment.index2)
plt.show()

Dieses Skript zeigt, wie man zwei Zeitreihen mit dem DTW-Algorithmus abgleicht und die Anpassung visualisiert. Der Code beginnt mit dem Import der erforderlichen Bibliotheken: „numpy“ für numerische Operationen, „matplotlib.pyplot“ für die grafische Darstellung und „dtw“ für die Implementierung des DTW-Algorithmus. Die Länge der Zeitreihe wird auf 10 festgelegt, und es wird ein Array arx mit 10 gleichmäßig verteilten Werten zwischen 1 und 6,28 erstellt. Eine Zeitreihe „query“ wird erzeugt, indem der Sinus von „arx“ genommen und etwas Zufallsrauschen hinzugefügt wird, während die Referenzzeitreihe „ref“ erzeugt wird, indem der Kosinus von „arx“ genommen wird. Der DTW-Abgleich wird dann zwischen den Serien „query“ und „ref“ durchgeführt. Der Abstand zwischen den Zeitreihen wird mit der Cosinus-Abstandsmethode gemessen, und auf den Normierungspfad wird ein symmetrisches Stufenmuster angewendet. Es wird kein Windowing-Constraint verwendet, und interne Details wie die Kostenmatrix und der Normierungspfad bleiben erhalten.

Der Code gibt dann die akkumulierte Kostenmatrix, die Gesamtausrichtungsdistanz, die normalisierte Distanz und die Indizes des Normierungspfads zwischen den beiden Reihen aus. Schließlich wird der Normierungspfad durch die Darstellung der Ausrichtungsindizes visualisiert, die zeigen, wie die Indizes der beiden Zeitreihen übereinstimmen, und die Darstellung wird angezeigt. Dieser Ansatz ermöglicht einen detaillierten Vergleich von zwei Zeitreihen, die möglicherweise phasenverschoben sind oder unterschiedliche Längen haben, sodass beobachtet werden kann, wie sich eine Reihe verformt, um sich der anderen anzugleichen.

Das MQL5-Äquivalent des soeben beschriebenen Python-Codes ist unten angegeben.

//+------------------------------------------------------------------+
//|                                                      dtwTest.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include<Math\Stat\Uniform.mqh>
#include<dtw.mqh>
//---
input ulong series_len = 10;
input bool  AddRandomNoise = false;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input bool WarpPathConstraint = false;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   if(series_len<10)
     {
      Alert(" Invalid input for series_len parameter. Should be >=10 ");
      return;
     }
//---
   vector arg = np::linspace(1.0,6.28,series_len);
   vector noise = vector::Zeros(series_len);

   if(AddRandomNoise)
     {
      double array[];
      if(!MathRandomUniform(0.0,1.0,int(series_len),array))
        {
         Print(__LINE__, " MathRandomUniform() failed ", GetLastError());
         return;
        }

      if(!noise.Assign(array))
        {
         Print(__LINE__, " vector assignment failure ", GetLastError());
         return;
        }
     }

   vector q = sin(arg) + noise; // candidate sequence
   vector rf =  cos(arg);       // reference sequence

   Cdtw cdtw;

   cdtw.dtw(q,rf,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize);

   Print(" local cm ", cdtw.localCostMatrix());
   Print(" final cm ", cdtw.costMatrix());
   Print(" direction matrix \n", cdtw.directionMatrix());
   matrix path = cdtw.warpPath();
   Print(" Warp path \n", cdtw.warpPath());
   Print(" Distance metric ", cdtw.distance());
   Print(" Normalized Distance metric ", cdtw.normalizedDistance());

   vector xx = path.Col(0);
   vector yy = path.Col(1);

   CGraphic *g = np::plotXY(xx,yy,"Warp Plot", " Query ", " Reference ");

   Sleep(20000);
   g.Destroy();
   ChartRedraw();
   delete g;
  }
//+------------------------------------------------------------------+

Die Ausgabe des Python-Skripts:

KQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Accumulated Cost Matrix is [[ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
RD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
FH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
JL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
NQ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 0.  2.  4.  6.  8. 10. 12. 12. 12. 12.]
GD      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 2.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
QH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 4.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
KL      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  0.  0.  0.  0.  0.  0.  2.  4.  6.]
GS      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  2.  2.  2.  2.  2.  2.  0.  0.  0.]
PJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  [ 6.  4.  4.  4.  4.  4.  4.  0.  0.  0.]]
LJ      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Distance is 0.0, 
MM      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily)  normalize distance is 0.0
CH      0       20:52:53.954    DTW (EURUSD DFX 10 Index,Daily) Warp Path is [0 1 2 3 4 5 5 5 5 6 7 8 8 9]:[0 0 0 0 0 1 2 3 4 5 6 7 8 9]

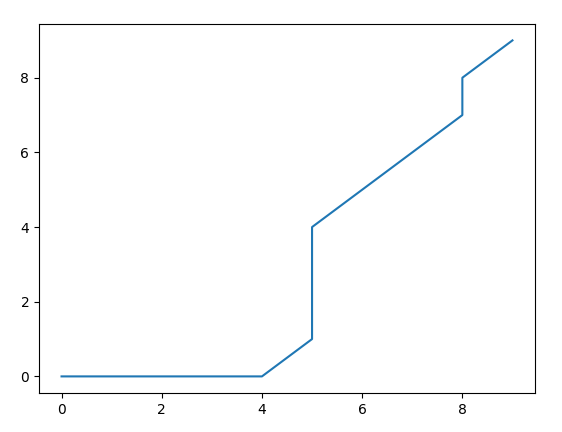
Die Ausgabe des MQL5-Skripts:

NE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         local cm [[0,2,2,2,2,2,2,0,0,0]
LH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
HE      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
RL      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
DF      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,0,0,2.220446049250313e-16,0,0,2,2,2]
ND      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,2,2,2]
FR      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,2.220446049250313e-16,2,2,2]
RS      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]
OH      0       20:56:48.971    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,2,2,2,2,2,0,0,0]]
ML      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         final cm [[0,2,4,6,8,10,12,12,12,12]
JR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
JD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,2,4,6,8,10,12,12,12,12]
EI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16,2,4,6]
CP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2,4,6]
EH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,2.220446049250313e-16,4.440892098500626e-16,2,4,6]
IN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,2,2,2,2,2,2,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4,4,4,4,4,4,4.440892098500626e-16,4.440892098500626e-16,4.440892098500626e-16]]
MO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         direction matrix 
QK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[-2147483648,1,1,1,1,1,1,1,1,1]
GN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
QQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
CK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
MR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,0,0,0,0,0,0,0,0]
OE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0,1,1,1,1,1,1,1,1]
HO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,1,1,1,0,0]
MF      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,0,0]
CH      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,0,1,1]
LN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,2,0,0,0,0,0,2,0,0]]
PK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Warp path 
HM      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)        [[9,9]
GJ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,8]
HS      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [8,7]
DK      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [7,6]
HP      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,5]
QI      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [6,4]
GQ      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,3]
RN      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,2]
MG      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [5,1]
CO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [4,0]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [3,0]
EL      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [2,0]
JE      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [1,0]
DO      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         [0,0]]
LD      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Distance metric 4.440892098500626e-16
NR      0       20:56:48.972    dtwTest (EURUSD DFX 10 Index,D1)         Normalized Distance metric 2.2204460492503132e-17

Der Vergleich der Ausgaben beider Skripte bestätigt, dass der Code gut genug zu funktionieren scheint. Wir können sie also für etwas Praktischeres verwenden. Dies bringt uns zu der Frage, wie die DTW bei der Strategieentwicklung eingesetzt werden kann.

Anwendung der dynamischen Zeitnormierung

Die DTW kann in der automatisierten Strategieentwicklung eingesetzt werden, indem sie flexible Mustererkennungs- und Vergleichstechniken von Finanzzeitreihen ermöglicht. DTW ermöglicht beispielsweise die Identifizierung wiederkehrender Preismuster, selbst wenn diese auf verschiedenen Skalen oder mit unterschiedlicher zeitlicher Dynamik auftreten. Durch den Abgleich dieser Muster mit historischen Daten ist es möglich, subtile Verschiebungen und Anomalien zu erkennen, die bedeutenden Marktbewegungen vorausgehen können.

Beim Backtesting kann DTW eingesetzt werden, um die Leistung verschiedener Strategien unter verschiedenen Marktbedingungen zu vergleichen, indem ihre jeweiligen Zeitreihenergebnisse abgeglichen werden. Dieser Ansatz hilft bei der Beurteilung, wie gut sich eine Strategie an Veränderungen des Marktverhaltens anpassen lässt, und ermöglicht ein tieferes Verständnis ihrer Robustheit. Darüber hinaus kann DTW verwendet werden, um ähnliche Handelssignale oder Marktzustände zu gruppieren, die dann analysiert werden können, um Handelsmöglichkeiten mit hoher Wahrscheinlichkeit zu identifizieren. Durch das Erkennen dieser Cluster kann eine Strategie feinabgestimmt werden, um wiederkehrende Marktverhaltensweisen effektiver zu nutzen.

Darüber hinaus kann DTW bei der Optimierung algorithmischer Strategien dabei helfen, die vielversprechendsten Parametersätze mit historischen Marktbedingungen abzugleichen, die der aktuellen Marktdynamik sehr ähnlich sind. Dadurch kann sich die Strategie dynamischer an die sich verändernden Marktbedingungen anpassen. Durch den Einsatz von DTW können automatisierte Strategien somit adaptiver und kontextbezogener werden und komplexe zeitliche Beziehungen in Finanzdaten erkennen. Das DTW mag ein nützliches Instrument sein, aber es ist kein Zauberstab. Es kann schwierig sein, damit zu arbeiten, besonders für unerfahrene Nutzer.

Eines der größten Probleme mit DTW liegt in der Konfiguration seiner Operationsparameter. Die richtige Kombination aus globalen und lokalen Beschränkungen ist entscheidend für die optimale Nutzung der Methode. DTW neigt dazu, falsche Treffer zu produzieren, und um die besten Ergebnisse zu erzielen, muss man oft viel ausprobieren. Dies wird im folgenden MQL5-Skript demonstriert.

//+------------------------------------------------------------------+
//|                                             dtwPatternSearch.mq5 |
//|                                  Copyright 2024, MetaQuotes Ltd. |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2024, MetaQuotes Ltd."
#property link      "https://www.mql5.com"
#property version   "1.00"
#resource "\\Indicators\\LogReturns.ex5"
#property script_show_inputs
#include<dtw.mqh>
#include<ErrorDescription.mqh>
enum ENUM_PRICE
  {
   CLOSE=0,//close price
   MEDIAN,//median price
   TYPICAL//typical price
  };

enum ENUM_TRANSFORM_TYPE
  {
   PERCENT_DIFF=0,//percent difference
   LOG_DIFF//log difference
  };
//--- input parameters
input string   Pattern = "0.0469,0.0093,0.0697,-0.0699";
input string   SymbolName="BTCUSD";
input datetime SearchStartDate=D'2024.06.01';
input datetime SearchStopDate=D'2018.04.22';
input double   NormalizedDistanceThreshold=0.01;
input ENUM_TIMEFRAMES      TimeFrame=PERIOD_D1;
input ENUM_DIST_METRIC AppliedDistanceMetric = DIST_EUCLIDEAN;
input ENUM_STEP_PATTERN AppliedStepPattern = STEP_SYMM2;
input ENUM_GLOBAL_CONSTRAINT AppliedGlobalConstraint = CONSTRAINT_NONE;
input ulong GlobalConstraintWinSize = 0;
input ENUM_PRICE AppliedPrice=CLOSE;
input ENUM_TRANSFORM_TYPE AppliedTransform=LOG_DIFF;
input int Lag = 1;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
   string pattern_values[];
//---
   int len = StringSplit(Pattern,StringGetCharacter(",",0),pattern_values);
   if(pattern_values[len-1]=="")
      len--;
//---
   if(len<3)
     {
      Alert("Pattern sequence is inadequately defined");
      return;
     }
//---
   vector pattern(len);
   for(ulong i = 0; i<pattern.Size(); i++)
      pattern[i]=StringToDouble(pattern_values[i]);
//---set prices handle
   int handle = INVALID_HANDLE;
   handle=iCustom(SymbolName!=""?SymbolName:NULL,TimeFrame,"::Indicators\\LogReturns.ex5",AppliedPrice,AppliedTransform,1);
   if(handle==INVALID_HANDLE)
     {
      Print("invalid handle ",ErrorDescription(GetLastError()));
      return;
     }
//---
   vector searchBuffer;
   if(!searchBuffer.CopyIndicatorBuffer(handle,0,SearchStartDate,SearchStopDate))
     {
      Print("History loading error ",ErrorDescription(GetLastError()));
      return;
     }
//---
   ulong stop = searchBuffer.Size()-pattern.Size();
   vector subv;
   Cdtw cdtw;
   ulong counter=0;
   for(ulong i = 0; i<stop; i++)
     {
      subv = np::sliceVector(searchBuffer,i,i+pattern.Size());

      if(!cdtw.dtw(subv,pattern,AppliedDistanceMetric,AppliedStepPattern,AppliedGlobalConstraint,GlobalConstraintWinSize))
        {
         Print(" dtw failed ");
         return;
        }

      if(cdtw.normalizedDistance()<NormalizedDistanceThreshold)
        {
         counter++;
         Print(" pattern found  ", datetime(SearchStopDate+(PeriodSeconds(TimeFrame)*(i+pattern.Size()-1))));
        }
     }
//---
   Print(" SearchBuffer size ", searchBuffer.Size());
   Print(" Reference pattern found ", counter, " times.");
  }
//+------------------------------------------------------------------+

Das Skript ermöglicht es dem Nutzer, ein beliebiges Muster zu definieren, das aus einer Folge von Log-Returns besteht, die mit dem Indikator „LogReturns.ex5“ berechnet werden. Das Skript dient der Suche nach einem bestimmten Muster in den Preisdaten eines Finanzinstruments, wobei zum Vergleich die dynamische Zeitnormierung (DTW) verwendet wird. Es enthält die notwendigen Bibliotheken, wie dtw.mqh für den DTW-Algorithmus und ErrorDescription.mqh für die Behandlung von Fehlerbeschreibungen. Das Skript definiert zwei Enumerationen: ENUM_PRICE, das die Art des zu verwendenden Preises angibt (close, median oder typical), und ENUM_TRANSFORM_TYPE, das festlegt, wie die Preisdaten transformiert werden (prozentuale Differenz oder logarithmische Differenz).

Mit den Eingabeparametern kann der Nutzer Details für die Suche angeben, einschließlich des abzugleichenden Musters, des Symbolnamens (z. B. „BTCUSD“), des Datumsbereichs für die Suche, eines Schwellenwerts für den normalisierten Abstand, des Zeitrahmens der Daten, der Abstandsmetrik, des Schrittmusters, der globalen Einschränkung, der Fenstergröße für die Einschränkung, der Art des zu verwendenden Preises, der Art der anzuwendenden Transformation und eines Verzögerungswerts. Beim Start des Skripts wird zunächst die Zeichenkette des Eingabemusters in ein Array von Werten zerlegt, wobei sichergestellt wird, dass das Muster mit mindestens drei Werten ausreichend definiert ist. Ist das Muster gültig, wird es zur weiteren Verarbeitung in ein Vektorformat umgewandelt. Das Skript versucht dann, die Preisdaten zu laden, indem es die Funktion iCustom verwendet, um einen nutzerdefinierten Indikator (LogReturns.ex5) aufzurufen, der den ausgewählten Preistyp und die Transformation auf die Daten anwendet. Wenn das von iCustom zurückgegebene Handle ungültig ist, wird eine Fehlermeldung ausgegeben und das Skript beendet.

Unter der Voraussetzung, dass die Preisdaten erfolgreich geladen wurden, werden sie in einem „searchBuffer“-Vektor gespeichert. Das Skript durchläuft dann den „searchBuffer“, unterteilt ihn in kleinere Untervektoren der gleichen Größe wie das Muster und vergleicht jeden Untervektor mit dem Muster unter Verwendung des DTW-Algorithmus. Der DTW-Vergleich verwendet die angegebene Abstandsmetrik, das Schrittmuster und die globale Einschränkung. Wenn bei jedem Vergleich der normalisierte Abstand zwischen dem Untervektor und dem Muster kleiner als der angegebene Schwellenwert ist, geht das Skript davon aus, dass das Muster an diesem Punkt in den Preisdaten gefunden wurde. Es gibt eine Meldung aus, die den Zeitstempel angibt, an dem das Muster gefunden wurde, und erhöht einen Zähler. Schließlich gibt das Skript die Größe des „searchBuffer“ und die Gesamtzahl der Funde des Musters innerhalb des angegebenen Zeitraums aus. Dieses Skript ermöglicht die automatische Erkennung von bestimmten Mustern in historischen Kursdaten, was bei der Entwicklung von Handelsstrategien auf der Grundlage von Mustererkennung nützlich sein kann.

Die Standardreihenfolge entspricht dem unten dargestellten Muster.

Wenn Sie das Skript mit verschiedenen Einschränkungen ausführen, ergibt sich eine unterschiedliche Anzahl von Übereinstimmungen. Dies ist die Ausgabe bei Verwendung der Standardeinstellungen.

RN      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Chosen Parameters
IJ      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    Distance Threshold 0.01
CS      0       22:00:09.210    dtwPatternSearch (BTCUSD,D1)    DIST_EUCLIDEAN
ND      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    STEP_SYMM2
CN      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)    CONSTRAINT_NONE
HG      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     WinSize 0
OO      0       22:00:09.211    dtwPatternSearch (BTCUSD,D1)     pattern found  2018.04.25 00:00:00
NJ      0       22:00:09.221    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.04.28 00:00:00
KD      0       22:00:09.222    dtwPatternSearch (BTCUSD,D1)     pattern found  2019.07.01 00:00:00
QO      0       22:00:09.230    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.04.27 00:00:00
II      0       22:00:09.234    dtwPatternSearch (BTCUSD,D1)     pattern found  2020.10.26 00:00:00
PD      0       22:00:09.237    dtwPatternSearch (BTCUSD,D1)     pattern found  2021.02.06 00:00:00
RN      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     pattern found  2024.01.29 00:00:00
DH      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     SearchBuffer size 2197
PQ      0       22:00:09.250    dtwPatternSearch (BTCUSD,D1)     Reference pattern found 7 times.

Der Parameter „NormalizedDistanceThreshold“ spielt offensichtlich eine wichtige Rolle bei der Feststellung, ob eine Übereinstimmung vorliegt. Dennoch können unterschiedliche Einschränkungen zu sehr unterschiedlichen Ergebnissen führen. Es geht nicht nur um die Einschränkungen, sondern auch um die Wahl der geeigneten Abstandsmetrik. Für die Anwendung des DTW-Algorithmus sind natürlich umfangreiche Fachkenntnisse erforderlich.

Schlussfolgerung

Die dynamische Zeitnormierung bietet einen ausgefeilten Ansatz zur Mustererkennung in der Finanzzeitreihenanalyse, hat aber auch einige Nachteile, die es zu beachten gilt. Erstens ist DTW rechenintensiv, insbesondere bei langen Zeitreihen oder großen Datensätzen. Bei diesem Algorithmus wird jeder Punkt einer Zeitreihe mit jedem Punkt einer anderen Zeitreihe verglichen, was zu einem erheblichen Zeit- und Speicherbedarf führen kann. Dies wird besonders problematisch, wenn man versucht, hochfrequente Finanzdaten zu analysieren oder Echtzeitanalysen durchzuführen. Zweitens ist DTW empfindlich gegenüber Rauschen und Ausreißern in Finanzdaten.

Finanzielle Zeitreihen sind aufgrund der Marktvolatilität oft verrauscht, und kleine Schwankungen oder Anomalien können dazu führen, dass der DTW-Algorithmus irreführende Ausrichtungen erzeugt. Diese Empfindlichkeit kann bei der Mustererkennung zu falsch-positiven Ergebnissen führen, d. h. es werden Muster erkannt, die keine signifikante Vorhersagekraft haben. Schließlich kann DTW Probleme mit der Interpretierbarkeit haben. Sie liefert zwar ein Maß für die Ähnlichkeit zwischen Zeitreihen, aber der Normierungspfad und die sich daraus ergebende Abstandsmetrik können schwer sinnvoll zu interpretieren sein, vor allem im Kontext der Finanzanalyse, wo klare und umsetzbare Erkenntnisse entscheidend sind. Diese Herausforderungen deuten darauf hin, dass DTW zwar ein nützliches Instrument für die Mustererkennung in Finanzzeitreihen sein kann, aber sorgfältig und oft in Kombination mit anderen Analysemethoden angewandt werden sollte, die ihre Grenzen ausgleichen können.

Datei	Beschreibung
Mql5\include\np.mqh	Header-Datei mit verschiedenen Vektor- und Matrix-Hilfsfunktionen
Mql5\include\dtw.mqh	Include-Datei mit der MQL5-Implementierung des Algorithmus Dynamische Zeitnormierung
Mql5\indicators\LogReturns.mq5	Indikator der logarithmischen Renditen einer Preisreihe
Mql5\scripts\dwTest.mq5	Skript, das zum Testen und zur Demonstration der Verwendung der MQL5-Implementierung von DTW verwendet wird
Mql5\scripts\dtwPatternSearch.mq5	Skript für die Suche nach einem beliebigen Muster in einer Datenprobe
Mql5\scripts\DTW.py	ein Python-Skript, das das Modul dtw-python verwendet, um zwei Reihen mit Hilfe des DTW-Algorithmus abzugleichen