MetaTrader 5 / テスター
English Русский 中文 Español Deutsch Português
preview
MQL5の圏論（第9回）：モノイド作用

MQL5の圏論（第9回）：モノイド作用

MetaTrader 5 — テスター | 1 8月 2023, 09:41
265 0
Stephen Njuki
Stephen Njuki

はじめに

前回の記事では、モノイドを紹介し、それらを教師あり学習で分類して取引の決定に情報を提供する方法を説明しました。引き続き、モノイド作用（英語）と、それらを教師なし学習で使用して入力データの次元を削減する方法を検討していきます。演算によるモノイド出力は常にその集合の要素になります。これは、それらが変換的ではないことを意味します。それらはモノイド作用です。したがって、作用集合はモノイド集合の部分集合である必要がないため、変換の能力が追加されます。変換とは、モノイド集合の要素ではない作業出力を持つ能力を意味します。

正式には、集合S上のモノイドM (e, *)のモノイド作用aは次のように定義されます。

a:M x S - - > S ;                                (1)

e a s - - > s;                                      (2)


m * (n * s) - - > (m * n) a s                (3)

ここで、m、nはモノイドMの要素、sは集合Sの要素です。


図解と方法

モデルの意思決定プロセスにおけるさまざまな特徴の相対的な重要性を理解することは重要です。前回の記事にあるように、私たちの場合、「特徴」は次のとおりです。

  • 振り返り期間
  • 時間枠
  • 適用価格
  • 指標
  • レンジかトレンドかの決定


モデルの特徴を重み付けし、予測の精度に最も敏感な特徴を特定するのに役立ついくつかの手法を見ていきます。1つの手法を選択し、その推奨に基づいて、モノイド作用を通じてモノイド集合を拡張することで、そのノードでモノイドに変換を追加し、これがトレーリングストップを正確に配置する能力にどのような影響を与えるかを確認します。前回の記事で検討した応用です。

訓練集合内の各データ列の相対的な重要性を判断する場合、使用できるツールと方法がいくつかあります。これらの手法は、モデルの予測に対する各特徴（データ列）の寄与を定量化するのに役立ち、どのデータ列を精緻化する必要があるのか​​、またどのデータ列にそれほど注意を払う必要がないのかを判断するのに役立ちます。一般的に使用されるいくつかの方法を次に示します。


特徴重要度のランク付け

このアプローチでは、モデルのパフォーマンスへの影響を考慮し、重要性に基づいて特徴をランク付けします。通常、ランダムフォレスト、勾配ブースティングマシン(GBM)、エクストラツリーなどのさまざまなアルゴリズムは、ツリーの構築に役立つだけでなく、モデルの訓練後に抽出できる組み込みの特徴重要度の測定値を提供します。

これを説明するために、前の記事と同様に、価格帯の変化を予測し、これをオープンポジションのトレーリングストップの調整に使用するシナリオを考えてみましょう。したがって、当時の決定点（特徴またはデータ列）をツリーとして考慮します。このタスクにランダムフォレスト分類器を使用する場合、訓練（英語）の後、各意思決定ポイントをツリーとして取得します。モデルを使用すると、特徴量の重要度ランク付けを抽出できます。

明確にするために、データ集合には次のツリーが含まれます。

  • 振り返り分析期間の長さ（整数データ）
  • 取引で選択された時間枠（列挙データ：1時間、2時間、3時間など）
  • 分析に使用される適用価格（列挙データ：始値、中央値、典型値、終値）
  • 分析に使用される指標の選択（RSIオシレーターまたはボリンジャーバンドエンベロープの列挙データ）


ランダムフォレスト分類器で訓練した後、ジニ不純度(Gini impurity)の重みを使用して特徴の重要度ランク付けを抽出できます。特徴重要度スコアは、モデルの意思決定プロセスにおける各データ列の相対的な重要性（重み付け）を示します。

特徴の重要度ランク付けの結果が次のようになったと仮定します。

  • 分析に使用される指標の選択:0.45
  • 振り返り分析期間の長さ:0.30
  • 分析に使用される適用価格:0.20
  • 取引で選択した時間枠:0.05


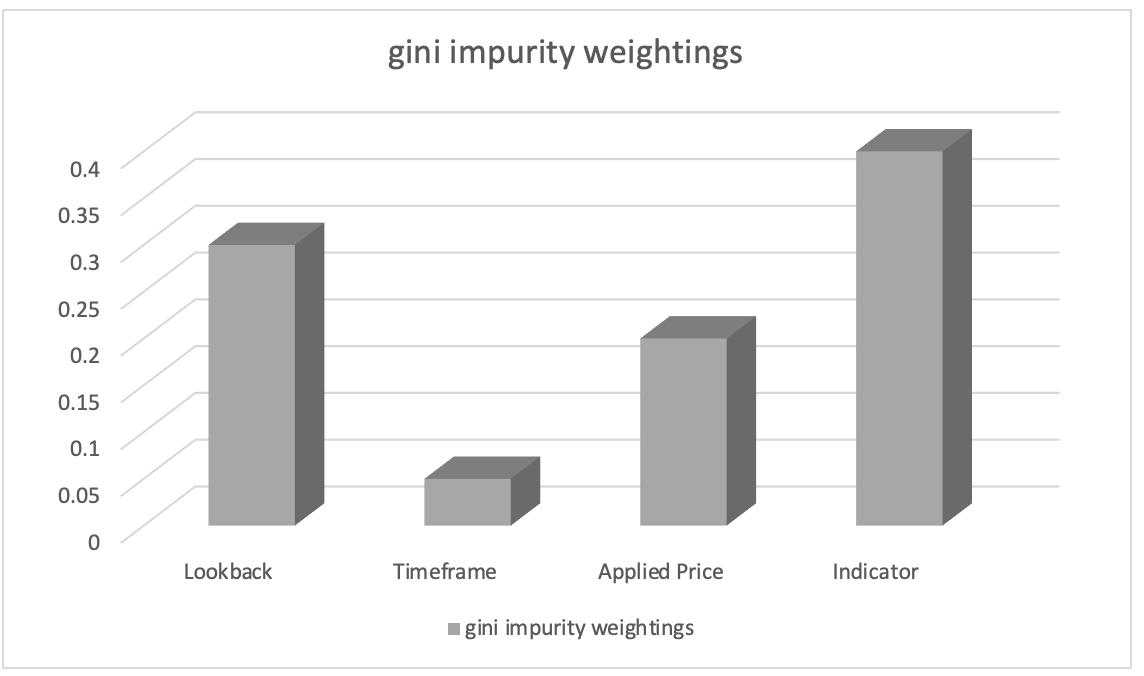
このことから、「分析に使用する指標の選択」特徴が最も重要であり、次に「振り返り分析期間の長さ」特徴が重要であると推測できます。「分析に使用される適用価格」特徴は3番目にランクされていますが、「取引で選択された時間枠」特徴の重要性は最も低くなります。

この情報は、どの特徴がモデルの予測に影響を与えるのに最も重要かを理解する際に役立ちます。また、この知識があれば、特徴エンジニアリング中により重要な特徴に焦点を当てたり、特徴の選択に優先順位を付けたり、これらの特徴に関連するドメイン固有の洞察をさらに探索したりすることができます。私たちの場合、他の指標のモノイド作用集合を導入することで指標のモノイド集合を変換し、それが予測にどのような影響を与えるかを調べることができます。したがって、私たちの作用集合は、RSIオシレーターとボリンジャーバンドエンベロープに代替指標を追加します。ただし、どの指標を追加する場合でも、前の記事のボリンジャーバンドの場合と同様に、その出力を正規化し、値が0から100の範囲内にあることを確認する必要があります。0は価格バー範囲の減少を示し、100は範囲の増加を示します。


順列の重要性

順列の重要度は、特徴（またはデータ列）の順序をランダムに並べ替え、予測をおこなうときにその後のモデルのパフォーマンスの変化を測定することによって、その順序の重要性を評価します。これまでの注文は、振り返り期間、次に時間枠、次に適用価格、次に指標、そして最後に取引決定タイプであることを思い出してください。意思決定の順序を変えるとどうなるでしょうか?これをおこなうには、一度に1つのデータ列（特徴）のみを並べ替える必要があります。これらのデータ列のいずれか1つの予測精度の低下が大きいほど、重要性が高いことを示します。この方法はモデルに依存せず、あらゆる機械学習アルゴリズムに適用できます。

これを説明するために、上記および前の記事と同じ5つの列のデータ集合を使用して、価格バー範囲の変化を予測するシナリオを考えてみましょう。このタスクには勾配ブースティング分類器を使用することにします。順列重要度を使用して各データ列の重要性を評価するには、基本的にモデルを訓練します。前回の記事で使用したモノイド演算子関数と同型写像設定を使用して勾配ブースティング分類器を訓練すると、データ集合は次の表のようになります。


データ集合を使用して勾配ブースト分類器を訓練するには、次の4つのステップバイステップガイドに従うことができます。

データの前処理:

このステップは、one-hotエンコーディングなどの手法を使用して、離散データ（つまり、価格チャートの時間枠、適用価格、指標の選択、取引決定などの列挙）を数値表現に変換することから始まります。次に、データ集合を特徴（データ列1～5）とモデル予測と実際の値（データ列6～7）に分割します。

データの分割:前処理の後、データ集合を訓練集合の行とテスト集合の行に分割する必要があります。これにより、訓練データで最適に機能した設定を使用しながら、目に見えないデータでのモデルのパフォーマンスを評価できます。通常は80対20の分割が使用されますが、データ集合内の行のサイズと特性に基づいて比率を調整できます。この記事で使用するデータ列については、60対40の分割をお勧めします。

勾配ブースト分類器を作成する:次に、C/MQL5で勾配ブースト分類に必要なライブラリを組み込むか、必要な関数を実装します。これは、エキスパートアドバイザー(EA)初期化関数に、推定器の数、学習率、最大深度などのハイパーパラメータも指定する勾配ブースト分類器モデルの作成されたインスタンスを含めることを意味します。

鉄道模型:意思決定プロセス中に訓練データを反復処理し、各データ列の順序を変更することにより、訓練集合を使用して勾配ブースト分類器を訓練します。その後、モデルの結果が記録されます。価格バー範囲調整の予測の精度を高めるために、各モノイド単位元や演算タイプ（前の記事で使用した演算リストから）などのモデルのパラメータを変更することもできます。

システムの評価:モデルは、訓練からの最適な設定を使用して、テストデータ行（分割で40%分離）でテストされます。これにより、十分に訓練されたモデル設定が訓練されていないデータに対してどのように機能するかを判断できます。その際、サンプル外データ（テストデータ行）のすべてのデータ行を実行して、目標価格バー範囲の変化を予測するためのモデルの最適な設定機能を評価することになります。テスト実行の結果は、F-scoreなどの方法を使用して評価できます。

パフォーマンスの改善が必要な場合は、勾配ブースト分類器のハイパーパラメータを変更することでモデルを微調整することもできます。最適なハイパーパラメータを見つけるには、グリッド検索や相互検証などの方法を利用する必要があります。モデルの開発が成功したら、そのモデルを使用して、新しいデータのカテゴリ変数を前処理およびエンコードして、訓練データと同じ形式であることを確認することで、新しい予期せぬデータについての仮定を立てることができます。これにより、訓練されたモデルを使用して、新しいデータの価格バー範囲の変化を予測できます。

MQL5での勾配ブースト分類の実装は、最初からおこなうのが難しく、時間がかかる場合があることに注意してください。したがって、Cで書かれた機械学習ライブラリ（XGBoostやLightGBMなど）を使用します。これらは、CAPIで効果的な勾配ブースティングの実装を提供します。強くお勧めします。

説明のために、データ列を並べ替えた後、次の結果が得られると想像してみましょう。

  • 振り返り期間を切り替えると、予測パフォーマンスは0.062低下します。
  • 順列の時間枠によりパフォーマンスが0.048低下します
  • 適用された価格に順列を適用すると、0.027のパフォーマンス損失が発生します。
  • 指標のデータ列の位置をシャッフルすると、パフォーマンスが0.014低下します。
  • 取引決定を変更した後のパフォーマンス損失は0.009につながる


これらの結果から、値を並べ替えるとモデルのパフォーマンスが最大に低下するため、価格バー範囲の変化を予測する際に「振り返り期間」がその位置において最も重要であるという結論に至りました。2番目に重要な特徴は「時間枠」で、次に「適用価格」、「指標」、最後に「取引決定」が続きます。

この方法では、モデルのパフォーマンスに対する各データ列の影響を定量化することで、それらの相対的な関連性を判断できます。各特徴（データ列）の相対的な重要性を評価することで、特徴をより適切に選択し、特徴を設計し、予測モデルでさらに研究開発が必要な領域を強調表示することもできます。

したがって、改善をさらに説明するために、まだモノイド集合に含まれていない追加の振り返り期間を追加することによってそれを変更する振り返りモノイド集合のモノイド作用を提案する場合があります。したがって、これにより、これらの追加期間がモデルによる価格バー範囲の変化の予測精度に影響を与えるかどうかを調査することができます。現在、モノイド集合は1～8の値で構成されており、それぞれは4の倍数です。倍数が3または2だったらどうなるでしょうか?これはパフォーマンスにどのような影響を及ぼしますか?現在では、振り返り期間が意思決定プロセスにおいてどのような位置を占めているか、そしてそれがシステム全体のパフォーマンスに最も影響を及ぼしやすいことが理解されているため、これらの問題や同等の問題に対処できる可能性があります。


SHAP値

SHAP(SHapleyAdditiveexPlanations)は、ゲーム理論の原則に基づいて各データ列に重要度の値を割り当てる統一フレームワークです。SHAP値は、あらゆる可能性を考慮して、特徴の寄与を公平に配分します。これらは、XGBoost、LightGBM、深層学習モデルなどの複雑なモデルにおける特徴の重要性を包括的に理解するのに役立ちます。


再帰的特徴削除(RFE)

RFEは、重みまたは重要度スコアに基づいて重要度の低い特徴を再帰的に削除することで特徴する反復的な特徴選択方法です。プロセスは、必要な特徴の数に達するか、パフォーマンスのしきい値に達するまで続行されます。これを説明するには、振り返り期間から取引意思決定タイプまでの5つの列のデータ集合があり、5つの特徴（データ列）のそれぞれに基づいて価格バー範囲の変化を予測する、上記の同様のシナリオを使用できます。このタスクにはサポートベクターマシン(SVM)分類子を使用します。再帰的特徴除去(RFE)がどのように適用されるかを次に示します。

  • データ集合内のすべてのデータ列を使用して、SVM分類器でモデルを訓練します。最初は訓練がすべてです。
  • 次に特徴のランク付けが行われ、SVM分類器によって各特徴に割り当てられた重みまたは重要度スコアが取得されます。これらは、分類タスクにおけるそれぞれの相対的な重要性を示します。
  • 次に、最も重要でない特徴の削除が行われ、SVMの重みに基づいて最も重要でないデータ列が省略されます。これは、重みが最も低いフィーチャを削除することで実行できます。
  • 次に、データ列を削減したモデルの再訓練が行われ、SVM分類器が残りの特徴のみに適用されます。
  • データ列を省略しないパフォーマンス評価は、精度やFスコアなどの適切な評価指標を使用して行われます。
  • プロセスは、必要な列数に到達するまでステップ2から5まで繰り返され、各反復で最も重要でない特徴（またはデータ列）が削除され、特徴集合が削減されたモデルが再訓練されます。


たとえば、5つの特徴から開始してRFEを適用し、3つの特徴を目標にしていると仮定します。反復1では、これが重要度スコアの降順に基づいた特徴のランク付けであると仮定します。

  • 振り返り期間
  • 時間枠
  • 適用価格
  • 指標
  • 通商決定


重要度スコアが最も低い特徴である貿易決定が削除されます。残りの特徴を使用してSVM分類器を再訓練する:その後、振り返り、時間枠、適用価格、指標が続きます。これを反復2でのランク付けとして考えてみましょう。

  • 振り返り期間
  • 指標
  • 時間枠
  • 適用価格

重要度スコアが最も低い特徴を削除します。これが適用価格になります。必要な特徴数に達したため、これ以上削除する特徴が残っていないため、反復は停止します。反復プロセスは、必要な特徴数（またはFスコアしきい値などの別の事前定義された停止基準）に達すると停止します。したがって、最終モデルは選択された特徴（振り返り期間、指標、時間枠）を使用して訓練されます。RFEは、関連性の低い特徴を繰り返し削除することで、分類タスクで最も重要な特徴を特定するのに役立ちます。RFEは、モデルのパフォーマンスに最も寄与する特徴の部分集合を選択することにより、モデルの効率を向上させ、過剰適合を軽減し、解釈可能性を高めることができます。


L1正則化(Lasso)

L1正則化は、モデルの目的関数に罰金項を適用し、スパースな特徴重みを促進します。その結果、重要度の低い特徴の重みはゼロまたはゼロに近い傾向があり、重みの大きさに基づいて特徴を選択できるようになります。トレーダーが不動産やREITへのエクスポージャーを評価したいシナリオを考えてみましょう。住宅価格のデータ集合があり、それを使用して、面積、寝室の数、住宅の価格傾向、バスルームの数、場所、築年数などのさまざまな特徴に基づいて住宅の価格傾向を予測します。L1正則化、特にLassoアルゴリズムを使用して、これらの特徴の重要性を評価できます。仕組みは次のとおりです。

  • データ集合内のすべての特徴を使用して、L1正則化(Lasso)を使用して線形回帰モデルを訓練することから始めます。L1正則化項は、モデルの目的関数に罰金を追加します。
  • Lassoモデルを訓練した後、各特徴に割り当てられた推定重みを取得します。これらの重みは、住宅価格を予測する際の各特徴の重要性を表します。L1正則化は、まばらな特徴の重みを促進します。つまり、重要度の低い特徴の重みがゼロまたはゼロに近い傾向があることを意味します。
  • ランクの特徴：重みの大きさに基づいて特徴をランク付けできます。絶対的な重みが大きい特徴はより重要であると見なされますが、重みがゼロに近い特徴は重要ではないと見なされます。


たとえば、住宅価格データ集合でLassoモデルを訓練し、次の特徴の重みを取得すると仮定します。

  • 面積：0.23
  • 寝室の数：0.56
  • バスルームの数：0.00
  • 場所：0.42
  • 築年：0.09


これらの特徴の重みに基づいて、住宅価格を予測するための重要性の観点から特徴をランク付けできます。

  • 寝室の数：0.56
  • 場所：0.42
  • 面積：0.23
  • 築年：0.09
  • バスルームの数：0.00

この例では、寝室数の絶対的な重みが最も高く、住宅価格の予測における重要性が高いことを示しています。重要度では場所と面積がそれに続きますが、築年の重みは比較的低くなります。この場合、バスルームの数の重みは0であり、重要ではないとみなされ、事実上モデルから除外されていることを示しています。

L1正則化(Lasso)を適用することで、住宅価格を予測するための最も重要な特徴を特定して選択できます。正則化罰金は特徴の重みの疎性を促進し、重みの大きさに基づいて特徴を選択できるようにします。この手法は、どの特徴がターゲット変数（住宅価格の傾向）に最も影響を与えるかを理解するのに役立ち、特徴エンジニアリング、モデルの解釈、および過剰適合の削減によるモデルのパフォーマンスの潜在的な向上に役立ちます。


主成分分析(PCA)

主成分分析は、元の特徴を低次元空間に変換することで特徴の重要性を間接的に評価できる次元削減手法であり、最大分散の方向を特定します。分散が最も高い主成分は、より重要であると考えることができます。


相関分析

相関分析では、特徴量とターゲット変数の間の線形関係を調べます。多くの場合、絶対相関値が高い特徴は、ターゲット変数を予測する上でより重要であると考えられます。ただし、相関関係は非線形関係を捉えるものではないことに注意することが重要です。


相互情報量

相互情報量は、変数間の統計的な依存性を測定します。ある変数に関する情報を別の変数からどれだけ取得できるかを定量化します。相互情報量の値が高いほど関係が強いことを示し、相対的な特徴の重要性を評価するために使用できます。

これを説明するために、トレーダー/投資家が、年齢、性別、収入、購読の種類、購入総額などの利用可能なさまざまな特徴（データ列）に基づいて顧客離れを予測することを目的として、顧客情報のデータ集合に基づいて、急成長中のプライベートエクイティのスタートアップでポジションをオープンしようとしているシナリオを考えることができます。）相互情報を使用して、これらの重要性を評価できます。その仕組みは次のとおりです。

  • まず、各特徴とターゲット変数（顧客離れ）の間の相互情報量を計算します。相互情報量は、ある変数に含まれる別の変数に関する情報の量を測定します。私たちの場合、利用可能なデータ列の各特徴から顧客の離脱に関する情報をどの程度取得できるかを定量化します。
  • 相互情報スコアを算出したら、その値に基づいてランク付けします。相互情報量の値が高いほど、特徴と顧客離れの間の関係が強いことを示し、重要性が高いことを示します。


たとえば、データ列の相互情報量スコアが次のようになると仮定します。

  • 築年：0.08
  • 性別：0.03
  • 所得：0.12
  • 購読の種類：0.10
  • 合計購入数：0.15


これらに基づいて、顧客離れを予測する上での重要性の観点から特徴をランク付けできます。

  • 合計購入数：0.15
  • 所得：0.12
  • 購読の種類：0.10
  • 築年：0.08
  • 性別：0.03

この例では、TotalPurchasesの相互情報スコアが最も高く、顧客離れに関するほとんどの情報が含まれていることを示しています。収入と購読タイプがそれに続きますが、年齢と性別の相互情報スコアは比較的低くなります。

相互情報を使用することで、各データ列に重みを付け、モノイド作用を追加することでどの列をさらに調査できるかを調べることができます。このデータ集合は前の記事とは異なり、まったく新しいものです。説明するには、最初にそれぞれの集合を定義して各データ列のモノイドを構築すると役立ちます。おそらく最高の相互情報量を持つデータ列の合計購入は連続データであり、離散的データではありません。つまり、基本モノイドの範囲外の列挙を導入することによってモノイド集合を簡単に拡張することはできません。したがって、さらに研究したり、モノイドでの総購入額を拡大したりするために、購入日のディメンションを追加できます。これは、作用集合に日時の連続データが含まれることを意味します。合計購入額に関するモノイドと（作用を介して）ペアリングすると、購入ごとに購入日を取得できるため、顧客離れにおける購入日と金額の重要性を調べることができます。これにより、より正確な予測が可能になる可能性があります。


モデル固有の手法

一部の機械学習アルゴリズムには、特徴の重要性を判断するための特定の方法があります。たとえば、決定木ベースのアルゴリズムは、データをさまざまなツリーに分割するために特徴が使用された回数に基づいて特徴重要度スコアを提供できます。

顧客情報のデータ集合があり、年齢、性別、収入、閲覧履歴などのさまざまな特徴に基づいて顧客が製品を購入するかどうかを予測したいシナリオを考えてみましょう。このタスクには、決定木ベースのアルゴリズムであるランダムフォレスト分類器を使用することにします。この分類器を使用して特徴の重要性を判断する方法は次のとおりです。

  • データ集合内のすべての特徴を使用してランダムフォレスト分類器を訓練することから始めます。ランダムフォレストは、複数の決定木を組み合わせたアンサンブルアルゴリズムです。
  • ランダムフォレストモデルを訓練した後、このアルゴリズムに固有の特徴重要度スコアを抽出できます。特徴重要度スコアは、分類タスクにおける各特徴の相対的な重要性を示します。
  • 次に、重要度スコアに基づいて特徴をランク付けします。スコアが高い特徴は、モデルのパフォーマンスに大きな影響を与えるため、より重要であるとみなされます。


たとえば、ランダムフォレスト分類器を訓練した後、次の特徴重要度スコアを取得します。

  • 築年：0.28
  • 性別：0.12
  • 所得：0.34
  • 閲覧履歴：0.46


これらの特徴重要度スコアに基づいて、顧客の購入を予測するための重要性の観点から特徴をランク付けできます。

  • 閲覧履歴：0.46
  • 所得：0.34
  • 築年：0.28
  • 性別：0.12

この例では、閲覧履歴の重要度スコアが最も高く、顧客の購入を予測する際に最も影響力のある特徴であることを示しています。収入がそれにほぼ続きますが、年齢と性別の重要度スコアは比較的低くなります。ランダムフォレストアルゴリズムの特定の方法を活用することで、アンサンブル内の異なるツリー間でデータを分割するために各特徴が使用された回数に基づいて特徴の重要度スコアを取得できます。この情報により、予測タスクに最も大きく貢献する主要な特徴を特定できます。これは、特徴の選択、データの根底にあるパターンの理解、およびモデルのパフォーマンスの潜在的な向上に役立ちます。


専門知識とドメインの理解

特徴の重要性を評価するには、定量的な方法に加えて、専門知識とドメインの理解を組み込むことが重要です。対象分野の専門家は、専門知識と経験に基づいて、特定の特徴の関連性と重要性についての洞察を常に提供できます。また、異なる方法ではわずかに異なる結果が得られる可能性があり、どの方法を選択するかは、使用されるデータ集合と機械学習アルゴリズムの特定の特性に依存する可能性があることに注意することも重要です。多くの場合、特徴の重要性を包括的に理解するために複数の手法を使用することが推奨されます。


実装

データ列/特徴の重み付けを実装するには、相関関係を使用します。前回の記事で使用したのと同じ特徴にこだわっているため、モノイド設定値の相関関係を価格バー範囲の変化と比較して、各データ列の重み付けを取得します。各データ列は、集合の値が列の値である集合を持つモノイドであることを思い出してください。テストしているため、最初は、最も相関性の高い列を展開する（モノイド作用によって変換する）必要があるのか​​、それとも相関性が最も低いデータ列にする必要があるのか​​がわかりません。そのために、さまざまなテスト実行にわたってこの選択をおこなうのに役立つ追加のパラメータを追加します。また、モノイド作用に対応するために追加のグローバルパラメータを導入しました。

//+------------------------------------------------------------------+
//|                                                   TrailingCT.mqh |
//|                   Copyright 2009-2013, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Math\Stat\Math.mqh>
#include <Expert\ExpertTrailing.mqh>
#include <ct_9.mqh>
// wizard description start
//+------------------------------------------------------------------+
//| Description of the class                                         |
//| Title=Trailing Stop based on 'Category Theory' monoid-action concepts  |
//| Type=Trailing                                                    |
//| Name=CategoryTheory                                              |
//| ShortName=CT                                                     |
//| Class=CTrailingCT                                                |
//| Page=trailing_ct                                                 |
//|....	
//| Parameter=IndicatorIdentity,int,0, Indicator Identity            |
//| Parameter=DecisionOperation,int,0, Decision Operation            |
//| Parameter=DecisionIdentity,int,0, Decision Identity              |
//| Parameter=CorrelationInverted,bool,false, Correlation Inverted   |
//+------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//| Class CTrailingCT.                                               |
//| Appointment: Class traling stops with 'Category Theory'          |
//|               monoid-action concepts.                            |
//| Derives from class CExpertTrailing.                              |
//+------------------------------------------------------------------+
int                        __LOOKBACKS[8] = {1,2,3,4,5,6,7,8};
ENUM_TIMEFRAMES            __TIMEFRAMES[8] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES[4] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE };
string                     __INDICATORS[2] = { "RSI", "BOLLINGER_BANDS" };
string                     __DECISIONS[2] = { "TREND", "RANGE" };

#define                    __CORR 5
int                        __LOOKBACKS_A[10] = {1,2,3,4,5,6,7,8,9,10};
ENUM_TIMEFRAMES            __TIMEFRAMES_A[10] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES_A[5] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE, PRICE_WEIGHTED };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CTrailingCT : public CExpertTrailing
  {
protected:
   //--- adjusted parameters
   double m_step;                // trailing step
   
   ...
   
   //
   
   CMonoidAction<double,double>  m_lookback_act;
   CMonoidAction<double,double>  m_timeframe_act;
   CMonoidAction<double,double>  m_appliedprice_act;
   
   bool                          m_correlation_inverted;
   
   int                           m_lookback_identity_act;
   int                           m_timeframe_identity_act;
   int                           m_appliedprice_identity_act;
   
   int                           m_source_size;       // Source Size

public:
   //--- methods of setting adjustable parameters
   
   
   
   
... 
   
   void                 CorrelationInverted(bool value)     { m_correlation_inverted=value;                 }
   
   
... 
   
  };


また、Operate_X関数は、Operateという1つの関数に整理されました。さらに、データ列の'Get'関数がモノイド作用に対応するように拡張され、それぞれのグローバル変数配列のインデックス付けを支援するためにそれぞれのオーバーロードが追加されました。

これが後続クラスの開発方法です。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate(CMonoid<double> &M,EOperations &O,int &OutputIndex)
   {
      OutputIndex=-1;
      //
      double _values[];
      ArrayResize(_values,M.Cardinality());ArrayInitialize(_values,0.0);
      //

      
... 
      
      //
      
      if(O==OP_LEAST)
      {
         OutputIndex=0;
         double _least=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_least>_values[i]){ _least=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_MOST)
      {
         OutputIndex=0;
         double _most=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_most<_values[i]){ _most=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_CLOSEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _closest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_closest>fabs(_values[i]-_mean)){ _closest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
      else if(O==OP_FURTHEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _furthest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_furthest<fabs(_values[i]-_mean)){ _furthest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback(CMonoid<double> &M,int &L[])
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      
... 
   
      int _i_out=-1;
      //
      Operate(M,m_lookback_operation,_i_out);
      
      if(_i_out==-1){ return(4); }
      
      return(4*L[_i_out]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(CMonoid<double> &M, ENUM_TIMEFRAMES &T[])
   {
      
... 
      
      int _i_out=-1;
      //
      Operate(M,m_timeframe_operation,_i_out);
      
      if(_i_out==-1){ return(INVALID_HANDLE); }
      
      return(T[_i_out]);
   }


EURUSDについて前の記事でおこなったように、ライブラリの組み込みRSIシグナルクラスを使用して2022.05.01から2023.05.15までの時間枠でテストを実行すると、これがテストレポートになります。



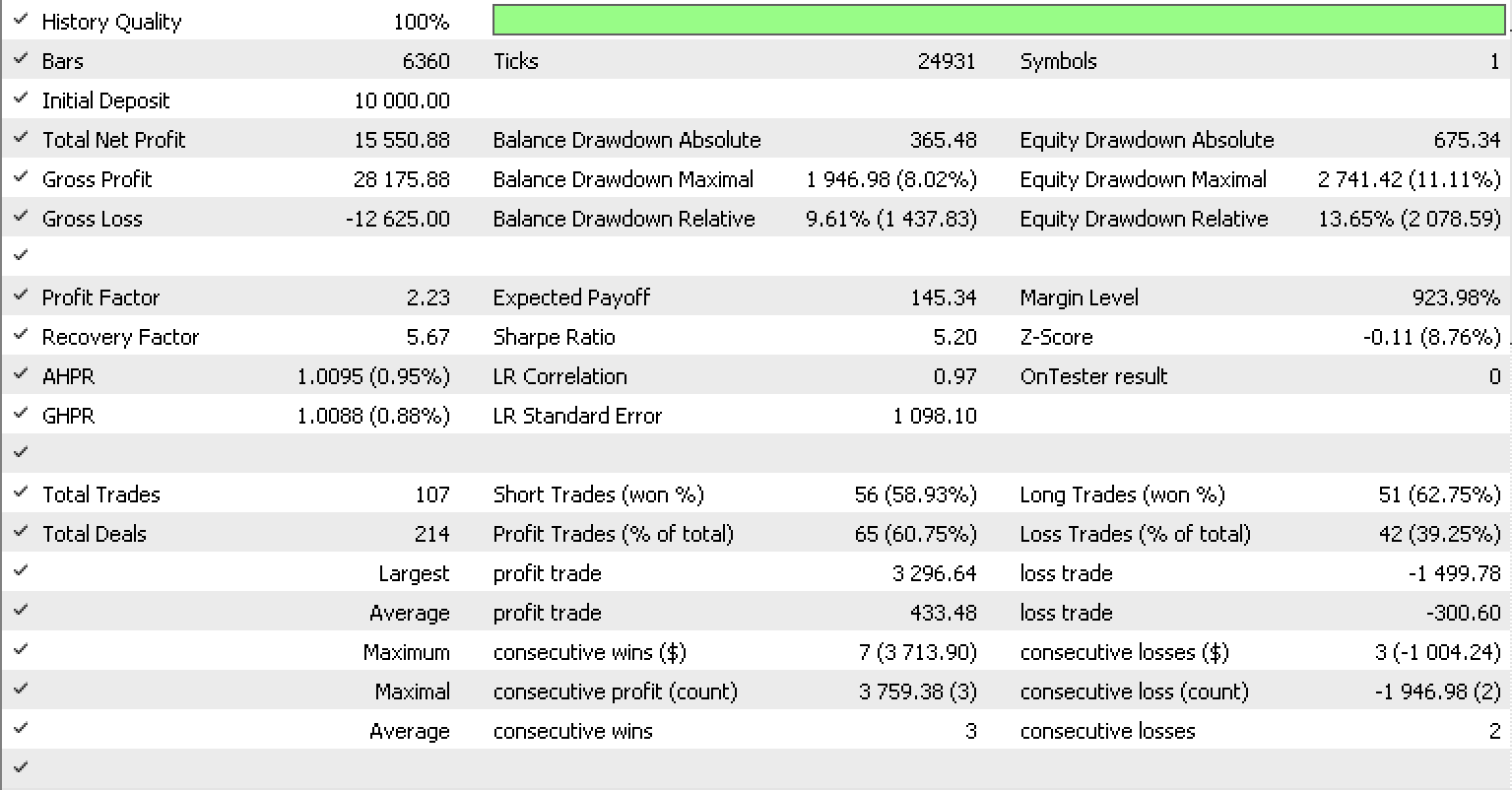
上記のレポートの結果は、前の記事の最良のレポートほど良好ではありませんが、モノイド作用を介したモノイド集合の変更に対するレポート結果の感度を強調しています。


結論

要約すると、ポジションのストップロスをより正確に調整するために、変換されたモノイド、別名モノイド作用が、ボラティリティを予測するトレーリングストップシステムをさらに微調整する方法について見てきました。これは、モデル、その感度、および精度を向上させるために拡張が必要な​​特徴（ある場合）をよりよく理解するために、モデルの特徴（この場合はデータ列）の重み付けに通常使用されるさまざまな方法と並行して検討されました。気に入っていただければ幸いです。ご精読ありがとうございました。

MetaQuotes Ltdにより英語から翻訳されました。
元の記事: https://www.mql5.com/en/articles/12739

添付されたファイル |
ZIPをダウンロード
TrailingCT_9.mqh (35.09 KB)
ct_9.mqh (65.06 KB)
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

この著者による他の記事

ディスカッションに移動
MQL5の圏論（第10回）：モノイド群 MQL5の圏論（第10回）：モノイド群
MQL5における圏論の実装についての連載を続けます。ここでは、モノイド集合を正規化して、より幅広いモノイド集合とデータ型にわたって比較しやすくする手段としてモノイド群を見ていきます。
MQL5.comでシグナルプロバイダーとして成功する方法 MQL5.comでシグナルプロバイダーとして成功する方法
この記事の主な目的は、MQL5.comでトップのシグナルプロバイダーになるための手順を簡単かつ正確に説明することです。私の知識と経験に基づいて、優れた戦略を見つけ、テストして最適化する方法など、成功するシグナルプロバイダーになるために何が必要かを説明します。さらに、シグナルの公開、説得力のある説明の作成、シグナルの効果的な宣伝と管理に関するヒントも提供します。
MQL5のインタラクティブGUIで取引チャートを改善する（前編）：移動可能なGUI (I) MQL5のインタラクティブGUIで取引チャートを改善する（前編）：移動可能なGUI (I)
MQL5で動かせるGUIを作成するための包括的なガイドで、取引戦略やユーティリティでのダイナミックなデータ表現の力を解き放ちましょう。チャートイベントのコアコンセプトに触れ、同じチャート上にシンプルで複数の移動可能なGUIをデザインし、実装する方法を学びます。この記事では、GUIに要素を追加し、機能性と美しさを向上させるプロセスについても説明します。
MQL5を使用してカスタムドンチャンチャネル指標を作成する方法 MQL5を使用してカスタムドンチャンチャネル指標を作成する方法
価格周辺のチャネルを視覚化するために使用できるテクニカルツールは数多くあります。これらのツールの1つが、ドンチャンチャネル指標です。この記事では、ドンチャンチャネル指標を作成する方法と、EAを使用してカスタム指標としてそれを取引する方法を学びます。