MQL5 中的范畴论 (第 9 部分)：幺半群（Monoid）— 动作

概述

在上一篇文章中，我们讲述了幺半群，并见识到它们在监督学习中如何分类和通知交易决策。 为了继续，我们将探讨幺半群 — 动作，以及如何将它们用于无监督学习，从而降低输入数据的维度。 出自幺半群操作的输出总会是其集合的成员，这意味着它们不具有变换性。 因此，幺半群动作增加了变换能力，因为动作集不必是幺半群集合的子集。 通过变换，我们指的是动作输出超出幺半群集合成员的能力。

从形式上讲，基于集合 S 的幺半群 M( e, *)，其幺半群动作 a 定义为：

a: M x S - - > S ;                                (1)

e a s - - > s;                                      (2)

m * (n * s) - - > (m * n) a s                (3)

其中 m、n 是幺半群 M 的成员，s 是集合 S 的成员。

阐明和方法

了解模型决策过程中不同特征的相对重要性很有价值。 在我们的例子中，根据之前的文章，我们的 “特征” 是：

• 回溯周期
• 时间帧
• 应用价格
• 指标
• 并决定范围或趋势。

我们将查看一些适用于对模型特征进行加权的技术，并帮助辨别对预测准确性最敏感的技术。 我们将选择一种技术，并基于其建议，通过扩展幺半群集合，以幺半群动作，在节点上添加幺半群变换，并看看这对我们准确放置尾随止损的能力有什么影响，正如我们在上一篇文章中研究的应用一样。

在判定训练集中每个数据列的相对重要性时，有若干种工具和方法可供使用。 这些技术有助于量化每个特征（数据列）对模型预测的贡献，并指导我们哪些数据列可能需要详查，以及哪些数据列应该较少关注。 以下是一些常用的方法：

特征重要性排位

此方式参考对模型性能的影响，基于重要性对特征进行排位。 通常，各种算法（例如随机森林、梯度提升机（GBM）、或额外树）提供内置的特征重要性度量，这些度量不仅有助于构建树，而且可在模型训练后提取。

为了阐明这一点，我们研究一个场景，譬如上一篇文章里，我们希望预测价格的变化范围，并用它来调整持仓的尾随止损。 故此，我们将把当时的决策点（特征或数据列）视为树。 如果我们使用随机森林分类器来完成这项任务，取我们的每个决策点作为一棵树，在训练模型后，我们可以提取特征重要性排位。

为了澄清，我们的数据集将包含以下树：

• 回溯分析周期的长度（整数型数据）
• 交易中选择的时间帧（枚举数据：1-小时、2-小时、3-小时、等等）
• 分析所用的应用价格（枚举数据：开盘价、中位数价、典型价、收盘价）
• 分析所用的指标选择（枚举数据：RSI 振荡器、或布林带轨道线线）

利用随机森林分类器进行训练后，我们可以依据 Gini 杂质权重提取特征重要性排位。 特征重要性分数表示模型决策过程中每个数据列的相对重要性（权重）。

我们假设特征重要性排位的结果如下：

• 分析所用的指标选择：0.45
• 回溯分析周期长度：0.30
• 分析所用的应用价格：0.20
• 交易中选择的时间帧：0.05

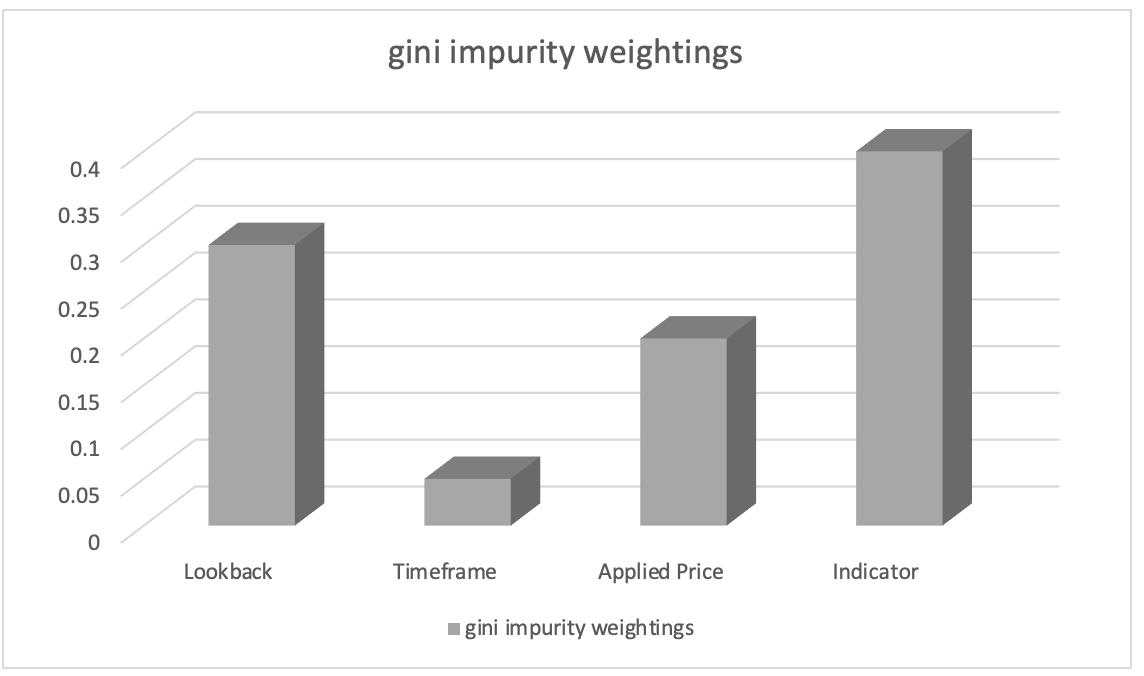
有基于此，我们可以推断出 “分析所用的指标选择” 特征最为重要，其次是 “回溯分析周期的长度” 特征。 “分析所用的应用价格” 特征排位第三，而 “交易中选择的时间帧” 特征重要性最低。

这些信息可以指导我们了解哪些特征在影响模型预测方面最明显，拥有这些知识，我们将在特征工程化期间专注于更重要的特征，优先选择特征，或深入探索与这些特征相关的特定领域见解。 在我们的例子中，我们可以通过引入其它指标的幺半群动作集合来查看转换指标的幺半群集合，并检验它如何影响我们的预测。 如此，我们的动作集将添加备用指标 RSI 振荡器和布林带轨道线。 但是，无论我们添加哪个指标，就像上一篇文章中的布林带一样，我们都需要对其输出进行正则化，并确保它在 0 到 100 的范围内，其中 0 表示价格柱线范围减小，而 100 表示范围增加。

重要性排列

重要性排列通过随机置换特征（或数据列）的顺序，并在进行预测时测量模型性能的后续变化，来评估特征（或数据列）顺序的重要性。 请记住，到目前为止，顺序是回溯周期，然后是时间帧，然后是应用价格，然后是指标，最后是交易决策类型。 如果我们的决策排序不同，将会发生什么？ 为此，我们只得一次仅置换一个数据列（特征）。 对于数据列中的任何一个，其预测准确性下降幅度越大，表明其重要性越高。 此方法与模型无关，并可应用于任意机器学习算法。

为了阐明这一点，我们研究一个场景，其中包含相同的五列数据集，如上文和上一篇文章，我们打算预测价格柱线范围的变化。 我们决定使用梯度提升分类器来完成该任务。 为了利用重要性排列来评估每个数据列的重要性，我们的模型要进行基础训练。 当我们用上一篇文章中的幺半群运算符函数和幺元设置训练梯度提升分类器之时，我们的数据集与下表相仿：

为了用我们的数据集训练梯度提升分类器，我们可遵循以下 4 个分步指南：

预处理数据：

这一步先用独热编码等技术将我们的离散数据（即那些枚举值，价格图表时间帧、应用价格、指标选择、交易决策）转换为数字表示。 然后，您将数据集拆分为特征（数据列 1-5），和模型预测加上实际值（数据列 6-7）。

拆分数据：预处理之后，我们需要将数据集切分若干行作为训练集、及若干行作为测试集。 这可令您基于未见过的数据上评估模型的性能，同时采用最适配训练数据的设置。 典型情况，按照 80-20 切分，但您可以根据数据集中的行数规模和特征调整比率。 至于本文中所用的数据列，我推荐按照 60-40 切分。

创建梯度提升分类器：然后，您要在 C/MQL5 中包含必要的函数库，或实现梯度提升分类所需的函数。 这意味着在智能系统初始化函数中要包括为梯度提升分类器模型创建实例，您还要在其中指定超参数，如评估器数量、学习率、和最大深度。

训练模型：通过迭代遍历训练数据，并在决策过程中改变每个数据列的顺序，训练集是用来训练梯度提升分类器。 然后记录模型结果。 为了提高针对价格柱线范围调整的预测准确性，您还可以更改模型的参数，例如每个幺半群幺元、或操作类型（来自上一篇文章中所用的操作清单）。

评估系统：采用来自训练时的最佳设置，基于测试数据行（切分时的 40%）测试模型。 这令您可以判定经过良好训练的模型设置，在未经训练数据上的性能如何。 在执行时，您将遍历样本数据（测试数据行）之外的所有数据行，来评估模型的最佳设置预测目标价格柱线范围变化的能力。 然后可用 F-分数 等方法评估测试运行的结果。

如果性能需要改进，您还可以通过更改梯度提升分类器的超参数来优调模型。 为了发现最佳超参数，您需要利用网格搜索和交叉验证等方法。 开发一个成功的模型之后，您可以用它来对新的、不可预见的数据做出假设，方法是为新数据中的分类变量进行预处理和编码，以确保它们与训练数据具有相同的格式。 这样一来，您就能用经过训练的模型来预测新数据的价格柱线范围变化。

请注意，在 MQL5 中实现梯度提升分类可能很困难，而且从头开始更耗时。 因此，强烈建议使用由 C 语言编写的机器学习函数库，例如 XGBoost 或 LightGBM，它们通过 C 语言 API 提供有效的梯度提升实现。

为了便于阐明，我们来想象一下，在对数据列进行置换后，我们得到以下结果：

• 切换回溯周期后，预测效果会下降 0.062。
• 时间帧置换导致性能下降 0.048
• 应用价格置换，导致性能损失 0.027
• 因指标数据列位置置换性能下降 0.014。
• 交易决策置换后的表现损失导致 0.009

这些发现令我们得出结论，在预测价格柱线范围的变化时，“回溯周期” 对其位置具有最大的意义，因为置换其值会导致模型性能的最大下降。 第二个最重要的特征是“时间帧”，其次是“应用价格”、“指标”，最后是“交易决策”。

通过量化每个数据列对模型性能的影响，该方法令我们能够判定它们的相对相关性。 通过评估每个特征（数据列）的相对重要性，我们能够更好地选择特征、工程化特征，甚至可能突显我们的预测模型需要更多研究和开发的区域。

故此，我们可以为回溯幺半群集提出幺半群动作，通过添加尚未在幺半群集中的额外回溯周期来改变它，从而进一步解释改进。 由此，这令我们能够调查这些额外的周期（如果有的话）是否对我们的模型预测价格柱线范围变化的程度有影响。 幺半群集目前由 1 到 8 数值组成，每个数值都是 4 的倍数。 如果我们的倍数是 3 或 2 会如何？ 这会对性能产生什么影响（如果有的话）？ 由于我们现在明白了回溯周期在决策过程中所处的位置，并且它对系统的整体性能最敏感，因此可以解决这些和类似的问题。

SHAP 值

SHAP（SHapley Additive exPlanations）是一个统一的框架，它根据博弈论原理为每个数据列分配重要性数值。 SHAP 值为特征贡献提供了公平分配，同时考虑了所有可能性。 它们提供了对复杂模型中特征重要性的全面理解，如 XGBoost、LightGBM 或深度学习模型。

递归特征消除（RFE）

RFE 是一种迭代特征选择方法，其工作原理是从特征权重或重要性分数之中递归消除不太重要的。 该过程持续进行，直至达到期望的特征数量、或性能阈值得到满足。 为了阐明这一点，我们可用类似上述的场景，此刻我们有一个五列数据集，从回顾周期到交易决策类型，且我们打算基于 5 个特征（数据列）中的每一个来预测价格柱线范围的变化。 我们使用支持向量机 （SVM） 分类器来完成此任务。 以下是递归特征消除（RFE）如何运用的：

• 使用数据集中的所有数据列，配以 SVM 分类器训练模型。 最初训练是依据所有一切。
• 接下来发生的是特征排位，此处我们获取由 SVM 分类器分配给每个特征的权重或重要性分数。 这些值表示在分类任务中每一个的相对重要性。
• 接下来，完成消除最不重要的特征，此处我们基于 SVM 权重忽略最不重要的数据列。 这可以通过删除权重最低的特征来完成。
• 接下来发生的是依减少的数据列重新训练模型，此处仅将 SVM 分类器应用于剩余特征。
• 在不忽略数据列的情况下完成性能评估，使用相应的评估度量（例如准确性、或 F-分数）。
• 从步骤 2 到步骤 5 重复该过程，直至达到期望的列数，从而在每次迭代中消除最不重要的特征（或数据列），并依据减少后的特征集重新训练模型。

举例，假设我们从 5 个特征开始，并应用 RFE，我们的目标是 3 个特征。 在第一次迭代中，假设特征排位基于重要性分数降序：

• 回溯周期
• 时间帧
• 应用价格
• 指标
• 交易决策

消除重要性得分最低的特征，即交易决策。 然后，依据剩余特征重新训练 SVM 分类器：回溯周期、时间帧、应用价格、和指标。 我们取其作为第二次迭代的排位：

• 回溯周期
• 指标
• 时间帧
• 应用价格

消除重要性得分最低的特征，这次是应用价格。 由于我们已经达到了期望的特征数量，因此无需消除更多的特征，因此迭代将停止。 当我们达到期望的特征数量（或其它预定义的停止准则，如 F-分数阈值）时，迭代过程就会停止。 故此，最终模型会依据选出的特征进行训练：回溯周期、指标、和时间帧。 RFE 通过迭代删除相关性不太强的特征，来帮助识别分类任务中最重要的特征。 通过选择对模型性能贡献最大的特征子集，RFE 可以提高模型效率、减少过拟合、并增强可解释性。

L1 正则化 （Lasso）

L1 正则化将惩罚项应用到模型的目标函数，从而鼓励稀疏特征权重。 结果就是，不太重要的特征往往具有零或接近零的权重，从而允许根据权重量级选择特征。 考虑一个场景，其中有一位交易者想要衡量他对房地产和房地产投资信托基金（REIT）的估值，我们已有一套房价数据集，我们打算基于各种特征（如面积、卧室数量、浴室数量、位置、和房龄）来预测住宅的价格趋势。 我们可以使用 L1 正则化，尤其是 Lasso 算法，来评估这些特征的重要性。 以下是它如何运作的：

• 我们先用数据集中的所有特征训练配以 L1 正则化（Lasso）的线性回归模型。 L1 正则化项为模型的目标函数增加了惩罚。
• 训练 Lasso 模型之后，我们获得了分配给每个特征的估算权重。 这些权重代表每个特征在预测房价方面的重要性。 L1 正则化鼓励稀疏特征权重，这意味着不太重要的特征往往权重为零，或接近零。
• 特征排位：我们可以根据权重量级对特征排位。 具有较高绝对权重的特征被认为更重要，而权重接近于零的特征则被认为不太重要。

例如，如果我们假设依据房价数据集训练 Lasso 模型，并获得以下特征权重：

• 面积： 0.23
• 卧室数量： 0.56
• 浴室数量： 0.00
• 位置： 0.42
• 房龄：0.09

基于这些特征权重，我们可以按照对预测房价的重要性进行特征排位：

• 卧室数量： 0.56
• 位置： 0.42
• 面积： 0.23
• 房龄：0.09
• 浴室数量： 0.00

在此示例中，卧室数量的绝对权重最高，表明其在预测房价方面的重要性较高。 “位置”和“面积”的重要性紧随其后，而“房龄”的权重相对较低。 在本例中，浴室数量的权重为零，表明它被认为不重要，并且已从模型中排除。

通过应用 L1 正则化（Lasso），我们可以识别和选择预测房价的最重要特征。 正则化惩罚促进了特征权重的稀疏性，允许根据权重量级选择特征。 该技术有助于了解哪些特征对目标变量（住宅价格趋势）影响最大，并且可用于特征工程化、模型解释、以及通过减少过拟合来潜在地提高模型性能。

主成分分析（PCA）

PCA 是一种降维技术，可以通过将原始特征转换为低维空间来间接评估特征重要性，PCA 识别最大方差的方向。 具有最高方差的主成分可认定为更重要。

相关性分析

相关性分析检验特征与目标变量之间的线性关系。 具有较高绝对相关性数值的特征通常被认为对预测目标变量更为重要。 不过，重点要注意的是，相关性并不能捕获非线性关系。

互动信息

互动信息衡量变量之间的统计依赖性。 它把一个变量可以从另一个变量获得多少信息进行了量化。 较高的互动信息值表示关系越强，可用于评估相对特征重要性。

为了阐明这一点，我们可以考虑一个场景，即交易者/投资者考察一家处于上升期的私募股权初创公司，并基于客户信息数据集进行投资，目标是根据各种可查特征（我们的数据列）预测客户黏性，例如年龄、性别、收入、订阅类型、和购买总数。 我们可以使用互动信息来评估这些特征的重要性。 以下是它如何运作的：

• 我们先计算每个特征和目标变量（客户黏性）之间的互动信息。 互动信息衡量一个变量包含的有关另一个变量的信息量。 在我们的例子中，它把我们从可查数据列中的每个特征中可以获得多少关于客户黏性的信息进行了量化。
• 一旦我们计算出互动信息分数，我们就会根据它们的值进行排位。 互动信息值越高，表示特征与客户黏性之间的关系越强，推崇的重要性越高。

例如，如果我们假设数据列的互动信息分数为：

• 年龄：0.08
• 性别：0.03
• 收入： 0.12
• 订阅类型：0.10
• 购买总数： 0.15

基于这些，我们就可以按照针对预测客户黏性的重要性进行特征排位：

• 购买总数： 0.15
• 收入： 0.12
• 订阅类型：0.10
• 年龄：0.08
• 性别：0.03

在此示例中，“购买总数”具有最高的互动信息分数，表明它包含有关客户黏性的大多数信息。 收入和订阅类型紧随其后，而年龄和性别的互动信息分数相对较低。

通过使用互动信息，我们能够对每个数据列进行加权，并探索哪些列可以通过添加幺半群动作来深入研究。 这个数据集是全新的，不像我们在之前文章中看到的，所以为了阐明这一点，它有助于通过定义各自的集合来构造每个数据列的幺半群。 具有最高互动信息的数据列“购买总数”是连续数据，而非离散数据，这意味着我们不能轻易地通过在基准幺半群中引入超出范围的枚举来扩展幺半群集。 那么，为了进一步研究或扩大幺半群的购买总数，我们可以添加购买日期的维度。 这意味着我们的动作集将具有连续的日期时间数据。 依据购买总数与幺半群配对（通过动作）时，对于每次购买，我们都可以获得购买日期，这将令我们能够探索购买日期和金额对客户黏性的重要性。 这可能会导致更准确的预测。

特定于模型的技术

一些机器学习算法拥有特殊方法来检测特征重要性。 例如，基于决策树的算法可以根据穿过不同树拆分数据时用到特征的次数来提供特征的重要性分数。

我们研究一个场景，此处我们已有一个客户信息数据集，我们希望根据年龄、性别、收入、和浏览历史记录等各种特征来预测客户是否会购买产品。 我们决定使用随机森林分类器来完成此任务，其是一种基于决策树的算法。 以下是如何用该分类器判定特征重要性的：

• 我们先用数据集中的所有特征训练随机森林分类器。 随机森林是一种结合了多个决策树的集成算法。
• 随机森林模型训练之后，我们可以提取特定于该算法的特征重要性分数。 特征重要性分数指示每个特征在分类任务中的相对重要性。
• 然后，我们根据特征的重要性分数进行特征排位。 分数较高的特征被认为更重要，因为它们对模型性能的影响更大。

例如，在训练随机森林分类器之后，我们得到以下特征重要性分数：

• 年龄：0.28
• 性别：0.12
• 收入： 0.34
• 浏览历史： 0.46

基于这些特征重要性分数，我们可以根据特征对预测客户购买的重要性进行特征排位：

• 浏览历史： 0.46
• 收入： 0.34
• 年龄：0.28
• 性别：0.12

在此示例中，浏览历史记录具有最高重要性分数，表明它是预测客户购买的最有影响力的特征。 收入紧随其后，而年龄和性别的重要性得分相对较低。 利用随机森林算法的特殊方法，我们可以基于融合体中穿过不同树拆分数据时每个特征用到的次数来获得特征重要性分数。 这些信息令我们能够识别对预测任务贡献最大的关键特征。 它有助于特征选择、了解数据中的潜在模式，并潜在提升模型的性能。

专业知识和领域理解

除了量化方法之外，结合专业知识和领域理解对于评估特征重要性至关重要。 主题专家始终能够基于他们的专业知识和经验，提供针对特定特征的相关性和重要性的见解。 还有重点要注意的是，不同方法产生的结果可能会略微不同，并且技术的选择可能取决于所使用的数据集和机器学习算法的特定特征。 往往推荐采用多种技术来全面了解特征的重要性。

实现

为了实现数据列/特征的权重，我们将使用相关性。 由于我们坚持使用与上一篇文章相同的特征，因此我们将比较幺半群集值与价格柱线范围变化的相关性，从而获得每个数据列的权重。 回想一下，每个数据列都是一个含有集合的幺半群，其中集合值是列值。 由于我们正在测试，因此在开始时，我们不知道是否应该扩展最相关的列（已通过幺半群动作转换），或者它应该是相关性最小的数据列。 为此，我们将添加一个额外的参数，其有助于从各种测试运行中做出选择。 此外，我们还引入了额外的全局参数来满足幺半群动作。

//+------------------------------------------------------------------+
//|                                                   TrailingCT.mqh |
//|                   Copyright 2009-2013, MetaQuotes Software Corp. |
//|                                              http://www.mql5.com |
//+------------------------------------------------------------------+
#include <Math\Stat\Math.mqh>
#include <Expert\ExpertTrailing.mqh>
#include <ct_9.mqh>
// wizard description start
//+------------------------------------------------------------------+
//| Description of the class                                         |
//| Title=Trailing Stop based on 'Category Theory' monoid-action concepts  |
//| Type=Trailing                                                    |
//| Name=CategoryTheory                                              |
//| ShortName=CT                                                     |
//| Class=CTrailingCT                                                |
//| Page=trailing_ct                                                 |
//|....	
//| Parameter=IndicatorIdentity,int,0, Indicator Identity            |
//| Parameter=DecisionOperation,int,0, Decision Operation            |
//| Parameter=DecisionIdentity,int,0, Decision Identity              |
//| Parameter=CorrelationInverted,bool,false, Correlation Inverted   |
//+------------------------------------------------------------------+
// wizard description end
//+------------------------------------------------------------------+
//| Class CTrailingCT.                                               |
//| Appointment: Class traling stops with 'Category Theory'          |
//|               monoid-action concepts.                            |
//| Derives from class CExpertTrailing.                              |
//+------------------------------------------------------------------+
int                        __LOOKBACKS[8] = {1,2,3,4,5,6,7,8};
ENUM_TIMEFRAMES            __TIMEFRAMES[8] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES[4] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE };
string                     __INDICATORS[2] = { "RSI", "BOLLINGER_BANDS" };
string                     __DECISIONS[2] = { "TREND", "RANGE" };

#define                    __CORR 5
int                        __LOOKBACKS_A[10] = {1,2,3,4,5,6,7,8,9,10};
ENUM_TIMEFRAMES            __TIMEFRAMES_A[10] = {PERIOD_H1,PERIOD_H2,PERIOD_H3,PERIOD_H4,PERIOD_H6,PERIOD_H8,PERIOD_H12,PERIOD_D1,PERIOD_W1,PERIOD_MN1};
ENUM_APPLIED_PRICE         __APPLIEDPRICES_A[5] = { PRICE_MEDIAN, PRICE_TYPICAL, PRICE_OPEN, PRICE_CLOSE, PRICE_WEIGHTED };
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
class CTrailingCT : public CExpertTrailing
  {
protected:
   //--- adjusted parameters
   double m_step;                // trailing step
   
   ...
   
   //
   
   CMonoidAction<double,double>  m_lookback_act;
   CMonoidAction<double,double>  m_timeframe_act;
   CMonoidAction<double,double>  m_appliedprice_act;
   
   bool                          m_correlation_inverted;
   
   int                           m_lookback_identity_act;
   int                           m_timeframe_identity_act;
   int                           m_appliedprice_identity_act;
   
   int                           m_source_size;       // Source Size

public:
   //--- methods of setting adjustable parameters
   
   
   
   
... 
   
   void                 CorrelationInverted(bool value)     { m_correlation_inverted=value;                 }
   
   
... 
   
  };

还有，“Operate_X” 函数经整理，并为 “Operate” 函数。 此外，获取数据列的 “Get” 函数已得到扩展，可适应幺半群动作，并且添加了重载函数，可按索引访问相应的全局变量数组。

这就是我们正开发的尾随类。

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate(CMonoid<double> &M,EOperations &O,int &OutputIndex)
   {
      OutputIndex=-1;
      //
      double _values[];
      ArrayResize(_values,M.Cardinality());ArrayInitialize(_values,0.0);
      //

      
... 
      
      //
      
      if(O==OP_LEAST)
      {
         OutputIndex=0;
         double _least=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_least>_values[i]){ _least=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_MOST)
      {
         OutputIndex=0;
         double _most=_values[0];
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_most<_values[i]){ _most=_values[i]; OutputIndex=i; }
         }
      }
      else if(O==OP_CLOSEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _closest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_closest>fabs(_values[i]-_mean)){ _closest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
      else if(O==OP_FURTHEST)
      {
         double _mean=0.0;
         for(int i=0;i<M.Cardinality();i++)
         {
            _mean+=_values[i];
         }
         _mean/=M.Cardinality();
         
         OutputIndex=0;
         double _furthest=fabs(_values[0]-_mean);
         for(int i=0;i<M.Cardinality();i++)
         {
            if(_furthest<fabs(_values[i]-_mean)){ _furthest=fabs(_values[i]-_mean); OutputIndex=i; }
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback(CMonoid<double> &M,int &L[])
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      
... 
   
      int _i_out=-1;
      //
      Operate(M,m_lookback_operation,_i_out);
      
      if(_i_out==-1){ return(4); }
      
      return(4*L[_i_out]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(CMonoid<double> &M, ENUM_TIMEFRAMES &T[])
   {
      
... 
      
      int _i_out=-1;
      //
      Operate(M,m_timeframe_operation,_i_out);
      
      if(_i_out==-1){ return(INVALID_HANDLE); }
      
      return(T[_i_out]);
   }

如果我们如同上一篇文章中一样，依据 EURUSD 从 2022.05.01 到 2023.05.15 的 H1 时间帧进行测试，使用函数库的内置 RSI 信号类，这就是我们的测试报告。

虽然我们上面报告的结果不如我们在上一篇文章中的最佳报告中那么好，但报告结果确实突显出幺半群动作对于幺半群集变化的敏感性。

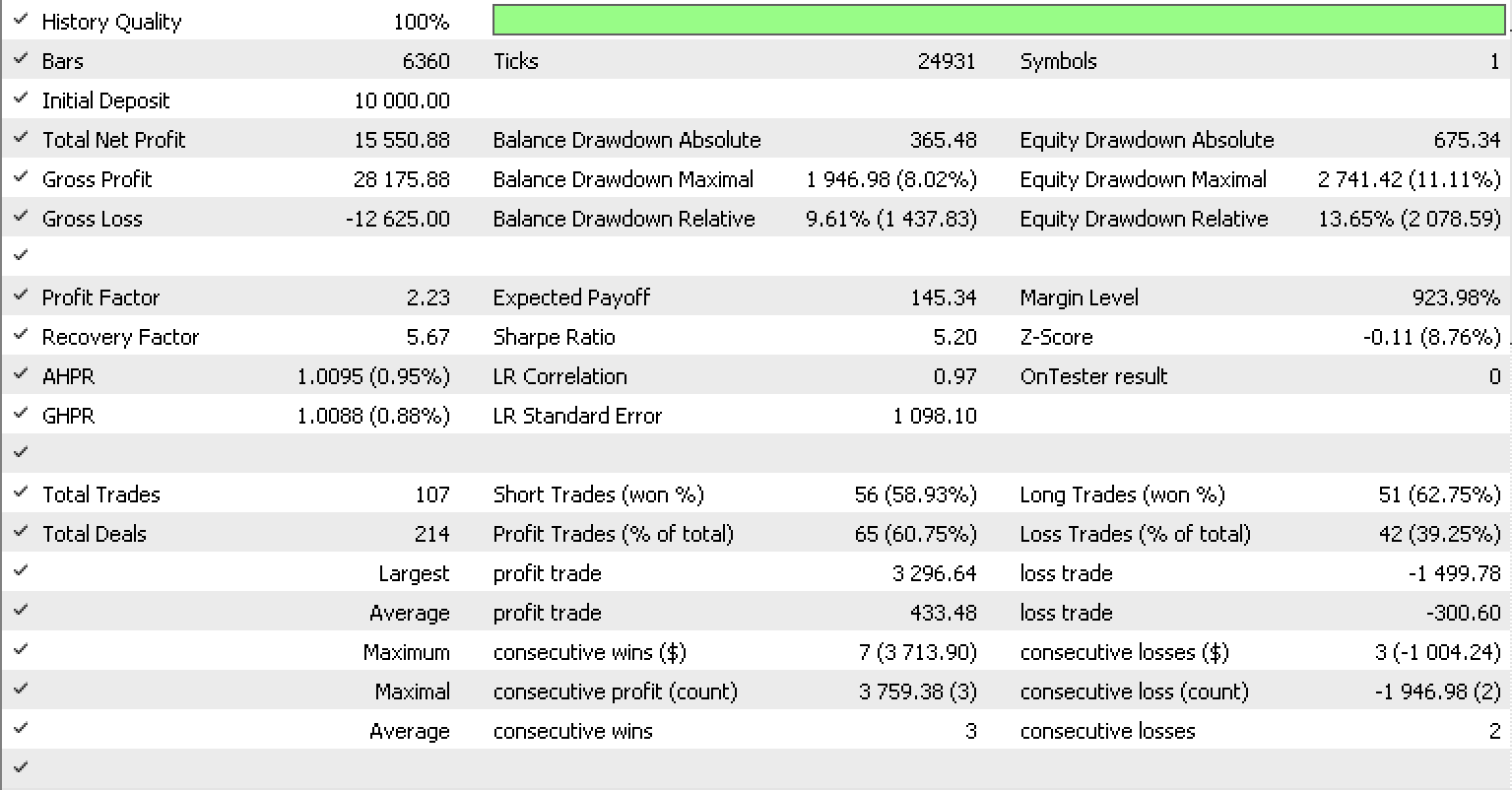
结束语

总而言之，我们已经查验了变换后的幺半群（又名幺半群行动）如何能进一步优调尾随止损系统，该系统可于波动当中进行预测，以便更准确地调整持仓的止损。 通常配合加权模型特征（在我们的例子中为数据列）的各种方法一起查验，以便更好地理解模型、其灵敏度、以及哪些特征（如果有的话）需要扩展，从而提高模型的准确性。 希望您喜欢它，感谢您的阅读。