Теория категорий в MQL5 (Часть 8): Моноиды

Введение

В предыдущей статье, посвященной теории категорий, мы раскрыли ключевые концепции мульти-, относительных и индексированных множеств и исследовали их значение в алгоритмической торговле. В продолжение темы введем понятие моноида. Моноиды занимают важное место в математике и информатике, обеспечивая структурированный подход к моделированию операций над множествами элементов.

По определению моноиды представляют собой набор из трех элементов, а именно множества, бинарной операции, которая принимает любые два элемента этого множества и всегда выводит элемент, который также является членом этого множества, и элемента равнозначности (identity element), который принадлежит множеству, так что при сопряжении с любым другим членом этого множества в вышеупомянутой бинарной операции на выходе мы всегда имеем элемент, отличающийся от того, с которым сопряжен текущий элемент равнозначности. Данная бинарная операция также является ассоциативной. Иными словами, моноид — это способ объединения элементов в множество с соблюдением предопределенных правил. Моноиды обеспечивают систематический и гибкий подход к агрегированию и обработке данных.

Формально моноид M с элементами-членами a, b и c; элемент равнозначности e; бинарная операция *; могут быть определены как:

M * M - - > M;                      1

e * a - - > a;                        2

a * e - - > a;                        3

a * (b * c) - - > (a * b) * c     4

В уравнении 1 подчеркивается, что объединение любых двух элементов множества в пару дает элемент множества. Уравнения 2 и 3 подчеркивают важность элемента равнозначности в том смысле, что в результате мы всегда получаем элемент бинарной операции, который не является равнозначностью. Наконец, уравнение 4 подчеркивает ассоциативность бинарной операции *.

Иллюстрация и методы

Чтобы проиллюстрировать возможное применение моноидов трейдерами, рассмотрим пять вопросов, с которыми некоторые или большинство трейдеров могут столкнуться перед совершением сделок:

1. Продолжительность периода ретроспективного анализа.
2. Используемый таймфрейм графика.
3. Применяемая цена.
4. Применяемый параметр.
5. И стоит ли, учитывая эту информацию, торговать в диапазоне или по тренду.

Для каждого из этих решений мы придумаем:

• набор возможных значений, из которых можно выбирать;
•  бинарную операцию, помогающую выбирать между любыми двумя элементами. Этой операцией может быть метод MQL5, который вызывается другим методом итеративно по всем элементам множеств, пока не будет сделан выбор.
• А также индекс элемента равнозначности данного множества. Именно индекс, так как этот элемент входит в множество, являющееся массивом.
• Выбор идеальной бинарной операции, которая просто выбирает между двумя элементами, представляет собой выбор из:
• Операции выбора меньшего из двух элементов.
•  Операции выбора наибольшего из двух оцениваемых элементов
•  Операции выбора из множества элемента, ближайшего к среднему значению двух элементов в бинарной операции.
•  И наконец операции выбора из множества элемента, который наиболее удален от среднего значения двух элементов в бинарной операции.

Рассмотрим пять точек принятия решений: ретроспективный период, таймфрейм, применяемую цену, индикатор и интерпретацию сигналов. У других трейдеров могут быть другие ключевые критерии принятия решений. Поэтому это не окончательное пошаговое руководство, а критерии, выбранные в рамках статьи.

При использовании моноидов теории категорий для классификации данных следует соблюдать некоторые меры предосторожности, чтобы обеспечить точные и содержательные результаты. Наиболее важные параметры:

1) Четко определенная моноидная структура:

Необходимо убедиться, что данные, с которыми вы работаете, образуют правильную моноидную структуру в соответствии с определением. Это означает проверку того, что они удовлетворяют аксиомам моноида, таким как наличие элемента равнозначности и ассоциативность при бинарной операции. Вот три примера ловушек, которые могут привести к плохо определенной моноидной структуре:

Отсутствие замыкания:

Если бинарная операция, используемая в моноиде, не приводит к элементам, принадлежащим одному и тому же множеству или домену, замыкание нарушается. Например, если вы попытаетесь определить моноид натуральных чисел с помощью операции вычитания, вы столкнетесь с элементами, которые не являются натуральными числами (например, вычитание 5 из 3 дает -2, что не является натуральным числом). Операция, строго говоря, не является ни сложением, ни вычитанием, ни умножением. Это просто метод с четко определенными правилами, который принимает любые два элемента множества и возвращает один элемент, являющийся членом этого множества.

Неассоциативность:

Другая трудность возникает, когда бинарная операция не удовлетворяет свойству ассоциативности. Если элементы в вашем моноиде не объединяются ассоциативным образом, это может привести к неоднозначным и противоречивым результатам. Например, рассмотрим моноид, в котором операция — умножение, а элементы — матрицы. Если у вас есть три матрицы a, b и c, то эта операция не является ассоциативной, т. е. (a * b) * c ≠ a * (b * c), поэтому моноидная структура нарушается.

Отсутствие элемента равнозначности:

Каждый моноид должен иметь элемент равнозначности, который действует как нейтральный элемент при бинарной операции. Если в моноиде отсутствует элемент равнозначности, становится проблематично выполнять операции с определенными элементами. Например, если вы определяете моноид вещественных чисел с помощью операции деления, то элемента равнозначности не будет, поскольку деление на ноль не определено.

Ниже представлены три примера правильных моноидных структур:

Добавление целых чисел:

Множество целых чисел с бинарной операцией сложения (+), образует моноид. Элемент равнозначности равен 0, а сложение ассоциативно и замкнуто на множестве целых чисел.

Умножение ненулевых рациональных чисел:

Множество ненулевых рациональных чисел (дробей) с бинарной операцией умножения (×) образует моноид. Элемент равнозначности равен 1, а умножение ассоциативно и замкнуто для ненулевых рациональных чисел.

Конкатенация строк:

Множество строк с бинарной операцией конкатенации образует моноид. Элемент равнозначности — это пустая строка (""), а конкатенация является ассоциативной и замкнутой для строк.

Эти примеры демонстрируют четко определенные моноидные структуры, которые удовлетворяют необходимым свойствам и могут быть эффективно использованы для целей классификации.

2) Семантика и интерпретируемость:

Необходимо понимать семантику моноидной операции и ее связь с вашими данными. Подумайте, соответствуют ли полученные классификации предполагаемым интерпретациям и имеют ли они смысл в контексте вашей предметной области. Ниже приведены пять примеров в качестве иллюстрации:

Классификация частоты слов:

Предположим, вы используете моноиды для классификации ежеквартальных прогнозов компании из расшифровки звонков на основе частоты слов. В то время как моноидная операция может включать простое суммирование количества слов, интерпретируемость полученных классификаций необходимо рассмотреть особенно тщательно, поскольку она зависит от семантики, присвоенной различным частотным диапазонам. Например, вы можете интерпретировать документы с высокой частотностью слов как более сфокусированные на определенной теме, в то время как низкая частота определенных слов может указывать на более широкий или разнообразный контент. Не следует фокусироваться только на общем количестве слов и использовать его в качестве основы в своих ключевых моноидных операциях.

Анализ настроений:

Допустим, вы используете моноид для классификации настроения текста. Моноидная операция может работать лучше, если агрегировать оценки настроений отдельных слов или предложений. Рассмотрим следующий пример. Предположим, у вас есть множество отзывов покупателей о продукте, и вы хотите классифицировать их по трем категориям настроений: положительные, нейтральные и отрицательные. Вы решаете использовать моноидный подход, при котором моноидная операция включает в себя агрегирование оценок настроений из отдельных предложений в каждом обзоре. В этом примере вы назначаете настроение в диапазоне от -1 до 1, где -1 представляет крайне негативное настроение, 0 — нейтральное, а 1 — очень позитивное настроение. Затем моноидная операция будет выполнять простое суммирование оценок настроения. Теперь давайте рассмотрим отзыв клиента:

Отзыв: "Продукт хорош. Однако работа с клиентами оставляет желать лучшего".

Правильный способ классифицировать этот отзыв — разбить его на отдельные предложения и присвоить баллы настроения каждому предложению:

Предложение 1: "Продукт хорош." - Оценка настроения: 0,8 (положительная)

Предложение 2: "Однако работа с клиентами оставляет желать лучшего." - Оценка настроения: -0,7 (отрицательная)

Чтобы затем общую оценку настроений для обзора, мы применяем моноидную операцию, которая в данном случае является суммированием:

Общая оценка настроения = 0,8 + (-0,7) = 0,1

Основываясь на семантике, назначенной диапазонам оценки настроения, мы интерпретируем общую оценку настроения 0,1 как слегка положительную. Поэтому мы классифицируем этот отзыв как "нейтральный" или "слегка положительный" на основе моноидной классификации. Если бы оба предложения рассматривались как единое целое, то оценка была бы положительной из-за наличия слова "хорош", что, разумеется, неверно. Как видите, необходимо учитывать детали.

Классификация изображений:

Моноид для классификации изображений на основе визуальных признаков, таких как цвет, текстура или форма, будет включать в себя объединение этих признаков, и интерпретируемость этих объединенных признаков, которые приводят к классификации, будет зависеть от того, как вы сопоставляете их с их предполагаемыми или значимыми категориями. Семантика, назначенная различным комбинациям признаков, может сильно повлиять на то, как вы понимаете результаты классификации.

Рассмотрим следующий пример, чтобы показать важность семантики и интерпретируемости в классификации изображений с использованием моноидов. Предположим, вы используете моноидный подход для классификации изображений по двум категориям - "Собака" и "Кошка" - на основе визуальных признаков. Для трейдеров классификацию изображений можно заменить на, скажем, бычьи и медвежьи паттерны "голова и плечи", но принцип остается тем же. Моноидная операция будет включать в себя комбинирование характеристик цвета и текстуры, считанных с изображений. Для наших целей предположим, что у нас есть две ключевые визуальные характеристики: "Цвет меха" и "Сложность текстуры". Цвет меха может быть классифицирован как "Светлый" или "Темный", а сложность текстуры может быть классифицирована как "Простая" или "Сложная". Теперь давайте рассмотрим два изображения.

Пусть на изображении 1 есть белая кошка с простой текстурой меха, что означает:

• Цвет меха: Светлый
• Сложность текстуры: Простая
• Пусть на изображении 2 есть черная собака со сложной текстурой меха, что подразумевает:
• Цвет меха: Темный
• Сложность текстуры: Сложная

Чтобы классифицировать эти изображения с использованием моноидного подхода, вы комбинируете визуальные признаки в соответствии с моноидной операцией (например, конкатенация, суммирование и т. д.):

Для изображения 1: "Легкий" + "Простой" = "ЛегкийПростой"

Для изображения 2: "Темный" + "Сложный" = "ТемныйСложный"

Теперь наступает самый важный момент - семантика и интерпретируемость. Вам нужно присвоить значение комбинированным функциям, чтобы сопоставить их обратно со значимыми категориями. В нашем случае, поскольку мы используем очень простой пример:

"ЛегкийПростой" можно интерпретировать как категорию "Кошки", потому что светлый цвет шерсти и простая текстура являются общими чертами кошек.

"ТемныйСложный" можно интерпретировать как категорию "Собаки", поскольку темный цвет шерсти и сложная текстура часто ассоциируются с собаками.

Присвоив соответствующую семантику и интерпретацию комбинированным функциям, вы сможете правильно классифицировать изображение 1 как "Кошку", а изображение 2 как "Собаку".

Сегментация клиентов:

Предположим, вы используете моноиды для сегментации клиентов на основе их покупательского поведения. Моноидная операция может включать в себя агрегирование данных транзакций или атрибутов клиента. Однако интерпретируемость результирующих сегментов зависит от того, как вы интерпретируете и маркируете эти сегменты. Например, вы можете назначить такие признаки, как "ценные клиенты" или "клиенты на грани ухода", на основе семантики и знаний предметной области.

Классификация временных рядов:

Рассмотрим возможность использования моноидов для классификации данных временных рядов, таких как тренды фондового рынка. Моноидная операция может включать в себя сочетание различных характеристик, таких как цена, объем и волатильность. Однако интерпретируемость классификаций зависит от того, как вы определяете семантику результирующих комбинаций по отношению к рыночным условиям. Различные интерпретации могут привести к различным выводам и последствиям для принятия решений.

Во всех этих примерах семантика, назначенная моноидной операции, и результирующие классификации имеют решающее значение для осмысленной интерпретации и принятия решений. Внимательное рассмотрение этой семантики гарантирует, что полученные классификации соответствуют необходимым интерпретациям и обеспечивают эффективный анализ и понимание данных.

3) Предварительная обработка данных:

Это важно для целей контроля качества данных перед их классификацией с помощью моноидов. Целесообразно провести предварительную обработку данных для обеспечения совместимости с моноидной структурой. Например, все выходные данные операционной функции должны быть определенными членами набора моноидов, а не плавающими данными с несколькими десятичными точками, которые при округлении могут быть неоднозначными. Добиться этого можно путем нормализации данных (регуляризации) или преобразования их в формат, подходящий для операции моноида. Но также необходимо решить проблему обработки пропущенных значений для лучшей общей согласованности вашей торговой системы.

4) Однородность данных:

Убедитесь, что данные, которые вы классифицируете, обладают определенной степенью однородности в каждой категории. Например, на этапе выбора параметра моноид множества, который мы будем использовать, должен иметь оба индикатора с согласованными и сопоставимыми значениями или весами. Учитывая, что мы используем осциллятор RSI и полосы Боллинджера, по умолчанию это явно не так. Однако мы нормализуем один из них, чтобы обеспечить их сопоставимость и однородность. Моноиды работают лучше всего, когда применяются к данным, которые демонстрируют схожие характеристики в каждом классе.

5) Кардинальное число категорий:

Рассмотрим кардинальное число или количество различных категорий, которые могут быть сформированы с помощью моноида. Если количество результирующих категорий слишком велико или слишком мало, это может повлиять на полезность классификации или интерпретируемость результатов.

Проиллюстрируем влияние кардинального числа данных категорий на примере:

Предположим, вы работаете над задачей классификации, чтобы предсказать направление валютной пары на основе настроений новостных событий календаря, и у вас есть набор данных с целевой переменной "Настроение", которая может принимать три возможных значения: "выше ожидаемого", "соответствует ожидаемому" и "ниже ожидаемого".

Вот пример набора данных:

Показатель	Настроение
Производство в обрабатывающей промышленности от ФРС м/м	ниже
Индекс цен от GDT	соответствует
Товарно-материальные запасы м/м	выше
Индекс рынка жилья от NAHB	ниже

В этом примере вы можете заметить, что переменная "Настроение" имеет три категории: "Выше", "Соответствует" и "Ниже". Кардинальное число относится к количеству различных категорий в переменной.

Кардинальное число переменной "Настроение" в этом наборе данных равно 3, поскольку переменная имеет три уникальные категории.

Кардинальное число данных категорий может иметь значение для задач классификации. Рассмотрим два сценария:

Сценарий 1:

Здесь у нас есть несбалансированное кардинальное число, ведущее к несбалансированному набору данных, где категория "Выше" имеет значительно большее количество выборок по сравнению с категориями "Соответствует" и "Ниже". Например, предположим, что 80% выборок помечены как "Выше", 10% — "Соответствует" и 10% — "Ниже".

В этом сценарии несбалансированное кардинальное число может привести к систематической ошибке в модели классификации. Модель может чаще предсказывать класса большинства ("Выше"). При этом она может испытывать трудности с предсказанием классов меньшинства ("Соответствует" и "Ниже"). Это может привести к снижению точности и полноты для классов меньшинства, влияя на общую производительность и интерпретируемость модели классификации.

Сценарий 2:

В этом случае вместо того, чтобы приписывать строковые значения элементам нашего множества моноидов, как в случае выше, мы используем данные с плавающей запятой для более точного взвешивания и описания каждого элемента в множестве моноидов. То есть у нас есть неограниченное кардинальное число, что означает отсутствие установленного количества возможных весов/значений для каждого из элементов множества, в отличие от сценария 1.

6) Масштабируемость:

Оценка масштабируемости классификации моноидов особенно нужна при работе с большими наборами данных. В зависимости от вычислительной сложности может потребоваться рассмотреть альтернативные методы или оптимизации для эффективной обработки значительных объемов данных. Один из подходов при работе с большими наборами данных состоит в том, чтобы сделать конструирование признаков. Моноидные гомоморфизмы могут использоваться в конструировании признаков для различных задач. Одной из них может быть оценка публичной компании.

Гомоморфизмы могут преобразовать входные признаки в новое пространство признаков с более точной предсказательной силой для моделей оценки. Давайте рассмотрим пример, когда у вас есть набор данных, содержащий различные финансовые показатели, такие как выручка, прибыль, активы и обязательства для набора публичных компаний.

Один из распространенных подходов состоит в том, чтобы использовать моноидные гомоморфизмы для получения и фокусировки на ключевых финансовых коэффициентах, которые широко используются в моделях оценки. Например, вы можете определить гомоморфизм, который сопоставляет множество моноидов доходов с новым нормализованным набором моноидов, представляющим скорость роста доходов. Это преобразование явно уменьшит ваши требования к данным, сделав ваши моноиды более масштабируемыми, потому что многие компании, перечисленные независимо друг от друга в множестве моноидов доходов, будут иметь одинаковые значения скорости роста доходов в кодомене.

Точно так же вы можете использовать моноидный гомоморфизм, чтобы сопоставить моноид прибыли с моноидом, представляющим прибыль на акцию (earnings per share, EPS). EPS — это широко используемый показатель оценки, который показывает прибыльность компании в расчете на одну акцию. Есть много других важных коэффициентов. Все они направлены на достижение одной и той же цели — сохранить масштабируемость модели классификации моноидов.

С другой стороны, нам необходимо свести к минимуму зависимость от распределенных вычислительных сред, таких как Apache Hadoop или Apache Spark, для параллельной обработки данных на нескольких узлах в кластере. Эти подходы позволяют распределять рабочую нагрузку и ускорять время обработки, позволяя обрабатывать большие наборы данных, однако это потребует значительных последующих затрат. "Последующих", так как все проблемы, которые они пытаются решить, могли бы быть решены более изящно еще на уровне проектирования моноидов.

7) Обобщаемость:

Необходимо оценить обобщаемость результатов классификации, используя новые и невидимые данные. Методы классификации на основе моноидов должны обеспечивать надежную и непротиворечивую категоризацию в различных наборах данных и контекстах.

Предположим, вы разрабатываете классификацию на основе моноидов для прогнозирования кредитоспособности потенциальных получателей кредита. Ваш набор данных будет содержать исторические данные о кредитах, такие как доход, кредитный рейтинг, отношение долга к доходу, история занятости и т.д.

Чтобы оценитьобобщаемость конечных результатов классификации, вам нужно будет оценить, насколько хорошо модель работает с новыми, невидимыми данными. Например, после обучения модели на наборе данных из определенного региона или периода времени вы должны протестировать ее на наборе данных из другого региона или периода времени. Если модель демонстрирует последовательную и надежную категоризацию в этом и других разнообразных наборах данных, это указывает на хорошую обобщаемость.

При достижении обобщаемости в методах классификации на основе моноидов потенциальные трудности включают подгонку, смещение данных и смещение выбора признаков. Подгонка имеет место, когда, например, функция моноидной операции становится слишком специфичной для обучающих данных, что приводит к плохой работе с новыми данными. И наоборот, смещение данных может произойти, если набор данных для обучения не является репрезентативным для более широкого множества, что приводит к необъективной классификации. При смещении выбора признаков выбор признаков, которые не отражают релевантную информацию для данного контекста, повлияет на обобщаемость модели.

8) Метрики оценки:

Необходимо определить соответствующие метрики оценки качества и эффективности классификации моноидов. Эти показатели должны соответствовать вашей конкретной проблеме и целям с учетом таких факторов как точность, достоверность, полнота или F1-мера.

9) Подгонка и недостаточное обучение:

Необходимо избегать подгонки и недостаточного обучения модели классификации моноидов. Применяйте такие методы, как перекрестная проверка, регуляризация или ранняя остановка, чтобы предотвратить эти проблемы и способствовать обобщению модели.

10) Интерпретируемость и объяснимость:

Учитывайте интерпретируемость и объяснимость полученных классификаций. Моноиды могут предоставить мощные возможности классификации, но важно понимать, как принимаются решения о классификации, и иметь возможность их объяснить.

Реализация

Период ретроспективного анализа:

Моноидный домен из 8 целых чисел от 1 до 8 будет использоваться для представления вариантов доступных периодов ретроспективного анализа. Одна единица периода будет эквивалентна четырем, а наши временные рамки тестирования будут фиксированными и равными одному часу, хотя временные рамки нашего анализа будут варьироваться, как описано в следующем разделе. На каждом новом баре нам нужно будет выбрать период. Единицей измерения для каждого из них будет относительный процент движения в этом периоде по сравнению с предыдущим периодом равной длины. Например, если изменение цены в пунктах за период 1 (4 бара) было A, а за один период до этого было B, то вес или значение периода 1 будет дано по формуле ниже:

= ABS(A)/(ABS(A) + ABS(B))

где функция ABS () представляет абсолютное значение. Эта формула проверяется на нулевое деление, гарантируя, что минимум знаменателя сопоставим со стоимостью рассматриваемой ценной бумаги.

Наша моноидная операция и элемент равнозначности будут выбраны из оптимизации по следующим методам, приведенным в начале статьи.

Таймфрейм:

Моноид, установленный для таймфрейма, будет иметь восемь периодов таймфрейма, а именно:

• PERIOD_H1
• PERIOD_H2
• PERIOD_H3,
• PERIOD_H4,
• PERIOD_H6,
• PERIOD_H8,
• PERIOD_H12,
• PERIOD_D1

Взвешивание и назначение значения каждого из этих таймфреймов будет следовать той же схеме, что и выше, в ретроспективном периоде, что означает, что мы будем сравнивать процентные изменения цены закрытия на основе предыдущих изменений ценового бара в соответствующем таймфрейме.

Применяемая цена:

Моноид множества применяемых цен будет иметь четыре возможных применяемых цены на выбор:

• MODE_MEDIAN ((High + Low) / 2)
• MODE_TYPICAL ((High + Low + Close) / 3)
• MODE_OPEN
• MODE_CLOSE

Взвешивание и присвоение значения здесь будут отличаться от того, что мы указали выше. В этом случае мы будем использовать стандартное отклонение каждой примененной цены за период, выбранный в ретроспективном периоде, чтобы определить вес или значение каждой примененной цены. Операция и выбор индекса равнозначности будут такими же, как описано выше.

Индикатор:

Множество моноидов для выбора индикатора будет иметь только два варианта, а именно:

• Осциллятор RSI
• Полосы Боллинджера

Осциллятор RSI нормализован в диапазоне от 0 до 100, полосы Боллинджера не только не нормализованы, но и имеют несколько буферных потоков. Чтобы нормализовать полосы Боллинджера и сделать их сопоставимыми с осциллятором RSI, мы возьмем разницу между текущей ценой и базовой полосой C и разделим ее на размер разрыва между верхними и нижними полосами D. Итак, наше значение для полос сначала будет выглядеть так:

= C/(ABS(C) + ABS(D))

Как и прежде, это значение будет проверяться на деление на ноль. Однако это значение может быть отрицательным и стремится к десятичному значению 1,0. Чтобы нормализовать эти два аспекта и получить их в диапазоне от 0 до 100, как RSI, мы добавляем 1,0, чтобы гарантировать, что он всегда положительный, а затем умножаем сумму на 50,0, чтобы убедиться, что она находится в диапазоне от 0 до 100. Таким образом, наши значения, которые теперь будут находиться в диапазоне от 0 до 100 как для RSI, так и для полос Боллинджера, будут представлять наш вес, а функция оператора и индекс элемента будут выбраны, как указано в приведенных выше методах.

Решение:

Для этого последнего моноида наше множество также будет иметь только два варианта.

• Торговля по тренду
• Торговля в диапазоне

Чтобы количественно оценить эти два элемента, мы рассмотрим за выбранный ретроспективный период количество ценовых пунктов, на которые ценные бумаги откатываются в противоположность своему возможному тренду в конце периода, в процентах от общего ценового диапазона этого периода. Это должно быть десятичное значение от 0,0 до 1,0. Оно будет напрямую измерять вес торговли с диапазоном, что означает, что торговля по тренду будет равна этому значению, вычтенному из 1,0. Метод работы и выбор индекса, как указано выше.

Ниже представлена реализация наших моноидных решений в виде экземпляра встроенного трейлинг-класса советника.

//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_8(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<8;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(O==OP_LEAST)
      {
         for(int i=0;i<8;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_MOST)
      {
         for(int i=0;i<8;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_CLOSEST)
      {
         for(int i=0;i<8;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<8;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
      else if(O==OP_FURTHEST)
      {
         for(int i=0;i<8;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<8;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_4(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<4;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            /*printf(__FUNCSIG__+
               " values size: "+IntegerToString(ArraySize(Values))+
               " in indices size: "+IntegerToString(ArraySize(InputIndices))+
               " in indices index: "+IntegerToString(InputIndices[i])
               );*/
               
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(O==OP_LEAST)
      {
         for(int i=0;i<4;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_MOST)
      {
         for(int i=0;i<4;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[i/2]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[i/2]=i+1; }
            else { OutputIndices[i/2]=m_lookback.Identity(); }
         }
      }
      else if(O==OP_CLOSEST)
      {
         for(int i=0;i<4;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<4;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
      else if(O==OP_FURTHEST)
      {
         for(int i=0;i<4;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<4;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[i/2]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
void CTrailingCT::Operate_2(CMonoid<double> &M,EOperations &O,double &Values[],int &InputIndices[],int &OutputIndices[])
   {
      for(int i=0;i<2;i++)
      {
         m_element.Let();
         if(m_lookback.Get(i,m_element))
         {
            if(!m_element.Get(0,Values[InputIndices[i]]))
            {
               printf(__FUNCSIG__+" Failed to get double for 1 at: "+IntegerToString(i+1));
            }
         }
         else{ printf(__FUNCSIG__+" Failed to get element for 1 at: "+IntegerToString(i+1)); }
      }
      
      //
      
      if(m_lookback_operation==OP_LEAST)
      {
         for(int i=0;i<2;i+=2)
         {
            if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i; }
            else if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; }
            else { OutputIndices[0]=m_lookback.Identity(); }
         }
      }
      else if(m_lookback_operation==OP_MOST)
      {
         for(int i=0;i<2;i+=2)
         {
            if(Values[InputIndices[i]]>Values[InputIndices[i+1]]){ OutputIndices[0]=i; }
            else if(Values[InputIndices[i]]<Values[InputIndices[i+1]]){ OutputIndices[0]=i+1; }
            else { OutputIndices[0]=m_lookback.Identity(); }
         }
      }
      else if(m_lookback_operation==OP_CLOSEST)
      {
         for(int i=0;i<2;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=DBL_MAX;
            for(int ii=0;ii<2;ii++)
            {
               if(_gap>fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[0]=_index;
         }
      }
      else if(m_lookback_operation==OP_FURTHEST)
      {
         for(int i=0;i<2;i+=2)
         {
            int _index=-1;
            double _mean=0.5*(Values[InputIndices[i]]+Values[InputIndices[i+1]]),_gap=0.0;
            for(int ii=0;ii<2;ii++)
            {
               if(_gap<fabs(_mean-Values[InputIndices[ii]])){ _gap=fabs(_mean-Values[InputIndices[ii]]); _index=ii;}
            }
            //
            if(_index==-1){ _index=m_lookback.Identity(); }
            
            OutputIndices[0]=_index;
         }
      }
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
int CTrailingCT::GetLookback()
   {
      m_close.Refresh(-1);
      
      int _x=StartIndex();
      
      for(int i=0;i<8;i++)
      {
         int _period=(__LOOKBACKS[i]*PeriodSeconds(PERIOD_H4))/PeriodSeconds(m_period);
         double _value=fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))/(fabs(m_close.GetData(_x)-m_close.GetData(_x+_period))+fabs(m_close.GetData(_x+_period)-m_close.GetData(_x+_period+_period)));
         
         m_element.Let();
         m_element.Cardinality(1);
         if(m_element.Set(0,_value))
         {
            ResetLastError();
            if(!m_lookback.Set(i,m_element,true))
            {
               printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
            }
         }
      }
      
      //r of 8
      double _v1[8];ArrayInitialize(_v1,0.0);
      int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; }
      int _i1_out[4];ArrayInitialize(_i1_out,-1);
      Operate_8(m_lookback,m_lookback_operation,_v1,_i1_in,_i1_out);
      
      
      //r of 4
      double _v2[8];ArrayInitialize(_v2,0.0);
      int _i2_out[2];ArrayInitialize(_i2_out,-1);
      Operate_4(m_lookback,m_lookback_operation,_v2,_i1_out,_i2_out);
      
      
      //r of 2
      double _v3[8];ArrayInitialize(_v3,0.0);
      int _i3_out[1];ArrayInitialize(_i3_out,-1);
      Operate_2(m_lookback,m_lookback_operation,_v2,_i2_out,_i3_out);
      
      return(4*__LOOKBACKS[_i3_out[0]]);
   }
//+------------------------------------------------------------------+
//|                                                                  |
//+------------------------------------------------------------------+
ENUM_TIMEFRAMES CTrailingCT::GetTimeframe(void)
   {
      for(int i=0;i<8;i++)
      {
         ResetLastError();
         double _value=0.0;
         double _buffer[];ArrayResize(_buffer,3);ArrayInitialize(_buffer,0.0);ArraySetAsSeries(_buffer,true);
         if(CopyClose(m_symbol.Name(),__TIMEFRAMES[i],0,3,_buffer)>=3)
         {
            _value=fabs(_buffer[0]-_buffer[1])/(fabs(_buffer[0]-_buffer[1])+fabs(_buffer[1]-_buffer[2]));
         }
         else{ printf(__FUNCSIG__+" Failed to copy: "+EnumToString(__TIMEFRAMES[i])+" close prices. err: "+IntegerToString(GetLastError())); }
         
         m_element.Let();
         m_element.Cardinality(1);
         if(m_element.Set(0,_value))
         {
            ResetLastError();
            if(!m_timeframe.Set(i,m_element,true))
            {
               printf(__FUNCSIG__+" Failed to assign element at index: "+IntegerToString(i)+", for lookback. ERR: "+IntegerToString(GetLastError()));
            }
         }
      }
      
      //r of 8
      double _v1[8];ArrayInitialize(_v1,0.0);
      int _i1_in[8];for(int i=0;i<8;i++){ _i1_in[i]=i; }
      int _i1_out[4];ArrayInitialize(_i1_out,-1);
      Operate_8(m_timeframe,m_timeframe_operation,_v1,_i1_in,_i1_out);
      
      
      //r of 4
      double _v2[8];ArrayInitialize(_v2,0.0);
      int _i2_out[2];ArrayInitialize(_i2_out,-1);
      Operate_4(m_timeframe,m_timeframe_operation,_v2,_i1_out,_i2_out);
      
      
      //r of 2
      double _v3[8];ArrayInitialize(_v3,0.0);
      int _i3_out[1];ArrayInitialize(_i3_out,-1);
      Operate_2(m_timeframe,m_timeframe_operation,_v2,_i2_out,_i3_out);
      
      return(__TIMEFRAMES[_i3_out[0]]);
   }

Таким образом, функция Operate_8 объединяет восемь элементов в наборе моноидов и предлагает выбор из четырех, по одному из каждой пары. Точно так же функция Operate_4 объединяет четыре элемента, полученных из Operate_8, и предлагает выбор из двух, снова по одному из каждой пары, и, наконец, функция Operate_2 объединяет эти два элемента из Operate_4, чтобы получить прибыльный элемент.

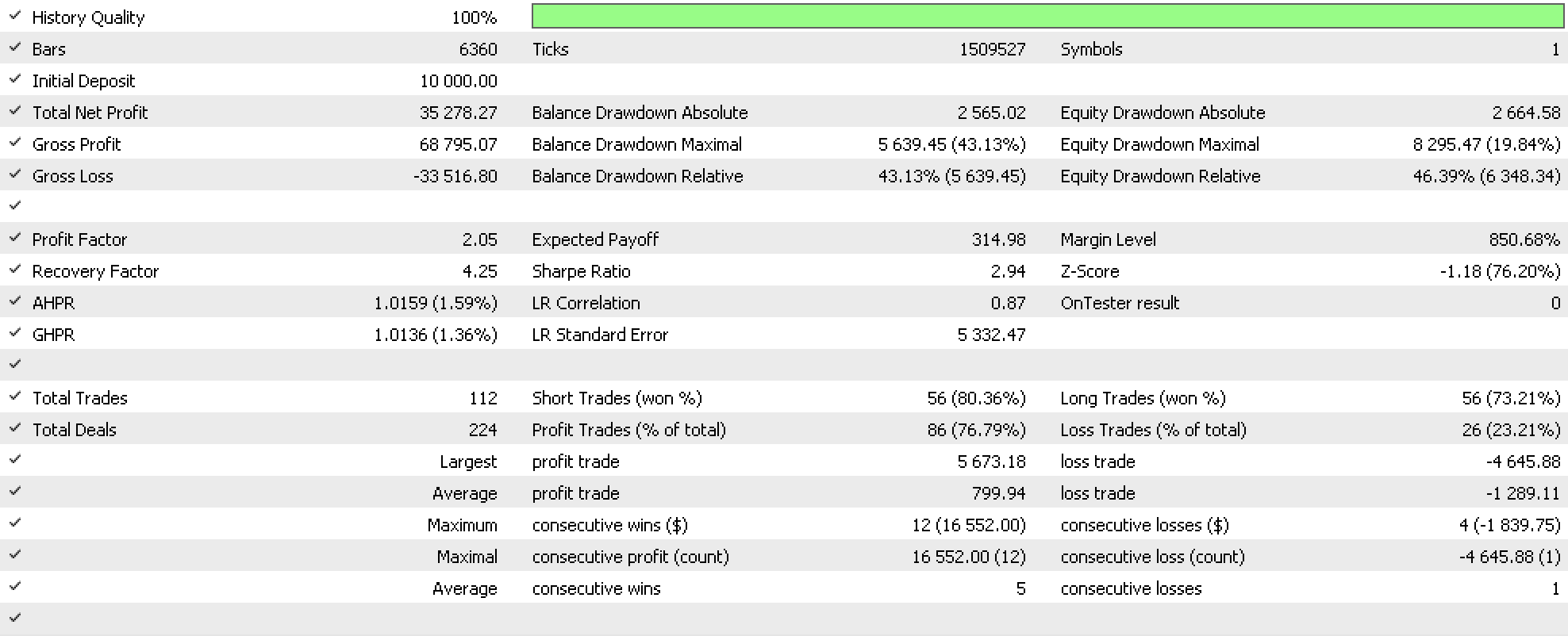
Если мы проведем тесты с этой системой для определения идеального трейлинг-стопа открытых позиций в составе советника, который использует встроенный сигнал RSI из экспертного класса сигналов и фиксированного управления капиталом из класса средств советника, мы получим следующий отчет.

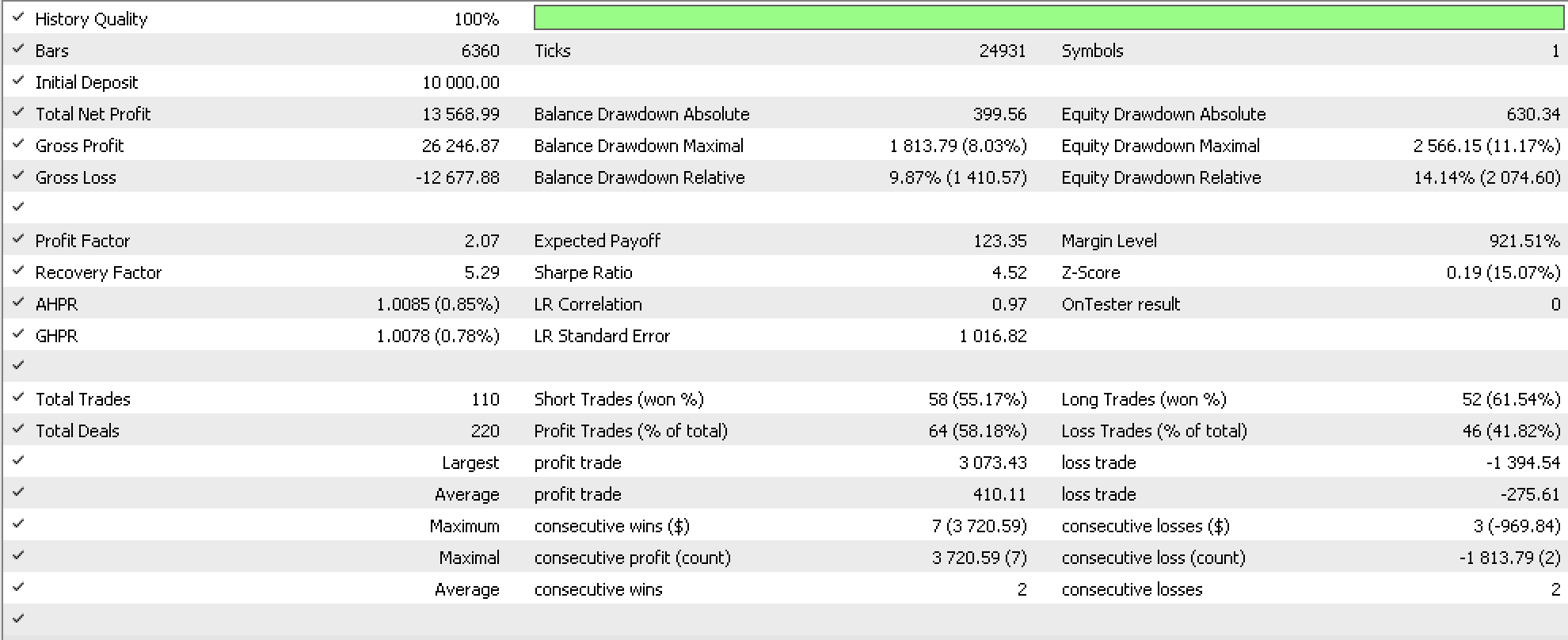
Аналогичный прогон на очень похожем советнике, единственное отличие которого — встроенный трейлинг-стоп на основе скользящей средней, дает следующие результаты.

Заключение

Мы рассмотрели моноиды как средство классификации данных и, следовательно, совокупность решений. Было подчеркнута важность хорошо сформированных обобщаемых моноидов без подгонки, а также на других мер предосторожности, которые могут быть ключевыми в реализации хорошо сбалансированной системы. Мы также рассмотрели возможную реализацию этой системы, которая корректирует позиции стоп-лосса, работая как экземпляр встроенного класса трейлинга советника.