MetaTrader 5 / 統計と分析
English Русский 中文 Español Deutsch Português
確率論と数理統計学と例(第1部): 基礎理論と初等理論

確率論と数理統計学と例(第1部): 基礎理論と初等理論

MetaTrader 5 — 統計と分析 | 9 11月 2020, 09:35
1 176 0
Aleksey Nikolayev
Aleksey Nikolayev

内容

  1. はじめに
  2. 理論的基礎
  3. 初等理論
    • 3.1. 組合せ確率
    • 3.2. ベルヌーイスキーム
  4. 数理統計学の基礎
  5. 初等理論の枠組みの中で数理統計学を適用する例
    • 5.1. 母数の推定
    • 5.2. 統計的仮説の検定
  6. 終わりに
  7. 添付ファイル

1.はじめに

取引とは、常に不確実性に直面して意思決定を行うことです。つまり、これらの決定が行われた時点では、決定の結果が明確ではありません。これには、そのようなケースを意味ある方法で説明できるようにする数学的モデルの構築への理論的アプローチの重要性が必然的に伴います。確率論とゲーム理論の2つのアプローチを強調したいと思います。確率的手法に関連するトピックでは、これらは「自然との戦い」の理論として組み合わされることがあります。これは、2つの異なるタイプの不確実性の存在を明確に示しています。最初のもの(確率論的)は通常、自然現象に関連しています。2つ目(純粋にゲーム関連)は、他の主題(個人またはコミュニティ)の活動に関連しています。ゲームの不確実性は、理論的に対処するのがはるかに困難です。これらの不確実性は、「悪い」および「良い」と呼ばれることさえあります。最初にゲームに関連する不確実性の理解の進歩は、多くの場合、それを確率的な形式に減らすことに関連しています。

金融市場の場合、人々の活動が重要な要素であるため、ゲームの性質の不確実性が明らかに重要です。ここでの確率モデルへの移行は、通常、多数のプレーヤーの考慮に基づいており、各プレーヤーは個別には価格変更にほとんど影響を与えません。部分的には、これは統計物理学で使用されているアプローチに似ており、経済物理学と呼ばれる科学的アプローチの出現につながりました。

実際、このような移行のトピックは非常に興味深く、重要であり、より詳細に検討する価値があります。うまくいけば、関連記事がいつかフォーラムに現れるでしょう。本稿では、確率論と数理統計学の基礎を見ていきます。

2. 理論的基礎

確率論は、コルモゴロフの公理として知られる形式体系に基づいています。「形式体系」とは何か、そして、どのように数学的公理的アプローチを正しく理解できるかについてはすべて数理論理学の分野に属する複雑すぎる質問であるため、詳しく説明しません。代わりに、確率論の基本的な目的である確率空間に焦点を当てます。これは、これらの事象の標本空間、事象集合、および確率で構成されています。さらに詳しく考えてみましょう。

1)標本空間は、確率実験のすべての可能な結果の集合で、通常、ギリシャ文字の「オメガ」大文字(Ω)で示されます。根元事象(標本点)は通常、小文字の「オメガ」(о)で示され、図上には点として示されます。コインを1回投げた結果を説明する最も単純な標準例はΩ={ω1, ω2}です。ここでω1=Hとω2=Tはそれぞれコインの表(Head)または裏(Tail)が出ることを意味し、中括弧はその要素の列挙によって与えられる集合を示します。

以下の図は、抽象的なΩを長方形といくつかの点(それに属する基本点ω1、ω2、ω3)として示しています。

標本空間

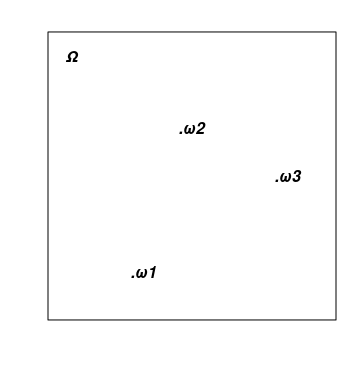
2)確率事象の集合。このような各事象は、根元事象の集合です(すべてのΩ根元事象の部分集合)。事象の集合には、空集合∅={}(決して発生しない事象)と全体集合Ω(常に発生する事象)が含まれます。集合からの2つの事象の結合(および共通事象)も集合に属している必要があります。数学では、このような集合の集合は通常、集合の代数学と呼ばれます。上記のコインの例には、{}=∅、{H}、{T}、{H,T}=Ωの4つの事象があります。(自己テストの質問: 根元事象は確率事象の例と見なすことができますか?)

確率事象は通常、大文字のラテン文字(A、B、C、...)で表され、図ではΩ内の図形として描かれます。事象の結合と共通事象は、さまざまな方法で示されます。通常の数値変数の加算と乗算に似たエントリ(АВおよびА+В)が使用される場合がありますが、 ∩記号と∪記号(А∩ВおよびА∪В)が使用されることもあります。

下の図は、Ωを長方形と2つの交差するА事象とВ事象として示します。

A_and_B

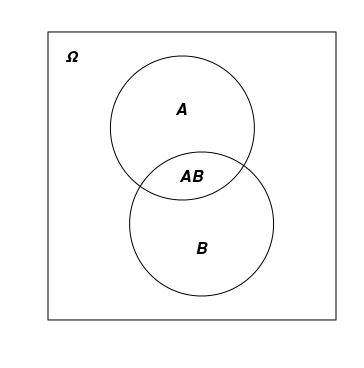
3)確率は数値関数P=P(A)で、各A確率事象を0から1の実数と一致させます。P(Ω)=1およびP(∅)=0です。さらに、加法性規則が満たされます。A事象が、重複しないB事象とC事象の組合せである場合、P(A)=P(B)+P(C)です。P()関数は、「確率」に加えて、「Ωの確率分布」を適用します(または単に「Ωの分布」)。この概念を同様の「確率変数の分布関数」の概念と混同しないでください。それらは互いに関連していますが、異なります。前者は数値を集合に一致させる関数であり、後者は数値を数値に一致させる通常の数値関数です。

図で確率分布を表現する方法は明確ではありませんが、直感的には、Ωの体積全体の単位質量の分布に例えることができます。この比較では、事象は体積の一部ですが、確率は体積のこの部分内の質量の割合です。

他のすべての確率論の概念は、これらから派生しています。ここで、確率的依存(独立)の非常に重要な概念を強調しましょう。これを行うために、B事象(P(B)>0)実行の対象となるА事象の条件付き確率の概念を紹介します。これはP(A|B)として表され、定義により、P(A|B)=P(AB)/P(B)(覚えているかもしれませんが、ABは、A事象とB事象の結合です)。定義上、A事象は、B事象の発生中に、条件付き確率が P(A|B)=P(A)に等しい場合に、B 事象から独立していると見なされます。条件付き確率式を使用する場合、独立性の定義はP(A)P(B)=P(AB)として書き直すことができます。この等式が満たされない場合、 A事象はB事象に依存すると言われます。

直感的には、独立性とは、B事象の発生が既知でも、A事象に関連する不確実性が変わらないことを意味します。 逆に、依存関係とは、B事象の発生がA事象に関する情報を伝達することを意味します。この直感的な理解の正確な表現は、クロード・シャノンの情報理論に示されています。

基本確率論は通常、個別に強調表示されます。根元理論と非根元理論の違いは、有限数の要素で構成される根元事象の集合を考慮することです。その結果、確率事象の集合も有限であることがわかります(自己テストの質問: これはなぜ本当ですか)。この理論はコルモゴロフの公理よりずっと前に発展し、実際には必要ありませんでした。本稿の残りの部分では、理論のこの部分に焦点を当てます。非初等理論については、次の記事で説明します。

3. 初等理論

根元結果の数は有限であるため、根元事象(単位集合)を1つだけ含む事象の確率を簡単に設定できます。そのようなすべての確率の合計が1に等しいことを確認する必要があります。事象の確率は、そのような確率の合計に等しくなります。これらの初期確率は必ずしも等しいとは限りませんが、通常は「組合せ確率」という名前で要約されるそのようなモデルから始めます。

3.1. 組合せ確率

Ωが正確にN個の基本結果で構成されているとすると、mの量でそれらを含む事象の確率はm/Nに等しくなります。ここでの確率計算は、オプションの数を数えることで構成されます。原則として、これには組合せ法が使用されるため、この名前が付けられています。ここではいくつかの例を示します。

例1: nの異なるアイテムがあるとします。それらを配置する(並べる)方法は何通りありますか。答えは、n!=1*2*3*....*(n-1)*n通りです。それぞれの方法は順列と呼ばれ、それぞれの順列は根元事象です。したがって、N=n!であり、mの順列からなる事象の確率はm/n! (m/N=m/n!)です。

簡単な問題を解決しましょう。ランダムな順列の後、特定のオブジェクトが最初の位置にある確率を定義します。最初の場所が選択されたアイテムで占められている場合、残りのn-1のアイテムを残りのn-1の場所に配置する方法は(n-1)!通りあります。したがって、m=(n-1)!は、望ましい確率がm/N=m/n!=(n-1)!/n!=1/nに等しいことを意味します。

例2: nの異なるアイテムがあるとします。k (k<=n)アイテムのさまざまな集合はいくつ分離できますか。アイテムの順序のみが異なる2つの集合を検討するかどうかに応じて、2つの可能なオプションがあります。検討する場合、答えはn!/(n-k)!です。検討しない場合、k!で割ることになるので、答えはn!/((n-k)!*k!)となります。順序を考慮した集合を割り当てと呼び、順序を考慮しない集合を組合せと呼びます。二項係数方程式としても知られる割り当て数の作成では、特別な記号が適用されます。次の図に示す2つのオプションがあります。

二項

したがって、集合内の要素の順序が重要でない場合は、組合せを根元事象の集合として使用して問題を解決できます。 順序が重要な場合は、割り当てを使用する必要があります。

例3: いわゆる超幾何分布につながる重要な例を考えてみましょう。nのアイテムがそれぞれ、「良い」または「悪い」のいずれかとして指定されているとします。b(b⋜n)を「悪い」、残りのn-bを「良い」にします。k要素の集合を、それらの順序を考慮せずに選択します(組合せ)。集合に正確にxの「悪い」アイテムが含まれている確率はどれくらいですか。この問題は、一致する組合せの数を数えることで解決されます。答えはかなり面倒なので、次の図に示すように、組合せの数を表記して書き留めておくことをお勧めします。ここで、目的の確率はpで表され、x、n、b、kで表されます。

hyperg

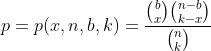
この例は、「確率変数」の概念の導入の背後にあるロジックを理解するのに適しています(次の記事で詳しく説明します)。事象の確率の計算に関連する特定の問題を解決するためには、x、n、b、およびkの知識で十分で、事象の初期集合全体の完全なデータは冗長である場合があります。その場合、不要な情報を破棄して元のモデルを単純化することは理にかなっています。次のように進めましょう。

  • n、b、kは固定母数と見なされます。
  • Ω標本空間の代わりに、それに基づいてΩх={0, 1, ..., k}を新しく構築します。新しい空間は、可能なх値で構成されます。
  • 各{х}事象(1つの根元事象で構成される)を、上記の超幾何分布方程式で指定された確率と一致させます。

結果のオブジェクトは「離散確率変数」と呼ばれ、Ωхからの可能な値の超幾何分布を持ちます。

3.2. ベルヌーイスキーム

これは、初等確率論の分野でよく知られているもう1つのモデルです。その例は通常、連続したコイントスの結果をモデル化することを含みますが、私はより正式な方法でスキームを構築するつもりです。

正の整数nと、p+q=1となるような非負の実数pとqのペアがあるとします。Ω標本空間は正確な長さがnの単語で構成され、H文字とT文字のみが許可されます(H - 表、T - 裏)。事象が1つの根元事象を含む確率は式pu({w})=p^nh*q^ntで設定されます。ここで、wは単語で、nh、nt、 nh+nt=nはそれぞれH文字およびT文字の数を表します。

組合せ確率とは対照的に、初期確率は一般に互いに等しくないことは容易に理解できます(p=q=0.5の場合にのみ、すべて類似しています )。

例としてn=2について考えましょう。この場合、Ω={HH, HT, TH, TT}です。ここでの根元事象の数は4で、確率事象の数は16です。(自己テストの質問: ベルヌーイスキームのnから、根元事象とすべての確率事象の数の依存関係を表す方程式の一般的な形式を導き出します。)

「1回目がH」={HH, HT}事象について考えましょう。確率はpq+p^2=pです。同じことがどの位置でも当てはまり、p母数を「各トスでを裏が出る可能性」として話すことができます。ここで、А=「2回目がH」={HH, TH}事象はВ=「1回目がH」={HH, HT}事象から独立しています。独立性の定義を使用してみましょう。АВ={HH}の結合、P(A)=p、 P(B)=pおよびP(AB)=p^2です。P(A)P(B)=p*p=p^2=P(AB)であるため、事象は独立しています。

各トスの結果の確率とその独立性に関する記述は、すべてのn>2に当てはまります。

他の方法で確率を指定して、等しい確率がないか、トスの結果に依存する可能性があります。ここでのポイントは、一連の事象を記述する有効なモデルはベルヌーイスキームだけではなく、それに限定すべきではないということです。

ここで、Hが正確にk回発生する単語で構成される事象の確率を計算してみましょう。これは、より砕けて言うと、n回のコイントスでk回表が出る確率です。この質問に対する答えは、次の図に示すいわゆる二項分布方程式を介して見つけることができます。pbは、k、 n、p、qに依存する、望まれた確率を示します。

PDFbinomial

二項分布と上記で検討した超幾何分布との関係を示す別の例を考えてみます。これは、それ自体でも、数理統計学(フィッシャーの直接確率検定)での適用に関連しても重要です。質問は非常に複雑で、数学的な観点からは意味があります。すべての推論を1つずつ強調してみましょう。

  • ベルヌーイスキームのΩ標本空間に基づいて、Hが正確にb回出現する言葉のみを含む、新しいΩ1を構築します。
  • Ω1内の任意の事象AはまたΩ内の事象でもあるので、それに対して確率P(A)が定義されています。その事実に基づいて、P1(A)=P(A)/Р(Ω1)の式に従って確率P1をΩ1に導入しましょう。 実際、ここでは条件付き確率方程式P1(A)=P(A|О1)が使用されます。
  • ここで、Ω1からの「kの長さの単語の接尾辞には正確にx個のH文字が含まれる」事象の確率P1()について考えます。この確率は、上記の超幾何分布方程式によって正確に設定されていることがわかります。 非常に注目すべきことに、方程式はp母数に影響を与えません。

4. 数理統計学の基礎

数理統計学と確率論の違いは、通常、それらが解決する問題の種類の違いとして説明されます。確率論では、通常、確率モデルは完全に既知であると想定されており、それに基づいていくつかの結論を導き出す必要があります。数理統計学では、モデルに関する知識は不完全ですが、モデルの改良に役立つ実験データの形式で追加情報があります。したがって、前の章で説明したすべての質問は、確率論の問題です。

私が今提供した数理統計学の定義は、従来のものと見なすことができます。数理統計を定義するための別のより現代的なアプローチもあります。それは決定理論の一部として定義されるかもしれません。この場合、エラーの平均コストを最小化するという意味で最適な決定ルールを構築することに重点が置かれます。ここでは、機械学習手法と非常に強力な収束が見られます。それらとの大きな違いは、数理統計学では、適用される数学的モデルのタイプが非常に明確に決定されるという事実にあります(たとえば、未知の母数の精度内で)。機械学習では、不確実性は通常、モデルタイプにも及びます。

ここで、従来の意味での数理統計学のサンプル問題について考えてみましょう。

5. 初等理論の枠組みの中で数理統計学を適用する例

問題には、母数の推定と仮説の確認の2種類があります。

母数の推定から始めましょう。これは、確率モデルに数値(非ランダム、決定論的)変数が存在することを前提としています。正確な数値は不明ですが、確率実験の結果得られたデータを使用して概算値を計算できます。

5.1. 母数の推定

ここでの最も一般的なアプローチは、 最尤推定法を使用することです。根元事象ωが実現された場合、尤度関数は{ω}事象の確率です(この根元事象のみで構成されます)。モデルの母数値に依存する限り、関数と呼ばれます。最尤推定(MLE)は、この関数が最大値に達する母数値です。

MLEに加えて、さまざまな母数推定が複数存在する可能性がありますが、数学的統計で証明されているように、MLEは精度の点で最高のものです。「精度」という言葉の意味についての説明は、次の確率変数に関する記事まで残しておきます。いずれにせよ、統計的推定はほとんどの場合、母数の真の値とは異なることに留意する必要があります。したがって、それらを区別することは非常に重要です。例はベルヌーイスキームでの事象の確率と頻度の形式でのその推定です。

例を使用してMLEの計算に移りましょう。

例1: 超幾何分布のb母数を推定します。n=1000のワークピースのバッチがあります。それらのうちk=20をチェックした後、欠陥のあるワークピースが1つ検出されました(x=1)。バッチ全体で欠陥のあるワークピースの数を推定します。

以下は、Pythonで記述されたhyperg_be.pyスクリプトです。このスクリプトは、bのすべての可能なオプションを列挙することで、この問題を解決します。答えは、超幾何分布方程式によって決定される尤度値が最大になるbe推定です。

from scipy.stats import hypergeom

n = 1000
k = 20
x = 1
lhx = 0.0
be = 0
for b in range(x, n - k + x):
    lh = hypergeom.pmf(x, n, b, k)
    if lh > lhx:
        be = b
        lhx = lh
        
print("be =",be)

回答は予想通りbe = 50(20個ごとのワークピース)です。

例2: 超幾何分布のn母数を推定します。水域の魚の量を推定する必要があります。このために、b=50の魚を網で捕獲し、印を付けて放しました。その後、k=55の魚が捕獲され、そのうちx=3に印があることが判明しました。

以下は、Pythonで記述されたhyperg_ne.pyスクリプトです。このスクリプトは、nの可能なオプションを列挙することでこの問題を解決します。回答は、最も高い確率値でのneの推定です。nの可能な値が理論的に50+(55-3)=102から無限大の範囲であるというささいなニュアンスがあります。これにより、無限の列挙ループが発生する可能性があります。しかし、尤度関数はあるn値まで増加することがわかります。 その後、減少し始め、ゼロになります。 したがって、答えは最初のne値であり、尤度関数値はその値よりne+1だけ大きくなります。

from scipy.stats import hypergeom

b = 50
k = 55
x = 3
lh0 = 0.0
ne = b + k - x - 1
while True:
    lh = hypergeom.pmf(x, ne+1, b, k)
    if lh < lh0:
        break
    else:
        lh0 = lh
        ne += 1
        
print("ne =",ne)

回答: ne = 916、 これもかなり期待通りです(ne/bはおよそk/xであり、よってne はおよそb*k/xとなります)。

以下のすべての例は、ベルヌーイスキームまたはその修正に関連しています。このモデルの従来の取引解釈には、資産価格の離散化バージョンとの照合が含まれます。例えば、練行足または点と図のチャートを使用して、そのような表現を得ることができます。

この従来の方法を守りましょう。HとTの文字の代わりに、1と-1の数列を見ていきます。これは明らかに個別の価格ステップ(それぞれ上昇と下降)に対応します。一般に、価格ステップは、価格グリッドの新しいレベルへの到達として定義できます。これらのレベルグリッドは通常、各レベルとその下位の隣接レベルとの違いまたは関係が同じになるように定義されます。ここでは、2番目の方法を使用します。この方法の欠点は負の価格のアセットに適用できないことですが、利点は各アセットのステップサイズを個別に選択する必要がないことです。また、ゼロレベルの選択にはある程度の恣意性があります。その役割は、離散化の対象となるものの最初の価格によって果たされます。

以下は、指定された間隔で指定されたパーセンテージステップで価格を離散化する簡単なスクリプトです。 Discr.mqhファイルには、価格の離散化が実際に行われるsetmv()関数のみが含まれています。簡単にするために、分バーの始値のみが開始価格として採用されています。

// 個別のmv[]の動きの配列を構築する
// (指定された時間間隔と指定されたパーセンテージステップ)
void setmv(int& mv[], datetime t1, datetime t2, double dpr)
{
  int ND = 1000;
  ArrayResize(mv, 0, ND);
// 価格履歴を取得する
  double price[];
  int nprice = CopyOpen(Symbol(), PERIOD_M1, t1, t2, price);
  if(nprice < 2)
  {
    Print("not enough price history");
    return;
  }
// mv[]を構築する
  int lvl = 0, dlvl, nmv = 0, dmv;
  double lp0 = log(price[0]), lstep = log(1 + 0.01 * dpr);
  for(int i = 1; i < nprice; ++i)
  {
    dlvl = (int)((log(price[i]) - lp0) / lstep - lvl);
    if(dlvl == 0) continue;
    lvl += dlvl;
    dmv = 1;
    if(dlvl < 0)
    {
      dmv = -1;
      dlvl = -dlvl;
    }
    ArrayResize(mv, nmv + dlvl, ND);
    for(int j = 0; j < dlvl; ++j) mv[nmv + j] = dmv;
    nmv += dlvl;
  }
}

discret_prices.mq5スクリプトは、結果を1と-1の列として表示するとともに、開始価格の離散アナログのグラフを表示します。

#include <Discr.mqh>
#include <Graphics\Graphic.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 考慮される時間間隔の開始
input datetime tstop = D'2020.06.20 00:00';   // 考慮される時間間隔の終了
input double   dprcnt = 0.5;                  // %単位の価格離散化ステップ
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[], nmv;
  setmv(mv, tstart, tstop, dprcnt);
  nmv = ArraySize(mv);
  if(nmv < 1)
  {
    Print("not enough moves");
    return;
  }
// mv[]を1と-1の数列として表示する
  string res = (string)mv[0];
  for(int i = 1; i < nmv; ++i) res += ", " + (string)mv[i];
  Print(res);
// mv[]累積合計チャートを表示する
  ChartSetInteger(0, CHART_SHOW, false);
  CGraphic graphic;
  graphic.Create(0, "G", 0, 0, 0, 750, 350);
  double x[], y[];
  ArrayResize(x, nmv + 1);
  ArrayResize(y, nmv + 1);
  x[0] = y[0] = 0.0;
  for(int i = 1; i <= nmv; ++i)
  {
    x[i] = i;
    y[i] = y[i-1] + mv[i-1];
  }
  ArrayPrint(x);
  ArrayPrint(y);
  graphic.CurveAdd(x, y, CURVE_LINES, "discret_prices");
  graphic.CurvePlotAll();
  graphic.Update();
  Sleep(30000);
  ChartSetInteger(0, CHART_SHOW, true);
  graphic.Destroy();
}

以下のすべての例では、2020年5月20日から6月20日まで0.5％刻みでEURUSDの価格離散化の結果を使用します。結果は、次の個別のステップの列です: 1、-1、1、1、-1、1、1、-1、1、1、1、-1、1、1、1、-1、- 1、1、1、1、-1、-1、-1、1、-1、-1。より明確にするために、元の価格とその個別のアナログのチャートを以下に示します。

EURUSD(2020.05.20～2020.06.20)

discret_prices

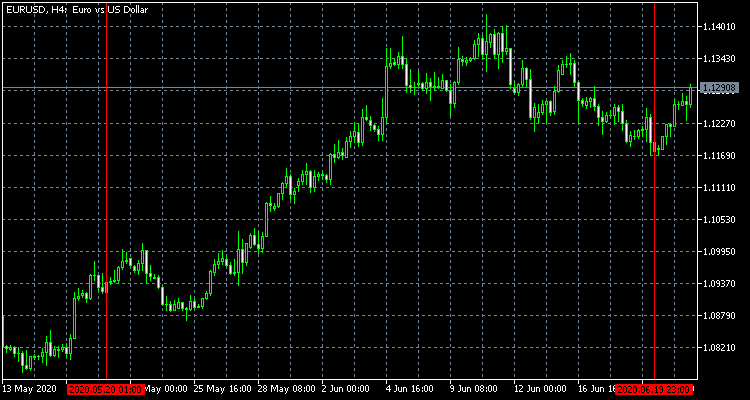
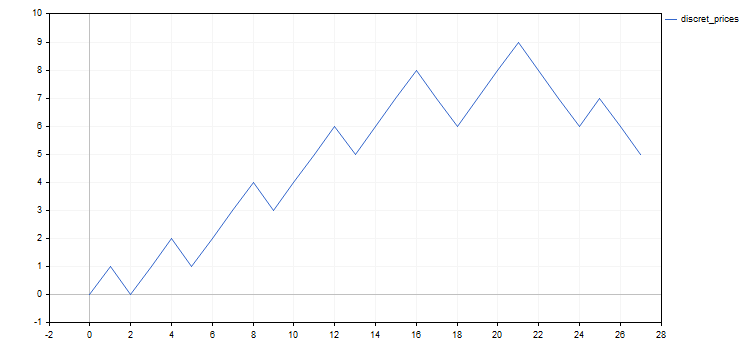
離散化された価格の振る舞いを研究することに加えて、ベルヌーイスキームまたはその修正を適用する他の方法があるかもしれません。取引に関連する2つのことを指摘しましょう。

  1. 固定ストップロスで取引が行われる取引の結果は、利益とボリュームレベルを取ります。一連の取引のすべての利益は互いにほぼ等しく、損失についても同じことが言えます。したがって、利益の確率は、取引結果を説明するのに十分な母数です。たとえば、既存の一連の取引で利益を上げる確率が十分に高いかどうかという疑問を提起することができます。 
  2. 投資する資産の選択。期間の開始時に投資方法の選択肢が豊富であると仮定します。それらのいずれかは、ある程度の確率で、最終的に投資された資金の完全な損失につながる可能性があります。資産を選択する方法がある場合、棄却された資産と比較して、選択された資産の破産の確率の違いについて疑問が生じる可能性があります。

    例に戻りましょう。

    例3: ベルヌーイスキームのp母数の推定。これは、問題が紙で解決できるまれなケースです。尤度関数はp^nup*(1-p)^ndnになります。pに関する導関数を取り、それをゼロに等しくして、рを頻度として推定するための期待値を取得します: pe=nup/(nup+ndn)=nup/nmv。通常の場合と同様に、検索は尤度関数の最大値ではなく、その対数に対して実行されます。これははるかに簡単です。対数は厳密に増加する関数であり、同じ母数値で最大値に達するため、答えは同じです。以下は、この推定を計算するp_model.mq5スクリプトです。

    #include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 考慮される時間間隔の開始
input datetime tstop = D'2020.06.20 00:00';   // 考慮される時間間隔の終了
input double   dprcnt = 0.5;                  // %単位の価格離散化ステップ
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 1)
  {
    Print("not enough moves");
    return;
  }
  double pe = calcpe(mv);
  Print("pe=", pe);
}
//+------------------------------------------------------------------+
// 確率推定を計算する
double calcpe(int& mv[])
{
  int nmv = ArraySize(mv);
  if(nmv < 1) return 0.0;
  int nup = 0;
  for(int i = 0; i < nmv; ++i) if(mv[i] > 0) ++nup;
  return ((double)nup) / nmv;
}

    回答: pe = 0.59(四捨五入)

    例4: 変更されたベルヌーイスキームの母数の推定。上で書いたように、モデリングの目的で必要な場合は、ベルヌーイスキームを変更できます。可能な変更オプションを考えてみましょう。

    おそらく、最も簡単なオプションは、一連の動きを2つの小さな動きに分割し、次々に移動し、母数n1、p1、n2=n-n1、およびp2を使用してベルヌーイスキームに対応することです。ここで、nは累積列の長さです。 したがってn1、p1、p2の3つの母数を推定する必要があります。p1およびp2に関連する対数尤度関数を最大化すると、n1を介してそれらを分析的に表現できます。 n1の推定は、p1とp2の式を対数尤度方程式に代入する単純な検索によって見つける必要があります。
    以下は、母数推定を計算するp1p2_model.mq5スクリプトです。

    #include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 考慮される時間間隔の開始
input datetime tstop = D'2020.06.20 00:00';   // 考慮される時間間隔の終了
input double   dprcnt = 0.5;                  // %単位の価格離散化ステップ
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  int n1e;
  calc_n1e_p1e_p2e(mv, n1e, p1e, p2e);
  Print("n1e=", n1e, " p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// 確率推定を計算する
void calc_n1e_p1e_p2e(int& mv[], int& n1e, double& p1e, double& p2e)
{
  n1e = 0;
  p1e = p2e = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  n1e = 1;
  double llhx = llhx_n1(mv, 1, p1e, p2e), llh, p1, p2;
  for(int n1 = 2; n1 < nmv; ++n1)
  {
    llh = llhx_n1(mv, n1, p1, p2);
    if(llh > llhx)
    {
      llhx = llh;
      n1e = n1;
      p1e = p1;
      p2e = p2;
    }
  }
}
//+------------------------------------------------------------------+
// n1に応じる最大の対数尤度関数
double llhx_n1(int& mv[], int n1, double& p1, double& p2)
{
  p1 = p2 = 0.0;
  int nmv = ArraySize(mv);
  if(nmv < 2 || n1 < 1 || n1 >= nmv) return 0.0;
  int nu1 = 0, nu2 = 0;
  for(int i = 0; i < n1; ++i) if(mv[i] > 0) ++nu1;
  for(int i = n1; i < nmv; ++i) if(mv[i] > 0) ++nu2;
  double l = 0.0;
  if(nu1 > 0)
  {
    p1 = ((double)nu1) / n1;
    l += nu1 * log(p1);
  }
  if(nu1 < n1) l += (n1 - nu1) * log(((double)(n1 - nu1)) / n1);
  if(nu2 > 0)
  {
    p2 = ((double)nu2) / (nmv - n1);
    l += nu2 * log(p2);
  }
  if(nu2 < nmv - n1) l += (nmv - n1 - nu2) * log(((double)(nmv - n1 - nu2)) / (nmv - n1));
  return l;
}

    回答: n1e = 21; p1e = 0.71; p2e = 0.17 (四捨五入)。私たちのモデルがそのセグメントの終わりに価格方向の変化(または修正)を「検出」したことは非常に明白なようです。これは、この場合のより複雑なモデルへの移行が無駄ではなかったことを示唆しています。

      例5: 前の例では、上向きの動きの確率はその数(時間内)に依存していました。この確率が前の動き自体に依存するベルヌーイスキームの別の修正を考えてみましょう。2つの状態を持つ最も単純なマルコフ連鎖の例であるモデルを構築してみましょう。

      動きに0からnまでの番号が付けられているとします。ゼロ移動の場合、上方向への移動の確率は、以前の移動がないため、単純に0.5に設定されます。他の位置の場合、上向きの動きの確率は、前に上向きの動きがあった場合はp1に等しく、前に下向きの動きがあった場合はp2に等しいです。これら2つの場合の下方向きの動きの確率はそれぞれq1=1-p1およびq2=1-p2に等しくなります。たとえば、事象に1つdown-up-up-downの根元事象がある確率は0.5*p2*p1*q1です。

      MLEを使用して推定できる2つの母数を持つモデルを取得しました。ここで、特に対数尤度関数を最大化すると、すべての計算を紙で再度実行できます。ベルヌーイスキームの場合のように、答えは頻度に要約されます。上向きの動きの後に下向きの動きが起こる回数はnud (u − up, d − down)として設定されます。同様に nuu、ndd、 nduを導入します。p1およびp2の推定は p1eおよびp2eで示されます。これらの推定はp1e=nuu/(nuu+nud)および p2e=ndu/(ndu+ndd)式を使用してみつかります。

      以下は、この推定を計算するmarkov_model.mq5スクリプトです。

      #include <Discr.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input datetime tstart = D'2020.05.20 00:00';  // 考慮される時間間隔の開始
input datetime tstop = D'2020.06.20 00:00';   // 考慮される時間間隔の終了
input double   dprcnt = 0.5;                  // %単位の価格離散化ステップ
//+------------------------------------------------------------------+
void OnStart()
{
  int mv[];
  setmv(mv, tstart, tstop, dprcnt);
  if(ArraySize(mv) < 2)
  {
    Print("not enough moves");
    return;
  }
  double p1e, p2e;
  calcpes(mv, p1e, p2e);
  Print("p1e=", p1e, " p2e=", p2e);
}
//+------------------------------------------------------------------+
// 確率推定を計算する
void calcpes(int& mv[], double& p1e, double& p2e)
{
  p1e = p2e = 0;
  int nmv = ArraySize(mv);
  if(nmv < 2) return;
  int nuu = 0, nud = 0, ndu = 0, ndd = 0, nu, nd;
  for(int i = 0; i < nmv - 1; ++i)
    if(mv[i] > 0)
    {
      if(mv[i + 1] > 0) ++nuu;
      else ++nud;
    }
    else
    {
      if(mv[i + 1] > 0) ++ndu;
      else ++ndd;
    }
  nu = nuu + nud;
  nd = ndu + ndd;
  if(nu > 0) p1e = ((double)nuu) / nu;
  if(nd > 0) p2e = ((double)ndu) / nd;
}

      回答:  p1e = 0.56、p2e = 0.60 (四捨五入)。両方の確率が互いにほぼ等しいことは、隣接する動きの間に依存関係がないことを示しています。両方の確率が0.5より大きい場合は、上昇傾向を示しています。両方の確率推定がより単純なモデル(3番目の例の単純なベルヌーイスキーム)の確率推定に近いことは、この特定のケースではこの複雑なモデルへの移行が不要であることが判明したことを示しています。

      5.2. 統計的仮説の検定

      同じ標本空間に異なる確率分布を設定できます。仮説は、分布のタイプを指定するステートメントです。解決策は1つの仮説を他の仮説よりも優先することにあるため、いくつかの仮説(少なくとも2つ)が必要です。仮説が分布のタイプを一意に決定する場合、その仮説は単純と呼ばれます。

      Bernoulliスキームの例を示しましょう。p母数が特定の数に等しいという仮説- 単純な 仮説(分布を明確に定義する1つの可能な母数値のみ)、母数が指定された数を超えるという仮説は複雑な仮説(可能な母数値の無限の量)です。

      次に、2つの仮説のうちの1つの選択について説明します。それらの1つは帰無仮説と呼ばれ、もう1つは対立仮説です。仮説は、統計的基準を使用して選択されます。基本的に、これは標本空間内に0と1の値を持つ関数です。ここで0は帰無仮説を受け入れることを意味し、1は対立仮説を受け入れることを示します。

      帰無仮説を受け入れるかことまたは棄却することができ、対立仮説を棄却することまたは受け入れることができます。これらの決定のそれぞれは、正しいか間違っている可能性があります。したがって、仮説を受け入れることで考えられる結果は4つあり、そのうち2つは正しく、2つは誤りです。

      1. タイプ1エラー - 帰無仮説の誤った棄却
      2. タイプ2エラー - 帰無仮説の誤った受け入れ

      タイプ1およびタイプ2のエラーの確率は、a1およびa2で示されます。当然、これらの確率を可能な限り低くするのがよいでしょう。しかし残念ながら、これは不可能です。さらに、あるタイプのエラーの確率を下げることにより、別のタイプのエラーの確率の増加に直面することはかなり予想されます。これが、これらのエラー間の特定の妥協が通常行われる理由です。

      1-a1は検定有意性と呼ばれ、1-a2はその検定力と呼ばれます。特に複雑な仮説の場合、テスト検定力の計算が難しい場合があります。したがって、通常は検定の有意性のみが使用されます。

      基準は通常、検定統計量と呼ばれる数値関数(標本空間に基づいて定義されます)に基づいています。その複数の値は2つの領域に分けられます。1つの領域は帰無仮説の受け入れに対応し、もう1つの領域はその棄却に対応します。帰無仮説が棄却される領域は、危険域と呼ばれます。

      以下は、「マイナスファースト」仮説に関する重要な注意事項です。この用語は、2つの仮説のいずれかが満たされていることを事前に確認する必要があることを意味します。大まかに言えば、チワワを他の品種の犬と体重で分ける場合は、常に体重計に犬(象、マウス、猫ではない)が乗っていることを確認する必要があります。そうでなければ、テストは無意味です。この原則は、計量経済学で使用される統計的基準が不正確に適用された場合に最も頻繁に破られます。

      以下は、ベルヌーイスキームの検定仮説の例です。

      例1: ベルヌーイスキームでの帰無仮説p=p0のテスト。この仮説は単純です。対立仮説は、次の2つのオプションのいずれかになります(どちらの場合も複雑です)。kup(列内の上向きの動きの数)は、どちらの場合も統計基準として使用されますが、危険域の定義は異なります。

      1. p>p0、危険域は右側にある、kup⋝kr
      2. p<p0、危険域は左側にある、kup⋜kl

      krおよびklの特定の値統計が危険域に分類される確率が、選択したタイプ1エラーの確率を超えないという条件を使用して検出されます。すでに述べたように、これらの確率はすべて、帰無仮説が満たされるという条件の下で計算されます(母数p=p0を使用したベルヌーイ分布によって)。

      同じ離散化された価格列でp0=0.5のこの仮説を確認しましょう。p0の値は、「ランダムウォーク」(「公正なコイン」)仮説に適合するという点で優れています。

      以下は、この仮説をテストするp0_hypothesis.mq5スクリプトです。

      #include <Math\Stat\Binomial.mqh>
#property script_show_inputs
//+------------------------------------------------------------------+
input int    nm = 27;          // シリーズの動きの総数
input int    kup = 16;         // 上向きの動きの数
input double p0 = 0.5;         // 確認された確率値
input double alpha1 = 0.05;    // タイプ1エラーの確率
//+------------------------------------------------------------------+
void OnStart()
{
  int kl, kr, er;
  kr=(int)MathQuantileBinomial(1.0-alpha1,nm,p0,er);
  kl=(int)MathQuantileBinomial(alpha1,nm,p0,er);
  Print("kl=", kl, " kup=", kup, " kr=", kr);
  Print("kup<=kl = ", kup<=kl);
  Print("kup>=kr = ", kup>=kr);
}

      応答:

      • kl=9; kup=16; kr=18
      • kup<=kl = false
      • kup>=kr = false

      結果は、このレベルの有意性では、対立仮説のいずれかを支持するために帰無仮説を棄却できないことを示しています。

      例2: 長さがn1およびn2でp1およびp2母数を持つ、ベルヌーイスキームから取得された2つの列があるとします。ここでの帰無仮説は、p1=p2の等式が満たされているというステートメントにあります。対立仮説は、不平等のさまざまなタイプであり、ここにも2つあります。k2は、これらすべての場合の統計基準として使用されます。2番目の列の危険域は異なって定義されていますが、2番目の列の上向きの動きの数です。

      • p2>p1、危険域は右側にある k2⋝kr
      • p2<p1、危険域は左側にある k2⋜kl

      前の例との大きな違いは、ここで話しているのは正確なp1とp2値に関連するステートメントについてではなく、それらの比率についてのみであるということです。危険域は前の例と同じ方法で定義されますが、帰無仮説の下での統計の分布は超幾何分布であり、二項分布ではありません。数理統計では、この基準はフィッシャーの直接確率検定として知られています。

      以下は、Pythonのp1p2_hypothesis.pyスクリプトで、離散化された価格を2つに分割してこの問題を解決しています。前の段落の4番目の例で取得した分割を使用します。

      from scipy.stats import hypergeom

n1 = 21; n2 = 6
k1 = 15; k2 = 1
alpha1 = 0.05

kl = int(hypergeom.ppf(alpha1, n1 + n2, k1 + k2, n2))
kr = int(hypergeom.ppf(1.0 - alpha1, n1 + n2, k1 + k2, n2))

print("kl =", kl, " k2 =", k2, " kr =", kr)
print("k2<=kl =", k2<=kl)
print("k2>=kr =", k2>=kr)

       応答:

      • kl = 2;  k2 = 2;  kr = 6
      • k2<=kl = True
      • k2>=kr = False
      結果は、帰無仮説がこの有意水準で棄却され、最初の選択肢が支持されることを示しています。これは、価格を異なる方法に動いている2つの部分に分割できることの追加の確認です。

      6. 終わりに

      この記事では、記述統計学、区間母数推定、漸近推定、統計におけるベイズアプローチなどの数理統計の重要な領域については説明していません。その理由は、意味のある考察のために確率変数の概念を明確にする必要があるということです。本稿を十分にコンパクトにするために、説明は次の記事で行います。

      7. 添付ファイル

      #
      		 名称
      		 種類 説明
       1 hyperg_be.py   Pythonスクリプト  b超幾何分布母数推定の計算(例5.1.1) 
       2 hyperg_ne.py   Pythonスクリプト   n超幾何分布母数推定の計算(例5.1.2)
       3  Discr.mqh  MQL5ヘッダファイル  以下のすべてのMQL5の例で価格の離散化に使用されているsetmv()関数を含むファイル
       4  discret_prices.mq5  MQL5スクリプト  価格の離散化を実行し、結果を1と-1の列のチャートに表示するスクリプト
       5  p_model.mq5  MQL5スクリプト  ベルヌーイスキームでのp母数推定の計算(例5.1.3)
       6  p1p2_model.mq5  MQL5スクリプト 2つのベルヌーイスキームで構成されるモデルでのn1、p1、p2母数の計算(例5.1.4) 
       7  markov_model.mq5  MQL5スクリプト マルコフ連鎖のp1およびp2母数推定の計算(例5.1.5)
       8  p0_hypothesis.mq5  MQL5スクリプト 
      		 ベルヌーイスキーム母数が指定された数に等しいという仮説の確認(例5.2.1) 
       9  p1p2_hypothesis.py  Pythonスクリプト  フィッシャーの直接確率検定(例5.2.2) 


      MetaQuotes Ltdによってロシア語から翻訳されました。
      元の記事: https://www.mql5.com/ru/articles/8038

      添付されたファイル |
      ZIPをダウンロード
      hyperg_be.py (0.22 KB)
      hyperg_ne.py (0.24 KB)
      Discr.mqh (1.71 KB)
      discret_prices.mq5 (2.67 KB)
      p_model.mq5 (1.86 KB)
      p1p2_model.mq5 (3.95 KB)
      markov_model.mq5 (2.51 KB)
      p0_hypothesis.mq5 (1.83 KB)
      p1p2_hypothesis.py (0.45 KB)
      警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。

      この著者による他の記事

      ディスカッションに移動
      買われすぎ・売られすぎゾーンの検出方法について。 第一部 買われすぎ・売られすぎゾーンの検出方法について。 第一部
      買われすぎ/売られすぎのゾーンは、相場の特定の状態を特徴づけ、有価証券の価格の弱い変化によって区別されます。 シナミクスにおけるこの不利な変化は、あらゆるスケールのトレンドの成長の最終段階で顕著です。 トレードにおける利益価値は、可能な限り大きなトレンド振幅をカバーできるかどうかに直接依存するため、このようなゾーンを検出する精度は、どのような証券でも重要な課題となります。
      クイック手動取引ツールキット: ポジションと指値注文の使用 クイック手動取引ツールキット: ポジションと指値注文の使用
      本稿では、ツールキットの機能を拡張します。特定の条件で取引ポジションを決済する機能を追加し、これらの注文を編集する機能を備えた、成行注文と指値注文を制御するための表を作成します。
      取引イベントおよびシグナルの音声通知システム 取引イベントおよびシグナルの音声通知システム
      今日では、ナビゲーター、音声検索、翻訳ツールがよく使用され、音声アシスタントは人間の生活において重要な役割を果たしています。本稿では、さまざまな取引イベント、市場の状態、取引シグナルによって生成されるシグナルに対するシンプルでユーザフレンドリーな音声通知システムの開発を試みます。
      DoEasyライブラリの時系列(第48部): 複数銘柄・複数期間指標バッファ DoEasyライブラリの時系列(第48部): 複数銘柄・複数期間指標バッファ
      本稿では、指標バッファオブジェクトのクラスを改善して、複数銘柄モードで動作するようにします。これにより、カスタムプログラムで複数銘柄・複数期間指標を作成するための道が開かれます。複数銘柄・複数期間指標標準指標を作成するために、不足している機能を計算バッファオブジェクトに追加します。