
计算数学表达式(第一部分)。 递归下降解析器
在自动执行交易任务时,可能需要在其执行阶段提供计算算法的灵活性。 例如,当微调程序以闭合(编译)模式分布时,我们可以从众多可能的组合中选择目标函数类型。 特别是在优化智能交易系统或快速评估指标原型时,这很有用。 除了更改对话框中的参数之外,用户还可以更改计算公式。 在这种情况下,我们只需从其文本表达形式计算其数学表达式,而无需更改 MQL 程序代码。
可以通过各种解析器来解决此任务,这些解析器可以即时解释公式,将其“编译”为语法树,生成所谓的字节码(计算指令序列),进而执行从而得出计算结果 。 在本文中,我们将研究几种类型的解析器和表达式计算方法。
问题的陈述
在本文中,算术表达式是单行序数据项和运算符的相关操作描述。 数据项是数字和已命名变量。 变量值可从外部设置和编辑,即并非在表达式内部,而是用特殊的解析器属性。 换句话说,没有赋值运算符('=')来存储中间结果。 以下是受支持的运算符列表,按计算优先级顺序显示:
- !, - , + — 一元逻辑非,减号和加号
- () — 括号分组
- *, /, % — 乘法,除法和除法模
- +, - — 加法和减法
- >, <, >=, <= — 大、小比较
- ==, != — 相等或不等比较
- &&, || — 逻辑与 AND 和逻辑或 OR(请注意,优先级相同,因此应使用括号)
- ?: — 三元条件运算符,可令您根据条件分支计算
我们还将允许在表达式中使用 MQL 的标准数学函数,共计 25 个。 其中之一是用于幂运算的 pow 函数。 有因于此,运算符列表中没有指数运算符('^')。 另外,运算符 '^' 仅支持整数幂,而该函数则无此限制。 还有一个更特殊的功能,即把 “^” 与其他研究的运算符区分开。
这与以下内容相关。 运算符属性之一是关联性,它判断如何从左或从右执行具有相同优先级的运算符。 还有其他关联类型,但它们不会在当前任务的前后环境里使用。
这是一个关联性如何影响计算结果的示例。
1 - 2 - 3
该表达式未明确指示两次减法的执行顺序。 由于运算符 '-' 是左关联的,因此首先从 1 中减去 2,然后从中间结果 -1 中减去 3,得到 -4,即等价于以下表达式:
((1 - 2) - 3)
如果假设运算符 “-” 为右关联,则将以相反的顺序执行操作:
(1 - (2 - 3))
我们会得到 2。 幸运的是,运算符 '-' 是左关联的。
因此,左或右关联会影响表达式的解析,从而令算法复杂化。 列出的所有二元运算符都是左关联的,只有 '^' 是右关联的。
例如,表达式:
3 ^ 2 ^ 5
意即首先计算 2 的 5 次幂,然后计算 3 的 32 次幂。
为简单起见,我们不再用指数运算符(而是改用 pow 函数),因此仅考虑左关联性来实现算法。 一元运算符始终是右关联的,因此统一对待。
在我们的表达式中,所有数字(包括那些写成常量和变量的数字)都是实数。 我们为比较它们是否相等而设置公差值。 逻辑表达式中的数字则采用一个简单的原理:零为假;非零为真。
未提供按位运算符。 不支持数组。
此处是一些表达式示例:
- "1 + 2 * 3" — 按操作优先级计算
- "(1 + 2) * 3" — 使用括号分组
- "(a + b) * c" — 使用变量
- "(a + b) * sqrt(1 / c)" — 使用函数
- "a > 0 && a != b ? a : c" — 按逻辑条件计算
变量按名称标识,该名称由 MQL 常规标识符规则组成:它们可以由字母、数字或下划线组成,并且不能以数字开头。 变量名称不得与内置函数重名。
输入的字符串将逐字符进行分析。 常规检查,诸如字符是否属于字母或数字,以及错误处理,变量设置和可扩展的标准函数表,将在基类中定义。 所有解析器类型都将从该基类继承。
我们来研究所有解析器类。 文章示意的类经过一些简化。完整的源代码附于下面。
解析器基类(AbstractExpressionProcessor 模板)
这是模板类,由于表达式分析结果不仅可以是标量值,而且还可以是描述表达式语法的节点树(特殊类的对象)。 稍后我们会研究如何完成此操作,以及这样做的目的是什么。
首先,类对象存储表达式(_expression),其长度(_length),读取字符串(_index)时的当前光标位置,和当前符号(_token)。 它还预留了指示表达式中错误的变量(_failed),和数值比较精度(_precision)。
template<typename T> class AbstractExpressionProcessor { protected: string _expression; int _index; int _length; ushort _token; bool _failed; double _precision;
提供了存储变量和链接的特殊表,但是稍后我们将研究相关的 VariableTable 和 FunctionTable 类。
VariableTable *_variableTable;
FunctionTable _functionTable;
这些表是由 “key=value” 对组成的关键字=数值对,其中关键字是变量或函数名称的字符串,而数值则是 double(对于变量),或 functor 对象(对于表) 。
变量表由引用描述,因为表达式不能包含变量。 对于函数表,解析器始终含有最少的内置函数集合(用户可以扩展),这就是为什么此表由已有对象表示的原因。
标准函数表是在方法中填充:
virtual void registerFunctions();
下一章节介绍的函数执行的子任务通用于各种解析器,例如切换到下一个字符,对照期望值检查字符(如果不匹配则显示错误),顺序读取满足格式要求的数字, 以及一些用于字符分类的静态辅助方法。
bool _nextToken(); void _match(ushort c, string message, string context = NULL); bool _readNumber(string &number); virtual void error(string message, string context = NULL, const bool warning = false); static bool isspace(ushort c); static bool isalpha(ushort c); static bool isalnum(ushort c); static bool isdigit(ushort c);
所有这些函数都在基类中定义,尤其是:
template<typename T> bool AbstractExpressionProcessor::_nextToken() { _index++; while(_index < _length && isspace(_expression[_index])) _index++; if(_index < _length) { _token = _expression[_index]; return true; } else { _token = 0; } return false; } template<typename T> void AbstractExpressionProcessor::_match(ushort c, string message, string context = NULL) { if(_token == c) { _nextToken(); } else if(!_failed) // prevent chained errors { error(message, context); } } template<typename T> bool AbstractExpressionProcessor::_readNumber(string &number) { bool point = false; while(isdigit(_token) || _token == '.') { if(_token == '.' && point) { error("Too many floating points", __FUNCTION__); return false; } number += ShortToString(_token); if(_token == '.') point = true; _nextToken(); } return StringLen(number) > 0; }
数字解析不支持指数的科学注释法。
该类还声明了主要的 “evaluate” 方法,该方法应在子类中被覆盖。 在此,它仅初始化变量。
public: virtual T evaluate(const string expression) { _expression = expression; _length = StringLen(_expression); _index = -1; _failed = false; return NULL; }
这是主要的类方法,该方法的输入接收表达式的字符串,并输出字符串处理结果:如果执行了计算,则为特定值;如果进行了分析,则为语法树。
该类的公开接口还包含构造函数,能够将变量及其值(作为字符串,例如 “name1 = value1; name2 = value2; ...”,或作为现成的 VariableTable 对象)传递给构造函数;为比较数字设置容差的方法;获取解析成功指示(表明没有语法错误)的方法;以及访问变量和函数表的方法。
public: AbstractExpressionProcessor(const string vars = NULL); AbstractExpressionProcessor(VariableTable &vt); bool success() { return !_failed; }; void setPrecision(const double p) { _precision = p; }; double getPrecision(void) const { return _precision; }; virtual VariableTable *variableTable(); virtual FunctionTable *functionTable(); };
请注意,即使没有语法错误,表达式计算也可能导致错误(例如,除零,负值开根,等等)。 为了控制这种情况,请用 MathIsValidNumber 函数检查结果是否为数字。 我们的解析器必须能够针对不同的 NaN(非数字)类型生成相应的数值,而不能在运行时崩溃。
最简单的方法是递归下降解析器。 因此,我们从这个解析器开始。
递归下降解析器(ExpressionProcessor 模板)
递归下降解析器是一组相互递归的函数,分别根据操作规则描述进行调用。 如果我们在扩展 BNF 注释法(Extended Backus–Naur Form)时,将某些最常见操作的语法表述为语法,则表达式可如下表示(每行是一条单独的规则):
Expr -> Sum
Sum -> Product { ('+' | '-') Product }
Product -> Value { ('*' | '/') Value }
Value -> [0-9]+ | '(' Expr ')'
这些规则在自然语言中类似于以下内容。 表达式解析从最低优先级操作开始,在本示例中则为加法/减法。 “Sum” 由两个 Product 操作数组成,它们之间用 “+” 或 “-” 号隔开,但运算本身,以及第二个操作数都是可选项。 'Product' 由两个 Value 操作数组成,数值之间以 '*' 或 '/' 分隔。 同样,该操作和第二个操作数可能会缺失。 'Value' 是任何数字,或括号中指定的嵌套表达式组成。
例如,表达式 “10”(一个数字)将扩展为以下规则序列:
Expr -> Sum -> Product -> Value -> 10
表达式 “1 + 2 * 3” 将具有更复杂的结构:
Expr -> Sum -> Product -> Value -> 1
| '+'
-> Product -> Value -> 2
| '*'
-> Value -> 3
根据该算法,执行语法解析,与输入字符流和操作规则之间的匹配一起执行。 解析是从主规则(整个表达式)到次要组件(直至单个数字)执行的。 递归下降解析器属于自上而下的类。
我们的解析器将支持更多操作(请参阅第一部分中的列表)。 在 ExpressionProcessor 派生类中为每个操作保留了一个单独的方法。
template<typename T> class ExpressionProcessor: public AbstractExpressionProcessor<T> { public: ExpressionProcessor(const string vars = NULL); ExpressionProcessor(VariableTable &vt); T evaluate(const string expression) override { AbstractExpressionProcessor<T>::evaluate(expression); if(_length > 0) { _nextToken(); return _parse(); } return NULL; } protected: T _parse(); T _if(); // ?: T _logic(); // && || T _eq(); // == != T _compare(); // ><>=<= T _expr(); // +- T _term(); // */% T _unary(); // !-+ T _factor(); // () T _identifier(); T _number(); T _function(const string &name); };
表达式 EBNF 语法的示例可作为编写方法代码的指南。
expression -> if
if -> logic { '?' if ':' if }
logic -> eq { ('&&' | '||' ) eq }
eq -> compare { ('==' | '!=' ) compare }
compare -> expr { ('>' | '<' | '>=' | '<=') expr }
expr -> term { ('+' | '-') term }
term -> unary { ('*' | '/' | '%') unary }
unary -> { ('!' | '-' | '+') } unary | factor
factor -> '(' if ')' | number | identifier
identifier -> function | variable
variable -> name
function -> name '(' { arglist } ')'
name -> char { char | digit }*
arglist -> if { ',' if }
下降点是 _parse 方法,该方法自公开的 “evaluate” 方法中调用。 根据运算符的优先级,_parse 方法将控制权转移到时间点最近的那个,即 _if。 解析整个表达式之后,当前字符必须为零(行终止符)。
template<typename T> T ExpressionProcessor::_parse(void) { T result = _if(); if(_token != '\0') { error("Tokens after end of expression.", __FUNCTION__); } return result; }
三元条件运算符由三个子表达式组成:布尔条件和两个计算选项(分别为真和假条件)。 布尔条件是语法的下一层:_logic 方法。 事实上,计算选项还可以是三元条件运算符,因此我们递归调用 _if。 在条件和 true 选项之间必须有 “?” 字符。 如果字符缺失,则说明它不是三元运算符,并且算法将按原样从 _logic 返回数值。 如果有 “?” 字符,我们需要另外检查 true 和 false 选项之间是否存在 ':' 字符。 如果所有组件均存在,则检查条件,并根据是 true 还是 false 返回第一个或第二个值。
template<typename T> T ExpressionProcessor::_if() { T result = _logic(); if(_token == '?') { _nextToken(); T truly = _if(); if(_token == ':') { _nextToken(); T falsy = _if(); return result ? truly : falsy; // NB: to be refined } else { error("Incomplete ternary if-condition", __FUNCTION__); } } return result; }
逻辑 AND(与)或 OR(或)操作由 _logic 方法表达。 在该方法中,我们期望在操作数之间有连续的字符 “&&” 或 “||”,表示比较(_eq 方法)。 如果没有逻辑运算,则直接从 _eq 方法返回结果。 如果找到逻辑运算,则对其进行计算。 借助 “while” 循环,解析器可以连续执行多个逻辑加法或乘法运算,例如 “a > 0 && b > 0 && c > 0”。
template<typename T> T ExpressionProcessor::_logic() { T result = _eq(); while(_token == '&' || _token == '|') { ushort previous = _token; _nextToken(); if(previous == '&' && _token == '&') { _nextToken(); result = _eq() && result; } else if(previous == '|' && _token == '|') { _nextToken(); result = _eq() || result; } else { error("Unexpected tokens " + ShortToString(previous) + " and " + ShortToString(_token), __FUNCTION__); } } return result; }
请注意,“&&” 和 “||” 在此实现中的优先级相等,故此,所需顺序应使用括号指定。
比较运算符('==','!=')与在 _eq 方法中的处理方式类似。
template<typename T> T ExpressionProcessor::_eq() { T result = _compare(); if(_token == '!' || _token == '=') { const bool equality = _token == '='; _nextToken(); if(_token == '=') { _nextToken(); const bool equal = fabs(result - _compare()) <= _precision; // NB: to be refined return equality ? equal : !equal; } else { error("Unexpected token " + ShortToString(_token), __FUNCTION__); } } return result; }
本文中跳过了某些方法(为了保持简洁)。 所有这些都可以在随附的源代码中找到。
在 _factor 方法中,我们实际处理操作数。 它可以是带括号的子表达式,针对它我们递归调用 _if,标识符或数字(常数,文字)。
template<typename T> T ExpressionProcessor::_factor() { T result; if(_token == '(') { _nextToken(); result = _if(); _match(')', ") expected!", __FUNCTION__); } else if(isalpha(_token)) { result = _identifier(); } else { result = _number(); } return result; }
标识符可以表示变量,或如果该名称后跟一个开放的括号则为函数名称。 此解析则是由 _identifier 方法执行的。 如果我们处理的是一个函数,则特殊的 _function 方法在 _functionTable 函数表中查找一个相应的对象,解析参数列表(每个参数可以是一个独立的表达式,并可通过 _if 的递归调用获得),然后将控制权转移到函子对象。
template<typename T> T ExpressionProcessor::_identifier() { string variable; while(isalnum(_token)) { variable += ShortToString(_token); _nextToken(); } if(_token == '(') { _nextToken(); return _function(variable); } return _variableTable.get(variable); // NB: to be refined }
_number 方法简单地调用 StringToDouble 将读取的数字序列转换为数字(上面已展示过 _readNumber 帮助函数)。
template<typename T> T ExpressionProcessor::_number() { string number; if(!_readNumber(number)) { error("Number expected", __FUNCTION__); } return StringToDouble(number); // NB: to be refined }
这就是整个递归下降解析器。 它几乎快准备好了。 “几乎”是因为这是一个模板类,故需要专门定制特定类型。 若要基于数字类型变量计算表达式,则为 double 提供定制,如下所示:
class ExpressionEvaluator: public ExpressionProcessor<double> { public: ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { } ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { } };
然而,该过程实际上更加复杂。 该算法在解析期间计算表达式。 解释器模式是最简单但也是最慢的一种。 想象一下,您需要使用变化的变量值(例如价格或数量)在每次即时报价上计算相同的公式。 为了加快计算速度,最好将这两个阶段分开:解析和操作执行。 在这种情况下,解析能够一次执行 - 表达式结构可按某种中间表示形式保存,该中间表示形式已针对计算进行了优化,然后可用该表示形式进行快速重新计算。
为此目的,必须将所有在中间方法中获得的中间结果以递归调用的形式传递,直到从公开的 “evaluate” 方法返回最终值为止,所有中间结果都必须替换为存储了以下内容的对象:包含运算符和操作数(及其所有关系)的特定表达式片段。 可用这样的描述以延迟的方式来计算表达式。 这样的对象称为 Promises。
惰性评估(Promises)
Promise 类描述的是与表达式元件不同的实体:操作数,或含有操作数引用的操作。 例如,如果在表达式中遇到变量名,则在 _identifier 方法中处理以下行:
return _variableTable.get(variable); // NB: to be refined
它按名称返回表中变量的当前值。 它是一个 double 类型值 — 当解析器为 double 类型定制,并即时执行计算时,此选项适用。 不过,如果需要推迟计算,则需要创建 Promise 对象,并将变量名称保存在其中,而不是变量值。 将来,当变量值变化时,我们可从 Promise 对象请求其新值,且按其名称查找其数值。 因此,很明显,含标记 “NB: to be refined” 的当前代码行不适用于 ExpressionProcessor 模板的一般情况,因此必须用其他内容替换。 ExpressionProcessor 中有若干这样的代码行,我们将为它们寻找一个单一的解决方案。 不过,我们首先需要完成 Promise 类。
Promise 类含有几个字段,用于描述任意操作数或操作。
class Promise { protected: uchar code; double value; string name; int index; Promise *left; Promise *right; Promise *last; public: Promise(const uchar token, Promise *l = NULL, Promise *r = NULL, Promise *v = NULL): code(token), left(l), right(r), last(v), value(0), name(NULL), index(-1) { } Promise(const double v): // value (const) code('n'), left(NULL), right(NULL), last(NULL), value(v), name(NULL), index(-1) { } Promise(const string n, const int idx = -1): // name of variable code('v'), left(NULL), right(NULL), last(NULL), value(0), name(n), index(idx) { } Promise(const int f, Promise *¶ms[]): // index of function code('f'), left(NULL), right(NULL), last(NULL), value(0), name(NULL) { index = f; if(ArraySize(params) > 0) left = params[0]; if(ArraySize(params) > 1) right = params[1]; if(ArraySize(params) > 2) last = params[2]; // more params not supported }
“code” 字段存储元素类型属性:“n” 是数字,“v” 是变量,“f” 是函数。 所有其他符号也被视为允许的操作之一(例如,“+”,“-”,“*”,“/”,“%”,等等)。 对于数字,其值存储在 “value” 字段中。 针对变量的情况,其名称存储在 “name” 字段中。 为了快速多次访问变量,Promise 会在第一次调用后尝试将变量编号缓存在 “index” 字段里,然后尝试按索引从表中检索变量,而非名称。 函数始终由 “index” 字段中的编号标识,因为与变量不同,“Functions” 表最初是用内置函数填充的,而变量表在表达式分析时可能依旧为空。
“left”,“right” 和 “last” 引用是可选项,它们可以存储操作数。 例如,对于数字或变量,所有三个引用均为 NULL。 一元运算仅使用 'left' 引用;二元运算用到 “left” 和 “right” 引用;而所有三个引用仅在三元条件运算符中使用:“left” 包含条件,“right” 是 true 条件的表达式,而 “last” 则是 false 条件。 另外,引用存储函数参数对象(在当前解析器实现中,函数参数的数量限制为三个)。
由于 Promise 对象参与计算,因此我们将覆盖其中的所有主要运算符。 例如,这就是处理带有 “promises” 的加法和减法运算的方式。
Promise *operator+(Promise *r) { return new Promise('+', &this, r); } Promise *operator-(Promise *r) { return new Promise('-', &this, r); }
当前对象(&this),即表达式中位于左侧的操作对象,以及下一个位于右侧的操作对象(r),将传递给按相关操作代码创建的新 Promise 对象的构造函数。
其他操作的处理方式相同。 结果就是,整个表达式显示为 Promise 类的对象树,其中根元素表示整个表达式。 有一个特殊的 “resolve” 方法,该方法接收任意 “promise” 对象的实际值,包括整个表达式。
double resolve() { switch(code) { case 'n': return value; // number constant case 'v': value = _variable(); // variable name return value; case 'f': value = _execute(); // function index return value; default: value = _calc(); return value; } return 0; };
这显示了如何从 value 字段返回数字常数值。 实现的 Helper 方法则针对变量、函数和操作。
static void environment(AbstractExpressionProcessor<Promise *> *e) { variableTable = e.variableTable(); functionTable = e.functionTable(); } protected: static VariableTable *variableTable; static FunctionTable *functionTable; double _variable() { double result = 0; if(index == -1) { index = variableTable.index(name); if(index == -1) { return nan; // error: Variable undefined } result = variableTable[index]; } else { result = variableTable[index]; } return result; } double _execute() { double params[]; if(left) { ArrayResize(params, 1); params[0] = left.resolve(); if(right) { ArrayResize(params, 2); params[1] = right.resolve(); if(last) { ArrayResize(params, 3); params[2] = last.resolve(); } } } IFunctor *ptr = functionTable[index]; // TBD: functors if(ptr == NULL) { return nan; // error: Function index out of bound } return ptr.execute(params); } double _calc() { double first = 0, second = 0, third = 0; if(left) { first = left.resolve(); if(right) { second = right.resolve(); if(last) { third = last.resolve(); } } } switch(code) { case '+': return first + second; case '-': return first - second; case '*': return first * second; case '/': return safeDivide(first, second); case '%': return fmod(first, second); case '!': return !first; case '~': return -first; case '<': return first < second; case '>': return first > second; case '{': return first <= second; case '}': return first >= second; case '&': return first && second; case '|': return first || second; case '`': return _precision < fabs(first - second); // first != second; case '=': return _precision > fabs(first - second); // first == second; case '?': return first ? second : third; } return nan; // error: Unknown operator }
此处省略了错误处理。 如果发生了错误,则返回一个特殊的 nan 值(“not a number - 非数字”,在单独的头文件 NaNs.mqh 中实现其生成,该文件附于后面)。 请注意,所有低层对象(在层次结构中),会在递归里按其引用调用 “resolve” 检查操作执行情况。 故此,调用 “resolve” 将启动表达式所有关联 “promises” 的一序列计算,并将计算结果作为 double 数值传输给更高的元素。 在末尾,所有数值“折叠”进表达式的最终值。
借助 Promise 类,我们可用它来定制递归下降解析器,该解析器返回一个类似对象的树作为结果,即它返回表达式的语法树。
如今,在 ExpressionProcessor 模板类的所有方法中,这些方法返回一些 T,该 T 现在必须等于(Promise *)。 特别是在 _identifier 方法中,有以下行:
return _variableTable.get(variable); // NB: to be refined
我们需要提供某种方式,它创建并返回一个新的 Promise 对象,替代 double,该对象指向一个名为 “variable” 的变量。
若要解决此问题,应将返回变量的 T 类型值的操作包装到单独的虚拟方法中,该方法将在 ExpressionProcessor<double> 和 ExpressionProcessor<Promise *> 派生类中执行不同的请求操作。 然而,还存在一个小问题。
ExpressionHelper 类
我们计划实现若干个解析器类,每个解析器类都将继承自 AbstractExpressionProcessor。 然而,并非所有方法都需要专用于递归下降方法。 我们可以在不需要它们的地方用空实现来覆盖它们,但就 OOP 而言,这并不正确。 如果 MQL 支持多重继承,我们可以使用特殊的 trait — 必要时可以在解析器类中包含其他方法集合。 由于这是不可能的,因此我们将相应的方法作为单独的模板类实现,并仅在需要该方法的解析器内部才创建其实例。
template<typename T> class ExpressionHelper { protected: VariableTable *_variableTable; FunctionTable *_functionTable; public: ExpressionHelper(AbstractExpressionProcessor<T> *owner): _variableTable(owner.variableTable()), _functionTable(owner.functionTable()) { } virtual T _variable(const string &name) = 0; virtual T _literal(const string &number) = 0; virtual T _negate(T result) = 0; virtual T _call(const int index, T &args[]) = 0; virtual T _ternary(T condition, T truly, T falsy) = 0; virtual T _isEqual(T result, T next, const bool equality) = 0; };
该类包含所有不同方式处理的方法,在即时和惰性评估中均可胜任。 例如,_variable 方法负责访问变量。 _literal 接收常量的值;_negate 执行逻辑非;_call 调用一个函数;_ternary 是三元运算符,_isEqual 用于比较值。 通过覆盖 Promise 类中的运算符,即可用相同的语法针对 double 和 Promise 处理所有其他计算用例。
有人可能想知道为什么逻辑非运算符 '!' 在 Promise 中没有被覆盖,而是使用 _negate 方法。 操作符 '!' 仅应用于对象,而不能应用于指针。 换句话说,对于 Promise *p 类型变量,我们不能把代码写成 !p,并期望被覆盖的运算符起作用。 取而代之的是,我们首先需要取消引用指针:!*p。 但是此注解符对于其他类型无效,包括 T=double。
此处是如何针对 double 数值实现 ExpressionHelper 方法。
class ExpressionHelperDouble: public ExpressionHelper<double> { public: ExpressionHelperDouble(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { } virtual double _variable(const string &name) override { if(!_variableTable.exists(name)) { return nan; } return _variableTable.get(name); } virtual double _literal(const string &number) override { return StringToDouble(number); } virtual double _call(const int index, double ¶ms[]) override { return _functionTable[index].execute(params); } virtual double _isEqual(double result, double next, const bool equality) override { const bool equal = fabs(result - next) <= _precision; return equality ? equal : !equal; } virtual double _negate(double result) override { return !result; } virtual double _ternary(double condition, double truly, double falsy) override { return condition ? truly : falsy; } };
此处是如何针对 Promise 对象实现它们。
class ExpressionHelperPromise: public ExpressionHelper<Promise *> { public: ExpressionHelperPromise(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { } virtual Promise *_negate(Promise *result) override { return new Promise('!', result); } virtual Promise *_call(const int index, Promise *¶ms[]) override { return new Promise(index, params); } virtual Promise *_ternary(Promise *condition, Promise *truly, Promise *falsy) override { return new Promise('?', condition, truly, falsy); } virtual Promise *_variable(const string &name) override { if(CheckPointer(_variableTable) != POINTER_INVALID) { int index = _variableTable.index(name); if(index == -1) { return new Promise(nan); // error: Variable is undefined } return new Promise(name, index); } return new Promise(name); } virtual Promise *_literal(const string &number) override { return new Promise(StringToDouble(number)); } virtual Promise *_isEqual(Promise *result, Promise *next, const bool equality) override { return new Promise((uchar)(equality ? '=' : '`'), result, next); } };
现在我们可以将 'helper' 字段添加到 AbstractExpressionProcessor 当中:
protected: ExpressionHelper<T> *helper; public: ~AbstractExpressionProcessor() { if(CheckPointer(helper) == POINTER_DYNAMIC) delete helper; }
并重新查看 ExpressionProcessor 方法的实现,该方法的字符串标记为 “NB”:它们都必须将操作委托给 “helper” 对象。 例如:
template<typename T> T ExpressionProcessor::_eq() { T result = _compare(); if(_token == '!' || _token == '=') { const bool equality = _token == '='; _nextToken(); if(_token == '=') { _nextToken(); return helper._isEqual(result, _compare(), equality); // OK } } return result; } template<typename T> T ExpressionProcessor::_identifier() { string variable; while(isalnum(_token)) { variable += ShortToString(_token); _nextToken(); } ... return helper._variable(variable); // OK } template<typename T> T ExpressionProcessor::_number() { string number; if(!_readNumber(number)) { error("Number expected", __FUNCTION__); } return helper._literal(number); // OK }
使用已给出的类,我们最终可以在解析表达式的同时,组装第一个执行计算的解析器:ExpressionEvaluator。
class ExpressionEvaluator: public ExpressionProcessor<double> { public: ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperDouble(&this); } ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperDouble(&this); } };
在此,我们得到了另一个用于延迟求值的解析器 — ExpressionCompiler。
class ExpressionCompiler: public ExpressionProcessor<Promise *> { public: ExpressionCompiler(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperPromise(&this); } ExpressionCompiler(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperPromise(&this); } virtual Promise *evaluate(const string expression) override { Promise::environment(&this); return ExpressionProcessor<Promise *>::evaluate(expression); } };
主要区别在于 'helper' 字段和 Promise::environment 的初步调用,以便将变量和函数表输入到 Promise。
在获得完整的解析器之前,只剩下一件事了:变量和函数表。
变量和函数表
这两个表都是由 key=value 对组成的模板映射类,其中 key 是字符串标识符,value 是类型 T 的某个值。它们的实现已在 VariableTable.mqh 当中提供。 基类定义了所有必需的映射操作:添加元素,更改数值,并按名称或按索引检索它们。
template<typename T> class Table { public: virtual T operator[](const int index) const; virtual int index(const string variableName); virtual T get(const string variableName) const; virtual int add(const string variableName, T value); virtual void update(const int index, T value); ... };
这是 T 型变量 double。
class VariableTable: public Table<double> { public: VariableTable(const string pairs = NULL) { if(pairs != NULL) assign(pairs); } void assign(const string pairs); };
利用 'assign' 方法,不仅可以将变量一一添加到表中,还可添加列表 - 如类型为 “name1=value1;name2=value2;...” 的字符串。
应该为该功能创建一个特殊的函子接口。 函子将包含函数计算的代码。
interface IFunctor { string name(void) const; int arity(void) const; double execute(const double ¶ms[]); };
每个函数都有一个名称和一个描述参数数量(arity)的属性。 该函数由 “execute” 方法依据所传递参数进行计算。 在此接口中包装所有内置的 MQL 数学函数,然后将相应的对象添加到表中(逐个或一个数组):
class FunctionTable: public Table<IFunctor *> { public: void add(IFunctor *f) { Table<IFunctor *>::add(f.name(), f); } void add(IFunctor *&f[]) { for(int i = 0; i < ArraySize(f); i++) { add(f[i]); } } };
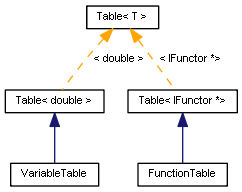
变量和函数表类的示意图
定义了一个存储类来存储所有函子。
class AbstractFuncStorage { protected: IFunctor *funcs[]; int total; public: ~AbstractFuncStorage() { for(int i = 0; i < total; i++) { CLEAR(funcs[i]); } } void add(IFunctor *f) { ArrayResize(funcs, total + 1); funcs[total++] = f; } void fill(FunctionTable &table) { table.add(funcs); } };
“fill” 方法用来自存储区(funcs 数组)中的标准函数填充该表。 为了令所有创建的函子自动传递到存储,请在 AbstractFunc 函数的基类中创建其静态实例,并用构造函数中 “this” 引用填充该实例。
class AbstractFunc: public IFunctor { private: const string _name; const int _arity; static AbstractFuncStorage storage; public: AbstractFunc(const string n, const int a): _name(n), _arity(a) { storage.add(&this); } string name(void) const override { return _name; } int arity(void) const override { return _arity; } static void fill(FunctionTable &table) { storage.fill(table); } }; static AbstractFuncStorage AbstractFunc::storage;
当然,构造函数会接收输入参数,从而令其能够识别函数的名称和属性。
还添加了中间模板类 FuncN,声明含有特殊含义的函数。 该类中的 Arity 由所传递类型的大小设置(截至目前,函数 arity 不超过 3,且不存在零大小的类型,因此我们用注解符 sizeof(T) % 4 — 故此大小 4 产生了 arity 0)。
template<typename T> class FuncN: public AbstractFunc { public: FuncN(const string n): AbstractFunc(n, sizeof(T) % 4) {} };
大小从 0 到 3 的类型都是用宏替换生成的。
struct arity0 { char x[4]; }; #define _ARITY(N) struct arity##N { char x[N]; }; _ARITY(1); _ARITY(2); _ARITY(3);
我们还需要参数列表来自动生成函数描述。
#define PARAMS0 #define PARAMS1 params[0] #define PARAMS2 params[0],params[1] #define PARAMS3 params[0],params[1],params[2]
现在,我们可以基于 FuncN<T> 类为函子定义一个宏。
#define FUNCTOR(CLAZZ,NAME,ARITY) \ class Func_##CLAZZ: public FuncN<arity##ARITY> \ { \ public: \ Func_##CLAZZ(): FuncN(NAME) {} \ double execute(const double ¶ms[]) override \ { \ return CLAZZ(PARAMS##ARITY); \ } \ }; \ Func_##CLAZZ __##CLAZZ;
最后,这是含有名称和参数数量的受支持函数的列表。
FUNCTOR(fabs, "abs", 1); FUNCTOR(acos, "acos", 1); FUNCTOR(acosh, "acosh", 1); FUNCTOR(asin, "asin", 1); FUNCTOR(asinh, "asinh", 1); FUNCTOR(atan, "atan", 1); FUNCTOR(atanh, "atanh", 1); FUNCTOR(ceil, "ceil", 1); FUNCTOR(cos, "cos", 1); FUNCTOR(cosh, "cosh", 1); FUNCTOR(exp, "exp", 1); FUNCTOR(floor, "floor", 1); FUNCTOR(log, "log", 1); FUNCTOR(log10, "log10", 1); FUNCTOR(fmax, "max", 2); FUNCTOR(fmin, "min", 2); FUNCTOR(fmod, "mod", 2); FUNCTOR(pow, "pow", 2); FUNCTOR(rand, "rand", 0); FUNCTOR(round, "round", 1); FUNCTOR(sin, "sin", 1); FUNCTOR(sinh, "sinh", 1); FUNCTOR(sqrt, "sqrt", 1); FUNCTOR(tan, "tan", 1); FUNCTOR(tanh, "tanh", 1);
广义形式的函子类示意图如下所示:
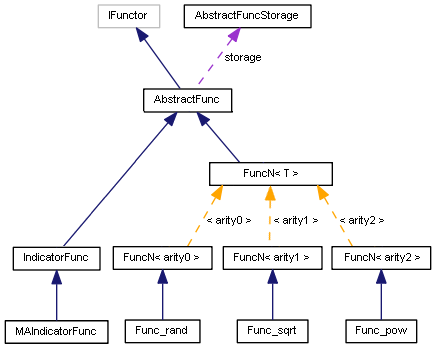
函子类示意图
该示意图未显示所有函数,仅显示了每种算法的一个函数。 还有一些函数,将在以后研究。
由此,一切准备就绪,两个递归下降解析器可以用了。 其中之一以解释模式计算表达式。 另一个使用语法树来计算表达式。
动态评估表达式(ExpressionEvaluator)
解释器对表达式的评估如下:我们创建一个 ExpressionEvaluator 实例,如有必要,将变量传递给它,然后用包含所需表达式的字符串调用 'evaluate' 方法。
ExpressionEvaluator ee("a=-10"); double result = ee.evaluate("1 + sqrt(a)"); // -nan(ind) bool success = ee.success(); // true
调用 “success” 方法,我们可以检查表达式在语法上是否正确。 只是,这不能保证它们在计算期间不会出错。 在上面的示例中,尝试负变量开根将返回 NaN。 因此,建议利用 MathIsValidNumber 函数检查结果。
开发其他解析器之后,我们将编写测试,并对该过程进行更详细的讲述。
"Compiling" 将表达式分解放入语法树,并评估该树(ExpressionCompiler)
通过构建语法树对表达式求值的步骤如下:我们创建 ExpressionCompiler 的实例,如有必要将初始变量传递给它,然后用包含所需表达式的字符串调用 'evaluate' 方法。 结果就是,我们得到 Promise 对象的引用,为此我们需要调用 “resolve” 评估表达式,并获取一个编号。 这看起来比较麻烦,但当您需要对变量的不同数值执行多次计算时,它的工作速度更快。
double a[10] = {...}, b[10] = {...}, c[10] = {...}; VariableTable vt; ExpressionCompiler с(vt); vt.adhocAllocation(true); const string expr = "(a + b) * sqrt(c)"; Promise *p = c.evaluate(expr); for(int i = 0; i < 10; i++) { vt.set("a", a[i]); vt.set("b", b[i]); vt.set("c", c[i]); Print(p.resolve()); }
首先在此处创建一个空变量表。 循环将变量 a、b、c 的变化值写入该表。 在解析和生成树阶段,于此处利用 adhocAllocation 方法设置一个标志,引导分析器接受并在表中保留任何变量名。 任何此类隐式变量都设置为 nan,因此调用者必须在计算 “promise” 之前将它们设置为实际值。
上面的示例中,如果在 c.evaluate 之前不调用 vt.adhocAllocation(true),则表达式中遇到的所有变量都会产生错误,因为默认情况下会假定变量已事先定义,但实际上表为空。 您可以在 c.evaluate() 之后调用 c.success() 来检查代码中的错误。 错误也会被记录。
与解释器类似,“evaluate” 方法无论如何都会返回一些结果。 因此,如果在解析阶段变量未知,则会在树中为其创建值为 nan 的节点。 依据这样的树进行计算是没有用的,因为一样也会返回 nan。 但存在一棵树是可以理解问题所在。 Promise 类拥有打印语法树的辅助方法 — print。
结束语
在本文中,我们研究了解析数学表达式的基础。 我们还创建了两个即用 MQL 解析器。 下面附有一个小的测试脚本,令您可开始在程序中运用该技术。 我们将在第二部分中继续探索其他解析器类型:我们将比较它们的性能,并提供有关如何运用它们来解决交易者任务的示例。
本文由MetaQuotes Ltd译自俄文
原文地址: https://www.mql5.com/ru/articles/8027
注意: MetaQuotes Ltd.将保留所有关于这些材料的权利。全部或部分复制或者转载这些材料将被禁止。
本文由网站的一位用户撰写,反映了他们的个人观点。MetaQuotes Ltd 不对所提供信息的准确性负责,也不对因使用所述解决方案、策略或建议而产生的任何后果负责。
 快捷手动交易工具箱:基本功能
快捷手动交易工具箱:基本功能
 神经网络在交易中的实际应用。 是时候进行实践了
神经网络在交易中的实际应用。 是时候进行实践了
在数学函数中添加更多 MQL 函数,并将优化标准 作为输入字符串。
或者指定带有 OnTester 函数源文件的文件名。解析器-解释器将进行计算。