Cálculo de expresiones matemáticas (Parte 1). Parsers de descenso recursivo

A la hora de automatizar las tareas comerciales, a veces necesitamos lograr que los algoritmos de cálculo sean flexibles en su estadio de ejecución. Así, por ejemplo, para el ajuste fino de los programas distribuidos en forma cerrada (compilada), podemos organizar la selección del tipo de función objetivo entre un amplio conjunto de combinacioes posibles. En particular, al optimizar el experto o realizar la evaluación rápida del prototipo de un indicador. Entonces, en la ventana de diálogo de propiedades, el usuario tendrá a su disposición no solo los parámetros, sino también la fórmula de cálculo. En estos casos, necesitaremos calcular la expresión matemática según su representación textual, sin cambiar el código MQL del programa.

Para solucionar esta tarea, se utilizan parsers de diferentes tipos, que permiten ejecutar la interpretación de fórmulas sobre la marcha, "compilar" estas en un árbol de sintaxis, generar el llamado código de bytes (secuencia de las instrucciones de cálculo), y ejecutar este posteriormente para calcular el resultado. En el presente artículo, analizaremos varios tipos de parsers y los métodos de cálculo de las expresiones.

Formulando la tarea

Entenderemos por expresión aritmética una secuencia unilateral de elementos de datos, y los operadores que describen las acciones sobre ellos. Como elementos de datos, tendremos números y variables nombradas. Los valores de las variables se podrán asignar y modificar desde el exterior, es decir, no en la propia expresión, sino usando los atributos especiales del analizador. En otras palabras, no habrá un operador de asignación ('=') para almacenar resultados intermedios. La lista de operadores soportados, considerando el orden de prioridad en los cálculos será la siguiente:

• !, - , + — negación lógica unaria, menos o más
• () — grupo con ayuda de paréntesis
• *, /, % — multiplicación, división y división euclidiana
• +, - — suma y resta
• >, <, >=, <= — comparación mayor-menor
• ==, != — comparación igualdad-desigualdad
• &&, || — Y u O lógico (atención, la prioridad es la misma, se necesitan paréntesis)
• ?: — operador condicional ternario que permite ramificar los cálculos según las condiciones

Además, permitiremos utilizar en las expresiones las funciones MQL matemáticas estándar, 25 en total. Entre ellas, en particular, tenemos también la función pow, para elevar a una determinada potencia. Por este motivo, en la lista de operadores no existe el operador de potenciación ('^'). Además, el operador '^' permite elevar solo a una potencia entera, mientras que la función no tiene esas limitaciones. Hay también otro matiz que distingue al operador '^' de los otros analizados.

La cuestión es que entre las propiedades de los operadores, hay una, llamada asociatividad, que define la dirección de ejecución de una secuencia de operadores con una misma prioridad (en concreto, del mismo tipo), o bien de izquierda a derecha, o bien de derecha izquierda. En principio, también existen otros tipos de asociatividad, pero no los encontraremos en el contexto de la nuestra tarea actual.

Aquí tenemos un ejemplo de cómo la asociativadad podría influir en el resultado del cálculo.

1 - 2 - 3

En esta expresión no existe una indicación explícita sobre la secuencia de ejecución de las dos restas con ayuda de paréntesis. Como el operador '-' tiene una asociatividad de derecha a izquierda, primero restaremos 2 a 1, y después 3 al -1 intermedio, obteniendo -4, lo cual equivale a:

((1 - 2) - 3)

Si, de forma puramente hipotética, el operador '-' tuviese una asociatividad de izquierda a derecha, la operación se realizaría en orden inverso:

(1 - (2 - 3))

y obtendríamos 2. Por fortuna, el operador '-' tiene una asociatividad hacia la izquierda.

De esta forma, la asociatividad hacia la izquierda o hacia la derecha influye en las reglas de análisis de las expresiones al realizar el parseo, complicando con ello el algoritmo. Entre los operadores binarios enumerados, todos tienen una asociatividad hacia la izquierda, y solo '^' hacia la derecha.

Por ejemplo, la expresión:

3 ^ 2 ^ 5

indica que primero 2 se eleva a 5, y después 3 se eleva a 32.

Para simplificar la tarea, tiene sentido eliminar el operador de potenciación (a favor de la función pow) e implementar los algoritmos solo considerando la asociatividad a la izquierda. Los operadores unarios siempre tienen asociatividad hacia la derecha, y por eso se procesan de las misma forma.

Todos los números en nuestras expresiones (tanto los anotados como constantes, como las variables) serán de tipo real. Para comparar si son iguales, estableceremos la magnitud permitida. En las expresiones lógicas, los números se usan según un principio sencillo: cero — false, no cero — true.

Los operadores a nivel de bits no se contemplan. Las matrices no tienen soporte.

Aquí tenemos varios ejemplos de expresiones:

• "1 + 2 * 3" — cálculos según la prioridad de las operaciones
• "(1 + 2) * 3" — grupo con ayuda de paréntesis
• "(a + b) * c" — uso de variables
• "(a + b) * sqrt(1 / c)" — uso de una función
• "a > 0 && a != b ? a : c" — cálculos según las condiciones lógicas

Las variables se identifican según el nombre compuesto conforme a las reglas habituales de los identificadores MQL: pueden constar de letras, cifras o guiones bajos, y no pueden comenzar por cifras. Los nombres de las variables no deberán coincidir con los nombres de las funciones incorporadas.

El análisis de la línea de entrada lo produciremos de forma simbólica. En la clase básica, que heredaremos todos los tipos de parsers, realizaremos las comprobaciones generales de pertenencia de los símbolos a un conjunto de letras y cifras, y también estableceremos las variables y el recuadro de funciones incorporadas (ampliado en caso necesario).

Vamos a analizar secuencialmente todas las clases de parsers. En los artículos, estas se representan con ciertas simplificaciones. Los códigos fuentes completos se adjuntan al artículo.

Clase básica de los parsers (plantilla AbstractExpressionProcessor)

Esta clase es una plantilla, dado que el resultado del análisis de una expresión puede ser no solo un valor escalar, sino también un árbol de nodos (objetos de la clase de señal) que describa la sintaxis de la expresión. Más tarde, hablaremos sobre cómo se hace esto y para qué lo necesitamos.

El objeto de clase guarda, ante todo, la propia expresión (_expression), su longitud (_length), la posición actual del cursor en el proceso de lectura de la línea (_index) y el símbolo actual (_token). Asimismo, se reservan variables para el signo del error en la expresión (_failed) y la precisión de la comparación de las magnitudes (_precision).

  template<typename T>
  class AbstractExpressionProcessor
  {
    protected:
      string _expression;
      int _index;
      int _length;
      ushort _token;
  
      bool _failed;
      double _precision;

Para guardar las variables y los enlaces a las funciones, hemos creado los recuadros correspondientes; no obstante, nos familiarizaremos con sus clases VariableTable y FunctionTable más tarde.

      VariableTable *_variableTable;
      FunctionTable _functionTable;

Por ahora, nos bastará con saber que los recuadros suponen mapas con parejas de "clave=valor", donde la clave es una línea con el nombre de la variable o función, mientras que el valor, o bien es un valor double (en el caso de las variables), o bien un objeto de funtor (en el caso de las funciones).

El recuadro de variables se describe con un enlace, porque en las expresiones podría no haber variables. Pero el conjunto mínimo de funciones incorporadas en el analizador siempre está presente (el usuario puede ampliarlo) y, por consiguiente, el recuadro de funciones estará representado por un objeto listo para usar.

El rellenado del recuadro de funciones incorporadas se realiza en el método:

      virtual void registerFunctions();

A continuación, se describen las funciones que efectúan subtareas comunes a varios analizadores, como pasar al siguiente carácter, comparar el carácter con lo esperado (dando error si no coincide), leer secuencialmente las cifras que cumplan con el formato numérico, y también varios métodos auxiliares estáticos para la clasificación de caracteres.

      bool _nextToken();
      void _match(ushort c, string message, string context = NULL);
      bool _readNumber(string &number);
      virtual void error(string message, string context = NULL, const bool warning = false);
      
      static bool isspace(ushort c);
      static bool isalpha(ushort c);
      static bool isalnum(ushort c);
      static bool isdigit(ushort c);

Todas estas funciones se definen en esta clase básica, en concreto:

  template<typename T>
  bool AbstractExpressionProcessor::_nextToken()
  {
    _index++;
    while(_index < _length && isspace(_expression[_index])) _index++;
    if(_index < _length)
    {
      _token = _expression[_index];
      return true;
    }
    else
    {
      _token = 0;
    }
    return false;
  }
  
  template<typename T>
  void AbstractExpressionProcessor::_match(ushort c, string message, string context = NULL)
  {
    if(_token == c)
    {
      _nextToken();
    }
    else if(!_failed) // prevent chained errors
    {
      error(message, context);
    }
  }
  
  template<typename T>
  bool AbstractExpressionProcessor::_readNumber(string &number)
  {
    bool point = false;
    while(isdigit(_token) || _token == '.')
    {
      if(_token == '.' && point)
      {
        error("Too many floating points", __FUNCTION__);
        return false;
      }
      number += ShortToString(_token);
      if(_token == '.') point = true;
      _nextToken();
    }
    return StringLen(number) > 0;
  }

Al realizar el parseo de un número, no se ofrece soporte de la entrada con función exponencial.

Aparte de estos, en la clase se declara el método principal evaluate, que será redefinido en los herederos. Aquí, el método solo inicializa las variables.

    public:
      virtual T evaluate(const string expression)
      {
        _expression = expression;
        _length = StringLen(_expression);
        _index = -1;
        _failed = false;
        return NULL;
      }

Se trata del método principal de la clase, encargado de recibir una línea con una expresión como entrada y de generar el resultado de su procesamiento en la salida: un valor específico si se ha realizado un cálculo, o un árbol de sintaxis, si se ha realizado un análisis.

La interfaz pública de clase contiene también constructores a los que se pueden transmitir en caso necesario las variables junto con sus valores (tanto en forma de lína del tipo "name1=value1;name2=value2;...", como de objeto VariableTable preparado), así como los métodos para establecer el permiso para la comparación de números, la obtención del signo de éxito del parseo (ausencia de errores de sintaxis) y el acceso a los recuadros de variables y funciones.

    public:
      AbstractExpressionProcessor(const string vars = NULL);
      AbstractExpressionProcessor(VariableTable &vt);
  
      bool success() { return !_failed; };
      void setPrecision(const double p) { _precision = p; };
      double getPrecision(void) const { return _precision; };
      virtual VariableTable *variableTable();
      virtual FunctionTable *functionTable();
  };

Preste atención: incluso de no haber errores de sintaxis, el cálculo de la expresión puede finalizar con un error (por ejemplo, división por 0, raíz cuadrada de un número negativo, etcétera). Para controlar semejantes situaciones, deberemos comprobar que el resultado verdaderamente es un número, usando para ello la función MathIsValidNumber. Nuestros parsers deberán saber generar las magnitudes correspondientes de los diversos tipos de NaN (Not A Number), y no "caerse" durante la ejecución.

El parser más sencillo de entender es el parser de descenso recursivo. Comenzaremos por él.

Parser de descenso recursivo (plantilla ExpressionProcessor)

Un parser de descenso recursivo supone un conjunto de funciones llamadas de forma recursiva una desde otra según reglas que describen operaciones aparte. Si reducimos la sintaxis de varias de las operaciones más utilizadas a la gramática en la anotación de BNF (Extended Backus–Naur Form), podremos presentar la expresión de la forma siguiente (cada línea es una regla aparte):

  Expr    -> Sum
  Sum     -> Product { ('+' | '-') Product }
  Product -> Value { ('*' | '/') Value }
  Value   -> [0-9]+ | '(' Expr ')'

En lenguaje natural, estas reglas son equivalentes a algo semejante a lo siguiente. La expresión empieza a ser analizada con la operación de menor prioridad; en este ejemplo, es la suma/resta. La suma (Sum) son dos operandos Product separados por los signos '+' o '-', pero la propia operación y el segundo operando son opcionales. El producto (Product) son dos operandos separados por los signos Value '*' o '/', pero, nuevamente, la propia operación y el segundo operando podrían no estar. El valor (Value) es, o bien un número que consta de cifras, o bien una expresión anidada realizada entre paréntesis.

Por ejemplo, la expresión "10" (simplemente el número) será desplegada en esta secuencia de reglas:

  Expr -> Sum -> Product -> Value -> 10

Mientras que la expresión "1 + 2 * 3" conllevará una construcción más compleja:

  Expr -> Sum -> Product -> Value -> 1
              |  '+'
              -> Product -> Value -> 2
                         |  '*'
                         -> Value -> 3

Como podemos ver fácilmente, el algoritmo presupone analizar la gramática seleccionando las correspondencias entre el flujo de caracteres de entrada y las reglas operacionales; dicho análisis, además, se realiza partiendo desde la regla principal (la expresión completa) hacia los componentes más pequeños (números individuales). El parser de descenso recursivo pertenece a la clase descendente (top-down)

Nuestro parser ofrecerá soporte a más operaciones (ver la lista mostrada en el primer apartado), reservando para cada una de ellas su propio método en la clase derivada ExpressionProcessor.

  template<typename T>
  class ExpressionProcessor: public AbstractExpressionProcessor<T>
  {
    public:
      ExpressionProcessor(const string vars = NULL);
      ExpressionProcessor(VariableTable &vt);
      T evaluate(const string expression) override
      {
        AbstractExpressionProcessor<T>::evaluate(expression);
        if(_length > 0)
        {
          _nextToken();
          return _parse();
        }
        return NULL;
      }
      
    protected:
      T _parse();
      T _if();        // ?:
      T _logic();     // && ||
      T _eq();        // == !=
      T _compare();   // ><>=<=
      T _expr();      // +-
      T _term();      // */%
      T _unary();     // !-+
      T _factor();    // ()
      T _identifier();
      T _number();
      T _function(const string &name);
  };

El aspecto aproximado de la gramática de EBNF de las expresiones servirá como instrucciones de escritura del código de los métodos.

  expression -> if
  if         -> logic { '?' if ':' if }
  logic      -> eq { ('&&' | '||' ) eq }
  eq         -> compare { ('==' | '!=' ) compare }
  compare    -> expr { ('>' | '<' | '>=' | '<=') expr }
  expr       -> term  { ('+' | '-') term }
  term       -> unary { ('*' | '/' | '%') unary }
  unary      -> { ('!' | '-' | '+') } unary | factor
  factor     -> '(' if ')' | number | identifier
  identifier -> function | variable
  variable   -> name
  function   -> name '(' { arglist } ')'
  name       -> char { char | digit }*
  arglist    -> if { ',' if } 

El punto de comienzo del descenso será el método _parse, que se llama desde el método público evaluate. Teniendo en cuenta las prioridades de los operadores, el método _parse transmite el control al más "joven", _if. Después de analizar toda la expresión, el carácter actual deberá ser cero (signo de final de la línea).

  template<typename T>
  T ExpressionProcessor::_parse(void)
  {
    T result = _if();
    if(_token != '\0')
    {
      error("Tokens after end of expression.", __FUNCTION__);
    }
    return result;
  }

El operador condicional ternario consta de tres subexpresiones: la condición lógica, y dos variantes de cálculos, una para la condición verdadera y otra para la condición falsa. La condición lógica es el siguiente nivel de la gramática: el método _logic. Las variantes de cálculo pueden a su vez ser operadores condicionales ternarios, en realción con lo cual, llamamos a _if de forma recursiva. Entre una condición y su variante verdadera debe estar el símbolo '?'. Si no se encuentra, no se tratará de un operador ternario, y el algoritmo retornará el valor de _logic como está. Si el signo '?' existe, compararemos adicionalmente que entre las variantes verdadera y falsa se encuentre el carácter ':'. Cuando tengamos todos los componentes, comprobaremos la condición y retornaremos el primer o el segundo valor, dependiendo de su veracidad.

  template<typename T>
  T ExpressionProcessor::_if()
  {
    T result = _logic();
    if(_token == '?')
    {
      _nextToken();
      T truly = _if();
      if(_token == ':')
      {
        _nextToken();
        T falsy = _if();
        return result ? truly : falsy; // NB: to be refined
      }
      else
      {
        error("Incomplete ternary if-condition", __FUNCTION__);
      }
    }
    return result;
  }

Los operadores del Y u O lógicos se presentan con el método _logic. En ellos, esperamos la aparición de los caracteres consecutivos "&&" o "||" entre los operandos que constituyen la comparación (método _eq). Si no hay operación lógica, el resultado se retornará directamente desde el método _eq. Si la hay, la calcularemos. Gracias al ciclo while, el parser puede ejecuctar varias sumas y multiplicaciones consecutivas, por ejemplo "a > 0 && b > 0 && c > 0".

  template<typename T>
  T ExpressionProcessor::_logic()
  {
    T result = _eq();
    while(_token == '&' || _token == '|')
    {
      ushort previous = _token;
      _nextToken();
      if(previous == '&' && _token == '&')
      {
        _nextToken();
        result = _eq() && result;
      }
      else
      if(previous == '|' && _token == '|')
      {
        _nextToken();
        result = _eq() || result;
      }
      else
      {
        error("Unexpected tokens " + ShortToString(previous) + " and " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Preste atención a que las prioridades de "&&" y "||" en esta implementación son iguales, y por eso, al registrar diferentes operaciones de forma consecutiva, necesitaremos indicar el orden deseado con ayuda de paréntesis.

Las operaciones de comparación ('==', '!=') se procesan de forma semejante en el método _eq.

  template<typename T>
  T ExpressionProcessor::_eq() 
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        const bool equal = fabs(result - _compare()) <= _precision; // NB: to be refined
        return equality ? equal : !equal;
      }
      else
      {
        error("Unexpected token " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Para mayor brevedad, vamos a omitir algunos métodos en el artículo; si el lector lo desea, podrá familiarizarse con los mismos en los códigos fuente.

En el método _factor, llegaremos prácticamente a los operandos. Puede tratarse de una subexpresión entre paréntesis para la que se llama a _if de forma recursiva, o bien un identificador, o bien un número (constante, literal).

  template<typename T>
  T ExpressionProcessor::_factor()
  {
    T result;
    
    if(_token == '(')
    {
      _nextToken();
      result = _if();
      _match(')', ") expected!", __FUNCTION__);
    }
    else if(isalpha(_token))
    {
      result = _identifier();
    }
    else
    {
      result = _number();
    }
    
    return result;
  }

El identificador puede indicar el nombre de una variable o función, si después del nombre hay un paréntesis inicial. De este análisis se encarga el método _identifier. En el caso de la función, el método especial _function encontrará en el recuadro de funciones _functionTable el objeto correspondiente, parseará la lista de parámetros (además, cada uno de ellos podrá ser una expresión independiente, y se obtendrá gracias a la llamada recursiva de _if) y después transmitirá el control a un objeto-funtor.

  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
  
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    
    if(_token == '(')
    {
      _nextToken();
      return _function(variable);
    }
    
    return _variableTable.get(variable); // NB: to be refined
  }

El método _number simplemente transforma la secuencia de cifras transmitida en un número con la ayuda de StringToDouble (la función auxiliar _readNumber se ha mostrado más arriba).

  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return StringToDouble(number); // NB: to be refined
  }

Aquí tenemos el parser de descenso recursivo, que ya está casi listo para funcionar. "Casi", porque la clase es una clase patrón y requiere la especialización con un tipo concreto. Para calcular una expresión basada en variables de tipo numérico, basta con hacer una especialización para double, aproximadamente así:

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { }
  };

Pero, en la práctica, las cosas son un poco más complicadas. El algoritmo analizado calcula una expresión en el proceso de análisis. Este modo del intérprete es el más sencillo, pero también el más lento. Imaginemos que debemos calcular la misma fórmula en cada tick para valores cambiantes de las variables (por ejemplo, los precios y volúmenes). Para acelerar los cálculos, sería deseable separar las etapas de análisis y ejecución de las operaciones. Después, el parseo solo podrá realizarse una vez, almacenando la estructura de la expresión en alguna representación intermedia y optimizada para los cálculos, y realizando luego un rápido cálculo de esta representación.

Para ello, todos los resultados intermedios obtenidos en los métodos analizados y transmitidos a lo largo de la cadena de llamadas recursivas hasta retornar el valor final del método público evaluate deberán ser sustituidos por objetos que guarden la descripción de los operadores y operandos de un fragmento particular de la expresión (junto con todas sus relaciones). Según esta descripción, se podrá realizar el cálculo de la expresión de forma diferida. Estos objetos se llaman Promise.

Cálculos diferidos (Promise)

La clase Promise describe una entidad aparte entre los componentes de la expresión: un operando u operación junto con los enlaces a los operandos. Por ejemplo, si en la expresión se encuentra el nombre de una variable, en el método _identifier se procesa la línea:

    return _variableTable.get(variable); // NB: to be refined

Esta retornará el valor actual de la variable desde el recuadro según su nombre. Se trata de un valor del tipo double, lo cual resulta adecuado en caso de que el parser esté especializado con el tipo double y ejecute los cálculos sobre la marcha. No obstante, si deseamos aplazar los cálculos, deberemos crear un objeto Promise en lugar del valor de la variable, y luego almacenar en él el nombre de la variable. En el futuro, cuando resulte probable que el valor de una variable cambie en el recuadro, deberíamos poder solicitar su nuevo valor desde el objeto Promise, que encontrará su valor según su nombre de la misma manera. De esta forma, queda claro que la línea de código actual, marcada con el comentario "NB: to be refined", no es conveniente para el caso general de la plantilla ExpressionProcessor, y deberá ser reemplazada con algo. En realidad, tenemos varias líneas de este tipo en ExpressionProcessor, y pronto hallaremos una solución uniforme para ellas, pero, por el momento, trataremos con la clase Promise.

Para describir un operando u operación aleatorios, tenemos varios campos en la clase Promise.

  class Promise
  {
    protected:
      uchar code;
      double value;
      string name;
      int index;
      Promise *left;
      Promise *right;
      Promise *last;
      
    public:
      Promise(const uchar token, Promise *l = NULL, Promise *r = NULL, Promise *v = NULL):
        code(token), left(l), right(r), last(v), value(0), name(NULL), index(-1)
      {
      }
      Promise(const double v): // value (const)
        code('n'), left(NULL), right(NULL), last(NULL), value(v), name(NULL), index(-1)
      {
      }
      Promise(const string n, const int idx = -1): // name of variable
        code('v'), left(NULL), right(NULL), last(NULL), value(0), name(n), index(idx)
      {
      }
      Promise(const int f, Promise *&params[]): // index of function
        code('f'), left(NULL), right(NULL), last(NULL), value(0), name(NULL)
      {
        index = f;
        if(ArraySize(params) > 0) left = params[0];
        if(ArraySize(params) > 1) right = params[1];
        if(ArraySize(params) > 2) last = params[2];
        // more params not supported
      }

El campo code guarda el signo del tipo de elemento: 'n' — número, 'v' — variable, 'f' — función, y todos los demás caracteres se analizan como operaciones permitidas (por ejemplo, '+', '-', '*', '/', '%', etcétera). En el caso de los números, su valor se guarda en el campo value. En el caso de las variables, su valor se guarda en el campo name. Para acceder rápidamente y de forma múltiple a las variables, tras la primera llamada, Promise intentará guardar en la caché el número de la variable en el campo index, y después tratará de extraerla del recuadro por el índice, y no por el nombre. Las funciones siempre se identifican según el número en el campo index, ya que, a diferencia de las variables, el recuadro de las funciones se rellena con las funciones incorporadas, mientras que el recuadro de variables puede encontrarse aún vacío en el momento en que se analiza la expresión.

Los enlaces left, right y last son opcionales, y pueden guardar operandos. Por ejemplo, para los números y variables, los tres enlaces son iguales a NULL. Para las operaciones unarias, se usa solo el enlace left, para las operaciones binarias, los enlaces left y right, mientras que los tres enlaces solo se implican en el operador condicional ternario: en ese caso, left contiene la condición, right, la expresión para la condición verdadera, y last, para la condición falsa. Asimismo, los enlaces contienen los objetos de parámetro de las funciones (la implementación actual del parser limita a tres el número de parámetros de las funciones).

Como los objetos Promise participan en los cálculos, hemos redefinido en ellos todos los operadores principales. Por ejemplo, aquí tenemos cómo se procesan las operaciones de suma y resta con Promise.

      Promise *operator+(Promise *r)
      {
        return new Promise('+', &this, r);
      }
      Promise *operator-(Promise *r)
      {
        return new Promise('-', &this, r);
      }

El objeto actual (&this), es decir, el que se encuentra dentro de la expresión, a la izquierda de la operación, y el objeto colindante (r), que se encuentra a la derecha de la operación, se transmiten al constructor del nuevo objeto Promise creado con el código de la operación correspondiente.

Las otras operaciones se procesan de forma similar. Como resultado, la expresión completa se representa en el árbol de objetos de la clase Promise; además, el elemento raíz presenta la expresión entera. Para obtener el valor actual de cualquier objeto Promise, incluyendo una expresión al completo, se ha previsto el método resolve.

      double resolve()
      {
        switch(code)
        {
          case 'n': return value;        // number constant
          case 'v': value = _variable(); // variable name
                    return value;
          case 'f': value = _execute();  // function index
                    return value;
          default:  value = _calc();
                    return value;
        }
        return 0;
      };

Aquí, podemos ver que el valor de la constante numérica es retornado desde el campo value, mientras que para las variables, funciones y operaciones, se han implementado métodos auxiliares.

      static void environment(AbstractExpressionProcessor<Promise *> *e)
      {
        variableTable = e.variableTable();
        functionTable = e.functionTable();
      }
      
    protected:
      static VariableTable *variableTable;
      static FunctionTable *functionTable;
  
      double _variable()
      {
        double result = 0;
        if(index == -1)
        {
          index = variableTable.index(name);
          if(index == -1)
          {
            return nan; // error: Variable undefined
          }
          result = variableTable[index];
        }
        else
        {
          result = variableTable[index];
        }
        return result;
      }
      
      double _execute()
      {
        double params[];
        if(left)
        {
          ArrayResize(params, 1);
          params[0] = left.resolve();
          if(right)
          {
            ArrayResize(params, 2);
            params[1] = right.resolve();
            if(last)
            {
              ArrayResize(params, 3);
              params[2] = last.resolve();
            }
          }
        }
        IFunctor *ptr = functionTable[index]; // TBD: functors
        if(ptr == NULL)
        {
          return nan; // error: Function index out of bound 
        }
        return ptr.execute(params);
      }
      
      double _calc()
      {
        double first = 0, second = 0, third = 0;
        if(left)
        {
          first = left.resolve();
          if(right)
          {
            second = right.resolve();
            if(last)
            {
              third = last.resolve();
            }
          }
        }
        
        switch(code)
        {
          case '+': return first + second;
          case '-': return first - second;
          case '*': return first * second;
          case '/': return safeDivide(first, second);
          case '%': return fmod(first, second);
          case '!': return !first;
          case '~': return -first;
          case '<': return first < second;
          case '>': return first > second;
          case '{': return first <= second;
          case '}': return first >= second;
          case '&': return first && second;
          case '|': return first || second;
          case '`': return _precision < fabs(first - second); // first != second;
          case '=': return _precision > fabs(first - second); // first == second;
          case '?': return first ? second : third;
        }
        return nan; // error: Unknown operator
      }

En este punto, hemos omitido el procesamiento de errores; en caso de que surja alguno, se retornará el valor especial nan ("no es un número"; la generación se ha sacado al archivo de inclusión aparte NaNs.mqh, con el que el lector podrá familiarizarse por sí mismo). Preste atención a que la ejecución de las operaciones se anticipa con la llamada recursiva de resolve en todos los objetos que se hallan más abajo en la jerarquía, mediante enlaces. De esta forma, la llamada de resolve en una expresión inicia el cálculo consecutivo de todos los objetos Promise, y la consecuente transmisión "hacia arriba" de los resultados de los cálculos, ya en forma de números double. Al final, estos "implosionan" en el valor final de la expresión.

Disponiendo de la clase Promise, podemos utilizar esta para especializar el parser de descenso recursivo que retorna como resultado del procesamiento un árbol de objetos semejantes, es decir, en la práctica, un árbol de sintaxis de las expresiones.

En todos los métodos de la clase de plantilla ExpressionProcessor donde se retorna un cierto T, ahora deberá ser igual a (Promise *). Concretamente, en el método _identifier, al que prestamos atención en la línea

    return _variableTable.get(variable); // NB: to be refined

es necesario posibilitar de alguna forma que, en lugar de double, podamos crear y retornar el nuevo objeto Promise, que indica la variable con el nombre "variable".

Para resolver esta tarea, deberíamos "envolver" la acción de retorno de un valor del tipo T para una variable en un método virtual que ejecutara en las clases derivadas ExpressionProcessor<double> y ExpressionProcessor<Promise *> las diferentes manipulaciones requeridas. Pero aquí surge un pequeño problema.

Clase ExpressionHelper

Planeamos implementar varias clases de parsers, y todas ellas se heredarán de AbstractExpressionProcessor. Pero los métodos característicos para el descenso recursivo no son necesarios en todas ellas, además en diferentes ramas de la jerarquía de herencia. Podríamos redefinirlas como vacías en los lugares que no sean necesarias, pero esto no resulta demasiado bonito desde el punto de vista de la POO. Si MQL ofreciera soporte de alguna forma a la herencia múltiple, podríamos utilizar el tipo especial (trait), un conjunto adicional de métodos que se podría incluir en la clase del parser, en caso necesario. Como esto no es posible, diseñaremos todos los métodos correspondientes como una clase de plantilla aparte, creando una instancia de ella solo dentro de aquellos parsers en los que se requiera.

  template<typename T>
  class ExpressionHelper
  {
    protected:
      VariableTable *_variableTable;
      FunctionTable *_functionTable;
  
    public:
      ExpressionHelper(AbstractExpressionProcessor<T> *owner): _variableTable(owner.variableTable()), _functionTable(owner.functionTable()) { }
  
      virtual T _variable(const string &name) = 0;
      virtual T _literal(const string &number) = 0;
      virtual T _negate(T result) = 0;
      virtual T _call(const int index, T &args[]) = 0;
      virtual T _ternary(T condition, T truly, T falsy) = 0;
      virtual T _isEqual(T result, T next, const bool equality) = 0;
  };

Aquí, hemos reunido todas las acciones que se procesan de forma distinta en los cálculos inmediatos y diferidos. Concretamente, el método _variable es responsable del acceso a las variables que hemos destacado antes. _literal obtiene el valor de la constante, _negate ejecuta la negación lógica, _call es la llamada de la función, _ternary es el operador condicional, y _isEqual ha sido creado para comparar magnitudes. En todos los otros casos, los cálculos se procesan para double y Promise con construcciones sintácticas idénticas, gracias a la redefinición de los operadores en el clase Promise.

El lecotr podría preguntarse por qué el operador de negación lógica '!' no ha sido redefinido en Promise y se ha requerido en su lugar _negate. La cuestión es que el operador '!' se aplica solo para los objetos, no para los punteros. Dicho de otra forma, teniendo la variable del tipo Promise *p, no podemos escribir de la forma acostumbrada !p, con la esperanza de que se active el operador redefinido. En lugar de ello, necesitaremos nombrar de forma preliminar el puntero: !*p. Debido a ello, la entrada se convertirá en no válida para los otros tipos, en concreto, para T=double.

Aquí tenemos cómo se pueden implementar los métodos ExpressionHelper para los números double.

  class ExpressionHelperDouble: public ExpressionHelper<double>
  {
    public:
      ExpressionHelperDouble(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual double _variable(const string &name) override
      {
        if(!_variableTable.exists(name))
        {
          return nan;
        }
        return _variableTable.get(name);
      }
      virtual double _literal(const string &number) override
      {
        return StringToDouble(number);
      }
      virtual double _call(const int index, double &params[]) override
      {
        return _functionTable[index].execute(params);
      }
      virtual double _isEqual(double result, double next, const bool equality) override
      {
        const bool equal = fabs(result - next) <= _precision;
        return equality ? equal : !equal;
      }
      virtual double _negate(double result) override
      {
        return !result;
      }
      virtual double _ternary(double condition, double truly, double falsy) override
      {
        return condition ? truly : falsy;
      }
  };

Y de esta forma se implementan para Promise.

  class ExpressionHelperPromise: public ExpressionHelper<Promise *>
  {
    public:
      ExpressionHelperPromise(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual Promise *_negate(Promise *result) override
      {
        return new Promise('!', result);
      }
      virtual Promise *_call(const int index, Promise *&params[]) override
      {
        return new Promise(index, params);
      }
      virtual Promise *_ternary(Promise *condition, Promise *truly, Promise *falsy) override
      {
        return new Promise('?', condition, truly, falsy);
      }
      virtual Promise *_variable(const string &name) override
      {
        if(CheckPointer(_variableTable) != POINTER_INVALID)
        {
          int index = _variableTable.index(name);
          if(index == -1)
          {
            return new Promise(nan); // error: Variable is undefined
          }
          return new Promise(name, index);
        }
        return new Promise(name);
      }
      virtual Promise *_literal(const string &number) override
      {
        return new Promise(StringToDouble(number));
      }
      virtual Promise *_isEqual(Promise *result, Promise *next, const bool equality) override
      {
        return new Promise((uchar)(equality ? '=' : '`'), result, next);
      }
  };

Ahora, podemos añadir a AbstractExpressionProcessor el campo helper:

    protected:
      ExpressionHelper<T> *helper;
      
    public:  
      ~AbstractExpressionProcessor()
      {
        if(CheckPointer(helper) == POINTER_DYNAMIC) delete helper;
      }

y revisar la implementación de los métodos ExpressionProcessor en los que había líneas marcadas con "NB": todas ellas deberán delegar las operaciones en el objeto helper. Por ejemplo, así:

  template<typename T>
  T ExpressionProcessor::_eq()
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        return helper._isEqual(result, _compare(), equality); // OK
      }
    }
    return result;
  }
  
  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    ...
    return helper._variable(variable); // OK
  }
  
  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return helper._literal(number); // OK
  }

Con la ayuda de las clases presentadas, al fin podremos componer el primer parser que ejecuta los cálculos durante el análisis de las expresiones, ExpressionEvaluator.

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperDouble(&this); }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperDouble(&this); }
  };

Y aquí, ya tenemos el segundo parser para los cálculos diferidos, ExpressionCompiler.

  class ExpressionCompiler: public ExpressionProcessor<Promise *>
  {
    public:
      ExpressionCompiler(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionCompiler(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperPromise(&this); }
      
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        return ExpressionProcessor<Promise *>::evaluate(expression);
      }
  };

Las principlaes diferencias residen solo en los objetos en el campo helper y la llamada preliminar Promise::environment para transmitir los recuadros de las variables y funciones dentro de Promise.

Para conseguir un parser completamente operativo, solo nos queda aclararnos con los recuadros de las variables y funciones.

Recuadros de las variables y funciones

Ambos recuadros constituyen clases de plantilla de mapas que constan de parejas de "clave=valor", donde la clave es un identificador de línea, y el valor es una cierta magnitud del tipo T. Su implementación se puede encontrar en el archivo VariableTable.mqh. La clase básica describe todas las operaciones requeridas con mapas: adición de elementos, modificación de valores y extracción de estos según el nombre o el índice.

  template<typename T>
  class Table
  {
    public:
      virtual T operator[](const int index) const;
      virtual int index(const string variableName);
      virtual T get(const string variableName) const;
      virtual int add(const string variableName, T value);
      virtual void update(const int index, T value);
      ...
  };

En el caso de las variables, el tipo T es double.

  class VariableTable: public Table<double>
  {
    public:
      VariableTable(const string pairs = NULL)
      {
        if(pairs != NULL) assign(pairs);
      }
      
      void assign(const string pairs);
  };

Con la ayuda del método assign, las variables se pueden añadir al recuadro, además de una a una, también como lista, en forma de línea del tipo "nombre1=valor1;nombre2=valor2;...".

Para las funciones, necesitaremos crear una interfaz de funtor especial que contenga el código para calcular las funciones.

  interface IFunctor
  {
    string name(void) const;
    int arity(void) const;
    double execute(const double &params[]);
  };

Cada función tiene un nombre, y una propiedad que describe el número de argumentos (aridad). El cálculo de la función se realiza con el método execute al que se transmiten los argumentos. Todas las funciones matemáticas MQL se deben envolver en esta interfaz, añadiendo después los objetos correspondientes al recuadro (uno a uno, o mediante una matriz):

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      void add(IFunctor *f)
      {
        Table<IFunctor *>::add(f.name(), f);
      }
      void add(IFunctor *&f[])
      {
        for(int i = 0; i < ArraySize(f); i++)
        {
          add(f[i]);
        }
      }
  };

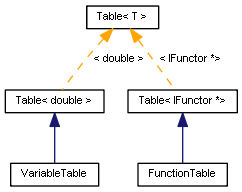
Diagrama de clases de los recuadros de variables y funciones

Para guardar todos los funtores, se ha definido una clase-repositorio.

  class AbstractFuncStorage
  {
    protected:
      IFunctor *funcs[];
      int total;
      
    public:
      ~AbstractFuncStorage()
      {
        for(int i = 0; i < total; i++)
        {
          CLEAR(funcs[i]);
        }
      }
      void add(IFunctor *f)
      {
        ArrayResize(funcs, total + 1);
        funcs[total++] = f;
      }
      void fill(FunctionTable &table)
      {
        table.add(funcs);
      }
  };

El método fill permite rellenar el recuadro que se le ha transmitido con las funciones incorporadas del repositorio (matriz funcs). Para que todos los funtores creados lleguen automáticamente al repositorio, lo convertiremos en una instancia estática dentro de la clase básica de las funciones AbstractFunc, y lo rellenaremos con los enlaces a "this" del constructor.

  class AbstractFunc: public IFunctor
  {
    private:
      const string _name;
      const int _arity;
      static AbstractFuncStorage storage;
  
    public:
      AbstractFunc(const string n, const int a): _name(n), _arity(a)
      {
        storage.add(&this);
      }
      string name(void) const override
      {
        return _name;
      }
      int arity(void) const override
      {
        return _arity;
      }
      static void fill(FunctionTable &table)
      {
        storage.fill(table);
      }
  };
  
  static AbstractFuncStorage AbstractFunc::storage;

Obviamente, el constructor tomará los parámetros de entrada que le permitan establecer el nombre y la aridad de la función.

Para declarar funciones de una aridad específica, hemos introducido la clase de plantilla intermedia FuncN, en la que la aridad se esteblece mediante el tamaño del tipo transmitido (como la aridad de las funciones, en nuestro caso, no supera aún 3, y no existen tipos con tamaño cero, se usa la entrada sizeof(T) % 4, de esta forma, el tamaño 4 dará una aridad 0).

  template<typename T>
  class FuncN: public AbstractFunc
  {
    public:
      FuncN(const string n): AbstractFunc(n, sizeof(T) % 4) {}
  };

Los propios tipos con los tamaños de 0 a 3 se generan con ayuda de macros.

  struct arity0 { char x[4]; };
  
  #define _ARITY(N)   struct arity##N { char x[N]; };
  
  _ARITY(1);
  _ARITY(2);
  _ARITY(3);

Asimismo, para automatizar la generación de la descripción de las funciones, necesitaremos las lista de argumentos.

  #define PARAMS0 
  #define PARAMS1 params[0]
  #define PARAMS2 params[0],params[1]
  #define PARAMS3 params[0],params[1],params[2]

Ahora, podemos definir una macro para el funtor basada en la clase FuncN<T>.

  #define FUNCTOR(CLAZZ,NAME,ARITY) \
  class Func_##CLAZZ: public FuncN<arity##ARITY> \
  { \
    public: \
      Func_##CLAZZ(): FuncN(NAME) {} \
      double execute(const double &params[]) override \
      { \
        return CLAZZ(PARAMS##ARITY); \
      } \
  }; \
  Func_##CLAZZ __##CLAZZ;

Y, finalmente, la lista de funciones soportadas con los nombres y el número de argumentos.

  FUNCTOR(fabs, "abs", 1);
  FUNCTOR(acos, "acos", 1);
  FUNCTOR(acosh, "acosh", 1);
  FUNCTOR(asin, "asin", 1);
  FUNCTOR(asinh, "asinh", 1);
  FUNCTOR(atan, "atan", 1);
  FUNCTOR(atanh, "atanh", 1);
  FUNCTOR(ceil, "ceil", 1);
  FUNCTOR(cos, "cos", 1);
  FUNCTOR(cosh, "cosh", 1);
  FUNCTOR(exp, "exp", 1);
  FUNCTOR(floor, "floor", 1);
  FUNCTOR(log, "log", 1);
  FUNCTOR(log10, "log10", 1);
  FUNCTOR(fmax, "max", 2);
  FUNCTOR(fmin, "min", 2);
  FUNCTOR(fmod, "mod", 2);
  FUNCTOR(pow, "pow", 2);
  FUNCTOR(rand, "rand", 0);
  FUNCTOR(round, "round", 1);
  FUNCTOR(sin, "sin", 1);
  FUNCTOR(sinh, "sinh", 1);
  FUNCTOR(sqrt, "sqrt", 1);
  FUNCTOR(tan, "tan", 1);
  FUNCTOR(tanh, "tanh", 1);

El aspecto general del diagrama de clases de los funtores es el siguiente.

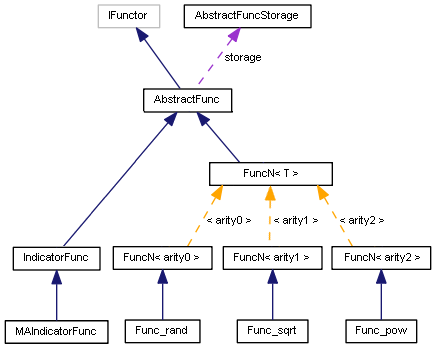
Diagrama de clases de los funtores

Aquí, no mostramos todas las funciones, sino solo una de cada aridad. Asimismo, aquí tenemos algunas clases que hemos visto anteriormente.

Teniendo en cuenta las funciones, todo está listo para explotar los dos parsers de descenso recursivo. Uno sabe calcular las expresiones en el modo de interpretación, mientras que el otro sabe calcular las expresiones según su árbol de sintaxis.

Cálculo de expresiones sobre la marcha (ExpressionEvaluator)

El método de cálculo de una expresión por parte del intérprete se corresponde con el sigueinete esquema: creamos una instancia de ExpressionEvaluator, en caso necesario, le transmitimos las variables, y llamamos al método evaluate con la línea que contiene la expresión necesaria.

  ExpressionEvaluator ee("a=-10");
  double result = ee.evaluate("1 + sqrt(a)"); // -nan(ind)
  bool success = ee.success();                // true

Con la ayuda del método success, podemos comprobar si la sintaxis de la expresión es correcta, pero dicha corrección no garantiza que no vayan a suceder errores en el proceso. En el ejemplo mostrado más arriba, la extracción de la raíz de la variable negativa provocará que se retorne un resultado NaN. Así que recomendamos comprobar siempre el resultado con la ayuda de la función MathIsValidNumber.

Después de desarrollar otros tipos de parsers, escribiremos tests que muestren las técnicas con más detalle.

"Compilación" de expresiones en un árbol de sintaxis y evaluación del árbol (ExpressionCompiler)

La evaluación de una expresión con la ayuda de la construcción de un árbol de sintaxis se efectúa de la siguiente forma: creamos una instancia de ExpressionCompiler, transmitimos las variables iniciales si fuera necesario y llamamos al método de evaluación con una línea que contenga la expresión necesaria. Como resultado, obtendremos un enlace al objeto Promise, para el cual necesitaremos llamar a resolve para evaluar la expresión y obtener un número. Parece más laborioso, pero funciona mucho más rápido cuando necesitamos realizar varios cálculos para diferentes valores de variables.

  double a[10] = {...}, b[10] = {...}, c[10] = {...};
  
  VariableTable vt;
  ExpressionCompiler с(vt);
  vt.adhocAllocation(true);
  const string expr = "(a + b) * sqrt(c)";
  Promise *p = c.evaluate(expr);
  
  for(int i = 0; i < 10; i++)
  {
    vt.set("a", a[i]);
    vt.set("b", b[i]);
    vt.set("c", c[i]);
    Print(p.resolve());
  }

En este ejemplo, creamos inicialmente unrecuadro de variables vacío, en el que se escribimos los valores cambiantes de las variables a, b, c dentro del ciclo. El método adhocAllocation usado aquí, que omitimos al analizar las clases de recuadro, establece una bandera que indica al parser que acepte y reserve cualquier nombre de variable en el recuadro en la etapa de análisis y generación del árbol. Cualquier variable implícita de este tipo es establecida en nan, por lo que el código que realiza la llamada tiene que preocuparse de establecerlas en valores reales antes de calcular el objeto Promise.

Si en el ejemplo mostrado no llamamos a vt.adhocAllocation(true) antes de c.evaluate, todas las variables que se encuentren en la expresión generarán errores, ya que por defecto, se supone que las variables deben ser descritas antes, y el recuadro tiene que encontrarse vacío. La presencia de errores se puede comprobar en el código llamando a c.success() después de c.evaluate(). Los errores también se muestran en el log.

Como sucede con el intérprete, el método evaluate, en cualquier caso, retornará un cierto resultado. Así, si las variables no era conocidas en el estadio de análisis, en el árbol se crearán para ellas nodos con el valor nan. Los cálculos según este árbol no tienen sentido, ya que también darán nan como resultado. Pero la presencia del árbol nos permitirá entender cuál es el problema. En la clase Promise, existe un método auxiliar para imprimir el árbol, print.

Conclusión

En el presente artículo, nos hemos familiarizado con los conceptos básicos del parseo de expresiones matemáticas, y también hemos creado dos parsers MQL listos para funcionar. En esta primera parte, adjuntamos un pequeño script de prueba que le permitirá comenzar a usar la tecnología en sus programas por sí mismo. Continuaremos analizando otros tipos de parsers en la segunda parte, comparando su rendimiento y ofreciendo ejemplos de uso del mismo para resolver las tareas del tráder.