
数式の計算(第1部)再帰下降パーサ
取引タスクを自動化する場合、実行段階で計算アルゴリズムの柔軟性を提供する必要がある場合があります。たとえば、プログラムをクローズド(コンパイル済み)モードで微調整する場合、さまざまな可能な組み合わせから選択した目的の関数タイプを実装できます。特に、これはエキスパートアドバイザーを最適化するとき、または指標のプロトタイプをすばやく評価するときに役立ちます。また、ユーザは、ダイアログボックスでパラメータを変更するだけでなく、計算式を変更することもできるため、MQLプログラムコードを変更せずに、テキスト表現から算術式を計算する必要があります。
このタスクは、さまざまなパーサを使用して、その場で数式を解釈し、構文木に「コンパイル」し、いわゆるバイトコード(計算命令のシーケンス)を生成し、結果を計算するためにさらに実行することで解決できます。本稿では、いくつかのタイプのパーサと式の計算方法について検討します。
問題の定式化
本稿での算術式は、関連するアクションを説明するデータ項目と演算子の1行のシーケンスです。データ項目は数値と名前付き変数です。変数値は、外部から、つまり式ではなく、特別なパーサ属性を使用して設定および編集できます。つまり、中間結果を格納するための代入演算子(=)はありません。以下は、サポートされている演算子を計算の優先順位の高い順に示します。
- !、- 、+ — 単項論理否定、マイナスおよびプラス
- () — 括弧でグループ化
- *、/、% — 乗算、除算、除算の余り
- +, - — 加算と減算
- >, <, >=, <= — より多い/より少ないの比較
- ==, != — 平等/不平等の比較
- &&, || — 論理ANDおよびOR(優先順位は同じであるため、括弧を使用する必要があることに注意してください)
- ?: — 条件に従って計算を分岐できる三項演算子(条件演算子)
また、合計25の式でMQL標準数学関数を使用できるようにします。それらの1つは、冪演算のためのpow関数です。このため、演算子のリストには冪乗演算子(^)がありません。さらに、演算子「^」は整数の冪乗のみをサポートしますが、この関数にはそのような制限はありません。「^」を他の考慮される演算子と区別するもう1つの特定の機能があります。
これは次に関連しています。演算子のプロパティの1つは結合性で、これは、同じ優先順位の演算子が左または右からどのように実行されるかを決定するものです。他の結合性タイプもありますが、現在のタスクの文脈では使用されません。
以下は、結合性が計算結果にどのように影響するかの一例です。
1 - 2 - 3
この式は、2つの減算が実行される順序を明示的に示していません。演算子「-」は左結合であるため、最初に2が1から減算され、次に3が中間の-1から減算され、-4が得られます。つまり、これは次の式に等しくなります。
((1 - 2) - 3)
仮に、演算子「-」が右結合であるとすると、操作は逆の順序で実行されます。
(1 - (2 - 3))
答えは2です。幸い、演算子「-」は左結合です。
したがって、結合性の左右は式の解析に影響を与え、アルゴリズムが複雑になります。リストされているすべての二項演算子は左結合であり、「^」のみが右結合です。
たとえば、式
3 ^ 2 ^ 5
では、まず2を5乗し、次に3を32(=2 ^ 5)乗します。
簡素化のために、冪乗演算子は使用せず、代わりにpow関数を使用します。そのため、アルゴリズムは左結合性のみを考慮して実装されます。単項演算子は常に右結合であるため、均一に扱われます。
式のすべての数値(定数および変数として記述された数値を含む)は実数型になります。それらが平等かどうかを比較するための許容値を設定します。論理式の数値はが利用する原則は、ゼロは偽でゼロ以外は真という、より単純なものです。
ビット演算子は提供されていません。配列はサポートされていません。
式の例を次に示します。
- 1 + 2 * 3 — 操作の優先度による計算
- (1 + 2) * 3 — 括弧を使用したグループ化
- (a + b) * c — 変数の使用
- (a + b) * sqrt(1 / c) — 関数の使用
- a > 0 && a != b ?a : c — 論理条件による計算
変数は、MQL識別子の通常の規則に従って構成された名前で識別されます。変数は、文字、数字、またはアンダースコアで構成でき、数字で始めることはできません。変数名は、組み込み関数名と一致してはなりません。
入力文字列は文字ごとに分析されます。文字が文字または数字に属しているかどうかなどの一般的な確認や、エラー処理、変数設定、拡張可能な標準関数テーブルは、基本クラスで定義されます。すべてのパーサタイプは、この基本クラスから継承されます。
すべてのパーサクラスについて考えてみましょう。記事では、クラスをいくつか簡略化して示しています。 完全なソースコードを以下に添付します。
パーサ基本クラス(AbstractExpressionProcessorテンプレート)
式の分析結果は、スカラー値だけでなく、式の構文を記述するノードの木(特別なクラスのオブジェクト)にもなり得るため、これはテンプレートクラスです。これがどのように行われるか、そしてそうする目的は何であるかについては後で検討します。
まず、クラスオブジェクトは、式(_expression)、その長さ(_length)、文字列の読み取り中の現在のカーソル位置(_index)、および現在のシンボル(_token)を格納します。また、式のエラー(_failed)と値の比較精度(_precision)を示す予約変数もあります。
template<typename T> class AbstractExpressionProcessor { protected: string _expression; int _index; int _length; ushort _token; bool _failed; double _precision;
変数とリンクを格納するための特別なテーブルが用意されていますが、関連するVariableTableクラスとFunctionTableクラスについては後で検討します。
VariableTable *_variableTable;
FunctionTable _functionTable;
テーブルは「key = value」のペアです。ここで、キーは変数または関数名を持つ文字列であり、値はdouble(変数の場合)または関手オブジェクト(テーブルの場合)のいずれかです。
式に変数を含めることはできないため、変数テーブルは参照によって記述されます。関数テーブルに関しては、パーサには常に最小限の組み込み関数のセット(ユーザによって拡張可能)があります。そのため、このテーブルは既製のオブジェクトで表されます。
標準関数のテーブルは、次のメソッド入力されます。
virtual void registerFunctions();
次のセクションでは、次の文字への切り替え、期待値に対する文字の確認(および一致しない場合はエラーの表示)、フォーマット要件を満たす数字の順次読み取りなど、さまざまなパーサに共通のサブタスクを実行する関数や、文字を分類するためのいくつかの静的な補助メソッドについて説明します。
bool _nextToken(); void _match(ushort c, string message, string context = NULL); bool _readNumber(string &number); virtual void error(string message, string context = NULL, const bool warning = false); static bool isspace(ushort c); static bool isalpha(ushort c); static bool isalnum(ushort c); static bool isdigit(ushort c);
これらの関数はすべて、特に次の基本クラスで定義されています。
template<typename T> bool AbstractExpressionProcessor::_nextToken() { _index++; while(_index < _length && isspace(_expression[_index])) _index++; if(_index < _length) { _token = _expression[_index]; return true; } else { _token = 0; } return false; } template<typename T> void AbstractExpressionProcessor::_match(ushort c, string message, string context = NULL) { if(_token == c) { _nextToken(); } else if(!_failed) // prevent chained errors { error(message, context); } } template<typename T> bool AbstractExpressionProcessor::_readNumber(string &number) { bool point = false; while(isdigit(_token) || _token == '.') { if(_token == '.' && point) { error("Too many floating points", __FUNCTION__); return false; } number += ShortToString(_token); if(_token == '.') point = true; _nextToken(); } return StringLen(number) > 0; }
指数を使用した科学的記数法は、数値の解析ではサポートされていません。
このクラスは、子クラスでオーバーライドされるメインの「evaluate」メソッドも宣言します。ここでは、変数を初期化するだけです。
public: virtual T evaluate(const string expression) { _expression = expression; _length = StringLen(_expression); _index = -1; _failed = false; return NULL; }
これはメインクラスのメソッドであり、式を入力として持つ文字列を受け取り、文字列処理の結果を出力します。計算が実行された場合は特定の値、分析が実行された場合は構文木です。
クラスのpublicインターフェイスにはコンストラクタも含まれており、変数をその値とともに(「name1 = value1; name2 = value2; ...」のような文字列として、または既製のVariableTableオブジェクトとして)渡すことができます。また、数値を比較するときに許容値を設定するメソッド、解析の成功を示すメソッド(構文エラーがなかったことを示す)、および変数と関数テーブルにアクセスするメソッドも含まれています。
public: AbstractExpressionProcessor(const string vars = NULL); AbstractExpressionProcessor(VariableTable &vt); bool success() { return !_failed; }; void setPrecision(const double p) { _precision = p; }; double getPrecision(void) const { return _precision; }; virtual VariableTable *variableTable(); virtual FunctionTable *functionTable(); };
構文エラーがない場合でも、式の計算でエラーが発生する可能性があることに注意してください(たとえば、ゼロ除算、負の値のルートなど)。このような状況を制御するには、MathIsValidNumber関数を使用して結果が数値であるかどうかを確認します。パーサは、実行時にクラッシュするのではなく、さまざまなNaN(Not A Number)タイプの適切な値を生成できる必要があります。
最も簡単な方法は、再帰降下パーサです。それでは、このパーサから始めましょう。
再帰下降パーサ(ExpressionProcessorテンプレート)
再帰下降パーサは、個別の操作を説明するルールに従って呼び出される相互再帰関数のセットです。最も一般的な操作の構文を拡張BNF表記(拡張バッカス・ナウア記法)の文法として表す場合、式は次のように表すことができます(各行は個別のルールです) 。
Expr -> Sum
Sum -> Product { ('+' | '-') Product }
Product -> Value { ('*' | '/') Value }
Value -> [0-9]+ | '(' Expr ')'
これらのルールは、自然言語では次のようなものです。式の解析は最も優先度の低い演算から始まります。この例ではこれは加算/減算です。「Sum」は、「+」または「-」記号で区切られた2つのProduct被演算子で構成されますが、演算自体と2番目の演算子はオプションです。「Product」は、「*」または「/」で区切られた2つのValue演算子で構成されます。この場合も、演算と第2演算子が欠落している可能性があります。「Value」は、数字または括弧内に指定されたネストされた式で構成される任意の数値です。
たとえば、式「10」(数値)は、次の一連のルールに展開されます。
Expr -> Sum -> Product -> Value -> 10
式「1+ 2 * 3」は、より複雑な構造になります。
Expr -> Sum -> Product -> Value -> 1
| '+'
-> Product -> Value -> 2
| '*'
-> Value -> 3
アルゴリズムに従って、文字の入力ストリームと操作ルールの間の一致作業とともに文法解析が実行されます。解析は、メインルール(式全体)から小さなコンポーネント(個々の数値)まで実行されます。再帰下降パーサはトップダウンクラスに属します。
私たちのパーサはより多くの操作をサポートします(最初のセクションのリストを参照してください)。個別のメソッドは、操作ごとにExpressionProcessor派生クラスで予約されています。
template<typename T> class ExpressionProcessor: public AbstractExpressionProcessor<T> { public: ExpressionProcessor(const string vars = NULL); ExpressionProcessor(VariableTable &vt); T evaluate(const string expression) override { AbstractExpressionProcessor<T>::evaluate(expression); if(_length > 0) { _nextToken(); return _parse(); } return NULL; } protected: T _parse(); T _if(); // ?: T _logic(); // && || T _eq(); // == != T _compare(); // ><>=<= T _expr(); // +- T _term(); // */% T _unary(); // !-+ T _factor(); // () T _identifier(); T _number(); T _function(const string &name); };
式のEBNF文法の例は、メソッドコードを記述するためのガイドとして役立ちます。
expression -> if
if -> logic { '?' if ':' if }
logic -> eq { ('&&' | '||' ) eq }
eq -> compare { ('==' | '!=' ) compare }
compare -> expr { ('>' | '<' | '>=' | '<=') expr }
expr -> term { ('+' | '-') term }
term -> unary { ('*' | '/' | '%') unary }
unary -> { ('!' | '-' | '+') } unary | factor
factor -> '(' if ')' | number | identifier
identifier -> function | variable
variable -> name
function -> name '(' { arglist } ')'
name -> char { char | digit }*
arglist -> if { ',' if }
降下点は_parseメソッドであり、publicの「evaluate」メソッドから呼び出されます。演算子の優先順位に従って、_parseメソッドは制御を順位が一番低い_ifに移します。式全体を解析した後、現在の文字はゼロ(行末記号)でなければなりません。
template<typename T> T ExpressionProcessor::_parse(void) { T result = _if(); if(_token != '\0') { error("Tokens after end of expression.", __FUNCTION__); } return result; }
三項条件演算子は、ブール条件と、真と偽の条件の2つの計算オプションの3つの部分式で構成されます。ブール条件は、文法の次のレベルである_logicメソッドです。計算オプションは三項条件演算子にすることができるため、再帰的に_ifを呼び出します。条件と真のオプションの間には文字「?」が必要です。文字が欠落している場合、これは三項演算子ではなく、アルゴリズムは_logicから値をそのまま返します。「?」 文字がある場合、trueオプションとfalseオプションの間に「:」文字があるかどうかをさらに確認する必要があります。すべてのコンポーネントが存在する場合は、条件を確認し、真か偽かに応じて、最初の値または2番目の値を返します。
template<typename T> T ExpressionProcessor::_if() { T result = _logic(); if(_token == '?') { _nextToken(); T truly = _if(); if(_token == ':') { _nextToken(); T falsy = _if(); return result ?truly : falsy; // NB: to be refined } else { error("Incomplete ternary if-condition", __FUNCTION__); } } return result; }
論理ANDまたはOR演算は、_logicメソッドで表されます。このメソッドでは、演算子間に連続する文字「&&」または「||」が必要です。これは比較(_eqメソッド)を表します。論理演算がない場合、結果は_eqメソッドから直接返されます。論理演算が見つかった場合は、それを計算します。「while」ループを使用すると、パーサは、たとえば「a> 0 && b> 0 && c> 0」のように、いくつかの論理的な加算または乗算を連続して実行できます。
template<typename T> T ExpressionProcessor::_logic() { T result = _eq(); while(_token == '&' || _token == '|') { ushort previous = _token; _nextToken(); if(previous == '&' && _token == '&') { _nextToken(); result = _eq() && result; } else if(previous == '|' && _token == '|') { _nextToken(); result = _eq() || result; } else { error("Unexpected tokens " + ShortToString(previous) + " and " + ShortToString(_token), __FUNCTION__); } } return result; }
この実装で「&&」と「||」の優先順位が等しく、かっこを使用して目的の順序を指定する必要があることに注意してください 。
比較演算子( 「==」、「!=」)は_eqメソッドでも同様に処理されます。
template<typename T> T ExpressionProcessor::_eq() { T result = _compare(); if(_token == '!' || _token == '=') { const bool equality = _token == '='; _nextToken(); if(_token == '=') { _nextToken(); const bool equal = fabs(result - _compare()) <= _precision; // NB: to be refined return equality ?equal : !equal; } else { error("Unexpected token " + ShortToString(_token), __FUNCTION__); } } return result; }
記事では一部のメソッドはスキップされます(簡潔にするため)が、それらはすべて、添付のソースコードで入手できます。
_factorメソッドでは、実際に演算子を使用します。括弧で囲まれた部分式の場合、_if、識別子、または数値(定数、リテラル)を再帰的に呼び出します。
template<typename T> T ExpressionProcessor::_factor() { T result; if(_token == '(') { _nextToken(); result = _if(); _match(')', ") expected!", __FUNCTION__); } else if(isalpha(_token)) { result = _identifier(); } else { result = _number(); } return result; }
名前の後に開き括弧が続く場合、識別子は変数または関数の名前を意味する場合があります。この解析は、_identifierメソッドによって実行されます。関数を扱う場合、特別な_functionメソッドは関数_functionTableのテーブルで適切なオブジェクトを見つけ、パラメータのリストを解析し(それぞれが独立した式であり、_ifの再帰呼び出しによって取得されます)、関手オブジェクトに制御を転送します。
template<typename T> T ExpressionProcessor::_identifier() { string variable; while(isalnum(_token)) { variable += ShortToString(_token); _nextToken(); } if(_token == '(') { _nextToken(); return _function(variable); } return _variableTable.get(variable); // NB: to be refined }
_numberメソッドは、StringToDoubleを使用して数字の読み取りシーケンスを数値に変換するだけです(_readNumberヘルパー関数は上に示されています)。
template<typename T> T ExpressionProcessor::_number() { string number; if(!_readNumber(number)) { error("Number expected", __FUNCTION__); } return StringToDouble(number); // NB: to be refined }
これが、再帰下降パーサ全体です。ほぼ準備完了です。「ほぼ」というのは、これは特定のタイプに特化する必要があるテンプレートクラスであるからです。数値型変数に基づいて式を計算するには、次のようにdoubleに特殊化します。
class ExpressionEvaluator: public ExpressionProcessor<double> { public: ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { } ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { } };
ただし、実際の手順は少し複雑です。アルゴリズムは、解析中に式を計算します。このインタプリタモードは最も単純ですが、最も遅いモードでもあります。変数値(価格やボリュームなど)を変更して、各ティックで同じ数式を計算する必要があると想像してください。計算を高速化するには、解析と操作の実行という2つの段階を分離することをお勧めします。この場合、式の構造を計算用に最適化された中間表現に保存でき、この表現を使用してすばやく再計算できるので、解析は1回実行できます。
この目的のために、考慮されたメソッドで取得され、再帰呼び出しのチェーンで渡される、publicの「evaluate」メソッドから最終値が返されるまでのすべての中間結果は、特定の式フラグメントの演算子と演算子(およびそれらのすべての関係)の記述を格納するオブジェクトに置き換える必要があります。式は、そのような記述を使用して、延期された方法で計算することができます。このようなオブジェクトはPromisesと呼ばれます。
遅延評価(Promises)
Promiseクラスは、式の構成とは別のエンティティ(被演算子、または被演算子参照を含む演算)を記述します。たとえば、式で変数名が検出された場合、次の行が_identifierメソッドで処理されます。
return _variableTable.get(variable); // NB: to be refined
テーブルから変数の現在の値を名前で返します。これはdouble型の値です。このオプションは、パーサがdouble型に特化していて、その場で計算を実行する場合に適しています。ただし、計算を延期する必要がある場合は、変数値の代わりに、Promiseオブジェクトを作成し、それに変数名を保存する必要があります。将来、変数値が変更されたときに、Promiseオブジェクトから新しい値を要求できるようになるはずです。Promiseオブジェクトは値をその名前で検索します。したがって、「NB: to be refined」とマークされた現在のコード行は、ExpressionProcessorテンプレートの一般的なケースには適していないため、別のものに置き換える必要があることは明らかです。ExpressionProcessorにはそのような行がいくつかあり、それらすべてに対して単一の実用的なソリューションを見つけます。ただし、最初にPromiseクラスを完了するべきです。
Promiseクラスには、任意の被演算子または演算を記述するためのいくつかのフィールドがあります。
class Promise { protected: uchar code; double value; string name; int index; Promise *left; Promise *right; Promise *last; public: Promise(const uchar token, Promise *l = NULL, Promise *r = NULL, Promise *v = NULL): code(token), left(l), right(r), last(v), value(0), name(NULL), index(-1) { } Promise(const double v): // value (const) code('n'), left(NULL), right(NULL), last(NULL), value(v), name(NULL), index(-1) { } Promise(const string n, const int idx = -1): // name of variable code('v'), left(NULL), right(NULL), last(NULL), value(0), name(n), index(idx) { } Promise(const int f, Promise *¶ms[]): // index of function code('f'), left(NULL), right(NULL), last(NULL), value(0), name(NULL) { index = f; if(ArraySize(params) > 0) left = params[0]; if(ArraySize(params) > 1) right = params[1]; if(ArraySize(params) > 2) last = params[2]; // more params not supported }
「code」フィールドには、要素タイプ属性が格納されます。「n」は数値、「 v」は変数、「f」は関数です。他のすべての記号は、許可される操作の1つとして扱われます(たとえば、「+」、「-」、「*」、「/」、「%」など)。数値の場合、その値は「値」フィールドに格納されます。変数の場合、その名前は「name」フィールドに格納されます。変数に高速で複数回アクセスするために、Promiseは最初の呼び出しの後で「index」フィールドに変数番号をキャッシュしてから、名前ではなくインデックスによってテーブルから変数を取得しようとします。関数は常に「index」フィールドの番号で識別されます。これは、変数とは異なり、関数テーブルには最初は組み込み関数が含まれているのに対し、式の分析時には変数のテーブルが空のままである可能性があるためです。
「left」、 「right」、「last」参照はオプションで、被演算子を格納できます。たとえば、数値または変数の3つの参照はすべてNULLです。単項演算には「left」参照のみが使用されます。「left」および「right」参照は二項演算に使用されます。 3つの参照がすべて使用されるのは三項(条件)演算子でのみで、「left」には条件が含まれ、「right」は真の条件の式で、「last」は偽の条件に使用されます。また、参照は関数パラメータオブジェクトを格納します(現在のパーサ実装では、関数パラメータの数は3つに制限されています)。
Promiseオブジェクトは計算に参加するため、オブジェクト内のすべての主要な演算子をオーバーライドします。たとえば、これは「promise」を使用した加算および減算演算の処理方法です。
Promise *operator+(Promise *r) { return new Promise('+', &this, r); } Promise *operator-(Promise *r) { return new Promise('-', &this, r); }
現在のオブジェクト(&this)、つまり操作の左側の式に配置されているオブジェクトと、操作の右側にある次のオブジェクト(r)は、関連する操作コードで作成された新しいPromiseオブジェクトのコンストラクタに渡されます。
他の操作も同様に処理されます。その結果、式全体がPromiseクラスのオブジェクトの木として表示され、ルート要素が式全体を表します。式全体を含む、「promise」オブジェクトの実際の値を受け取るために使用される特別な「resolve」メソッドがあります。
double resolve() { switch(code) { case 'n': return value; // number constant case 'v': value = _variable(); // variable name return value; case 'f': value = _execute(); // function index return value; default: value = _calc(); return value; } return 0; };
これは、数値定数値が値フィールドからどのように返されるかを示しています。ヘルパーメソッドは、変数、関数、および操作に対して実装されます。
static void environment(AbstractExpressionProcessor<Promise *> *e) { variableTable = e.variableTable(); functionTable = e.functionTable(); } protected: static VariableTable *variableTable; static FunctionTable *functionTable; double _variable() { double result = 0; if(index == -1) { index = variableTable.index(name); if(index == -1) { return nan; // error: Variable undefined } result = variableTable[index]; } else { result = variableTable[index]; } return result; } double _execute() { double params[]; if(left) { ArrayResize(params, 1); params[0] = left.resolve(); if(right) { ArrayResize(params, 2); params[1] = right.resolve(); if(last) { ArrayResize(params, 3); params[2] = last.resolve(); } } } IFunctor *ptr = functionTable[index]; // TBD: functors if(ptr == NULL) { return nan; // error: Function index out of bound } return ptr.execute(params); } double _calc() { double first = 0, second = 0, third = 0; if(left) { first = left.resolve(); if(right) { second = right.resolve(); if(last) { third = last.resolve(); } } } switch(code) { case '+': return first + second; case '-': return first - second; case '*': return first * second; case '/': return safeDivide(first, second); case '%': return fmod(first, second); case '!': return !first; case '~': return -first; case '<': return first < second; case '>': return first > second; case '{': return first <= second; case '}': return first >= second; case '&': return first && second; case '|': return first || second; case '`': return _precision < fabs(first - second); // first != second; case '=': return _precision > fabs(first - second); // first == second; case '?': return first ?second : third; } return nan; // error: Unknown operator }
ここではエラー処理は省略されています。エラーが発生した場合、特別なNaN(「数値ではありません」)値が返されます。その生成は、以下に添付されている別のヘッダーファイルNaNs.mqhに実装されます)。操作の実行は、参照によって(階層内の)すべての下位オブジェクトの「resolve」の再帰呼び出しでチェックされることに注意してください。したがって、式に対して「resolve」を呼び出すと、関連するすべての「promise」の順次計算が開始され、計算結果がdouble数値として上位の要素にさらに転送されます。最後に、すべての値が式の最終値に「折りたたまれ」ます。
Promiseクラスを使用すると、これを使用して、結果として類似したオブジェクトの木を返す再帰下降パーサを特殊化できます。つまり、式の構文木を返します。
Tを返すExpressionProcessorテンプレートクラスのすべてのメソッドで、このTは(Promise *)と等しくなければなりません。特に、
return _variableTable.get(variable); // NB: to be refined
行を持つ_identifierメソッドでは、どういうわけか、doubleの代わりに、「variable」という名前の変数を指す新しいPromiseオブジェクトを作成して返す必要があります。
この問題を解決するには、変数のTタイプ値を返すアクションを別の仮想メソッドにラップする必要があります。このメソッドは、ExpressionProcessor <double>およびExpressionProcessor <Promise *>派生クラスで必要なさまざまな操作を実行します。ただし、小さな問題があります。
ExpressionHelperクラス
いくつかのパーサクラスを実装する予定です。各クラスはAbstractExpressionProcessorから継承されます。ただし、再帰下降に固有のメソッドがすべてに必要なわけではありません。不要な場合は空のものでオーバーライドできますが、これはOOPの観点からは正しくありません。MQLが多重継承をサポートしていたら、特別なトレイトを使用できたでしょう。これは、必要に応じてパーサクラスに含めることができる追加のメソッドセットです。これは不可能なので、適切なメソッドを個別のテンプレートクラスとして実装し、メソッドが必要なパーサ内にのみインスタンスを作成します。
template<typename T> class ExpressionHelper { protected: VariableTable *_variableTable; FunctionTable *_functionTable; public: ExpressionHelper(AbstractExpressionProcessor<T> *owner): _variableTable(owner.variableTable()), _functionTable(owner.functionTable()) { } virtual T _variable(const string &name) = 0; virtual T _literal(const string &number) = 0; virtual T _negate(T result) = 0; virtual T _call(const int index, T &args[]) = 0; virtual T _ternary(T condition, T truly, T falsy) = 0; virtual T _isEqual(T result, T next, const bool equality) = 0; };
このクラスには、即時評価と遅延評価でさまざまな方法で処理されるすべてのメソッドが含まれています。たとえば、_variableメソッドは変数へのアクセスを担当します。_literalは定数の値を受け取ります。 _negateは論理否定を実行します。 _callは関数を呼び出します。 _ternaryは三項演算子であり、_isEqualは値の比較に使用されます。他のすべての計算では、Promiseクラスの演算子をオーバーライドすることにより、同じ構文を使用してdoubleとPromiseに対して処理されます。
なぜ論理否定演算子「!」がPromiseではオーバーライドされず、代わりに_negateメソッドが使用されたのかを不思議に思うかもしれません。 「!」演算子はオブジェクトにのみ適用され、ポインタには適用されません。つまり、Promise *p型変数の場合、オーバーライドされた演算子が機能することを期待して!pを書き込むことはできません。代わりに、まずポインタを逆参照する必要があります(!*p)。ただし、この表記は、T=doubleを含む他のタイプでは無効になります。
以下のように、ExpressionHelperメソッドをdouble数用に実装します。
class ExpressionHelperDouble: public ExpressionHelper<double> { public: ExpressionHelperDouble(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { } virtual double _variable(const string &name) override { if(!_variableTable.exists(name)) { return nan; } return _variableTable.get(name); } virtual double _literal(const string &number) override { return StringToDouble(number); } virtual double _call(const int index, double ¶ms[]) override { return _functionTable[index].execute(params); } virtual double _isEqual(double result, double next, const bool equality) override { const bool equal = fabs(result - next) <= _precision; return equality ?equal : !equal; } virtual double _negate(double result) override { return !result; } virtual double _ternary(double condition, double truly, double falsy) override { return condition ?truly : falsy; } };
Promiseでの実装方法は次のとおりです。
class ExpressionHelperPromise: public ExpressionHelper<Promise *> { public: ExpressionHelperPromise(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { } virtual Promise *_negate(Promise *result) override { return new Promise('!', result); } virtual Promise *_call(const int index, Promise *¶ms[]) override { return new Promise(index, params); } virtual Promise *_ternary(Promise *condition, Promise *truly, Promise *falsy) override { return new Promise('?', condition, truly, falsy); } virtual Promise *_variable(const string &name) override { if(CheckPointer(_variableTable) != POINTER_INVALID) { int index = _variableTable.index(name); if(index == -1) { return new Promise(nan); // error: Variable is undefined } return new Promise(name, index); } return new Promise(name); } virtual Promise *_literal(const string &number) override { return new Promise(StringToDouble(number)); } virtual Promise *_isEqual(Promise *result, Promise *next, const bool equality) override { return new Promise((uchar)(equality ?'=' : '`'), result, next); } };
これで、「ヘルパー」フィールドをAbstractExpressionProcessorに追加できます。
protected: ExpressionHelper<T> *helper; public: ~AbstractExpressionProcessor() { if(CheckPointer(helper) == POINTER_DYNAMIC) delete helper; }
そして、「NB」でマークされた文字列を持つExpressionProcessorメソッドの実装を再検討します。これらはすべて、操作を「ヘルパー」オブジェクトに委任する必要があります。以下は例です。
template<typename T> T ExpressionProcessor::_eq() { T result = _compare(); if(_token == '!' || _token == '=') { const bool equality = _token == '='; _nextToken(); if(_token == '=') { _nextToken(); return helper._isEqual(result, _compare(), equality); // OK } } return result; } template<typename T> T ExpressionProcessor::_identifier() { string variable; while(isalnum(_token)) { variable += ShortToString(_token); _nextToken(); } ... return helper._variable(variable); // OK } template<typename T> T ExpressionProcessor::_number() { string number; if(!_readNumber(number)) { error("Number expected", __FUNCTION__); } return helper._literal(number); // OK }
提示されたクラスを使用して、式を解析しながら計算を実行する最初のパーサを最終的に組み立てることができます: ExpressionEvaluator。
class ExpressionEvaluator: public ExpressionProcessor<double> { public: ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperDouble(&this); } ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperDouble(&this); } };
ここでは、遅延評価用に別のパーサ(ExpressionCompiler)を取得します。
class ExpressionCompiler: public ExpressionProcessor<Promise *> { public: ExpressionCompiler(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperPromise(&this); } ExpressionCompiler(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperPromise(&this); } virtual Promise *evaluate(const string expression) override { Promise::environment(&this); return ExpressionProcessor<Promise *>::evaluate(expression); } };
主な違いは、「ヘルパー」フィールドと、変数と関数のテーブルをPromiseに入力するためのPromise::environment の予備呼び出しにあります。
完全に機能するパーサを取得する前に、変数と関数のテーブルが1つだけ残っています。
変数と関数のテーブル
両方のテーブルは、key=valueのペアで構成されるテンプレートマップクラスです。ここで、keyは文字列識別子であり、valueはタイプTの値です。それらの実装はVariableTable.mqhで利用できます。基本クラスは、要素の追加、値の変更、名前またはインデックスによる取得など、必要なすべてのマップ操作を記述します。
template<typename T> class Table { public: virtual T operator[](const int index) const; virtual int index(const string variableName); virtual T get(const string variableName) const; virtual int add(const string variableName, T value); virtual void update(const int index, T value); ... };
これは、T型変数の場合はdoubleです。
class VariableTable: public Table<double> { public: VariableTable(const string pairs = NULL) { if(pairs != NULL) assign(pairs); } void assign(const string pairs); };
「assign」メソッドを使用すると、変数を1つずつテーブルに追加するだけでなく、リストとして「name1=value1;name2=value2;...」タイプの文字列として追加することもできます。
関数用に特別な関手インターフェイスを作成する必要があります。関手には、関数計算用のコードが含まれます。
interface IFunctor { string name(void) const; int arity(void) const; double execute(const double ¶ms[]); };
各関数には、引数の数(アリティ)を説明する名前とプロパティがあります。関数は、引数が渡される「execute」メソッドによって計算されます。このインターフェイスですべての組み込みMQL数学関数をラップしてから、対応するオブジェクトをテーブルに(1つずつまたは配列で)追加します。
class FunctionTable: public Table<IFunctor *> { public: void add(IFunctor *f) { Table<IFunctor *>::add(f.name(), f); } void add(IFunctor *&f[]) { for(int i = 0; i < ArraySize(f); i++) { add(f[i]); } } };
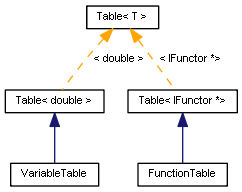
変数と関数のテーブルクラスの図
ストレージクラスは、すべての関手を格納するために定義されています。
class AbstractFuncStorage { protected: IFunctor *funcs[]; int total; public: ~AbstractFuncStorage() { for(int i = 0; i < total; i++) { CLEAR(funcs[i]); } } void add(IFunctor *f) { ArrayResize(funcs, total + 1); funcs[total++] = f; } void fill(FunctionTable &table) { table.add(funcs); } };
「fill」メソッドは、ストレージ(funcs配列)からの標準関数でテーブルを埋めます。作成されたすべての関手をストレージに自動的に渡すことができるようにするには、AbstractFunc関数の基本クラス内に静的インスタンスを作成し、コンストラクタからの「this」参照を入力します。
class AbstractFunc: public IFunctor { private: const string _name; const int _arity; static AbstractFuncStorage storage; public: AbstractFunc(const string n, const int a): _name(n), _arity(a) { storage.add(&this); } string name(void) const override { return _name; } int arity(void) const override { return _arity; } static void fill(FunctionTable &table) { storage.fill(table); } }; static AbstractFuncStorage AbstractFunc::storage;
もちろん、コンストラクタは入力パラメータを受け取り、関数の名前とアリティを識別できるようにします。
特別なアリティを持つ関数を宣言するための中間テンプレートクラスFuncNが追加されました。このクラスのアリティは、渡された型のサイズによって設定されます(現在、関数のアリティは3を超えず、ゼロサイズの型はないため、sizeof(T)%4という表記を使用します。したがって、サイズ4はアリティ0を生成します)。
template<typename T> class FuncN: public AbstractFunc { public: FuncN(const string n): AbstractFunc(n, sizeof(T) % 4) {} };
サイズが0から3のタイプは、マクロを使用して生成されます。
struct arity0 { char x[4]; }; #define _ARITY(N) struct arity##N { char x[N]; }; _ARITY(1); _ARITY(2); _ARITY(3);
関数記述の生成を自動化するための引数のリストも必要です。
#define PARAMS0 #define PARAMS1 params[0] #define PARAMS2 params[0],params[1] #define PARAMS3 params[0],params[1],params[2]
これで、FuncN<T>クラスに基づいて、関手のマクロを定義できます。
#define FUNCTOR(CLAZZ,NAME,ARITY) \ class Func_##CLAZZ: public FuncN<arity##ARITY> \ { \ public: \ Func_##CLAZZ(): FuncN(NAME) {} \ double execute(const double ¶ms[]) override \ { \ return CLAZZ(PARAMS##ARITY); \ } \ }; \ Func_##CLAZZ __##CLAZZ;
最後に、サポートされている関数の名前と引数の数のリストを示します。
FUNCTOR(fabs, "abs", 1); FUNCTOR(acos, "acos", 1); FUNCTOR(acosh, "acosh", 1); FUNCTOR(asin, "asin", 1); FUNCTOR(asinh, "asinh", 1); FUNCTOR(atan, "atan", 1); FUNCTOR(atanh, "atanh", 1); FUNCTOR(ceil, "ceil", 1); FUNCTOR(cos, "cos", 1); FUNCTOR(cosh, "cosh", 1); FUNCTOR(exp, "exp", 1); FUNCTOR(floor, "floor", 1); FUNCTOR(log, "log", 1); FUNCTOR(log10, "log10", 1); FUNCTOR(fmax, "max", 2); FUNCTOR(fmin, "min", 2); FUNCTOR(fmod, "mod", 2); FUNCTOR(pow, "pow", 2); FUNCTOR(rand, "rand", 0); FUNCTOR(round, "round", 1); FUNCTOR(sin, "sin", 1); FUNCTOR(sinh, "sinh", 1); FUNCTOR(sqrt, "sqrt", 1); FUNCTOR(tan, "tan", 1); FUNCTOR(tanh, "tanh", 1);
一般化された形式の関手クラス図は次のようになります。
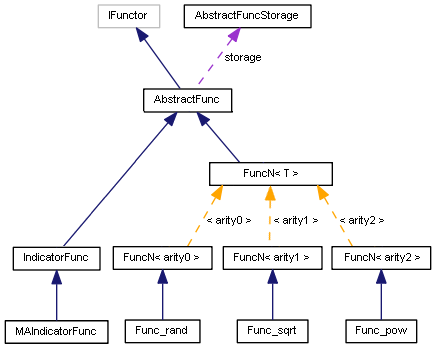
関手クラス図
この図はすべての機能を示しているわけではありませんが、各アリティの1つの機能のみを示しています。 また、後で検討するいくつかの関数もあります。
したがって、すべてが2つの再帰下降パーサを使用できます。そのうちの1つは、解釈モードで式を計算します。もう1つは、構文木を使用して式を計算します。
その場での式の評価(ExpressionEvaluator)
インタプリタによる式の評価は次のとおりです。ExpressionEvaluatorインスタンスを作成し、必要に応じて変数を渡し、必要な式を含む文字列を使用して「evaluate」メソッドを呼び出します。
ExpressionEvaluator ee("a=-10"); double result = ee.evaluate("1 + sqrt(a)"); // -nan(ind) bool success = ee.success(); // true
「success」メソッドを使用して、式が構文的に正しいかどうかを確認できます。ただし、これは計算中にエラーが発生しないことを保証するものではありません。上記の例では、負の変数のルートを抽出しようとすると、NaNが返されます。したがって、MathIsValidNumber関数を使用して結果を確認することをお勧めします。
他のパーサを開発した後、プロセスのより詳細な説明を含むテストを作成します。
式を構文木に「コンパイル」した後の木の評価(ExpressionCompiler)
構文木を構築することによる式の評価は、次のように実行されます。ExpressionCompilerのインスタンスを作成し、必要に応じて初期変数を渡し、必要な式を含む文字列を使用して「evaluate」メソッドを呼び出します。その結果、Promiseオブジェクトへの参照を受け取ります。このオブジェクトに対して、式を評価して数値を取得するために「resolve」を呼び出す必要があります。これはより面倒に見えますが、変数の異なる値に対して複数の計算を実行する必要がある場合は、はるかに高速に動作します。
double a[10] = {...}, b[10] = {...}, c[10] = {...}; VariableTable vt; ExpressionCompiler с(vt); vt.adhocAllocation(true); const string expr = "(a + b) * sqrt(c)"; Promise *p = c.evaluate(expr); for(int i = 0; i < 10; i++) { vt.set("a", a[i]); vt.set("b", b[i]); vt.set("c", c[i]); Print(p.resolve()); }
変数の空のテーブルが最初にここに作成されます。変数a、b、cの変更値は、反復処理でこのテーブルに書き込まれます。ここで使用されるadhocAllocationメソッドは、解析および木の生成の段階で、テーブル内の変数名を受け入れて予約するようにパーサに指示するフラグを設定します。このような暗黙の変数はすべてNaNに設定されるため、呼び出し元は「promise」を計算する前にそれらを実際の値に設定する必要があります。
上記の例でc.evaluateの前にvt.adhocAllocation(true)を呼び出さないと、式で検出されたすべての変数はエラーを生成します。これは、デフォルトでは、変数は事前に記述されている必要があるが、テーブルは空であると想定されているためです。c.evaluate()の後にc.success()を呼び出すことで、コードのエラーをチェックできます。また、エラーはログに記録されます。
インタプリタと同様に、「evaluate」メソッドはとにかく何らかの結果を返します。したがって、解析段階で変数が不明な場合は、NaN値を持つノードが木に作成されます。このような木での計算はNaNを返すため、役に立ちません。しかし、木の存在によって問題が何であるかを理解することができます。Promiseクラスには、木を印刷するためのヘルパーメソッド(print)があります。
終わりに
本稿では、数式の解析の基本について考察しました。また、すぐに使用できる2つのMQLパーサを作成しました。以下には小さなテストスクリプトが添付されているので、この技術をプログラムで使い始められます。第2部では、引き続き他のパーサタイプを調査します。パフォーマンスを比較し、トレーダーのタスクを解決するためにそれらを使用する方法の例を示します。
MetaQuotes Ltdによってロシア語から翻訳されました。
元の記事: https://www.mql5.com/ru/articles/8027
警告: これらの資料についてのすべての権利はMetaQuotes Ltd.が保有しています。これらの資料の全部または一部の複製や再プリントは禁じられています。
この記事はサイトのユーザーによって執筆されたものであり、著者の個人的な見解を反映しています。MetaQuotes Ltdは、提示された情報の正確性や、記載されているソリューション、戦略、または推奨事項の使用によって生じたいかなる結果についても責任を負いません。
 クイック手動取引ツールキット: 基本機能
クイック手動取引ツールキット: 基本機能
- 無料取引アプリ
- 8千を超えるシグナルをコピー
- 金融ニュースで金融マーケットを探索

数学関数にさらにいくつかのMQL関数を追加し、最適化基準を 入力文字列にすることができます。
またはOnTester関数のソースを含むファイル名を指定します。パーサー・インタープリターが計算します。