Berechnung mathematischer Ausdrücke (Teil 1). Ein Parser mit rekursivem Abstieg

Bei der Automatisierung von Handelsaufgaben kann es erforderlich sein, die Flexibilität von Berechnungsalgorithmen in ihrer Ausführungsphase zu gewährleisten. Bei der Feinabstimmung von Programmen, die in einem geschlossenen (kompilierten) Modus verteilt sind, können wir beispielsweise die Auswahl des Zielfunktionstyps aus einer Vielzahl von möglichen Kombinationen implementieren. Dies kann insbesondere bei der Optimierung eines Expert Advisors oder bei der schnellen Evaluierung eines Indikatorprototyps nützlich sein. Zusätzlich zur Änderung der Parameter im Dialogfeld können die Nutzer auch die Berechnungsformel ändern. In diesem Fall müssen wir den arithmetischen Ausdruck aus seiner textuellen Darstellung berechnen, ohne den MQL-Programmcode zu ändern.

Diese Aufgabe kann durch die Verwendung verschiedener Parser gelöst werden, die eine Formelinterpretation im laufenden Betrieb, ihre "Kompilierung" in einen Syntaxbaum, die Erzeugung des sogenannten Bytecodes (Folge von Rechenanweisungen) und seine weitere Ausführung zur Berechnung des Ergebnisses ermöglichen. In diesem Artikel werden wir verschiedene Arten von Parsern und Ausdrucksberechnungsmethoden betrachten.

Formulierung des Problems

In diesem Artikel ist ein arithmetischer Ausdruck eine einzeilige Folge von Datenelementen und Operatoren, die die relevanten Aktionen beschreiben. Datenelemente sind Zahlen und benannte Variablen. Variablenwerte können von außen gesetzt und bearbeitet werden, d.h. nicht im Ausdruck, sondern unter Verwendung spezieller Parser-Attribute. Mit anderen Worten, es gibt keinen Zuweisungsoperator ('=') zur Speicherung von Zwischenergebnissen. Unten finden Sie eine Liste der unterstützten Operatoren, die in der Reihenfolge der Berechnungspriorität angezeigt werden:

• !, - , + — unäre logische Negation, Minus und Plus
• () — Gruppierung mit Klammern
• *, /, % — Multiplikation, Division und Modulo-Division
• +, - — Addition und Subtraktion
• >, <, >=, <= — größer, kleiner Vergleiche
• ==, != — gleich oder ungleich
• &&, || — logische UND und ODER (bitte beachten Sie, dass die Priorität gleiche ist, daher sollten Klammern verwendet werden)
• ?: — ternäre Bedingung, mit der Sie Berechnungen nach Bedingungen verzweigen können

Wir werden auch die Verwendung von mathematischen MQL-Standardfunktionen in Ausdrücken erlauben, die insgesamt 25 sind. Eine davon ist die Potenzfunktion für das Potenzieren. Aus diesem Grund enthält die Liste der Operatoren keinen Exponentenoperator ('^'). Darüber hinaus unterstützt der Operator '^' nur eine ganzzahlige Potenz, während die Funktion keine solchen Einschränkungen hat. Es gibt ein weiteres spezifisches Merkmal, das '^' von den anderen betrachteten Operatoren unterscheidet.

Dies hängt mit folgendem zusammen. Eine der Operator-Eigenschaften ist die Assoziativität, die bestimmt, wie Operatoren mit gleicher Priorität entweder von links oder von rechts ausgeführt werden. Es gibt auch andere Assoziativität Typen, aber sie werden im Kontext der aktuellen Aufgabe nicht verwendet.

Hier ist ein Beispiel dafür, wie sich die Assoziativität auf das Berechnungsergebnis auswirken könnte.

1 - 2 - 3

Dieser Ausdruck gibt nicht ausdrücklich die Reihenfolge an, in der die beiden Subtraktionen durchgeführt werden. Da der Operator '-' links-assoziativ ist, wird zuerst 2 von 1 subtrahiert und dann 3 vom Zwischenergebnis -1, was -4 ergibt, d.h. dies ist gleich den folgenden Ausdrücken:

((1 - 2) - 3)

Wenn, einmal hypothetisch, der Operator "-" eine rechte Assoziativität hätte, würden die Operationen in umgekehrter Reihenfolge ausgeführt werden:

(1 - (2 - 3))

Das ergäbe 2. Glücklicherweise ist der Operator '-' links-assoziativ.

Daher beeinflusst die Links- oder Rechts-Assoziativität das Parsen der Ausdrücke und verkompliziert dadurch den Algorithmus. Alle aufgeführten binären Operatoren sind links-assoziativ, und nur '^' ist rechts-assoziativ.

Zum Beispiel der Ausdruck:

3 ^ 2 ^ 5

bedeutet, dass zuerst 2 hoch 5 und dann 3 hoch 32 berechnet wird.

Der Einfachheit halber verzichten wir auf den Exponentenoperator (und verwenden stattdessen die Funktion pow()), so dass die Algorithmen nur unter Berücksichtigung der linken Assoziativität implementiert werden. Unäre Operatoren sind immer rechts-assoziativ und werden daher einheitlich behandelt.

Alle Zahlen in unseren Ausdrücken (einschließlich derer, die als Konstanten und als Variablen geschrieben werden) werden vom reellen Typ sein. Lassen Sie uns den Toleranzwert festlegen, um sie auf Gleichheit zu vergleichen. Zahlen in logischen Ausdrücken beruhen auf einem einfachen Prinzip: Null ist falsch, Nicht-Null ist wahr.

Bitweise Operatoren sind nicht vorgesehen. Arrays werden nicht unterstützt.

Hier sind einige Beispiele für Ausdrücke:

• "1 + 2 * 3" — Berechnung nach Operationspriorität
• "(1 + 2) * 3" — Gruppierung durch Klammern
• "(a + b) * c" — Verwendung von Variablen
• "(a + b) * sqrt(1 / c)" — Verwendung der Funktion
• "a > 0 && a != b ? a : c" — Berechnung durch logische Bedingungen

Variablen werden durch einen Namen identifiziert, der nach den regulären Regeln der MQL-Bezeichner zusammengesetzt ist: Sie können aus Buchstaben, Zahlen oder Unterstrichen bestehen und dürfen nicht mit einer Zahl beginnen. Variablennamen dürfen nicht mit eingebauten Funktionsnamen übereinstimmen.

Die eingegebene Zeichenkette wird Zeichen für Zeichen analysiert. Allgemeine Prüfungen, z.B. ob ein Zeichen zu Buchstaben oder Zahlen gehört, sowie die Fehlerbehandlung, das Setzen von Variablen und die erweiterbare Tabelle der Standardfunktionen, werden in der Basisklasse definiert. Alle Parsertypen werden von dieser Basisklasse geerbt.

Wir realisieren alles in Parserklassen. Die Artikel stellen die Klassen mit einigen Vereinfachungen vor. Die vollständigen Quellcodes sind unten angehängt.

Die Parser-Basisklasse (AbstractExpressionProcessor-Vorlage)

Dies ist eine Vorlagenklasse (template), da das Ergebnis der Ausdrucksanalyse nicht nur ein skalarer Wert, sondern auch ein Baum von Knoten (Objekte einer speziellen Klasse) sein kann, der die Ausdruckssyntax beschreibt. Wie dies geschieht und zu welchem Zweck dies geschieht, werden wir später besprechen.

Zunächst einmal speichert das Klassenobjekt den Ausdruck (_expression), seine Länge (_length), die aktuelle Cursorposition beim Lesen der Zeichenkette (_index) und das aktuelle Symbol (_token). Außerdem verfügt es über reservierte Variablen, die einen Fehler im Ausdruck (_failed) und die Genauigkeit des Wertevergleichs (_precision) anzeigen.

  template<typename T>
  class AbstractExpressionProcessor
  {
    protected:
      string _expression;
      int _index;
      int _length;
      ushort _token;
  
      bool _failed;
      double _precision;

Für die Speicherung von Variablen und Verknüpfungen stehen spezielle Tabellen zur Verfügung, wir werden jedoch die entsprechenden Klassen von VariableTable und FunctionTable später betrachten.

      VariableTable *_variableTable;
      FunctionTable _functionTable;

Die Tabellen sind Paares von "Schlüssel=Wert", wobei der Schlüssel die Zeichenkette mit dem Variablen- oder Funktionsnamen ist und der Wert entweder ein Double (bei Variablen) oder ein Funktor Objekt (bei Tabellen) ist.

Die Variablentabelle wird durch eine Referenz beschrieben, da ein Ausdruck keine Variablen haben kann. Was die Funktionstabelle betrifft, so hat der Parser immer ein Minimum an eingebauten Funktionen (die ein Benutzer erweitern kann), deshalb wird diese Tabelle durch ein vorgefertigtes Objekt dargestellt.

Die Tabelle der Standardfunktionen wird in der Methode gefüllt:

      virtual void registerFunctions();

Der folgende Abschnitt beschreibt Funktionen, die Unteraufgaben ausführen, die verschiedenen Parsern gemeinsam sind, wie z.B. das Umschalten zum nächsten Zeichen, die Prüfung des Zeichens gegen den erwarteten Wert (und das Anzeigen eines Fehlers, wenn er nicht übereinstimmt), das sequentielle Lesen von Ziffern, die den Formatanforderungen entsprechen, sowie einige statische Hilfsmethoden zur Klassifizierung von Zeichen.

      bool _nextToken();
      void _match(ushort c, string message, string context = NULL);
      bool _readNumber(string &number);
      virtual void error(string message, string context = NULL, const bool warning = false);
      
      static bool isspace(ushort c);
      static bool isalpha(ushort c);
      static bool isalnum(ushort c);
      static bool isdigit(ushort c);

Alle diese Funktionen sind insbesondere in dieser Basisklasse definiert:

  template<typename T>
  bool AbstractExpressionProcessor::_nextToken()
  {
    _index++;
    while(_index < _length && isspace(_expression[_index])) _index++;
    if(_index < _length)
    {
      _token = _expression[_index];
      return true;
    }
    else
    {
      _token = 0;
    }
    return false;
  }
  
  template<typename T>
  void AbstractExpressionProcessor::_match(ushort c, string message, string context = NULL)
  {
    if(_token == c)
    {
      _nextToken();
    }
    else if(!_failed) // prevent chained errors
    {
      error(message, context);
    }
  }
  
  template<typename T>
  bool AbstractExpressionProcessor::_readNumber(string &number)
  {
    bool point = false;
    while(isdigit(_token) || _token == '.')
    {
      if(_token == '.' && point)
      {
        error("Too many floating points", __FUNCTION__);
        return false;
      }
      number += ShortToString(_token);
      if(_token == '.') point = true;
      _nextToken();
    }
    return StringLen(number) > 0;
  }

Die wissenschaftliche Notation mit Exponent wird beim Parsen von Zahlen nicht unterstützt.

Die Klasse deklariert auch die Hauptmethode 'evaluieren', die in Kinderklassen außer Kraft gesetzt wird. Hier initialisiert sie nur Variablen.

    public:
      virtual T evaluate(const string expression)
      {
        _expression = expression;
        _length = StringLen(_expression);
        _index = -1;
        _failed = false;
        return NULL;
      }

Dies ist die Methode der Hauptklasse, die eine Zeichenkette mit dem Ausdruck als Eingabe erhält und das Ergebnis der Zeichenkettenverarbeitung ausgibt: einen bestimmten Wert, wenn eine Berechnung durchgeführt wurde, oder einen Syntaxbaum, wenn eine Analyse durchgeführt wurde.

Die öffentliche Schnittstelle der Klasse enthält auch Konstruktoren, an die Variablen zusammen mit ihren Werten übergeben werden können (als Zeichenfolge wie "name1 = Wert1; name2 = Wert2; ..." oder als vorgefertigtes Objekt VariableTable), Methoden zum Festlegen der Toleranz beim Vergleich von Zahlen, zum Erhalten der Parsing-Erfolgsanzeige (die zeigt, dass es keine Syntaxfehler gab) und zum Zugreifen auf Variablen und Funktionstabellen.

    public:
      AbstractExpressionProcessor(const string vars = NULL);
      AbstractExpressionProcessor(VariableTable &vt);
  
      bool success() { return !_failed; };
      void setPrecision(const double p) { _precision = p; };
      double getPrecision(void) const { return _precision; };
      virtual VariableTable *variableTable();
      virtual FunctionTable *functionTable();
  };

Bitte beachten Sie, dass selbst wenn keine Syntaxfehler vorliegen, eine Ausdrucksberechnung zu einem Fehler führen kann (z.B. Null Division, Wurzel eines negativen Wertes usw.). Um solche Situationen zu kontrollieren, überprüfen Sie mit der Funktion MathIsValidNumber, ob das Ergebnis eine Zahl ist. Unsere Parser müssen in der Lage sein, geeignete Werte verschiedener NaN-Typen (Not A Number (keine Zahl)) zu erzeugen, anstatt zur Laufzeit abzustürzen.

Die einfachste Methode ist der Parser mit rekursivem Abstieg. Beginnen wir also mit diesem Parser.

Parser mit rekursivem Abstieg (Vorlage ExpressionProcessor)

Ein Parser mit rekursivem Abstieg ist eine Menge von wechselseitig rekursiven Funktionen, die nach den Regeln aufgerufen werden, die separate Operationen beschreiben. Wenn wir die Syntax einiger der gebräuchlichsten Operationen als Grammatik in erweiterter BNF-Notation darstellen (Erweiterte Backus-Naur-Form), dann kann der Ausdruck wie folgt dargestellt werden (jede Zeile ist eine separate Regel):

  Expr    -> Sum
  Sum     -> Product { ('+' | '-') Product }
  Product -> Value { ('*' | '/') Value }
  Value   -> [0-9]+ | '(' Expr ')'

Diese Regeln ähneln den folgenden in natürlicher Sprache. Das Parsen des Ausdrucks beginnt mit der Operation mit der niedrigsten Priorität, die in diesem Beispiel Addition/Subtraktion ist. 'Sum' besteht aus zwei Produktoperanden, die durch die Zeichen '+' oder '-' getrennt sind, aber die Operation selbst sowie der zweite Operand sind optional. 'Product' besteht aus zwei Wertoperanden, die durch '*' oder '/' getrennt sind. Auch hier können die Operation und der zweite Operand fehlen. 'Value' ist eine beliebige Zahl, die aus Ziffern oder einem verschachtelten, in Klammern angegebenen Ausdruck besteht.

Zum Beispiel wird der Ausdruck "10" (eine Zahl) in die folgende Folge von Regeln erweitert:

  Expr -> Sum -> Product -> Value -> 10

Der Ausdruck "1 + 2 * 3" hat dann eine komplexere Struktur:

  Expr -> Sum -> Product -> Value -> 1
              |  '+'
              -> Product -> Value -> 2
                         |  '*'
                         -> Value -> 3

Dem Algorithmus zufolge wird die Grammatikanalyse zusammen mit dem Abgleich zwischen dem Eingabestrom von Zeichen und den Operationsregeln durchgeführt. Das Parsing wird von der Hauptregel (dem gesamten Ausdruck) zu kleineren Komponenten (bis hinunter zu einzelnen Zahlen) durchgeführt. Der Parser mit rekursivem Abstieg gehört zur Klasse von oben nach unten (top-down).

Unser Parser wird mehr Operationen unterstützen (siehe die Liste im ersten Abschnitt). Für jede der Operationen ist eine eigene Methode in der von ExpressionProcessor abgeleiteten Klasse reserviert.

  template<typename T>
  class ExpressionProcessor: public AbstractExpressionProcessor<T>
  {
    public:
      ExpressionProcessor(const string vars = NULL);
      ExpressionProcessor(VariableTable &vt);
      T evaluate(const string expression) override
      {
        AbstractExpressionProcessor<T>::evaluate(expression);
        if(_length > 0)
        {
          _nextToken();
          return _parse();
        }
        return NULL;
      }
      
    protected:
      T _parse();
      T _if();        // ?:
      T _logic();     // && ||
      T _eq();        // == !=
      T _compare();   // ><>=<=
      T _expr();      // +-
      T _term();      // */%
      T _unary();     // !-+
      T _factor();    // ()
      T _identifier();
      T _number();
      T _function(const string &name);
  };

Ein Beispiel für die EBNF-Grammatik von Ausdrücken dient als Leitfaden für das Schreiben von Methodencodes.

  expression -> if
  if         -> logic { '?' if ':' if }
  logic      -> eq { ('&&' | '||' ) eq }
  eq         -> compare { ('==' | '!=' ) compare }
  compare    -> expr { ('>' | '<' | '>=' | '<=') expr }
  expr       -> term  { ('+' | '-') term }
  term       -> unary { ('*' | '/' | '%') unary }
  unary      -> { ('!' | '-' | '+') } unary | factor
  factor     -> '(' if ')' | number | identifier
  identifier -> function | variable
  variable   -> name
  function   -> name '(' { arglist } ')'
  name       -> char { char | digit }*
  arglist    -> if { ',' if } 

Der Ausgangspunkt des Abstiegs ist die Methode _parse - sie wird von der 'public' Bewertungsmethode aufgerufen. Unter Berücksichtigung der Vorgehensprioritäten gibt die Methode _parse die Kontrolle an die jüngste, und die ist _if. Nach dem Parsen des gesamten Ausdrucks muss das aktuelle Symbol Null sein (das Zeilenendezeichen).

  template<typename T>
  T ExpressionProcessor::_parse(void)
  {
    T result = _if();
    if(_token != '\0')
    {
      error("Tokens after end of expression.", __FUNCTION__);
    }
    return result;
  }

Ein ternärer Bedingungsoperator besteht aus drei Unterausdrücken: einer booleschen Bedingung und zwei Berechnungsoptionen, eine für die wahre und eine für die falsche Bedingung. Die boolesche Bedingung ist die nächste Ebene der Grammatik: die Methode _logische. Berechnungsoptionen können wiederum ternäre Bedingungsoperatoren sein, und deshalb rufen wir rekursiv _if auf. Es muss das Zeichen '?' zwischen der Bedingung und der wahren Option stehen. Fehlt das Zeichen, dann ist dies kein ternärer Operator, und der Algorithmus liefert einen Wert aus _logic so wie er ist. Wenn es das Zeichen '?' gibt, müssen wir zusätzlich prüfen, ob es das Zeichen ':' zwischen der wahren und der falschen Option gibt. Wenn alle Komponenten vorhanden sind, überprüfen wir die Bedingung und geben den ersten oder zweiten Wert zurück, je nachdem, ob er wahr oder falsch ist.

  template<typename T>
  T ExpressionProcessor::_if()
  {
    T result = _logic();
    if(_token == '?')
    {
      _nextToken();
      T truly = _if();
      if(_token == ':')
      {
        _nextToken();
        T falsy = _if();
        return result ? truly : falsy; // NB: to be refined
      }
      else
      {
        error("Incomplete ternary if-condition", __FUNCTION__);
      }
    }
    return result;
  }

Logische UND- oder ODER-Operationen werden durch die Methode _logic umgesetzt. Bei dieser Methode erwarten wir aufeinander folgende Zeichen "&&" oder "||" zwischen Operanden, die einen Vergleich darstellen (die Methode _eq). Wenn es keine logische Operation gibt, wird das Ergebnis direkt von der Methode _eq zurückgegeben. Wenn die logische Operation gefunden wird, werten wir sie aus. Mit der 'while'-Schleife kann der Parser mehrere logische Additionen oder Multiplikationen in einer Zeile ausführen, zum Beispiel "a > 0 && b > 0 && c > 0".

  template<typename T>
  T ExpressionProcessor::_logic()
  {
    T result = _eq();
    while(_token == '&' || _token == '|')
    {
      ushort previous = _token;
      _nextToken();
      if(previous == '&' && _token == '&')
      {
        _nextToken();
        result = _eq() && result;
      }
      else
      if(previous == '|' && _token == '|')
      {
        _nextToken();
        result = _eq() || result;
      }
      else
      {
        error("Unexpected tokens " + ShortToString(previous) + " and " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Beachten Sie, dass die Prioritäten von "&&" und "||" in dieser Implementierung gleich sind und es daher notwendig ist, die gewünschte Reihenfolge durch Klammern anzugeben, wenn verschiedene Operationen nacheinander geschrieben werden.

Vergleichsoperatoren ('==', '!=') werden in der Methode _eq ähnlich gehandhabt.

  template<typename T>
  T ExpressionProcessor::_eq() 
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        const bool equal = fabs(result - _compare()) <= _precision; // NB: to be refined
        return equality ? equal : !equal;
      }
      else
      {
        error("Unexpected token " + ShortToString(_token), __FUNCTION__);
      }
    }
    return result;
  }

Einige der Methoden in dem Artikel werden übersprungen (um ihn kurz zu halten). Sie sind alle in den beigefügten Quellcodes verfügbar.

Bei der Methode _Faktor arbeiten wir eigentlich mit Operanden. Es kann ein eingeklammerter Unterausdruck sein, für den wir rekursiv _if aufrufen, ein Bezeichner oder eine Zahl (Konstante, Literal).

  template<typename T>
  T ExpressionProcessor::_factor()
  {
    T result;
    
    if(_token == '(')
    {
      _nextToken();
      result = _if();
      _match(')', ") expected!", __FUNCTION__);
    }
    else if(isalpha(_token))
    {
      result = _identifier();
    }
    else
    {
      result = _number();
    }
    
    return result;
  }

Ein Bezeichner kann den Namen einer Variablen oder einer Funktion bedeuten, wenn der Name von einer offenen Klammer gefolgt wird. Dieses Parsen wird mit der Methode _Identifier durchgeführt. Wenn wir es mit einer Funktion zu tun haben, findet die spezielle Funktion _function ein geeignetes Objekt in der Funktionstabelle _functionTable, parst die Liste der Parameter (jeder von ihnen kann ein unabhängiger Ausdruck sein und wird durch einen rekursiven Aufruf von _if erhalten) und übergibt dann die Kontrolle an das Funktorobjekt.

  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
  
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    
    if(_token == '(')
    {
      _nextToken();
      return _function(variable);
    }
    
    return _variableTable.get(variable); // NB: to be refined
  }

Die _number-Methode wandelt einfach die gelesene Ziffernfolge mit StringToDouble in eine Zahl um (die Hilfsfunktion _readNumber wurde oben vorgestellt).

  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return StringToDouble(number); // NB: to be refined
  }

Dies ist der ganze Parser mit rekursivem Abstieg. Er ist fast fertig. "Fast", weil es sich um eine Vorlagenklasse handelt, die auf einen bestimmten Typ spezialisiert werden muss. Um einen Ausdruck auf der Grundlage von Variablen numerischen Typs zu berechnen, bieten Sie eine Spezialisierung für Double wie folgt an:

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { }
  };

Allerdings ist das Verfahren in der Praxis etwas komplizierter. Der Algorithmus wertet während des Parsens einen Ausdruck aus. Dieser Modus interpreter ist der einfachste, aber auch der langsamste. Stellen Sie sich vor, Sie müssten bei jedem Tick die gleiche Formel berechnen, wobei sich ändernde Variablenwerte (wie Preise oder Volumen) verwendet werden. Um die Berechnungen zu beschleunigen, ist es besser, diese beiden Phasen zu trennen: Parsing und Ausführung der Operation. In diesem Fall kann das Parsing einmal durchgeführt werden - die Ausdrucksstruktur kann in einer Zwischendarstellung gespeichert werden, die für Berechnungen optimiert ist, und dann kann eine schnelle Neuberechnung unter Verwendung dieser Darstellung durchgeführt werden.

Zu diesem Zweck müssen alle Zwischenergebnisse, die in den betrachteten Methoden erhalten und in einer Kette rekursiver Aufrufe bis zur Rückgabe des Endwertes aus der 'public' Methode 'evaluate' übergeben werden, durch Objekte ersetzt werden, die die Beschreibung der Operatoren und Operanden eines bestimmten Ausdrucksfragments (zusammen mit allen ihren Beziehungen) speichern. Ausdruck kann unter Verwendung einer solchen Beschreibung zeitversetzt berechnet werden. Solche Objekte werden Promises genannt.

Abwartende Auswertung (Promises)

Die Klasse Promise beschreibt eine von der Ausdruckskomposition getrennte Entität: einen Operanden oder eine Operation mit Operandenreferenzen. Wenn z.B. ein Variablenname in einem Ausdruck vorkommt, wird die folgende Zeile in der Methode _identifier verarbeitet:

    return _variableTable.get(variable); // NB: to be refined

Es gibt den aktuellen Wert einer Variablen aus der Tabelle nach ihrem Namen zurück. Es ist ein Wert vom Typ double — diese Option ist geeignet, wenn der Parser auf den Typ double spezialisiert ist und Berechnungen im laufenden Betrieb durchführt. Wenn Berechnungen jedoch zurückgestellt werden müssen, müssen wir anstelle des Variablenwertes das Objekt Promise erstellen und den Variablennamen darin speichern. In Zukunft, wenn sich der Variablenwert ändert, sollten wir in der Lage sein, seinen neuen Wert vom Promise-Objekt anzufordern, das den Wert anhand seines Namens findet. Es ist also klar, dass die aktuelle Codezeile, die mit "NB: zu verfeinern" gekennzeichnet ist, nicht für den allgemeinen Fall der Vorlage ExpressionProcessor geeignet ist und durch etwas anderes ersetzt werden muss. Es gibt mehrere solcher Zeilen in ExpressionProcessor, und wir werden eine einzige funktionierende Lösung für alle diese Zeilen finden. Zuerst müssen wir jedoch die Klasse Promise fertig stellen.

Die Promise-Klasse hat mehrere Felder zur Beschreibung eines beliebigen Operanden oder einer Operation.

  class Promise
  {
    protected:
      uchar code;
      double value;
      string name;
      int index;
      Promise *left;
      Promise *right;
      Promise *last;
      
    public:
      Promise(const uchar token, Promise *l = NULL, Promise *r = NULL, Promise *v = NULL):
        code(token), left(l), right(r), last(v), value(0), name(NULL), index(-1)
      {
      }
      Promise(const double v): // value (const)
        code('n'), left(NULL), right(NULL), last(NULL), value(v), name(NULL), index(-1)
      {
      }
      Promise(const string n, const int idx = -1): // name of variable
        code('v'), left(NULL), right(NULL), last(NULL), value(0), name(n), index(idx)
      {
      }
      Promise(const int f, Promise *&params[]): // index of function
        code('f'), left(NULL), right(NULL), last(NULL), value(0), name(NULL)
      {
        index = f;
        if(ArraySize(params) > 0) left = params[0];
        if(ArraySize(params) > 1) right = params[1];
        if(ArraySize(params) > 2) last = params[2];
        // more params not supported
      }

Das Feld 'code' speichert ein Elementtyp-Attribut: 'n' ist eine Zahl, 'v' ist eine Variable, 'f' ist eine Funktion. Alle anderen Symbole werden als eine der erlaubten Operationen behandelt (z.B. '+', '-', '*', '/', '%', usw.). Im Falle einer Zahl wird ihr Wert im Feld 'value' gespeichert. Im Falle einer Variablen wird ihr Name im Feld "name" gespeichert. Für einen schnellen Mehrfachzugriff auf Variablen wird Promise versuchen, die Variablennummer nach dem ersten Aufruf im Feld 'index' zwischenzuspeichern, und dann versuchen, sie nicht über den Namen, sondern über den Index aus der Tabelle abzurufen. Funktionen werden immer durch eine Nummer im Feld 'index' identifiziert, da die Tabelle der Funktionen im Gegensatz zu den Variablen anfangs mit eingebauten Funktionen gefüllt ist, während die Tabelle der Variablen zum Zeitpunkt der Ausdrucksanalyse noch leer sein kann.

Die linke, 'left', rechte, 'right' und letzte, 'last', Referenz sind optional und können Operanden speichern. Zum Beispiel sind alle drei Referenzen NULL für Zahlen oder Variablen. Nur die linke Referenz wird für unäre Operationen verwendet; die linke und rechte Referenz werden für binäre Operationen verwendet; während alle drei Referenzen nur im ternären Bedingungsoperator verwendet werden: 'left' enthält die Bedingung, 'right' ist der Ausdruck für die wahre Bedingung und 'last' wird für die falsche Bedingung verwendet. Auch Referenzen speichern Funktionsparameterobjekte (in der aktuellen Parser-Implementierung ist die Anzahl der Funktionsparameter auf drei begrenzt).

Da Promise-Objekte an Berechnungen teilnehmen, werden wir alle Hauptoperatoren in ihnen überschreiben. So werden z.B. Additions- und Subtraktionsoperationen mit "Promise"-Objekten behandelt.

      Promise *operator+(Promise *r)
      {
        return new Promise('+', &this, r);
      }
      Promise *operator-(Promise *r)
      {
        return new Promise('-', &this, r);
      }

Das aktuelle Objekt (&this), d.h. dasjenige, das sich im Ausdruck links von der Operation befindet, und das nächste Objekt (r), das sich rechts von der Operation befindet, werden an den Konstruktor des neuen Promise-Objekts übergeben, das mit dem entsprechenden Operationscode erstellt wird.

Andere Operationen werden auf die gleiche Weise behandelt. Als Ergebnis wird der gesamte Ausdruck als Baum von Objekten der Klasse Promise angezeigt, in dem das Wurzelelement den gesamten Ausdruck darstellt. Es gibt eine spezielle 'resolve'-Methode, die verwendet wird, um den tatsächlichen Wert eines beliebigen "Promise"-Objekts, einschließlich des Ausdrucks als Ganzes, zu erhalten.

      double resolve()
      {
        switch(code)
        {
          case 'n': return value;        // number constant
          case 'v': value = _variable(); // variable name
                    return value;
          case 'f': value = _execute();  // function index
                    return value;
          default:  value = _calc();
                    return value;
        }
        return 0;
      };

Dies zeigt, wie der Wert einer numerischen Konstanten aus dem Feld value zurückgegeben wird. Hilfsmethoden sind für Variablen, Funktionen und Operationen implementiert.

      static void environment(AbstractExpressionProcessor<Promise *> *e)
      {
        variableTable = e.variableTable();
        functionTable = e.functionTable();
      }
      
    protected:
      static VariableTable *variableTable;
      static FunctionTable *functionTable;
  
      double _variable()
      {
        double result = 0;
        if(index == -1)
        {
          index = variableTable.index(name);
          if(index == -1)
          {
            return nan; // error: Variable undefined
          }
          result = variableTable[index];
        }
        else
        {
          result = variableTable[index];
        }
        return result;
      }
      
      double _execute()
      {
        double params[];
        if(left)
        {
          ArrayResize(params, 1);
          params[0] = left.resolve();
          if(right)
          {
            ArrayResize(params, 2);
            params[1] = right.resolve();
            if(last)
            {
              ArrayResize(params, 3);
              params[2] = last.resolve();
            }
          }
        }
        IFunctor *ptr = functionTable[index]; // TBD: functors
        if(ptr == NULL)
        {
          return nan; // error: Function index out of bound 
        }
        return ptr.execute(params);
      }
      
      double _calc()
      {
        double first = 0, second = 0, third = 0;
        if(left)
        {
          first = left.resolve();
          if(right)
          {
            second = right.resolve();
            if(last)
            {
              third = last.resolve();
            }
          }
        }
        
        switch(code)
        {
          case '+': return first + second;
          case '-': return first - second;
          case '*': return first * second;
          case '/': return safeDivide(first, second);
          case '%': return fmod(first, second);
          case '!': return !first;
          case '~': return -first;
          case '<': return first < second;
          case '>': return first > second;
          case '{': return first <= second;
          case '}': return first >= second;
          case '&': return first && second;
          case '|': return first || second;
          case '`': return _precision < fabs(first - second); // first != second;
          case '=': return _precision > fabs(first - second); // first == second;
          case '?': return first ? second : third;
        }
        return nan; // error: Unknown operator
      }

Eine Fehlerbehandlung entfällt hier. Tritt ein Fehler auf, wird der spezielle Wert Nan zurückgegeben ("keine Zahl", seine Erzeugung ist in einer separaten Header-Datei NaNs.mqh implementiert, die unten angehängt ist). Bitte beachten Sie, dass die Ausführung von Operationen in einem rekursiven Aufruf von 'resolve' aller unteren Objekte (in der Hierarchie) per Referenz überprüft wird. So löst der Aufruf von 'resolve' für einen Ausdruck eine sequentielle Berechnung aller zugehörigen Promises und die weitere Übertragung der Berechnungsergebnisse als doppelte Zahlen an höhere Elemente aus. Am Ende "kollabieren" alle Werte in den Endwert des Ausdrucks.

Mit der Klasse Promise können wir sie zur Spezialisierung des rekursiven Abstiegsparsers verwenden, der als Ergebnis einen Baum ähnlicher Objekte liefert, d.h. er liefert den Syntaxbaum des Ausdrucks.

In allen Methoden der Template-Klasse ExpressionProcessor, die etwas T zurückgeben, muss dieses T nun gleich (Promise *) sein. Insbesondere in der Methode _Identifikator mit der Zeile:

    return _variableTable.get(variable); // NB: to be refined

müssen wir irgendwie dafür sorgen, dass anstelle der Verdoppelung ein neues Promise-Objekt erzeugt und zurückgegeben wird, das auf eine Variable mit dem Namen 'variable' zeigt.

Um dieses Problem zu lösen, sollte die Aktion, die einen Wert vom Typ T für eine Variable zurückgibt, in eine separate virtuelle Methode verpackt werden, die verschiedene erforderliche Manipulationen in den abgeleiteten Klassen ExpressionProcessor<double> und ExpressionProcessor<Promise *> ausführen würde. Es gibt jedoch ein kleines Problem.

Die Klasse ExpressionHelper

Wir planen die Implementierung mehrerer Parser-Klassen, von denen jede von AbstractExpressionProcessor abgeleitet wird. Die für rekursive Ableitungen spezifischen Methoden sind jedoch nicht in allen von ihnen erforderlich. Wir könnten sie mit leeren überschreiben, wo sie nicht benötigt werden, aber das ist im Hinblick auf OOP nicht richtig. Da MQL Mehrfachvererbung unterstützt, könnten wir ein spezielles Trait verwenden — ein zusätzlicher Satz von Methoden, der bei Bedarf in die Parserklasse eingebunden werden könnte. Da dies nicht möglich ist, sollten wir die entsprechenden Methoden als separate Vorlagenklasse implementieren und ihre Instanz nur innerhalb derjenigen Parser erzeugen, in denen die Methode benötigt wird.

  template<typename T>
  class ExpressionHelper
  {
    protected:
      VariableTable *_variableTable;
      FunctionTable *_functionTable;
  
    public:
      ExpressionHelper(AbstractExpressionProcessor<T> *owner): _variableTable(owner.variableTable()), _functionTable(owner.functionTable()) { }
  
      virtual T _variable(const string &name) = 0;
      virtual T _literal(const string &number) = 0;
      virtual T _negate(T result) = 0;
      virtual T _call(const int index, T &args[]) = 0;
      virtual T _ternary(T condition, T truly, T falsy) = 0;
      virtual T _isEqual(T result, T next, const bool equality) = 0;
  };

Die Klasse enthält alle Methoden, die in der sofortigen und abwartende Auswertung auf unterschiedliche Weise verarbeitet werden. Beispielsweise ist die Methode _variable für den Zugriff auf Variablen zuständig. _literal erhält den Wert einer Konstanten; _negate führt eine logische Negation aus; _call ruft eine Funktion auf; _ternary ist ein ternärer Operator, und _isEqual wird für den Vergleich von Werten verwendet. Alle anderen Berechnungsfälle werden für double und Promise mit derselben Syntax verarbeitet, indem Operatoren in der Klasse Promise überschrieben werden.

Man könnte sich fragen, warum der logische Negationsoperator '!' in Promise nicht außer Kraft gesetzt wurde und stattdessen die Methode _Negate verwendet wurde. Der Operator '!' wird nur auf Objekte angewendet, nicht aber auf Zeiger. Mit anderen Worten, für eine Variable vom Typ Promise *p können wir nicht !p schreiben und erwarten, dass der überschriebene Operator funktioniert. Stattdessen müssen wir zuerst den Zeiger dereferenzieren: !*p. Aber diese Notation wäre für andere Typen, einschließlich T=double, ungültig.

Hier ist, wie die Methode ExpressionHelper für reelle Zahlen implementiert werden können.

  class ExpressionHelperDouble: public ExpressionHelper<double>
  {
    public:
      ExpressionHelperDouble(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual double _variable(const string &name) override
      {
        if(!_variableTable.exists(name))
        {
          return nan;
        }
        return _variableTable.get(name);
      }
      virtual double _literal(const string &number) override
      {
        return StringToDouble(number);
      }
      virtual double _call(const int index, double &params[]) override
      {
        return _functionTable[index].execute(params);
      }
      virtual double _isEqual(double result, double next, const bool equality) override
      {
        const bool equal = fabs(result - next) <= _precision;
        return equality ? equal : !equal;
      }
      virtual double _negate(double result) override
      {
        return !result;
      }
      virtual double _ternary(double condition, double truly, double falsy) override
      {
        return condition ? truly : falsy;
      }
  };

Hier ist, wie sie für Promise implementiert ist.

  class ExpressionHelperPromise: public ExpressionHelper<Promise *>
  {
    public:
      ExpressionHelperPromise(AbstractExpressionProcessor<T> *owner): ExpressionHelper(owner) { }
  
      virtual Promise *_negate(Promise *result) override
      {
        return new Promise('!', result);
      }
      virtual Promise *_call(const int index, Promise *&params[]) override
      {
        return new Promise(index, params);
      }
      virtual Promise *_ternary(Promise *condition, Promise *truly, Promise *falsy) override
      {
        return new Promise('?', condition, truly, falsy);
      }
      virtual Promise *_variable(const string &name) override
      {
        if(CheckPointer(_variableTable) != POINTER_INVALID)
        {
          int index = _variableTable.index(name);
          if(index == -1)
          {
            return new Promise(nan); // error: Variable is undefined
          }
          return new Promise(name, index);
        }
        return new Promise(name);
      }
      virtual Promise *_literal(const string &number) override
      {
        return new Promise(StringToDouble(number));
      }
      virtual Promise *_isEqual(Promise *result, Promise *next, const bool equality) override
      {
        return new Promise((uchar)(equality ? '=' : '`'), result, next);
      }
  };

Jetzt können wir das Feld 'helper' zu AbstractExpressionProcessor hinzufügen:

    protected:
      ExpressionHelper<T> *helper;
      
    public:  
      ~AbstractExpressionProcessor()
      {
        if(CheckPointer(helper) == POINTER_DYNAMIC) delete helper;
      }

und die Implementierung der Methode ExpressionProcessor überprüfen, die mit "NB" markierte Zeichenketten hatten: Sie alle müssen Operationen an das Objekt 'helper' delegieren. Zum Beispiel:

  template<typename T>
  T ExpressionProcessor::_eq()
  {
    T result = _compare();
    if(_token == '!' || _token == '=')
    {
      const bool equality = _token == '=';
      _nextToken();
      if(_token == '=')
      {
        _nextToken();
        return helper._isEqual(result, _compare(), equality); // OK
      }
    }
    return result;
  }
  
  template<typename T>
  T ExpressionProcessor::_identifier()
  {
    string variable;
    while(isalnum(_token))
    {
      variable += ShortToString(_token);
      _nextToken();
    }
    ...
    return helper._variable(variable); // OK
  }
  
  template<typename T>
  T ExpressionProcessor::_number()
  {
    string number;
    if(!_readNumber(number))
    {
      error("Number expected", __FUNCTION__);
    }
    return helper._literal(number); // OK
  }

Mithilfe der vorgestellten Klassen können wir schließlich den ersten Parser zusammenstellen, der während des Parsens von Ausdrücken Berechnungen durchführt: ExpressionEvaluator.

  class ExpressionEvaluator: public ExpressionProcessor<double>
  {
    public:
      ExpressionEvaluator(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperDouble(&this); }
      ExpressionEvaluator(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperDouble(&this); }
  };

Hier erhalten wir einen weiteren Parser für die abwartende Auswertung — ExpressionCompiler.

  class ExpressionCompiler: public ExpressionProcessor<Promise *>
  {
    public:
      ExpressionCompiler(const string vars = NULL): ExpressionProcessor(vars) { helper = new ExpressionHelperPromise(&this); }
      ExpressionCompiler(VariableTable &vt): ExpressionProcessor(vt) { helper = new ExpressionHelperPromise(&this); }
      
      virtual Promise *evaluate(const string expression) override
      {
        Promise::environment(&this);
        return ExpressionProcessor<Promise *>::evaluate(expression);
      }
  };

Die Hauptunterschiede liegen im Feld 'helper' und im vorläufigen Aufruf von Promise::environment zur Eingabe der Tabellen mit Variablen und Funktionen in Promise.

Es bleibt nur noch eines übrig, bevor wir einen voll funktionsfähigen Parser erhalten können: die Tabellen mit Variablen und Funktionen.

Variablen- und Funktionstabellen

Beide Tabellen sind Template-Map-Klassen, die aus Schlüssel=Wert-Paaren bestehen, wobei Schlüssel ein Text-Bezeichner und Wert ein Wert vom Typ T ist. Ihre Implementierung ist in VariableTable.mqh verfügbar. Die Basisklasse beschreibt alle erforderlichen Abbildungsoperationen: Hinzufügen von Elementen, Ändern von Werten und Abrufen nach Name oder Index.

  template<typename T>
  class Table
  {
    public:
      virtual T operator[](const int index) const;
      virtual int index(const string variableName);
      virtual T get(const string variableName) const;
      virtual int add(const string variableName, T value);
      virtual void update(const int index, T value);
      ...
  };

Dies ist ein reeller Wert die Variable vom Typ T.

  class VariableTable: public Table<double>
  {
    public:
      VariableTable(const string pairs = NULL)
      {
        if(pairs != NULL) assign(pairs);
      }
      
      void assign(const string pairs);
  };

Mit der Methode 'assign' können Variablen der Tabelle nicht nur einzeln, sondern auch als Liste — als Zeichenkette mit der Struktur "name1=Wert1;name2=Wert2;..." — hinzugefügt werden.

Für Funktionen sollte eine spezielle Functor-Schnittstelle erstellt werden. Der Functor wird Code für Funktionsberechnungen enthalten.

  interface IFunctor
  {
    string name(void) const;
    int arity(void) const;
    double execute(const double &params[]);
  };

Jede Funktion hat einen Namen und eine Eigenschaft, die die Anzahl der Argumente beschreibt (Arität). Die Funktion wird durch die Methode 'execute' berechnet, an die Argumente übergeben werden. Fügen Sie alle eingebauten MQL-Mathematikfunktionen in diese Schnittstelle ummantelt ein und fügen Sie dann die entsprechenden Objekte zur Tabelle hinzu (eines nach dem anderen oder in einem Array):

  class FunctionTable: public Table<IFunctor *>
  {
    public:
      void add(IFunctor *f)
      {
        Table<IFunctor *>::add(f.name(), f);
      }
      void add(IFunctor *&f[])
      {
        for(int i = 0; i < ArraySize(f); i++)
        {
          add(f[i]);
        }
      }
  };

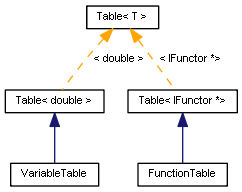
Diagramm der Tabellenklassen für Variablen und Funktionen

Für die Speicherung aller Funktoren wird eine Speicherklasse definiert.

  class AbstractFuncStorage
  {
    protected:
      IFunctor *funcs[];
      int total;
      
    public:
      ~AbstractFuncStorage()
      {
        for(int i = 0; i < total; i++)
        {
          CLEAR(funcs[i]);
        }
      }
      void add(IFunctor *f)
      {
        ArrayResize(funcs, total + 1);
        funcs[total++] = f;
      }
      void fill(FunctionTable &table)
      {
        table.add(funcs);
      }
  };

Die Methode 'fill' füllt die Tabelle mit Standardfunktionen aus dem Speicher (dem Array funcs). Um die automatische Übergabe aller erstellten Funktoren an den Speicher zu ermöglichen, erstellen Sie seine statische Instanz innerhalb der Basisklasse der Funktion AbstractFunc und füllen Sie sie mit 'this'-Referenzen aus dem Konstruktor.

  class AbstractFunc: public IFunctor
  {
    private:
      const string _name;
      const int _arity;
      static AbstractFuncStorage storage;
  
    public:
      AbstractFunc(const string n, const int a): _name(n), _arity(a)
      {
        storage.add(&this);
      }
      string name(void) const override
      {
        return _name;
      }
      int arity(void) const override
      {
        return _arity;
      }
      static void fill(FunctionTable &table)
      {
        storage.fill(table);
      }
  };
  
  static AbstractFuncStorage AbstractFunc::storage;

Natürlich erhält der Konstruktor Eingabeparameter, die es ihm ermöglichen, den Namen und die Arität der Funktion zu identifizieren.

Für die Deklaration von Funktionen mit spezieller Arität wurde eine Template-Zwischenklasse FuncN hinzugefügt. Die Arität in dieser Klasse wird durch die Größe des übergebenen Typs festgelegt (da die Arität der Funktion derzeit nicht größer als 3 ist und es keine Typen mit Null-Größe gibt, verwenden wir eine Notationsgröße von (T) % 4 — und somit ergibt Größe 4 die Arität 0).

  template<typename T>
  class FuncN: public AbstractFunc
  {
    public:
      FuncN(const string n): AbstractFunc(n, sizeof(T) % 4) {}
  };

Typen mit Größen von 0 bis 3 werden mit Hilfe von Makros generiert.

  struct arity0 { char x[4]; };
  
  #define _ARITY(N)   struct arity##N { char x[N]; };
  
  _ARITY(1);
  _ARITY(2);
  _ARITY(3);

Wir brauchen auch Argumentlisten, um die Erzeugung von Funktionsbeschreibungen zu automatisieren.

  #define PARAMS0 
  #define PARAMS1 params[0]
  #define PARAMS2 params[0],params[1]
  #define PARAMS3 params[0],params[1],params[2]

Jetzt können wir ein Makro für einen Funktor definieren, basierend auf der Klasse FuncN<T>.

  #define FUNCTOR(CLAZZ,NAME,ARITY) \
  class Func_##CLAZZ: public FuncN<arity##ARITY> \
  { \
    public: \
      Func_##CLAZZ(): FuncN(NAME) {} \
      double execute(const double &params[]) override \
      { \
        return CLAZZ(PARAMS##ARITY); \
      } \
  }; \
  Func_##CLAZZ __##CLAZZ;

Abschließend finden Sie hier eine Liste der unterstützten Funktionen mit Namen und Anzahl der Argumente.

  FUNCTOR(fabs, "abs", 1);
  FUNCTOR(acos, "acos", 1);
  FUNCTOR(acosh, "acosh", 1);
  FUNCTOR(asin, "asin", 1);
  FUNCTOR(asinh, "asinh", 1);
  FUNCTOR(atan, "atan", 1);
  FUNCTOR(atanh, "atanh", 1);
  FUNCTOR(ceil, "ceil", 1);
  FUNCTOR(cos, "cos", 1);
  FUNCTOR(cosh, "cosh", 1);
  FUNCTOR(exp, "exp", 1);
  FUNCTOR(floor, "floor", 1);
  FUNCTOR(log, "log", 1);
  FUNCTOR(log10, "log10", 1);
  FUNCTOR(fmax, "max", 2);
  FUNCTOR(fmin, "min", 2);
  FUNCTOR(fmod, "mod", 2);
  FUNCTOR(pow, "pow", 2);
  FUNCTOR(rand, "rand", 0);
  FUNCTOR(round, "round", 1);
  FUNCTOR(sin, "sin", 1);
  FUNCTOR(sinh, "sinh", 1);
  FUNCTOR(sqrt, "sqrt", 1);
  FUNCTOR(tan, "tan", 1);
  FUNCTOR(tanh, "tanh", 1);

Das Funktor-Klassendiagramm sieht in verallgemeinerter Form wie folgt aus:

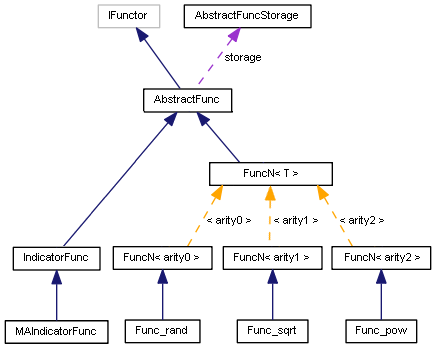
Funktor-Klassendiagramm

Das Diagramm zeigt nicht alle Funktionen, sondern nur eine Funktion jeder Arität. Es hat auch einige Funktionen, die später betrachtet werden.

Und so ist alles bereit für die Verwendung von zwei Parser mit rekursivem Abstieg. Einer von ihnen berechnet Ausdrücke im Interpretationsmodus. Der andere wertet Ausdrücke mit Hilfe von Syntaxbäumen aus.

Ausdrücke im laufenden Betrieb auswerten (ExpressionEvaluator)

Die Ausdrucksauswertung durch den Interpreter sieht folgendermaßen aus: Wir erzeugen eine ExpressionEvaluator-Instanz, übergeben ihr gegebenenfalls Variablen und rufen die Methode 'evaluate' mit einer Zeichenfolge auf, die den gewünschten Ausdruck enthält.

  ExpressionEvaluator ee("a=-10");
  double result = ee.evaluate("1 + sqrt(a)"); // -nan(ind)
  bool success = ee.success();                // true

Mit der Methode 'success' können wir überprüfen, ob der Ausdruck syntaktisch korrekt ist. Dies garantiert jedoch nicht, dass bei den Berechnungen keine Fehler auftreten. Im obigen Beispiel ergibt der Versuch, die Wurzel einer negativen Variablen zu extrahieren, NaN. Es wird daher empfohlen, das Ergebnis mit der Funktion MathIsValidNumber zu überprüfen.

Nachdem wir andere Parser entwickelt haben, werden wir Tests mit einer detaillierteren Beschreibung des Prozesses schreiben.

"Kompilieren" von Ausdrücken in einen Syntaxbaum und Auswerten des Baumes (ExpressionCompiler)

Die Auswertung eines Ausdrucks durch den Aufbau eines Syntaxbaums wird wie folgt durchgeführt: Wir erzeugen eine Instanz von ExpressionCompiler, übergeben ihm gegebenenfalls Anfangsvariablen und rufen die Methode 'evaluate' mit einer Zeichenfolge auf, die den gewünschten Ausdruck enthält. Als Ergebnis erhalten wir eine Referenz auf das Promise-Objekt, für das wir 'resolve' aufrufen müssen, um den Ausdruck auszuwerten und eine Zahl zu erhalten. Das sieht umständlicher aus, aber es funktioniert viel schneller, wenn Sie mehrere Berechnungen für verschiedene Werte von Variablen durchführen müssen.

  double a[10] = {...}, b[10] = {...}, c[10] = {...};
  
  VariableTable vt;
  ExpressionCompiler с(vt);
  vt.adhocAllocation(true);
  const string expr = "(a + b) * sqrt(c)";
  Promise *p = c.evaluate(expr);
  
  for(int i = 0; i < 10; i++)
  {
    vt.set("a", a[i]);
    vt.set("b", b[i]);
    vt.set("c", c[i]);
    Print(p.resolve());
  }

Hier wird zunächst eine leere Variablentabelle erstellt. Die sich ändernden Werte für die Variablen a, b, c werden in einer Schleife in diese Tabelle geschrieben. Die Ad-hoc-Zuweisungsmethode, die hier verwendet wird, setzt ein Flag, das den Parser anweist, alle Variablennamen in der Tabelle zu akzeptieren und zu reservieren, und zwar im Stadium des Parsing und der Baumerzeugung. Jede solche implizite Variable wird auf nan gesetzt, so dass der Aufrufer sie vor der Auswertung von "Promise" auf reelle Werte setzen muss.

Wenn wir im obigen Beispiel vt.adhocAllocation(true) vor c.evaluate nicht aufrufen, werden alle im Ausdruck vorkommenden Variablen Fehler erzeugen, weil standardmäßig angenommen wird, dass die Variablen im Voraus beschrieben werden müssen, die Tabelle aber leer ist. Sie können Ihren Code auf Fehler überprüfen, indem Sie c.success() nach c.evaluate() aufrufen. Fehler werden ebenfalls protokolliert.

Ähnlich wie der Interpreter wird auch die Methode 'evaluate' trotzdem ein Ergebnis liefern. Wenn also die Variablen im Parsing-Stadium nicht bekannt sind, werden für sie Knoten mit dem Nan-Wert im Baum erstellt. Das Rechnen mit einem solchen Baum ist nutzlos, da auch dieser Nan-Wert zurückgegeben wird. Aber das Vorhandensein eines Baumes erlaubt es, das Problem zu verstehen. Die Klasse Promise hat eine Hilfsmethode zum Drucken des Baumes — print.

Schlussfolgerung

In diesem Artikel haben wir die Grundlagen des Parsens mathematischer Ausdrücke betrachtet. Wir haben auch zwei einsatzbereite MQL-Parser erstellt. Ein kleines Testskript ist unten angefügt, mit dem Sie beginnen können, die Technologie in Ihren Programmen zu verwenden. Andere Parsertypen werden wir im zweiten Teil weiter untersuchen: Wir werden ihre Leistung vergleichen und Beispiele dafür geben, wie sie zur Lösung von Händleraufgaben eingesetzt werden können.