Previsão de séries temporais (parte 2): método de vetores de suporte por mínimos quadrados (LS-SVM)

Palavras-chave: LS-SVM, SOM-LS-SVM, SOM

Introdução

Neste artigo, continuamos a falar sobre algoritmos de previsão de séries temporais. Na primeira parte, destacamos o método de decomposição de modo empírico (EMD) e o indicador TSA para análise estatística de séries temporais. Na segunda parte, tratamos o algoritmo de vetores de suporte (support-vector machine, SVM), em particular sua modificação de mínimos quadrados (Least-squares support-vector machine, LS-SVM). Embora este abordagem ainda não tenha sido implementada em MQL, em primeiro lugar, precisamos conhecer determinado modelo matemático.

Modelo matemático LS-SVM

O método de vetores de suporte (Support Vector Machine, SVM) é um nome genérico para um grupo de algoritmos de análise de dados usados para classificação e regressão. Nós estamos especialmente interessados na regressão (artigo em inglês da Wikipedia), uma vez que ela revela a relação entre variáveis dependentes e independentes (preditores). A previsão pode ser formulada através de uma regressão como o fato de encontrar uma determinada função, que dependa de amostras da série temporal (isto é, dos preditores), de modo que seus valores descrevam de maneira mais plausível as amostras futuras da série.

O algoritmo do SVM é baseado na conversão de dados de origem num espaço de maior dimensão, onde cada vetor de entrada é gerado como uma sequência de pontos de origem com atrasos no tempo. Em seguida, estes vetores são usados como amostras de suporte, cuja combinação permite calcular um hiperplano que descreve a distribuição dos dados com determinada precisão. Os cálculos são uma soma de todas as amostras dos núcleos (kernels), isto é, de funções uniformes a partir de dados de entrada. Essas funções podem ser lineares ou não lineares (geralmente em forma de sino) e controladas por parâmetros que afetam a precisão da regressão. Os núcleos mais comuns abrangem:

• linear ;
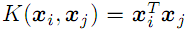• polinômio de grau d ;
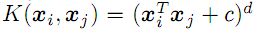• função de base radial com dispersão "sigma" (Gaussian, ver abaixo);
• sigmóide (tangente hiperbólica) ;

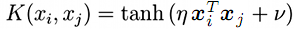Também existe uma modificação do SVM que é chamada de método de vetores de suporte por mínimos quadrados, Least-Squares SVM (LS-SVM). Esse método permite resolver, em vez de um problema não linear, um equivalente na forma de um sistema de equações lineares.

Digamos que temos uma série temporal y e assumimos que podemos descobrir seu valor no momento t como uma função de p de pontos anteriores e de determinadas variáveis externas q, com erro e. Em termos gerais, fica assim:

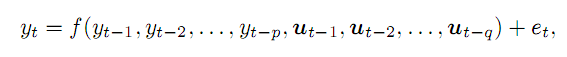 (1)

Como exemplos de variáveis externas (para a área de aplicação do trading) podemos falar do número para o dia da semana, do número da hora em dias ou do volume da barra correspondente. Neste artigo, nos abordaremos apenas aos pontos anteriores da série temporal de preços. A complexidade do material não permite considerar todos os aspectos de uma só vez.

Os pontos anteriores retirados da série p formam um vetor no espaço tridimensional p. Após nos deslocarmos ao longo da série inicial, da esquerda para a direita, obtemos o conjunto de vetores-preditores, que designamos como x, para um momento t eles corresponderem à previsão y, vamos expressar essa correspondência como:

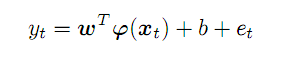 (2)

O vetor desconhecido dos coeficientes w e as funções transformadoras f trabalham num espaço abstrato de signos, cuja dimensão é potencialmente ilimitada e até pode ser maior do que p. O tipo de f, bem como os valores dos coeficientes w devem ser encontrados no processo de otimização:

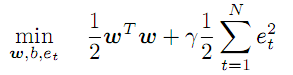 (3)

Esta condição ordena minimizar a magnitude dos coeficientes w e introduz um coeficiente "gama" que regulariza a magnitude dos erros. Quanto maior "gama", com mais precisão a regressão deve aproximar os dados de origem. Se "gama" diminuir, a tolerância aos desvios aumenta, incrementando a suavidade do modelo.

O sistema de equações (2) age como limitação para todos os t de 1 a N (número de vetores).

Para simplificar a tarefa, são utilizados truques matemáticos (um deles é chamado 'kernel trick') que, em vez da tarefa de otimização inicial, resolvem a chamada dualidade que é, em essência, equivalente - nela é possível se livrar dos coeficientes w e das transformações f em troca de funções nucleares (veja mais abaixo) Como resultado, a solução se reduz a um sistema linear:

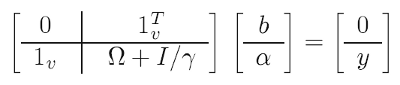 (4)

Dados conhecidos:

• y - vetor que consiste em todos os valores meta (de aprendizado) de previsão;
• 1 - vetores unitários (linha e coluna);
• I - matriz única;
• gama - parâmetro de regularização descrito acima (deve ser selecionado com base na qualidade da previsão na amostra de teste);
• omega - matriz calculada segundo a fórmula:

 (5)

Aqui finalmente vemos as funções de núcleo K, mencionadas anteriormente, calculadas aos pares entre todos os vetores de entrada x. Para uma função de base radial na forma de uma função de Gauss, a fórmula de K fica assim:

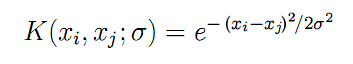 (6)

O parâmetro "sigma" descreve a largura da campainha, sendo este outro parâmetro que precisa ser selecionado iterativamente na prática. Quanto maior o "sigma", maior o número de vetores "vizinhos" que participará da regressão. Quando o "sigma" é pequeno, a função passa com precisão pelos pontos do conjunto de dados de aprendizado e deixa de responder a formas desconhecidas (deixa de generalizar).

Usando os dados de origem (x, y), de acordo com as fórmulas (4), (5) e (6), obtemos todas as incógnitas pelo método dos mínimos quadrados:

• b - termo livre que aparece em (2) e (7);
• a - vetor dos coeficientes "alfa", incluídos na fórmula final do modelo de regressão:

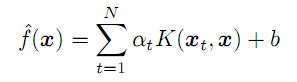 (7)

Para qualquer vetor arbitrário x (não do conjunto de aprendizado), ela permite calcular a previsão como a soma dos produtos dos coeficientes "alfa" e núcleos com base em todos os vetores N iniciais, ajustados para o termo livre b.

Na parte teórica, resta responder a 2 perguntas. Em primeiro lugar, como devemos reconhecer os parâmetros livres "gama" e "sigma". Em segundo lugar, que atraso de profundidade de tempo p deve ser escolhido para formar vetores de entrada x desde uma série de cotações.

Os parâmetros são realmente determinados pelo método "tentativa e erro": num ciclo de uma grade bidimensional de valores muito ampla, é calculado o modelo para cada combinação e é determinada sua qualidade. Por qualidade, entenderemos minimizar erros de previsão com base num conjunto de dados de teste que não seja o conjunto de aprendizado. O processo se assemelha e pode envolver otimização no testador MetaTrader, mas para estudar amplas faixas, será necessário realmente alterar os valores não com um incremento constante, mas, sim, em progressão geométrica com a ajuda da multiplicação. Por isso, precisaremos considerar essa particularidade no estágio de implementação.

Quanto ao tamanho do espaço de entrada p, recomenda-se determiná-lo com base nas características da séries a sere prevista, em particular, usando a função de autocorrelação privada (PACF). No artigo anterior, preparamos um conjunto de ferramentas para calcular a PACF e vimos como fica com base no EURUSD D1 diferenciado para uma parte específica do histórico. Cada barra do histograma descreve o efeito das barras com o atraso correspondente na barra atual (ou seja, em toda a amostra, em pares entre barras com índices diferentes do valor do intervalo). As duas linhas curvas tracejadas acima e abaixo indicam os limites do intervalo de confiança de 95%. A maioria das leituras da PACF fica dentro do intervalo, mas algumas ficam fora dos seus limites. A rigor, ao formar vetores de entrada, faz sentido, em primeiro lugar, coletar amostras com valores grandes, pois indicam a conexão da nova barra e das barras anteriores correspondentes. Em outras palavras, no vetor y poderíamos adicionar nem todas as amostras anteriores em sequência, mas, sim, por exemplo, as 6ª, 8ª e 50ª, como na imagem do último artigo. No entanto, essa situação é típica apenas para uma amostra específica. Se tomarmos, não 500 barras D1, mas, sim, 1000 ou 250, obteremos uma nova PACF com outros "picos". Assim, o “afinamento” das amostras da série inicial precisará ser feito durante qualquer alteração de dados, e isso, por sua vez, exigirá uma otimização das configurações da LS-SVM (em particular, dos parâmetros gama e sigma). Por isso, a fim de aumentar a universalidade do algoritmo, embora permitindo alguma perda de eficiência, foi decidido formar vetores de entrada a partir de todas as barras consecutivas com base numa determinada profundidade p, para que nesta seção inicial da PACF haja um intervalo de confiança dos principais "aumentos repentinos". Na prática, isso significa p variando de 20 a 50 barras, para EURUSD D1.

Por fim, vale ressaltar que a complexidade computacional da LS-SVM depende quadraticamente do comprimento da amostra N, pois o tamanho da matriz é (N+1)*(N+1). Para amostras de várias centenas e milhares de barras, isso pode afetar adversamente o desempenho. Existem muitos tipos de LS-SVMs que tentam enfrentar essa "maldição dimensional". Um deles, por exemplo, envolve primeiro agrupar todos os vetores usando uma rede neural de Kohonen (SOM) e, em seguida, realizar o treinamento de modelos M individuais para cada cluster (M é o número de clusters).

Eu sugiro uma abordagem diferente. Após agrupar o conjunto inicial de vetores por meio da rede SOM, os clusters encontrados serão usados como kernels em vez dos vetores originais. Por exemplo, uma amostra de 1000 vetores pode ser representada numa camada Kohonen 7*7, ou seja, 49 vetores de referência, que fornecem, em média, cerca de 20 amostras iniciais para cada célula da rede.

A rede Kohonen já foi discutida nos artigos "Uso prático das redes neurais Kohonen na negociação algorítmica (Parte I, Parte II), portanto, é relativamente fácil integrá-lo ao mecanismo LS-SVM.

Agora, implementemos o algoritmo em MQL.

LS-SVM em MQL

Reduziremos todos os cálculos a uma classe LSSVM, que usará os "solucionadores" lineares da biblioteca ALGLIB. Portanto, vamos anexá-la ao código fonte e à biblioteca CSOM.

  #include <Math/Alglib/dataanalysis.mqh>
  #include <CSOM/CSOM.mqh>

Na classe, fornecemos armazenamento de todos os vetores de entrada e matrizes LS-SVM:

  class LSSVM
  {
    protected:
      double X[];
      double Y[];
      double Alpha[];
      double Omega[];
      double Beta;
      
      double Sigma;
      double Sigma22; // 2 * Sigma * Sigma;
      double Gamma;
      
      int VectorNumber;
      int VectorSize;
      int Offset;
      int DifferencingOrder;
      ...

A classe preencherá X e Y com dados de cotações, guiada pelo número de vetores VectorNumber, tamanho VectorSize e deslocamento no histórico Offset (por padrão, 0 é o preço mais recente), tudo isso é passado através dos parâmetros para o construtor.

A classe suporta o processamento não apenas da série original (DifferencingOrder равно 0), mas também sua diferença de ordens de 1 a 3. Mais para frente, as nuances dessa técnica serão discutidas em mais detalhes.

O armazenamento em cluster opcional usando a rede Kohonen é fornecido pelo objeto KohonenMap e os clusters encontrados entram na matriz Kernels.

      double Kernels[];  // SOM clusters
      int KernelNumber;
      CSOM KohonenMap;
      ...

O tamanho da rede (é assumida uma camada quadrada, ou seja, o KernelNumber deve ser o quadrado de um número inteiro) é definido pelo usuário e esse parâmetro também pode ser otimizado. Se KernelNumber for 0 (o padrão) ou o número total de vetores, o SOM será desativado e entrará em jogo o processamento padrão usando LS-SVM. O trabalho com a rede está além do escopo do artigo; aqueles que desejam podem se familiarizar com os métodos de preparação, treinamento e integração nos códigos fonte anexados. Observe que a rede é inicialmente aleatória e, portanto, para obter resultados reproduzíveis, é necessário chamar srand com um valor específico.

Por padrão, os dados são lidos a partir das séries temporais de preços de abertura no método buildXYVectors. Neste artigo, trabalharemos apenas com eles. O método feedXYVectors é fornecido para a inserção de dados arbitrários, mas não foi testado.

    bool buildXYVectors()
    {
      ArrayResize(X, VectorNumber * VectorSize);
      ArrayResize(Y, VectorNumber);
      double open[];
      int k = 0;
      const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y
      CopyOpen(_Symbol, _Period, Offset, size, open);
      
      double diff[];
      ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction
      
      for(int i = 0; i < VectorNumber; i++)     // loop through anchor bars
      {
        for(int j = 0; j < VectorSize; j++)     // loop through successive bars
        {
          differentiate(open, i + j, diff);
          
          X[k++] = diff[0];
        }
        
        differentiate(open, i + VectorSize, diff);
        Y[i] = diff[0];
      }
      
      return true;
    }

O método auxiliar diferenciado chamado aqui permite calcular a diferença em ordem arbitrária para a matriz passada: o resultado é retornado através da matriz diff, cujo comprimento é 1 vez maior que o DifferencingOrder.

    void differentiate(const double &open[], const int ij, double &diff[])
    {
      for(int q = 0; q <= DifferencingOrder; q++)
      {
        diff[q] = open[ij + q];
      }
      
      int d = DifferencingOrder;
      while(d > 0)
      {
        for(int q = 0; q < d; q++)
        {
          diff[q] = diff[q + 1] - diff[q];
        }
        d--;
      }
    }

A classe suporta a normalização de vetores subtraindo a média e dividindo pelo desvio padrão no método normalizeXYVectors (não mostrado aqui).

A classe também possui alguns métodos para calcular núcleos, tanto para vetores de X[] por seus índices quanto para vetores externos, por exemplo:

    double kernel(const double &x1[], const double &x2[]) const
    {
      double sum = 0;
      for(int i = 0; i < VectorSize; i++)
      {
        sum += (x1[i] - x2[i]) * (x1[i] - x2[i]);
      }
      return exp(-1 * sum / Sigma22);
    }

O cálculo da matriz omega é realizado pelo método buildOmega (usa o método kernel com acesso aos vetores X[] por índice):

    void buildOmega()
    {
      KernelNumber = VectorNumber;
      
      ArrayResize(Omega, VectorNumber * VectorNumber);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        for(int j = i; j < VectorNumber; j++)
        {
          const double k = kernel(i, j);
          Omega[i * VectorNumber + j] = k;
          Omega[j * VectorNumber + i] = k;
          
          if(i == j)
          {
            Omega[i * VectorNumber + j] += 1 / Gamma;
            Omega[j * VectorNumber + i] += 1 / Gamma;
          }
        }
      }
    }

A solução direta do sistema de equações e a obtenção dos coeficientes desejados "alfa" e "beta" ocorrem no método resolveSoLE.

    bool solveSoLE()
    {
      // |  0              |1|             |   |  Beta   |   |  0  |
      // |                                 | * |         | = |     |
      // | |1|  |Omega| + |Identity|/Gamma |   | |Alpha| |   | |Y| |
      
      CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1);
      
      for(int i = 1; i <= KernelNumber; i++)
      {
        for(int j = 1; j <= KernelNumber; j++)
        {
          MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]);
        }
      }
      
      MATRIX[0].Set(0, 0);
      for(int i = 1; i <= KernelNumber; i++)
      {
        MATRIX[i].Set(0, 1);
        MATRIX[0].Set(i, 1);
      }
      
      double B[];
      ArrayResize(B, KernelNumber + 1);
      B[0] = 0;
      for(int j = 1; j <= KernelNumber; j++)
      {
        B[j] = Y[j - 1];
      }
      
      int info;
      CDenseSolverLSReport rep;
      double x[];
      
      CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x);
      
      Beta = x[0];
      ArrayResize(Alpha, KernelNumber);
      ArrayCopy(Alpha, x, 0, 1);
      
      return true;
    }

O principal método de classe para executar a regressão é process. A partir disso, inicia-se a formação dos dados de entrada/saída, normalização, cálculo da matriz ômega, solução do sistema de equações e obtenção de erros da amostra.

    bool process()
    {
      if(!buildXYVectors()) return false;
      normalizeXYVectors();
      
      // least squares linear regression for demo purpose only
      if(KernelNumber == -1 || KernelNumber > VectorNumber)
      {
        return regress();
      }
      
      if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
      {
        buildOmega();
      }
      else                                                  // proposed SOM-LS-SVM
      {
        if(!buildKernels()) return false;
      }
      if(!solveSoLE()) return false;
      
      LSSVM_Error result;
      checkAll(result);
      ErrorPrint(result);
      return true;
    }

Para avaliar a qualidade da otimização na classe, são utilizados vários indicadores que são calculados automaticamente para todo o conjunto de dados: erro de desvio padrão, coeficiente de correlação, coeficiente de determinação (R-squared) e % de coincidência no sinal (faz sentido apenas em modos diferenciados). Todos os indicadores estão resumidos na estrutura LSSVM_Error:

    struct LSSVM_Error
    { // indices: 0 - training set, 1 - test set
      double RMSE[2]; // RMSE
      double CC[2];   // Correlation Coefficient
      double R2[2];   // R-squared
      double PCT[2];  // %
    };

O índice zero de matrizes corresponde ao conjunto de treinamento, primeiro, ao conjunto de testes. Seria desejável usar uma avaliação mais rigorosa da significância estatística da previsão, por exemplo, com um teste de Fisher, já que uma correlação bonita ou valores de R2 podem ser enganosos, mas, é necessário considerar que nem sempre é possível usar todas as ferramentas de uma só vez.

O método de cálculo do erro para toda a amostra é checkAll.

    void checkAll(LSSVM_Error &result)
    {
      result.RMSE[0] = result.RMSE[1] = 0;
      result.CC[0] = result.CC[1] = 0;
      result.R2[0] = result.R2[1] = 0;
      result.PCT[0] = result.PCT[1] = 0;
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      double out[];
      getResult(out);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        double given = Y[i];
        double trained = out[i];
        result.RMSE[0] += (given - trained) * (given - trained);
        // mean is 0 after normalization
        xy += (given) * (trained);
        x2 += (given) * (given);
        y2 += (trained) * (trained);
        
        if(given * trained > 0) correct++;
      }
      
      result.R2[0] = 1 - result.RMSE[0] / x2;
      result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber);
      result.CC[0] = xy / sqrt(x2 * y2);
      result.PCT[0] = correct * 100.0 / VectorNumber;
      
      crossvalidate(result); // fill metrics for test set (if attached)
    }

Antes do ciclo, é chamado o método getResult, que executa a aproximação para todos os vetores de entrada e preenche a matriz out com esses valores.

    void getResult(double &out[], const bool reverse = false) const
    {
      double data[];
      ArrayResize(out, VectorNumber);
      for(int i = 0; i < VectorNumber; i++)
      {
        vector(i, data);
        out[i] = approximate(data);
      }
      if(reverse) ArrayReverse(out);
    }

Ele usa a função de previsão padrão para um modelo já construído, approximate:

    double approximate(const double &x[]) const
    {
      double sum = 0;
      double data[];
      
      if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference)
      {
        for(int i = 0; i < ArraySize(x); i++)
        {
          sum += Solution[i] * x[i];
        }
        sum += Solution[ArraySize(x)];
      }
      else
      {
        if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
        {
          for(int i = 0; i < VectorNumber; i++)
          {
            vector(i, data);
            sum += Alpha[i] * kernel(x, data);
          }
        }
        else                                                  // proposed SOM-LS-SVM
        {
          for(int i = 0; i < KernelNumber; i++)
          {
            ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize);
            sum += Alpha[i] * kernel(x, data);
          }
        }
      }
      return sum + Beta;
    }

Nele, os coeficientes encontrados Alpha[] e Beta são aplicados à soma das funções nucleares (casos LS-SVM e SOM-LS-SVM).

Uma amostra de teste é formada da mesma maneira que uma amostra de treinamento: com a ajuda de outro objeto LSSVM e, no objeto principal, é definida uma referência ao "teste".

  protected:
    LSSVM *crossvalidator;
  
  public:
    bool bindCrossValidator(LSSVM *tester)
    {
      if(tester.getVectorSize() == VectorSize)
      {
        crossvalidator = tester;
        return true;
      }
      return false;
    }
    
    void crossvalidate(LSSVM_Error &result)
    {
      const int vectorNumber = crossvalidator.getVectorNumber();
      
      double out[];
      double _Y[];
      crossvalidator.getY(_Y); // assumed normalized by validator
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      for(int i = 0; i < vectorNumber; i++)
      {
        crossvalidator.vector(i, out);
        
        double z = approximate(out);
        
        result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z);
        xy += (_Y[i]) * (z);
        x2 += (_Y[i]) * (_Y[i]);
        y2 += (z) * (z);
        
        if(_Y[i] * z > 0) correct++;
      }
      
      result.R2[1] = 1 - result.RMSE[1] / x2;
      result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber);
      result.CC[1] = xy / sqrt(x2 * y2);
      result.PCT[1] = correct * 100.0 / vectorNumber;
    }

A classe permite, se necessário, executar, em vez de uma otimização não linear pelo algoritmo LS-SVM / SOM-LS-SVM, uma regressão linear de mínimos quadrados num sistema com variáveis VectorSize e equações VectorNumber. Para fazer isso, é implementado o método regress.

    bool regress(void)
    {
      CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column
      
      for(int i = 0; i < VectorNumber; i++)
      {
        MATRIX[i].Set(VectorSize, Y[i]);
      }
      
      for(int i = 0; i < VectorSize; i++)
      {
        for(int j = 0; j < VectorNumber; j++)
        {
          MATRIX[j].Set(i, X[j * VectorSize + i]);
        }
      }
      
      CLinearModel LM;
      CLRReport AR;
      int info;
      
      CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR);
      if(info != 1)
      {
        Alert("Error in regression model!");
        return false;
      }
      
      int _size;
      CLinReg::LRUnpack(LM, Solution, _size);
      
      Print("RMSE=" + (string)AR.m_rmserror);
      ArrayPrint(Solution);
      
      return true;
    }

Obviamente, esse método perde a precisão do LS-SVM e é adicionado para demonstrar isso. Por outro lado, pode ser necessário para a regressão de dados de natureza mais simples do que cotações. A inclusão desse modo ocorre ao definir o KernelNumber = -1. Nesse caso, a solução é gravada na matriz Solution (Alpha[] e Beta não estão envolvidos nisso).

Vamos criar um indicador de previsão com base na classe LSSVM.

Indicador preditivo LS-SVM

A tarefa do indicador SOMLSSVM.mq5 é criar 2 objetos LSSVM (um para a amostra de treinamento e outro para a de teste), executar a regressão e exibir os valores iniciais e previstos com a avaliação da qualidade da previsão em ambas as amostras. Os parâmetros gama e sigma serão considerados já selecionados e definidos pelo usuário. É mais conveniente otimizá-los num EA usando o testador regular (a próxima seção será dedicada a isso). Em princípio, o testador também pode suportar o otimização de indicadores, uma vez que, essa restrição é artificial. Nesse sentido, podemos otimizar o modelo diretamente no indicador.

O indicador terá 4 buffers numa janela separada. 2 buffers exibirão os valores originais e previstos para a amostra de treinamento e 2 outros buffers exibirão os mesmos para a amostra de teste.

Parâmetros de entrada:

  input int _VectorNumber = 250; // VectorNumber (training)
  input int _VectorNumber2 = 50; // VectorNumber (validating)
  input int _VectorSize = 20; // VectorSize
  input double _Gamma = 0; // Gamma (0 - auto)
  input double _Sigma = 0; // Sigma (0 - auto)
  input int _KernelNumber = 0; // KernelNumber (0 - auto)
  input int _TrainingOffset = 50; // Offset of training bars
  input int _ValidationOffset = 0; // Offset of validation bars
  input int DifferencingOrder = 1;

Os dois primeiros definem o tamanho das amostras de treinamento e teste. O tamanho do vetor é especificado em VectorSize. Os parâmetros Gamma e Sigma podem ser deixados iguais a 0 para a seleção automática de seus valores com base nos dados de entrada, mas a qualidade desse modo trivial está longe de ser ótima, ele é necessário apenas para que o indicador funcione com os valores padrão. KernelNumber deve ser deixado como 0 para regressão usando o método LS-SVM. Por padrão, o conjunto de testes está localizado no final do histórico de cotações e o conjunto de treinamento fica à esquerda dele (cronologicamente antes).

Com base nos parâmetros de entrada, são inicializados os objetos.

  LSSVM *lssvm = NULL;
  LSSVM *test = NULL;
  
  int OnInit()
  {
    static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"};
    
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetString(i, PLOT_LABEL, titles[i]);
    }
    
    lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset);
    test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset);
    lssvm.setDifferencingOrder(DifferencingOrder);
    test.setDifferencingOrder(DifferencingOrder);
    
    return INIT_SUCCEEDED;
  }

O indicador é calculado apenas uma vez, pois é criado para fins de demonstração. Se necessário, é fácil adaptá-lo para que as leituras sejam atualizadas em cada barra.

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {
    ArraySetAsSeries(Open, true);
    ArraySetAsSeries(Time, true);
    
    static bool calculated = false;
    if(calculated) return rates_total;
    calculated = true;
    
    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }
    
    lssvm.bindCrossValidator(test);
    bool processed = lssvm.process(true);

No manipulador OnCalculate, anexamos o conjunto de testes ao conjunto de treinamento e executamos a regressão. Se for bem-sucedida, exibimos todos os dados: as previsões inicial e a recebida:

  if(processed)
  {
    const double m1 = lssvm.getMean();
    const double s1 = lssvm.getStdDev();
    const double m2 = test.getMean();
    const double s2 = test.getStdDev();
    
    // training
    
    double out[];
    lssvm.getY(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[0].set(_TrainingOffset, out);
    
    lssvm.getResult(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[1].set(_TrainingOffset, out);
    
    // validation
    
    test.getY(out, true);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      out[i] = out[i] * s2 + m2;
    }
    
    buffers[2].set(_ValidationOffset, out);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      test.vector(i, out);
      
      double z = lssvm.approximate(out);
      z = z * s2 + m2;
      buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z;
      ...
    }
  }

Como temos a opção de analisar uma série diferenciada, o indicador é exibido numa janela separada. No entanto, de fato, ainda trabalhamos com preços e é aconselhável exibir a previsão no gráfico principal. Para fazer isso, podemos usar objetos. Suas coordenadas ao longo do eixo dos preços devem ser restauradas a partir da série de diferenças. A indexação de elementos na série original e na série de diferenças de diferentes ordens derivadas é ilustrada pelo seguinte esquema (indexação em ordem cronológica):

    d0:  0   1   2   3   4   5  :y
    d1:    0   1   2   3   4
    d2:      0   1   2   3
    d3:        0   1   2

Por exemplo, se a diferença de primeira ordem (d1), é óbvio que:

y[i+1] = y[i] + d1[i]

Para as diferenças da segunda (d2) e terceira (d3) ordens, as equações serão as seguintes:

y[i+2] = 2 * y[i+1] - y[i] + d2[i]

y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]

Vemos que quanto maior a ordem de diferenciação, maior o número de amostras anteriores y envolvido nos cálculos.

Aplicando essas fórmulas, podemos descrever a previsão por objetos no gráfico de preços.

      if(ShowPredictionOnChart)
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2]
                 + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z;
        }
        else
        {
          // unsupported yet
        }
        
        string name = prefix + (string)i;
        ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target);
        ObjectSetString(0, name, OBJPROP_TEXT, "l");
        ObjectSetString(0, name, OBJPROP_FONT, "Wingdings");
        ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER);
        ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed);
      }

Ordens superiores a 3 não foram consideradas, uma vez que possuem não apenas um efeito positivo, mas também um efeito negativo. Lembremo-nos de que o positivo é que a qualidade da previsão aumenta com o aumento da ordem devido ao aumento da estacionariedade. No entanto, isso se aplica precisamente à previsão de uma derivada da ordem correspondente, e não à série inicial. O efeito negativo da diferenciação de ordens mais altas é que mesmo um erro muito pequeno aumenta significativamente com o subsequente "desdobramento" de incrementos nas séries integradas. Portanto, para o parâmetro DifferencingOrder, você também deve encontrar o meio-termo por meio de otimização ou seleção.

Ambos os efeitos podem ser observados nas duas capturas de tela a seguir (linha verde e verde clara - dados reais das amostras de treinamento e de teste; linha ciano e azul - previsão para as amostras de treinamento e de teste):

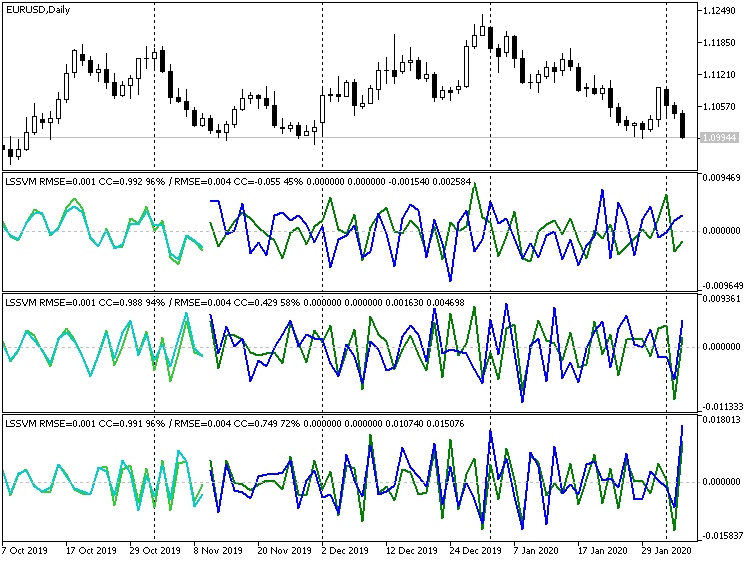
Indicadores LSSVM com ordem de diferenciação diferente da série EURUSD D1

Aqui são mostrados 3 exemplos do indicador com configurações gerais e com diferentes ordens de diferenciação. Configurações gerais:

• _VectorNumber = 250; // VectorNumber (training)
• _VectorNumber2 = 60; // VectorNumber (validating)
• _VectorSize = 20; // VectorSize
• _Gamma = 2048; // Gamma (0 - auto)
• _Sigma = 8; // Sigma (0 - auto)
• _KernelNumber = 0; // KernelNumber (0 - auto)
• _TrainingOffset = 60; // Offset of training bars
• _ValidationOffset = 0; // Offset of validation bars

A ordem de diferenciação é 1, 2 e 3, respectivamente. Na barra de título de cada janela, após a linha oblíqua, são exibidos os indicadores de previsão para a amostra de teste (neste caso, validação): eles aumentam para melhor (coeficiente de correlação: -0,055, 0,429, 0,749; porcentagem de sinais de incremento correspondentes: 45%, 58%, 72%). Em princípio, a melhoria na coincidência da linha é visível mesmo visualmente. No entanto, se restaurarmos a previsão de terceira ordem para o gráfico de preços, obteremos a seguinte imagem:

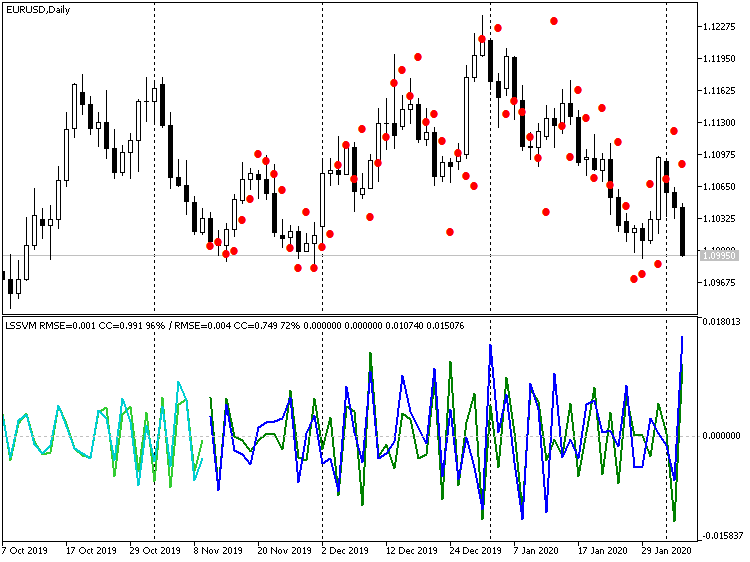
Indicador LSSVM da terceira ordem de diferenciação com os valores restaurados da previsão de preço EURUSD D1

Obviamente, muitos pontos podem ser descritos como aumentos repentinos. Por outro lado, se desativarmos completamente a diferenciação, obteremos:

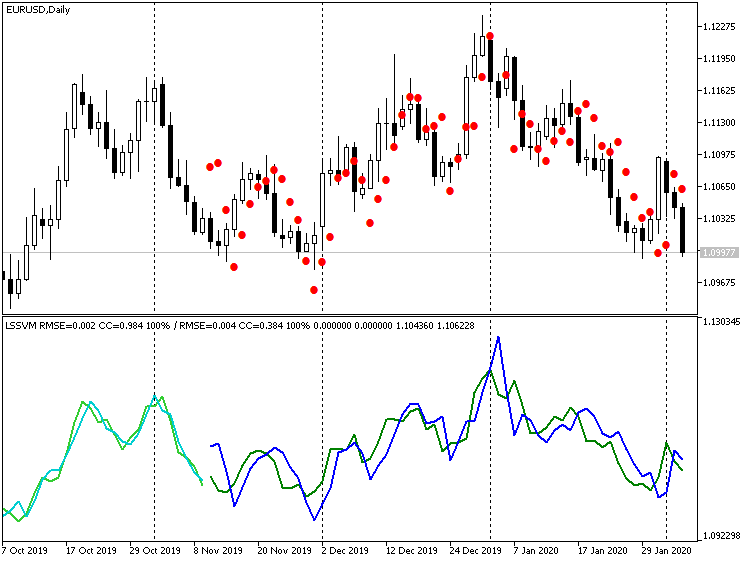
Indicador LSSVM sem diferenciação com os valores restaurados da previsão de preço EURUSD D1

Aqui, os valores dos preços estão muito mais próximos dos reais, mas é perceptível um atraso da previsão segundo a fase em cerca de 1 barra. Esse efeito é explicado pelo fato de que nosso algoritmo é realmente equivalente a um filtro digital, um tipo de média móvel baseada em N vetores de amostra. Dada a semelhança no nível de preços, faz sentido com que esse atraso de 1 a 2 barras seja nivelado prevendo vários passos adiante de uma só vez, ou seja, depois de receber a previsão para -1 barra, assumir como uma entrada para a previsão de -2 barras e assim por diante. Forneceremos esse modo ao criar um EA na próxima seção.

Expert Advisor LS-SVM

O Expert Advisor LSSVMbot.mq5 serve para realizar duas tarefas:

• otimização dos parâmetros "gama" e "sigma" LS-SVM no modo virtual (sem negociação);
• negociação no testador e otimização opcional de outros parâmetros no modo de negociação;

No modo virtual, bem como no indicador, são usadas 2 instâncias do LSSVM: uma contendo uma amostra de treinamento e outra com uma de teste. São os indicadores da amostra de teste que são levados em consideração. A otimização é realizada de acordo com critérios personalizados. Todos eles estão listados na enumeração:

  enum CUSTOM_ESTIMATOR
  {
    RMSE,   // RMSE
    CC,     // correlation
    R2,     // R-squared
    PCT,    // %
    TRADING // trading
  };

A opção TRADING é usada para colocar um EA no modo de negociação. Nela, o EA pode ser otimizado da maneira usual, de acordo com um dos critérios internos (lucro, rebaixamento, etc.).

O grupo principal de parâmetros de entrada define os mesmos valores que no indicador.

  input int _VectorNumber = 250;  // VectorNumber (training)
  input int _VectorNumber2 = 25;  // VectorNumber (validating)
  input int _VectorSize = 20;     // VectorSize
  input double _Gamma = 0;        // Gamma (0 - auto)
  input double _Sigma = 0;        // Sigma (0 - auto)
  input int _KernelNumber = 0;    // KernelNumber (sqrt, 0 - auto)
  input int DifferencingOrder = 1;
  input int StepsAhead = 0;

No entanto, os deslocamentos TrainingOffset e ValidationOffset se tornaram variáveis internas e são definidas automaticamente. ValidationOffset é sempre 0. TrainingOffset é igual ao tamanho da amostra de teste VectorNumber2 no modo virtual ou 0 no modo de negociação (pois implica que todos os parâmetros já foram encontrados, não há amostra de teste e a regressão deve ser feita com os dados mais recentes).

Para usar o SOM no parâmetro KernelNumber, é necessário especificar o tamanho de um lado, enquanto o tamanho total do mapa será calculado como o quadrado desse valor.

O segundo grupo de parâmetros de entrada é projetado para otimizar gama e sigma:

  input int _GammaIndex = 0;     // Gamma Power Iterator
  input int _SigmaIndex = 0;     // Sigma Power Iterator
  input double _GammaStep = 0;   // Gamma Power Multiplier (0 - off)
  input double _SigmaStep = 0;   // Sigma Power Multiplier (0 - off)
  input CUSTOM_ESTIMATOR Estimator = R2;

Como o intervalo de pesquisa é muito amplo e o testador regular oferece suporte à iteração apenas adicionando uma determinada etapa, o EA usa a seguinte abordagem. A otimização deve ser ativada pelos parâmetros GammaIndex e SigmaIndex. Cada um deles determina quantas vezes é preciso multiplicar os valores iniciais de Gamma e Sigma pelos fatores GammaStep e SigmaStep, respectivamente, para obter o valor de trabalho "gama" e "sigma". Por exemplo, se Gamma é 1, GammaStep é 2 e a otimização é executada para GammaIndex no intervalo de 0 a 5, o algoritmo avaliará os valores de gama de 1, 2, 4, 8, 16, 32. Se GammaStep e SigmaStep não forem iguais a 0, eles sempre serão usados para calcular os valores operacionais de "gama" e "sigma", inclusive durante uma única execução do testador.

O EA trabalha com base em barras. O EA inicia o cálculo não antes que o número solicitado de barras (vetores) esteja disponível no histórico. Se não houver barras suficientes no testador, a execução poderá terminar em vão, vejas os logs. Infelizmente, o número de barras de histórico carregadas pelo testador durante a inicialização depende de muitos fatores (período gráfico, números de dias dentro do ano etc.) e pode variar significativamente. Se necessário, desloque o tempo inicial do teste para o passado.

No modo virtual, o modelo é treinado apenas uma vez; uma das características (selecionadas no parâmetro Estimator) é retornada da função OnTester como um indicador de qualidade (se for selecionado RMSE, o erro será retornado com o sinal oposto).

  bool optimize()
  {
    if(Estimator != TRADING) lssvm.bindCrossValidator(test);
    iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep);
    bool success = lssvm.process();
    if(success)
    {
      LSSVM::LSSVM_Error result;
      lssvm.checkAll(result);
      
      Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma());
      Print("  training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]);
      Print("  test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]);
      
      customResult = Estimator == CC ? result.CC[1]
                  : (Estimator == RMSE ? -result.RMSE[1] // the lesser |absolute error value| the better
                  : (Estimator == PCT ? result.PCT[1] : result.R2[1]));
    }
    return success;
  }
  
  void OnTick()
  {
    ...
    if(Estimator != TRADING)
    {
      if(!processed)
      {
        processed = optimize();
      }
    }
    ...
  }
  
  double OnTester()
  {
    return processed ? customResult : -1;
  }

No modo de negociação, o modelo também é treinado por padrão apenas uma vez, mas é possível definir a reconstrução a cada ano, trimestre ou mês. Para fazer isso, escreva OPTIMIZATION (no código ele chamado de _2), respectivamente, "y", "q" ou "m" (letras maiúsculas também são suportadas). Lembre-se de que esse processo afeta apenas a solução do sistema de equações com base em novos dados, mas os parâmetros gama e sigma permanecem os mesmos. Em princípio, é possível complicar o processo e selecionar parâmetros durante cada aprendizado (o que confiamos anteriormente ao otimizador habitual), mas isso deve ser feito pelo EA e, portanto, será executado por um único fluxo.

Agora está implícito que os parâmetros "gama" e "sigma", selecionados para dados durante um período suficientemente longo (ano ou mais), não devem perder sua relevância durante períodos de negociação de menor duração.

Após a construção do modelo, uma instância de teste do LSSVM é usada para ler os preços conhecidos mais recentes, gerear um vetor de entrada a partir deles e normalizá-lo. Em seguida, o vetor é passado para o método lssvm.approximate:

    static bool solved = false;
    if(!solved)
    {
      const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0);
      solved = opt ? optimize() : lssvm.process();
    }
    
    if(solved)
    {
      // test is used to read latest _VectorNumber2 prices
      if(!test.buildXYVectors())
      {
        Print("No vectors");
        return;
      }
      test.normalizeXYVectors();
      
      double out[];
      
      // read latest vector
      if(!test.buildVector(out))
      {
        Print("No last price");
        return;
      }
      test.normalizeVector(out);
      
      double z = lssvm.approximate(out);

Dependendo do parâmetro de entrada StepsAhead, o EA quer usa imediatamente o valor obtido de z, convertendo-o numa previsão de preço por meio de desnormalização, quer repete a previsão um número especificado de vezes e só depois a converte em preço.

      for(int i = 0; i < StepsAhead; i++)
      {
        ArrayCopy(out, out, 0, 1);
        out[ArraySize(out) - 1] = z;
        z = lssvm.approximate(out);
      }
      
      z = test.denormalize(z);

Como a série temporal pode ser diferenciada, usamos os últimos valores de preço para restaurar o próximo valor de preço e o incremento da previsão.

      double open[];
      if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = open[2] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * open[2] - open[1] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * open[2] - 3 * open[1] + open[0] + z;
        }
        else
        {
          // unsupported yet
        }

Dependendo da posição do preço previsto em relação ao nível atual, o EA abre uma transação. Se já estiver aberta uma posição na direção desejada, ela será salva. Se a posição estiver na direção oposta, será feita uma reversão.

        int mode = target >= open[2] ? +1 : -1;
        int dir = CurrentOrderDirection();
        if(dir * mode <= 0)
        {
          if(dir != 0) // there is an order
          {
            OrdersCloseAll();
          }
          
          if(mode != 0)
          {
            const int type = mode > 0 ? OP_BUY : OP_SELL;
            const double p = type == OP_BUY ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID);
            OrderSend(_Symbol, type, Lot, p, 100, 0, 0);
          }
        }
      }
    }

Verificaremos como o EA funciona nos dois modos. Como ferramenta de trabalho, adotamos o XAUUSD, como menos sujeito a notícias nacionais (em comparação com moedas). Período gráfico — D1.

O arquivo de configurações está anexado (LSSVMbot.set). O tamanho do conjunto de treinamento VectorNumber é escolhido voluntariamente como 200. Isso é um pouco menos de um ano. Grandes valores na região de 1000 já podem desacelerar significativamente a solução do sistema de equações. Conjunto de teste VectorNumber2=50. Tamanho do vetor VectorSize=20 (месяц). O SOM não é usado (KernelNumber=0). A diferenciação está desativada (DifferencingOrder=0), mas para o estágio de verificação no modo de negociação, a previsão está 2 passos à frente (StepsAhead=2), porque, com a ajuda do indicador, observamos um pequeno atraso na previsão em relação aos preços. No modo virtual, o parâmetro de entrada StepsAhead não é usado ao calcular o modelo.

Os valores base de Gamma e Sigma são iguais a 1, mas seus multiplicadores Power Multiplier (GammaStep, SigmaStep) são iguais a 2, e o número de multiplicações que são executadas durante o processo de otimização são especificados nos iteradores GammaIndex e SigmaIndex, respectivamente, como intervalos de 5 a 35 e de 5 até 20 em incrementos de 5. Assim, quando GammaIndex é igual a 15, Gamma obterá um valor igual a 1 * (2 à potência de 15), ou seja, 32768.

A seleção dos intervalos corretos para a pesquisa de "gama" e "sigma" é uma tarefa bastante rotineira, porque para ela, infelizmente, não há outra solução a não ser cálculos primeiro numa grade grossa e depois numa mais fina. Nós nos restringimos a uma grade, porque na preparação do artigo, foram feitas muitas amostras que podem ser consideradas uma pesquisa numa faixa mais ampla.

Portanto, existem apenas 2 parâmetros otimizados: GammaIndex e SigmaIndex. Eles alteram indiretamente Gamma e Sigma num intervalo amplo, com um passo variável exponencialmente.

Iniciamos a otimização com base em 2018, segundo preços de abertura. Fazemos otimização com base no critério personalizado, Estimator = R2.

Lembremo-nos de que o EA não negocia nesse modo, em vez disso, preenche um sistema de equações a partir de cotações e o resolve usando o algoritmo LS-SVM. O cálculo envolve uma quantidade suficiente de barras para formar VectorNumber de vetores de tamanho VectorSize, ajustados para possível diferenciação (cada ordem adicional para obter diferenças requer uma barra adicional nos dados de entrada). Além disso, o EA exige adicionalmente vetores de teste VectorNumber2, localizados cronologicamente após o treinamento, ou seja, nas barras mais recentes. É nas barras de teste (mais precisamente, os vetores formados a partir delas) que as habilidades preditivas do modelo resultante para retorno do OnTester são avaliadas.

Tudo isso é importante, pois o testador nem sempre possui um número suficiente de barras no histórico no início, e o EA poderá preencher o sistema apenas alguns meses após a data de início. Por outro lado, não esqueça que as barras de treinamento sempre começam antes da data do teste (otimização), pois o EA recebe imediatamente um histórico de um determinado comprimento.

Após a conclusão da otimização, classificamos os resultados pelo critério R2 (em ordem decrescente, ou seja, os melhores no topo). Suponhamos que, no início, irão as configurações GammaIndex=15 e SigmaIndex=5 ("suponhamos" porque é provável que a ordem dos passagens com resultados iguais mude).

Clique duas vezes no primeiro registro para executar um único teste (ainda no modo virtual). No log, veremos algo como o seguinte:

  2018.01.01 00:00:00   Bars required: 270
  2018.01.02 00:00:00   247 2017.01.03 00:00:00
  2018.02.02 00:00:00   Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270
  2018.02.02 00:00:00   G[15]=32768.0 S[5]=32.0
  2018.02.02 00:00:00   RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985
  2018.02.02 00:00:00   Parameters: 32768.0 32.0
  2018.02.02 00:00:00     training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0
  2018.02.02 00:00:00     test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0
  final balance 10000.00 USD
  OnTester result 0.9598497541714557

Isso pode ser interpretado da seguinte maneira: para concluir o procedimento completo, eram necessárias 270 barras, mas no início do 01.08.2018 apenas 247 estavam disponíveis. Um número suficiente apareceu apenas em 2018.02.02 (ou seja, um mês depois), e os dados de treinamento (histórico disponível) começaram em 01.01.03.03. A seguir estão os parâmetros operacionais de Gamma e Sigma (G[15]=32768.0 S[5]=32.0, entre colchetes estão os parâmetros-iteradores otimizados). Finalmente, na linha com os indicadores da qualidade do treinamento, vemos o valor de R2 (0,95985), que foi retornado do OnTester.

Agora desativamos a otimização, expandimos o período de 2017 a fevereiro de 2020, definimos Estimator = TRADING nos parâmetros do EA (isso significa que o EA executará operações de negociação). No parâmetro OPTIMIZATION (no código, _2), introduzimos o símbolo "q", que instrui o EA a recalcular o modelo de regressão uma vez por trimestre com base nos novos dados (os vetores VectorNumber mais recentes). Mas a gama e o sigma permanecem os mesmos.

Executamos um único teste.

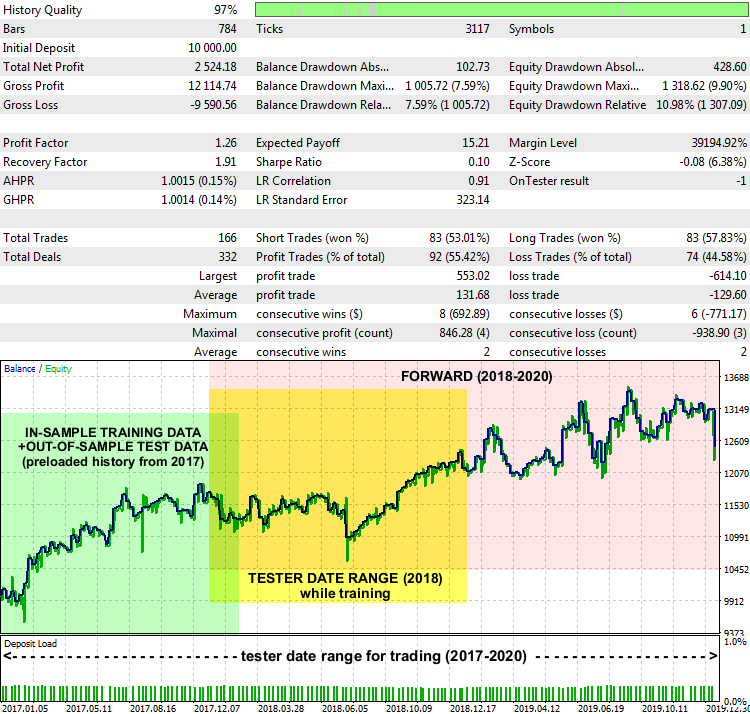
Relatório do EA LSSVMbot com base no XAUUSD D1, 2017-2020

Os indicadores não são excelentes, mas o sistema como um todo funciona. No gráfico do relatório são destacados os intervalos de datas de onde os dados de treinamento foram obtidos para encontrar a gama e o sigma ideais (destacados em verde), o intervalo definido no testador no modo de treinamento (destacado em amarelo) e o intervalo em que o EA negociou com base em dados desconhecidos (destacado em rosa).

O método de interpretar a previsão e criar uma estratégia de negociação em torno dela pode ser diferente. Em particular, nosso EA de testes possui um parâmetro de entrada PreviousTargetCheck (false por padrão). Se for ativado, a negociação de previsão será realizada usando uma estratégia diferente: a direção da transação será determinada pela posição relativa da nova previsão em relação à anterior. Também há espaço para experimentos com outras configurações, como com o clustering do SOM, com a alteração do lote dependendo da força do movimento previsto, etc.

Fim do artigo

Neste artigo, abordamos um algoritmo de previsão de séries temporais baseado em LS-SVM, que requer o uso ativo de modelos matemáticos e ajustes cuidadosos. O uso bem-sucedido de métodos semelhantes (EMD e LS-SVM) na prática pode depender muito das particularidades das séries temporais e, no que diz respeito ao trading, depende da natureza do instrumento financeiro e do período gráfico. Por isso, a escolha de um mercado que seja adequado às capacidades de um algoritmo específico não é menos importante do que a implementação de cálculos que usem intensivamente recursos e alta tecnologia. Em particular, as moedas são ativos menos previsíveis e mais suscetíveis a choques externos, o que reduz a eficácia da previsão com base apenas em dados históricos. Metais, índices ou cestas balanceadas devem ser considerados mais adequados para os dois métodos considerados. Além disso, não importa quão maravilhosa possa parecer a previsão, não se deve esquecer do gerenciamento de riscos, de ordens stop e do monitoramento de notícias.

Os códigos fonte fornecidos permitem incorporar novos métodos em seus próprios projetos MQL.