Forecasting Time Series (Part 2): Least-Square Support-Vector Machine (LS-SVM)

Keywords: LS-SVM, SOM-LS-SVM, SOM

Introduction

In this article, we will continue telling about the algortihms of forecasting times series. In Part 1, we presented the method of forecasting empiric mode decomposition (EMD) and indicator TSA for the statistical analysis of times series. In this second part, the object of our studies is the support-vector machine (SVM) in its version named Least-squares support-vector machine ( LS-SVM)). This technology has not been implemented in MQL yet. But first, we have to get to know math for it.

Math for LS-SVM

Support Vector Machine (SVM) is an umbrella term for a group of data analysis algorithms used in classification and regression. It is regression that is of special interest for us (article in Wikipedia in English), because it identifies the interrelation between regressands and predictors. Forecasting problem can be stated through regression as finding a certain function depending on the previous counts of the time series (predictors mentioned above), so that its values describe the future counts of the time series as reasonably as possible.

SVM algorithm is based on transferring source data into a space of higher dimensionality, where each input vector is formed as a sequence of seed points with time delays. Then these vectors are used as key samples that, being combined in a special manner, allow computing a regression hyperplane defining the data distribution with a specified accuracy. These computations represent a summarization by all samples of the so-called "kernels", i.e., the uniform functions of inputs. These functions may be linear or nonlinear (normally bell-shaped) and guided by the parameters affecting the accuracy of regression. Most common kernels are:

• Linear ;
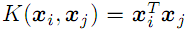• d-degree polynomial;
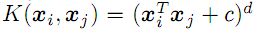• Radial basis function with the sigma dispersion (Gaussian, see below);
• Sigmoid (hyperbolic tangent) ;

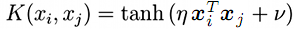There is a SVM modification, Least-Squares SVM (LS-SVM), or least-squares support-vector method. It allows to solve a problem as a system of linear equations, instead of solving the equivalent initial non-linear problem.

Suggest we have a time series, y, and we suppose that we can get to know its value at moment t as a function of p of preceding points and some external q variables, with error e. In general, this will be written as follows:

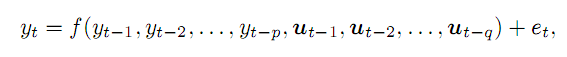 (1)

External variables (in the applied trading) can be exemplified by the week day number, day hour number, or the relevant bar volume. In this article, we will be limited by only the preceding points of a price time series. Complexity of the material does not allow considering all the aspects.

Taken from the series, p preceding points form a vector in the p-dimensional space. Moving along the initial series from left to right, we will get a set of predictor vectors that we will denote as x; for the time moment t, their compliance with the forecast y is expressed as follows:

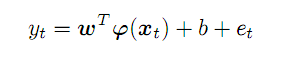 (2)

Unknown vector of coefficients w and transforming functions f work in an abstract feature space, the dimensionality of which is potentially unlimited and can even be higher than p, while appearance f, as well as the values of coefficients w, should exactly be found in the process of optimization:

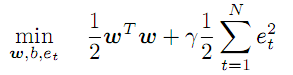 (3)

This condition prescribes minimizing the value of coefficients w and introduces the regularizing/penalty factor, gamma, for error rates. The larger the gamma is, the more accurately regression must approximate the source data. If the gamma decreases, the tolerance of deviations increases, thereby increasing the model smoothness.

System of equations (2) acts as limitations for all t's from 1 to N (number of vectors).

To facilitate the problem, mathematical "tricks" are used (one of them is even called "kernel trick"): Instead of the initial optimization problem, they solve the so-called dual one that is essentially equivalent, in which we manage to eliminate coefficients w and transformations f in exchange for kernel functions (see below). As a result, solution is reduced to linear system:

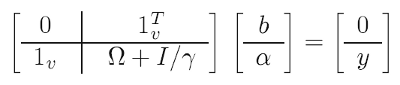 (4)

Known data in it:

• y - вvector consisting of all the target (training) values of the forecast;
• 1 - unit vector (row and column);
• I - unit matrix;
• gamma - regularizing parameter described above (to be searched guided by the forecast quality on a test set);
• omega - matrix calculated by the following formula:

 (5)

And here, we finally see the kernel functions, K, announced above and computed on the pairwise combinations among all input vectors x. For a radial basis function as a symmetric Gaussian (we are going to use it), formula K appears as follows:

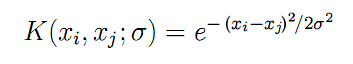 (6)

Parameter "sigma" desctibes the bell width — it is another parameter that should be searched iteratively in practice. The larger the sigma is, the larger number of "neighboring" vectors will be involved in regression. Where sigma is small, the function goes, in fact, exactly along the points of the training data set and stops responding to unknown images, i.e., generalizing.

Using source data (x, y) and formulas (4), (5), and (6), we apply the least-squares method to obtain all the unknown ones:

• b - intercept term involved in (2) and (7);
• a - vector of "alpha" coefficients included in the final regression model formula:

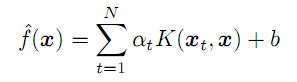 (7)

For any arbitrary vector x (not from the training set), it allows computing the forecast as the sum of products of "alpha" coefficients and kernels for all source N vectors, as adjusted for the intercept term b.

There remain to answer 2 questions in the theoretical part. First, how do we know the free parameters, "Gamma" and "sigma"? Second, what depth should we choose for time delays p to form input vectors x from the series of quotes?

In fact, the parameters are found by the trial-and-error method: In the loop, we use a very broad two-dimensional value grid to evaluate the models for each combination and to assess its quality. Quality shall mean minimizing the forecast error on a test data set other than the training set. The process resembles and may involve optimization in the MetaTrader Tester. However, studying larger ranges will require to actually change values not at a fixed increment, but exponentially, i.e., using multiplying. Therefore, we will have to consider this aspect at the implementation stage.

As to the size of the input space p, it is recommended to define it based on the characteristics of the series to be forecasted, particularly using the partical autocorrelation function (PACF). In our next paper, we prepared tools for computing the PACF and saw how it appeared on a differentiated EURUSD D1 for a specific part of history. Each chart bar describes how the bars with the relevant time lag affect the current bar (i.e., in general, throughout the selection, pair-wise between bars with the indexes that differ by the value of the lag). 2 point graphs above and below set the boundaries of the 95% confidence interval. Most PACF computations are within the interval, but some go beyond it. Technically, when forming input vectors, it is reasonable to first take computations with larger values, since they indicate the link between the new bar and the relevant of the past bars. In other words, not all the past computations could be placed into vector y, but, for instance, the 6th, the 8th, and the 50th ones, as in the picture from our preceding article. However, this situation is typical of a specific selection only. If we take not 500 bars of D1, but 1000 or 250, then we will obtain a new PACF with other "wavelets." Thus, computations of the source series will require "thinning" at any change in data, which, in turn, will require to re-optimize the LS-SVM settings, particularly the "gamma" and "sigma" parameters. Therefore, to enhance the universality of the algorithm, if even at the price of some loss of efficiency, we decided to form input vectors from all the successive bars at a given depth p for the confidence interval to cover the basic "runs" on this initial section of the PACF. In practice, this means p within the range of 20-50 bars for EURUSD D1.

Finally, it should be noted that the complexity of LS-SVM depends quadratically on the length of the N selection, since the matrix size is (N+1)*(N+1). For the selections amounting to several hundreds and thousands of bars, this may adversely impact the performance. There are many versions of LS-SVM that try to deal with this "curse of dimensionality." One of them, for example, suggests firstly clusterizing all vectors using a Kohonen self-organizing map (SOM) and then train individual M models for each cluster (M is the number of clusters).

I propose another approach. Upon clusterization of the initial set of vectors by the SOM, the clusters found will be used as kernels instead of the source vectors. For instance, a selection of 1000 vectors can be displayed on a Kohonen layer sized 7*7, i.e., 49 support vectors, which averagely provides about 20 source samples per network element.

Kohonen network (self-organizing map, SOM) has already been considered in a series of articles titled Practical Use of Kohonen Neural Networks in Algorithmic Trading (Part I and Part II), so it is relatively easy to bed it in into the LS-SVM engine being created.

Let us implement the algorithm in MQL.

LS-SVM in MQL

We are going to include all computations into one class, LSSVM, that will use the linear solvers of ALGLIB. Therefore, let us include it into the source code, as well as the CSOM library.

  #include <Math/Alglib/dataanalysis.mqh>
  #include <CSOM/CSOM.mqh>

Ensure the storage of all LS-SVM input vectors and matrices in the class:

  class LSSVM
  {
    protected:
      double X[];
      double Y[];
      double Alpha[];
      double Omega[];
      double Beta;
      
      double Sigma;
      double Sigma22; // 2 * Sigma * Sigma;
      double Gamma;
      
      int VectorNumber;
      int VectorSize;
      int Offset;
      int DifferencingOrder;
      ...

The class will independently fill X and Y with the quotes data, guided by the number of vectors requested, VectorNumber, their size VectorSize, and their offset on history, Offset (by default, 0 — the latest prices), all this being sent to the constructor through parameters.

This class supports processing of both the source code (DifferencingOrder is 0) and its differences of degrees from 1 through 3. This technique will be considered in more details below.

Object KohonenMap ensures optional clusterization, while clusters found by it get into the Kernels array.

      double Kernels[];  // SOM clusters
      int KernelNumber;
      CSOM KohonenMap;
      ...

User defines the network size (a square layer is suggested, i.e., KernelNumber must be an integral square), and this parameter can also be optimized. If KernelNumber is 0 (by default) or the total number of vectors, SOM gets disabled, and standard processing starts using LS-SVM. Working with the network goes beyond this paper, and those willing to know can find the methods of preparing, training, and integrating it in the source codes attached hereto. Note that the network is initially randomized; therefore, to get reproducible results, strand with a specific value must be called.

By default, data is read from the open price time series in the buildXYVectors method. In this article, we will only work with them. To enter random data, method feedXYVectors is provided, but it has not been tested.

    bool buildXYVectors()
    {
      ArrayResize(X, VectorNumber * VectorSize);
      ArrayResize(Y, VectorNumber);
      double open[];
      int k = 0;
      const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y
      CopyOpen(_Symbol, _Period, Offset, size, open);
      
      double diff[];
      ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction
      
      for(int i = 0; i < VectorNumber; i++)     // loop through anchor bars
      {
        for(int j = 0; j < VectorSize; j++)     // loop through successive bars
        {
          differentiate(open, i + j, diff);
          
          X[k++] = diff[0];
        }
        
        differentiate(open, i + VectorSize, diff);
        Y[i] = diff[0];
      }
      
      return true;
    }

Helper method "differentiate" called here allows computing for the array passed the difference of a random dimension — the result is returned through the "diff" array, the length of which is by 1 larger than DifferencingOrder.

    void differentiate(const double &open[], const int ij, double &diff[])
    {
      for(int q = 0; q <= DifferencingOrder; q++)
      {
        diff[q] = open[ij + q];
      }
      
      int d = DifferencingOrder;
      while(d > 0)
      {
        for(int q = 0; q < d; q++)
        {
          diff[q] = diff[q + 1] - diff[q];
        }
        d--;
      }
    }

The class supports normalization of vectors using subtracting the mean value and dividing by the standard deviation in the normalizeXYVectors method (not presented here).

In the class, there is also a couple of methods to compute the kernels — for vectors from X[] by their indexes and for external vectors, for instance:

    double kernel(const double &x1[], const double &x2[]) const
    {
      double sum = 0;
      for(int i = 0; i < VectorSize; i++)
      {
        sum += (x1[i] - x2[i]) * (x1[i] - x2[i]);
      }
      return exp(-1 * sum / Sigma22);
    }

Matrix "omega" is computed using the buildOmega method (it applies the "kernel" method calling the X[] vectors by indexes):

    void buildOmega()
    {
      KernelNumber = VectorNumber;
      
      ArrayResize(Omega, VectorNumber * VectorNumber);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        for(int j = i; j < VectorNumber; j++)
        {
          const double k = kernel(i, j);
          Omega[i * VectorNumber + j] = k;
          Omega[j * VectorNumber + i] = k;
          
          if(i == j)
          {
            Omega[i * VectorNumber + j] += 1 / Gamma;
            Omega[j * VectorNumber + i] += 1 / Gamma;
          }
        }
      }
    }

System of equations is solved and the "alpha" and "beta" coefficients searched for are obtained in the solveSoLE method.

    bool solveSoLE()
    {
      // |  0              |1|             |   |  Beta   |   |  0  |
      // |                                 | * |         | = |     |
      // | |1|  |Omega| + |Identity|/Gamma |   | |Alpha| |   | |Y| |
      
      CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1);
      
      for(int i = 1; i <= KernelNumber; i++)
      {
        for(int j = 1; j <= KernelNumber; j++)
        {
          MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]);
        }
      }
      
      MATRIX[0].Set(0, 0);
      for(int i = 1; i <= KernelNumber; i++)
      {
        MATRIX[i].Set(0, 1);
        MATRIX[0].Set(i, 1);
      }
      
      double B[];
      ArrayResize(B, KernelNumber + 1);
      B[0] = 0;
      for(int j = 1; j <= KernelNumber; j++)
      {
        B[j] = Y[j - 1];
      }
      
      int info;
      CDenseSolverLSReport rep;
      double x[];
      
      CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x);
      
      Beta = x[0];
      ArrayResize(Alpha, KernelNumber);
      ArrayCopy(Alpha, x, 0, 1);
      
      return true;
    }

"process" is the main method of the class to execute regression. From it, we launch forming inputs/outputs, normalization, computing the "omega" matrix, solving the system of equations, and getting an error for the selection.

    bool process()
    {
      if(!buildXYVectors()) return false;
      normalizeXYVectors();
      
      // least squares linear regression for demo purpose only
      if(KernelNumber == -1 || KernelNumber > VectorNumber)
      {
        return regress();
      }
      
      if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
      {
        buildOmega();
      }
      else                                                  // proposed SOM-LS-SVM
      {
        if(!buildKernels()) return false;
      }
      if(!solveSoLE()) return false;
      
      LSSVM_Error result;
      checkAll(result);
      ErrorPrint(result);
      return true;
    }

To assess the optimization quality, there are several different values in the class, which are automatically computed for the entire data set. These are mean-square error, correlation coefficient, determination coefficient (R-squared), and the ratio of concordance of signs (only reasonable in the modes implying differentiation). All aspects are brought into the structure of LSSVM_Error:

    struct LSSVM_Error
    { // indices: 0 - training set, 1 - test set
      double RMSE[2]; // RMSE
      double CC[2];   // Correlation Coefficient
      double R2[2];   // R-squared
      double PCT[2];  // %
    };

Zero index of the array means a training selection, while index 1 means a test selection. It would be desirable to use a more rigorous evaluation of the statistical significance of the forecast, such as Fisher test, since the nice correlation and R2 values can be deceptive. However, it seems to be impossible to cover all at once.

Method of computing the error over the entire selection is checkAll.

    void checkAll(LSSVM_Error &result)
    {
      result.RMSE[0] = result.RMSE[1] = 0;
      result.CC[0] = result.CC[1] = 0;
      result.R2[0] = result.R2[1] = 0;
      result.PCT[0] = result.PCT[1] = 0;
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      double out[];
      getResult(out);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        double given = Y[i];
        double trained = out[i];
        result.RMSE[0] += (given - trained) * (given - trained);
        // mean is 0 after normalization
        xy += (given) * (trained);
        x2 += (given) * (given);
        y2 += (trained) * (trained);
        
        if(given * trained > 0) correct++;
      }
      
      result.R2[0] = 1 - result.RMSE[0] / x2;
      result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber);
      result.CC[0] = xy / sqrt(x2 * y2);
      result.PCT[0] = correct * 100.0 / VectorNumber;
      
      crossvalidate(result); // fill metrics for test set (if attached)
    }

Before the loop, the getResult method is called that executes approximation for all input vectors and fills the "out" array with these values.

    void getResult(double &out[], const bool reverse = false) const
    {
      double data[];
      ArrayResize(out, VectorNumber);
      for(int i = 0; i < VectorNumber; i++)
      {
        vector(i, data);
        out[i] = approximate(data);
      }
      if(reverse) ArrayReverse(out);
    }

Here, the regular forecasting function, "approximate," is used for the model already constructed:

    double approximate(const double &x[]) const
    {
      double sum = 0;
      double data[];
      
      if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference)
      {
        for(int i = 0; i < ArraySize(x); i++)
        {
          sum += Solution[i] * x[i];
        }
        sum += Solution[ArraySize(x)];
      }
      else
      {
        if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
        {
          for(int i = 0; i < VectorNumber; i++)
          {
            vector(i, data);
            sum += Alpha[i] * kernel(x, data);
          }
        }
        else                                                  // proposed SOM-LS-SVM
        {
          for(int i = 0; i < KernelNumber; i++)
          {
            ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize);
            sum += Alpha[i] * kernel(x, data);
          }
        }
      }
      return sum + Beta;
    }

In it, the found coefficients Alpha[] and Beta are applied to the sum of kernel functions (cases LS-SVM and SOM-LS-SVM).

Test selection is formed in a manner similar to that for the training one — with another object, LSSVM, binding to the "checking" one in the main object.

  protected:
    LSSVM *crossvalidator;
  
  public:
    bool bindCrossValidator(LSSVM *tester)
    {
      if(tester.getVectorSize() == VectorSize)
      {
        crossvalidator = tester;
        return true;
      }
      return false;
    }
    
    void crossvalidate(LSSVM_Error &result)
    {
      const int vectorNumber = crossvalidator.getVectorNumber();
      
      double out[];
      double _Y[];
      crossvalidator.getY(_Y); // assumed normalized by validator
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      for(int i = 0; i < vectorNumber; i++)
      {
        crossvalidator.vector(i, out);
        
        double z = approximate(out);
        
        result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z);
        xy += (_Y[i]) * (z);
        x2 += (_Y[i]) * (_Y[i]);
        y2 += (z) * (z);
        
        if(_Y[i] * z > 0) correct++;
      }
      
      result.R2[1] = 1 - result.RMSE[1] / x2;
      result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber);
      result.CC[1] = xy / sqrt(x2 * y2);
      result.PCT[1] = correct * 100.0 / vectorNumber;
    }

Where necessary, the class allows executing, instead of non-linear optimization by the LS-SVM/SOM-LS-SVM algorithm, the linear regression by the least-squares method within the system with VeсtorSize variables and VectorNumber equations. For this purpose, the "regress" method is implemented.

    bool regress(void)
    {
      CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column
      
      for(int i = 0; i < VectorNumber; i++)
      {
        MATRIX[i].Set(VectorSize, Y[i]);
      }
      
      for(int i = 0; i < VectorSize; i++)
      {
        for(int j = 0; j < VectorNumber; j++)
        {
          MATRIX[j].Set(i, X[j * VectorSize + i]);
        }
      }
      
      CLinearModel LM;
      CLRReport AR;
      int info;
      
      CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR);
      if(info != 1)
      {
        Alert("Error in regression model!");
        return false;
      }
      
      int _size;
      CLinReg::LRUnpack(LM, Solution, _size);
      
      Print("RMSE=" + (string)AR.m_rmserror);
      ArrayPrint(Solution);
      
      return true;
    }

this method is a priori behind LS-SVM in accuracy and added here to demonstrate this. On the other hand, it can be used to regress data that is more primitive by its nature than quotes. This mode is enabled by setting KernelNumber = -1. In this case, the solution is written to the Solution array, Alpha[] and Beta are not being involved.

Let us create a forecasting indicator based on class LSSVM.

Forecasting Indicator LS-SVM

The task of indicator SOMLSSVM.mq5 is to create 2 LSSVM objects (one for the training selection and one for the testing one), perform regression, and display the initial and the forecasted values with the quality assessments in both sets. Parameters "gamma" and "sigma" will be considered as already found and set by the user. It is more convenient to optimize them in an EA, using the standard tester (the next Section hereof deals with that). Technically, the tester could also support the possibility of optimizing indicators, since this limitation is quite artificial. Then we could optimize the model in the indicator directly.

The indicator will have 4 buffers in a separate window. 2 buffers will display initial and forecasted values for the training set, while the 2 other ones will display those for the test set.

Inputs:

  input int _VectorNumber = 250; // VectorNumber (training)
  input int _VectorNumber2 = 50; // VectorNumber (validating)
  input int _VectorSize = 20; // VectorSize
  input double _Gamma = 0; // Gamma (0 - auto)
  input double _Sigma = 0; // Sigma (0 - auto)
  input int _KernelNumber = 0; // KernelNumber (0 - auto)
  input int _TrainingOffset = 50; // Offset of training bars
  input int _ValidationOffset = 0; // Offset of validation bars
  input int DifferencingOrder = 1;

The two first ones set the sizes of training and testing sets. Vector size is specified in VectorSize. Parameters Gamma and Sigma can be left being 0 to automatically select their values based on inputs; however, the quality of this trivial mode is far cry from optimal — we only need it for the indicator to work with the default values. KernelNumber should be left being 0 for the regression by the LS-SVM method. By default, the testing set is placed at the very end of the quotes history, while the training one is to the left of it (chronologically earlier).

Objects are initialized based on inputs.

  LSSVM *lssvm = NULL;
  LSSVM *test = NULL;
  
  int OnInit()
  {
    static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"};
    
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetString(i, PLOT_LABEL, titles[i]);
    }
    
    lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset);
    test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset);
    lssvm.setDifferencingOrder(DifferencingOrder);
    test.setDifferencingOrder(DifferencingOrder);
    
    return INIT_SUCCEEDED;
  }

Indicator is computed only once, since it has been created for demonstration purposes. Where necessary, it can be easily adapted so that the indications are updated at each bar, but the system should be solved potentially costly only once or repeatedly, after a rather large time interval.

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {
    ArraySetAsSeries(Open, true);
    ArraySetAsSeries(Time, true);
    
    static bool calculated = false;
    if(calculated) return rates_total;
    calculated = true;
    
    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }
    
    lssvm.bindCrossValidator(test);
    bool processed = lssvm.process(true);

In OnCalculate, we connect the testing set to the training one and launch regression. If it is completed successfully, we will display all data, both initial and forecasted:

  if(processed)
  {
    const double m1 = lssvm.getMean();
    const double s1 = lssvm.getStdDev();
    const double m2 = test.getMean();
    const double s2 = test.getStdDev();
    
    // training
    
    double out[];
    lssvm.getY(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[0].set(_TrainingOffset, out);
    
    lssvm.getResult(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[1].set(_TrainingOffset, out);
    
    // validation
    
    test.getY(out, true);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      out[i] = out[i] * s2 + m2;
    }
    
    buffers[2].set(_ValidationOffset, out);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      test.vector(i, out);
      
      double z = lssvm.approximate(out);
      z = z * s2 + m2;
      buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z;
      ...
    }
  }

Since we have the option of analyzing the differentiated series, the indicator is displayed in a separate window. However, in fact, we are still working with prices, and it is desirable to display the forescast in the main chart. For this purpose, objects can be used. Their coordinates by the price axis should be restored from the difference series. Indexation of elements in the initial series and in the various-dimension difference series derived from it is illustrated by the scheme below (indexation in chronological order):

    d0:  0   1   2   3   4   5  :y
    d1:    0   1   2   3   4
    d2:      0   1   2   3
    d3:        0   1   2

For example, if the difference is of the first dimension (d1), it is obvious that:

y[i+1] = y[i] + d1[i]

For the differences of the second (d2) and third (d3) dimensions, the equations will be as follows:

y[i+2] = 2 * y[i+1] - y[i] + d2[i]

y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]

We can see that the higher the order of differentiation is, the larger number of the preceding computations y is involved in calculations.

Having applied these formulas, we can display the forecast with the objects in the price chart.

      if(ShowPredictionOnChart)
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2]
                 + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z;
        }
        else
        {
          // unsupported yet
        }
        
        string name = prefix + (string)i;
        ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target);
        ObjectSetString(0, name, OBJPROP_TEXT, "l");
        ObjectSetString(0, name, OBJPROP_FONT, "Wingdings");
        ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER);
        ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed);
      }

We did not consider any dimensions higher than 3, since they have both positive effects and a negative one. It should be reminded that the positive one consists in the fact that the forecast quality increases with increasing the dimension due to the growing stationarity. However, this is particularly true of the forecast for a derivative of the relevant order, not of the initial series. Negative effect high-order differentiating is that even a minor error on them increases essentially at the subsequent "deployment" of increments into an integrated series. Thus, for DifferencingOrder, a "golden mean" should also be found by optimizing or trial and error.

Both effects can be observed on two screenshots below (light green and green lines are the real data of the training and testing sets, respectively, while light blue and blue lines are the forecast for the same):

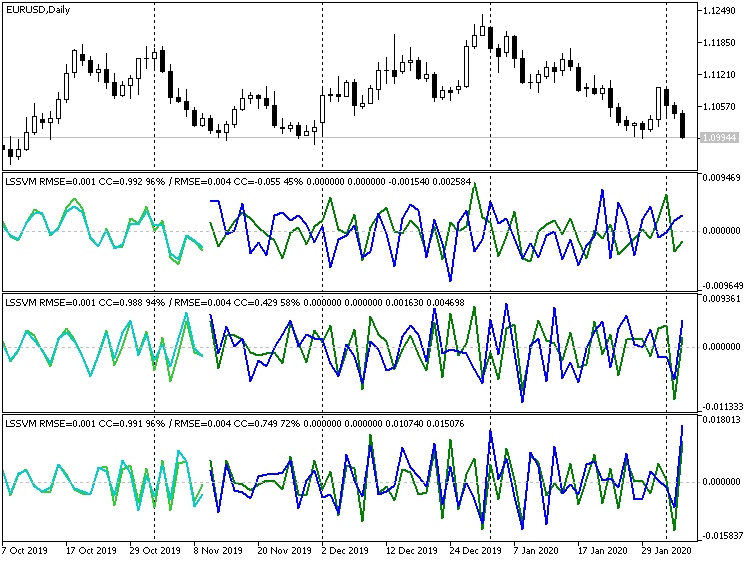
Indicators LSSVM with Various Differentiation Orders for the Series of EURUSD D1

Here, 3 indicator instances are shown here with general settings and with different orders of differentiation. General Settings:

• _VectorNumber = 250; // VectorNumber (training)
• _VectorNumber2 = 60; // VectorNumber (validating)
• _VectorSize = 20; // VectorSize
• _Gamma = 2048; // Gamma (0 - auto)
• _Sigma = 8; // Sigma (0 - auto)
• _KernelNumber = 0; // KernelNumber (0 - auto)
• _TrainingOffset = 60; // Offset of training bars
• _ValidationOffset = 0; // Offset of validation bars

Differentiation orders are 1, 2, and 3, respectively. After the slope line in the heading of each window, the forecast indications are shown for the testing (in this case, validating) selection: They increase for the better (correlation coefficient: -0.055, 0.429, and 0.749; while the percentage of the matching signs of increments is 45%, 58%, and 72%, respectively). In fact, the better coincidence of lines can be seen even visually. However, if we restore the third-order forecast in the price chart, we will have the following picture:

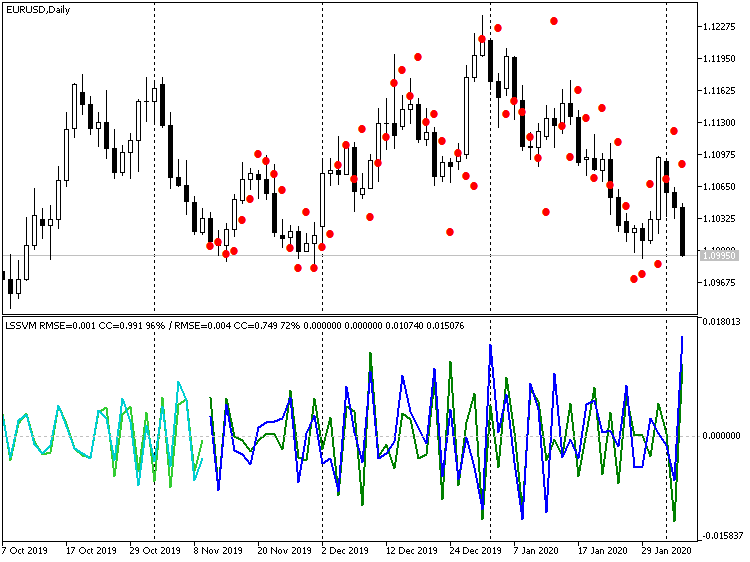
Third-Order Differentiation Indicator LSSVM with the Restored Values of Forecast for EURUSD D1

Obviously, many points can be characterized as runouts. On the other hand, if we disable differentiation at all, we will get:

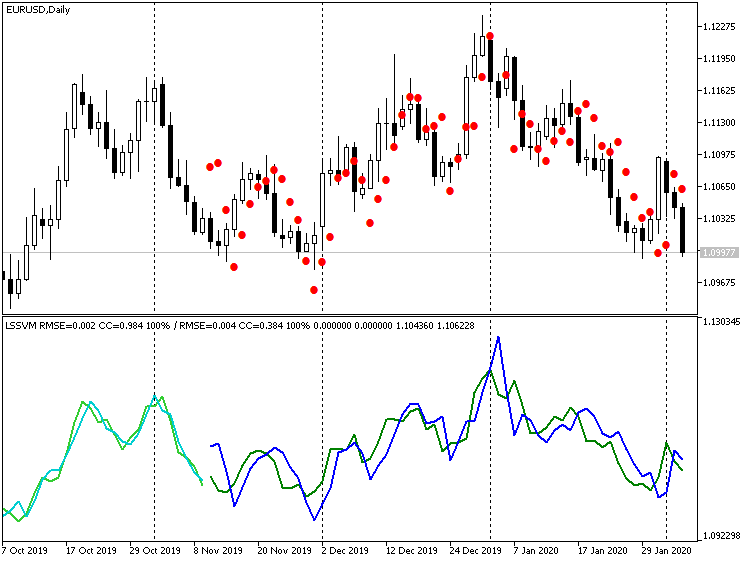
Indicator LSSVM without Differentiation, with the Restored Values of Forecast for EURUSD D1

Here, the price values are much closer to real ones, but there is a visible lag of about 1 bar. This effect is due to the fact that, in fact, our algorithm is equivalent to digital filter, a kind of a moving average based on N instance vectors. Considering the proximity of price level, it is reasonable to level out this lag of 1-2 bars by forecasting several steps forward at once, i.e., upon obtaining a forecast for bar -1, feed it as the input for forecasting bar -2, etc. We are going to provide for this mode when creating an EA in the next Section.

Expert Advisor LS-SVM

Exper Advisor LSSVMbot.mq5 is designed to perform two tasks:

• Optimizing the "Gamma" and "Sigma" parameters of LS-SVM in virtual mode (without trading); and
• Trading in Tester and, optionally, optimizing other parameters in the trading mode.

In virtual mode, like in the indicator, 2 instances of LSSVM are used: One with a training set, and another one with a testing set. These are testing set indications that are taken into consideration. Optimization is performed by the custom criterion. They are all listed as follows:

  enum CUSTOM_ESTIMATOR
  {
    RMSE,   // RMSE
    CC,     // correlation
    R2,     // R-squared
    PCT,    // %
    TRADING // trading
  };

The TRADING option is used to set the EA in the trading mode. In it, the EA can be optimized in a conventional manner, by one of the embedded criteria, such as profit, drawdown, etc.

The main group of inputs sets the same values as in the indicator.

  input int _VectorNumber = 250;  // VectorNumber (training)
  input int _VectorNumber2 = 25;  // VectorNumber (validating)
  input int _VectorSize = 20;     // VectorSize
  input double _Gamma = 0;        // Gamma (0 - auto)
  input double _Sigma = 0;        // Sigma (0 - auto)
  input int _KernelNumber = 0;    // KernelNumber (sqrt, 0 - auto)
  input int DifferencingOrder = 1;
  input int StepsAhead = 0;

However, TrainingOffset and ValidationOffset have become internal variables and are set automatically. ValidationOffset is always 0. TrainingOffset is the size of the validation set VectorNumber2 in the virtual mode, or it is 0 in the trading mode (since it is implied here that all parameters have already been found, there is no testing set, and regression should be performed on the latest data).

To use SOM in KernelNumber, you should specify the size of one side, while the full map size will be computed as the squared value of this value.

The second group of inputs is intended for optimizing "Gamma" and "Sigma":

  input int _GammaIndex = 0;     // Gamma Power Iterator
  input int _SigmaIndex = 0;     // Sigma Power Iterator
  input double _GammaStep = 0;   // Gamma Power Multiplier (0 - off)
  input double _SigmaStep = 0;   // Sigma Power Multiplier (0 - off)
  input CUSTOM_ESTIMATOR Estimator = R2;

Since the search range is very broad and the standard tester only supports iteration by adding a predefined step, the following approach is used in the EA. Optimization must be enabled by parameters GammaIndex and SigmaIndex. Each of them defines how many times the initial values of Gamma and Sigma must be multiplied by GammaStep and SigmaStep, respectively, to get the working value of the "gamma" and "sigma." For example, if Gamma is 1, GammaStep is 2, and optimization is being performed for GammaIndex within the range of 0-5, then the algorithm will evaluate the "gamma" values 1, 2, 4, 8, 16, and 32. If GammaStep and SigmaStep are not 0, then they are always used to compute the working values of "gamma" and "sigma,' including within a single tester run.

The EA works on bars. EA does not start computing before the requested number of bars (vectors) becomes available in history. If there is no sufficient number of bars in tester, the run may be finished idly — see the logs. Unfortunately, the number of historical bars loaded by the tester at starting depends on many factors, such as timeframe, day number within the year, etc., and can vary considerably. If necessary, move the initial test time to the past.

In virtual mode, the model is trained only once, and one of the characteristics (selected in Estimator) is returned from function OnTester as a quality indicator (in case of selecting RMSE, the error is given with a reversed sign).

  bool optimize()
  {
    if(Estimator != TRADING) lssvm.bindCrossValidator(test);
    iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep);
    bool success = lssvm.process();
    if(success)
    {
      LSSVM::LSSVM_Error result;
      lssvm.checkAll(result);
      
      Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma());
      Print("  training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]);
      Print("  test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]);
      
      customResult = Estimator == CC ? result.CC[1]
                  : (Estimator == RMSE ? -result.RMSE[1] // the lesser |absolute error value| the better
                  : (Estimator == PCT ? result.PCT[1] : result.R2[1]));
    }
    return success;
  }
  
  void OnTick()
  {
    ...
    if(Estimator != TRADING)
    {
      if(!processed)
      {
        processed = optimize();
      }
    }
    ...
  }
  
  double OnTester()
  {
    return processed ? customResult : -1;
  }

In trading mode, the model is trained by default only once, too, but you can set redrawing each year, quarter, or month. For this purpose, in the OPTIMIZATION parameter (it is named _2 in the code), you should write "y", "q," or "m" (uppercase is supported, too). Remember that this process only involves solving a system of equations on new (latest) data; however, the "gamma" and "sigma" parameters remain the same. Technically, we can sophisticate the process and, at each re-training, try parameters on-the-fly (what we previously assigned to the standard optimizer); however, this must then be organized within the EA and, therefore, will be executed by a single stream.

It is implying now that the "gamma" and "simga" parameters matched for the data over a quite long period (a year or more) must be relevant during shorter trading periods.

After the model has been built, the test instance of LSSVM is used to read the latest known prices, form input vector from them, and normalize it. Then the vector is passed to method lssvm.approximate:

    static bool solved = false;
    if(!solved)
    {
      const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0);
      solved = opt ? optimize() : lssvm.process();
    }
    
    if(solved)
    {
      // test is used to read latest _VectorNumber2 prices
      if(!test.buildXYVectors())
      {
        Print("No vectors");
        return;
      }
      test.normalizeXYVectors();
      
      double out[];
      
      // read latest vector
      if(!test.buildVector(out))
      {
        Print("No last price");
        return;
      }
      test.normalizeVector(out);
      
      double z = lssvm.approximate(out);

Depending on the input, StepsAhead, the EA either puts to use the obtained value, z, transforming it into a price forecast by denormalizing, or repeats the forecast a predefined number of times and only then transforms it into a price.

      for(int i = 0; i < StepsAhead; i++)
      {
        ArrayCopy(out, out, 0, 1);
        out[ArraySize(out) - 1] = z;
        z = lssvm.approximate(out);
      }
      
      z = test.denormalize(z);

Since the time series might be differentiated, we take several latest price values to restore the next price value by them and by the forecast increment.

      double open[];
      if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = open[2] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * open[2] - open[1] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * open[2] - 3 * open[1] + open[0] + z;
        }
        else
        {
          // unsupported yet
        }

Depending on the location of the forecasted price relative to the current level, the EA opens a trade. If the position has already been opened in the required direction, it remains open. If the position is in the opposite direction, a reverse is performed.

        int mode = target >= open[2] ? +1 : -1;
        int dir = CurrentOrderDirection();
        if(dir * mode <= 0)
        {
          if(dir != 0) // there is an order
          {
            OrdersCloseAll();
          }
          
          if(mode != 0)
          {
            const int type = mode > 0 ? OP_BUY : OP_SELL;
            const double p = type == OP_BUY ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID);
            OrderSend(_Symbol, type, Lot, p, 100, 0, 0);
          }
        }
      }
    }

Let us check how the EA works in both modes. Let us take XAUUSD as a working tool that is less exposed to national news, as compared to currencies. Timeframe is D1.

File with settings is attached (LSSVMbot.set). Size of the training set VectorNumber is voluntarily taken as 200. This is slightly less than a year. Large values around 1000 may already considerably inhibit solving the system of equations. Testing set VectorNumber2=50. Vector size VectorSize=20 (a month). SOM is not used (KernelNumber=0). Differencing is disabled (DifferencingOrder=0), but for the verifying stage in trading mode, forecasting is set to 2 steps ahead (StepsAhead=2), since we have noticed a slight delay of the forecast vs. prices, using the indicator. In virtual mode, the input parameter StepsAhead is not used in evaluating the model.

Basic values of Gamma and Sigma are 1, but their multipliers, Power Multiplier (GammaStep, SigmaStep), are equal to 2, while the number of multiplications to be performed in optimization are defined in iterators GammaIndex and SigmaIndex as intervals from 5 to 35 and from 5 to 20 with step 5, respectively. Thus, when GammaIndex is 15, Gamma will take the value of 1 * (2 raised to the power of 15), that is 32768.

Trying correct ranges to find "gamma" and "sigma" is quite a routine task, since for it, unfortunately, there is no other solutions than computing, firstly, by a coarse grid and, secondly, by a finer one. We will limit ourselves to one grid, since many trials were made while preparing this paper, which can be considered as search in a broader range.

Thus, there are only 2 parameters to be optimized: GammaIndex and SigmaIndex. they indirectly change Gamma and Sigma within a broader range, with a variable step, exponentially.

Let us start optimization by open prices on the year 2018. Optimization is performed by the custom criterion, Estimator = R2.

Remember that, in this mode, the EA does not trade, but fills from quote a system of equations and solves it by the LS-SVM algorithm. Bars are involved in the computation in the amounts sufficient to form VectorNumber vectors sized VectorSize adjusted for possibly enabled differentiation (each additional procedure of taking differences requires an additional bar in inputs). Moreover, the EA additionally requires VectorNumber2 test vectors that are chronologically located after the training ones, i.e., on the latest bars. It is on test bars (more exactly: On the vectors fromed from them), where the forecasting abilities of the obtained model are assessed for returning from OnTester.

All this is important, since the tester does not always have a right number of bars in history at starting, and the EA will only be able to fill the system several months after the initial date. On the other hand, we should remember that training bars always start prior to the test (optimization) date, since the EA is immediately provided with the history of a certain length.

Upon completion of optimization, we sort the findings by criterion R2 (in descending order, i.e., the best ones on top). Suppose, in the beginning there will be settings GammaIndex=15 and SigmaIndex=5 (we say "suppose", because the order of runs with equal results may probably change).

Double-click on the first record to run a single test (still in the virtual mode). We will see something like the following in the log:

  2018.01.01 00:00:00   Bars required: 270
  2018.01.02 00:00:00   247 2017.01.03 00:00:00
  2018.02.02 00:00:00   Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270
  2018.02.02 00:00:00   G[15]=32768.0 S[5]=32.0
  2018.02.02 00:00:00   RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985
  2018.02.02 00:00:00   Parameters: 32768.0 32.0
  2018.02.02 00:00:00     training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0
  2018.02.02 00:00:00     test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0
  final balance 10000.00 USD
  OnTester result 0.9598497541714557

This can be interpreted as follows: 270 bars were required to perform the complete procedure, while only 247 ones were available as of 2018.01.02. Sufficient number of bars only appeared on 2018.02.02, i.e., a month later, training data (available history) starting on 2017.01.03. Then the working parameters, Gamma and Sigma (G[15]=32768.0 S[5]=32.0 are specified, optimized iterator parameters being given in square brackets. Finally, we can see the value of R2 (0.95985) in the string containing training quality indicators, which value has been returned from OnTester.

Let us now disable optimization, broaden the date range from 2017 to February, 2020, and set in the EA's parameters Estimator = TRADING (it means that the EA will perform trade operations). In parameter OPTIMIZATION (_2 in the code), let us introduce symbol "q," which instructs the EA to quarterly recalculate the regression model on new data (the latest then-current VectorNumber vectors). However, "gamma" and "sigma" remain the same.

Let us run a single test.

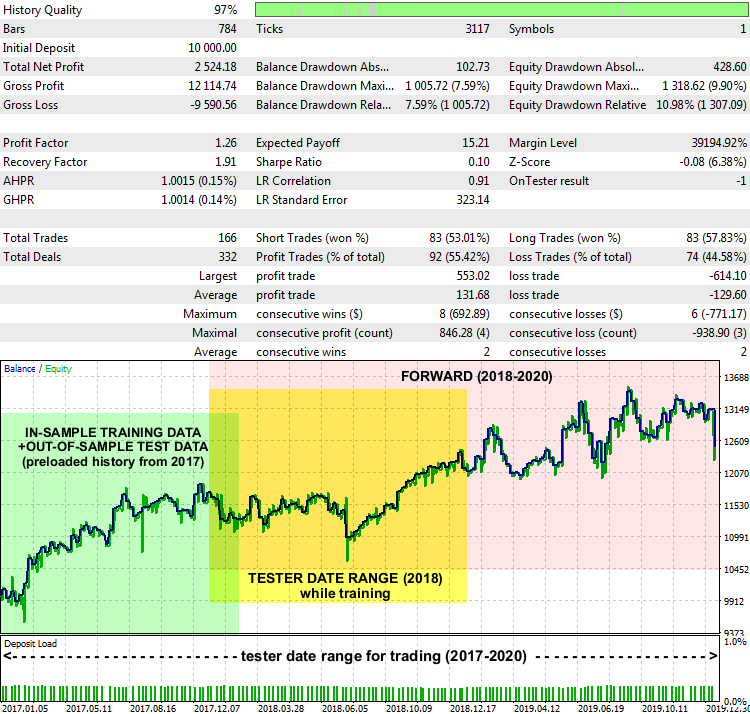
EA LSSVMbot Report on XAUUSD D1, 2017-2020

Not really amazing performance, but basically, the system works. Date ranges are marked on the report chart, from which the training data was taken to find optimal "gamma" and "sigma" (highlighted in green),which range was defined in the tester in training mode (highlighted in yellow), and the range where the EA traded on unknown data (highlighted in pink).

The ways of interpreting the forecast and constructing a trading strategy around it can be different. In particular, in our test EA, there is an input, PreviousTargetCheck (false, by default). It being enabled, the forecast-based trading will be performed using another strategy: Transaction direction is determined by the location of the newest forecast relative to the preceding one. There is also some further scope for experimenting with other settings, such as SOM clusterization, changing the lot size depending on the strength of the forecasted movement, refilling, etc.

Conclusions

In this article, we have got to know the LS-SVM-based algorithm for forecasting time series requiring the active use of mathematical methods and careful configuration. Successfully using the said methods (EMD from Part 1 and LS-SVM from this Part 2) in practice may considerably depend on the special aspects of time series, while applied to trading, also on the nature of a financial instrument and timeframe. Therefore, selecting a market relevant to the capabilities of a specific algorithm is as important as implementing knowledge-intensive and/or resource-intensive computations. Particularly, Forex currencies are less predictable and more exposed to external shocks, which reduces the efficiency of a forecast that is exclusively constructed on historical quotes. Metals, indices, or balanced baskets/portfolios should be considered more suitable for the two methods described. Moreover, no matter how fascinating a forecast appears to be, we should not forget about risk management, protective stop orders, and news background monitoring.

Source codes provided allow you to embed the new methods in your own MQL projects.