预测时间序列（第 2 部分）：最小二乘支持向量机（LS-SVM）

关键字: LS-SVM, SOM-LS-SVM, SOM

概述

在本文中，我们将继续讲述预测时间序列的算法。 在第 1 部分中，我们曾述及预测经验模式分解（EMD），和统计分析时间序列的指标 TSA。 在第二部分中，我们要研究的对象是支持向量机（SVM），其一版本名为最小二乘支持向量机（LS-SVM）。 该技术尚未在 MQL 中实现。 但是首先，我们必须了解相关的数学知识。

LS-SVM 的数学知识

支持向量机（SVM）是数据分类和回归的一套分析算法的总称。 回归是我们特别感兴趣的（英文维基百科中的文献），因为它可识别回归与预测量之间的相互关系。 预测问题可由回归表述，即根据时间序列的先前计数（上述预测量）来找到某个函数，从而令其值尽可能合理地表述时间序列的未来计数。

SVM 算法基于将源数据变换到更高维度的空间中，其中的每个输入向量，形成了含有时间延迟的种子点序列。 然后，这些向量会作为关键样本，以特殊方式进行组合，从而能够以指定的精度计算定义数据分布的回归超平面。 这些计算代表称之为“内核”的全部样本的总和，即输入的统合函数。 这些函数可以是线性的、或非线性的（常态为钟形），且指导参数会影响回归精度。 最常见的内核是：

• 线性;
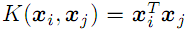• d 次多项式;
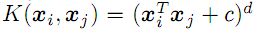• 带有西格玛（sigma）色散的径向基函数（高斯，见下文）；
• Sigmoid (双曲正切) ;

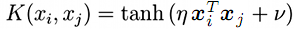有一个 SVM 修正版，最小二乘 SVM（LS-SVM），或最小二乘支持向量法。 它能够作为线性方程组解决问题，替代解决等效初始非线性问题。

若我们有一个时间序列 y，且假设我们可以得到其在 t 时刻的值，以前置点 p 和某些外部 q 变量构成函数，误差为 e。 通常，它会如下所示：

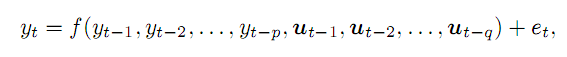 (1)

举例来说，外部变量（在所应用的交易中）可以是工作日编号，日内时辰编号，或相关的柱线交易量。 在本文中，我们将仅受价格时间序列的前置点限制。 资料的复杂性不允许考虑所有方面。

从该序列中抽取 p 前置点，在 p-维空间中形成一个向量。 沿着初始序列从左到右移动，我们将获得一组预测向量，将其表示为 x； 对于 t 时刻，它们与预测值 y 的依从关系表示为：

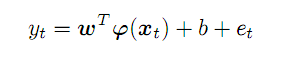 (2)

系数 w 的未知向量，和变换函数 f 在抽象特征空间中工作，其维数潜在无限制，甚至可以高于 p，而特征函数 f，以及系数 w，应能在优化过程中准确发现：

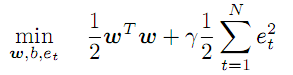 (3)

此条件规定最小化系数 w 的值，并引入误差率的正则化/惩罚因子 gamma。 gamma 值越大，则回归越精确就必须越近似于源数据。 如果 gamma 减小，则偏差冗余增大，从而提高了模型的平滑度。

方程组（2）限定在所有 t 值从 1 到 N（向量数）。

为了纾解这个问题，利用了数学“技巧”（其中之一甚至被称为“内核技巧”）：它们解决了所谓的 二重问题，替代原本的优化问题，但本质上它们是等效的，其中我们设法消除系数 w，并将 f 转换为内核函数（请参见下文）。 结果则为，解决方案简化为线性系统：

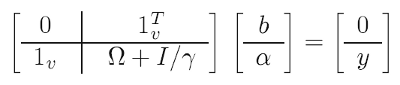 (4)

其中的已知数据：

• y - 由预测的所有目标（训练）值组成的向量；
• 1 - 单位向量（行和列）；
• I - 单位矩阵;
• gamma - 上述正则化参数（将以测试集上的预测品质为指导进行搜索）；
• omega - 按以下公式计算的矩阵：

 (5)

在此，我们终于看到了上面宣布的内核函数 K，它取所有输入向量 x 之间的成对组合进行计算。 对于对称高斯的径向基函数（我们将用到它），公式 K 如下所示：

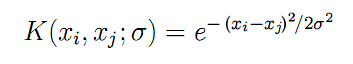 (6)

参数 “sigma” 描述钟形宽度—在实践中，这是另一个应迭代搜索的参数。 sigma 越大，回归中将涉及更多数量的“相邻”向量。 实际上，在 sigma 较小的情况下，该函数正好沿着训练数据集的点前进，且对于未知图像停止响应（即泛化）。

利用源数据（x，y）和公式（4），（5）和（6），我们应用最小二乘法获得所有未知数：

• b - （2）和（7）所涉及的截距项；
• a - 最终回归模型公式中包含的 “alpha” 系数向量：

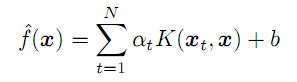 (7)

对于任意向量 x（不是来自训练集），它计算预测的方式为：所有 N 个源向量的 “alpha” 系数和内核的乘积之和， 根据截取项 b 进行调整。

在理论部分仍有两个问题涵待解答。 第一，我们如何知道自变量 “Gamma” 和 “sigma”？ 第二，为了依据报价的时间序列形成输入向量 x，我们应该如何选择时间延迟 p 的深度？

实际上，这些参数是通过穷举法反复试验找到的：在循环中，我们利用非常广泛的二维值网格来评估每种组合的模型，并评估其品质。 品质应意味着依据测试数据集的预测误差比之训练集要更小。 这个过程类似于 MetaTrader 测试器，且可能涉及到优化。 然而，研究较大的范围不能只用固定增量，实际上需要以指数方式（即，乘法）来改变数值。 所以，我们将在实现阶段再研究这个方面。

至于输入空间 p 的大小，建议根据要预测序列的特征对其进行定义，尤其是使用部分自相关函数（PACF） 。 在我们的下一篇文章中，我们准备了计算 PACF 的工具，并看看它在不同历史特定部分的 EURUSD D1 上如何表现。 每个图表柱线都描述了含有相关时间滞后的柱线对当前柱线的影响（即，通常情况下，贯穿整个选择部分，索引之间的成对柱线之间的时间滞后值会有所不同）。 上下两个点图则设定了 95％ 置信区间的边界。 大多数 PACF 计算都在该间隔内，但有些会超出。 从技术上讲，当形成输入向量时，首先取较大值进行计算是合理的，因为它们能指明新柱线与旧柱线相关部分之间的联系。 换句话说，并非所有过去的计算都可以放入向量 y 当中，举例，我们以前所发表文章中的第 6、8 和 50。 不过，这种情况仅是特定选择的典型情况。 如果我们从 D1 取柱线时，不只选 500 根，而是1000 或 250 根，那么我们将得到带有其他“小波” 的新 PACF。 因此，源序列的计算将需要针对数据的任何变化进行“细化”，进而需要重新优化 LS-SVM 设置，尤其是 “gamma” 和 “sigma” 参数。 故此，为了增强算法的通用性，即使以牺牲一些效率为代价，我们决定从给定深度 p 的所有连续柱线形成输入向量，从而置信区间涵盖了 PACF 初始部分的基本“运行”。 实际上，这表示 p 处于 EURUSD D1 图表上 20 至 50 根柱线范围内。

最后，应当注意的是，由于矩阵大小为 (N+1)*(N+1)，因此 LS-SVM 的复杂度取决于所选长度 N 的二次方。 对于所选柱线数量达数百和数千根的，可能会对性能产生不利影响。 有许多版本的 LS-SVM 试图破解这个“维数诅咒”。 例如，其中之一建议首先利用 Kohonen 自组织映射（SOM）对所有向量进行集簇，然后针对每个集簇训练 M 个模型（M 为集簇数量）。

我提议采用另一种方法。 依据 SOM 的初始向量集进行集簇后，发现的集簇将用作内核，替代源向量。 举例，可以在大小为 7*7 的 Kohonen 层上显示 1000 个选择的向量，即 49 个支持向量，平均每个网络元素提供约 20 个源样本。

题目为 “Kohonen 神经网络在算法交易中的实际应用” 的系列文章（第一部分和第二部分）已经研究过 Kohonen 网络（自组织映射，SOM），因此将其嵌入正在创建的 LS-SVM 引擎则相对容易。

我们以 MQL 实现该算法。

以 MQL 实现 LS-SVM

我们将把所有计算都纳入一个类，LSSVM，它会利用 ALGLIB 的线性求解器。 所以，我们将其包含在源代码，还有 CSOM 函数库。

  #include <Math/Alglib/dataanalysis.mqh>
  #include <CSOM/CSOM.mqh>

确保在该类中所有 LS-SVM 输入向量和矩阵的存储：

  class LSSVM
  {
    protected:
      double X[];
      double Y[];
      double Alpha[];
      double Omega[];
      double Beta;
      
      double Sigma;
      double Sigma22; // 2 * Sigma * Sigma;
      double Gamma;
      
      int VectorNumber;
      int VectorSize;
      int Offset;
      int DifferencingOrder;
      ...

该类将分别用报价数据填充 X 和 Y，并根据请求的向量数 VectorNumber，大小 VectorSize，以及它们在历史记录中的偏移量 Offset（默认为 0 — 最新价格）作为指导，所有这些都将作为参数发送到构造函数。

该类即支持源代码（DifferencingOrder 为 0），以及度数差从 1 到 3 的处理。 下文会更详尽地研究此技术。

对象 KohonenMap 确保可选的集簇，同时将已发现的集簇放入 Kernels 数组。

      double Kernels[];  // SOM clusters
      int KernelNumber;
      CSOM KohonenMap;
      ...

用户定义网络大小（建议使用平方层，即 KernelNumber 必须为整数的平方），当然此参数也可优化。 如果 KernelNumber 为 0（默认情况下），或是向量总数，则会禁用 SOM，且开始使用 LS-SVM 进行标准处理。 网络的操作超出了本文的范畴，而且那些想了解的人可在本文所附的源代码中找到网络准备、训练和集成的方法。 请注意，网络最初是随机的。 因此，为了获得可重现的结果，数据链必须调用相同的特定值。

默认情况下，在 buildXYVectors 方法中从时间序列中读取开盘数据。 在本文中，我们仅操控它们。 为了输入随机数据，提供了 feedXYVectors 方法，但它尚未经过测试。

    bool buildXYVectors()
    {
      ArrayResize(X, VectorNumber * VectorSize);
      ArrayResize(Y, VectorNumber);
      double open[];
      int k = 0;
      const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y
      CopyOpen(_Symbol, _Period, Offset, size, open);
      
      double diff[];
      ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction
      
      for(int i = 0; i < VectorNumber; i++)     // loop through anchor bars
      {
        for(int j = 0; j < VectorSize; j++)     // loop through successive bars
        {
          differentiate(open, i + j, diff);
          
          X[k++] = diff[0];
        }
        
        differentiate(open, i + VectorSize, diff);
        Y[i] = diff[0];
      }
      
      return true;
    }

此处调用 Helper 的方法 “differentiate”，能够依据所传递的随机维度的差值数组进行计算 — 结果会经 “diff” 数组返回，其长度比 DifferencingOrder 大 1。

    void differentiate(const double &open[], const int ij, double &diff[])
    {
      for(int q = 0; q <= DifferencingOrder; q++)
      {
        diff[q] = open[ij + q];
      }
      
      int d = DifferencingOrder;
      while(d > 0)
      {
        for(int q = 0; q < d; q++)
        {
          diff[q] = diff[q + 1] - diff[q];
        }
        d--;
      }
    }

该类支持向量的常规化，实施则是在 normalizeXYVectors 方法（此处未提供）中减去平均值，并除以标准差。

在该类中，还存在几种计算内核的方法 — 对于向量，按它们的索引从 X[] 里获取，对于外部向量，举例：

    double kernel(const double &x1[], const double &x2[]) const
    {
      double sum = 0;
      for(int i = 0; i < VectorSize; i++)
      {
        sum += (x1[i] - x2[i]) * (x1[i] - x2[i]);
      }
      return exp(-1 * sum / Sigma22);
    }

矩阵 “omega” 是利用 buildOmega 方法计算的（它应用 “kernel” 方法按索引调用X[] 向量）：

    void buildOmega()
    {
      KernelNumber = VectorNumber;
      
      ArrayResize(Omega, VectorNumber * VectorNumber);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        for(int j = i; j < VectorNumber; j++)
        {
          const double k = kernel(i, j);
          Omega[i * VectorNumber + j] = k;
          Omega[j * VectorNumber + i] = k;
          
          if(i == j)
          {
            Omega[i * VectorNumber + j] += 1 / Gamma;
            Omega[j * VectorNumber + i] += 1 / Gamma;
          }
        }
      }
    }

求解方程组，并利用 solveSoLE 方法搜索 “α” 和 “β” 系数。

    bool solveSoLE()
    {
      // |  0              |1|             |   |  Beta   |   |  0  |
      // |                                 | * |         | = |     |
      // | |1|  |Omega| + |Identity|/Gamma |   | |Alpha| |   | |Y| |
      
      CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1);
      
      for(int i = 1; i <= KernelNumber; i++)
      {
        for(int j = 1; j <= KernelNumber; j++)
        {
          MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]);
        }
      }
      
      MATRIX[0].Set(0, 0);
      for(int i = 1; i <= KernelNumber; i++)
      {
        MATRIX[i].Set(0, 1);
        MATRIX[0].Set(i, 1);
      }
      
      double B[];
      ArrayResize(B, KernelNumber + 1);
      B[0] = 0;
      for(int j = 1; j <= KernelNumber; j++)
      {
        B[j] = Y[j - 1];
      }
      
      int info;
      CDenseSolverLSReport rep;
      double x[];
      
      CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x);
      
      Beta = x[0];
      ArrayResize(Alpha, KernelNumber);
      ArrayCopy(Alpha, x, 0, 1);
      
      return true;
    }

“process” 是该类执行回归的主要方法。 我们启动它，从中形成输入/输出，常规化，计算 “omega” 矩阵，求解方程组，并得到所选的误差。

    bool process()
    {
      if(!buildXYVectors()) return false;
      normalizeXYVectors();
      
      // least squares linear regression for demo purpose only
      if(KernelNumber == -1 || KernelNumber > VectorNumber)
      {
        return regress();
      }
      
      if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
      {
        buildOmega();
      }
      else                                                  // proposed SOM-LS-SVM
      {
        if(!buildKernels()) return false;
      }
      if(!solveSoLE()) return false;
      
      LSSVM_Error result;
      checkAll(result);
      ErrorPrint(result);
      return true;
    }

为了评估优化品质，类中有若干个不同的数值，这些数值是针对整个数据集自动计算的。 这些是均方误差，相关系数，确定系数（R-平方），和符号的一致性比率（合理性仅存在于表示微分的模式中）。 所有方面都纳入 LSSVM_Error 的结构中：

    struct LSSVM_Error
    { // indices: 0 - training set, 1 - test set
      double RMSE[2]; // RMSE
      double CC[2];   // Correlation Coefficient
      double R2[2];   // R-squared
      double PCT[2];  // %
    };

数组的零索引表示训练选择，而索引 1 表示测试选择。 期望针对预测统计意义进行更严谨的评估，例如费舍尔（Fisher）测试，因为漂亮的相关性和 R2 值可能具有欺骗性。 不过，似乎不可能一次性覆盖所有内容。

计算整个选择误差的方法是 checkAll。

    void checkAll(LSSVM_Error &result)
    {
      result.RMSE[0] = result.RMSE[1] = 0;
      result.CC[0] = result.CC[1] = 0;
      result.R2[0] = result.R2[1] = 0;
      result.PCT[0] = result.PCT[1] = 0;
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      double out[];
      getResult(out);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        double given = Y[i];
        double trained = out[i];
        result.RMSE[0] += (given - trained) * (given - trained);
        // mean is 0 after normalization
        xy += (given) * (trained);
        x2 += (given) * (given);
        y2 += (trained) * (trained);
        
        if(given * trained > 0) correct++;
      }
      
      result.R2[0] = 1 - result.RMSE[0] / x2;
      result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber);
      result.CC[0] = xy / sqrt(x2 * y2);
      result.PCT[0] = correct * 100.0 / VectorNumber;
      
      crossvalidate(result); // fill metrics for test set (if attached)
    }

在循环之前，将调用 getResult 方法，该方法针对所有输入向量执行近似运算，并用这些数值填充 “out” 数组。

    void getResult(double &out[], const bool reverse = false) const
    {
      double data[];
      ArrayResize(out, VectorNumber);
      for(int i = 0; i < VectorNumber; i++)
      {
        vector(i, data);
        out[i] = approximate(data);
      }
      if(reverse) ArrayReverse(out);
    }

在此，常规预测函数 “approximate” 则用于已构建的模型：

    double approximate(const double &x[]) const
    {
      double sum = 0;
      double data[];
      
      if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference)
      {
        for(int i = 0; i < ArraySize(x); i++)
        {
          sum += Solution[i] * x[i];
        }
        sum += Solution[ArraySize(x)];
      }
      else
      {
        if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
        {
          for(int i = 0; i < VectorNumber; i++)
          {
            vector(i, data);
            sum += Alpha[i] * kernel(x, data);
          }
        }
        else                                                  // proposed SOM-LS-SVM
        {
          for(int i = 0; i < KernelNumber; i++)
          {
            ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize);
            sum += Alpha[i] * kernel(x, data);
          }
        }
      }
      return sum + Beta;
    }

在其中，找到的系数 Alpha[] 和 Beta 被应用于内核函数的总和（LS-SVM 和 SOM-LS-SVM 的情况）。

测试选择的形成方式类似于训练的方式 — 与另一个对象，LSSVM 绑定到主对象中的 “checking” 对象。

  protected:
    LSSVM *crossvalidator;
  
  public:
    bool bindCrossValidator(LSSVM *tester)
    {
      if(tester.getVectorSize() == VectorSize)
      {
        crossvalidator = tester;
        return true;
      }
      return false;
    }
    
    void crossvalidate(LSSVM_Error &result)
    {
      const int vectorNumber = crossvalidator.getVectorNumber();
      
      double out[];
      double _Y[];
      crossvalidator.getY(_Y); // assumed normalized by validator
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      for(int i = 0; i < vectorNumber; i++)
      {
        crossvalidator.vector(i, out);
        
        double z = approximate(out);
        
        result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z);
        xy += (_Y[i]) * (z);
        x2 += (_Y[i]) * (_Y[i]);
        y2 += (z) * (z);
        
        if(_Y[i] * z > 0) correct++;
      }
      
      result.R2[1] = 1 - result.RMSE[1] / x2;
      result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber);
      result.CC[1] = xy / sqrt(x2 * y2);
      result.PCT[1] = correct * 100.0 / vectorNumber;
    }

必要时，该类能够利用带有 Ve_torSize 变量和 VectorNumber 方程的最小二乘法执行线性回归，替代按 LS-SVM/SOM-LS-SVM 算法的非线性优化。 为此目的，实现 “regress” 方法。

    bool regress(void)
    {
      CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column
      
      for(int i = 0; i < VectorNumber; i++)
      {
        MATRIX[i].Set(VectorSize, Y[i]);
      }
      
      for(int i = 0; i < VectorSize; i++)
      {
        for(int j = 0; j < VectorNumber; j++)
        {
          MATRIX[j].Set(i, X[j * VectorSize + i]);
        }
      }
      
      CLinearModel LM;
      CLRReport AR;
      int info;
      
      CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR);
      if(info != 1)
      {
        Alert("Error in regression model!");
        return false;
      }
      
      int _size;
      CLinReg::LRUnpack(LM, Solution, _size);
      
      Print("RMSE=" + (string)AR.m_rmserror);
      ArrayPrint(Solution);
      
      return true;
    }

该方法在准确性上是 LS-SVM 的先验算法，放于此处只为演示。 另一方面，它可用于回归数据，在本质上比报价更原始。 通过设置 KernelNumber=-1 启用此模式。 在此情况下，方程解将写入 Solution 数组，且不涉及 Alpha[] 和 Beta。

我们基于 LSSVM 类创建一个预测指标。

预测指标 LS-SVM

指标 SOMLSSVM.mq5 的任务是创建 2 个 LSSVM 对象（一个用于训练选择，一个用于测试），执行回归，并显示初始和预测两组的数值，并带有品质评估。 参数 “gamma” 和 “sigma” 可认为已找到，并由用户设置。 利用标准测试器在 EA 中优化它们更为方便（本文的下一部分将对此进行讲解）。 从技术上讲，测试器还可以支持优化指标，因为这种限制是人为的。 然后，我们可以直接在指标中优化模型。

该指标将在一个单独的窗口中运行，并有 4 个缓冲区。 2 个缓冲区显示训练集的初始值和预测值，其他 2 个缓冲区将显示测试集的值。

输入:

  input int _VectorNumber = 250; // VectorNumber (training)
  input int _VectorNumber2 = 50; // VectorNumber (validating)
  input int _VectorSize = 20; // VectorSize
  input double _Gamma = 0; // Gamma (0 - auto)
  input double _Sigma = 0; // Sigma (0 - auto)
  input int _KernelNumber = 0; // KernelNumber (0 - auto)
  input int _TrainingOffset = 50; // Offset of training bars
  input int _ValidationOffset = 0; // Offset of validation bars
  input int DifferencingOrder = 1;

前两个设置了训练和测试集的大小。 向量大小则在 VectorSize 中指定。 参数 Gamma 和 Sigma 可保留为 0，以便根据输入自动选择其值。 不过，这种非主流模式的品质远非最佳 — 我们只需要令指标采用默认值操作即可。 利用 LS-SVM 方法进行回归时，KernelNumber 应该保留为 0。 默认情况下，测试集位于报价历史记录的末尾，而训练集位于报价历史记录的左侧（时间顺序更早）。

根据输入初始化对象。

  LSSVM *lssvm = NULL;
  LSSVM *test = NULL;
  
  int OnInit()
  {
    static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"};
    
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetString(i, PLOT_LABEL, titles[i]);
    }
    
    lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset);
    test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset);
    lssvm.setDifferencingOrder(DifferencingOrder);
    test.setDifferencingOrder(DifferencingOrder);
    
    return INIT_SUCCEEDED;
  }

因为指标是为演示目的而创建的，故此它仅计算一次。 在必要时，可以轻松进行调整，从而在每根柱线上刷新指标，但出于成本考虑，该系统仅会解题一次，或每隔相当长的时间之后才重复。

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {
    ArraySetAsSeries(Open, true);
    ArraySetAsSeries(Time, true);
    
    static bool calculated = false;
    if(calculated) return rates_total;
    calculated = true;
    
    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }
    
    lssvm.bindCrossValidator(test);
    bool processed = lssvm.process(true);

在 OnCalculate 当中，我们将测试集与训练集相连接，然后启动回归。 如果成功完成，我们将显示所有数据，包括初始数据和预测数据：

  if(processed)
  {
    const double m1 = lssvm.getMean();
    const double s1 = lssvm.getStdDev();
    const double m2 = test.getMean();
    const double s2 = test.getStdDev();
    
    // training
    
    double out[];
    lssvm.getY(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[0].set(_TrainingOffset, out);
    
    lssvm.getResult(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[1].set(_TrainingOffset, out);
    
    // validation
    
    test.getY(out, true);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      out[i] = out[i] * s2 + m2;
    }
    
    buffers[2].set(_ValidationOffset, out);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      test.vector(i, out);
      
      double z = lssvm.approximate(out);
      z = z * s2 + m2;
      buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z;
      ...
    }
  }

由于我们有分析差值序列的选项，因此指标显示在单独的窗口中。 然而，实际上，我们仍在操控价格，故更希望在主图表中显示预测。 为此目的，可以使用对象。 它们在价格轴上的坐标应从差值序列中恢复。 下面的规化图描绘了初始序列和由此衍生的多维差值序列中元素的索引（按时间顺序索引）：

    d0:  0   1   2   3   4   5  :y
    d1:    0   1   2   3   4
    d2:      0   1   2   3
    d3:        0   1   2

例如，如果差值为第一维（d1），则很明显：

y[i+1] = y[i] + d1[i]

对于第二维（d2）和第三维（d3）的差值，方程如下：

y[i+2] = 2 * y[i+1] - y[i] + d2[i]

y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]

我们可以看到，微分的阶数越高，前置计算 y 的数量就越大。

应用这些公式后，我们可以在价格图表中利用对象显示预测。

      if(ShowPredictionOnChart)
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2]
                 + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z;
        }
        else
        {
          // unsupported yet
        }
        
        string name = prefix + (string)i;
        ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target);
        ObjectSetString(0, name, OBJPROP_TEXT, "l");
        ObjectSetString(0, name, OBJPROP_FONT, "Wingdings");
        ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER);
        ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed);
      }

我们没有考虑任何大于 3 的维度，因为它们既有正面影响，也有负面影响。 应当提醒您，正面在于，由于平稳性的提高，预测品质随维数的增加而增长。 然而，这尤其适用于相关阶导数的预测，而非初始序列。 高阶微分的负面影响是，即使它们只有一点很小的误差增长，那么随后增量也会“部署”到一个完整系列里。 因此，对于 DifferencingOrder，还应该利用优化或反复试验找到“黄金均值”。

可以在下面的两个屏幕截图中观察到这两种影响（浅绿色和绿色线分别是训练和测试集的真实数据，而浅蓝色和蓝色线是同期的预测）：

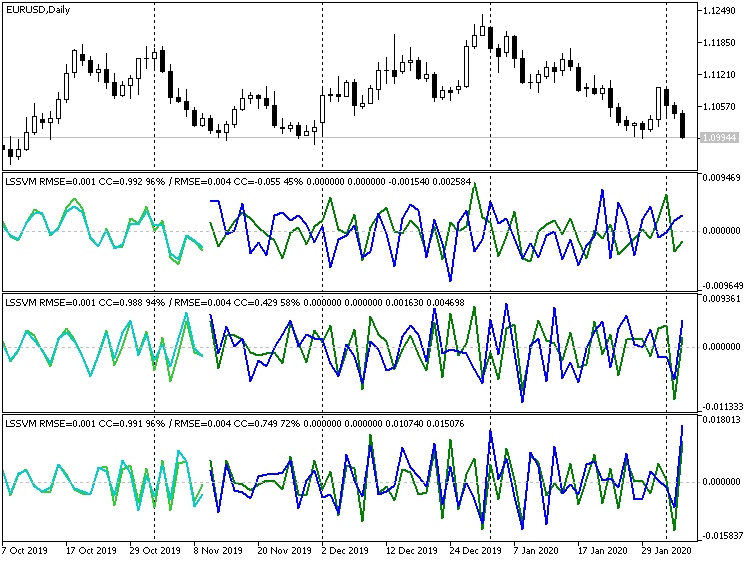
取 EURUSD D1 序列的各种微分阶数的 LSSVM 指标

此处，显示了 3 个指标实例，它们的常规设置含有不同的微分阶数。 常规设置：

• _VectorNumber = 250; // VectorNumber (training)
• _VectorNumber2 = 60; // VectorNumber (validating)
• _VectorSize = 20; // VectorSize
• _Gamma = 2048; // Gamma (0 - auto)
• _Sigma = 8; // Sigma (0 - auto)
• _KernelNumber = 0; // KernelNumber (0 - auto)
• _TrainingOffset = 60; // Offset of training bars
• _ValidationOffset = 0; // Offset of validation bars

微分阶数分别为 1、2 和 3。 在每个窗口标题上的斜线之后，显示了所选测试（在这种情况下为验证）的预测指示：它们增长得很好（相关系数：-0.055、0.429 和 0.749；而匹配的增量分别为 45％，58％ 和 72％）。 实际上，即便肉眼也能看出线条的重合性很好。 然而，如果我们恢复价格图表中的三阶预测，则会得到以下图片：

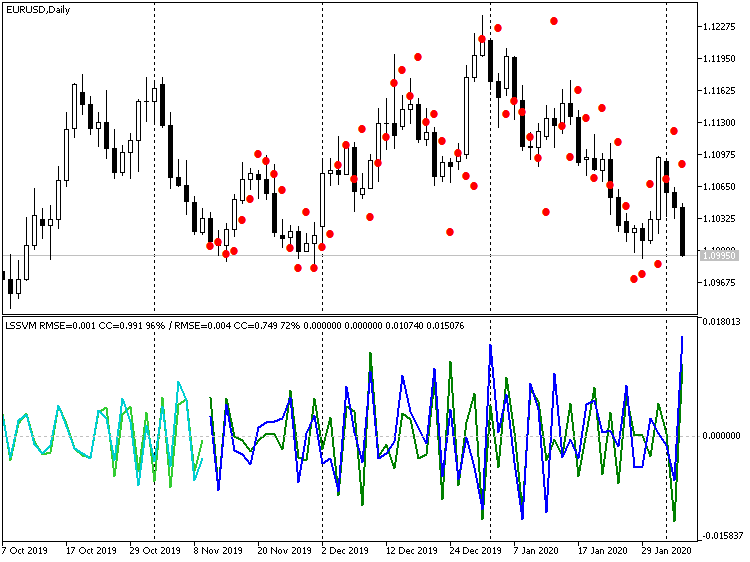
三阶微分 LSSVM 指标，预测恢复值，EURUSD D1

显然，许多点的特征为跳动。 另一方面，如果我们完全禁用微分，我们将得到：

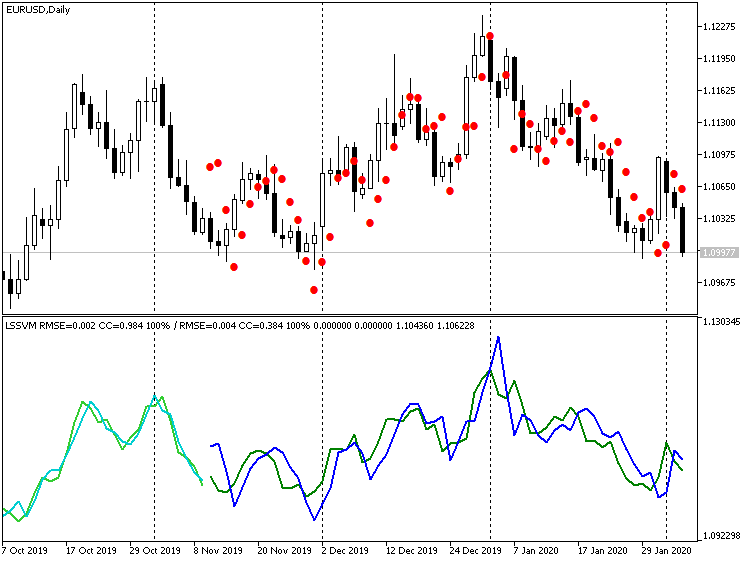
指标 LSSVM 未用微分，预测恢复值，,EURUSD D1

在此，价格值非常接近真实价格，但有大约 1 根柱线的可见滞后。 产生这种效果的原因是，事实上，我们的算法等效于数字滤波器，这是一种基于 N 个实例向量的移动平均值。 考虑到价位的接近性，一次性预测超前若干步来消除 1-2 根柱线的滞后是合理的，即，获得柱线 - 1 的预测后，将其作为预测柱线 - 2 的输入， 等等 在下一章节中创建 EA 时，我们将提供此模式。

LS-SVM 智能交易系统

智能交易系统 LSSVMbot.mq5 旨在执行两个任务：

• 在虚拟模式下（不进行交易）优化 LS-SVM 的 “Gamma” 和 “Sigma” 参数；
• 在测试器中进行交易，以及（可选）在交易模式下优化其他参数。

在虚拟模式下，如指标一般，用到 2 个 LSSVM 实例：一个含训练集，另一个含测试集。 这些是需要考虑的测试集指示。 按自定义条件执行优化。 它们全部列出如下：

  enum CUSTOM_ESTIMATOR
  {
    RMSE,   // RMSE
    CC,     // correlation
    R2,     // R-squared
    PCT,    // %
    TRADING // trading
  };

TRADING 选项可将 EA 设置为交易模式。 在其中，可按嵌入标准之一，诸如盈利、亏损、回撤、等等，以常规方式优化 EA。

主要输入组应设置为指标中相同的值。

  input int _VectorNumber = 250;  // VectorNumber (training)
  input int _VectorNumber2 = 25;  // VectorNumber (validating)
  input int _VectorSize = 20;     // VectorSize
  input double _Gamma = 0;        // Gamma (0 - auto)
  input double _Sigma = 0;        // Sigma (0 - auto)
  input int _KernelNumber = 0;    // KernelNumber (sqrt, 0 - auto)
  input int DifferencingOrder = 1;
  input int StepsAhead = 0;

然而，TrainingOffset 和 ValidationOffset 已变为内部变量，并且会自动设置。 ValidationOffset 则一直为 0。 TrainingOffset 是在虚拟模式下验证集 VectorNumber2 的大小，或者在交易模式下为 0（因为这里暗示已经找到了所有参数，因此没有测试集，应依据最新数据执行回归）。

若要在 KernelNumber 中使用 SOM，您应该指定一侧的大小，而完整映射的大小计算为该值的平方值。

第二组输入旨在优化 “Gamma” 和 “Sigma”：

  input int _GammaIndex = 0;     // Gamma Power Iterator
  input int _SigmaIndex = 0;     // Sigma Power Iterator
  input double _GammaStep = 0;   // Gamma Power Multiplier (0 - off)
  input double _SigmaStep = 0;   // Sigma Power Multiplier (0 - off)
  input CUSTOM_ESTIMATOR Estimator = R2;

由于搜索范围非常广泛，并且标准测试器仅支持预定义步长的迭代，因此在 EA 中采用了以下方式。 必须按参数 GammaIndex 和 SigmaIndex 启用优化。 它们分别定义必须将 Gamma 和 Sigma 的初始值乘以 GammaStep 和 SigmaStep 多少次才能获得 “gamma” 和 “sigma” 的工作值。 例如，如果 Gamma 为 1，GammaStep 为 2，并且正在为 0-5 范围内的 GammaIndex 执行优化，则该算法将评估 “gamma” 值 1、2、4、8、16 和 32。 如果 GammaStep 和 SigmaStep 不为 0，则始终采用1它们来计算 “gamma” 和 “sigma” 的工作值，包括在一次测试仪运行中。

EA 依据柱线操作。 请求的历史柱线（向量）数量可用之前，EA 不会开始计算。 如果测试器中的柱线数量不足，则运行可能会空转 — 请参阅日志。 不幸的是，测试器在启动时加载的历史柱线数量取决于许多因素，例如时间帧，一年中的天数等，并且可能相差很大。 如有必要，将初始测试时间移到过去。

在虚拟模式下，模型仅训练一次，并且特征之一（在 Estimator 中选择）从函数 OnTester 返回，作为品质指标（在选择 RMSE 的情况下，误差带有逆反的符号）。

  bool optimize()
  {
    if(Estimator != TRADING) lssvm.bindCrossValidator(test);
    iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep);
    bool success = lssvm.process();
    if(success)
    {
      LSSVM::LSSVM_Error result;
      lssvm.checkAll(result);
      
      Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma());
      Print("  training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]);
      Print("  test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]);
      
      customResult = Estimator == CC ? result.CC[1]
                  : (Estimator == RMSE ? -result.RMSE[1] // the lesser |absolute error value| the better
                  : (Estimator == PCT ? result.PCT[1] : result.R2[1]));
    }
    return success;
  }
  
  void OnTick()
  {
    ...
    if(Estimator != TRADING)
    {
      if(!processed)
      {
        processed = optimize();
      }
    }
    ...
  }
  
  double OnTester()
  {
    return processed ? customResult : -1;
  }

在交易模式下，默认情况下也仅对模型进行一次训练，但是您可以设置每年、每季度或每月重绘。 为此目的，在 OPTIMIZATION 参数（在代码里是 named_2）中，应输入 “y”，“q” 或 “m”（也支持大写）。 请记住，此过程仅涉及根据新（最新）数据求解方程组； 但是，“gamma” 和 “sigma” 参数保持不变。 从技术上讲，我们可以完善该过程，并在每次重新训练时即时尝试参数（我们先前分配给标准优化程序的参数）；但是，这必须在 EA 中进行组织，因此将在单一线程里执行。

这意味着在相当长的一段时间（一年或更长时间）内与数据匹配的 “gamma” 和 “simga” 参数必须在较短的交易期间内具有相关性。

建立模型后，将使用 LSSVM 的测试实例读取最新的已知价格，依其形成输入向量，并将其常规化。 然后将向量传递给方法 lssvm.approximate：

    static bool solved = false;
    if(!solved)
    {
      const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0);
      solved = opt ? optimize() : lssvm.process();
    }
    
    if(solved)
    {
      // test is used to read latest _VectorNumber2 prices
      if(!test.buildXYVectors())
      {
        Print("No vectors");
        return;
      }
      test.normalizeXYVectors();
      
      double out[];
      
      // read latest vector
      if(!test.buildVector(out))
      {
        Print("No last price");
        return;
      }
      test.normalizeVector(out);
      
      double z = lssvm.approximate(out);

取决于输入 StepsAhead，EA 要么使用获得的值 z，然后通过逆常规化将其转换为价格预测，要么将预测重复预设次数，然后将其转换为价格。

      for(int i = 0; i < StepsAhead; i++)
      {
        ArrayCopy(out, out, 0, 1);
        out[ArraySize(out) - 1] = z;
        z = lssvm.approximate(out);
      }
      
      z = test.denormalize(z);

由于时间序列可能会有所不同，因此我们采用几个最新的价格值，通过它们和预测增量来恢复下一个价格值。

      double open[];
      if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = open[2] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * open[2] - open[1] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * open[2] - 3 * open[1] + open[0] + z;
        }
        else
        {
          // unsupported yet
        }

根据相对于当前价格的预测价位，EA 开仓交易。 如果所请求方向已有开仓，则它继续持仓。 如果持仓为逆向，则执行相反操作。

        int mode = target >= open[2] ? +1 : -1;
        int dir = CurrentOrderDirection();
        if(dir * mode <= 0)
        {
          if(dir != 0) // there is an order
          {
            OrdersCloseAll();
          }
          
          if(mode != 0)
          {
            const int type = mode > 0 ? OP_BUY : OP_SELL;
            const double p = type == OP_BUY ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID);
            OrderSend(_Symbol, type, Lot, p, 100, 0, 0);
          }
        }
      }
    }

我们查验 EA 在两种模式下如何工作。 我们取 XAUUSD 作为操作工具，与货币对相比，它很少受到国家消息影响。 时间帧是 D1。

附上设置文件（LSSVMbot.set）。 训练集 VectorNumber 的大小自行选取为 200。 这略少于一年。 大约 1000 的值可能太大，已经大大抑制了方程组的求解。 测试集 VectorNumber2=50。 向量大小 VectorSize=20（一个月）。 不使用 SOM（KernelNumber=0）。 禁用微分（DifferencingOrder=0），但在交易模式下的验证阶段，由于我们注意到预测值相对于价格略有延迟，因此将预测设置为提前 2 步（StepsAhead=2）。 在虚拟模式下，在评估模型里未使用输入参数 StepsAhead。

Gamma 和 Sigma 的基本值为 1，但它们的乘数，幂次（GammaStep，SigmaStep）等于 2，而要在优化中执行的乘法次数在迭代器 GammaIndex 和 SigmaIndex 中分别定义为从 5 到 35，以及从 5 到 20，步长为 5。 因此，当 GammaIndex 为 15 时，Gamma 将取值 1*(2 的 15 次幂)，即 32768。

尝试找到正确的范围，以便查找 “gamma” 和 “sigma” 是一项常规任务，因为对于它来讲，不幸的是，除了先用粗网格，其次是用细网格来计算之外，没有其他解。 我们自行限定为一个网格，因为在准备本文时进行了许多试验，且考虑它能在更广范围搜索。

因此，只有两个参数需要优化：GammaIndex 和 SigmaIndex。 它们在更大范围内间接改变Gamma 和 Sigma，步长可变，且呈指数性。

我们从 2018 年开始，采用开盘价优化。 遵照自定义条件 Estimator=R2 进行优化。

请记住，在这种模式下，EA不 会进行交易，而是用报价方程组来填充，并利用 LS-SVM 算法求解。 计算中涉及的柱线要有足够数量，以便形成 VectorNumber 向量，其大小为 VectorSize，并可依据可能的微分进行调整（每个附加取微分过程都需要在输入中附加柱线）。 此外，EA 还要求 VectorNumber2 测试向量按时间顺序位于训练样本之后，即位于最新的柱线上。 它在测试柱线上（更确切地说：在由它们组成的向量上），其中评估从 OnTester 返回得到的模型预测能力。

所有这些都很重要，因为测试器在启动时并不总是拥有正确的历史柱线数量，并且 EA 只能为系统填充初始日期后几个月的数据。 另一方面，我们应该记住，训练柱线总是在测试（优化）日期之前开始，因为 EA 会立即提供一定长度的历史记录。

优化完成后，我们将按条件 R2 对搜索结果进行排序（降序排列，即最佳搜索结果排在最前面）。 假设，在开始时设置 GammaIndex=15 和 SigmaIndex=5（我们说“假设”，因为运行顺序相同，但结果可能会改变）。

双击第一个记录以便运行单次测试（仍处于虚拟模式）。 我们将在日志中看到类似以下内容：

  2018.01.01 00:00:00   Bars required: 270
  2018.01.02 00:00:00   247 2017.01.03 00:00:00
  2018.02.02 00:00:00   Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270
  2018.02.02 00:00:00   G[15]=32768.0 S[5]=32.0
  2018.02.02 00:00:00   RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985
  2018.02.02 00:00:00   Parameters: 32768.0 32.0
  2018.02.02 00:00:00     training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0
  2018.02.02 00:00:00     test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0
  final balance 10000.00 USD
  OnTester result 0.9598497541714557

可以解释如下：完成整个过程需要 270 根柱线，而截至 2018 年 1 月 2 日，只有 247 根柱线可用。 仅在 2018.02.02 才出现足够数量的柱线，即一个月后，那么训练数据（可用历史记录）从 2017.01.03 开始。 然后指定工作参数 Gamma 和 Sigma（G[15]=32768.0 S[5]=32.0），优化的迭代参数在方括号中给出。 最后，我们可以在包含训练品质指标的字符串中看到 R2 的值（0.95985），该值已从 OnTester 返回。

现在我们禁用优化，将日期范围从 2017 年扩展到 2020 年 2 月，并设置 EA 的参数 Estimator=TRADING（这意味着 EA 将执行交易操作）。 在参数 OPTIMIZATION（代码里的 _2）中，我们引入符号 “q”，该符号指示 EA 每季度重新计算新数据（当时最新的 VectorNumber 向量）的回归模型。 不过，“gamma” 和 “sigma” 保持不变。

我们运行一遍测试。

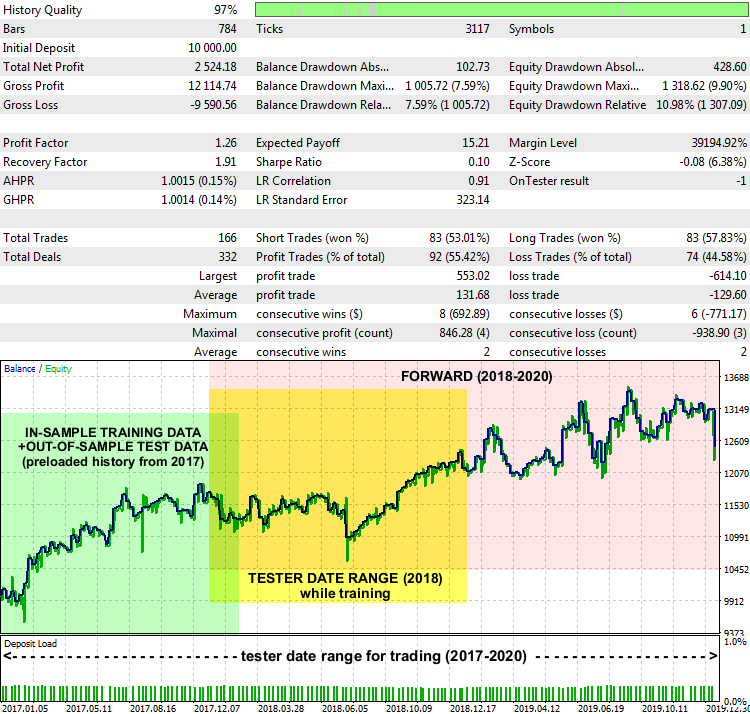
EA LSSVMbot Report on XAUUSD D1, 2017-2020

性能并不是很令人惊奇，但基本上，该系统可以运行。 日期范围标记在报告图表上，从中获取训练数据，以便找到最佳的 “gamma” 和 “sigma”（以绿色突出显示），这些范围在测试器中以训练模式定义（以黄色突出显示），以及 EA 在未知数据上进行交易的范围（以粉色突出显示）。

解释预测和围绕该预测构建交易策略的方式可以不同。 特别是，在我们的测试 EA 中，有一个输入 PreviousTargetCheck（默认为 false）。 若启用它，将用另一套策略执行基于预测的交易：业务方向由最新预测相对于前一个预测的位置判定。 还有其他一些进一步的构想，则是尝试其他设置，例如 SOM 集簇，根据预测的走势强度更改手数大小，重新填充等。

结束语

在本文中，我们已了解了基于 LS-SVM 预测时间序列的算法，运用这些数学方法需要行动，和精心配置。 在实践中成功地运用上述方法（第 1 部分中的 EMD 和第 2 部分中的 LS-SVM），可能在很大程度上取决于时间序列的特殊层面，而应用于交易，也要取决于金融工具的性质和时间帧。 所以，选择与特定算法能力相关的行情，与实现知识密集型和/或资源密集型计算一样重要。 特别是，外汇货币的可预测性较差，更容易受到外部冲击的影响，仅基于历史报价进行预测，会因此而降低效率。 贵金属、指数、或均衡性篮子/资产组合应被认为更适合于上述两种方法。 甚而，无论预测多么令人着迷，我们都不应忘记风险管理，保护性止价单，和消息面监控。

在自己的 MQL 项目里，您可将提供的源代码嵌入到新方法之中。