
Prognose von Zeitreihen (Teil 2): Least-Square Support-Vector Machine (LS-SVM)
Schlüsselwörter: LS-SVM, SOM-LS-SVM, SOM
Einführung
In diesem Artikel werden wir weiter über die Algorithmen zur Vorhersage von Zeitreihen berichten. In Teil 1 stellten wir die Methode der Vorhersage der empirischen Moduszerlegung (EMD) und den Indikator TSA für die statistische Analyse von Zeitreihen vor. In diesem zweiten Teil ist der Gegenstand unserer Untersuchungen die Support-Vektor-Maschine (SVM) in ihrer Version Least-Squares Support-Vektor-Maschine (LS-SVM)). Diese Technologie ist noch nicht in MQL implementiert worden. Aber zuerst müssen wir uns mit der Mathematik dafür vertraut machen.
Mathe der LS-SVM
Support Vector Machine (SVM) ist ein Überbegriff für eine Gruppe von Datenanalyse-Algorithmen, die bei Klassifikation und Regression verwendet werden. Es ist die Regression, die für uns von besonderem Interesse ist (Artikel in Wikipedia auf Englisch), da sie die Wechselbeziehung zwischen den Regressand (abhängige Variablen der Regressionsanalyse) und den Prädiktoren identifiziert. Das Prognoseproblem kann durch die Regression als das Auffinden einer bestimmten Funktion in Abhängigkeit von den vorherigen Zählungen der Zeitreihe (oben erwähnte Prädiktoren) angegeben werden, so dass ihre Werte die zukünftigen Zählungen der Zeitreihe so vernünftig wie möglich beschreiben.
Der SVM-Algorithmus basiert auf der Übertragung der Quelldaten in einen Raum mit höherer Dimensionalität, wo jeder Eingangsvektor als eine Folge von Saatpunkten mit Zeitverzögerungen gebildet wird. Dann werden diese Vektoren als Schlüsselstichproben verwendet, die, wenn sie auf spezielle Weise kombiniert werden, die Berechnung einer Regressionshyperebene ermöglichen, die die Datenverteilung mit einer bestimmten Genauigkeit definiert. Diese Berechnungen stellen eine Zusammenfassung aller Stichproben der sogenannten "Kernls", d.h. der einheitlichen Funktionen der Eingaben, dar. Diese Funktionen können linear oder nichtlinear (normalerweise glockenförmig) sein und durch die Parameter geführt werden, die die Genauigkeit der Regression beeinflussen. Die gebräuchlichsten Kernel sind:
- Linear
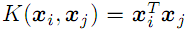 ;
; - Polynom vom Grad d
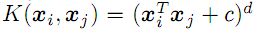
- Radiale Basisfunktion mit der Sigma-Dispersion (nach Gauß, siehe unten);
- Sigmoid (Hyperbolische Tangs)
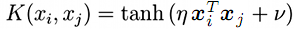 ;
;
Es gibt eine SVM-Modifikation, Least-Squares SVM (LS-SVM), oder die Support-Vektor-Methode der kleinsten Quadrate. Sie erlaubt es, ein Problem als ein System von linearen Gleichungen zu lösen, anstatt das äquivalente nichtlineare Anfangsproblem zu lösen.
Angenommen, wir haben eine Zeitreihe y mit die einen uns bekannten Wert im Zeitpunkt t alsa Funktion p von vorhergehenden Punkten und einigen externen Variablen q und einem Fehler e. Im Allgemeinen wird dies wie folgt geschrieben:
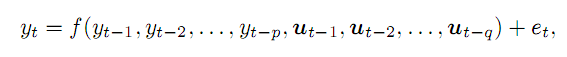 (1)
(1)
Externe Variablen (im angewandten Handel) können durch die Wochentagsnummer, die Tagesstundenzahl oder das relevante Balkenvolumen veranschaulicht werden. In diesem Artikel werden wir uns nur auf die vorhergehenden Punkte einer Preiszeitreihe beschränken. Die Komplexität des Materials erlaubt es nicht, alle Aspekte zu berücksichtigen.
Aus der Reihe genommen, bilden p vorhergehende Punkte einen Vektor im p-dimensionalen Raum. Wenn wir uns entlang der Anfangsreihe von links nach rechts bewegen, erhalten wir einen Satz von Vorhersagevektoren, die wir als x bezeichnen werden; für den Zeitpunkt t wird ihre Übereinstimmung mit der Vorhersage y wie folgt ausgedrückt:
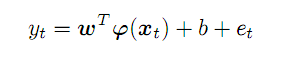 (2)
(2)
Der unbekannte Vektor der Koeffizienten w und transformierenden Funktionen f arbeiten in einem abstrakten Merkmalsraum, dessen Dimensionalität potentiell unbegrenzt ist und sogar höher als p sein kann, während das Aussehen f, sowie die Werte der Koeffizienten w, genau im Prozess der Optimierung gefunden werden sollten:
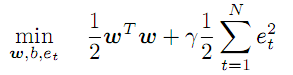 (3)
(3)
Diese Bedingung schreibt die Minimierung des Wertes der Koeffizienten w vor und führt den Regularisierungs-/Strafungsfaktor Gamma für Fehlerraten ein. Je größer das Gamma ist, desto genauer muss die Regression die Quelldaten approximieren. Wenn das Gamma abnimmt, nimmt die Toleranz von Abweichungen zu, wodurch die Modellglätte erhöht wird.
Das Gleichungssystem (2) wirkt als Begrenzung für alle t von 1 bis N (Anzahl der Vektoren).
Um das Problem zu erleichtern, werden mathematische "Tricks" verwendet (einer davon wird sogar "Kernel-Trick" genannt): Anstelle des anfänglichen Optimierungsproblems lösen wir das sogenannte duale, ein im wesentlichen äquivalentes Problem, bei dem es uns gelingt, Koeffizienten w und Transformationen f im Austausch gegen Kernel-Funktionen (siehe unten) zu eliminieren. Als Ergebnis wird die Lösung auf ein lineares System reduziert:
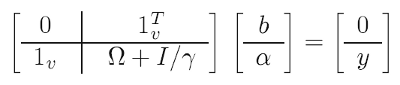 (4)
(4)
Enthaltene bekannte Daten:
- y - Vektor, bestehend aus allen Ziel- (Trainings-) Werten der Prognose;
- 1 - Einheitsvektor (Zeile und Spalte);
- I - Einheitsmatrix;
- gamma - oben beschriebener Regularisierungsparameter (der anhand der Vorhersagequalität auf einem Testsatz zu suchen ist);
- omega - Matrix, die nach folgender Formel berechnet wird:
![]() (5)
(5)
Und hier sehen wir schließlich die oben angekündigten Kernelfunktionen, K, die auf den paarweisen Kombinationen unter allen Eingangsvektoren x berechnet wurden. Für eine radiale Basisfunktion als symmetrische Gaußsche Funktion (wir werden sie verwenden) ergibt sich die Formel K wie folgt:
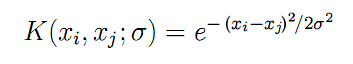 (6)
(6)
Der Parameter "sigma" beschreibt die Glockenbreite — es ist ein weiterer Parameter, der in der Praxis iterativ gesucht werden sollte. Je größer das Sigma ist, desto mehr "benachbarte" Vektoren sind an der Regression beteiligt. Wo das Sigma klein ist, geht die Funktion tatsächlich genau entlang der Punkte des Trainingsdatensatzes und hört auf, auf unbekannte Bilder zu reagieren, d.h. zu verallgemeinern.
Unter Verwendung der Quelldaten (x, y) und der Formeln (4), (5) und (6) wenden wir die Methode der kleinsten Quadrate an, um alle unbekannten Bilder zu erhalten:
- b - Abstandsterm, der in (2) und (7) involviert ist;
- a - Vektor der "alpha"-Koeffizienten, die in der endgültigen Formel des Regressionsmodells enthalten sind:
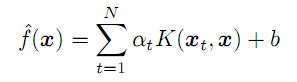 (7)
(7)
Für jeden beliebigen Vektor x (nicht aus dem Trainingsset) erlaubt sie die Berechnung der Vorhersage als Summe der Produkte der "alpha"-Koeffizienten und der Kernel für alle Quell-N-Vektoren, bereinigt um den Abstands-Term b.
Es bleiben noch 2 Fragen im theoretischen Teil zu beantworten. Erstens: Woher kennen wir die freien Parameter "gamma" und "sigma"? Zweitens: Welche Tiefe sollten wir für Zeitverzögerungen p wählen, um aus der Zeitreihe der Kurse die Eingangsvektoren x zu bilden?
Tatsächlich werden die Parameter durch Probieren gefunden: In der Schleife verwenden wir ein sehr breites, zweidimensionales Wertraster, um die Modelle für jede Kombination zu bewerten und ihre Qualität einzuschätzen. Qualität bedeutet das Minimieren des Vorhersagefehlers auf einem anderen Testdatensatz als dem Trainingssatz. Das Verfahren ähnelt dem MetaTrader Tester und kann eine Optimierung im MetaTrader Tester beinhalten. Bei der Untersuchung größerer Bereiche ist es jedoch erforderlich, die Werte tatsächlich nicht mit einer festen Schrittweite, sondern exponentiell, d.h. durch Multiplikation, zu ändern. Daher werden wir diesen Aspekt in der Implementierungsphase berücksichtigen müssen.
Es wird empfohlen, die Größe des Eingabebereichs p auf der Grundlage der Eigenschaften der zu prognostizierenden Reihe zu definieren, insbesondere unter Verwendung der partikulären Autokorrelationsfunktion (PACF). In unserem nächsten Beitrag bereiteten wir Werkzeuge zur Berechnung der PACF vor und sahen, wie sie auf einer differenzierten EURUSD D1 für einen bestimmten Teil der Geschichte erschien. Jeder Diagrammbalken beschreibt, wie sich die Balken mit der jeweiligen Zeitverzögerung auf den aktuellen Balken auswirken (d.h. im Allgemeinen während der gesamten Auswahl paarweise zwischen den Balken mit den Indizes, die sich durch den Wert der Verzögerung unterscheiden). 2-Punkt-Diagramme oberhalb und unterhalb legen die Grenzen des 95%-Konfidenzintervalls fest. Die meisten PACF-Berechnungen liegen innerhalb des Intervalls, aber einige gehen darüber hinaus. Technisch gesehen ist es sinnvoll, bei der Bildung von Eingabevektoren zunächst Berechnungen mit größeren Werten durchzuführen, da diese die Verbindung zwischen dem neuen Balken und den relevanten der vergangenen Balken anzeigen. Mit anderen Worten, es könnten nicht alle bisherigen Berechnungen in den Vektor y gelegt werden, sondern z.B. die 6., 8. und 50. wie im Bild aus unserem vorhergehenden Artikel. Diese Situation ist jedoch nur für eine bestimmte Auswahl typisch. Wenn wir nicht 500 Bars von D1 nehmen, sondern 1000 oder 250, erhalten wir einen neuen PACF mit anderen "Wavelets". Daher erfordern die Berechnungen der Quellenserie bei jeder Datenänderung eine "Ausdünnung", was wiederum eine erneute Optimierung der LS-SVM-Einstellungen, insbesondere der Parameter "gamma" und "sigma", erforderlich macht. Um die Universalität des Algorithmus zu verbessern, wenn auch um den Preis eines gewissen Effizienzverlustes, haben wir uns daher entschieden, aus allen aufeinanderfolgenden Bars in einer gegebenen Tiefe p Eingangsvektoren für das Konfidenzintervall zu bilden, um die grundlegenden "Durchläufe" auf diesem ersten Abschnitt der PACF abzudecken. In der Praxis bedeutet dies p innerhalb des Bereichs von 20-50 Bars für EURUSD D1.
Schließlich ist zu beachten, dass die Komplexität der LS-SVM quadratisch von der Länge der N-Auswahl abhängt, da die Matrixgröße (N+1)*(N+1) beträgt. Bei den Selektionen, die mehrere Hundert und Tausende von Bars umfassen, kann sich dies nachteilig auf die Leistung auswirken. Es gibt viele Versionen von LS-SVM, die versuchen, mit diesem "Fluch der Dimensionalität" umzugehen. Eine von ihnen schlägt zum Beispiel vor, zunächst alle Vektoren mit Hilfe einer Kohonen Self-Organizing Map (SOM) zu clustern und dann für jeden Cluster individuelle M-Modelle zu trainieren (M ist die Anzahl der Cluster).
Ich schlage einen anderen Ansatz vor. Nach der Clusterbildung der anfänglichen Menge von Vektoren durch die SOM werden die gefundenen Cluster anstelle der Quellvektoren als Kernel verwendet. Zum Beispiel kann eine Auswahl von 1000 Vektoren auf einer Kohonen-Schicht der Größe 7*7 dargestellt werden, d.h. 49 Unterstützungsvektoren, was im Durchschnitt etwa 20 Quell-Samples pro Netzwerkelement liefert.
Das Kohonen-Netzwerk (selbstorganisierende Karte, SOM) wurde bereits in einer Reihe von Artikeln mit dem Titel Die praktische Verwendung eines neuronalen Kohonen-Netzes im algorithmischen Handel (Teil I und Teil II) behandelt, so dass es relativ einfach ist, es in die zu erstellende LS-SVM-Engine einzubetten.
Lassen Sie uns den Algorithmus in MQL implementieren.
LS-SVM in MQL
Wir werden alle Berechnungen in einer Klasse, LSSVM, zusammenfassen, die die Lineargleichungslöser von ALGLIB verwenden wird. Daher sollten wir sie in den Quellcode sowie in die CSOM-Bibliothek aufnehmen.
#include <Math/Alglib/dataanalysis.mqh> #include <CSOM/CSOM.mqh>
Stellen Sie das Speichern aller LS-SVM-Eingangsvektoren und -matrizen in der Klasse sicher:
class LSSVM { protected: double X[]; double Y[]; double Alpha[]; double Omega[]; double Beta; double Sigma; double Sigma22; // 2 * Sigma * Sigma; double Gamma; int VectorNumber; int VectorSize; int Offset; int DifferencingOrder; ...
Die Klasse füllt X und Y unabhängig voneinander mit den Kursen, geleitet von der Anzahl der angeforderten Vektoren, VectorNumber, ihrer Größe VectorSize und ihrem Offset auf die Historie, Offset (standardmäßig 0 - die neuesten Preise), wobei all dies über Parameter an den Konstrukteur gesendet wird.
Diese Klasse unterstützt sowohl die Verarbeitung des Quellcodes (DifferencingOrder ist 0) als auch seiner Gradunterschiede von 1 bis 3. Auf diese Technik wird weiter unten näher eingegangen.
Das Objekt KohonenMap gewährleistet eine optionale Clusterbildung, während die von ihm gefundenen Cluster in das Kernels-Array gelangen.
double Kernels[]; // SOM clusters int KernelNumber; CSOM KohonenMap; ...
Der Nutzer definiert die Netzwerkgröße (es wird eine quadratische Schicht vorgeschlagen, d.h. KernelNumber muss ein ganzzahliges Quadrat sein), und dieser Parameter kann ebenfalls optimiert werden. Wenn KernelNumber 0 (standardmäßig) oder die Gesamtzahl der Vektoren ist, wird SOM deaktiviert, und die Standardverarbeitung beginnt mit LS-SVM. Die Arbeit mit dem Netzwerk geht über dieses Papier hinaus, und diejenigen, die es wissen wollen, können die Methoden zur Vorbereitung, Schulung und Integration in den beigefügten Quellcodes finden. Beachten Sie, dass das Netzwerk zunächst randomisiert ist; um reproduzierbare Ergebnisse zu erhalten, muss daher ein Strang mit einem bestimmten Wert aufgerufen werden.
Standardmäßig werden die Daten in der Methode buildXYVectors aus der Zeitreihe der offenen Preise gelesen. In diesem Artikel werden wir nur mit ihnen arbeiten. Zur Eingabe von Zufallsdaten wird die Methode feedXYVectors angeboten, die jedoch nicht getestet wurde.
bool buildXYVectors() { ArrayResize(X, VectorNumber * VectorSize); ArrayResize(Y, VectorNumber); double open[]; int k = 0; const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y CopyOpen(_Symbol, _Period, Offset, size, open); double diff[]; ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction for(int i = 0; i < VectorNumber; i++) // loop through anchor bars { for(int j = 0; j < VectorSize; j++) // loop through successive bars { differentiate(open, i + j, diff); X[k++] = diff[0]; } differentiate(open, i + VectorSize, diff); Y[i] = diff[0]; } return true; }
Die hier genannte Hilfsmethode "differentiate" ermöglicht es, für das übergebene Array die Differenz einer zufälligen Dimension zu berechnen — das Ergebnis wird durch das "diff"-Array zurückgegeben, dessen Länge um 1 größer ist als Differenzierungsordnung.
void differentiate(const double &open[], const int ij, double &diff[]) { for(int q = 0; q <= DifferencingOrder; q++) { diff[q] = open[ij + q]; } int d = DifferencingOrder; while(d > 0) { for(int q = 0; q < d; q++) { diff[q] = diff[q + 1] - diff[q]; } d--; } }
Die Klasse unterstützt die Normalisierung von Vektoren durch Subtraktion des Mittelwerts und Division durch die Standardabweichung in der Methode normalizeXYVectors (hier nicht dargestellt).
In der Klasse gibt es auch eine Reihe von Methoden zur Berechnung der Kerne — für Vektoren aus X[] durch ihre Indizes und für externe Vektoren, zum Beispiel:
double kernel(const double &x1[], const double &x2[]) const { double sum = 0; for(int i = 0; i < VectorSize; i++) { sum += (x1[i] - x2[i]) * (x1[i] - x2[i]); } return exp(-1 * sum / Sigma22); }
Die Matrix "omega" wird mit der Methode "buildOmega" berechnet (sie verwendet die Methode "kernel", bei der die X[]-Vektoren durch Indizes aufgerufen werden):
void buildOmega() { KernelNumber = VectorNumber; ArrayResize(Omega, VectorNumber * VectorNumber); for(int i = 0; i < VectorNumber; i++) { for(int j = i; j < VectorNumber; j++) { const double k = kernel(i, j); Omega[i * VectorNumber + j] = k; Omega[j * VectorNumber + i] = k; if(i == j) { Omega[i * VectorNumber + j] += 1 / Gamma; Omega[j * VectorNumber + i] += 1 / Gamma; } } } }
Das Gleichungssystem wird gelöst und die gesuchten Koeffizienten "alpha"- und "beta" werden mit der Methode solveSoLE ermittelt.
bool solveSoLE() { // | 0 |1| | | Beta | | 0 | // | | * | | = | | // | |1| |Omega| + |Identity|/Gamma | | |Alpha| | | |Y| | CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1); for(int i = 1; i <= KernelNumber; i++) { for(int j = 1; j <= KernelNumber; j++) { MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]); } } MATRIX[0].Set(0, 0); for(int i = 1; i <= KernelNumber; i++) { MATRIX[i].Set(0, 1); MATRIX[0].Set(i, 1); } double B[]; ArrayResize(B, KernelNumber + 1); B[0] = 0; for(int j = 1; j <= KernelNumber; j++) { B[j] = Y[j - 1]; } int info; CDenseSolverLSReport rep; double x[]; CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x); Beta = x[0]; ArrayResize(Alpha, KernelNumber); ArrayCopy(Alpha, x, 0, 1); return true; }
"process" ist die Hauptmethode der Klasse zur Durchführung der Regression. Davon ausgehend beginnen wir mit der Bildung von Inputs/Outputs, der Normalisierung, der Berechnung der Matrix "omega", der Lösung des Gleichungssystems und dem Erhalten eines Fehlers für die Auswahl.
bool process() { if(!buildXYVectors()) return false; normalizeXYVectors(); // least squares linear regression for demo purpose only if(KernelNumber == -1 || KernelNumber > VectorNumber) { return regress(); } if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM { buildOmega(); } else // proposed SOM-LS-SVM { if(!buildKernels()) return false; } if(!solveSoLE()) return false; LSSVM_Error result; checkAll(result); ErrorPrint(result); return true; }
Zur Beurteilung der Optimierungsqualität gibt es mehrere, verschiedene Werte in der Klasse, die automatisch für den gesamten Datensatz berechnet werden. Dabei handelt es sich um den mittleren quadratischen Fehler, den Korrelationskoeffizienten, den Bestimmungskoeffizienten (R-Quadrat) und das Verhältnis der Übereinstimmung der Vorzeichen (nur sinnvoll in den Modi, die eine Differenzierung implizieren). Alle Aspekte werden in die Struktur von LSSVM_Error gebracht:
struct LSSVM_Error { // indices: 0 - training set, 1 - test set double RMSE[2]; // RMSE double CC[2]; // Correlation Coefficient double R2[2]; // R-squared double PCT[2]; // % };
Ein Index von Null des Arrays bedeutet eine Trainingsauswahl und Index 1 eine Testauswahl. Es wäre wünschenswert, eine strengere Bewertung der statistischen Signifikanz der Vorhersage zu verwenden, wie z.B. den Fisher-Test, da die schöne Korrelation und die R2-Werte trügerisch sein können. Es scheint jedoch unmöglich zu sein, alles auf einmal abzudecken.
Die Methode zur Berechnung des Fehlers über die gesamte Auswahl ist checkAll.
void checkAll(LSSVM_Error &result) { result.RMSE[0] = result.RMSE[1] = 0; result.CC[0] = result.CC[1] = 0; result.R2[0] = result.R2[1] = 0; result.PCT[0] = result.PCT[1] = 0; double xy = 0; double x2 = 0; double y2 = 0; int correct = 0; double out[]; getResult(out); for(int i = 0; i < VectorNumber; i++) { double given = Y[i]; double trained = out[i]; result.RMSE[0] += (given - trained) * (given - trained); // mean is 0 after normalization xy += (given) * (trained); x2 += (given) * (given); y2 += (trained) * (trained); if(given * trained > 0) correct++; } result.R2[0] = 1 - result.RMSE[0] / x2; result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber); result.CC[0] = xy / sqrt(x2 * y2); result.PCT[0] = correct * 100.0 / VectorNumber; crossvalidate(result); // fill metrics for test set (if attached) }
Vor der Schleife wird die Methode getResult aufgerufen, die eine Approximation für alle Eingangsvektoren ausführt und das Array "out" mit diesen Werten füllt.
void getResult(double &out[], const bool reverse = false) const { double data[]; ArrayResize(out, VectorNumber); for(int i = 0; i < VectorNumber; i++) { vector(i, data); out[i] = approximate(data); } if(reverse) ArrayReverse(out); }
Hier wird für das bereits konstruierte Modell die reguläre Prognosefunktion, "approximate", verwendet:
double approximate(const double &x[]) const { double sum = 0; double data[]; if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference) { for(int i = 0; i < ArraySize(x); i++) { sum += Solution[i] * x[i]; } sum += Solution[ArraySize(x)]; } else { if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM { for(int i = 0; i < VectorNumber; i++) { vector(i, data); sum += Alpha[i] * kernel(x, data); } } else // proposed SOM-LS-SVM { for(int i = 0; i < KernelNumber; i++) { ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize); sum += Alpha[i] * kernel(x, data); } } } return sum + Beta; }
Darin werden die gefundenen Koeffizienten Alpha[] und Beta auf die Summe der Kernel-Funktionen angewendet (Fälle LS-SVM und SOM-LS-SVM).
Die Testauswahl wird in ähnlicher Weise wie bei der Trainingsfunktion gebildet — mit einem weiteren Objekt, LSSVM, das an das "kontrollierende" Objekt im Hauptobjekt gebunden ist.
protected: LSSVM *crossvalidator; public: bool bindCrossValidator(LSSVM *tester) { if(tester.getVectorSize() == VectorSize) { crossvalidator = tester; return true; } return false; } void crossvalidate(LSSVM_Error &result) { const int vectorNumber = crossvalidator.getVectorNumber(); double out[]; double _Y[]; crossvalidator.getY(_Y); // assumed normalized by validator double xy = 0; double x2 = 0; double y2 = 0; int correct = 0; for(int i = 0; i < vectorNumber; i++) { crossvalidator.vector(i, out); double z = approximate(out); result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z); xy += (_Y[i]) * (z); x2 += (_Y[i]) * (_Y[i]); y2 += (z) * (z); if(_Y[i] * z > 0) correct++; } result.R2[1] = 1 - result.RMSE[1] / x2; result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber); result.CC[1] = xy / sqrt(x2 * y2); result.PCT[1] = correct * 100.0 / vectorNumber; }
Wo erforderlich, erlaubt die Klasse, anstelle der nichtlinearen Optimierung durch den LS-SVM/SOM-LS-SVM-Algorithmus, die lineare Regression durch die Methode der kleinsten Quadrate innerhalb des Systems mit VeсtorSize Variablen und VectorNumber-Gleichungen durchzuführen. Dafür wird die Methode "regress" implementiert.
bool regress(void) { CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column for(int i = 0; i < VectorNumber; i++) { MATRIX[i].Set(VectorSize, Y[i]); } for(int i = 0; i < VectorSize; i++) { for(int j = 0; j < VectorNumber; j++) { MATRIX[j].Set(i, X[j * VectorSize + i]); } } CLinearModel LM; CLRReport AR; int info; CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR); if(info != 1) { Alert("Error in regression model!"); return false; } int _size; CLinReg::LRUnpack(LM, Solution, _size); Print("RMSE=" + (string)AR.m_rmserror); ArrayPrint(Solution); return true; }
Diese Methode steht a priori in der Genauigkeit hinter LS-SVM und wurde hier hinzugefügt, um dies zu demonstrieren. Andererseits kann sie zur Regression von Daten verwendet werden, die ihrer Natur nach primitiver sind als Zitate. Dieser Modus wird aktiviert, indem KernelNumber = -1 gesetzt wird. In diesem Fall wird die Lösung in das Lösungsarray geschrieben, Alpha[] und Beta sind nicht beteiligt.
Lassen Sie uns einen Prognose-Indikator erstellen, der auf der Klasse LSSVM basiert.
Der Prognose-Indikator LS-SVM
Die Aufgabe des Indikators SOMLSSVM.mq5 besteht darin, 2 LSSVM-Objekte zu erstellen (eines für die Trainingsauswahl und eines für die Testauswahl), eine Regression durchzuführen und die Anfangs- und Prognosewerte mit den Qualitätsbeurteilungen in beiden Sets anzuzeigen. Die Parameter "gamma" und "sigma" werden als vom Nutzer bereits gefunden und eingestellt betrachtet. Es ist bequemer, sie in einer EA unter Verwendung des Standardtesters zu optimieren (der nächste Abschnitt befasst sich damit). Technisch gesehen könnte der Tester auch die Möglichkeit der Optimierung von Indikatoren unterstützen, da diese Einschränkung recht künstlich ist. Dann könnten wir das Modell im Indikator direkt optimieren.
Der Indikator wird 4 Puffer in einem separaten Fenster haben. 2 Puffer zeigen die Anfangs- und Prognosewerte für das Trainingsset an, während die 2 anderen Puffer die Werte für das Testset anzeigen.
Eingaben:
input int _VectorNumber = 250; // VectorNumber (training) input int _VectorNumber2 = 50; // VectorNumber (validating) input int _VectorSize = 20; // VectorSize input double _Gamma = 0; // Gamma (0 - auto) input double _Sigma = 0; // Sigma (0 - auto) input int _KernelNumber = 0; // KernelNumber (0 - auto) input int _TrainingOffset = 50; // Offset of training bars input int _ValidationOffset = 0; // Offset of validation bars input int DifferencingOrder = 1;
Die beiden ersten legen den Umfang der Trainings- und Testsätze fest. Die Vektorgröße wird in VectorSize angegeben. Die Parameter Gamma und Sigma können auf 0 belassen werden, um ihre Werte auf der Grundlage der Eingaben automatisch auszuwählen; die Qualität dieses trivialen Modus ist jedoch alles andere als optimal — wir brauchen ihn nur, damit der Indikator mit den Standardwerten arbeitet. KernelNumber sollte für die Regression nach der LS-SVM-Methode auf 0 belassen werden. Standardmäßig wird der Testsatz ganz am Ende der historischen Kurse platziert, während der Trainingssatz links davon steht (chronologisch früher).
Die Objekte werden auf der Grundlage der Eingaben initialisiert.
LSSVM *lssvm = NULL; LSSVM *test = NULL; int OnInit() { static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"}; for(int i = 0; i < BUF_NUM; i++) { PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE); PlotIndexSetString(i, PLOT_LABEL, titles[i]); } lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset); test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset); lssvm.setDifferencingOrder(DifferencingOrder); test.setDifferencingOrder(DifferencingOrder); return INIT_SUCCEEDED; }
Der Indikator wird nur einmal berechnet, da er zu Demonstrationszwecken erstellt wurde. Falls erforderlich, kann er leicht angepasst werden, so dass die Indikationen bei jedem Balken aktualisiert werden, aber das System sollte, weil vielleicht zu aufwendig, nur einmal oder wiederholt, nach einem größeren Zeitintervall, gelöst werden.
int OnCalculate(const int rates_total, const int prev_calculated, const datetime& Time[], const double& Open[], const double& High[], const double& Low[], const double& Close[], const long& Tick_volume[], const long& Volume[], const int& Spread[]) { ArraySetAsSeries(Open, true); ArraySetAsSeries(Time, true); static bool calculated = false; if(calculated) return rates_total; calculated = true; for(int k = 0; k < BUF_NUM; k++) { buffers[k].empty(); } lssvm.bindCrossValidator(test); bool processed = lssvm.process(true);
In OnCalculate verbinden wir die Testeinstellungen mit den Trainings-Einstellungen und starten die Regression. Wenn sie erfolgreich abgeschlossen wird, zeigen wir alle Daten an, sowohl die Anfangs- als auch die Prognosedaten:
if(processed) { const double m1 = lssvm.getMean(); const double s1 = lssvm.getStdDev(); const double m2 = test.getMean(); const double s2 = test.getStdDev(); // training double out[]; lssvm.getY(out, true); for(int i = 0; i < _VectorNumber; i++) { out[i] = out[i] * s1 + m1; } buffers[0].set(_TrainingOffset, out); lssvm.getResult(out, true); for(int i = 0; i < _VectorNumber; i++) { out[i] = out[i] * s1 + m1; } buffers[1].set(_TrainingOffset, out); // validation test.getY(out, true); for(int i = 0; i < _VectorNumber2; i++) { out[i] = out[i] * s2 + m2; } buffers[2].set(_ValidationOffset, out); for(int i = 0; i < _VectorNumber2; i++) { test.vector(i, out); double z = lssvm.approximate(out); z = z * s2 + m2; buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z; ... } }
Da wir die Möglichkeit haben, die differenzierten Reihen zu analysieren, wird der Indikator in einem separaten Fenster angezeigt. Tatsächlich arbeiten wir aber noch mit den Preisen, und es ist wünschenswert, die Vorhersage im Hauptdiagramm anzuzeigen. Zu diesem Zweck können Objekte verwendet werden. Ihre Koordinaten durch die Preisachse sollten aus der Differenzreihe wiederhergestellt werden. Die Indexierung der Elemente in der Ausgangsreihe und in den daraus abgeleiteten Differenzreihen verschiedener Dimensionen wird durch das folgende Schema veranschaulicht (Indexierung in chronologischer Reihenfolge):
d0: 0 1 2 3 4 5 :y
d1: 0 1 2 3 4
d2: 0 1 2 3
d3: 0 1 2
Wenn der Unterschied z.B. in der ersten Dimension (d1) liegt, ist das offensichtlich:
y[i+1] = y[i] + d1[i]
Für die Differenzen der zweiten (d2) und dritten (d3) Dimension werden die Gleichungen wie folgt lauten:
y[i+2] = 2 * y[i+1] - y[i] + d2[i]
y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]
Man kann sehen, dass je höher die Ordnung der Differenzierung ist, desto mehr fließen die vorhergehenden Berechnungen y in die Berechnungen ein.
Wenn wir diese Formeln angewendet haben, können wir die Prognose mit den Objekten im Preisdiagramm anzeigen.
if(ShowPredictionOnChart) { double target = 0; if(DifferencingOrder == 0) { target = z; } else if(DifferencingOrder == 1) { target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z; } else if(DifferencingOrder == 2) { target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z; } else if(DifferencingOrder == 3) { target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z; } else { // unsupported yet } string name = prefix + (string)i; ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target); ObjectSetString(0, name, OBJPROP_TEXT, "l"); ObjectSetString(0, name, OBJPROP_FONT, "Wingdings"); ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER); ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed); }
Wir haben keine höheren Dimensionen als 3 in Betracht gezogen, da das sowohl positive als auch negative Auswirkungen haben. Es sei daran erinnert, dass der positive Effekt darin besteht, dass die Prognosegüte mit zunehmender Dimension aufgrund der wachsenden Stationarität zunimmt. Dies gilt jedoch insbesondere für die Prognose für eine Ableitung der relevanten Ordnung, nicht für die der Anfangsreihe. Der negative Effekt der Differenzierung höherer Ordnung besteht darin, dass selbst ein kleiner Fehler auf ihnen im Wesentlichen bei der anschließenden "Entfaltung" der Inkremente zu einer integrierten Serie zunimmt. Daher sollte für die DifferencingOrder auch durch Optimierung oder Versuch und Irrtum eine "goldene Mitte" gefunden werden.
Beide Effekte können auf zwei Screenshots unten beobachtet werden (hellgrüne und grüne Linien sind die tatsächlichen Daten der Trainings- bzw. Testsätze, während hellblaue und blaue Linien die Prognose für dieselben sind):
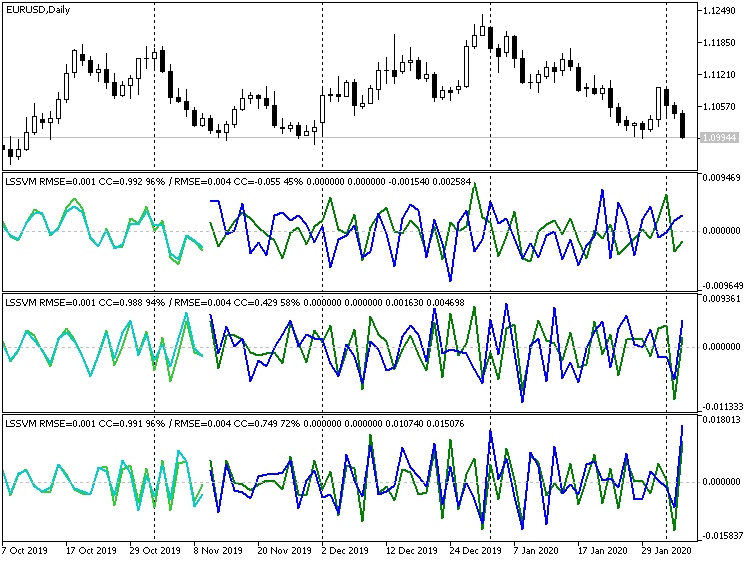
Die Indikatoren LSSVM mit verschiedenen Differenzierungsordnungen für die Serie EURUSD D1
Hier werden 3 Indikatorinstanzen mit allgemeinen Einstellungen und mit unterschiedlichen Differenzierungsordnungen gezeigt. Allgemeine Einstellungen:
- _VectorNumber = 250; // VectorNumber (Training)
- _VectorNumber2 = 60; // VectorNumber (Validierung)
- _VectorSize = 20; // VectorSize
- _Gamma = 2048; // Gamma (0 - auto)
- _Sigma = 8; // Sigma (0 - auto)
- _KernelNumber = 0; // KernelNumber (0 - auto)
- _TrainingOffset = 60; // Offset der Trainings-Bars
- _ValidationOffset = 0; // Offset der Validierungs-Bars
Die Differenzierungsreihenfolge ist 1, 2 bzw. 3. Nach der Steigungslinie in der Kopfzeile jedes Fensters werden die Vorhersagehinweise für die Auswahl des Tests (in diesem Fall der Validierung) angezeigt: Sie nehmen zum Besseren hin zu (Korrelationskoeffizient: -0,055, 0,429 und 0,749; während der Prozentsatz der übereinstimmenden Vorzeichen der Inkremente 45%, 58% bzw. 72% beträgt). Tatsächlich kann die bessere Übereinstimmung der Linien sogar visuell gesehen werden. Wenn wir jedoch die Prognose dritter Ordnung im Preisdiagramm wiederherstellen, ergibt sich folgendes Bild:
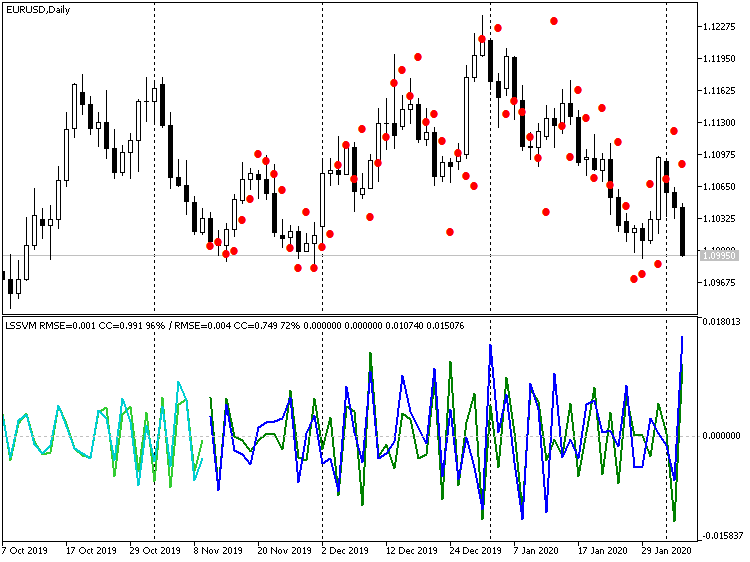
Dritt-Order-Differenzierungsindikator LSSVM mit den wiederhergestellten Prognosewerten für EURUSD D1
Offensichtlich können viele Punkte als Ausreißer charakterisiert werden. Auf der anderen Seite werden wir, wenn wir die Differenzierung überhaupt ausschalten, einen Auslauf bekommen:
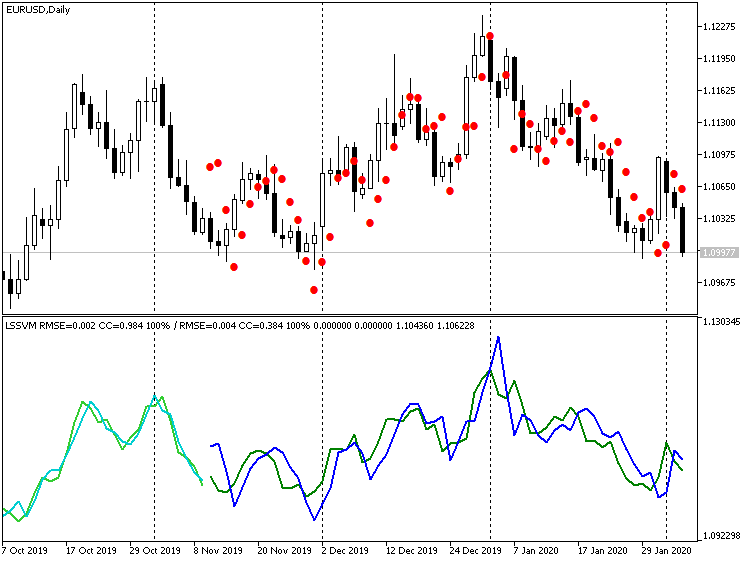
Indikator LSSVM ohne Differenzierung, mit den wiederhergestellten Prognosewerten für EURUSD D1
Hier sind die Werte der Preis viel näher an den realen Werten, aber es gibt eine sichtbare Verzögerung von etwa 1 bar. Dieser Effekt ist darauf zurückzuführen, dass unser Algorithmus in der Tat einem digitalen Filter entspricht, einer Art gleitender Durchschnitt auf der Grundlage von N-Instanzvektoren. In Anbetracht der Nähe des Preisniveaus ist es vernünftig, diese Verzögerung von 1-2 Balken auszugleichen, indem man mehrere Schritte auf einmal prognostiziert, d.h. wenn man eine Prognose für Balken -1 erhält, diese als Input für die Prognose von Balken -2 einspeist, usw. Wir werden diesen Modus bei der Erstellung eines EA im nächsten Abschnitt berücksichtigen.
Der Expert Advisor LS-SVM
Exper Advisor LSSVMbot.mq5 ist für zwei Aufgaben vorgesehen:
- der Optimierung der Parameter "Gamma"- und "Sigma" von LS-SVM im virtuellen Modus (kein Handel); und
- dem Handel im Tester und, optional, Optimierung anderer Parameter im Handelsmodus.
Im virtuellen Modus werden, wie im Indikator, 2 Instanzen von LSSVM verwendet: Eine mit einem Trainingsset und eine weitere mit einem Testset. Dabei handelt es sich um Testsatz-Indikatoren, die berücksichtigt werden. Die Optimierung erfolgt durch das nutzerdefinierte Kriterium. Sie sind alle wie folgt aufgelistet:
enum CUSTOM_ESTIMATOR { RMSE, // RMSE CC, // Korrelation R2, // R-Quadrat PCT, // % TRADING // Handel };
Die Option TRADING wird verwendet, um den EA in den Handelsmodus zu setzen. Darin kann der EA auf konventionelle Weise durch eines der eingebetteten Kriterien, wie Gewinn, Drawdown usw., optimiert werden.
Die Hauptgruppe der Eingaben setzt die gleichen Werte wie im Indikator.
input int _VectorNumber = 250; // VectorNumber (training) input int _VectorNumber2 = 25; // VectorNumber (validating) input int _VectorSize = 20; // VectorSize input double _Gamma = 0; // Gamma (0 - auto) input double _Sigma = 0; // Sigma (0 - auto) input int _KernelNumber = 0; // KernelNumber (sqrt, 0 - auto) input int DifferencingOrder = 1; input int StepsAhead = 0;
TrainingOffset und ValidationOffset sind jedoch zu internen Variablen geworden und werden automatisch gesetzt. ValidationOffset ist immer 0. TrainingOffset ist die Größe des Validierungssatzes VectorNumber2 im virtuellen Modus, oder er ist 0 im Handelsmodus (da hier impliziert wird, dass alle Parameter bereits gefunden wurden, gibt es keinen Testsatz, und die Regression sollte mit den neuesten Daten durchgeführt werden).
Um SOM in KernelNumber zu verwenden, sollten Sie die Größe einer Seite angeben, während die volle Kartengröße als quadratischer Wert dieses Wertes berechnet wird.
Die zweite Gruppe von Eingaben ist für die Optimierung von "Gamma" und "Sigma" vorgesehen:
input int _GammaIndex = 0; // Gamma Power Iterator input int _SigmaIndex = 0; // Sigma Power Iterator input double _GammaStep = 0; // Gamma Power Multiplier (0 - off) input double _SigmaStep = 0; // Sigma Power Multiplier (0 - off) input CUSTOM_ESTIMATOR Estimator = R2;
Da der Suchbereich sehr breit ist und der Standard-Tester die Iteration nur durch Hinzufügen eines vordefinierten Schrittes unterstützt, wird in der EA der folgende Ansatz verwendet. Die Optimierung muss durch die Parameter GammaIndex und SigmaIndex aktiviert werden. Jeder von ihnen definiert, wie viele Male die Anfangswerte von Gamma und Sigma mit GammaStep bzw. SigmaStep multipliziert werden müssen, um den Arbeitswert von "Gamma" und "Sigma" zu erhalten. Wenn z.B. Gamma gleich 1, GammaStep gleich 2 ist und die Optimierung für GammaIndex im Bereich von 0-5 durchgeführt wird, dann bewertet der Algorithmus die "Gamma"-Werte 1, 2, 4, 8, 16 und 32. Wenn GammaStep und SigmaStep ungleich 0 sind, werden sie immer verwendet, um die Arbeitswerte von "gamma" und "sigma" zu berechnen, auch innerhalb eines einzigen Testdurchlaufs.
Der EA arbeitet mit Bars. Der EA beginnt erst dann mit der Berechnung, wenn die gewünschte Anzahl von Balken (Vektoren) in der Historie verfügbar ist. Wenn keine ausreichende Anzahl von Balken im Tester vorhanden ist, kann der Lauf ohne Ergebnis beendet werden — siehe die Protokolle. Leider hängt die Anzahl der historischen Balken, die vom Tester beim Start geladen werden, von vielen Faktoren ab, wie z.B. Zeitrahmen, Tagesanzahl innerhalb des Jahres usw., und kann erheblich variieren. Verschieben Sie gegebenenfalls die anfängliche Testzeit weiter in die Vergangenheit.
Im virtuellen Modus wird das Modell nur einmal trainiert, und eines der (im Estimator ausgewählten) Merkmale wird von der Funktion OnTester als Qualitätsindikator zurückgegeben (im Falle der Auswahl von RMSE wird der Fehler mit umgekehrtem Vorzeichen angegeben).
bool optimize() { if(Estimator != TRADING) lssvm.bindCrossValidator(test); iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep); bool success = lssvm.process(); if(success) { LSSVM::LSSVM_Error result; lssvm.checkAll(result); Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma()); Print(" training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]); Print(" test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]); customResult = Estimator == CC ? result.CC[1] : (Estimator == RMSE ? -result.RMSE[1] // the lesser |absolute error value| the better : (Estimator == PCT ? result.PCT[1] : result.R2[1])); } return success; } void OnTick() { ... if(Estimator != TRADING) { if(!processed) { processed = optimize(); } } ... } double OnTester() { return processed ? customResult : -1; }
Im Handelsmodus wird das Modell standardmäßig ebenfalls nur einmal trainiert, aber Sie können festlegen, dass es jedes Jahr, Quartal oder Monat neu gezeichnet wird. Zu diesem Zweck sollten Sie im Parameter OPTIMIZATION (er wird im Code mit _2 bezeichnet) "y", "q" oder "m" schreiben (Großschreibung wird ebenfalls unterstützt). Denken Sie daran, dass dieser Vorgang nur die Lösung eines Gleichungssystems auf neuen (aktuellen) Daten beinhaltet; die Parameter "gamma" und "sigma" bleiben jedoch gleich. Technisch gesehen können wir den Prozess verfeinern und bei jedem Neustart Parameter on-the-fly ausprobieren (was wir zuvor dem Standard-Optimierer zugewiesen haben); dies muss dann jedoch innerhalb der EA organisiert werden und wird daher von einem einzigen Datenstrom ausgeführt.
Das bedeutet nun, dass die Parameter "gamma" und "simga", die für die Daten über einen ziemlich langen Zeitraum (ein Jahr oder mehr) abgestimmt werden, auch während kürzerer Handelsperioden relevant sein müssen.
Nach der Erstellung des Modells wird die Testinstanz von LSSVM verwendet, um die letzten bekannten Preise zu lesen, einen Eingangsvektor daraus zu bilden und ihn zu normalisieren. Dann wird der Vektor an die Methode lssvm.approximate übergeben:
static bool solved = false; if(!solved) { const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0); solved = opt ? optimize() : lssvm.process(); } if(solved) { // test is used to read latest _VectorNumber2 prices if(!test.buildXYVectors()) { Print("No vectors"); return; } test.normalizeXYVectors(); double out[]; // read latest vector if(!test.buildVector(out)) { Print("No last price"); return; } test.normalizeVector(out); double z = lssvm.approximate(out);
Je nach Eingabe, StepsAhead, verwendet der EA entweder den erhaltenen Wert z und wandelt ihn durch Denormalisierung in eine Preisprognose um, oder er wiederholt die Prognose eine vordefinierte Anzahl von Malen und wandelt sie erst dann in einen Preis um.
for(int i = 0; i < StepsAhead; i++) { ArrayCopy(out, out, 0, 1); out[ArraySize(out) - 1] = z; z = lssvm.approximate(out); } z = test.denormalize(z);
Da die Zeitreihe differenziert sein könnte, nehmen wir mehrere aktuelle Preise, um den nächsten Preis durch sie und durch den Prognosezuschlag wiederherzustellen.
double open[]; if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current { double target = 0; if(DifferencingOrder == 0) { target = z; } else if(DifferencingOrder == 1) { target = open[2] + z; } else if(DifferencingOrder == 2) { target = 2 * open[2] - open[1] + z; } else if(DifferencingOrder == 3) { target = 3 * open[2] - 3 * open[1] + open[0] + z; } else { // unsupported yet }
Je nachdem, wo sich der prognostizierte Preis im Verhältnis zum aktuellen Niveau befindet, eröffnet der EA eine Position. Wenn die Position bereits in der gewünschten Richtung eröffnet wurde, bleibt sie offen. Liegt die Position in der entgegengesetzten Richtung, wird ein Reverse durchgeführt.
int mode = target >= open[2] ? +1 : -1; int dir = CurrentOrderDirection(); if(dir * mode <= 0) { if(dir != 0) // there is an order { OrdersCloseAll(); } if(mode != 0) { const int type = mode > 0 ? OP_BUY : OP_SELL; const double p = type == OP_BUY ? SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID); OrderSend(_Symbol, type, Lot, p, 100, 0, 0); } } } }
Lassen Sie uns prüfen, wie der EA in beiden Modi funktioniert. Nehmen wir XAUUSD als ein Arbeitsinstrument, das im Vergleich zu Währungen weniger den nationalen Nachrichten ausgesetzt ist. Der Zeitrahmen ist D1.
Datei mit Einstellungen ist angehängt (LSSVMbot.set). Die Größe des Trainingssets VectorNumber wird bewusst als 200 angenommen. Dies ist etwas weniger als ein Jahr. Große Werte um 1000 können das Lösen des Gleichungssystems bereits erheblich erschweren. Testeinstellung VectorNumber2=50. Vektorgröße VectorSize=20 (ein Monat). SOM wird nicht verwendet (KernelNumber=0). Die Differenzierung ist deaktiviert (DifferencingOrder=0), aber für die Verifizierungsphase im Handelsmodus wird die Prognose auf 2 Schritte im Voraus gesetzt (StepsAhead=2), da wir bei der Verwendung des Indikators eine leichte Verzögerung der Prognose gegenüber den Preisen festgestellt haben. Im virtuellen Modus wird der Eingabeparameter StepsAhead bei der Auswertung des Modells nicht verwendet.
Die Grundwerte von Gamma und Sigma sind 1, aber ihre Multiplikatoren, der Leistungsmultiplikator (GammaStep, SigmaStep), sind gleich 2, während die Anzahl der in der Optimierung durchzuführenden Multiplikationen in den Iteratoren GammaIndex und SigmaIndex als Intervalle von 5 bis 35 bzw. von 5 bis 20 mit Schritt 5 definiert werden. Wenn also GammaIndex 15 ist, nimmt Gamma den Wert 1 * (2 hoch 15) an, d.h. 32768.
Das Ausprobieren korrekter Bereiche, um "gamma" und "sigma" zu finden, ist eine ziemliche Routineaufgabe, da es dafür leider keine andere Lösung gibt, als erstens mit einem groben und zweitens mit einem feineren Gitter zu rechnen. Wir werden uns auf ein Gitter beschränken, da bei der Vorbereitung dieses Papiers viele Versuche unternommen wurden, die als Suche in einem breiteren Bereich betrachtet werden können.
Es gibt also nur 2 Parameter, die optimiert werden müssen: GammaIndex und SigmaIndex. Sie verändern Gamma und Sigma indirekt in einem breiteren Bereich, mit einem variablen Schritt, exponentiell.
Beginnen wir die Optimierung durch offene Preise auf das Jahr 2018. Die Optimierung wird durch das benutzerdefinierte Kriterium Estimator = R2 durchgeführt.
Denken Sie daran, dass der EA in diesem Modus nicht handelt, sondern aus dem Kurs ein Gleichungssystem erstellt und es mit dem LS-SVM-Algorithmus löst. Die Balken sind an der Berechnung in den Mengen beteiligt, die ausreichen, um die Vektoren VectorNumber in der Größe VectorSize zu bilden, die für eine möglicherweise aktivierte Differenzierung angepasst sind (jedes zusätzliche Verfahren zur Differenzbildung erfordert einen zusätzlichen Balken in den Eingaben). Darüber hinaus erfordert der EA zusätzlich VectorNumber2-Testvektoren, die chronologisch nach den Trainingsvektoren liegen, d.h. auf den letzten Balken. Es handelt sich um Testbalken (genauer: auf den von ihnen abgeleiteten Vektoren), auf denen die Prognosefähigkeiten des erhaltenen Modells für die Rückkehr von OnTester bewertet werden.
All dies ist wichtig, da der Tester beim Start nicht immer die richtige Anzahl von Balken in der Historie hat und der EA das System erst einige Monate nach dem Startdatum füllen kann. Andererseits sollten wir daran denken, dass die Trainingsbalken immer vor dem Test- (Optimierungs-) Datum beginnen, da der EA sofort mit der Historie einer bestimmten Länge versehen wird.
Nach Abschluss der Optimierung sortieren wir die Ergebnisse nach Kriterium R2 (in absteigender Reihenfolge, d.h. die besten oben). Nehmen wir an, am Anfang gibt es die Einstellungen GammaIndex=15 und SigmaIndex=5 (wir sagen "nehmen wir an", weil sich die Reihenfolge der Läufe mit gleichen Ergebnissen wahrscheinlich ändern wird).
Machen Sie einen Doppelklick auf den ersten Datensatz, um einen einzelnen Test durchzuführen (immer noch im virtuellen Modus). Wir werden im Protokoll etwas wie das Folgende sehen:
2018.01.01 00:00:00 Bars required: 270 2018.01.02 00:00:00 247 2017.01.03 00:00:00 2018.02.02 00:00:00 Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270 2018.02.02 00:00:00 G[15]=32768.0 S[5]=32.0 2018.02.02 00:00:00 RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985 2018.02.02 00:00:00 Parameters: 32768.0 32.0 2018.02.02 00:00:00 training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0 2018.02.02 00:00:00 test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0 final balance 10000.00 USD OnTester result 0.9598497541714557
Dies kann wie folgt interpretiert werden: Für die Durchführung des gesamten Verfahrens waren 270 Balken erforderlich, während ab 2018.01.02 nur 247 Balken zur Verfügung standen. Eine ausreichende Anzahl von Balken erschien erst am 2018.02.02, d.h. einen Monat später, Trainingsdaten (verfügbare Historie) ab 2017.01.03. Dann werden die Arbeitsparameter Gamma und Sigma (G[15]=32768,0 S[5]=32,0 angegeben, wobei die optimierten Iteratorparameter in eckigen Klammern angegeben sind. Schließlich sehen wir den Wert von R2 (0,95985) in der Zeichenfolge mit Trainingsqualitätsindikatoren, welcher Wert von OnTester zurückgegeben wurde.
Deaktivieren wir nun die Optimierung, erweitern den Datumsbereich von 2017 bis Februar 2020 und setzen die Parameter Estimator = TRADING in den EA-Parametern (das bedeutet, dass der EA Handelsoperationen durchführen wird). Im Parameter OPTIMIZATION (_2 im Code) führen wir das Symbol "q" ein, das den EA anweist, das Regressionsmodell vierteljährlich auf der Grundlage neuer Daten (die letzten damals aktuellen VectorNumber-Vektoren) neu zu berechnen. Allerdings bleiben "gamma" und "sigma" gleich.
Lassen Sie uns einen einzigen Test durchführen.
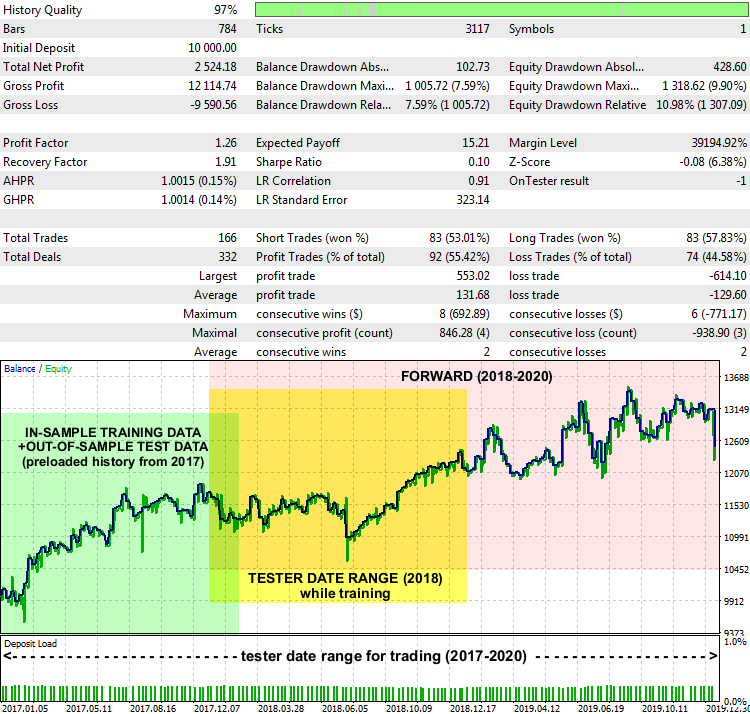
Bericht des EA LSSVMbot mit XAUUSD D1, 2017-2020
Keine wirklich erstaunliche Leistung, aber im Grunde genommen funktioniert das System. Auf dem Berichtsdiagramm sind Datumsbereiche markiert, aus denen die Trainingsdaten entnommen wurden, um ein optimales "gamma" und "sigma" zu finden (grün hervorgehoben), welcher Bereich im Trainingsmodus im Tester definiert wurde (gelb hervorgehoben) und der Bereich, in dem der EA mit unbekannten Daten gehandelt hat (rosa hervorgehoben).
Die Art und Weise, wie die Prognose interpretiert und eine Handelsstrategie um sie herum konstruiert wird, kann unterschiedlich sein. Insbesondere gibt es in unserem Test-EA eine Eingabe, PreviousTargetCheck (standardmäßig false). Wenn sie aktiviert ist, wird der prognosegestützte Handel mit einer anderen Strategie durchgeführt: Die Transaktionsrichtung wird durch die Lage der neuesten Prognose im Verhältnis zur vorhergehenden bestimmt. Es gibt auch noch etwas Spielraum für das Experimentieren mit anderen Einstellungen, wie z.B. SOM-Clusterisierung, Änderung der Losgröße in Abhängigkeit von der Stärke der prognostizierten Bewegung, Nachfüllen usw.
Schlussfolgerungen
In diesem Artikel haben wir den LS-SVM-basierten Algorithmus zur Vorhersage von Zeitreihen kennen gelernt, der den aktiven Einsatz mathematischer Methoden und eine sorgfältige Konfiguration erfordert. Die erfolgreiche Anwendung der genannten Methoden (EMD aus Teil 1 und LS-SVM aus diesem Teil 2) in der Praxis kann in erheblichem Maße von den besonderen Aspekten der Zeitreihen abhängen, während sie auf den Handel angewandt werden, aber auch von der Art eines Finanzinstruments und dem Zeitrahmen. Daher ist die Auswahl eines Marktes, der für die Fähigkeiten eines bestimmten Algorithmus relevant ist, genauso wichtig wie die Implementierung wissensintensiver und/oder ressourcenintensiver Berechnungen. Insbesondere Forex-Währungen sind weniger vorhersehbar und externen Schocks stärker ausgesetzt, was die Effizienz einer Prognose, die ausschließlich auf historischen Kursen beruht, verringert. Metalle, Indizes oder ausgewogene Körbe/Portfolios sollten für die beiden beschriebenen Methoden als besser geeignet angesehen werden. Darüber hinaus sollten wir, egal wie faszinierend eine Prognose zu sein scheint, das Risikomanagement, schützende Stopp-Verfügungen und die Überwachung des Nachrichtenhintergrunds nicht vergessen.
Die mitgelieferten Quellcodes ermöglichen es Ihnen, die neuen Methoden in Ihre eigenen MQL-Projekte einzubetten.
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/7603
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
Dieser Artikel wurde von einem Nutzer der Website verfasst und gibt dessen persönliche Meinung wieder. MetaQuotes Ltd übernimmt keine Verantwortung für die Richtigkeit der dargestellten Informationen oder für Folgen, die sich aus der Anwendung der beschriebenen Lösungen, Strategien oder Empfehlungen ergeben.
 Anwendung von OLAP im Handel (Teil 4): Quantitative und visuelle Analyse der Testberichte
Anwendung von OLAP im Handel (Teil 4): Quantitative und visuelle Analyse der Testberichte
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.