時系列の予測(第2部):最小二乗サポートベクターマシン(LS-SVM)

キーワード: LS-SVM, SOM-LS-SVM, SOM

はじめに

この記事では、引き続き予測時系列のアルゴリズムについて説明します。第1部では、時系列の統計分析のための経験的モード分解(EMD)および指標TSAの予測方法を示しました。この第2部では、調査の対象は、最小二乗サポートベクターマシン(LS-SVM)と呼ばれるバージョンのサポートベクターマシン(SVM)です。このテクノロジーはまだMQLに実装されていません。まず、そのための数学を理解する必要があります。

LS-SVMの数学

サポートベクターマシン(SVM)は分類と回帰で使用されるデータ分析アルゴリズムのグループを表す包括的な用語です。回帰と予測子の相互関係を特定するため、私たちにとって特に興味深いのは回帰です(Wikipediaの英語の記事)。予測の問題は、回帰を通じて、時系列の以前のカウント(上記の予測子)に応じて特定の関数を見つけることで説明できます。その値は時系列の将来のカウントを可能な限り合理的に表します。

SVMアルゴリズムは、ソースデータをより高次元の空間に転送することに基づいており、それぞれの入力ベクトルは、時間遅延のあるシードポイントのシーケンスとして形成されます。次に、これらのベクトルを主要なサンプルとして使用し、特別な方法で組み合わせることで、指定された精度でデータ分布を定義する回帰超平面を計算できるようにします。これらの計算は、いわゆる「カーネル」のすべてのサンプルによる要約、つまり入力の均一関数を表しています。これらの関数は、線形または非線形(通常はベル型)であり、回帰の精度に影響を与えるパラメータによってガイドされます。最も一般的なカーネルは次のとおりです。

• 線形
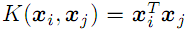
• d次多項式
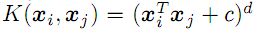
• sigma分散を伴う動径基底関数(ガウス、以下を参照)
• シグモイド(双曲線正接)

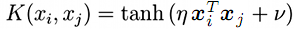
SVMを修正した最小二乗SVM(LS-SVM)(最小二乗サポートベクター法)では、同等の初期非線形問題を解く代わりに、線形方程式のシステムとして問題を解くことができます。

時系列yがあり、先行する点pと変数qの関数として、誤差eで瞬間tでの値を知ることができると仮定します。一般に、これは次のように記述されます。

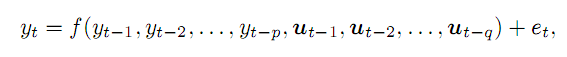 (1)

(適用される取引における)外部変数は、曜日番号、時間番号、または関連するバーボリュームによって例示できます。この記事では、価格時系列の先行する点のみに制限されます。題材が複雑であるため、すべての側面を考慮することはできません。

系列から抜粋したpの先行する点は、p次元空間のベクトルを形成します。最初の系列に沿って左から右に移動するとxとして示す一連の予測ベクトルが得られます。瞬間tでの予測yへの準拠は次のように表されます。

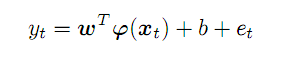 (2)

係数の未知のベクトルwおよび変換関数fは抽象的な特徴空間で機能します。ここでの次元は潜在的に無制限でpを超える可能性がある一方、外観fと係数wは最適化のプロセスで正確に見つける必要があります。

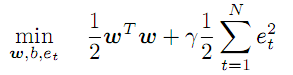 (3)

この条件は、係数wの値の最小化を規定し、誤り率の正則化/ペナルティ項(gamma)を導入します。gammaが大きいほど、回帰はより正確にソースデータを近似する必要があります。gammaが減少すると、偏差の許容値が増加し、モデルの滑らかさが増します。

方程式系(2)は、1からN(ベクトルの数)までのすべてのtの制限として機能します。

問題を容易にするために、数学的「トリック」が使用されます(そのうちの1つは「カーネルトリック」とも呼ばれます)。最初の最適化問題の代わりに、本質的に同等である、いわゆるdualを解決します。ここでは、カーネル関数と引き換えに、係数wと変換fを削除します(下記参照)。その結果、解は線形システムに削減されます。

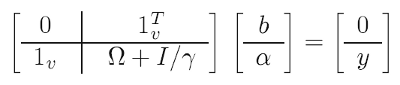 (4)

以下が既知のデータです。

• y - 予測のすべてのターゲット(訓練)値で構成されるベクトル
• 1 - 単位ベクトル(行と列)
• I - 単位行列
• gamma - 上記のパラメータの正則化(テストセットの予測品質に基づいて検索)
• omega - 次の式で計算された行列

 (5)

ここではついに、上述のすべての入力ベクトルxの対ごとの組み合わせで計算されたカーネル関数Kを確認できます。対称なガウスとしての放射基底関数の場合(本稿で使用)、式Kは次のようになります。

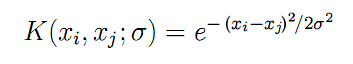 (6)

パラメータ「sigma」はベルの幅を示し、現実では繰り返し検索される必要があります。sigmaが大きいほど、より多くの「隣接する」ベクトルが回帰に関与します。sigmaが小さい場合、関数は実際には訓練用データセットの点に正確に沿って進み、未知の画像への応答、つまり一般化を停止します。

ソースデータ(x, y)と(4)、(5)、(6)の各式を使用して、最小二乗法を適用し、未知のすべてを取得します。

• b - (2)と(7)の切片項
• a - 最終回帰モデル式に含まれる「alpha」係数のベクトル

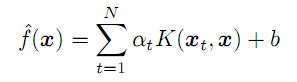 (7)

任意のベクトルx(訓練用セットではない)の場合、切片項bに合わせて調整された、すべてのソースNベクトルの「alpha」係数とカーネルの積の合計として予測を計算できます。

理論的な部分では2つの質問に答える必要があります。1つ目は、どのようにして「gamma」と「sigma」というフリーパラメータ(free parameters)がわかるかということです。2つ目は、一連の相場から入力ベクトルpを形成するために、時間遅延pにどの深さを選択するかということです。

実際、パラメータは試行錯誤法によって検出されます。ループでは、非常に幅広い2次元の値グリッドを使用して、各組み合わせのモデルを評価し、その品質を評価します。品質とは、訓練用セット以外のテストデータセットの予測誤差を最小限に抑えることを意味します。プロセスはMetaTraderテスターでの最適化に似ており、それを伴う場合があります。ただし、より大きな範囲を調査するには、固定の増分ではなく、指数関数的に、つまり乗算を使用して値を実際に変更する必要があります。したがって、実装段階でこの点を考慮する必要があります。

入力スペースpのサイズについては、特に部分自己相関関数(PACF)を使用して、予測系列の特性に基づいて定義することをお勧めします。次の記事では、PACFを計算するためのツールを準備し、特定の履歴の部分について、差別化されたEURUSD D1でそれがどのように現れるかを見ました。各チャートのバーは、バーが関連するタイムラグで現在のバーにどのように影響するかを示します(つまり、一般に、選択全体で、ラグの値が異なるインデックスを持つバーの間で対で)。上下の2点グラフは、95％信頼区間の境界を設定します。ほとんどのPACF計算は間隔内にありますが、間隔外のものもあります。技術的には、入力ベクトルを形成するとき、新しいバーと過去のバーの関連との間のリンクを示すため、最初に大きな値で計算を行うのが妥当です。つまり、過去のすべての計算をベクトルyに配置できるわけではなく、たとえば、前の記事の図のように6番目、8番目、50番目の計算を行うことができます。 ただし、この状況は特定の選択の典型的なものにすぎません。D1の500バーではなく、1000または250を取る場合、他の「ウェーブレット」を備えた新しいPACFを取得します。したがって、ソース系列の計算では、データの変更時に「間引き」が必要になるため、LS-SVM設定、特に「gamma」と「sigma」パラメータを再最適化する必要があります。したがって、アルゴリズムの普遍性を高めるために、このPACFの最初のセクションでは、効率がいくらか犠牲になったとしても、信頼区間の所定の深さpですべての連続するバーから入力ベクトルを形成し、これに関する基本的な「実行」をカバーすることにしました。 現実的には、EURUSD D1に対するpの範囲は20～50バーになります。

最後に、行列のサイズは(N+1)*(N+1)であるため、LS-SVMの複雑さはN選択の長さに二次的に依存することに注意してください。選択が数百および数千バーに相当すると、パフォーマンスに悪影響を与える可能性があります。この「次元の呪い」に対処しようとするLS-SVMには多くのバージョンがあります。 例えば、そのうちの1つは、Kohonen自己組織化マップ(SOM)を使用してすべてのベクトルをクラスタ化してから各クラスタの個々のMモデルを訓練することを提案します(Mはクラスタの数です)。

別のアプローチを提案します。SOMによる初期ベクトルセットのクラスタ化時に、検出されたクラスタは、ソースベクトルの代わりにカーネルとして使用されます。例えば、選択した1000個のベクトルは、7*7サイズのKohonen層に表示できます。つまりサポートベクトルは49個で、平均してネットワーク要素ごとに約20個のソースサンプルを提供します。

Kohonenネットワーク(自己組織化マップ、SOM)は、「アルゴリズムトレードにおけるKOHONENニューラルネットワークの実用的利用」稿(第1部および第2部)ですでに検討されているため、作成されるLS-SVMエンジンに組み込むのは比較的簡単です。

MQLでアルゴリズムを実装してみましょう。

MQLでのLS-SVM

ALGLIBの線形ソルバーを使用する1つのクラスLSSVMにすべての計算を含めます。したがって、それをソースコードとCSOMライブラリにインクルードします。

  #include <Math/Alglib/dataanalysis.mqh>
  #include <CSOM/CSOM.mqh>

クラス内のすべてのLS-SVM入力ベクトルと行列のストレージを確保します。

  class LSSVM
  {
    protected:
      double X[];
      double Y[];
      double Alpha[];
      double Omega[];
      double Beta;
      
      double Sigma;
      double Sigma22; // 2 * Sigma * Sigma;
      double Gamma;
      
      int VectorNumber;
      int VectorSize;
      int Offset;
      int DifferencingOrder;
      ...

クラスは、要求されたベクトルの数、VectorNumber、それらのサイズVectorSize、および履歴上のオフセット、Offset(デフォルトでは最新の価格である0)に基づいて、XとYに個別に相場データを入力します。これらすべてはパラメータによってコンストラクタに渡されます。

このクラスは、ソースコード(DifferencingOrderが0)および次数1から3までの違いの両方の処理をサポートします。この手法については、以下で詳しく説明します。

オブジェクトKohonenMapはオプションのクラスタ化を保証しますが、オブジェクトによって検出されたクラスタはKernels配列に入ります。

      double Kernels[];  // SOM clusters
      int KernelNumber;
      CSOM KohonenMap;
      ...

ユーザがネットワークサイズを定義し(正方形の層が推奨されます。つまり、KernelNumberは積分平方である必要があります)、このパラメータも最適化できます。KernelNumberが0(デフォルト)またはベクトルの総数である場合、SOMは無効になり、LS-SVMを使用して標準処理が開始されます。 ネットワークでの作業はこのホワイトペーパーを超えており、知りたい人は、ネットワークを準備、訓練、およびここに添付されているソースコードに統合する方法を見つけることができます。ネットワークは最初はランダム化されています。したがって、再現可能な結果を得るには、特定の値を持つストランドを呼び出す必要があります。

デフォルトでは、データはbuildXYVectorsメソッドの始値時系列から読み取られます。この記事では、それらのみを扱います。ランダムデータを入力するためにはfeedXYVectorsメソッドが提供されていますが、テストされていません。

    bool buildXYVectors()
    {
      ArrayResize(X, VectorNumber * VectorSize);
      ArrayResize(Y, VectorNumber);
      double open[];
      int k = 0;
      const int size = VectorNumber + VectorSize + DifferencingOrder; // +1 is included for future Y
      CopyOpen(_Symbol, _Period, Offset, size, open);
      
      double diff[];
      ArrayResize(diff, DifferencingOrder + 1); // order 1 means 2 values, 1 subtraction
      
      for(int i = 0; i < VectorNumber; i++)     // loop through anchor bars
      {
        for(int j = 0; j < VectorSize; j++)     // loop through successive bars
        {
          differentiate(open, i + j, diff);
          
          X[k++] = diff[0];
        }
        
        differentiate(open, i + VectorSize, diff);
        Y[i] = diff[0];
      }
      
      return true;
    }

ここで呼ばれるヘルパーメソッド「differentiate」により、ランダムな次元の差を渡された配列の計算が可能になります。結果は「diff」配列を介して返され、長さはDifferencingOrderより1大きくなります。

    void differentiate(const double &open[], const int ij, double &diff[])
    {
      for(int q = 0; q <= DifferencingOrder; q++)
      {
        diff[q] = open[ij + q];
      }
      
      int d = DifferencingOrder;
      while(d > 0)
      {
        for(int q = 0; q < d; q++)
        {
          diff[q] = diff[q + 1] - diff[q];
        }
        d--;
      }
    }

このクラスは、平均値を差し引き、normalizeXYVectorsメソッドで標準偏差で除算することにより、ベクトルの正規化をサポートします(ここには示されていません)。

クラスには、カーネルを計算するためのいくつかのメソッドもあります。例えば、X []からのベクトルとそのインデックス、および外部ベクトルの場合は以下となります。

    double kernel(const double &x1[], const double &x2[]) const
    {
      double sum = 0;
      for(int i = 0; i < VectorSize; i++)
      {
        sum += (x1[i] - x2[i]) * (x1[i] - x2[i]);
      }
      return exp(-1 * sum / Sigma22);
    }

行列「omega」は、buildOmegaメソッドを使用して計算されます(インデックスによってX[]ベクトルを呼び出す「kernel」メソッドが適用されます)。

    void buildOmega()
    {
      KernelNumber = VectorNumber;
      
      ArrayResize(Omega, VectorNumber * VectorNumber);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        for(int j = i; j < VectorNumber; j++)
        {
          const double k = kernel(i, j);
          Omega[i * VectorNumber + j] = k;
          Omega[j * VectorNumber + i] = k;
          
          if(i == j)
          {
            Omega[i * VectorNumber + j] += 1 / Gamma;
            Omega[j * VectorNumber + i] += 1 / Gamma;
          }
        }
      }
    }

連立方程式が解かれ、検索された「alpha」および「beta」係数がsolveSoLEメソッドで取得されます。

    bool solveSoLE()
    {
      // |  0              |1|             |   |  Beta   |   |  0  |
      // |                                 | * |         | = |     |
      // | |1|  |Omega| + |Identity|/Gamma |   | |Alpha| |   | |Y| |
      
      CMatrixDouble MATRIX(KernelNumber + 1, KernelNumber + 1);
      
      for(int i = 1; i <= KernelNumber; i++)
      {
        for(int j = 1; j <= KernelNumber; j++)
        {
          MATRIX[j].Set(i, Omega[(i - 1) * KernelNumber + (j - 1)]);
        }
      }
      
      MATRIX[0].Set(0, 0);
      for(int i = 1; i <= KernelNumber; i++)
      {
        MATRIX[i].Set(0, 1);
        MATRIX[0].Set(i, 1);
      }
      
      double B[];
      ArrayResize(B, KernelNumber + 1);
      B[0] = 0;
      for(int j = 1; j <= KernelNumber; j++)
      {
        B[j] = Y[j - 1];
      }
      
      int info;
      CDenseSolverLSReport rep;
      double x[];
      
      CDenseSolver::RMatrixSolveLS(MATRIX, KernelNumber + 1, KernelNumber + 1, B, Threshold, info, rep, x);
      
      Beta = x[0];
      ArrayResize(Alpha, KernelNumber);
      ArrayCopy(Alpha, x, 0, 1);
      
      return true;
    }

「process」は、回帰を実行するクラスのメインメソッドです。そこから、入力/出力の形成、正規化、「オメガ」行列の計算、連立方程式の解、選択のエラーの取得を開始します。

    bool process()
    {
      if(!buildXYVectors()) return false;
      normalizeXYVectors();
      
      // least squares linear regression for demo purpose only
      if(KernelNumber == -1 || KernelNumber > VectorNumber)
      {
        return regress();
      }
      
      if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
      {
        buildOmega();
      }
      else                                                  // proposed SOM-LS-SVM
      {
        if(!buildKernels()) return false;
      }
      if(!solveSoLE()) return false;
      
      LSSVM_Error result;
      checkAll(result);
      ErrorPrint(result);
      return true;
    }

最適化の品質を評価するために、クラスにはいくつかの異なる値があり、データセット全体に対して自動的に計算されます。これらは、平均二乗誤差、相関係数、決定係数(R二乗)、および符号の一致率(微分を意味するモードでのみ妥当)です。すべての側面がLSSVM_Errorの構造に組み込まれます。

    struct LSSVM_Error
    { // indices: 0 - training set, 1 - test set
      double RMSE[2]; // RMSE
      double CC[2];   // Correlation Coefficient
      double R2[2];   // R-squared
      double PCT[2];  // %
    };

配列のインデックス0は訓練の選択を意味し、インデックス1はテストの選択を意味します。フィッシャー検定など、予測の統計的有意性のより厳密な評価を使用することが望ましいでしょう。これは、良好な相関とR2値が誤っている可能性があるためです。ただし、一度にすべてをカバーすることは不可能のようです。

選択全体のエラーを計算するメソッドは、checkAllです。

    void checkAll(LSSVM_Error &result)
    {
      result.RMSE[0] = result.RMSE[1] = 0;
      result.CC[0] = result.CC[1] = 0;
      result.R2[0] = result.R2[1] = 0;
      result.PCT[0] = result.PCT[1] = 0;
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      double out[];
      getResult(out);
      
      for(int i = 0; i < VectorNumber; i++)
      {
        double given = Y[i];
        double trained = out[i];
        result.RMSE[0] += (given - trained) * (given - trained);
        // mean is 0 after normalization
        xy += (given) * (trained);
        x2 += (given) * (given);
        y2 += (trained) * (trained);
        
        if(given * trained > 0) correct++;
      }
      
      result.R2[0] = 1 - result.RMSE[0] / x2;
      result.RMSE[0] = sqrt(result.RMSE[0] / VectorNumber);
      result.CC[0] = xy / sqrt(x2 * y2);
      result.PCT[0] = correct * 100.0 / VectorNumber;
      
      crossvalidate(result); // fill metrics for test set (if attached)
    }

ループの前に、すべての入力ベクトルの近似を実行し、「out」配列にこれらの値を入力するgetResultメソッドが呼び出されます。

    void getResult(double &out[], const bool reverse = false) const
    {
      double data[];
      ArrayResize(out, VectorNumber);
      for(int i = 0; i < VectorNumber; i++)
      {
        vector(i, data);
        out[i] = approximate(data);
      }
      if(reverse) ArrayReverse(out);
    }

ここでは、すでに作成されたモデルに通常の予測関数「approximate」が使用されています。

    double approximate(const double &x[]) const
    {
      double sum = 0;
      double data[];
      
      if(ArraySize(x) + 1 == ArraySize(Solution)) // Least Squares Linear System (just for reference)
      {
        for(int i = 0; i < ArraySize(x); i++)
        {
          sum += Solution[i] * x[i];
        }
        sum += Solution[ArraySize(x)];
      }
      else
      {
        if(KernelNumber == 0 || KernelNumber == VectorNumber) // standard LS-SVM
        {
          for(int i = 0; i < VectorNumber; i++)
          {
            vector(i, data);
            sum += Alpha[i] * kernel(x, data);
          }
        }
        else                                                  // proposed SOM-LS-SVM
        {
          for(int i = 0; i < KernelNumber; i++)
          {
            ArrayCopy(data, Kernels, 0, i * VectorSize, VectorSize);
            sum += Alpha[i] * kernel(x, data);
          }
        }
      }
      return sum + Beta;
    }

その中で、見つかった係数Alpha[]とBetaはカーネル関数の合計に適用されます(ケースLS-SVMおよびSOM-LS-SVM)。

テストの選択は、訓練用オブジェクトの場合と同様の方法で形成されます。別のオブジェクト、LSSVMを使用して、メインオブジェクトの「チェック」オブジェクトにバインドします。

  protected:
    LSSVM *crossvalidator;
  
  public:
    bool bindCrossValidator(LSSVM *tester)
    {
      if(tester.getVectorSize() == VectorSize)
      {
        crossvalidator = tester;
        return true;
      }
      return false;
    }
    
    void crossvalidate(LSSVM_Error &result)
    {
      const int vectorNumber = crossvalidator.getVectorNumber();
      
      double out[];
      double _Y[];
      crossvalidator.getY(_Y); // assumed normalized by validator
      
      double xy = 0;
      double x2 = 0;
      double y2 = 0;
      int correct = 0;
      
      for(int i = 0; i < vectorNumber; i++)
      {
        crossvalidator.vector(i, out);
        
        double z = approximate(out);
        
        result.RMSE[1] += (_Y[i] - z) * (_Y[i] - z);
        xy += (_Y[i]) * (z);
        x2 += (_Y[i]) * (_Y[i]);
        y2 += (z) * (z);
        
        if(_Y[i] * z > 0) correct++;
      }
      
      result.R2[1] = 1 - result.RMSE[1] / x2;
      result.RMSE[1] = sqrt(result.RMSE[1] / vectorNumber);
      result.CC[1] = xy / sqrt(x2 * y2);
      result.PCT[1] = correct * 100.0 / vectorNumber;
    }

必要に応じて、クラスは、LS-SVM / SOM-LS-SVMアルゴリズムによる非線形最適化の代わりに、VeсtorSize変数とVectorNumber方程式を使用したシステム内の最小二乗法による線形回帰の実行を許可します。この目的のために、「regress」メソッドが実装されています。

    bool regress(void)
    {
      CMatrixDouble MATRIX(VectorNumber, VectorSize + 1); // +1 stands for b column
      
      for(int i = 0; i < VectorNumber; i++)
      {
        MATRIX[i].Set(VectorSize, Y[i]);
      }
      
      for(int i = 0; i < VectorSize; i++)
      {
        for(int j = 0; j < VectorNumber; j++)
        {
          MATRIX[j].Set(i, X[j * VectorSize + i]);
        }
      }
      
      CLinearModel LM;
      CLRReport AR;
      int info;
      
      CLinReg::LRBuildZ(MATRIX, VectorNumber, VectorSize, info, LM, AR);
      if(info != 1)
      {
        Alert("Error in regression model!");
        return false;
      }
      
      int _size;
      CLinReg::LRUnpack(LM, Solution, _size);
      
      Print("RMSE=" + (string)AR.m_rmserror);
      ArrayPrint(Solution);
      
      return true;
    }

このメソッドはLS-SVMの精度の先験的なものであり、これを実証するためにここに追加されています。一方、これは相場よりも本質的にプリミティブなデータを回帰するために使用できます。このモードを有効にするには、KernelNumber = -1を設定します。この場合、ソリューションはソリューション配列に書き込まれ、Alpha[]とBetaは関与していません。

クラスLSSVMに基づいて予測指標を作成してみましょう。

予測指標LS-SVM

指標SOMLSSVM.mq5のタスクは、2つのLSSVMオブジェクト(1つは訓練用、もう1つはテスト用)を作成し、回帰を実行して、両方のセットの品質評価で初期値と予測値を表示します。パラメータ「gamma」と「sigma」は、ユーザが既に見つけて設定したものと見なされます。標準のテスターを使用して、EAでそれらを最適化する方が便利です(次のセクションでこれを扱います)。この制限はかなり人工的なものであるため、技術的には、テスターは指標を最適化する可能性をサポートすることもできます。この場合、指標のモデルを直接最適化できます。

指標には、別のウィンドウに4つのバッファーがあります。2つのバッファには訓練用セットの初期値と予測値が表示され、他の2つのバッファにはテスト用セットの値が表示されます。

入力:

  input int _VectorNumber = 250; // VectorNumber (training)
  input int _VectorNumber2 = 50; // VectorNumber (validating)
  input int _VectorSize = 20; // VectorSize
  input double _Gamma = 0; // Gamma (0 - auto)
  input double _Sigma = 0; // Sigma (0 - auto)
  input int _KernelNumber = 0; // KernelNumber (0 - auto)
  input int _TrainingOffset = 50; // Offset of training bars
  input int _ValidationOffset = 0; // Offset of validation bars
  input int DifferencingOrder = 1;

最初の2つは、訓練用セットとテスト用セットのサイズを設定します。ベクトルサイズはVectorSizeで指定されます。パラメータgammaとSigmaを0のままにして、入力に基づいてそれらの値を自動的に選択できます。ただし、このトリビアルモードは品質が最適とはほど遠く、指標がデフォルト値で機能するためにのみ必要です。KernelNumberメソッドによる回帰では、KernelNumberを0のままにする必要があります。デフォルトでは、テストセットは相場履歴の最後に配置されますが、訓練用セットはその左側にあります(年代順で)。

オブジェクトは入力に基づいて初期化されます。

  LSSVM *lssvm = NULL;
  LSSVM *test = NULL;
  
  int OnInit()
  {
    static string titles[BUF_NUM] = {"Training set", "Trained output", "Test input", "Test output"};
    
    for(int i = 0; i < BUF_NUM; i++)
    {
      PlotIndexSetInteger(i, PLOT_DRAW_TYPE, DRAW_LINE);
      PlotIndexSetString(i, PLOT_LABEL, titles[i]);
    }
    
    lssvm = new LSSVM(_VectorNumber, _VectorSize, _KernelNumber, _Gamma, _Sigma, _TrainingOffset);
    test = new LSSVM(_VectorNumber2, _VectorSize, _KernelNumber, 1, 1, _ValidationOffset);
    lssvm.setDifferencingOrder(DifferencingOrder);
    test.setDifferencingOrder(DifferencingOrder);
    
    return INIT_SUCCEEDED;
  }

指標はデモ用に作成されているため、一度だけ計算されます。必要に応じて、各バーで表示が更新されるように簡単に調整できますが、かなり長い時間間隔を置いた後で、システムを1回だけまたは繰り返して潜在的に高コストで解決する必要があります。

  int OnCalculate(const int rates_total,
                  const int prev_calculated,
                  const datetime& Time[],
                  const double& Open[],
                  const double& High[],
                  const double& Low[],
                  const double& Close[],
                  const long& Tick_volume[],
                  const long& Volume[],
                  const int& Spread[])
  {
    ArraySetAsSeries(Open, true);
    ArraySetAsSeries(Time, true);
    
    static bool calculated = false;
    if(calculated) return rates_total;
    calculated = true;
    
    for(int k = 0; k < BUF_NUM; k++)
    {
      buffers[k].empty();
    }
    
    lssvm.bindCrossValidator(test);
    bool processed = lssvm.process(true);

OnCalculateでは、テストセットを訓練セットに接続し、回帰を開始します。 正常に完了すると、初期データと予測データの両方のすべてのデータが表示されます。If it is completed successfully, we will display all data, both initial and forecasted:

  if(processed)
  {
    const double m1 = lssvm.getMean();
    const double s1 = lssvm.getStdDev();
    const double m2 = test.getMean();
    const double s2 = test.getStdDev();
    
    // training
    
    double out[];
    lssvm.getY(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[0].set(_TrainingOffset, out);
    
    lssvm.getResult(out, true);
    
    for(int i = 0; i < _VectorNumber; i++)
    {
      out[i] = out[i] * s1 + m1;
    }
    
    buffers[1].set(_TrainingOffset, out);
    
    // validation
    
    test.getY(out, true);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      out[i] = out[i] * s2 + m2;
    }
    
    buffers[2].set(_ValidationOffset, out);
    
    for(int i = 0; i < _VectorNumber2; i++)
    {
      test.vector(i, out);
      
      double z = lssvm.approximate(out);
      z = z * s2 + m2;
      buffers[3][_VectorNumber2 - i - 1 + _ValidationOffset] = z;
      ...
    }
  }

微分系列を分析するオプションがあるため、指標は別のウィンドウに表示されます。ただし、実際にはまだ価格を扱っており、予測をメインチャートに表示することが望ましいです。この目的のために、オブジェクトを使用できます。価格軸による座標は、差分系列から復元する必要があります。初期系列およびそれから派生したさまざまな次元の差分系列の要素の索引付けは、以下のスキームで示されています(年代順の索引付け)。

    d0:  0   1   2   3   4   5  :y
    d1:    0   1   2   3   4
    d2:      0   1   2   3
    d3:        0   1   2

例えば、違いが最初の次元(d1)である場合、次のことが明らかです。

y[i+1] = y[i] + d1[i]

2番目(d2)と3番目(d3)の次元の違いについて、方程式は次のようになります。

y[i+2] = 2 * y[i+1] - y[i] + d2[i]

y[i+3] = 3 * y[i+2] - 3 * y[i+1] + y[i] + d3[i]

微分の次数が高いほど、yの計算の数が多くなることがわかります。

これらの数式を適用すると、価格チャートにオブジェクトとともに予測を表示できます。

      if(ShowPredictionOnChart)
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 1]
                 - 3 * Open[_VectorNumber2 - i - 1 + _ValidationOffset + 2]
                 + Open[_VectorNumber2 - i - 1 + _ValidationOffset + 3] + z;
        }
        else
        {
          // unsupported yet
        }
        
        string name = prefix + (string)i;
        ObjectCreate(0, name, OBJ_TEXT, 0, Time[_VectorNumber2 - i - 1 + _ValidationOffset], target);
        ObjectSetString(0, name, OBJPROP_TEXT, "l");
        ObjectSetString(0, name, OBJPROP_FONT, "Wingdings");
        ObjectSetInteger(0, name, OBJPROP_ANCHOR, ANCHOR_CENTER);
        ObjectSetInteger(0, name, OBJPROP_COLOR, clrRed);
      }

3より大きい次元には、プラスの効果とマイナスの効果の両方があるため、考慮しませんでした。プラスは、定常性の増大による次元の増加に伴って予測品質が向上することです。ただし、これは、最初の系列ではなく、関連する注文の派生物の予測に特に当てはまります。高次の差別化のマイナスの効果は、小さな誤差でさえ、基本的に、統合された系列への増分の後続の「展開」で増加します。したがって、DifferencingOrderの場合、最適化または試行錯誤によって「黄金の平均」も見つかるはずです。

両方の効果は、以下の2つのスクリーンショットで確認できます(薄い緑色と緑色の線は、それぞれ訓練用セットとテスト用セットの実際のデータで、水色と青色の線は予測です)。

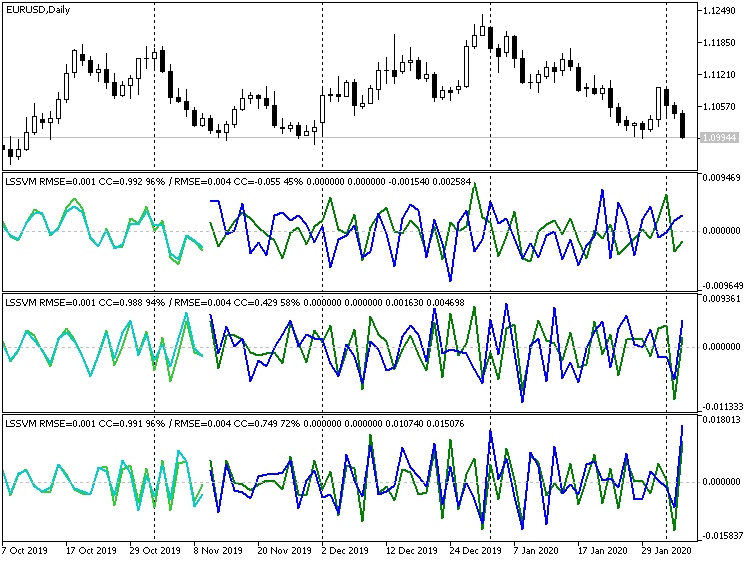
一連のEURUSD D1に対するさまざまな微分順序の指標LSSVM

ここでは、3つの指標インスタンスが、一般的な設定と異なる微分の階で表示されます。以下が全体的な設定です。

• _VectorNumber = 250; // ベクトル番号(訓練)
• _VectorNumber2 = 60; // ベクトル番号(検証)
• _VectorSize = 20; // ベクトルサイズ
• _Gamma = 2048; // Gamma (0 - 自動)
• _Sigma = 8; // Sigma (0 - 自動)
• _KernelNumber = 0; // カーネル番号(0 - 自動)
• _TrainingOffset = 60; // 訓練バーのオフセット
• _ValidationOffset = 0; // 検証バーのオフセット

微分の階は、それぞれ1、2、3です。各ウィンドウの見出しのスロープラインの後に、テスト(この場合は検証)の選択のために予測指標が表示されます。予測指標はより良い(相関係数: -0.055、0.429、0.749、増分の一致する符号は、それぞれ45％、58％、72％)。実際、線の一致性は視覚的にもよくわかります。ただし、価格チャートで3次予測を復元すると、次の図のようになります。

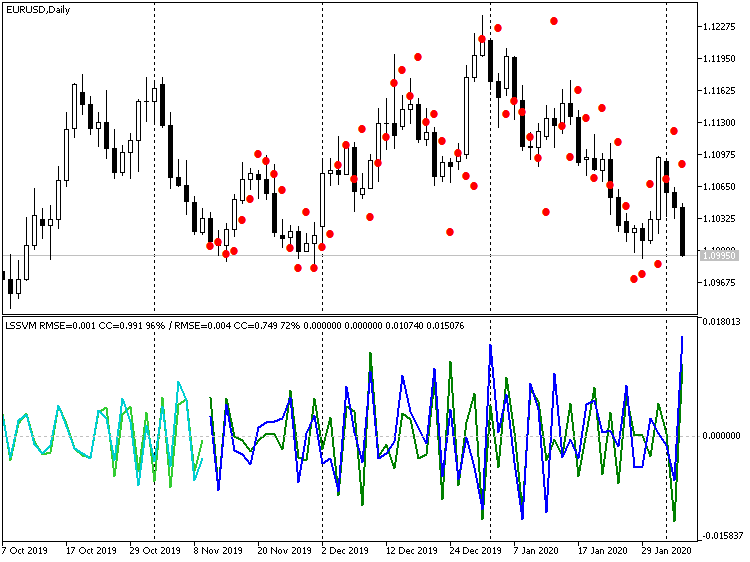
EURUSD D1の予測値が復元された3次微分指標LSSVM

明らかに、多くのポイントが振れとして特徴付けられます。一方、差別化をまったく無効にすると、次のようになります。

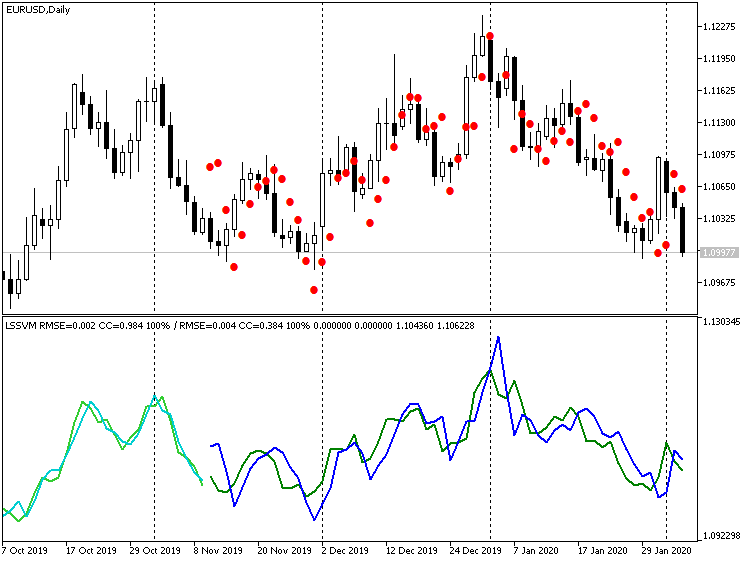
EURUSD D1の予測の復元された値を含む、微分なしの指標LSSVM

ここでは、価格の値は実際の値に非常に近いですが、約1バーの目に見える遅れがあります。この効果は、実際には、アルゴリズムがN個のインスタンスベクトルに基づく移動平均の一種であるデジタルフィルタに相当するという事実によるものです。価格レベルの近さを考慮して、一度に数歩先を予測することにより、この1〜2本のバーのラグを平準化することは合理的です。つまり、バー-1の予測を取得したら、バー-2の予測の入力としてフィードする、等です。次のセクションでEAを作成するときに、このモードを提供します。

エキスパートアドバイザーLS-SVM

エキスパートアドバイザーLSSVMbot.mq5は、次の2つのタスクを実行するように設計されています。

• 仮想モード(取引なし)でのLS-SVMの「gamma」および「Sigma」パラメータの最適化。 そして
• テスターでの取引、およびオプションで、取引モードでの他のパラメータの最適化。

指標と同様に、仮想モードでは、LSSVMの2つのインスタンスが使用されます。1つは訓練用セットを持ち、もう1つはテスト用セットを持ちます。これらは考慮に入れられるテストセットの兆候です。最適化はカスタム基準によって実行されます。それらはすべて次のようにリストされます。

  enum CUSTOM_ESTIMATOR
  {
    RMSE,   // RMSE
    CC,     // correlation
    R2,     // R-squared
    PCT,    // %
    TRADING // trading
  };

TRADINGオプションは、EAを取引モードに設定するために使用されます。その中で、EAは、利益、ドローダウンなどの埋め込まれた基準の1つによって、従来の方法で最適化できます。

入力のメイングループは、指標と同じ値を設定します。

  input int _VectorNumber = 250;  // VectorNumber (training)
  input int _VectorNumber2 = 25;  // VectorNumber (validating)
  input int _VectorSize = 20;     // VectorSize
  input double _Gamma = 0;        // Gamma (0 - auto)
  input double _Sigma = 0;        // Sigma (0 - auto)
  input int _KernelNumber = 0;    // KernelNumber (sqrt, 0 - auto)
  input int DifferencingOrder = 1;
  input int StepsAhead = 0;

ただし、TrainingOffsetとValidationOffsetは内部変数になり、自動的に設定されます。ValidationOffsetは常に0です。TrainingOffsetは、仮想モードの検証セットVectorNumber2のサイズ、または取引モードでは0です(すべてのパラメータがすでに検出されていることがここに示されているため、テストセットはなく、最新のデータで回帰を実行する必要があります)。

KernelNumberでSOMを使用するには、片側のサイズを指定する必要がありますが、フルマップサイズはこの値の2乗値として計算されます。

2番目の入力グループは、「gamma」と「Sigma」を最適化するためのものです。

  input int _GammaIndex = 0;     // Gamma Power Iterator
  input int _SigmaIndex = 0;     // Sigma Power Iterator
  input double _GammaStep = 0;   // Gamma Power Multiplier (0 - off)
  input double _SigmaStep = 0;   // Sigma Power Multiplier (0 - off)
  input CUSTOM_ESTIMATOR Estimator = R2;

検索範囲は非常に広く、標準テスターは事前定義されたステップを追加することによってのみ反復をサポートするため、EAでは次のアプローチが使用されます。最適化は、パラメータgammaIndexおよびSigmaIndexによって有効にする必要があります。それらのそれぞれは、「gamma」と「sigma」の実際の値を取得するために、gammaとsigmaの初期値にそれぞれgammaStepとSigmaStepを掛ける必要がある回数を定義します。たとえば、gammaが1、gammaStepが2で、0〜5の範囲内のgammaIndexに対して最適化が実行されている場合、アルゴリズムは「gamma」値1、2、4、8、16、32を評価します。gammaStepとSigmaStepが0でない場合、「gamma」と「sigma」の実際の値を計算するために常に使用され、単一のテスター実行内を含みます。

EAはバーで機能します。EAは、要求された数のバー(ベクトル)が履歴で利用可能になるまで計算を開始しません。テスターに十分な数のバーがない場合は、実行が無駄に終了する可能性があります。ログを参照してください。残念ながら、開始時にテスターによって読み込まれる履歴バーの数は、時間枠、年内の日数などの多くの要因に依存し、かなり変動する可能性があります必要に応じて、初期テスト時間を過去に移動します。

仮想モードでは、モデルは1回だけ訓練され、特性(Estimatorで選択)の1つが関数OnTesterから品質指標として返されます(RMSEを選択した場合、エラーは逆符号で示されます)。

  bool optimize()
  {
    if(Estimator != TRADING) lssvm.bindCrossValidator(test);
    iterate(_GammaIndex, _GammaStep, _SigmaIndex, _SigmaStep);
    bool success = lssvm.process();
    if(success)
    {
      LSSVM::LSSVM_Error result;
      lssvm.checkAll(result);
      
      Print("Parameters: ", lssvm.getGamma(), " ", lssvm.getSigma());
      Print("  training: ", result.RMSE[0], " ", result.CC[0], " ", result.R2[0], " ", result.PCT[0]);
      Print("  test: ", result.RMSE[1], " ", result.CC[1], " ", result.R2[1], " ", result.PCT[1]);
      
      customResult = Estimator == CC ?result.CC[1]
                  : (Estimator == RMSE ?-result.RMSE[1] // the lesser |absolute error value| the better
                  : (Estimator == PCT ?result.PCT[1] : result.R2[1]));
    }
    return success;
  }
  
  void OnTick()
  {
    ...
    if(Estimator != TRADING)
    {
      if(!processed)
      {
        processed = optimize();
      }
    }
    ...
  }
  
  double OnTester()
  {
    return processed ?customResult : -1;
  }

取引モードでは、モデルもデフォルトで1回だけ訓練されますが、年、四半期、または月ごとに再描画を設定できます。このためには、OPTIMIZATIONパラメータ(コードでは_2という名前)に、「y」、「q」、または「m」と記述します(大文字もサポートされています)。このプロセスには、新しい(最新の)データに関する方程式系の解法のみが含まれることに注意してください。ただし、「gamma」パラメータと「sigma」パラメータは同じままです。技術的には、プロセスを洗練し、再訓練するたびに、オンザフライでパラメータを試すことができます(以前に標準オプティマイザに割り当てたもの)。ただし、これはEA内で編成する必要があるため、単一のストリームによって実行されます。

かなり長い期間(1年以上)にわたってデータに一致する「gamma」および「sigma」パラメータが、より短い取引期間で有効である必要があることを今意味しています。

モデルが構築された後、LSSVMのテストインスタンスを使用して、最新の既知の価格を読み取り、それらから入力ベクトルを形成し、正規化します。次に、ベクトルはメソッドlssvm.approximateに渡されます。

    static bool solved = false;
    if(!solved)
    {
      const bool opt = (bool)MQLInfoInteger(MQL_OPTIMIZATION) || (_GammaStep != 0 && _SigmaStep != 0);
      solved = opt ?optimize() : lssvm.process();
    }
    
    if(solved)
    {
      // test is used to read latest _VectorNumber2 prices
      if(!test.buildXYVectors())
      {
        Print("No vectors");
        return;
      }
      test.normalizeXYVectors();
      
      double out[];
      
      // read latest vector
      if(!test.buildVector(out))
      {
        Print("No last price");
        return;
      }
      test.normalizeVector(out);
      
      double z = lssvm.approximate(out);

入力に応じて、EAは取得した値zを使用して、非正規化することで価格予測に変換するか、事前定義された回数だけ予測を繰り返してから、それを価格に変換します。

      for(int i = 0; i < StepsAhead; i++)
      {
        ArrayCopy(out, out, 0, 1);
        out[ArraySize(out) - 1] = z;
        z = lssvm.approximate(out);
      }
      
      z = test.denormalize(z);

時系列は区別される可能性があるため、最新の価格値をいくつか使用して、それらと予測増分によって次の価格値を復元します。

      double open[];
      if(3 == CopyOpen(_Symbol, _Period, 0, 3, open)) // open[1] - previous, open[2] - current
      {
        double target = 0;
        if(DifferencingOrder == 0)
        {
          target = z;
        }
        else if(DifferencingOrder == 1)
        {
          target = open[2] + z;
        }
        else if(DifferencingOrder == 2)
        {
          target = 2 * open[2] - open[1] + z;
        }
        else if(DifferencingOrder == 3)
        {
          target = 3 * open[2] - 3 * open[1] + open[0] + z;
        }
        else
        {
          // unsupported yet
        }

現在のレベルに対する予測価格の場所に応じて、EAは取引を開始します。ポジションが必要な方向にすでに開かれている場合は開いたままになります。反対方向にある場合は、反転が実行されます。

        int mode = target >= open[2] ?+1 : -1;
        int dir = CurrentOrderDirection();
        if(dir * mode <= 0)
        {
          if(dir != 0) // there is an order
          {
            OrdersCloseAll();
          }
          
          if(mode != 0)
          {
            const int type = mode > 0 ?OP_BUY : OP_SELL;
            const double p = type == OP_BUY ?SymbolInfoDouble(_Symbol, SYMBOL_ASK) : SymbolInfoDouble(_Symbol, SYMBOL_BID);
            OrderSend(_Symbol, type, Lot, p, 100, 0, 0);
          }
        }
      }
    }

EAが両方のモードでどのように機能するかを確認してみましょう。XAUUSDを、通貨に比べて全国ニュースにさらされる機会が少ない作業ツールとして考えてみましょう。時間枠はD1です。

構成ファイルは添付されています(LSSVMbot.set)。訓練セットVectorNumberのサイズは自発的に200と見なされます。これは1年弱です。1000前後の大きな値は、すでに方程式系の解決をかなり妨げている可能性があります。テストセットVectorNumber2=50ベクトルサイズVectorSize=20 (1か月)SOM未使用(KernelNumber=0)差分は無効になっていますが(DifferencingOrder=0)、取引モードの検証ステージでは、指標を使用して予測と価格のわずかな遅延に気づいたため、予測は2ステップ先に設定されています。仮想モードでは、入力パラメータStepsAheadはモデルの評価に使用されません。

gammaとSigmaの基本的な値は1ですが、それらの乗数、Power Multiplier(gammaStep、SigmaStep)は2に等しく、最適化で実行される乗算の数は、イテレータgammaIndexとSigmaIndexでそれぞれ5〜35と5～20の間隔として定義されます(ステップ5)。したがって、gammaIndexが15の場合、gammaは1 *(2の15乗)の値、つまり32768になります。

「gamma」と「sigma」を見つけるために正しい範囲を試すことは、非常に日常的な作業です。残念ながら、最初は粗いグリッドで、次に細かいグリッドで計算する以外に解決策はありません。本稿の準備中に多くの試行が行われたため、より広い範囲の検索と見なすことができるので、1つのグリッドに制限します。

したがって、最適化するパラメータはgammaIndexとSigmaIndexの2つだけです。これらは間接的にgammaとSigmaをより広い範囲で、可変ステップで指数関数的に変化させます。

2018年の始値から最適化を始めましょう。最適化はカスタム基準(Estimator = R2)によって実行されます。

このモードでは、EAはトレードしないが、見積りから方程式系を埋め、LS-SVMアルゴリズムで解くことを覚えておいてください。バーは、可能性のある微分のために調整されたVectorSizeサイズのVectorNumberベクトルを形成するのに十分な量で計算に関与します(差分を取る各追加手順には、入力に追加バーが必要です)。 さらに、EAはさらに、訓練の後に、つまり最新のバーに時系列に配置されているVectorNumber2テストベクトルを必要とします。これはテストバー上(より正確には、それらから取得したベクトル上)であり、取得したモデルの予測能力がOnTesterからの戻りに対して評価されます。

テスターは、開始時に常に正しい数のバーを履歴に持つとは限らず、EAは最初の日付から数か月後にのみシステムに入力できるため、これらすべてが重要です。一方、EAには特定の長さの履歴がすぐに提供されるため、訓練バーは常にテスト(最適化)日付の前に開始されることに注意してください。

最適化が完了すると、結果を基準R2で並び替えします(降順、つまり一番上にあるもの)。最初に、設定gammaIndex = 15とSigmaIndex = 5があると仮定します(結果が等しい実行の順序はおそらく変わる可能性があるため、「仮定」と言います)。

最初のレコードをダブルクリックして、単一のテストを実行します(仮想モードのままです)。ログには次のようなものが表示されます。

  2018.01.01 00:00:00   Bars required: 270
  2018.01.02 00:00:00   247 2017.01.03 00:00:00
  2018.02.02 00:00:00   Starting at 2017.01.03 00:00:00 - 2018.02.02 00:00:00, bars=270
  2018.02.02 00:00:00   G[15]=32768.0 S[5]=32.0
  2018.02.02 00:00:00   RMSE: 0.21461 / 0.26944; CC: 0.97266 / 0.97985; R2: 0.94606 / 0.95985
  2018.02.02 00:00:00   Parameters: 32768.0 32.0
  2018.02.02 00:00:00     training: 0.2146057434536685 0.9726640597702653 0.9460554570543925 93.0
  2018.02.02 00:00:00     test: 0.2694416925009446 0.9798483835616107 0.9598497541714557 96.0
  final balance 10000.00 USD
  OnTester result 0.9598497541714557

これは次のように解釈できます。手順全体を実行するには270バーが必要でしたが、2018.01.02の時点では247バーしか使用できませんでした。十分な数のバーが2018.02.02、つまり1か月後の2017.01.03以降の訓練データ(利用可能な履歴)に表示されました。次に、作業パラメータのgammaとsigma(G [15] = 32768.0 S [5] = 32.0が指定され、最適化されたイテレーターパラメータが角括弧で示されます。最後に、OnTesterから返された訓練品質指標を含む文字列でR2(0.95985)の値を確認できます。

次に、最適化を無効にして、日付範囲を2017年から2020年2月に拡大し、EAのパラメータEstimator = TRADINGに設定します(EAがトレード操作を実行することを意味します)。パラメータOPTIMIZATION(コードの_2)で、新しいデータ(最新の当時最新のVectorNumberベクトル)の回帰モデルを四半期ごとに再計算するようにEAに指示する記号「q」を導入しましょう。ただし、「gamma」と「sigma」は同じままです。

単一のテストを実行してみましょう。

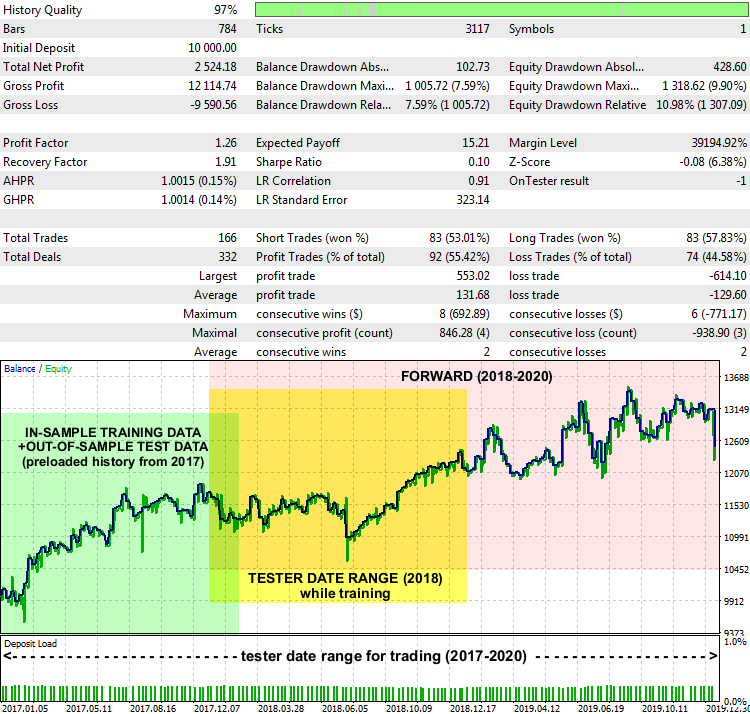
EA LSSVMbot Report on XAUUSD D1, 2017-2020

パフォーマンスはそれほど驚くべきではありませんが、基本的に言って、システムは機能します。最適な「gamma」と「sigma」を見つけるために訓練データが取得された日付範囲(緑色で強調表示)、テスターで訓練モードで定義された日付範囲(黄色で強調表示)、EAが不明なデータで取引した日付範囲(ピンク色で強調表示)はレポートチャートに示されます。

予測を解釈し、その周囲の取引戦略を構築する方法は異なる場合があります。特に、テストEAには、PreviousTargetCheckという入力があります(デフォルトではfalse)。これが有効になっていると、予測に基づいた取引は、前の予測に関連した最新の予測の場所によって取引方向を決めるという、別の戦略を使用して実行されます。また、SOMのクラスタ化、予測される移動の強さに応じたロットサイズの変更、補充など、他の設定を試す余地もあります。

終わりに

本稿では、数学的な方法の積極的な使用と慎重な構成を必要とする時系列を予測するためのLS-SVMベースのアルゴリズムを紹介しました。前述の方法(第1部のEMDおよび本第2部のLS-SVM)を実際にうまく使用できるかどうかは、時系列の特殊な側面に大きく依存しますが、取引に適用される場合は、金融商品と時間枠の性質にも依存します。したがって、特定のアルゴリズムの機能に関連する市場を選択することは、知識集約型および/またはリソース集約型の計算を実装することと同じくらい重要です。特に、外国為替通貨は予測可能性が低く、外部からの衝撃にさらされているため、履歴相場のみに基づいて構築される予測の効率が低下します。金属、インデックス、またはバランスの取れたバスケット/ポートフォリオは、説明された2つの方法により適していると見なされます。さらに、予測がどれほど魅力的であるように見えても、リスク管理、ストップオーダーによる保護、ニュースのバックグラウンドモニタリングを忘れてはなりません。

提供されているソースコードを使用すると、独自のMQLプロジェクトに新しいメソッドを埋め込むことができます。