Aplicação do método de coordenadas de Eigen para a análise estrutural de distribuições estatísticas não extensivas

Introdução

Em 1988, Constantino Tsallis propôs a generalização da mecânica estatística de Boltzmann-Gibbs-Shannon [1], onde ele apresentou a noção de entropia não extensiva.

Uma consequência importante da generalização de entropia parece ser a existência de novos tipos de distribuição [2] desempenhando o papel principal na nova mecânica estatística:

Verificou-se que estes tipos de distribuição podem ser utilizados para descrever uma grande quantidade de dados experimentais em sistemas com memória de longo alcance, com sistemas de forças de longo alcance e sistemas fortemente correlacionados.

A entropia está estreitamente relacionada à informação [7]. A generalização da mecânica estatística com base na teoria da informação foi apresentada em [8-9]. A mecânica estatística não extensiva tem se mostrado muito útil para econometria [10-17]. Por exemplo, a distribuição Q-Gaussian descreve bem as asas largas (caudas) de distribuições de aumento de cotas de instrumento financeiro (q~1.5). Dito isso, a maioria das distribuições de aumentos de séries temporais financeiras transformam-se em distribuições normais (q=1) em grandes escalas (meses, anos) [10].

Foi naturalmente esperado que tal generalização de mecânica estatística resultasse em um equivalente do teorema limite central para as distribuições q-Gaussian. Mas isso foi demonstrado estar errado em [18] - a distribuição limite da soma de variáveis aleatórias fortemente correlacionadas é analiticamente diferente de q-Gaussians.

No entanto, um problema de outro tipo apareceu: descobriu-se que os valores numéricos da solução exata encontrada estavam muito perto de Q-Gaussian ("numericamente semelhantes, analiticamente diferentes"). Para analisar as diferenças entre as funções e obter os melhores parâmetros de distribuição de Q-Gaussian, uma expansão em série foi utilizada em [18]. As relações entre essas funções levaram à expansão de energia no parâmetro q caracterizando o grau de sistema não extensivo.

O maior problema de estatísticas aplicadas é o problema de aceitar a hipótese estatística. Foi durante muito tempo considerada impossível de ser resolvida [19-20] exigindo uma ferramenta especial (algo como um microscópio eletrônico), que permitiria ver mais do que o possível através de métodos de estatísticas modernos aplicados.

O método de coordenadas de eigen introduzido em [21] permite-nos chegar a um nível mais profundo - a análise das propriedades estruturais de relações funcionais. Este método muito refinado pode ser utilizado para resolver uma variedade de problemas. As funções de expansões de operador correspondentes a distribuições não extensivas acima foram demonstradas em [22].

Este artigo lidará com o método de coordenadas de eigen e exemplos de seu uso prático. Ele contém uma grande quantidade de fórmulas que são de grande importância para a compreensão da essência do método. Depois de repetir todos os cálculos, você será capaz de representar expansões de funções para funções de seu próprio interesse.

1. Q-Gaussians em Econometria

A distribuição Q-Gaussians executa um papel importante em econometria [4,10-17].

Para se ter uma compreensão geral do nível de pesquisa atual, pode-se consultar as obras do Dr. Claudio Antonini "q-Gaussians em Finanças" [23] e "O Uso da Distribuição q-Gaussian em Finanças" [24].

Vamos destacar brevemente os resultados principais.

Fig. 1. Metodologia da ciência (Slide 4 "O Uso da Distribuição q-Gaussian em Finanças")

Os principais detalhes da série temporal estão apresentados na fig. 2:

Fig. 2. Propriedades da série temporal financeira (Slide 3 "O Uso da Distribuição q-Gaussian em Finanças")

Muitos modelos teóricos que são usados​para descrever a série temporal financeira levam à distribuição Q-Gaussian:

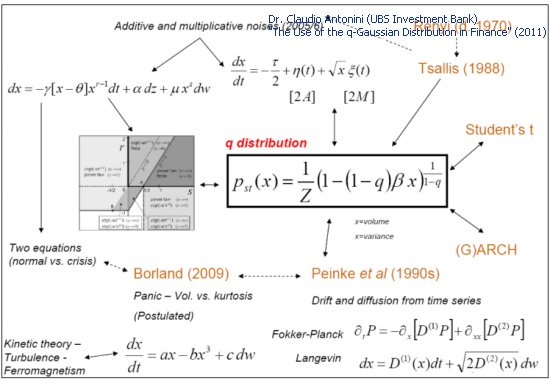
Fig. 3. Modelos teóricos e Q-Gaussian (Slide 27 "O Uso da Distribuição q-Gaussian em Finanças")

A distribuição Q-Gaussian é também utilizada para descrição fenomenológica de distribuição de cotas:

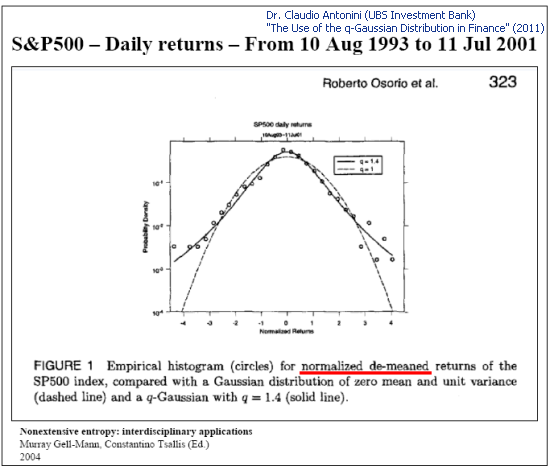
Fig. 4. Análise de amostra da S&P 500 retorna diariamente (Slide 8 "O Uso da Distribuição q-Gaussian em Finanças")

Ao se trabalhar com dados reais, planta-se um problema de identificação de função:

Fig. 5. O problema de identificação de função de distribuição (Slide 14 "q-Gaussians em Finanças")

Ambos os documentos do Dr. Claudio Antonini enfatizam a importância da identificação correta de funções para construir modelos adequados de processos físicos:

Fig. 6. As conclusões desenhadas em "q-Gaussians em Finanças" e "O Uso da Distribuição q-Gaussian em Finanças" (Dr. Claudio Antonini, 2010, 2011)

Exemplos do uso de estatísticas q-Gaussian em finanças (folhas de trabalho + arquivos MathCad):

• Dinâmicas de preços de ações q-Gaussian, (Michael English, 2008)
• Opções européias q-Gaussian (Michael English, 2008)
• Distribuição e desvios aleatórios q-Gaussian, (Michael English, 2008)
• Portfólios q-Gaussian (Michael English, 2008)
• Medidas de risco q-Gaussian (Michael English, 2008)
• Valor esperado e valor em risco para ativo de distribuição log-normal (Michael English, 2008)

2. Coordenadas de Eigen

A expansão de coordenadas de Eigen é como a seguir:

onde C1…CN são constantes e X1(t),..,XN(t) são as "coordenadas de eigen".

Tais expansões lineares são muito úteis e geralmente utilizadas em análise de dados. Por exemplo, uma função exponencial em uma escala logarítmica se transforma em uma linha reta (sua inclinação pode ser facilmente calculada por meio de regressão linear). Assim, não há necessidade de otimização não linear (encaixe), a fim de determinar os parâmetros de função.

Escala logarítmica vai, porém, ser de pouca ajuda ao lidar com funções mais complexas (por exemplo, a soma de dois expoentes) - a função não será exibida como uma linha reta. E uma otimização não-linear será necessária para determinar os coeficientes de função.

Há casos em que os dados experimentais podem ser igualmente bem explicados usando várias funções, os quais correspondem a diferentes modelos de processos físicos. Qual função escolher? Qual delas fornecerá uma imagem mais adequada da realidade fora dos dados experimentais?

Identificação da função correta é vital para a análise de sistemas complexos (por exemplo, série temporal financeira) - cada distribuição corresponde a um determinado processo físico e seremos capazes de compreender melhor a dinâmica e as propriedades gerais de sistemas complexos ao escolher um modelo adequado.

A estatística aplicada [19, 20] afirma que não existe um critério que lhe permite rejeitar uma hipótese estatística errada. O método de coordenadas de Eigen lança uma luz completamente nova sobre este problema (aceitação de hipótese).

A função utilizada para a descrição dos dados experimentais pode ser vista como uma solução para uma determinada equação diferencial. A sua forma determina a estrutura da expansão de coordenadas de Eigen.

Uma característica peculiar da expansão de coordenadas de Eigen é que todos os dados gerados pela função Y(t) são lineares em estrutura na base das coordenadas de Eigen X1(t)..XN(t) da função Y(t). Os dados gerados por qualquer outra função F(t) nesta base não aparecerão mais como uma linha reta (eles parecerão lineares na base de coordenadas de Eigen da função F(t)).

Este fato permite identificar com precisão as funções, assim facilitando muito o trabalho com hipótese estatística.

2.1. O método de coordenadas de Eigen

O conceito por trás do método é o de construir as coordenadas de Eigen Xk(t) sob a forma de operadores com base na função de Y(t).

Isso pode ser feito usando a análise matemática da qual as coordenadas de Eigen Xk(t) assumem a forma de enrolamentos integrais e a expansão é determinada pela estrutura da equação diferencial que é satisfeita pela função Y(t). A seguir, um problema em determinar os coeficientes C1.. CN aparecem.

Na expansão de base ortogonal (por exemplo, ao determinar os coeficientes da transformada de Fourier), coeficientes de expansão são calculados projetando o vetor na base e o resultado desejado é obtido devido à ortogonalidade de funções de base.

Isto não é apropriado no nosso caso, pois não há qualquer informação sobre a ortogonalidade de X1(t)… XN(t).

2.2. Cálculo de coeficientes de expansão utilizando método de mínimos quadrados

Os coeficientes Ck podem ser calculados com o uso do método dos mínimos quadrados. Este problema se reduz a resolver um sistema de equações lineares.

Suponha que:

Para praticamente toda medida de há um erro :

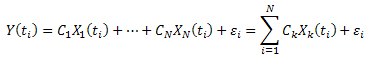
Minimizar a soma de desvios quadrados:

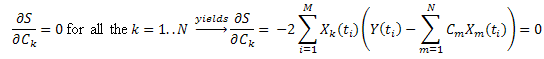
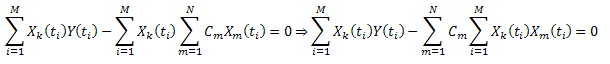
A introdução da notificação: 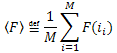, pode ser escrita da seguinte forma:

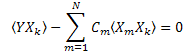
Assim, obtemos um sistema de equações lineares em C1...CN (k=1..N):

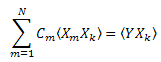
A matriz "correlação" é simétrica: .

Em alguns casos, a expansão de coordenadas de eigen pode aparecer mais conveniente na forma integral:

Isso permite reduzir o impacto de erros (devido à média), mas requer cálculos adicionais.

2.3. Um exemplo da expansão de função R(x)

Vamos olhar para a expansão de coordenadas de Eigen da seguinte função:

Esta função gera muitas distribuições estatísticas [21]:

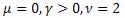1. - A distribuição (Gaussian) normal;
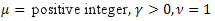2. - a distribuição Poisson;
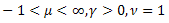3. - a distribuição gamma;
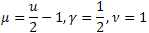4. - a distribuição ;
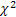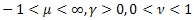5. - a distribuição Schtauffer que inclui a distribuição Weibull como um caso especial .

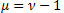Além disso, também é bem adequado descrever processos de relaxamento:

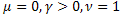1. - a função exponencial ordinária;
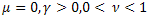2. - a função exponencial esticada;
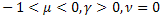3. - a função de atenuação de força.

Tendo R(x) distintos com respeito a x, temos que:

Multiplicar ambos os lados por x:

Transformar :

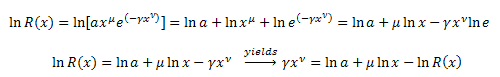
Substituir na equação:

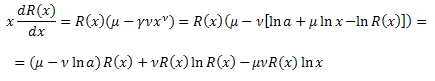
Obtemos a equação diferencial para a função R(x):

Integrar ambos os lados com respeito a x no intervalo [xm,x]:

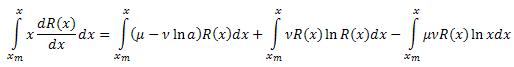
Integral o lado esquerdo da equação por partes:

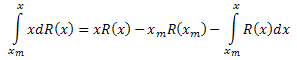
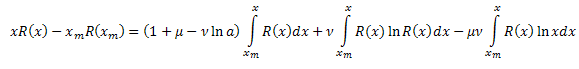
Como um resultado, temos:

Onde:

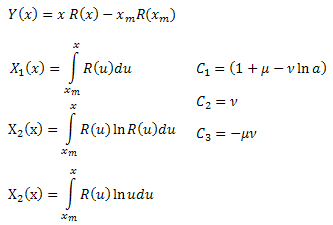
Por meio do cálculo dos coeficientes , podemos determinar os parâmetros de função . O quarto parâmetro pode derivar da fórmula para R(x).

2.4. Implementação

O cálculo dos coeficientes de expansão exige para resolver o sistema de equações linear. Por conveniência do trabalho com matrizes, ele pode ser providenciado como uma classe CMatrix (o arquivo CMatrix.mqh). Usando métodos desta classe, você pode definir os parâmetros de matriz, os valores de elemento da matriz e resolver o sistema de equações lineares, empregando o método de Gaussian.

//+------------------------------------------------------------------+
//| CMatrix class                                                    |
//+------------------------------------------------------------------+
class CMatrix
  {
   double            m_matrix[];
   int               m_rows;
   int               m_columns;
public:
   void              SetSize(int nrows,int ncolumns);
   double            Get(int i,int j);
   void              Set(int i,int j,double val);
   void              GaussSolve(double &v[]);
   void              Test();
  };

Vamos dar um exemplo do script (EC_Example1.mq5), que calcula as coordenadas de Eigen e parâmetros da função R(x).

//+------------------------------------------------------------------+
//|                                                  EC_Example1.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <CMatrix.mqh>
//+------------------------------------------------------------------+
//| CECCalculator                                                    |
//+------------------------------------------------------------------+
class CECCalculator
  {
protected:
   int               m_size;
   //--- x[i]
   double            m_x[];
   //--- y[i]
   double            m_y[];
   //--- matrix
   CMatrix           m_matrix;
   //--- Y[i]
   double            m_ec_y[];
   //--- eigen-coordinates X1[i],X2[i],X3[i]
   double            m_ec_x1[];
   double            m_ec_x2[];
   double            m_ec_x3[];
   //--- coefficients C1,C2,C3
   double            m_ec_coefs[];
   //--- function f1=Y-C2*X2-C3*X3
   double            m_f1[];
   //--- function f2=Y-C1*X1-C3*X3
   double            m_f2[];
   //--- function f3=Y-C1*X1-C2*X2
   double            m_f3[];
private:
   //--- function for data generation
   double            R(double x,double a,double mu,double gamma,double nu);
   //--- calculation of the integral
   double            Integrate(double &x[],double &y[],int ind);
   //--- calculation of the function Y(x)
   void              CalcY(double &y[]);
   //--- calculation of the function X1(x)
   void              CalcX1(double &x1[]);
   //--- calculation of the function X2(x)
   void              CalcX2(double &x2[]);
   //--- calculation of the function X3(x)
   void              CalcX3(double &x3[]);
   //--- calculation of the correlator
   double            Correlator(int ind1,int ind2);
public:
   //--- method for generating the test function data set x[i],y[i]
   void              GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu);
   //--- loading data from the file
   bool              LoadData(string filename);
   //--- saving data into the file
   bool              SaveData(string filename);
   //--- saving the calculation results
   void              SaveResults(string filename);
   //--- calculation of the eigen-coordinates
   void              CalcEigenCoordinates();
   //--- calculation of the linear expansion coefficients
   void              CalcEigenCoefficients();
   //--- calculation of the function parameters
   void              CalculateParameters();
   //--- calculation of the functions f1,f2,f3
   void              CalculatePlotFunctions();
  };
//+------------------------------------------------------------------+
//| Function R(x)                                                    |
//+------------------------------------------------------------------+
double CECCalculator::R(double x,double a,double mu,double gamma,double nu)
  {
   return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x)))));
  }
//+-----------------------------------------------------------------------+
//| Method for generating the data set x[i],y[i] of the test function R(x)|
//+-----------------------------------------------------------------------+
void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu)
  {
   if(size<=0) return;
   if(x1>=x2) return;
   m_size=size;
   ArrayResize(m_x,m_size);
   ArrayResize(m_y,m_size);
   double delta=(x2-x1)/(m_size-1);
//---
   for(int i=0; i<m_size; i++)
     {
      m_x[i]=x1+i*delta;
      m_y[i]=R(m_x[i],a,mu,gamma,nu);
     }
  };
//+------------------------------------------------------------------+
//| Method for loading data from the .CSV file                       |
//+------------------------------------------------------------------+
bool CECCalculator::LoadData(string filename)
  {
   int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   m_size=0;
   while(!FileIsEnding(filehandle))
     {
      string str=FileReadString(filehandle);
      if(str!="")
        {
         string astr[];
         StringSplit(str,';',astr);
         if(ArraySize(astr)==2)
           {
            ArrayResize(m_x,m_size+1);
            ArrayResize(m_y,m_size+1);
            m_x[m_size]=StringToDouble(astr[0]);
            m_y[m_size]=StringToDouble(astr[1]);
            m_size++;
           }
         else
           {
            m_size=0;
            return(false);
           }
        }
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for saving data into the .CSV file                        |
//+------------------------------------------------------------------+
bool CECCalculator::SaveData(string filename)
  {
   if(m_size==0) return(false);
   if(ArraySize(m_x)!=ArraySize(m_y)) return(false);
   if(ArraySize(m_x)==0) return(false);
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   for(int i=0; i<ArraySize(m_x); i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the integral                       |
//+------------------------------------------------------------------+
double CECCalculator::Integrate(double &x[],double &y[],int ind)
  {
   double sum=0;
   for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5;
   return(sum);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function Y(x)                  |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the function X1(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X2(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i]));
   ArrayResize(x2,m_size);
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X3(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i]));
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the eigen-coordinates              |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoordinates()
  {
   CalcY(m_ec_y);
   CalcX1(m_ec_x1);
   CalcX2(m_ec_x2);
   CalcX3(m_ec_x3);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the correlator                     |
//+------------------------------------------------------------------+
double CECCalculator::Correlator(int ind1,int ind2)
  {
   if(m_size==0) return(0);
   if(ind1<=0 || ind1>4) return(0);
   if(ind2<=0 || ind2>4) return(0);
//---
   double arr1[];
   double arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
//---
   switch(ind1)
     {
      case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
   switch(ind2)
     {
      case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
//---
   double sum=0;
   for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i];  }
   sum=sum/m_size;
   return(sum);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the linear expansion coefficients  |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoefficients()
  {
//--- setting the matrix size 3x4
   m_matrix.SetSize(3,4);
//--- calculation of the correlation matrix 
   for(int i=3; i>=1; i--)
     {
      string s="";
      for(int j=1; j<=4; j++)
        {
         double corr=Correlator(i,j);
         m_matrix.Set(i,j,corr);
         s=s+" "+DoubleToString(m_matrix.Get(i,j));
        }
      Print(i," ",s);
     }
//--- solving the system of the linear equations
   m_matrix.GaussSolve(m_ec_coefs);
//--- displaying the solution - the obtained coefficients C1,..CN 
   for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]);
  };
//+--------------------------------------------------------------------+
//| Method for the calculation of the function parameters a,mu,nu,gamma|
//+--------------------------------------------------------------------+
void CECCalculator::CalculateParameters()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//--- calculate a
   double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1]));
//--- calculate mu
   double mu=-m_ec_coefs[2]/m_ec_coefs[1];
//--- calculate nu
   double nu=m_ec_coefs[1];
//--- calculate gamma
   double arr1[],arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
   double corr1=0;
   double corr2=0;
   for(int i=0; i<m_size; i++)
     {
      arr1[i]=MathPow(m_x[i],nu);
      arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]);
      corr1+=arr1[i]*arr2[i];
      corr2+=arr1[i]*arr1[i];
     }
   double gamma=-corr1/corr2;
//---
   Print("a=",a);
   Print("mu=",mu);
   Print("nu=",nu);
   Print("gamma=",gamma);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the functions                      |
//| f1=Y-C2*X2-C3*X3                                                 |
//| f2=Y-C1*X1-C3*X3                                                 |
//| f3=Y-C1*X1-C2*X2                                                 |
//+------------------------------------------------------------------+
void CECCalculator::CalculatePlotFunctions()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//---
   ArrayResize(m_f1,m_size);
   ArrayResize(m_f2,m_size);
   ArrayResize(m_f3,m_size);
//---
   for(int i=0; i<m_size; i++)
     {
      //--- plot function f1=Y-C2*X2-C3*X3
      m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f2=Y-C1*X1-C3*X3
      m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f3=Y-C1*X1-C2*X2
      m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i];
     }
  }
//+------------------------------------------------------------------+
//| Method for saving the calculation results                        |
//+------------------------------------------------------------------+
void CECCalculator::SaveResults(string filename)
  {
   if(m_size==0) return;
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename," for writing, error",GetLastError());
      return;
     }
   for(int i=0; i<m_size; i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+=DoubleToString(m_ec_y[i],8)+";";
      s+=DoubleToString(m_ec_x1[i],8)+";";
      s+=DoubleToString(m_f1[i],8)+";";
      s+=DoubleToString(m_ec_x2[i],8)+";";
      s+=DoubleToString(m_f2[i],8)+";";
      s+=DoubleToString(m_ec_x3[i],8)+";";
      s+=DoubleToString(m_f3[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CECCalculator ec;
//--- model function data preparation
   ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3);
//--- saving into the file
   ec.SaveData("ex1.csv");
//--- calculation of the eigen-coordinates
   ec.CalcEigenCoordinates();
//--- calculation of the coefficients
   ec.CalcEigenCoefficients();
//--- calculation of the parameters
   ec.CalculateParameters();
//--- calculation of the functions f1,f2,f3
   ec.CalculatePlotFunctions();
//--- saving the results into the file
   ec.SaveResults("ex1-results.csv");
  }

2.5. Os resultados de cálculo de função do modelo R(x)

Produziremos 100 valores da função R(x) no intervalo [0.25,15.25] conforme os dados do modelo:

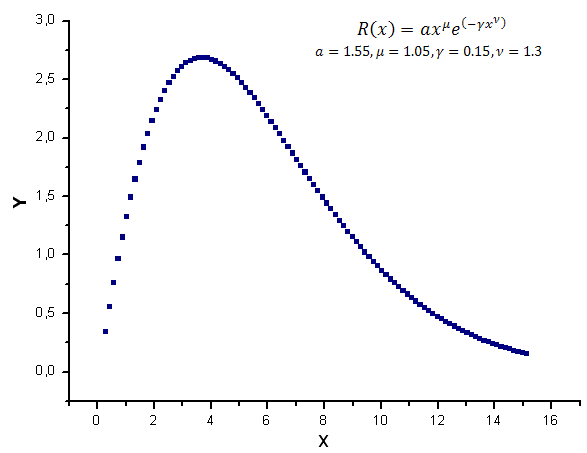
Fig. 7. Função de modelo usado para cálculos

Estes dados fornecem a base para traçar a função Y(x) e sua expansão nas funções X1(x), X2(x) e X3(x).

A fig. 8 mostra a função Y(x) e suas "coordenadas de eigen" X1(x), X2(x) e X3(x).

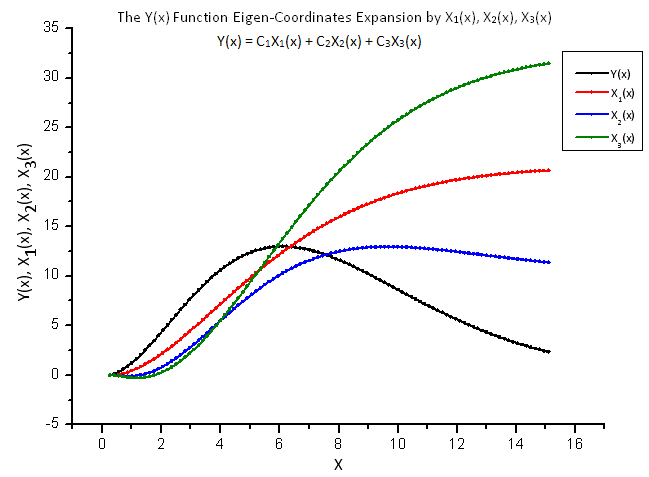
Fig. 8. Forma geral da função Y(x) e as coordenadas de eigen X1(x), X2(x) e X3(x)

Observe a suavização de tais funções que resultam de natureza integral dos operadores X1(x), X2(x) e X3(x).

Seguindo o cálculo das funções Y(x), X1(x), X2(x) e X3(x), a matriz de correlação é construída, em seguida as equações para os coeficientes C1, C2 e C3 são salvas e os parâmetros de função R(x) são calculados baseados nos valores obtidos:

2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1  221.03637620 148.53278281 305.48547011 101.93843241
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2  148.53278281 101.63995012 202.85142688 74.19784681
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3  305.48547011 202.85142688 429.09345292 127.82779760

Verificaremos agora a linearidade da expansão calculada. Para este processo, precisamos calcular 3 funções:

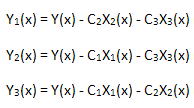
cada qual que seja projetada na sua base de coordenadas de eigen X1(x), X2(x) e X3(x):

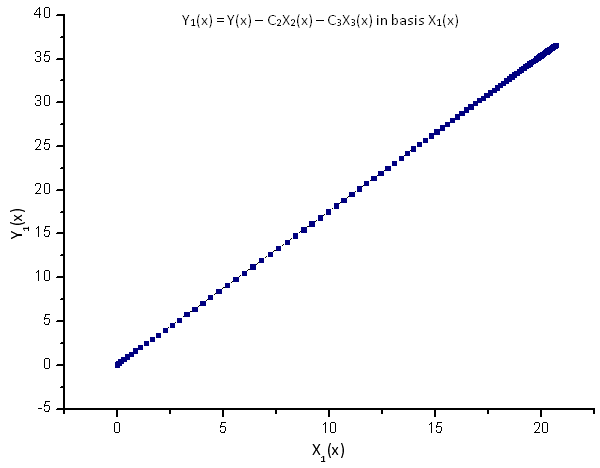
Fig. 9. Representação da função Y1(x) na base X1(x)

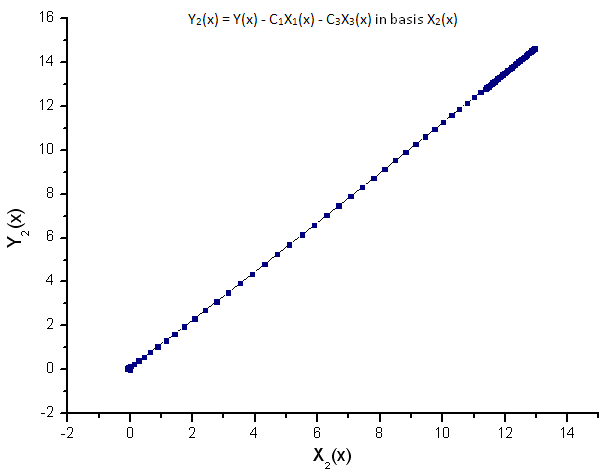
Fig. 10. Representação da função Y2(x) na base X2(x)

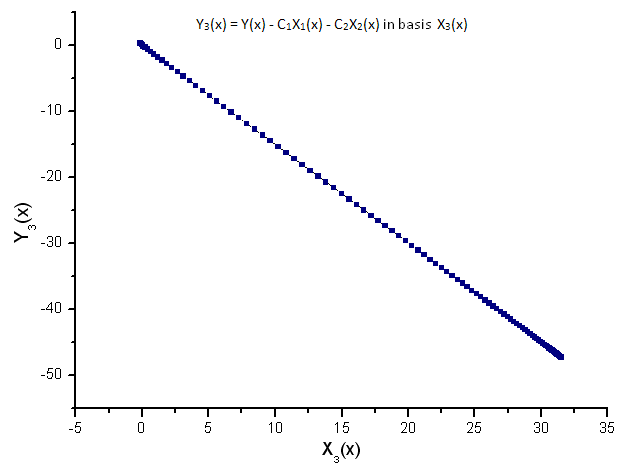
Fig. 11. Representação da função Y3(x) na base X3(x)

A dependência linear das funções representadas sugere que a série de dados na fig. 7 corresponda estritamente à função R(x).

Qualquer outra função (mesmo semelhante em forma) representada nas coordenadas de eigen R(x) não terá mais uma forma linear. Este fato nos permite identificar funções.

A precisão do cálculo de valores numéricos dos parâmetros de função de modelo pode ser melhorada, se o número de pontos for aumentado para 10000 (enquanto mantém-se o mesmo intervalo):

2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1  225.47846911 151.22066473 311.86134419 104.65062550
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2  151.22066473 103.30005101 206.66297964 76.03285182
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3  311.86134419 206.66297964 438.35625824 131.91955339

Neste caso, os parâmetros de função foram calculados de forma mais precisa.

2.6 Efeito ruído

Dados experimentais reais sempre contêm ruídos.

No método GenerateData() da classe ECCCalculator, substituímos:

m_y[i]=R(m_x[i],a,mu,gamma,nu);

com

m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;

adição de um ruído aleatório, sendo aproximadamente 10% do valor máximo da função.

O resultado do script EC_Example1-noise.mq5 é como a seguir:

2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1  254.45082565 185.19087989 354.25574000 125.17343164
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2  185.19087989 136.81028987 254.92996885 97.14705491
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3  354.25574000 254.92996885 501.76021715 159.49440494

O gráfico da função de modelo com um ruído aleatório é demonstrado na fig. 12.

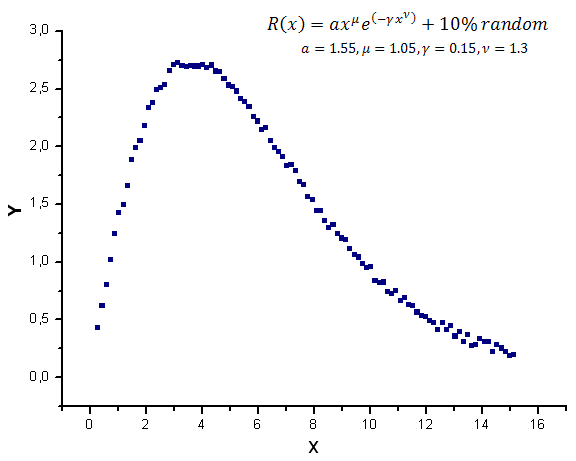
Fig. 12. Função de modelo com ruído usado para cálculos

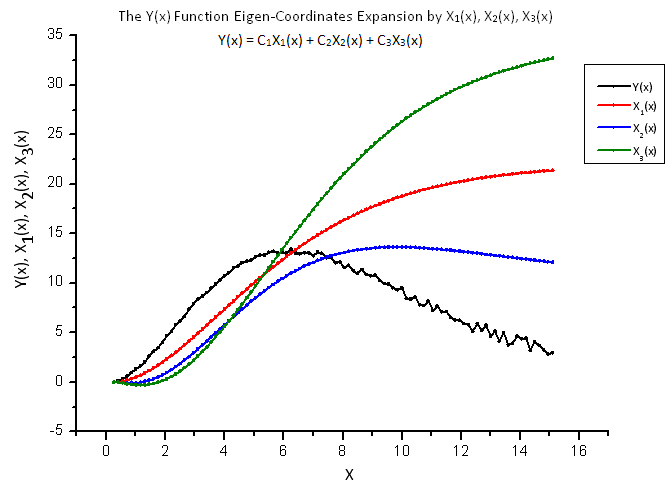
Fig. 13. Forma geral da função Y(x) e as coordenadas de eigen X1(x), X2(x) e X3(x)

As funções X1(x), X2(x) e X3(x) que servem de" coordenadas de eigen" ainda possuem uma aparência suave, no entanto, o Y(x) traçado conforme sua combinação linear parece ser diferente (fig. 13).

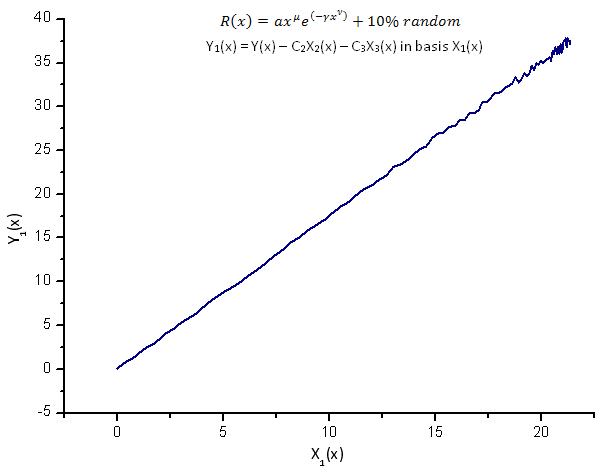
Fig. 14. Representação da função Y1(x) na base X1(x)

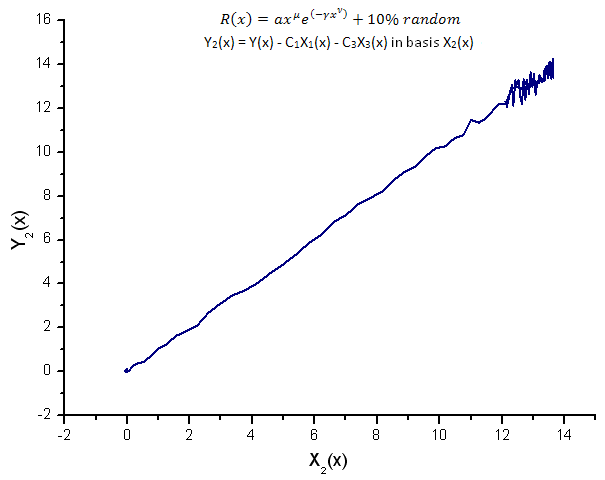
Fig. 15. Representação da função Y2(x) na base X2(x)

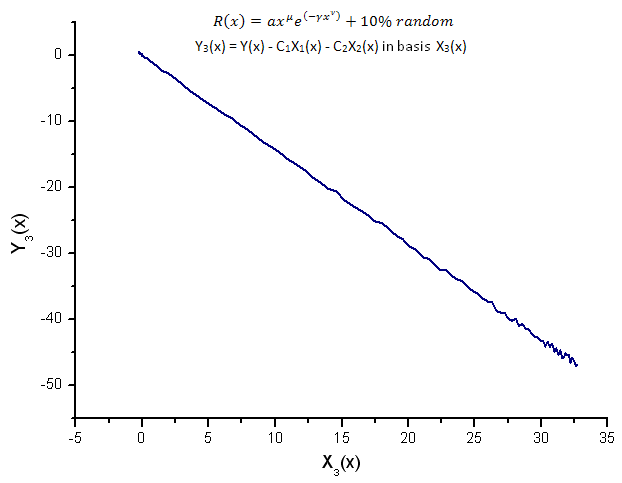
Fig. 16. Representação da função Y3(x) na base X3(x)

A representação das funções Y1(x),Y2(x) e Y3(x) na base das coordenadas de eigen (figuras 8-10) ainda possuem uma forma linear que ainda pode-se notar flutuações em torno da linha reta, devido à presença de ruído. Ele é mais pronunciado em relação a maiores X onde o sinal/ruído torna-se mínimo.

Aqui, os componentes de ruído estão deitados em ambos os lados da linha reta e, neste caso, portanto, é conveniente usar a expansão das coordenadas de eigen integrais (Seção 2.2).

3. Distribuições de probabilidade não extensiva

A generalização de resultados de mecânica estatística na distribuição [2, 22]:

onde , .

A distribuição q-Gaussian é um caso especial da função P2(x).

3.1. A expansão de coordenadas de eigen da função P1(x)

Diferenciamos P1(x):

A equação diferencial resultante é como se segue:

Integrada no intervalo [xm,x]:

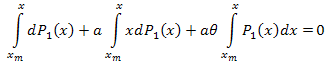
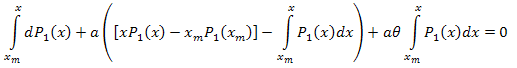
Assim:

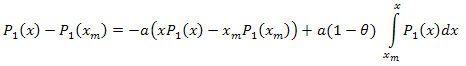
A expansão de coordenadas eigen é como a seguir:

Onde:

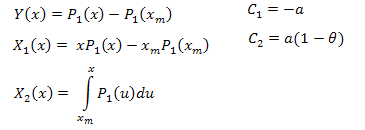
As funções para cálculos são apresentadas abaixo (EC_Example2.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
//--- Y=P(x)-P(xm)
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
//--- X1=x*P(x)-xm*P(xm)
   for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
//--- X2=Integrate(P1(x)) 
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i);
  }

Neste momento o tamanho da matriz de correlação é de 2x3; os valores dos parâmetros a e teta da função P1(x) são determinados com base nos coeficientes С1 e C2. O valor numérico do parâmetro B pode ser obtido a partir da necessidade de normalização.

Abaixo está o resultado de cálculo da função de modelo P1(x,1,0.5,2) no intervalo x [0,10]; o número de pontos usados é 1000:

2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1  0.15420524 0.48808959 -0.32145543
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2  0.48808959 1.79668322 -1.14307410

A função P1(x) e sua expansão de coordenadas de eigen são mostradas nas figuras 17-20.

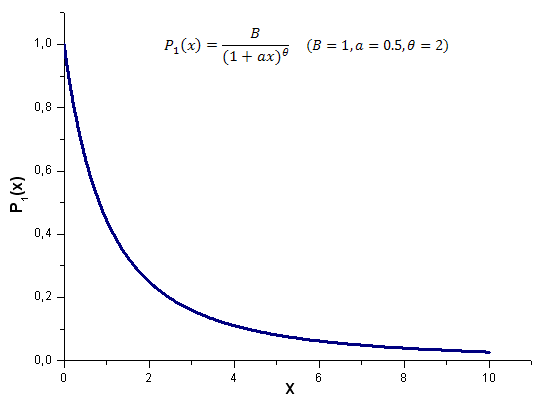
Fig. 17. Função de modelo P1(x, 1, 0.5, 2) usada para cálculos, 1000 pontos

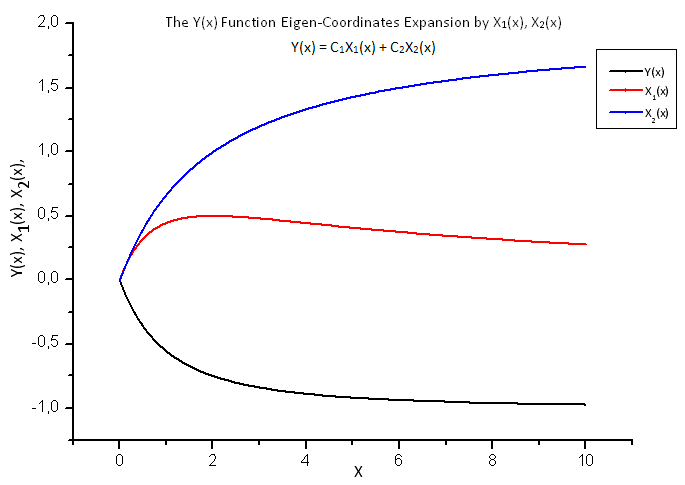
Fig. 18. Forma geral da função Y(x) e as coordenadas de eigen X1(x) e X2(x)

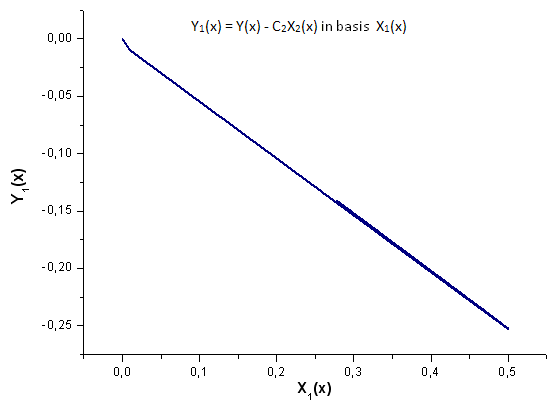
Fig. 19. Representação da função Y1(x) na base X1(x)

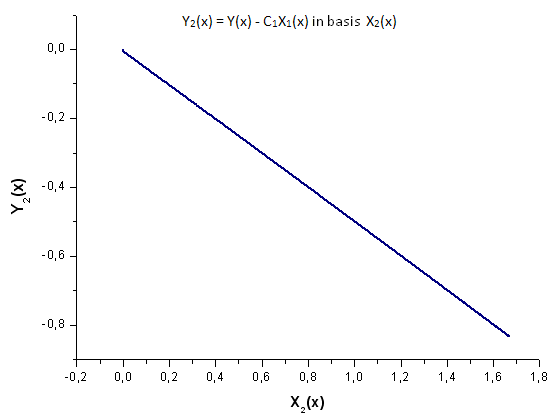
Fig. 20. Representação da função Y2(x) na base X2(x)

Dê uma olhada na fig. 19. Há uma ligeira distorção da dependência linear bem no início e no segundo terço do gráfico. Isto está associado com as peculiaridades da expansão calculada - X1(x) não ser de natureza integral.

3.2. A expansão de coordenadas de eigen da função P2(x)

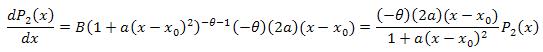
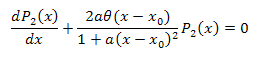
A equação diferencial:

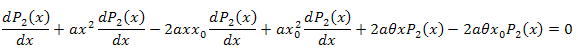
Nós integramos em relação a x no intervalo [xm, x]:

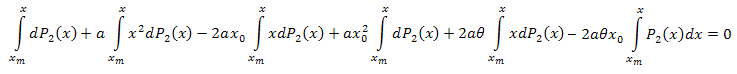
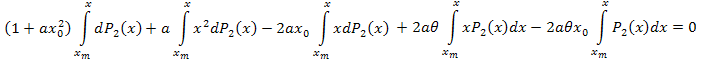
Integrando por partes, temos:

Simplifique:

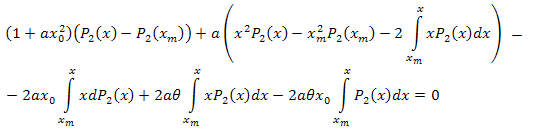
Após as manipulações algébricas, obtemos:

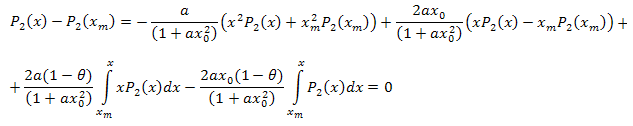
Assim, a expansão resultante é a seguinte:

onde:

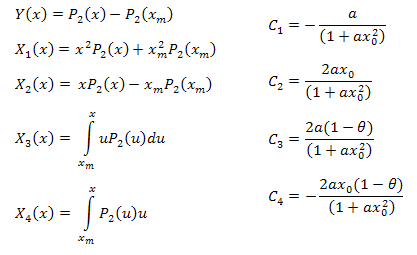
Os parâmetros da função podem ser calculados usando as fórmulas abaixo:

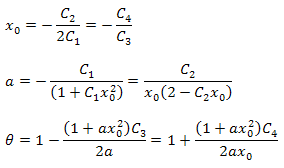
Deve notar-se que existe uma relação adicional entre os parâmetros na expansão resultante. Este fato pode ser usado para verificar a regularidade da função selecionada para a análise. Estas relações são sempre exatas para os dados estritamente correspondentes à função P2(x).

O valor numérico do parâmetro B pode ser obtido a partir da necessidade de normalização.

As funções para cálculo de coordenadas de Eigen são como se segue (EC_Example3.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm)
   for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
   //--- X2=(x)*P2(x)-(xm)*P2(xm)
   for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX3                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i];
   //--- X3=Integrate(X*P2(x)) 
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);  
  }
//+------------------------------------------------------------------+
//| CalcX4                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX4(double &x4[])
  {
   if(m_size==0) return;
   //--- X4=Integrate(P2(x))
   ArrayResize(x4,m_size);
   for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i);
  }

Abaixo está o resultado de cálculo de função de modelo P2(x) de (B=1, a=0.5, theta=2, x0=1); o número de ponto usado é 1000:

2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1  1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2  0.60684314 0.37995888 0.55974145 0.58899739 0.06731011
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3  1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4  1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168

A função P2(x) e sua expansão de coordenadas de eigen são mostradas nas figuras 21-26.

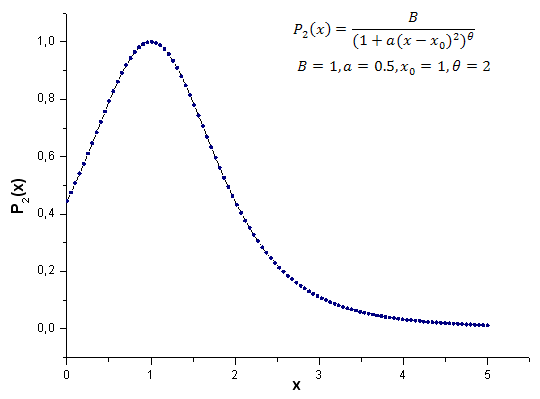
Fig. 21. Função de modelo P2(x,1,0.5,2,1) usado para cálculos, 100 pontos

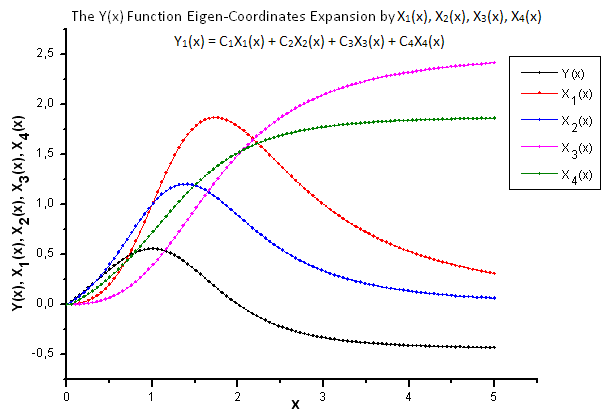
Fig. 22. Forma geral da função Y(x) e as coordenadas de eigen X1(x), X2(x), X3(x) e X4(x)

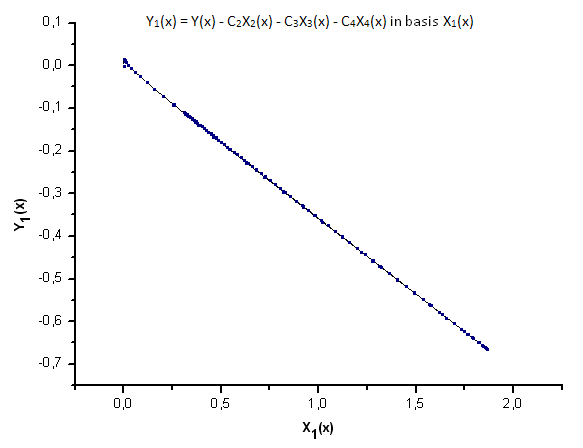
Fig. 23. Representação da função Y1(x) na base X1(x)

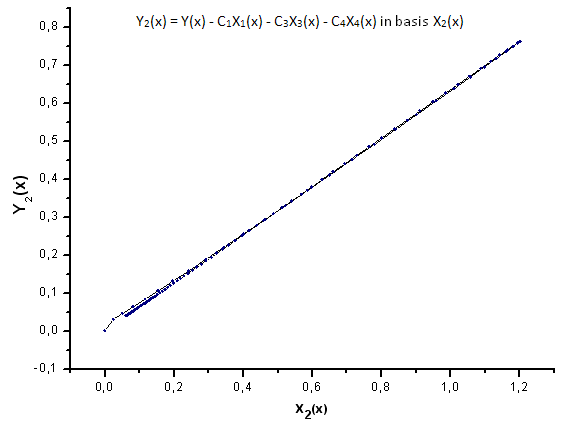
Fig. 24. Representação da função Y2(x) na base X2(x)

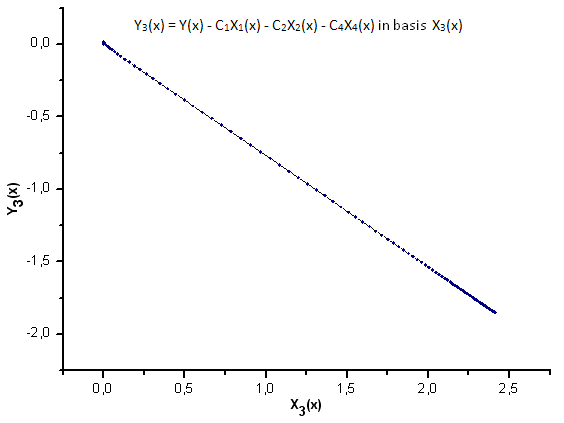
Fig. 25. Representação da função Y3(x) na base X3(x)

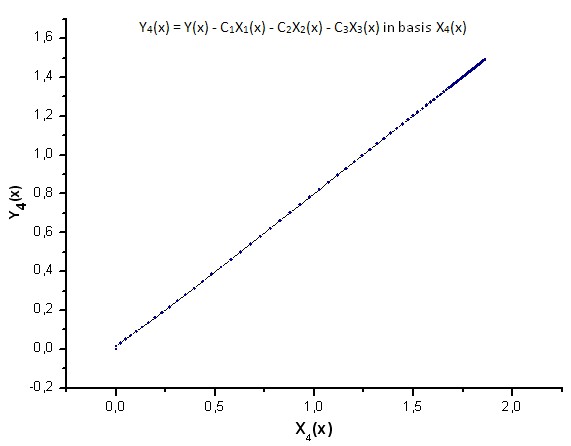
Fig. 26. Representação da função Y4(x) na base X4(x)

4. Se parece-se como um gato... Pode não ser um gato

A família das distribuições q-Gaussian está bem no coração da mecânica estatística não extensiva e, portanto, era natural esperar que ela apareceria no teorema de limite central generalizado. Considerações de entropia serviram como o principal argumento a seu favor [26].

Entretanto, a [apresentação] do artigo 18 mostrou que as distribuições, como o q-Gaussian, não são universais, o que levanta dúvidas sobre o seu papel especial como distribuições limite.

Por exemplo, a função (solução analítica a um dos problemas):

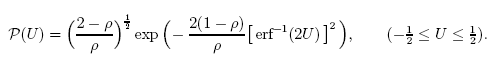
pode ser descrita muito precisamente ao se usar a distribuição q-Gaussian.

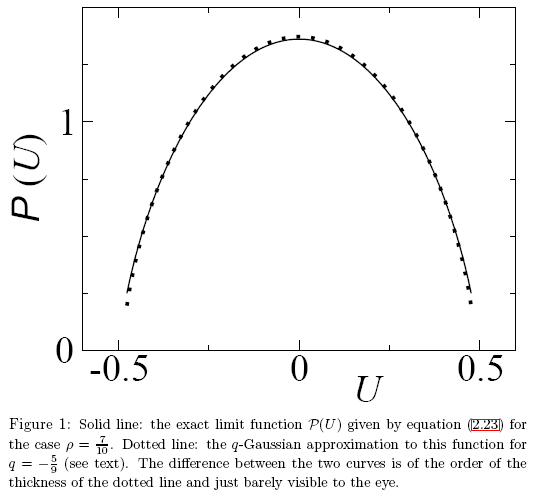
Fig. 27. Um exemplo do artigo "Uma nota sobre q-gaussian e não-gaussian em mecânica estatística"

Neste caso, funções analiticamente diferentes têm valores numéricos semelhantes e as diferenças são, portanto, pouco visíveis a olho. Um método de identificação de função preciso é necessário. Este problema pode ser bem resolvido ao utilizar o método de coordenadas de Eigen.

Vamos analisar um exemplo da expansão de função de coordenadas de Eigen P(U) e mostrar o que exatamente faz a diferença em relação a q-Gaussian. As funções parecem muito semelhantes a olho (Fig. 27).

Geramos um sinal (100 valores da função P(U)) e "o projetamos" no sistema das coordenadas de Eigen da função P2(x) traçada na seção 3.2.

O script Hilhorst-Schehr-problem.mq5 calcula a função P(U) e constrói série de dados que são salvos no arquivo MQL5\Files\test-data.csv. Estes dados são analisados por EC_Example3_Test.mq5.

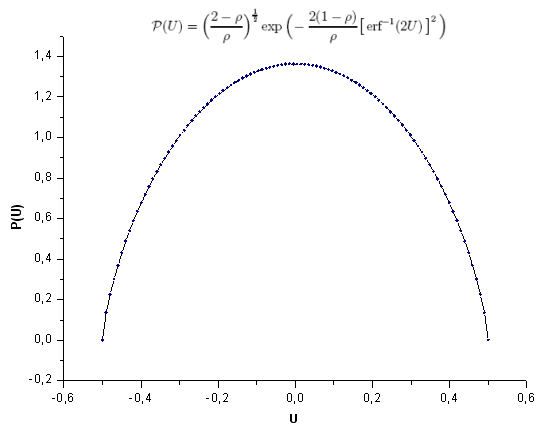
Fig. 28. Função de modelo P(U), 100 pontos

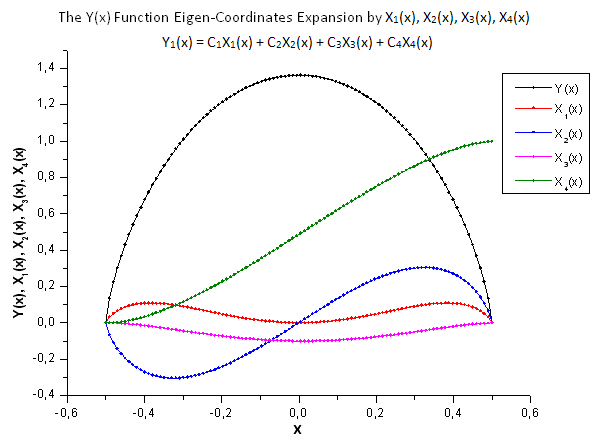
Fig. 29. Forma geral da função Y(x) e as coordenadas de eigen X1(x), X2(x), X3(x) e X4(x)

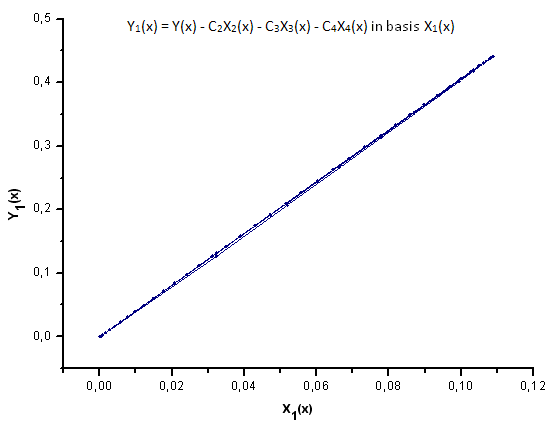
Fig. 30. Representação da função Y1(x) na base X1(x)

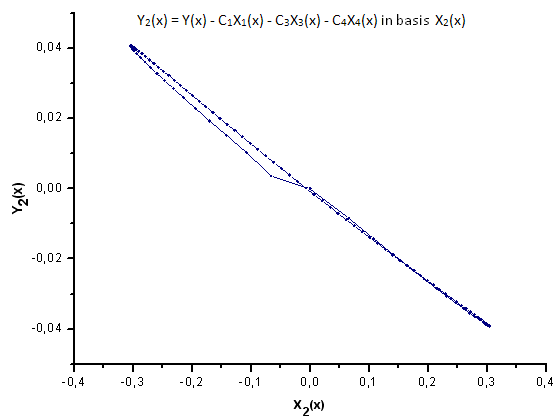
Fig. 31. Representação da função Y2(x) na base X2(x)

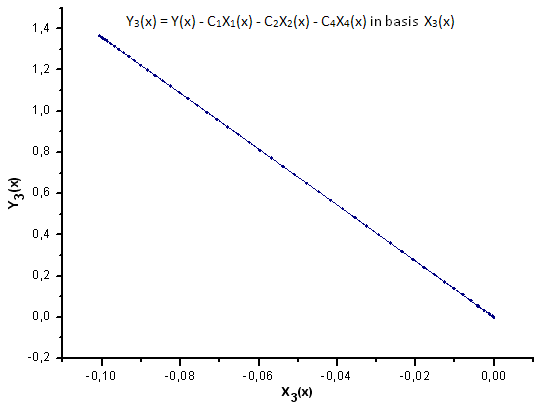
Fig. 32. Representação da função Y3(x) na base X3(x)

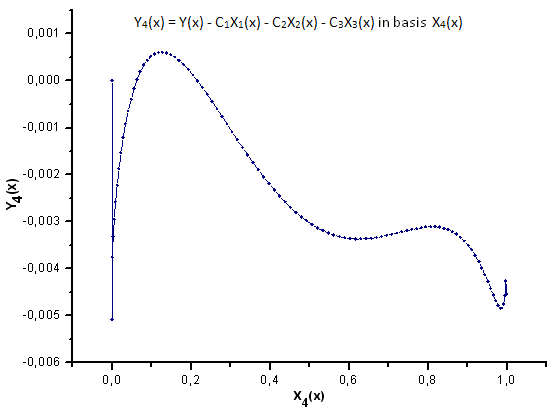
Fig. 33. Representação da função Y4(x) na base X4(x)

Conforme as fig. 30-33 sugerem, as funções de P2(x) e P(U) são muito semelhantes em termos de coordenadas X1(x), X2(x) e X3(x) - pode-se observar uma boa dependência linear entre Xi(x) e Yi(x). Uma diferença significativa pode ser vista no componente X4(x) (fig. 33).

A ausência de uma dependência linear para o componente X4(x) mostra o fato de que o conjunto de dados gerados por P(U), apesar de parecer semelhante à distribuição q-Gaussian, de fato, não é a q-Gaussian.

Podemos olhar de forma diferente para as funções (figuras 34-37) ao representar Xi(x) e Yi(x) juntas.

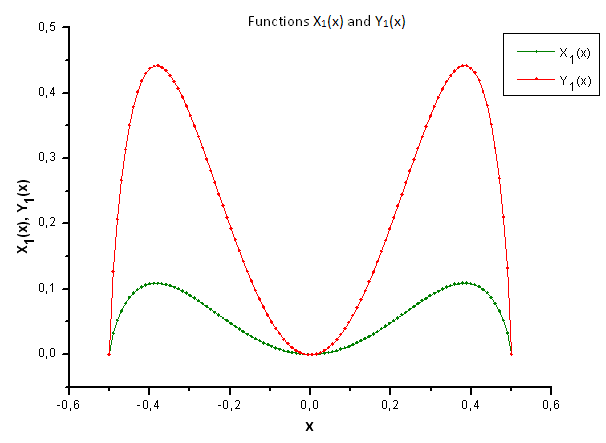
Fig. 34. Forma geral das funções X1(x) e Y1(x)

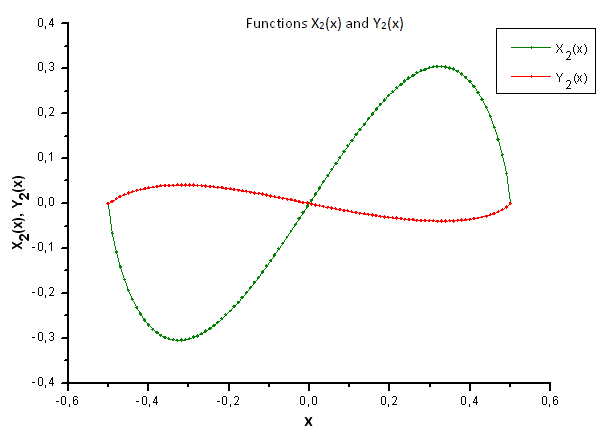
Fig. 35. Forma geral das funções X2(x) e Y2(x)

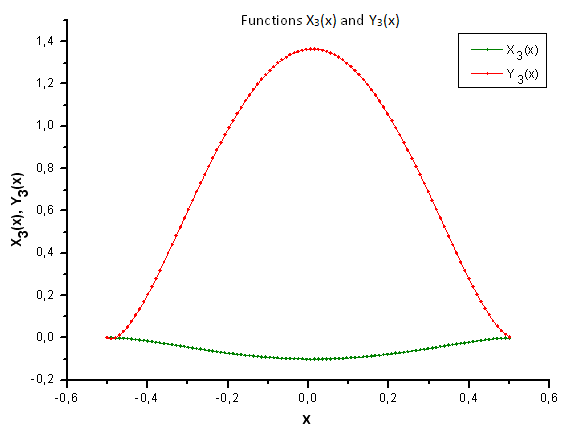
Fig. 36. Forma geral das funções X3(x) e Y3(x)

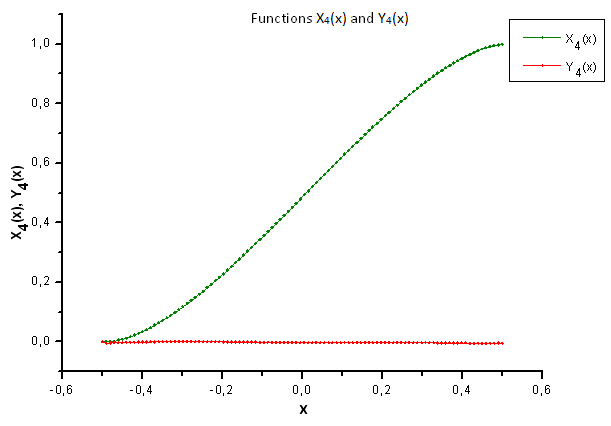
Fig. 37. Forma geral das funções X4(x) e Y4(x)

Como a fig. 37 sugere, a diferença estrutural no componente X4(x) parece óbvia ao projetarmos dados gerados pela função P(U) nas coordenadas de Eigen da função P2(x). Assim, podemos dizer com evidência que os dados experimentais não correspondem à função P2(x).

O cálculo descrito abaixo (EC_Example3_test) fala a favor deste fato:

2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1  0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2  0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3  -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4  0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994

Ele também prejudicou as relações entre os parâmetros.

Conclusão

O método de coordenadas de Eigen é uma ferramenta única para a análise de propriedades estruturais de relações funcionais que permitem simplificar substancialmente a análise e interpretação de dados.

O conceito por trás deste método é utilizar conjuntos de dados experimentais {xi,yi} para construir novas funções ao modelo proposto. A forma de expansões de operador é determinada pela estrutura da equação diferencial que é satisfeita pela função de servir como uma "candidata" para a descrição de dados. Se a função for nativa, as funções de expansão calculadas utilizando os dados {xi,yi}, na base das coordenadas de Eigen tomarão uma forma linear. Os desvios de linearidade na base das coordenadas de Eigen da "função candidata" sugerem que os dados {xi,yi} não poderiam ser gerados pela função dada e o modelo construído não é apropriado.

Em alguns casos complicados a função candidata e a função nativa podem aparecer de modo tão similar que uma grande parte das expansões calculadas acabam por ser lineares. No entanto, o método de coordenadas de Eigen nos permite identificar a diferença entre essas funções que torna sua presença conhecida por linearidade deficiente da expansão - o exemplo de Hilhorst e Schehr serviu como uma ilustração da diferença ficando óbvio ao último membro de expansão quando projetando X4(x).

Esta informação pode também ser útil com uma equação diferencial (seção 3.2) que é satisfeita pela função P2(x) - o membro em questão corresponde à parte linear com respeito a P2(x). Pode não ser tão interessante no caso de descrição fenomenológica de dados experimentais ("estamos procurando uma solução na forma do q-Gaussian"). No entanto, se o modelo é baseado nas equações diferenciais (fig. 3), o papel de cada um dos mecanismos considerados em modelos de processos físicos podem ser melhor compreendidos.

Referências

1. C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
2. C. Tsallis, "Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
3. C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
4. Europhysics News "Special Issue: Nonextensive Statistical Mechanics: New Trends, New Perspectives", Vol. 36 No. 6 (Novebro-Dezembro 2005).
5. M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
6. Constantino Tsallis, the Official Website Nonextensive Statistical Mechanics and Thermodynamics.
7. Chumak, O.V. "Entropy and Fractals in Data Analysis", М.-Izhevsk: RDC "Regular and Chaotic Dynamics", Institute for Computer Research, 2011. - 164 p.
8. Qiuping A. Wang, "Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
9. Qiuping A. Wang, "Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory", Entropy, 5(2003).
10. Lisa Borland, "Long-Range Memory and Nonextensivity in Financial Markets", Europhysics News 36, 228-231 (2005)
11. T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
12. S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-Law Distributions in Economics: A Nonextensive Statistical Approach", Proceedings of SPIE (2005) Volume: 5848, Editor: SPIE, Páginas: 151-164, (preprint)
13. R Hanel, S Thurner, "Derivation of Power-Law Distributions within Standard Statistical Mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Edição: 2-4, Editor: Elsevier, Páginas: 260-268. (preprint)
14. A K Rajagopal, Sumiyoshi Abe, "Statistical Mechanical Foundations of Power-Law Distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Edição: 1-4, Páginas: 19 (preprint)
15. T. Kaizoji, "An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
16. V. Gontis, J. Ruseckas, A. Kononovičius, "A Long-Range Memory Stochastic Model of the Return in Financial Markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
17. H.E. Roman, M. Porto, "Self-Generated Power-Law Tails in Probability Distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Edição: 3 Pt 2, Páginas: 036-128.
18. H. J. Hilhorst, G. Schehr, "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" (2007, preprint, presentation).
19. D. J. Hudson, "Lectures on Elementary Statistics and Probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
20. D. J. Hudson, "Statistics Lectures II : Maximum Likelihood and Least Squares Theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
21. R. R. Nigmatullin, "Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
22. R.R. Nigmatullin, "Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method", Physica A: Statistical Mechanics and its Applications Volume 285, Edições 3–4, 1 Outubro 2000, pp. 547–565.
23. C. Antonini "q-Gaussians in Finance" (2010).
24. C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
25. L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical Indications of a q-Generalised Central Limit Theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
26. T. Dauxois, "Non-Gaussian Distributions under Scrutiny", J. Stat. Mech. (2007) N08001. (preprint)