Anwendung des Verfahrens der eigenen Koordinaten auf die Analyse des Aufbaus einfacher statistischer Verteilungen

Inhalt

• Einleitung
• 1. Das Q-Analogon der Normalverteilung (Q-Gaußverteilung) in der Ökonometrie
• 2. Eigen-Koordinaten
  • 2.1. Das Eigen-Koordinaten-Verfahren
  • 2.2. Die Berechnung der Zerlegungskoeffizienten mithilfe der Methode der kleinsten Quadrate
  • 2.3. Beispielhafte Zerlegung der Funktion R(x)
  • 2.4. Umsetzung in ein Programm
  • 2.5. Ergebnisse der Berechnung der Beispielfunktion R(x)
  • 2.6. Auswirkungen des Rauschens
• 3. Nicht mitwachsende Wahrscheinlichkeitsverteilungen
  • 3.1. Zerlegung der Funktion P1(x) in Eigen-Koordinaten
  • 3.2. Zerlegung der Funktion P2(x) in Eigen-Koordinaten
• 4. Nicht alles, was wie eine Katze aussieht, muss auch eine Katze sein
• Fazit
  
• Literaturhinweise:
• Anhang. Analyse der SP500-Verteilung mittels Q-Gaußverteilung

Einleitung

1988 schlug Constantino Tsallis eine Verallgemeinerung der statistischen Mechanik von Boltzmann, Gibbs und Shannon [1] vor, durch die der Begriff der nicht mitwachsenden Entropie eingeführt wurde.

Als ein bedeutendes Ergebnis der Verallgemeinerung der Entropie erwies sich das Zustandekommen neuer Arten von Verteilungen [2], die eine Schlüsselrolle in der neuen statistischen Mechanik (die Q-Analoga der Exponential- und Normalverteilung):

Es hat sich gezeigt, dass es mithilfe dieser Verteilungen möglich ist, eine Vielzahl von Versuchsdaten [3-6] von Systemen mit Langzeitspeicher, weitreichender Wirkung und starker Korrelation zu beschreiben.

Die Entropie ist sehr eng mit Informationen [7] verknüpft. Die Verallgemeinerung der statistischen Mechanik auf der Grundlage der Informationstheorie erfolgte in den Arbeiten unter [8-9] in den Literaturhinweisen. Die neue nicht mitwachsende statistische Mechanik hat sich als überaus nützlich für die Ökonometrie erwiesen [10-17]. Das Q-Analogon der Normalverteilung (Q-Gaußverteilung) beschreibt sehr schön die breiten Schwingen (Schwänze) der Verteilungen der Inkremente der Kursnotierungen von Finanzinstrumenten (q~1,5), wobei sich die Mehrzahl der Inkrementverteilungen finanzieller Zeitreihen bei langen Zeiträumen (Monaten, Jahren) in eine Normalverteilung (q=1) verwandeln [10].

Natürlich wurde erwartet, dass eine vergleichbare Verallgemeinerung der statistischen Mechanik zu einem Analogon des zentralen Grenzwertsatzes für Verteilungen des Typs Q-Gauß führen würde. In der unter [18] in den Literaturhinweisen aufgeführten Arbeit wurde gezeigt, dass dem nicht so ist, die Grenzverteilung der Summe stark korrelierender Zufallsvariablen weicht analytisch von der der Q-Gaußverteilung ab.

Es trat jedoch ein ganz anders geartetes Problem auf: es ergab sich, die Zahlenwerte der ermittelten exakten Lösung sehr dicht bei denen einer Q-Gaußverteilung lagen („zahlenmäßig ähnlich, analytisch anders“). Zur Untersuchung der Unterschiede zwischen den Funktionen und, um die besten Parameter für die Q-Gaußverteilung zu erhalten, wurde in der genannten Arbeit [18] die Zerlegung in Reihen angewendet. Das Verhalten dieser Funktionen führte zu einer allmählichen Zerlegung des den Grad der Unveränderlichkeit des Systems beschreibenden Parameters q.

Das große Problem der angewandten Statistik besteht in der Annahme statistischer Hypothesen. Es galt lange Zeit als unlösbar [19-20], da dazu ein besonderes Hilfsmittel (in der Art eines Elektronenmikroskops) benötigt würde, um mehr zu sehen, als mit den Methoden der zeitgenössischen angewandten Statistik möglich ist.

In der Arbeit unter [21] wird das Eigen-Koordinaten-Verfahren vorgeschlagen, mit dessen Hilfe wir zu einer tiefer liegenden Ebene vordringen können, der Analyse der strukturellen Eigenschaften der Abhängigkeiten zwischen Funktionen. Mit diesem feinen Instrument lässt sich eine Reihe von Aufgaben lösen. In der Arbeit unter [22] wurden den oben aufgeführten nicht mitwachsenden Verteilungen entsprechende Funktionen in ihre Operatoren zerlegt.

In dem hier vorliegenden Beitrag betrachten wir das Eigen-Koordinaten-Verfahren (kurz: EKV) und untersuchen einige konkrete Anwendungsbeispiele. Der Beitrag selbst enthält eine Fülle für das Verständnis der Natur des Verfahrens unverzichtbarer Formeln. Durch Wiederholen aller Berechnungen können Sie selbst praktikable Zerlegungen der für Sie interessantesten Funktionen durchführen.

1. Das Q-Analogon der Normalverteilung (Q-Gaußverteilung) in der Ökonometrie

Die Q-Gaußverteilung hat für die Ökonometrie eine große Bedeutung [4,10-17].

Eine allgemeine Vorstellung von dem aktuellen Forschungsstand vermitteln die Vorträge Dr. Claudio Antoninis „q-Gaussians in Finance“ [23] und „The Use of the q-Gaussian Distribution in Finance“ [24].

Es folgt eine Kurzfassung der wesentlichen Ergebnisse:

Abb. 1. Wissenschaftliche Methoden (Folie 4 Verwendung des Q-Analogons der Normalverteilung im Finanzwesen [The Use of the q-Gaussian Distribution in Finance])

Die wesentlichen Besonderheiten von Finanzzeitreihen zeigt die Abbildung 2:

Abb. 2. Eigenschaften von Finanzzeitreihen (Folie 3 Verwendung des Q-Analogons der Normalverteilung im Finanzwesen [The Use of the q-Gaussian Distribution in Finance])

Zahlreiche zur Beschreibung von Finanzzeitreihen verwendete theoretische Modelle führen zu einer Q-Gaußverteilung:

Abb. 3. Theoretische Modelle und die Q-Gaußverteilung (Folie 27 Verwendung des Q-Analogons der Normalverteilung im Finanzwesen [The Use of the q-Gaussian Distribution in Finance])

Die Q-Gaußverteilung wird auch zur phänomenologischen Beschreibung der Verteilung von Kursnotierungen verwendet:

Abb. 4. Beispiel der Analyse der Tagesrendite von S&P500 (Folie 8 Verwendung des Q-Analogons der Normalverteilung im Finanzwesen [The Use of the q-Gaussian Distribution in Finance])

Bei der Arbeit mit echten Daten stellt sich die Frage der Ermittlung der richtigen Funktionen:

Abb. 5. Das Problem der Ermittlung der Verteilungsfunktion (Folie 14 Q-Gaußverteilungen im Finanzwesen [q-Gaussians in Finance])

In beiden Vorträgen betont Antonini die Bedeutung der Ermittlung der richtigen Funktionen für die Erstellung angemessener Modelle physischer Vorgänge:

Abb. 6. Schlussfolgerungen der Vorträge „q-Gaussians in Finance“ und „The Use of the q-Gaussian Distribution in Finance“ (Claudio Antonini, 2010, 2011)

Anwendungsbeispiele für Q-Gauß-Statistiken im Finanzwesen (Methodisches Material [worksheets]) + Dateien für MathCad):

• q-Gaussian Stock Price Dynamics, (Michael English, 2008)
• q-Gaussian European Options (Michael English, 2008)
• q-Gaussian Random Deviates & Distribution, (Michael English, 2008)
• q-Gaussian Portfolios (Michael English, 2008)
• q-Gaussian Risk Measures (Michael English, 2008)
• Expected Value & Value at Risk for Lognormal Asset (Michael English, 2008)

2. Eigen-Koordinaten

Eine Zerlegung in eigene Koordinaten sieht folgendermaßen aus:

mit C1…CN als Konstanten und X1(t),..,XN(t) als „Eigen-Koordinaten“.

Solche linearen Zerlegungen sind recht unproblematisch und kommen bei der Datenanalyse häufig zur Anwendung. In logarithmischem Maßstab verwandelt sich die Musterfunktion beispielsweise in eine Gerade (deren Neigung sich leicht mithilfe der linearen Regression berechnen lässt). Mithin besteht zum Auffinden der Funktionsparameter nicht die Notwendigkeit der Durchführung einer nichtlinearen Optimierung („Fitting“).

Bei komplexeren Funktionen (z. B. der Summer zweier Exponenten) könnte der logarithmische Maßstab allerdings bereits nicht mehr von Nutzen sein, da die Funktion nicht aussieht wie eine Gerade. Zur Ermittlung ihrer Koeffizienten bedarf es einer nichtlinearen Optimierung.

Es gibt Fälle, in denen die Versuchsdaten mithilfe einiger Funktionen, denen jeweils unterschiedliche Modelle physischer Vorgänge entsprechen, mit gleichbleibender Genauigkeit erklärt werden können. Welche Funktion ist die geeignetste? Welche von ihnen bildet die Wirklichkeit jenseits der Versuchsdaten am besten ab?

Für die Analyse komplexer Systeme (z. B. von Finanzzeitreihen) ist die Ermittlung der richtigen Funktion überaus wichtig, jeder der Verteilungen entspricht ein jeweils eigener physischer Vorgang, und die Auswahl des richtigen Modells führt zu einem besseren Verständnis der Dynamik sowie der allgemeinen Eigenschaften komplexer Systeme.

In der angewandten Statistik [19, 20] heißt es, dass es kein Kriterium gibt, das die Zurückweisung einer fehlerhaften statistischen Hypothese zulässt. Das Verfahren der Eigen-Koordinaten eröffnet eine neue Sicht auf dieses Problem (das der Annahme von Hypothesen).

Die zur Beschreibung der Versuchsdaten verwendete Funktion kann als Lösung einer bestimmten Differentialgleichung betrachtet werden. Ihre Form bestimmt den Aufbau der Zerlegung in eigene Koordinaten.

Eine Besonderheit der Zerlegung in Eigen-Koordinaten besteht darin, dass alle von der Funktion Y(t) hervorgebrachten Daten in der Basis der Eigen-Koordinaten X1(t)..XN(t) derselben Funktion ihrem Aufbau nach linear sind. Von einer beliebigen anderen Funktion F(t) hervorgebrachte Daten erscheinen in dieser Basis nicht mehr als gerade Linie (sie sehen in der Basis der Eigen-Koordinaten der entsprechenden Funktion F(t) linear aus).

Dieser Umstand ermöglicht die exakte Ermittlung der Funktionen, was die Arbeit mit statistischen Hypothesen beträchtlich erleichtert.

2.1. Das Eigen-Koordinaten-Verfahren

Der Grundgedanke dieses Verfahrens besteht in der Schaffung eigener Koordinaten Xk(t) in der Form in der Basis der Funktion Y(t) angelegter Operatoren.

Das kann mittels mathematischer Analyse geschehen, die Eigen-Koordinaten Xk(t) nehmen dann das Aussehen integraler Faltungen an, während die Anlage der Zerlegung durch den Aufbau der durch die Funktion Y(t) erfüllten Differentialgleichung bestimmt. Darüber hinaus ergibt sich das Problem der Ermittlung der Koeffizienten C1... CN.

Bei der Zerlegung orthogonaler Basen (etwa zur Ermittlung der Koeffizienten der Fourier-Transformation) werden die Zerlegungskoeffizienten mittels Projektion eines Vektors auf die Basis ermittelt, und das gewünschte Ergebnis wird dank der Orthogonalität der Basisfunktionen erhalten.

In unserem Fall ist dieser Ansatz nicht geeignet, es liegen keine Angaben zur Orthogonalität von X1(t)… XN(t) vor.

2.2. Die Berechnung der Zerlegungskoeffizienten mithilfe der Methode der kleinsten Quadrate

Die Berechnung der Koeffizienten Ck kann mithilfe der Methode der kleinsten Quadrate ausgeführt werden. Diese Aufgabe reduziert sich auf die Lösung eines Systems linearer Gleichungen.

Angenommen:

Real liegt bei jeder Messung der Fehler vor:

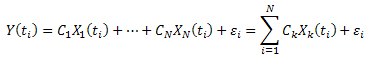
Wir minimieren die Summe der Abweichungsquadrate:

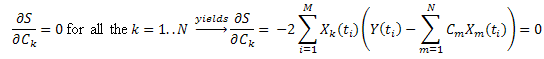
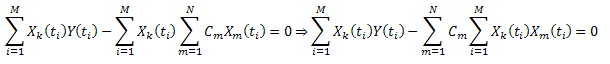
Nach Einführung der Bezeichnung: 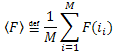, können wir sie wie folgt aufzeichnen:

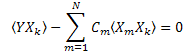
So erhalten wir ein System linearer Gleichungen für C1...CN (k=1..N):

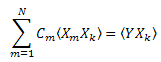
Die „Korrelatorenmatrix“ ist symmetrisch: .

In manchen Fällen ist es besser, die Zerlegung in eigene Koordinaten in integraler Form anzulegen:

Dadurch kann die Auswirkung von Fehlern (aufgrund der Mittelung) verringert werden, allerdings sind dazu weitere Berechnungen erforderlich.

2.3. Beispielhafte Zerlegung der Funktion R(x)

Sehen wir uns das Beispiel der Zerlegung der folgenden Funktion in eigene Koordinaten an:

Diese Funktion bringt mehrere statistische Verteilungen hervor [21]:

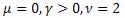1. - die Normal- oder Gaußverteilung;
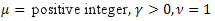2. - die Poisson-Verteilung;
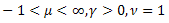3. - die Gamma-Verteilung;
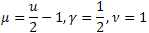4. - die 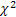-Verteilung; und
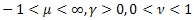5. - Stauffer-Verteilung mit der Weibull-Verteilung als Sonderfall .

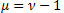Darüber hinaus eignet sie sich gut für die Beschreibung von Entspannungsvorgängen:

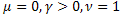1. - die gewöhnliche exponentielle Funktion;
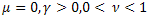2. - die gestreckte (stretched) exponentielle Funktion;
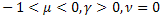3. - die graduelle Entspannungsfunktion.

Nach der Differenzierung von R(x) bezüglich x, erhalten wir:

Wir multiplizieren beide Seiten mit x:

wandeln um:

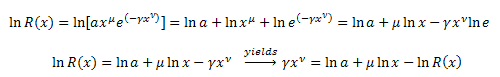
und setzen es in die Gleichung ein;

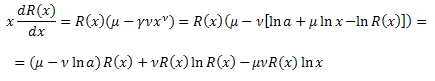
Wir erhalten eine Differentialgleichung für die Funktion R(x):

Wir setzen beide Seiten in Bezug auf x in das Intervall [xm,x] ein:

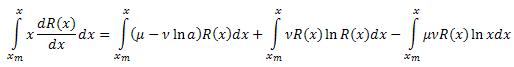
setzen den linken Teil des Ausdrucks in Teilen ein:

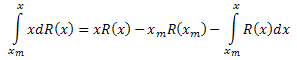
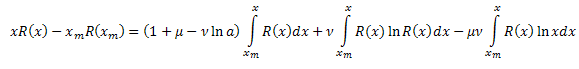
und erhalten:

mit:

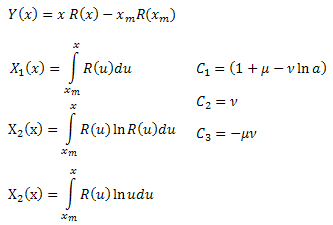
Durch Berechnung der Koeffizienten können die Funktionsparameter ermittelt werden. Der vierte Parameter kann aus dem Ausdruck für R(x) abgeleitet werden.

2.4. Umsetzung in ein Programm

Zur Berechnung der Zerlegungskoeffizienten muss ein System linearer Gleichungen gelöst werden. Die Arbeit mit Matrizen kann der Einfachheit halber in Form der gesonderten Klasse CMatrix (in der Datei CMatrix.mqh) angelegt werden. Mit den Methoden dieser Klasse können sowohl die Parameter und die Werte der Elemente der Matrix festgelegt als auch das System der linearen Gleichungen mithilfe des Verfahrens von Gauß gelöst werden.

//+------------------------------------------------------------------+
//| CMatrix class                                                    |
//+------------------------------------------------------------------+
class CMatrix
  {
   double            m_matrix[];
   int               m_rows;
   int               m_columns;
public:
   void              SetSize(int nrows,int ncolumns);
   double            Get(int i,int j);
   void              Set(int i,int j,double val);
   void              GaussSolve(double &v[]);
   void              Test();
  };

Wir zeigen als Beispiel ein Skript (EC_Example1.mq5) zur Berechnung der Eigen-Koordinaten und Parameter der Funktion R(x).

//+------------------------------------------------------------------+
//|                                                  EC_Example1.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <CMatrix.mqh>
//+------------------------------------------------------------------+
//| CECCalculator                                                    |
//+------------------------------------------------------------------+
class CECCalculator
  {
protected:
   int               m_size;
   //--- x[i]
   double            m_x[];
   //--- y[i]
   double            m_y[];
   //--- matrix
   CMatrix           m_matrix;
   //--- Y[i]
   double            m_ec_y[];
   //--- eigen-coordinates X1[i],X2[i],X3[i]
   double            m_ec_x1[];
   double            m_ec_x2[];
   double            m_ec_x3[];
   //--- coefficients C1,C2,C3
   double            m_ec_coefs[];
   //--- function f1=Y-C2*X2-C3*X3
   double            m_f1[];
   //--- function f2=Y-C1*X1-C3*X3
   double            m_f2[];
   //--- function f3=Y-C1*X1-C2*X2
   double            m_f3[];
private:
   //--- function for data generation
   double            R(double x,double a,double mu,double gamma,double nu);
   //--- calculation of the integral
   double            Integrate(double &x[],double &y[],int ind);
   //--- calculation of the function Y(x)
   void              CalcY(double &y[]);
   //--- calculation of the function X1(x)
   void              CalcX1(double &x1[]);
   //--- calculation of the function X2(x)
   void              CalcX2(double &x2[]);
   //--- calculation of the function X3(x)
   void              CalcX3(double &x3[]);
   //--- calculation of the correlator
   double            Correlator(int ind1,int ind2);
public:
   //--- method for generating the test function data set x[i],y[i]
   void              GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu);
   //--- loading data from the file
   bool              LoadData(string filename);
   //--- saving data into the file
   bool              SaveData(string filename);
   //--- saving the calculation results
   void              SaveResults(string filename);
   //--- calculation of the eigen-coordinates
   void              CalcEigenCoordinates();
   //--- calculation of the linear expansion coefficients
   void              CalcEigenCoefficients();
   //--- calculation of the function parameters
   void              CalculateParameters();
   //--- calculation of the functions f1,f2,f3
   void              CalculatePlotFunctions();
  };
//+------------------------------------------------------------------+
//| Function R(x)                                                    |
//+------------------------------------------------------------------+
double CECCalculator::R(double x,double a,double mu,double gamma,double nu)
  {
   return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x)))));
  }
//+-----------------------------------------------------------------------+
//| Method for generating the data set x[i],y[i] of the test function R(x)|
//+-----------------------------------------------------------------------+
void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu)
  {
   if(size<=0) return;
   if(x1>=x2) return;
   m_size=size;
   ArrayResize(m_x,m_size);
   ArrayResize(m_y,m_size);
   double delta=(x2-x1)/(m_size-1);
//---
   for(int i=0; i<m_size; i++)
     {
      m_x[i]=x1+i*delta;
      m_y[i]=R(m_x[i],a,mu,gamma,nu);
     }
  };
//+------------------------------------------------------------------+
//| Method for loading data from the .CSV file                       |
//+------------------------------------------------------------------+
bool CECCalculator::LoadData(string filename)
  {
   int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   m_size=0;
   while(!FileIsEnding(filehandle))
     {
      string str=FileReadString(filehandle);
      if(str!="")
        {
         string astr[];
         StringSplit(str,';',astr);
         if(ArraySize(astr)==2)
           {
            ArrayResize(m_x,m_size+1);
            ArrayResize(m_y,m_size+1);
            m_x[m_size]=StringToDouble(astr[0]);
            m_y[m_size]=StringToDouble(astr[1]);
            m_size++;
           }
         else
           {
            m_size=0;
            return(false);
           }
        }
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for saving data into the .CSV file                        |
//+------------------------------------------------------------------+
bool CECCalculator::SaveData(string filename)
  {
   if(m_size==0) return(false);
   if(ArraySize(m_x)!=ArraySize(m_y)) return(false);
   if(ArraySize(m_x)==0) return(false);
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   for(int i=0; i<ArraySize(m_x); i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the integral                       |
//+------------------------------------------------------------------+
double CECCalculator::Integrate(double &x[],double &y[],int ind)
  {
   double sum=0;
   for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5;
   return(sum);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function Y(x)                  |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the function X1(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X2(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i]));
   ArrayResize(x2,m_size);
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X3(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i]));
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the eigen-coordinates              |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoordinates()
  {
   CalcY(m_ec_y);
   CalcX1(m_ec_x1);
   CalcX2(m_ec_x2);
   CalcX3(m_ec_x3);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the correlator                     |
//+------------------------------------------------------------------+
double CECCalculator::Correlator(int ind1,int ind2)
  {
   if(m_size==0) return(0);
   if(ind1<=0 || ind1>4) return(0);
   if(ind2<=0 || ind2>4) return(0);
//---
   double arr1[];
   double arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
//---
   switch(ind1)
     {
      case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
   switch(ind2)
     {
      case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
//---
   double sum=0;
   for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i];  }
   sum=sum/m_size;
   return(sum);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the linear expansion coefficients  |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoefficients()
  {
//--- setting the matrix size 3x4
   m_matrix.SetSize(3,4);
//--- calculation of the correlation matrix 
   for(int i=3; i>=1; i--)
     {
      string s="";
      for(int j=1; j<=4; j++)
        {
         double corr=Correlator(i,j);
         m_matrix.Set(i,j,corr);
         s=s+" "+DoubleToString(m_matrix.Get(i,j));
        }
      Print(i," ",s);
     }
//--- solving the system of the linear equations
   m_matrix.GaussSolve(m_ec_coefs);
//--- displaying the solution - the obtained coefficients C1,..CN 
   for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]);
  };
//+--------------------------------------------------------------------+
//| Method for the calculation of the function parameters a,mu,nu,gamma|
//+--------------------------------------------------------------------+
void CECCalculator::CalculateParameters()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//--- calculate a
   double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1]));
//--- calculate mu
   double mu=-m_ec_coefs[2]/m_ec_coefs[1];
//--- calculate nu
   double nu=m_ec_coefs[1];
//--- calculate gamma
   double arr1[],arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
   double corr1=0;
   double corr2=0;
   for(int i=0; i<m_size; i++)
     {
      arr1[i]=MathPow(m_x[i],nu);
      arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]);
      corr1+=arr1[i]*arr2[i];
      corr2+=arr1[i]*arr1[i];
     }
   double gamma=-corr1/corr2;
//---
   Print("a=",a);
   Print("mu=",mu);
   Print("nu=",nu);
   Print("gamma=",gamma);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the functions                      |
//| f1=Y-C2*X2-C3*X3                                                 |
//| f2=Y-C1*X1-C3*X3                                                 |
//| f3=Y-C1*X1-C2*X2                                                 |
//+------------------------------------------------------------------+
void CECCalculator::CalculatePlotFunctions()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//---
   ArrayResize(m_f1,m_size);
   ArrayResize(m_f2,m_size);
   ArrayResize(m_f3,m_size);
//---
   for(int i=0; i<m_size; i++)
     {
      //--- plot function f1=Y-C2*X2-C3*X3
      m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f2=Y-C1*X1-C3*X3
      m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f3=Y-C1*X1-C2*X2
      m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i];
     }
  }
//+------------------------------------------------------------------+
//| Method for saving the calculation results                        |
//+------------------------------------------------------------------+
void CECCalculator::SaveResults(string filename)
  {
   if(m_size==0) return;
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename," for writing, error",GetLastError());
      return;
     }
   for(int i=0; i<m_size; i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+=DoubleToString(m_ec_y[i],8)+";";
      s+=DoubleToString(m_ec_x1[i],8)+";";
      s+=DoubleToString(m_f1[i],8)+";";
      s+=DoubleToString(m_ec_x2[i],8)+";";
      s+=DoubleToString(m_f2[i],8)+";";
      s+=DoubleToString(m_ec_x3[i],8)+";";
      s+=DoubleToString(m_f3[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CECCalculator ec;
//--- model function data preparation
   ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3);
//--- saving into the file
   ec.SaveData("ex1.csv");
//--- calculation of the eigen-coordinates
   ec.CalcEigenCoordinates();
//--- calculation of the coefficients
   ec.CalcEigenCoefficients();
//--- calculation of the parameters
   ec.CalculateParameters();
//--- calculation of the functions f1,f2,f3
   ec.CalculatePlotFunctions();
//--- saving the results into the file
   ec.SaveResults("ex1-results.csv");
  }

2.5. Ergebnisse der Berechnung der Beispielfunktion R(x)

Als Versuchsdaten erzeugen wir 100 Werte der Funktion R(x) in dem Intervall [0,25;15,25].

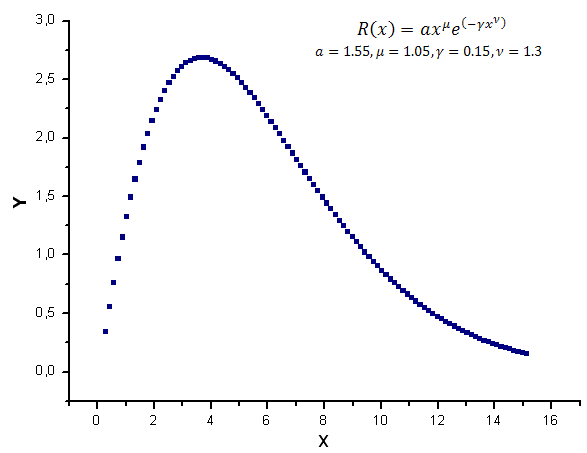
Abb. 7. Die zur Berechnung verwendete Musterfunktion

Auf der Grundlage dieser Daten werden die Funktion Y(x) und ihre Zerlegung in die Funktionen X1(x), X2(x) und X3(x) angelegt.

In der Abbildung 8 sehen wir die Funktion Y(x) und ihre „eigenen Koordinaten“ X1(x), X2(x) und X3(x).

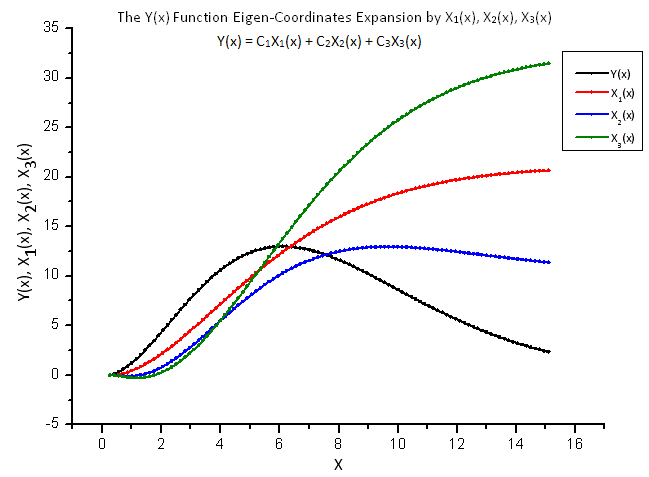
Abb. 8. Allgemeine Ansicht der Funktion Y(x) und ihrer Eigen-Koordinaten X1(x), X2(x) und X3(x).

Zu beachten ist dabei die durch die integrale Natur der Operatoren X1(x), X2(x) und X3(x) bedingte „Glattheit“ dieser Funktionen.

Nach der Berechnung der Funktionen Y(x), X1(x), X2(x) und X3(x) wird die Korrelatorenmatrix angelegt, danach erfolgt die Lösung der Gleichungen für die Koeffizienten C1, C2 und C3, auf deren Grundlage die Rechenparameter der Funktion R(x) ermittelt werden:

2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1  221.03637620 148.53278281 305.48547011 101.93843241
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2  148.53278281 101.63995012 202.85142688 74.19784681
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3  305.48547011 202.85142688 429.09345292 127.82779760

Wir überprüfen die Linearität der angelegten Zerlegung. Dazu müssen 3 Funktionen berechnen:

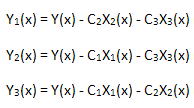
jede von ihnen wird auf die Basis ihrer entsprechenden Eigen-Koordinate X1(x), X2(x) oder X3(x) projiziert:

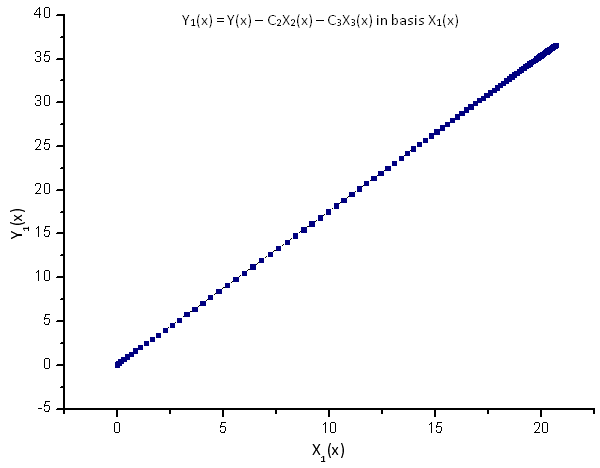
Abb. 9. Darstellung der Funktion Y1(x) mit der Basis X1(x)

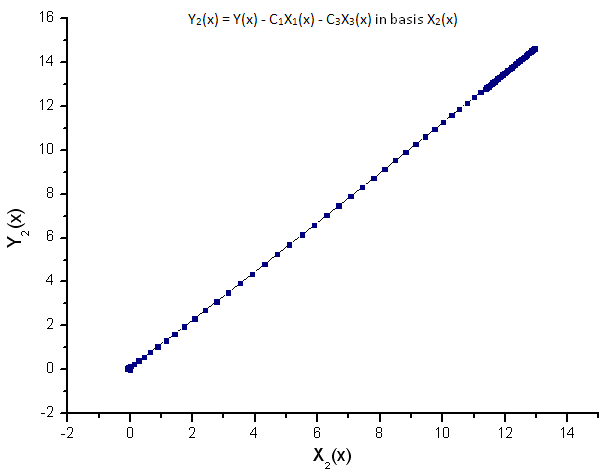
Abb. 10. Darstellung der Funktion Y2(x) mit der Basis X2(x)

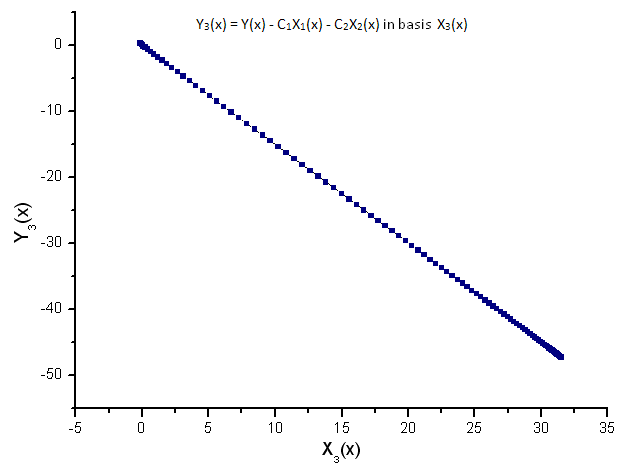
Abb. 11. Darstellung der Funktion Y3(x) mit der Basis X3(x)

Die lineare Abhängigkeit der angelegten Funktionen zeugt davon, dass die in der Abbildung 7 wiedergegebene Datenfolge genau der Funktion R(x) entspricht.

Jede andere in den Eigen-Koordinaten von R(x) wiedergegebene Funktion (auch solche von ähnlicher Form) wird nicht mehr linear aussehen. Dieser Umstand ermöglicht die Ermittlung der Funktionen.

Die Genauigkeit der Berechnung der Zahlenwerte der Parameter der Musterfunktion kann durch eine Erhöhung der Anzahl der der Punkte auf 10.000 (bei gleichbleibendem Intervall) gesteigert werden:

2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1  225.47846911 151.22066473 311.86134419 104.65062550
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2  151.22066473 103.30005101 206.66297964 76.03285182
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3  311.86134419 206.66297964 438.35625824 131.91955339

In diesem Fall wurden die Funktionsparameter mit größerer Genauigkeit ermittelt.

2.6. Auswirkungen des Rauschens

Echte Versuchsdaten enthalten stets ein gewisses Rauschen.

In der Methode GenerateData() der Klasse ECCCalculator ändern wir:

m_y[i]=R(m_x[i],a,mu,gamma,nu);

in

m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;

wobei wir ein zufälliges Rauschen im Umfang von etwa 10% des Höchstwertes der Funktion hinzufügen.

Hier sehen wir das Ergebnis der Ausführung des Skripts EC_Example1-noise.mq5:

2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1  254.45082565 185.19087989 354.25574000 125.17343164
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2  185.19087989 136.81028987 254.92996885 97.14705491
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3  354.25574000 254.92996885 501.76021715 159.49440494

Das Diagramm der Musterfunktion mit Rauschen zeigt die Abbildung 12:

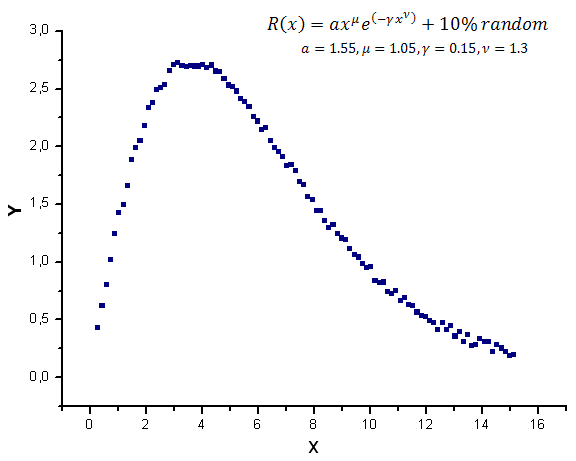
Abb. 12. Die zur Berechnung verwendete Musterfunktion mit Rauschen

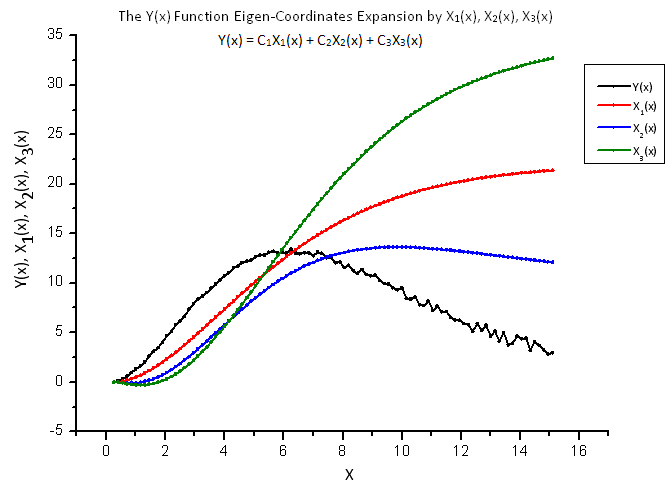
Abb. 13. Allgemeine Ansicht der Funktion Y(x) und ihrer Eigen-Koordinaten X1(x), X2(x) und X3(x).

Die als „Eigen-Koordinaten“ auftretenden Funktionen X1(x), X2(x) und X3(x) scheinen nach wie vor „glatt“ zu sein, die als ihre lineare Kombination angelegte Funktion Y(x) dagegen sieht anders aus (s. Abb. 13).

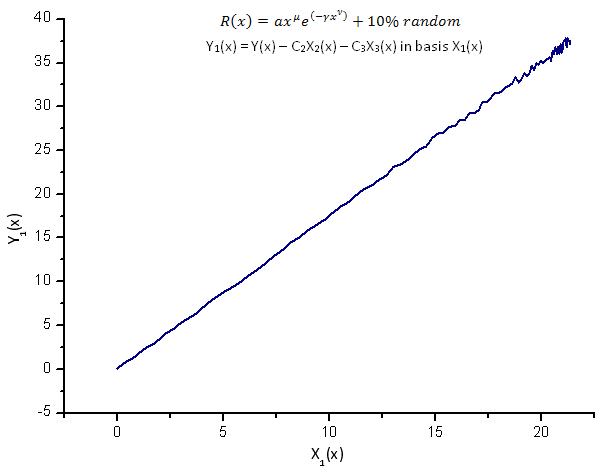
Abb. 14. Darstellung der Funktion Y1(x) mit der Basis X1(x)

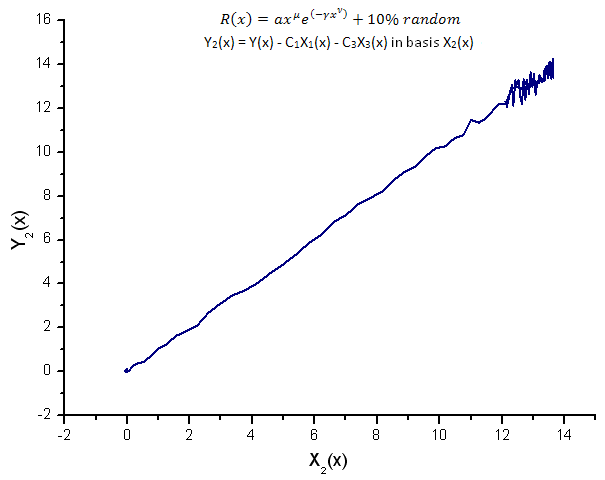
Abb. 15. Darstellung der Funktion Y2(x) mit der Basis X2(x)

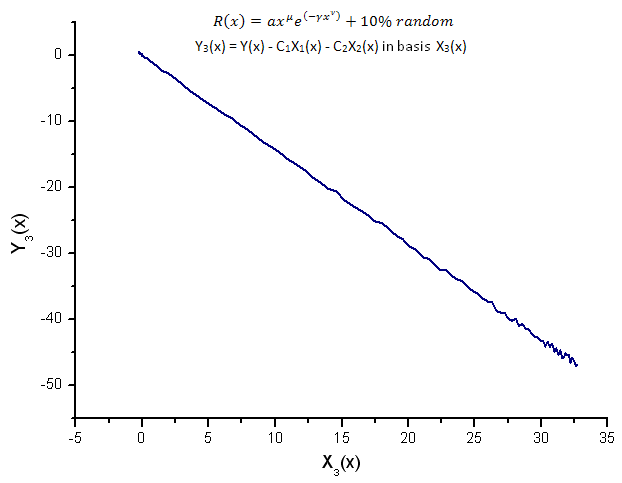
Abb. 16. Darstellung der Funktion Y3(x) mit der Basis X3(x)

Die Darstellung der Funktionen Y1(x), Y2(x) und Y3(x) in der Basis der Eigen-Koordinaten (Abbildung 8-10) weist wie gehabt eine lineare Form auf, wobei um die Gerade herum bereits durch das Vorhandensein von Rauschen bedingte Fluktuationen zu beobachten sind. Das wird am deutlichsten bei großen X-Werten, bei denen das Signal/Rauschen minimal wird.

Dabei befinden sich die Bestandteile des Rauschens auf beiden Seiten der Geraden, weswegen sich in diesen Fällen die Verwendung der integralen Form der Zerlegung in Eigen-Koordinaten (s. Abschnitt 2.2) empfiehlt.

 

3. Nicht mitwachsende Wahrscheinlichkeitsverteilungen

Die Verallgemeinerung der statistischen Mechanik führt zu folgenden Verteilungen [s. 2 und 22]:

mit , .

Das Q-Analogon der Exponentialverteilung ist ein Sonderfall der Funktion P1(x) und die Q-Gaußverteilung ein Sonderfall der Funktion P2(x).

3.1. Zerlegung der Funktion P1(x) in Eigen-Koordinaten

Wir differenzieren P1(x):

und erhalten folgende Differentialgleichung:

dann integrieren wir aus dem Intervall [xm,x]:

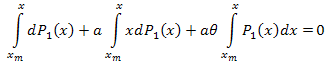
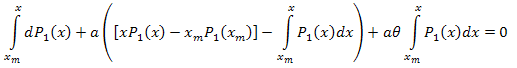
und erhalten:

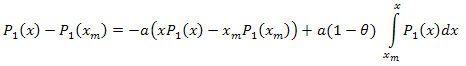
Die Zerlegung in eigene Koordinaten sieht folgendermaßen aus:

mit:

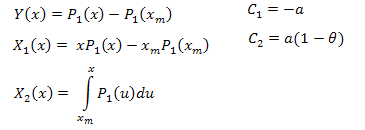
Die Rechenfunktionen haben folgendes Aussehen (s. das Skript EC_Example2.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
//--- Y=P(x)-P(xm)
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
//--- X1=x*P(x)-xm*P(xm)
   for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
//--- X2=Integrate(P1(x)) 
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i);
  }

Diesmal weist die Korrelatorenmatrix die Dimension 2x3 auf; die Werte der Parameter „a“ und „Theta“ der Funktion P1(x) werden mithilfe der Koeffizienten С1 und C2 bestimmt. Den Zahlenwert für den Parameter B erhalten wir aus der Normalisierungsbedingung.

Das Ergebnis der Berechnung der Musterfunktion P1(x; 1; 0,5; 2) für 1.000 Punkte in dem Intervall x [0,10] lautet:

2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1  0.15420524 0.48808959 -0.32145543
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2  0.48808959 1.79668322 -1.14307410

Die Funktion P1(x) sowie ihre Zerlegung in eigene Koordinaten werden in den Abbildungen 17 - 20 wiedergegeben.

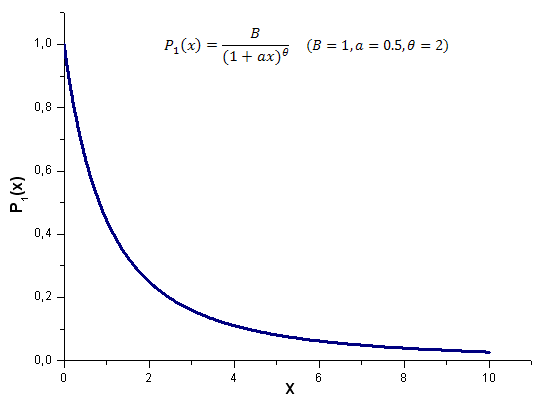
Abb. 17. Die für die Berechnung verwendete Musterfunktion P1(x; 1; 0,5; 2) mit 1.000 Punkten

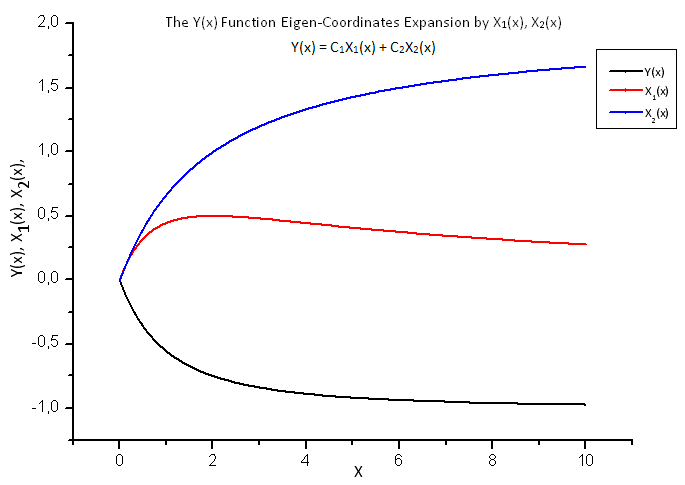
Abb. 18. Die allgemeine Ansicht der Funktion Y(x) und ihrer Eigen-Koordinaten X1(x) und X2(x).

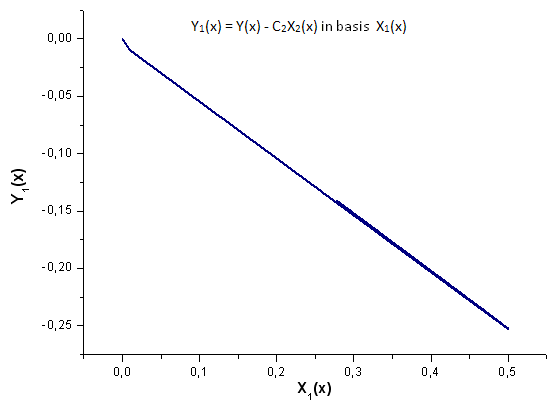
Abb. 19. Darstellung der Funktion Y1(x) mit der Basis X1(x)

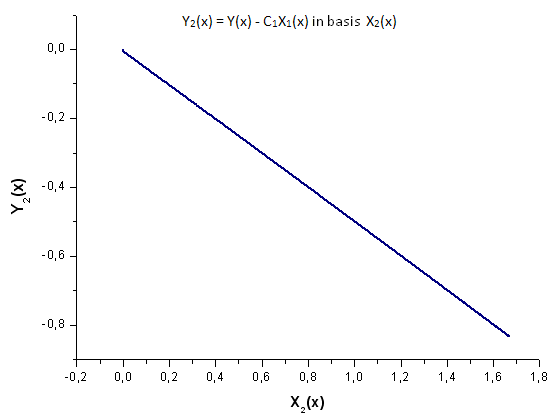
Abb. 20. Darstellung der Funktion Y2(x) mit der Basis X2(x)

Achten Sie einmal auf Abbildung 19. Ganz am Anfang sowie im zweiten Drittel des Diagramms liegt eine leichte Verformung der linearen Abhängigkeit vor.

Diese ist durch die Besonderheiten der ausgeführten Zerlegung bedingt - X1(x) ist nicht von integraler Natur.

3.2. Zerlegung der Funktion P2(x) in Eigen-Koordinaten

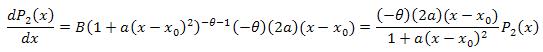
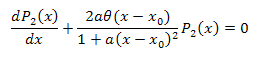
Die Differentialgleichung:

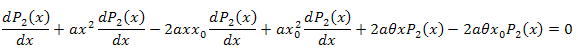
Wir integrieren mit Bezug auf x im Intervall [xm,x]:

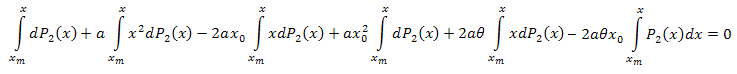
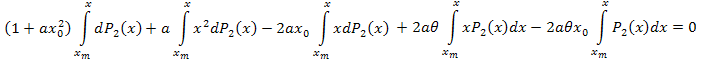
Durch Integration in Teilen erhalten wir:

Wir vereinfachen:

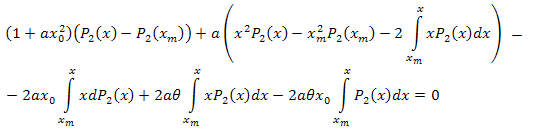
Nach algebraischer Umwandlung erhalten wir:

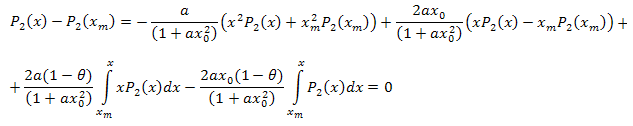
Also haben wir folgende Zerlegung:

mit:

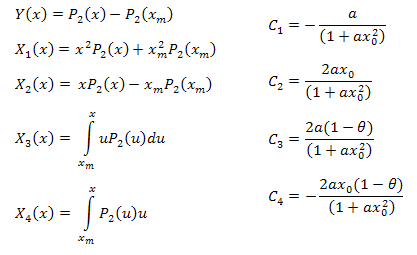
Die Funktionsparameter können mithilfe folgender Formeln berechnet werden:

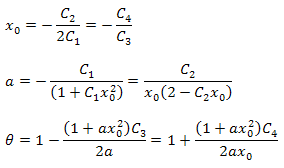
Es ist zu beachten, dass in der resultierenden Zerlegung weitere Beziehungen zwischen den Parametern vorhanden sind. Diesen Umstand können wir zur Überprüfung der Richtigkeit der Wahl der Funktion für die Analyse nutzen. Bei der Funktion P2(x) genau entsprechenden Daten sind diese Beziehungen stets berechtigt.

Den Zahlenwert für den Parameter B erhalten wir aus der Normalisierungsbedingung.

Die Funktionen zur Berechnung der Eigen-Koordinaten (s. EC_Example3.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm)
   for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
   //--- X2=(x)*P2(x)-(xm)*P2(xm)
   for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX3                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i];
   //--- X3=Integrate(X*P2(x)) 
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);  
  }
//+------------------------------------------------------------------+
//| CalcX4                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX4(double &x4[])
  {
   if(m_size==0) return;
   //--- X4=Integrate(P2(x))
   ArrayResize(x4,m_size);
   for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i);
  }

Das Ergebnis der Berechnung der Musterfunktion P22(x) (B=1; a=0,5; Theta=2; x0=1) für 1.000 Punkte lautet:

2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1  1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2  0.60684314 0.37995888 0.55974145 0.58899739 0.06731011
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3  1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4  1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168

Die Funktion P2(x) sowie ihre Zerlegung in eigene Koordinaten werden in den Abbildungen 21 - 26 wiedergegeben.

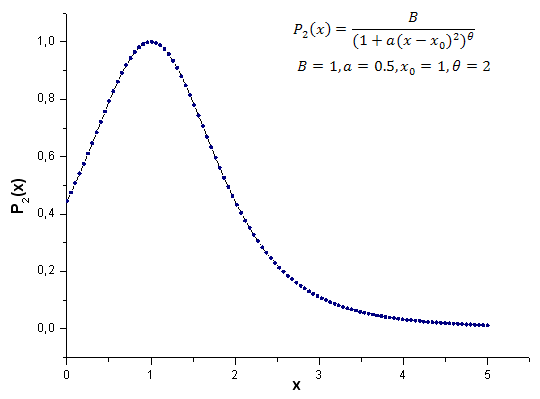
Abb. 21. Die für die Berechnung verwendete Musterfunktion P2(x; 1; 0,5; 2; 1) mit 100 Punkten

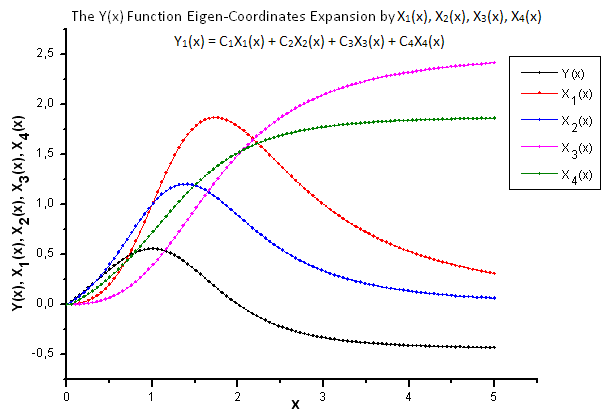
Abb. 22. Allgemeine Ansicht der Funktion Y(x) und ihrer Eigen-Koordinaten X1(x), X2(x),X3(x) und X4(x).

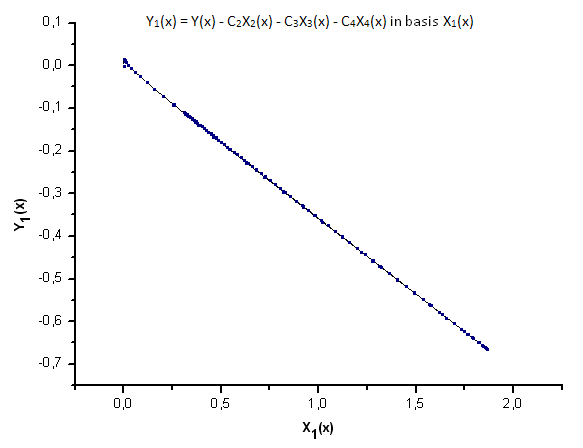
Abb. 23. Darstellung der Funktion Y1(x) mit der Basis X1(x)

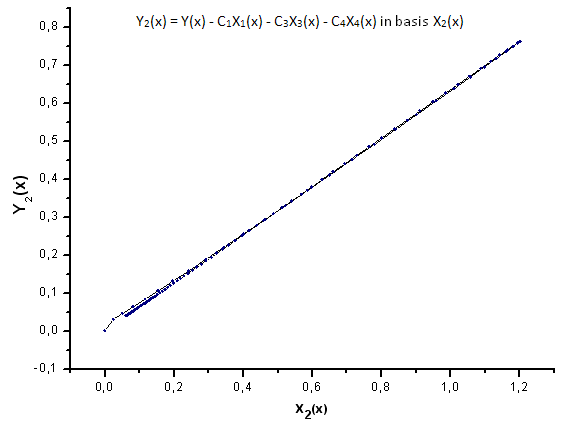
Abb. 24. Darstellung der Funktion Y2(x) mit der Basis X2(x)

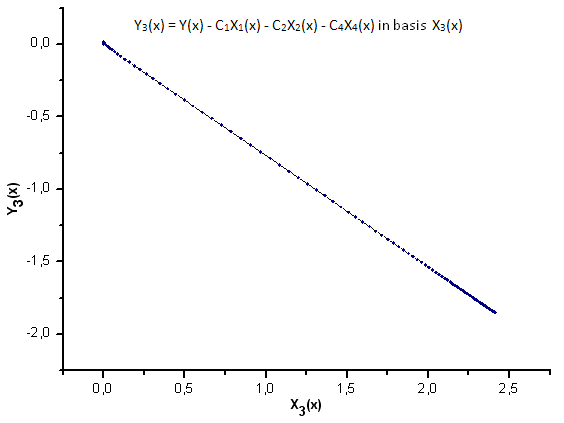
Abb. 25. Darstellung der Funktion Y3(x) mit der Basis X3(x)

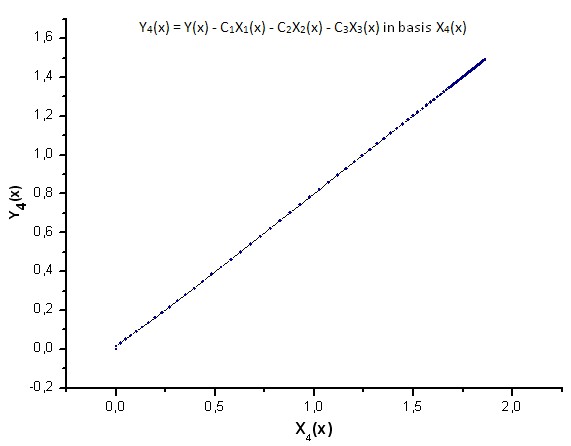
Abb. 26. Darstellung der Funktion Y4(x) mit der Basis X4(x)

4. Nicht alles, was wie eine Katze aussieht, muss auch eine Katze sein

Die Familie der Q-Analoga der Normalverteilungen (der Q-Gaußverteilungen) bildet das Herzstück der statistischen Mechanik, weshalb natürlich erwartet wurde, dass sie bei der Verallgemeinerung als zentraler Grenzsatz erscheinen würde. Das Hauptargument dafür lieferten die Überlegungen zur Entropie [26].

Und trotzdem wurde in einem Vortrag [18] gezeigt, dass Verteilungen vom Typ Q-Gauß nicht allumfassend sind, wodurch auch ihre besondere Rolle als Grenzverteilungen infrage gestellt wird.http://www.ens-lyon.fr/PHYSIQUE/PHENIX_ISIS/SCHER.pdf

Die Funktion (die analytische Lösung einer der gestellten Aufgaben):

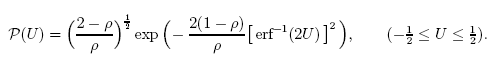
wird zum Beispiel mithilfe der Q-Gaußverteilung mit großer Genauigkeit dargestellt.

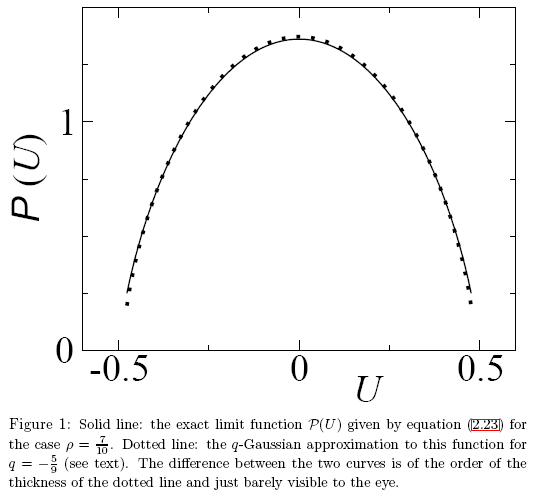
Abb. 27. Beispiel aus dem Artikel „Eine Anmerkung zu den Q-Gauß- und Nicht-Gaußverteilungen in der statistischen Mechanik“ (A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics)

In diesem Fall weisen analytisch unterschiedliche Funktionen vergleichbare Zahlenwerte auf, weswegen die Unterschiede mit bloßem Auge schwer zu erkennen sind. Es ist ein exaktes Verfahren zur Ermittlung der Funktionen vonnöten. Das Eigen-Koordinaten-Verfahren stellt eine elegante Lösung für diese Aufgabe dar.

Wir betrachten die Zerlegung der Funktion P(U) in deren eigene Koordinaten und zeigen, worin genau es sich von der Q-Gaußverteilung unterscheidet. Dem Aussehen nach sind beide Funktionen recht ähnlich (s. Abb. 27).

Wir erzeugen ein Signal (100 Werte der Funktion P(U)) und „projizieren“ es auf das System der Eigen-Koordinaten der in Abschnitt 3.2 angelegten Funktion P2(x).

Das Skript Hilhorst-Schehr-problem.mq5 berechnet die Funktion P(U) und erstellt eine Datenfolge, beides wird in der Datei MQL5\Files\test-data.csv gespeichert. Die Analyse dieser Daten wird von dem Skript EC_Example3_Test.mq5 ausgeführt.

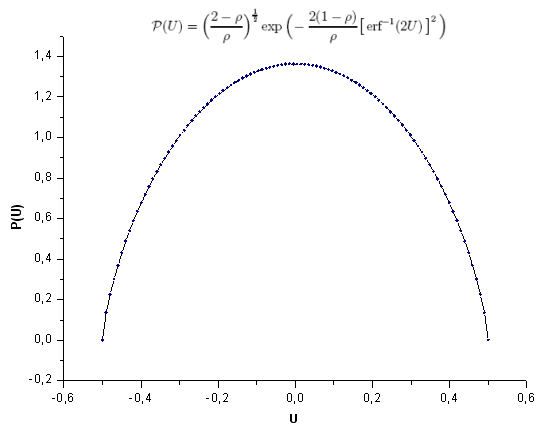
Abb. 28. Die Musterfunktion P(U) mit 100 Punkten

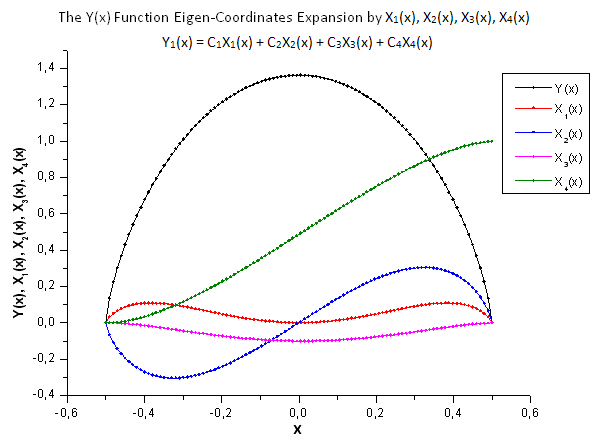
Abb. 29. Allgemeine Ansicht der Funktion Y(x) und ihrer Eigen-Koordinaten X1(x), X2(x),X3(x) und X4(x).

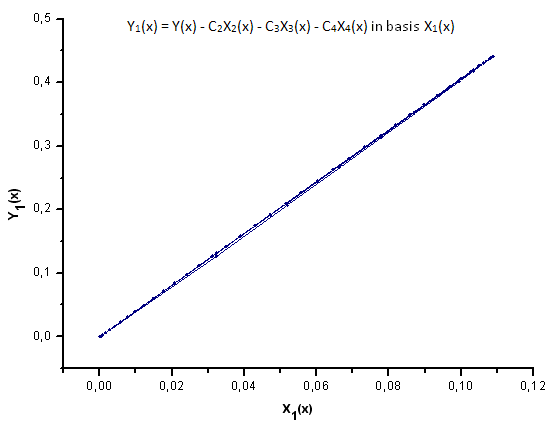
Abb. 30. Darstellung der Funktion Y1(x) mit der Basis X1(x)

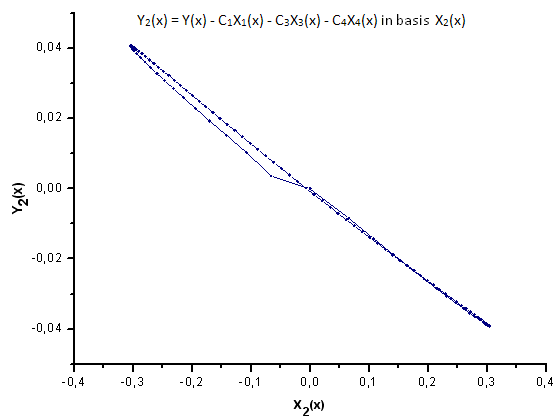
Abb. 31. Darstellung der Funktion Y2(x) mit der Basis X2(x)

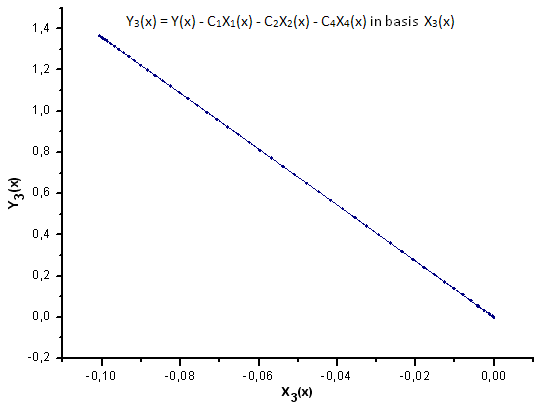
Abb. 32. Darstellung der Funktion Y3(x) mit der Basis X3(x)

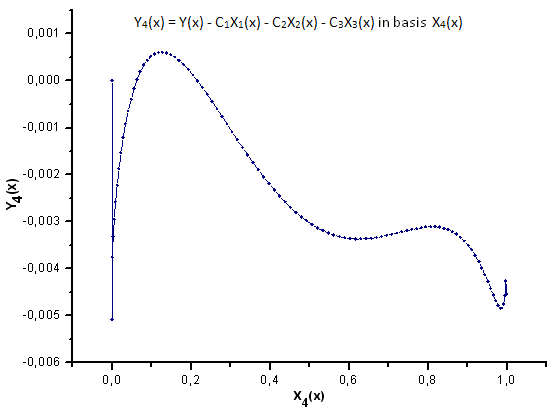
Abb. 33. Darstellung der Funktion Y4(x) mit der Basis X4(x)

Wie die Abbildungen 30 - 33 zeigen, sind die Funktionen P2(x) und P(U) in Bezug auf die Koordinaten X1(x), X2(x) und X3(x) recht ähnlich, es lässt sich eine schöne lineare Abhängigkeit zwischen Xi(x) und Yi(x) beobachten. Ein deutlicher Unterschied zeigt sich in X4(x) (s. Abb. 33).

Das Fehlen der linearen Abhängigkeit bei X4(x) belegt, dass der von P(U) erzeugte Datensatz trotz der optischen Ähnlichkeit mit einer Q-Gaußverteilung kein solche darstellt.

Die Funktionen erscheinen in einem anderen Licht (s. die Abbildungen 34 - 37), wenn wir sie auf Xi(x) und Yi(x) gemeinsam aufbauen.

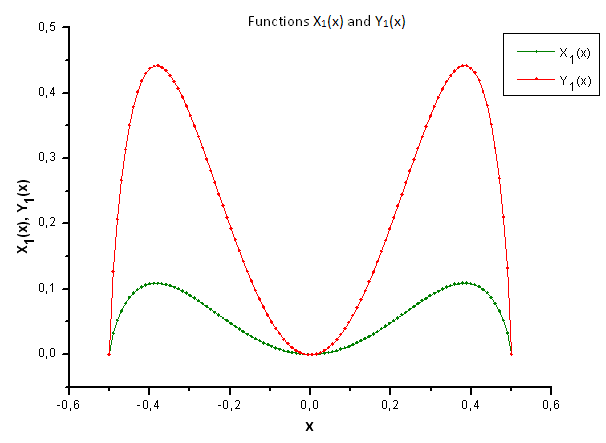
Abb. 34. Allgemeine Ansicht der Funktionen X1(x) und Y1(x)

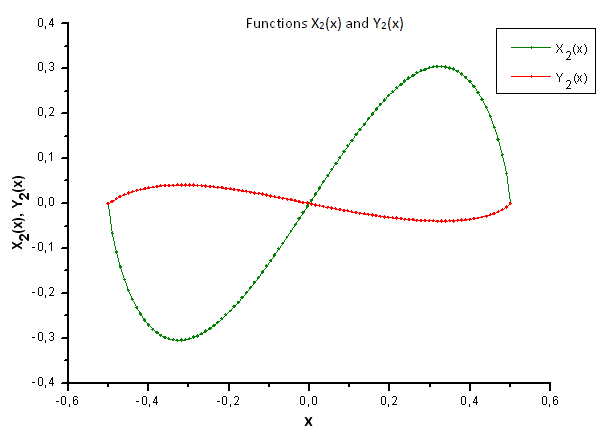
Abb. 35. Allgemeine Ansicht der Funktionen X2(x) und Y2(x)

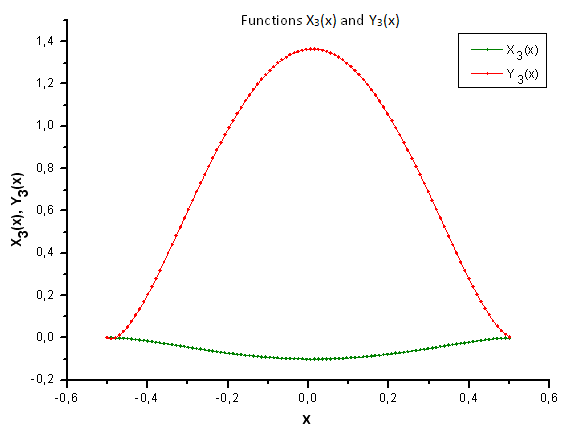
Abb. 36. Allgemeine Ansicht der Funktionen X3(x) und Y3(x)

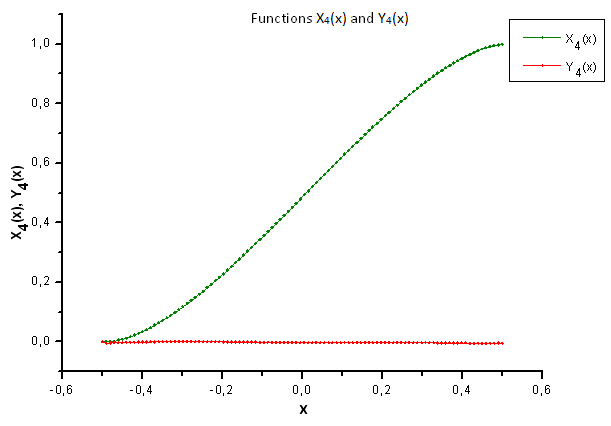
Abb. 37. Allgemeine Ansicht der Funktionen X4(x) und Y4(x)

Aus der Abbildung 37 geht hervor, dass bei der Projektion der von der Funktion P(U) erzeugten Daten auf die Eigen-Koordinaten der Funktion P2(x) eine Abweichung im Aufbau des Elements X4(x) aufgetreten ist. Somit lässt sich mit Bestimmtheit sagen, dass die Versuchsdaten nicht mit der Funktion P2(x) übereinstimmen.

Die Berechnung (EC_Example3_test) bestätigt diesen Umstand:

2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1  0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2  0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3  -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4  0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994

Die Beziehungen zwischen den Parametern wurden ebenfalls zerstört.

Fazit

Das Verfahren der eigenen Koordinaten ist ein einzigartiges Instrument zur Analyse der strukturellen Eigenschaften der Abhängigkeiten von Funktionen, das die Analyse und Auswertung von Daten erheblich erleichtert.

Die Idee hinter diesem Verfahren ist die Schaffung neuer, dem vorgeschlagenen Modell entsprechender Funktionen aus dem Versuchsdatenbestand {xi, yi}. Die Form der Zerlegung in Operatoren wird durch den Aufbau der Differentialgleichung bestimmt, die durch die als „Kandidat“ für die Beschreibung der Daten dienende Funktion erfüllt wird. Wenn die Funktion richtig gewählt wurde (native function), nehmen die anhand der Daten {xi, yi} angelegten Zerlegungen der Funktionen in der Eigen-Koordinatenbasis eine lineare Form an. Abweichungen von der Linearität in der Basis der Eigen-Koordinaten der „Kandidatenfunktion“ sprechen dafür, dass die Daten {xi, yi} nicht von dieser Funktion hervorgebracht wurden und das aufgestellte Modell nicht das richtige ist.

In einigen komplizierten Fällen sind die „Kandidatenfunktion“ und die „native Funktion“ einander so ähnlich, dass ein großer Teil der gebildeten Zerlegungen sich als linear erweist. Nichtsdestoweniger gelingt es mithilfe des Eigen-Koordinaten-Verfahrens, den Unterschied zwischen diesen Funktionen auszumachen, der in der Aufhebung der Linearität der Zerlegung zutage tritt. In dem Beispiel von Hilhorst und Schehr hat sich der Unterschied in dem letzten Glied der Zerlegung bei der Projektion auf X4(x) gezeigt.

Diese Information kann auch bei einer Differentialgleichung (s. Abschnitt 3.2) hilfreich sein, die durch die Funktion P2(x) erfüllt wird, ein solches Glied entspricht dem linearen Teil in Bezug auf P2(x). Bei der phänomenologischen Beschreibung der Versuchsdaten („wir suchen nach einer Lösung in der Form eines Q-Analogons der Normalverteilung“) ist das nicht sonderlich interessant, obwohl bei einem auf Differentialgleichungen beruhenden Modell (s. Abb. 3) die Funktion der einzelnen in Modellen physischer Vorgänge zu berücksichtigenden Mechanismen verständlicher wird,

Literaturhinweise:

1. C. Tsallis, Mögliche Verallgemeinerung der Boltzmann-Gibbs-Statistik (Possible Generalization of Boltzmann-Gibbs Statistics), Journal of Statistical Physics, Bd. 52, Nr. 1/2, 1988.
2. C. Tsallis, Nicht mitwachsende Statistik: Theoretische, experimentelle und rechnerische Beweise und Verbindungen (Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections). Brazilian Journal of Physics, (1999) Bd. 29. S.1.
3. C. Tsallis, Einige Anmerkungen zur statistischen Mechanik von Boltzmann und Gibbs (Some Comments on Boltzmann-Gibbs Statistical Mechanics), Chaos, Solitons & Fractals Band 6, 1995, S. 539–559.
4. Europhysics News Sonderausgabe: Nicht mitwachsende statistische Mechanik: Neue Trend, neue Perspektiven (Nonextensive Statistical Mechanics: New Trends, New Perspectives), Bd. 36 Nr. 6 (November-Dezember 2005).
5. M. Gell-Mann, C. Tsallis, Nicht mitwachsende Entropie: Interdisziplinäre Anwendungen (Nonextensive Entropy: Interdisciplinary Applications), Oxford University Press, 15. 04. 2004, S. 422.
6. Constantino Tsallis, offizielle Webseite Nicht mitwachsende statistische Mechanik und Thermodynamik (Nonextensive Statistical Mechanics and Thermodynamics).
7. Tschumak, O.V. Entropie und Fraktale in der Datenanalyse (Entropy and Fractals in Data Analysis), Мoskau-Izhevsk: RDC Geordnete und chaotische Dynamik (Regular and Chaotic Dynamics), Institut für Rechnerforschung (Institute for Computer Research), 2011. 164 Seiten.
8. Qiuping A. Wang, Unvollständige Statistik und nicht mitwachsende Verallgemeinerungen der statistischen Mechanik (Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics), Chaos, Solitone und Fraktale (Chaos, Solitons and Fractals), 12(2001) 1431-1437.
9. Qiuping A. Wang, Mitwachsende Verallgemeinerung der statistischen Mechanik auf der Grundlage der Theorie unvollständiger Informationen (Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory), Entropie (Entropy), 5(2003).
10. Lisa Borland, Langzeitgedächtnis und Gleichmaß auf Finanzmärkten (Long-Range Memory and Nonextensivity in Financial Markets), Europhysics News 36, 228-231 (2005)
11. T. S. Biró, R. Rosenfeld, Der mikroskopische Ursprung der Nicht-Normalverteilung von Finanzrenditen (Microscopic Origin of Non-Gaussian Distributions of Financial Returns), Physica A: Statistische Mechanik und ihre Anwendungen (Statistical Mechanics and its Applications), Bd. 387, Nr. 7 (1. März 2008), S. 1603-1612 (Vorabdruck).
12. S. M. D. Queiros, C. Anteneodo, C. Tsallis, Exponentielle Verteilungen in den Wirtschaftswissenschaften: Ein nicht mitwachsender statistischer Ansatz (Power-Law Distributions in Economics: A Nonextensive Statistical Approach), Sitzungsberichte des SPIE (2005) Band: 5848, Herausgeber: SPIE, Seiten: 151 - 164, (Vorabdruck)
13. R. Hanel, S. Thurner, Ableitung von exponentiellen Verteilungen in der gewöhnlichen statistischen Mechanik (Derivation of Power-Law Distributions within Standard Statistical Mechanics), Physica A: Statistische Mechanik und ihre Anwendungen (Statistical Mechanics and its Applications) (2005), Band: 351, Ausgabe: 2-4, Herausgeber: Elsevier, Seiten: 260 - 268. (Vorabdruck)
14. A. K. Rajagopal, Sumiyoshi Abe, Statistisch mechanische Grundlagen exponentieller Verteilungen (Statistical Mechanical Foundations of Power-Law Distributions), Physica D: Nichtlineare Erscheinungen (Nonlinear Phenomena) (2003), Band: 193, Ausgabe: 1-4, Seiten: 19 (Vorabdruck)
15. T. Kaizoji, Ein Finanzmarktmodell mit interagierenden Maklern aus Sicht der nicht mitwachsenden statistischen Mechanik (An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics), Physica A: Statistische Mechanik und ihre Anwendungen (Statistical Mechanics and its Applications), Bd. 370, Nr. 1 (1. Okt. 2008), S. 109-113. (Vorabdruck)
16. V. Gontis, J. Ruseckas, A. Kononovičius, Ein stochastisches Finanzmarktrenditemodell mit Langzeitgedächtnis (A Long-Range Memory Stochastic Model of the Return in Financial Markets), Physica A: Statistische Mechanik und ihre Anwendungen (Statistical Mechanics and its Applications) 389 (2010), 100 - 106: (Vorabdruck)
17. H.E. Roman, M. Porto, Selbst erzeugte Exponentialschwänze bei Wahrscheinlichkeitsverteilungen (Self-Generated Power-Law Tails in Probability Distributions), Physical Review E - Statistische, nichtlineare und Weichmateriephysik (Statistical, Nonlinear and Soft Matter Physics) (2001), Bd.: 63, Ausgabe: 3 Teil 2, Seiten: 036 - 128.
18. H. J. Hilhorst, G. Schehr, Eine Anmerkung zu den Q-Gauß- und Nicht-Gaußverteilungen in der statistischen Mechanik (A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics) (2007, Vorabdruck, Präsentation).
19. D. J. Hudson, Vorlesungen zu Elementarstatistik und Wahrscheinlichkeit (Lectures on Elementary Statistics and Probability), CERN-63-29, Genf: CERN, 1963. 101 Seiten.
20. D. J. Hudson, Statistikvorlesungen II: Maximale Wahrscheinlichkeit und die Theorie der kleinsten Quadrate ("Statistics Lectures II: Maximum Likelihood and Least Squares Theory), CERN-64-18. - Genf: CERN, 1964. 115 Seiten.
21. R. R. Nigmatullin, Eigen-Koordinaten: Ein neues Verfahren zur Ermittlung der Analysefunktionen bei experimentellen Messungen (Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements), Angewandte Magnetresonanz (Applied Magnetic Resonance) Band 14, Nummer 4 (1998), 601-633.
22. R.R. Nigmatullin, Erkennen nicht mitwachsender statistischer Verteilungen mittels Eigen-Koordinaten-Verfahren (Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method), Physica A: Statistische Mechanik und ihre Anwendungen (Statistical Mechanics and its Applications) Band 285, Ausgaben 3 -4, 1. Oktober 2000, S. 547-565.
23. C. Antonini Q-Gaußverteilungen im Finanzwesen (q-Gaussians in Finance) (2010).
24. C. Antonini, Die Verwendung der Q-Gaußverteilung im Finanzwesen (The Use of the q-Gaussian Distribution in Finance) (2011).
25. L. G. Moyano, C. Tsallis, M. Gell-Mann, Nummerische Indikationen eines Q-verallgemeinerten zentralen Grenzwertsatzes (Theorem), Europhysics Briefe 73, 813-819, 2006, (Vorabdruck).
26. T. Dauxois, Nicht-Gaußverteilungen unter der Lupe (Non-Gaussian Distributions under Scrutiny), J. Stat. Mech. (2007) Nr. 8001. (Vorabdruck)

Anhang. Analyse der SP500-Verteilung mittels Q-Gaußverteilung

Wir betrachten hier das klassische Beispiel (Abb. 4) zur Erläuterung der Verteilung der SP500-Tagesrendite mithilfe des Q-Analogons der Normalverteilung (in Form der Funktion P2(x).

Die Tagesdaten zu den Schlusskursen stammen aus: http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500/

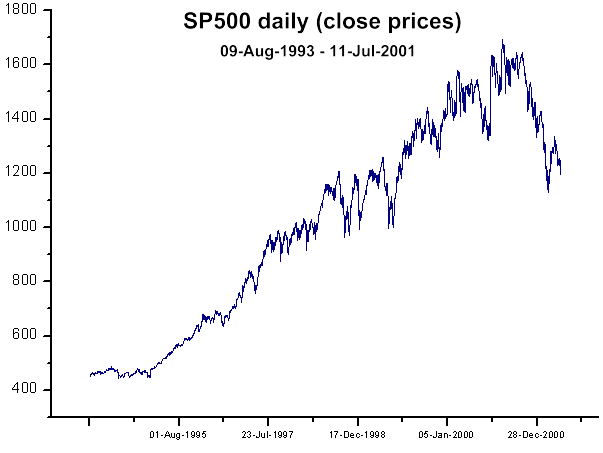
Abb. 38. Diagramm der täglichen Schlusskurse für SP500

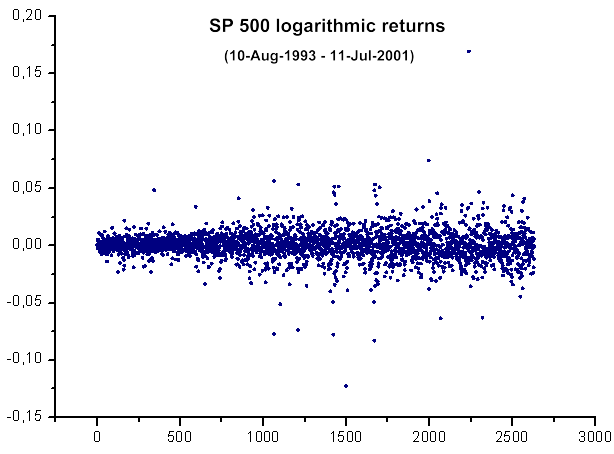
Abb. 39. Diagramm des Logarithmus der Inkremente der täglichen Kursnotierungen für SP500

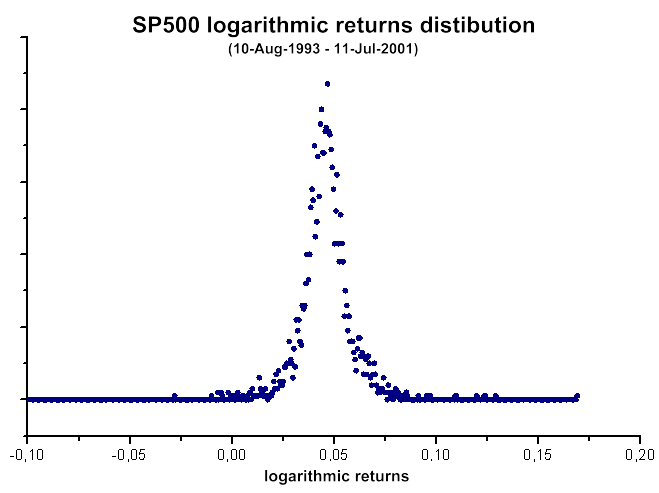
Abb. 40. Verteilung des Logarithmus der Inkremente der täglichen Kursnotierungen für SP500

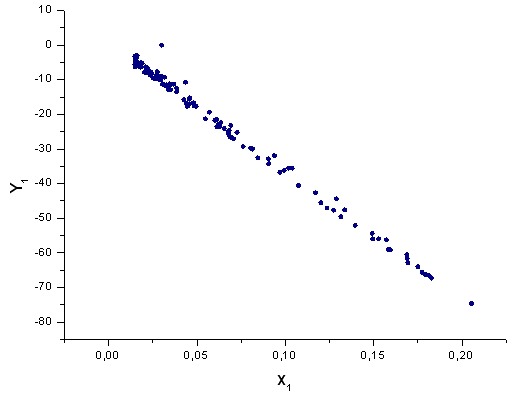
Abb. 41. Darstellung der Funktion Y1(x) mit der Basis X1(x)

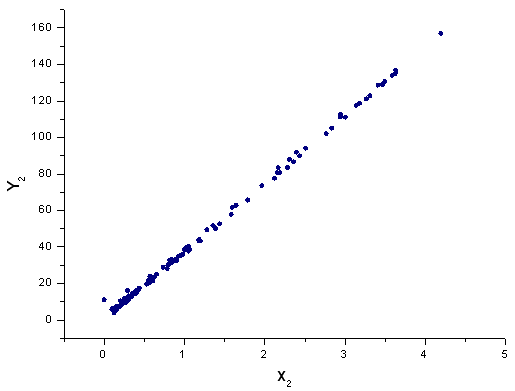
Abb. 42. Darstellung der Funktion Y2(x) mit der Basis X2(x)

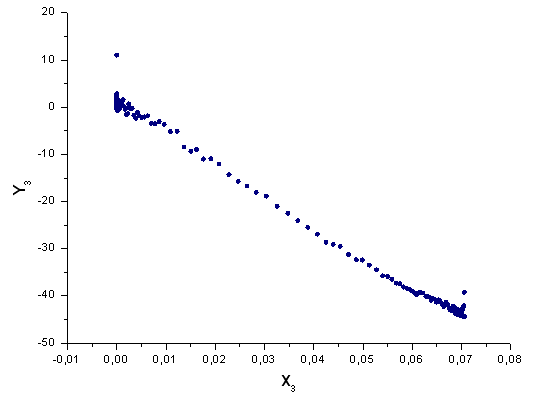
Abb. 43. Darstellung der Funktion Y3(x) mit der Basis X3(x)

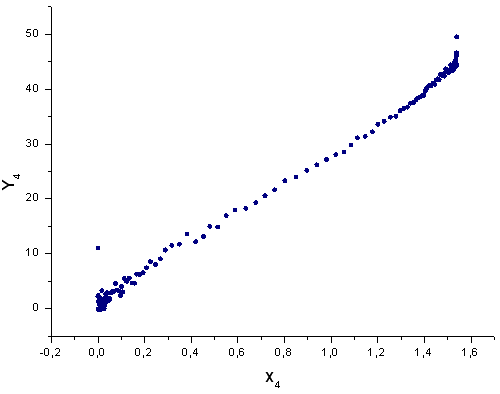
Abb. 44. Darstellung der Funktion Y4(x) mit der Basis X4(x)

Zur Überprüfung muss die Datei SP500-data.csv auf Ihrem Ausgabegerät (Terminal) in den Ordner \Files\ kopiert werden.

Anschließend muss zunächst das Skript

1. CalcDistr_SP500.mq5 (zur Berechnung der Verteilung) ausgeführt werden und
2. dann das Skript q-gaussian-SP500.mq5 (für die Analyse mithilfe des Eigen-Koordinaten-Verfahrens).

Die Berechnungsergebnisse lauten:

2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: theta=1.770125768485269
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: theta=1.864132228192338
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: a=2798.166930885822
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: a=8676.207867097581
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: x0=0.04567518783335043
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: x0=0.0512505923716428
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C1=-364.7131366394939
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C2=37.38352859698793
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C3=-630.3207508306047
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C4=28.79001868944634
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1  0.00177913 0.03169294 0.00089521 0.02099064 0.57597695
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2  0.03169294 0.59791579 0.01177430 0.28437712 11.55900584
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    3  0.00089521 0.01177430 0.00193200 0.04269286 0.12501732
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    4  0.02099064 0.28437712 0.04269286 0.94465120 3.26179090
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    checking distibution cnt=2632.0 n=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Total data=2633

Die mithilfe des Verfahrens der Eigen-Koordinaten (q=1+1/Theta) gewonnenen Schätzwerte für den Parameter q lauten: q~1,55

bzw. q~1.4 in dem Beispiel (s. Abb. 4).

Schlussfolgerung: Generell lassen sich diese Daten recht gut auf eine Q-Gaußverteilung projizieren, was ihre beschriebene erfolgreiche Interpretation mit deren Hilfe erklärt.