Aplicación del método de coordenadas de Eigen al análisis estructural de distribuciones estadísticas no extensivas

Introducción

En 1988, Constantino Tsallis propuso la generalización de la mecánica estadística de Boltzmann-Gibbs-Shannon [1] donde presentó la noción de entropía no extensiva.

Una importante consecuencia de la generalización de la entropía parecía ser la existencia de nuevos tipos de distribuciones [2] que desempeñaban un papel clave en la nueva mecánica estadística:

Se encontró que estos tipos de distribución podían utilizarse para describir una gran cantidad de datos experimentales en sistemas con memorias a largo plazo, sistemas con fuerzas de largo alcance y sistemas fuertemente correlacionados.

La entropía está íntimamente relacionada con la información [7]. La generalización de la mecánica estadística basada en la teoría de la información fue presentada en [8-9]. La nueva mecánica estadística no extensiva demostró ser muy útil para la econometría [10-17]. Por ejemplo, la distribución q-gausiana describe bien a las (colas) de distribuciones amplias de incrementos de cotizaciones de instrumentos financieros (q~1,5). Dicho esto, la mayoría de distribuciones de incrementos de series de tiempo financieras se transforman en distribuciones normales (q=1) a escalas mayores (meses, años) [10].

Era natural esperar que dicha generalización de la mecánica estadística resultara análoga al teorema central del límite para las distribuciones q-gausianas. Pero esto resultó ser erróneo en [18], ya que la distribución límite de la suma de variables aleatorias fuertemente correlacionadas es analíticamente distinta de las q-gausianas.

Sin embargo, apareció un problema distinto: resultó que los valores numéricos encontrados para la solución exacta estaban muy cerca de la distribución q-gausiana ("numéricamente similar, analíticamente distintos). Para analizar las diferencias entre las funciones y obtener los mejores parámetros de la distribución q-gausiana se usó un desarrollo de las series en [18]. Las relaciones de estas funciones llevaron a un desarrollo exponencial en el parámetro q que caracteriza el grado de no extensividad del sistema.

El mayor problema de la estadística aplicada es la aceptación de hipótesis estadísticas. Durante mucho tiempo se consideró un problema imposible de resolver [19-20] y que requería una herramienta especial (algo similar a un microscopio de electrones) que permitiera ver más de lo que es posible utilizando métodos de la estadística moderna aplicada.

El método de las coordenadas de Eigen presentado en [21] nos permite alcanzar un nivel más profundo: el análisis de las propiedades estructurales de las relaciones funcionales. Este extraordinario método puede utilizarse para resolver una gran variedad de problemas. Los desarrollos del operador de funciones correspondientes a las distribuciones no extensivas anteriores fueron mostrados en [22].

Este artículo tratará sobre el método de las coordenadas de Eigen e incluirá ejemplos prácticos de su utilización. Contiene una gran cantidad de fórmulas de gran importancia para comprender la esencia del método. Después de repetir todos los cálculos podrá trazar los desarrollos de las funciones que más le interesen.

 

1. Distribuciones q-gausianas en econometría

La distribución q-gausiana desempeña un importante papel en la econometría [4, 10-17].

Para tener un conocimiento general del nivel de la investigación actual, uno puede consultar los trabajos del Dr. Claudio Antonini "Distribuciones q-gausianas en las finanzas" [23] y "El uso de la distribución q-gausiana en las finanzas" [24].

Vamos a presentar brevemente los resultados principales.

Fig. 1. Metodología de la ciencia (Lámina 4 "El uso de la distribución q-gausiana en las finanzas")

Los rasgos fundamentales de las series de tiempo financieras se expusieron en la Fig. 2:

Fig. 2. Propiedades de las series de tiempo financieras (Lámina 3 "El uso de la distribución q-gausiana en las finanzas")

El uso de una gran cantidad de modelos para describir las series de tiempo financieras llevó al descubrimiento de la distribución q-gausiana:

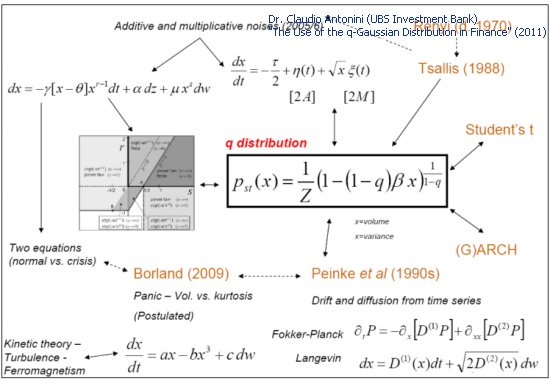
Fig. 3. Modelos teóricos y la q-gausiana (Lámina 27 "El uso de la distribución q-gausiana en las finanzas")

La distribución q-gausiana también se utiliza para la descripción de los fenómenos de las distribuciones de las cotizaciones:

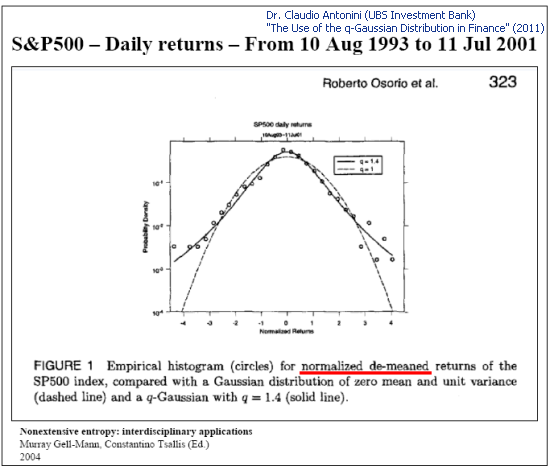
Fig. 4. Análisis de muestras de la rentabilidad diaria de S&P 500 (Lámina 8 "El uso de la distribución q-gausiana en las finanzas")

El trabajo con datos reales plantea el problema de la identificación de la función:

Fig. 5. El problema de la identificación de la función de distribución (Lámina 14 "Distribuciones q-gausianas en las finanzas")

Ambos documentos del Dr. Claudio Antonini destacan la importancia de la correcta identificación de las funciones para construir modelos adecuados de procesos físicos:

Fig. 6. Conclusiones a las que se llaga en "Distribuciones q-gausianas en las finanzas" y "El uso de la distribución q-gausiana en las finanzas" (Dr. Claudio Antonini, 2010, 2011)

Ejemplos de uso de la estadística q-gausiana en las finanzas (hojas de trabajo + archivos MathCad):

• q-Gaussian Stock Price Dynamics, (Michael English, 2008)
• q-Gaussian European Options (Michael English, 2008)
• q-Gaussian Random Deviates & Distribution, (Michael English, 2008)
• q-Gaussian Portfolios (Michael English, 2008)
• q-Gaussian Risk Measures (Michael English, 2008)
• Expected Value & Value at Risk for Lognormal Asset (Michael English, 2008)

 

2. Coordenadas Eigen

El desarrollo de las coordenadas Eigen es como se muestra a continuación:

donde C1…CN son constantes y X1(t),..,XN(t) son las "coordenadas Eigen".

Dichos desarrollos lineales son muy adecuados y a menudo utilizados en el análisis de datos. Por ejemplo, una función exponencial en una escala logarítmica se convierte en una línea recta (su pendiente puede calcularse fácilmente usando una regresión lineal). Por tanto, no es necesario realizar una optimización no lineal (ajuste) para determinar los parámetros de la función.

No obstante, la escala logarítmica será de poca ayuda a la hora de trabajar con funciones más complejas (por ejemplo, la suma de dos exponentes), ya que la función no aparecerá como una línea recta. Y será necesaria una optimización no lineal para calcular los coeficientes de la función.

Hay casos en los que los datos experimentales pueden ser explicados de igual forma usando varias funciones, cada una de ellas correspondientes a modelos de los procesos físicos. ¿Qué función elegir? ¿Cuál proporcionará una descripción más adecuada de la realidad existente al margen de los datos experimentales?

La correcta identificación de la función es esencial para el análisis de sistemas complejos (p.ej. las series de tiempo financieras, ya que cada distribución se corresponde con un determinado proceso físico y podremos comprender mejor la dinámica y las propiedades generales de los sistemas complejos si hemos elegido el modelo adecuado.

La estadística aplicada [19, 20] establece que no existe un criterio que nos permita rechazar una hipótesis estadística errónea. El método de las coordenadas Eigen arroja nueva luz sobre este problema (aceptación de la hipótesis).

La función utilizada para la descripción de los datos experimentales puede considerarse una solución para ciertas ecuaciones diferenciales. Su forma determina la estructura del desarrollo de las coordenadas Eigen.

Un rasgo peculiar del desarrollo de las coordenadas Eigen es que todos los datos generados por la función Y(t) tienen una estructura lineal en las coordenadas Eigen X1(t)..XN(t) de la función Y(t). Los datos generados por cualquier otra función F(t) no aparecerán como una línea recta (parecerán lineales en las coordenadas Eigen de la función F(t)).

Este método permite identificar las funciones con precisión, lo que facilita enormemente el trabajo con los hipótesis estadísticas.

2.1. El método de las coordenadas Eigen

El concepto que subyace detrás del método es construir las coordenadas Eigen Xk(t) en forma de operadores basados en la función Y(t).

Esto puede realizarse usando el análisis matemática por medio del cual las coordenadas Eigen Xk(t) adoptan la forma de espirales y el desarrollo se determina por la estructura de la ecuación diferencial que es satisfecha por la función Y(t). Posteriormente surge el problema de determinar los coeficientes C1. CN .

En el desarrollo ortogonal (p.ej. al calcular los coeficientes de la transformada de Fourier), los coeficientes de desarrollo se calculan proyectando el vector sobre la base y el resultado deseado se obtiene debido a la ortogonalidad de las funciones base.

Esto no es adecuado en nuestro caso, ya que no hay información sobre la ortogonalidad de X1(t)… XN(t).

2.2. Cálculo de los coeficientes de desarrollo usando el método de mínimos cuadrados

Los coeficientes Ck pueden calcularse usando el método de mínimos cuadrados. Este problema se reduce a resolver un sistema de ecuaciones lineales.

Supongamos que:

Para casi cualquier medida de hay un error :

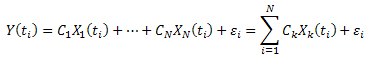
Minimizar la suma de los cuadrados de las deviaciones:

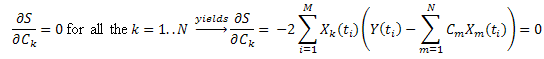
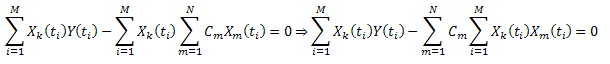
Introducir la notación: 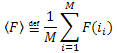, puede escribirse de esta forma:

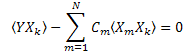
Por tanto, tenemos un sistema de ecuaciones lineales en C1...CN (k=1..N):

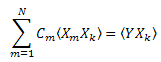
La matriz de "correlación" es simétrica: .

En algunos casos el desarrollo de las coordenadas Eigen puede ser más adecuada en su forma integral:

Esto permite reducir el impacto de los errores (debidos a la promediación), aunque requiere cálculos adicionales.

2.3. Un ejemplo del desarrollo de la función R(x)

Vamos a echar un vistazo al desarrollo de las coordenadas Eigen de la siguiente función:

Esta función genera varias distribuciones estadísticas [21]:

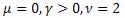1. - la distribución normal (gausiana);
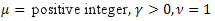2. - la distribución de Poisson;
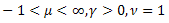3. - la distribución gamma;
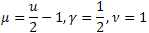4. - la distribución ;
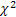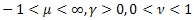5. - la distribución de Schtauffer, que incluye la distribución de Weibull como caso especial .

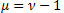Además, es conveniente describir los procesos de relajación:

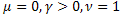1. - la función exponencial ordinaria;
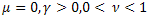2. - la función exponencial alargada;
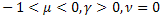3. - la función de relajación de potencia;

Una vez derivada R(x) con respecto a x, tenemos:

Multiplicamos ambos lados por x:

Transformada :

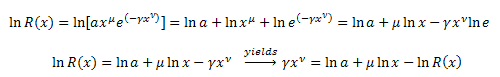
Sustituimos en la ecuación:

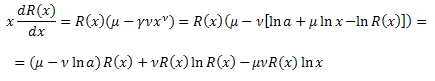
Obtenemos la ecuación diferencial para la función R(x):

Integramos ambos lados con respecto a x sobre el intervalo [xm,x]:

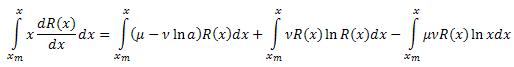
Integramos por partes el lado izquierdo de la ecuación:

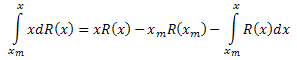
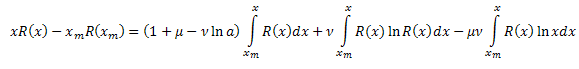
Como resultado tenemos:

donde:

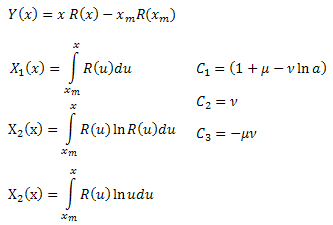
Calculando los coeficientes , podemos determinar los parámetros de la función . El cuarto parámetro puede obtenerse a partir de la fórmula de R(x).

2.4. Implementación

El cálculo de los coeficientes de desarrollo requiere resolver el sistema de ecuaciones lineales. Para facilitar el trabajo con las matrices, estas pueden ubicarse en una clase separada CMatrix (el archivo CMatrix.mqh). Al utilizar los métodos de esta clase podemos establecer los parámetros de la matriz, los valores de los elementos de la matriz y resolver el sistema de ecuaciones lineales gracias al método gausiano.

//+------------------------------------------------------------------+
//| CMatrix class                                                    |
//+------------------------------------------------------------------+
class CMatrix
  {
   double            m_matrix[];
   int               m_rows;
   int               m_columns;
public:
   void              SetSize(int nrows,int ncolumns);
   double            Get(int i,int j);
   void              Set(int i,int j,double val);
   void              GaussSolve(double &v[]);
   void              Test();
  };

Vamos a proporcionar un ejemplo del script (EC_Example1.mq5) que calcula las coordenadas Eigen y los parámetros de la función R(x).

//+------------------------------------------------------------------+
//|                                                  EC_Example1.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <CMatrix.mqh>
//+------------------------------------------------------------------+
//| CECCalculator                                                    |
//+------------------------------------------------------------------+
class CECCalculator
  {
protected:
   int               m_size;
   //--- x[i]
   double            m_x[];
   //--- y[i]
   double            m_y[];
   //--- matrix
   CMatrix           m_matrix;
   //--- Y[i]
   double            m_ec_y[];
   //--- eigen-coordinates X1[i],X2[i],X3[i]
   double            m_ec_x1[];
   double            m_ec_x2[];
   double            m_ec_x3[];
   //--- coefficients C1,C2,C3
   double            m_ec_coefs[];
   //--- function f1=Y-C2*X2-C3*X3
   double            m_f1[];
   //--- function f2=Y-C1*X1-C3*X3
   double            m_f2[];
   //--- function f3=Y-C1*X1-C2*X2
   double            m_f3[];
private:
   //--- function for data generation
   double            R(double x,double a,double mu,double gamma,double nu);
   //--- calculation of the integral
   double            Integrate(double &x[],double &y[],int ind);
   //--- calculation of the function Y(x)
   void              CalcY(double &y[]);
   //--- calculation of the function X1(x)
   void              CalcX1(double &x1[]);
   //--- calculation of the function X2(x)
   void              CalcX2(double &x2[]);
   //--- calculation of the function X3(x)
   void              CalcX3(double &x3[]);
   //--- calculation of the correlator
   double            Correlator(int ind1,int ind2);
public:
   //--- method for generating the test function data set x[i],y[i]
   void              GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu);
   //--- loading data from the file
   bool              LoadData(string filename);
   //--- saving data into the file
   bool              SaveData(string filename);
   //--- saving the calculation results
   void              SaveResults(string filename);
   //--- calculation of the eigen-coordinates
   void              CalcEigenCoordinates();
   //--- calculation of the linear expansion coefficients
   void              CalcEigenCoefficients();
   //--- calculation of the function parameters
   void              CalculateParameters();
   //--- calculation of the functions f1,f2,f3
   void              CalculatePlotFunctions();
  };
//+------------------------------------------------------------------+
//| Function R(x)                                                    |
//+------------------------------------------------------------------+
double CECCalculator::R(double x,double a,double mu,double gamma,double nu)
  {
   return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x)))));
  }
//+-----------------------------------------------------------------------+
//| Method for generating the data set x[i],y[i] of the test function R(x)|
//+-----------------------------------------------------------------------+
void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu)
  {
   if(size<=0) return;
   if(x1>=x2) return;
   m_size=size;
   ArrayResize(m_x,m_size);
   ArrayResize(m_y,m_size);
   double delta=(x2-x1)/(m_size-1);
//---
   for(int i=0; i<m_size; i++)
     {
      m_x[i]=x1+i*delta;
      m_y[i]=R(m_x[i],a,mu,gamma,nu);
     }
  };
//+------------------------------------------------------------------+
//| Method for loading data from the .CSV file                       |
//+------------------------------------------------------------------+
bool CECCalculator::LoadData(string filename)
  {
   int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   m_size=0;
   while(!FileIsEnding(filehandle))
     {
      string str=FileReadString(filehandle);
      if(str!="")
        {
         string astr[];
         StringSplit(str,';',astr);
         if(ArraySize(astr)==2)
           {
            ArrayResize(m_x,m_size+1);
            ArrayResize(m_y,m_size+1);
            m_x[m_size]=StringToDouble(astr[0]);
            m_y[m_size]=StringToDouble(astr[1]);
            m_size++;
           }
         else
           {
            m_size=0;
            return(false);
           }
        }
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for saving data into the .CSV file                        |
//+------------------------------------------------------------------+
bool CECCalculator::SaveData(string filename)
  {
   if(m_size==0) return(false);
   if(ArraySize(m_x)!=ArraySize(m_y)) return(false);
   if(ArraySize(m_x)==0) return(false);
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   for(int i=0; i<ArraySize(m_x); i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the integral                       |
//+------------------------------------------------------------------+
double CECCalculator::Integrate(double &x[],double &y[],int ind)
  {
   double sum=0;
   for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5;
   return(sum);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function Y(x)                  |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the function X1(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X2(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i]));
   ArrayResize(x2,m_size);
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X3(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i]));
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the eigen-coordinates              |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoordinates()
  {
   CalcY(m_ec_y);
   CalcX1(m_ec_x1);
   CalcX2(m_ec_x2);
   CalcX3(m_ec_x3);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the correlator                     |
//+------------------------------------------------------------------+
double CECCalculator::Correlator(int ind1,int ind2)
  {
   if(m_size==0) return(0);
   if(ind1<=0 || ind1>4) return(0);
   if(ind2<=0 || ind2>4) return(0);
//---
   double arr1[];
   double arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
//---
   switch(ind1)
     {
      case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
   switch(ind2)
     {
      case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
//---
   double sum=0;
   for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i];  }
   sum=sum/m_size;
   return(sum);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the linear expansion coefficients  |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoefficients()
  {
//--- setting the matrix size 3x4
   m_matrix.SetSize(3,4);
//--- calculation of the correlation matrix 
   for(int i=3; i>=1; i--)
     {
      string s="";
      for(int j=1; j<=4; j++)
        {
         double corr=Correlator(i,j);
         m_matrix.Set(i,j,corr);
         s=s+" "+DoubleToString(m_matrix.Get(i,j));
        }
      Print(i," ",s);
     }
//--- solving the system of the linear equations
   m_matrix.GaussSolve(m_ec_coefs);
//--- displaying the solution - the obtained coefficients C1,..CN 
   for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]);
  };
//+--------------------------------------------------------------------+
//| Method for the calculation of the function parameters a,mu,nu,gamma|
//+--------------------------------------------------------------------+
void CECCalculator::CalculateParameters()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//--- calculate a
   double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1]));
//--- calculate mu
   double mu=-m_ec_coefs[2]/m_ec_coefs[1];
//--- calculate nu
   double nu=m_ec_coefs[1];
//--- calculate gamma
   double arr1[],arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
   double corr1=0;
   double corr2=0;
   for(int i=0; i<m_size; i++)
     {
      arr1[i]=MathPow(m_x[i],nu);
      arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]);
      corr1+=arr1[i]*arr2[i];
      corr2+=arr1[i]*arr1[i];
     }
   double gamma=-corr1/corr2;
//---
   Print("a=",a);
   Print("mu=",mu);
   Print("nu=",nu);
   Print("gamma=",gamma);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the functions                      |
//| f1=Y-C2*X2-C3*X3                                                 |
//| f2=Y-C1*X1-C3*X3                                                 |
//| f3=Y-C1*X1-C2*X2                                                 |
//+------------------------------------------------------------------+
void CECCalculator::CalculatePlotFunctions()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//---
   ArrayResize(m_f1,m_size);
   ArrayResize(m_f2,m_size);
   ArrayResize(m_f3,m_size);
//---
   for(int i=0; i<m_size; i++)
     {
      //--- plot function f1=Y-C2*X2-C3*X3
      m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f2=Y-C1*X1-C3*X3
      m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f3=Y-C1*X1-C2*X2
      m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i];
     }
  }
//+------------------------------------------------------------------+
//| Method for saving the calculation results                        |
//+------------------------------------------------------------------+
void CECCalculator::SaveResults(string filename)
  {
   if(m_size==0) return;
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename," for writing, error",GetLastError());
      return;
     }
   for(int i=0; i<m_size; i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+=DoubleToString(m_ec_y[i],8)+";";
      s+=DoubleToString(m_ec_x1[i],8)+";";
      s+=DoubleToString(m_f1[i],8)+";";
      s+=DoubleToString(m_ec_x2[i],8)+";";
      s+=DoubleToString(m_f2[i],8)+";";
      s+=DoubleToString(m_ec_x3[i],8)+";";
      s+=DoubleToString(m_f3[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CECCalculator ec;
//--- model function data preparation
   ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3);
//--- saving into the file
   ec.SaveData("ex1.csv");
//--- calculation of the eigen-coordinates
   ec.CalcEigenCoordinates();
//--- calculation of the coefficients
   ec.CalcEigenCoefficients();
//--- calculation of the parameters
   ec.CalculateParameters();
//--- calculation of the functions f1,f2,f3
   ec.CalculatePlotFunctions();
//--- saving the results into the file
   ec.SaveResults("ex1-results.csv");
  }

2.5. Resultados del cálculo de la función modelo R(x)

Vamos a generar 100 valores para la función R(x) sobre el intervalo [0,25,15,25] como datos del modelo

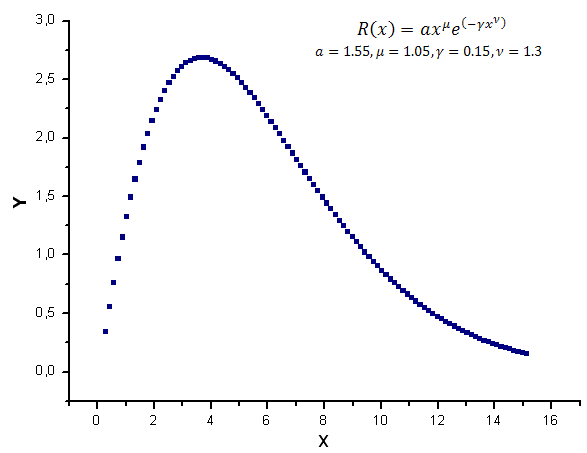
Fig. 7. Función modelo utilizada para los cálculos

Estos datos proporcionan la base para trazar la función Y(x) y su desarrollo en las funciones X1(x), X2(x) y X3(x).

La Fig. 8 muestra la función Y(x) y sus "coordenadas Eigen" X1(x), X2(x) y X3(x).

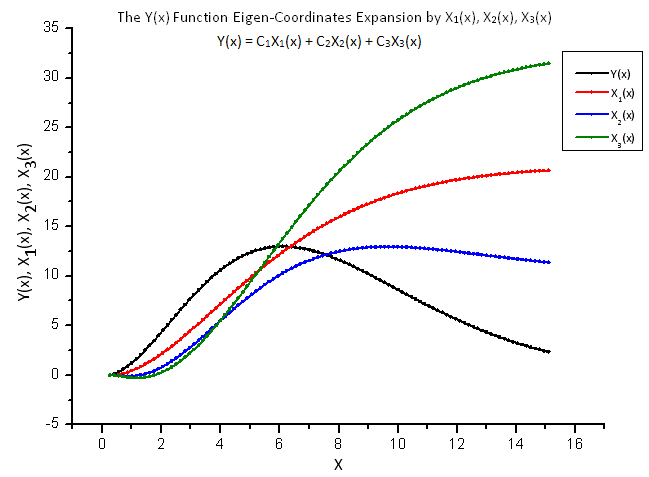
Fig. 8. Forma general de la función Y(x) y de las coordenadas Eigen X1(x), X2(x) y X3(x)

Observe el ajuste de estas funciones debido a la naturaleza integral de los operadores X1(x), X2(x) y X3(x).

Tras el cálculo de las funciones Y(x), X1(x), X2(x) y X3(x), se construye la matriz de correlación y a continuación se resuelven las ecuaciones para los coeficientes C1, C2 y C3 y se calculan los parámetros de la función R(x) en base a los valores obtenidos:

2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1  221.03637620 148.53278281 305.48547011 101.93843241
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2  148.53278281 101.63995012 202.85142688 74.19784681
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3  305.48547011 202.85142688 429.09345292 127.82779760

Vamos a comprobar ahora la linealidad del desarrollo calculado. Para este propósito, necesitamos calcular 3 funciones:

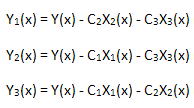
cada una se proyecta sobre la base de las coordenadas Eigen X1(x), X2(x) y X3(x):

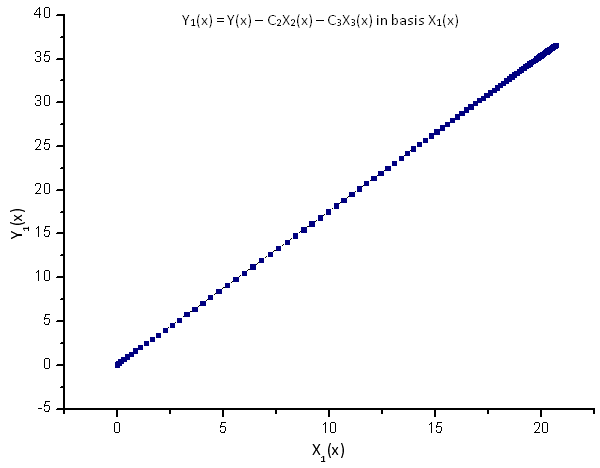
Fig. 9. Representación de la función Y1(x) sobre la base de X1(x)

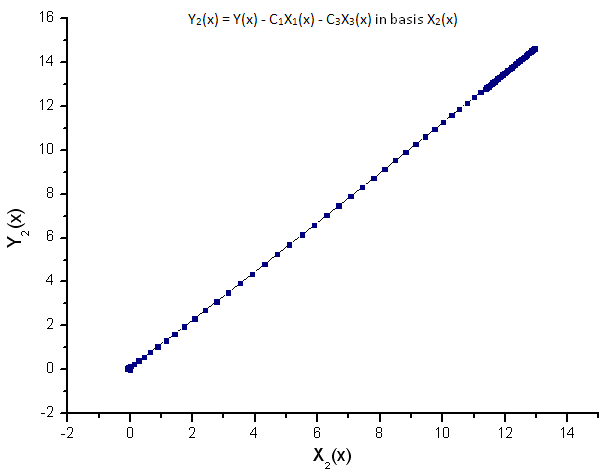
Fig. 10. Representación de la función Y2(x) sobre la base de X2(x)

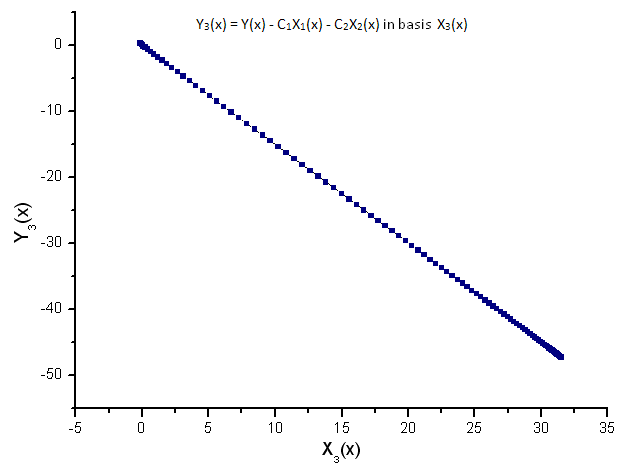
Fig. 11. Representación de la función Y3(x) sobre la base de X3(x)

La dependencia lineal de las funciones trazadas sugiere que las series de datos en la Fig. 7 se corresponden estrictamente con la función R(x).

Como cualquier otra función (incluso similar en la forma) representada en R(x), las coordenadas Eigen ya no tendrán más una forma lineal. Este hecho nos permite identificar las funciones.

La precisión del cálculo de los valores numéricos de los parámetros de la función modelo puede mejorarse si el número de puntos se incrementa a 10.000 (manteniendo el mismo intervalos):

2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1  225.47846911 151.22066473 311.86134419 104.65062550
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2  151.22066473 103.30005101 206.66297964 76.03285182
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3  311.86134419 206.66297964 438.35625824 131.91955339

En este caso, los parámetros de la función se han calculado con mayor precisión.

2.6 Efecto ruido

Los datos experimentales reales siempre contienen ruido.

En el método GenerateData() de la clase ECCCalculator reemplazamos:

m_y[i]=R(m_x[i],a,mu,gamma,nu);

con

m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;

añadiendo un ruido aleatorio, siendo aproximadamente el 10% del valor máximo de la función.

El resultado del script EC_Example1-noise.mq5 es el siguiente:

2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1  254.45082565 185.19087989 354.25574000 125.17343164
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2  185.19087989 136.81028987 254.92996885 97.14705491
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3  354.25574000 254.92996885 501.76021715 159.49440494

El gráfico de la función modelo con un ruido aleatorio se muestra en la Figura 12.

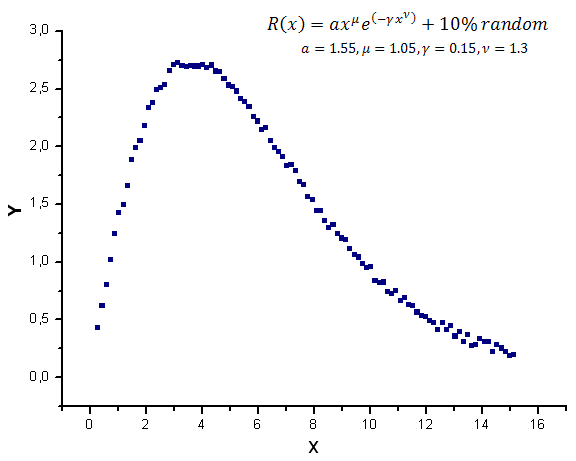
Fig. 12. Función modelo con ruido utilizada para los cálculos

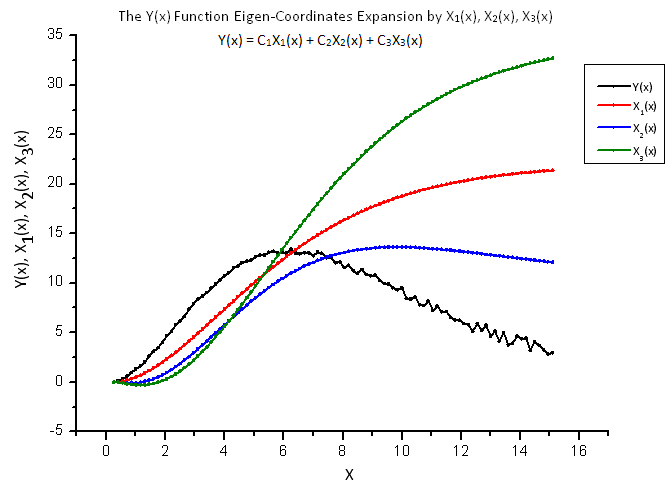
Fig. 13. Forma general de la función Y(x) y de las coordenadas Eigen X1(x), X2(x) y X3(x)

Las funciones X1(x), X2(x) and X3(x) que sirven como "coordenadas Eigen" aún parecen ajustadas, a pesar de que la Y(x) trazada como su combinación lineal parece ser distinta (Fig. 13).

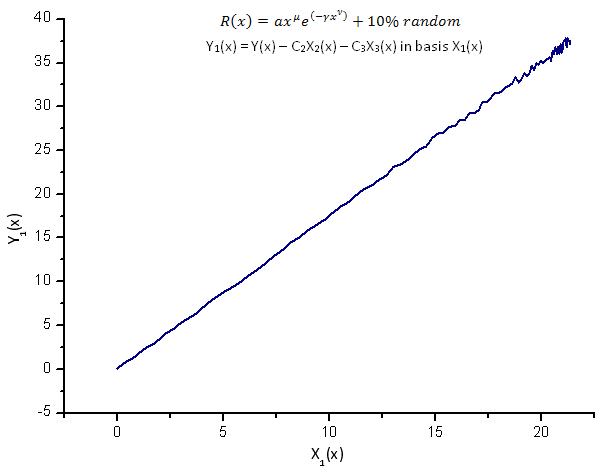
Fig. 14. Representación de la función Y1(x) sobre la base de X1(x)

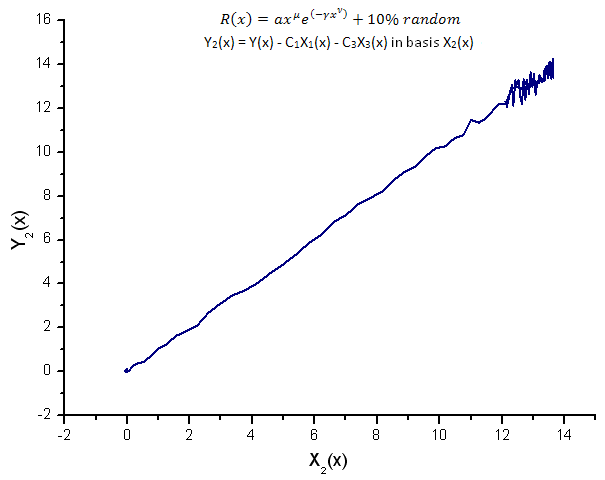
Fig. 15. Representación de la función Y2(x) sobre la base de X2(x)

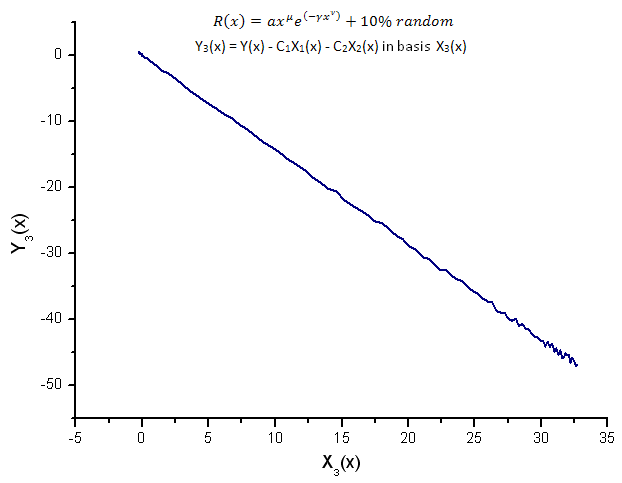
Fig. 16. Representación de la función Y3(x) sobre la base de X3(x)

La representación de las funciones Y1(x),Y2(x) y Y3(x) en la base de las coordenadas Eigen (Figuras 8-10) todavía tiene la forma lineal y uno puede apreciar fluctuaciones alrededor de la línea recta debidas a la presencia de ruido. Es más pronunciado con respecto a las X mayores donde la señal o el ruido se hacen mínimos.

Aquí, los componentes del ruido descansan en ambos lados de la línea recta y, en este caso, es conveniente utilizar el desarrollo integral de las coordenadas Eigen (Sección 2.2).

 

3. Distribuciones estadísticas de probabilidad no extensivas

La generalización de la mecánica estadística da como resultado las distribuciones [2, 22]:

donde , .

La distribución q-gausiana es un caso particular de la función P2(x).

3.1. El desarrollo de las coordenadas Eigen de la función P1(x)

Derivamos P1(x):

El resultado de la ecuación diferencial es el siguiente:

Integramos en el intervalo [xm,x]:

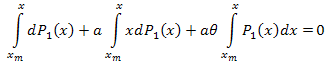
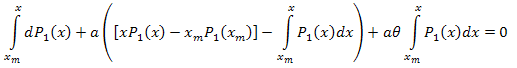
Por tanto:

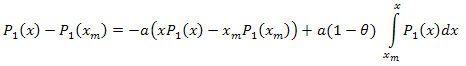
El desarrollo de las coordenadas Eigen es como se muestra a continuación:

donde:

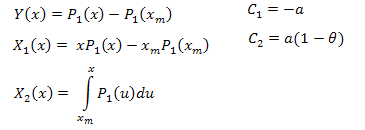
Las funciones para los cálculos son como se describen a continuación (EC_Example2.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
//--- Y=P(x)-P(xm)
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
//--- X1=x*P(x)-xm*P(xm)
   for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
//--- X2=Integrate(P1(x)) 
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i);
  }

Esta vez el tamaño de la matriz de correlación es 2x3 y los valores de los parámetros y el valor theta de la función P1(x) se determinan en función de los coeficientes С1 y C2. El valor numérico del parámetro B puede obtenerse a partir del requisito de normalización.

A continuación se muestra el cálculo del modelo de la función P1(x,1,0.5,2) en el intervalo x [0,10] y el número de puntos usados es 1.000:

2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1  0.15420524 0.48808959 -0.32145543
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2  0.48808959 1.79668322 -1.14307410

La función P1(x) y su desarrollo en coordenadas Eigen se muestran en las Figuras 17-20.

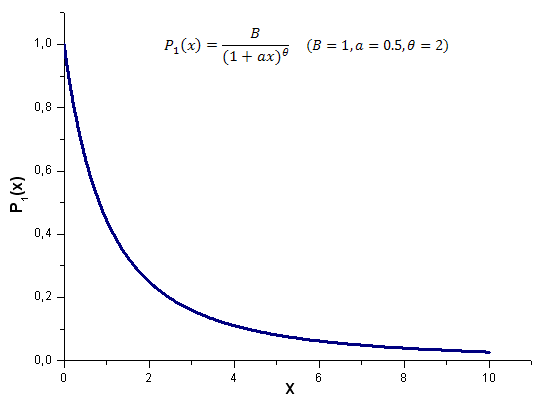
Fig. 17. Función modelo P1(x, 1, 0.5, 2) usada para los cálculos, 1.000 puntos

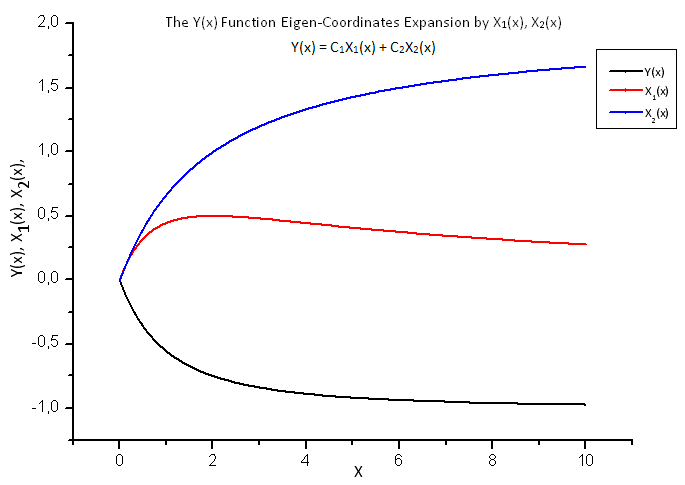
Fig. 18. Forma general de la función Y(x) y de las coordenadas Eigen X1(x) y X2(x)

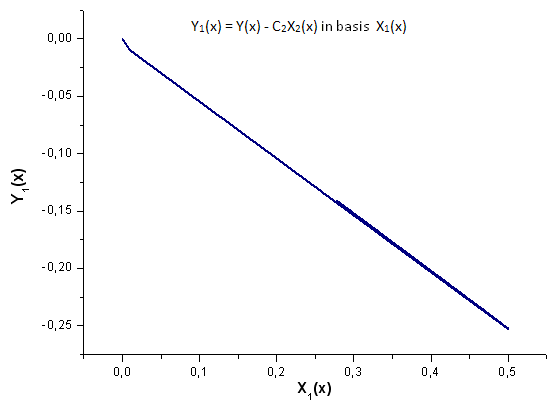
Fig. 19. Representación de la función Y1(x) sobre la base de X1(x)

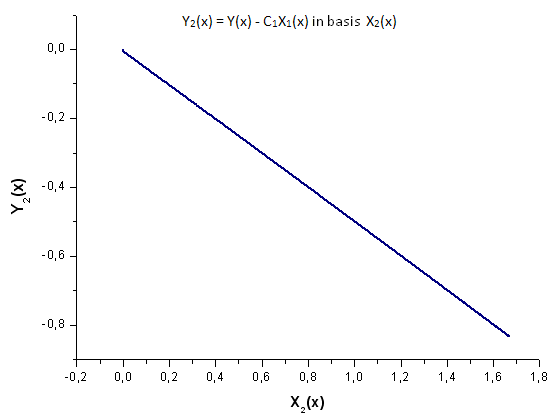
Fig. 20. Representación de la función Y2(x) sobre la base de X2(x)

Observe con atención la Figura 19. Hay una ligera distorsión de la dependencia lineal al inicio y en el segundo tercio del gráfico. Esto está relacionado con las peculiaridades del desarrollo calculado, X1(x) no es de naturaleza integral.

3.2. Desarrollo de las coordenadas Eigen de la función P2(x)

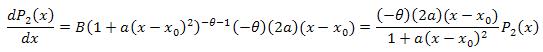
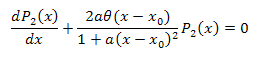
La ecuación diferencial:

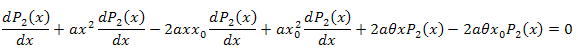
Integramos con respecto a x en el intervalo [xm,x]:

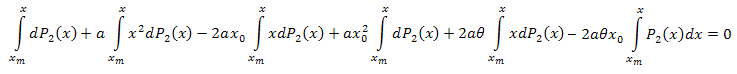
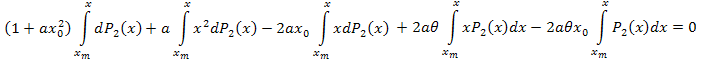
Integrando por partes tenemos:

Simplificamos:

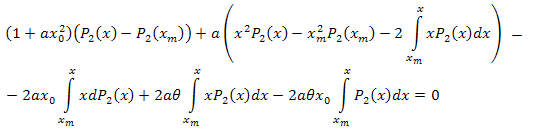
Siguiendo las modificaciones algebraicas tenemos:

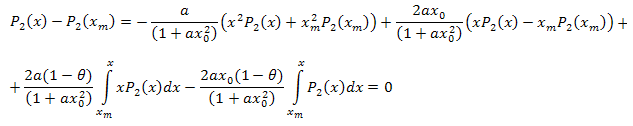
De esta forma, el desarrollo que se obtiene es el siguiente:

donde:

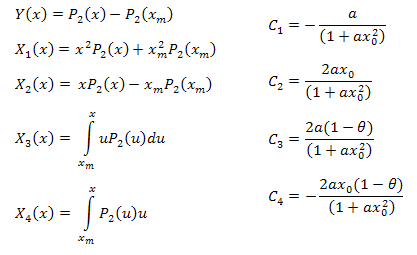
Los parámetros de la función pueden calcularse usando las formulas siguientes:

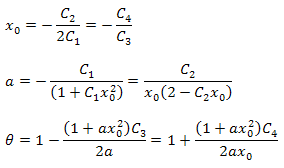
Debe señalarse que hay una relación adicional entre los parámetros en el desarrollo resultante. Este hecho puede usarse para verificar si la función elegida para el análisis es correcta. Estas relaciones son siempre verdaderas para los datos que se corresponden estrictamente con la función P2(x).

El valor numérico del parámetro B puede obtenerse a partir del requisito de normalización.

Las funciones para el cálculo de las coordenadas Eigen son las siguientes (EC_Example3.mq5):

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm)
   for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
   //--- X2=(x)*P2(x)-(xm)*P2(xm)
   for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX3                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i];
   //--- X3=Integrate(X*P2(x)) 
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);  
  }
//+------------------------------------------------------------------+
//| CalcX4                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX4(double &x4[])
  {
   if(m_size==0) return;
   //--- X4=Integrate(P2(x))
   ArrayResize(x4,m_size);
   for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i);
  }

A continuación se muestra el resultado del cálculo de la función modelo P2(x) (B=1, a=0.5, theta=2, x0=1) y el número de puntos usados es 1.000:

2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1  1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2  0.60684314 0.37995888 0.55974145 0.58899739 0.06731011
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3  1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4  1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168

La función P2(x) y su desarrollo en coordenadas Eigen se muestran en las Figuras 21-26.

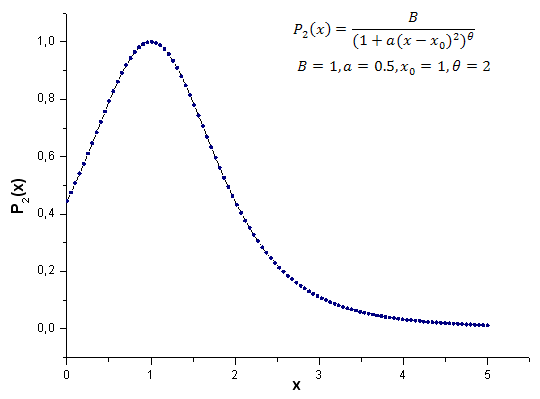
Fig. 21. Función modelo P2(x,1,0.5,2,1) usada para los cálculos, 100 puntos

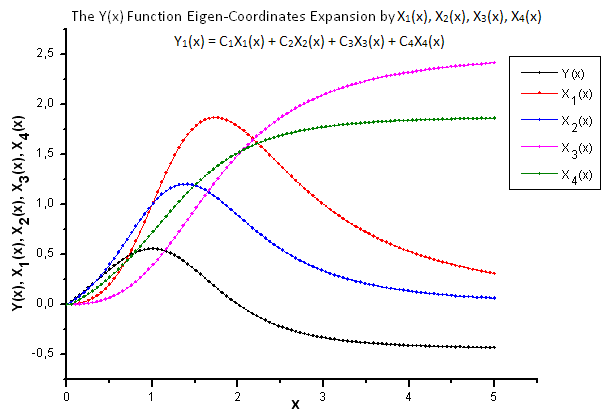
Fig. 22. Forma general de la función Y(x) y de las coordenadas Eigen X1(x), X2(x), X3(x) y X4(x)

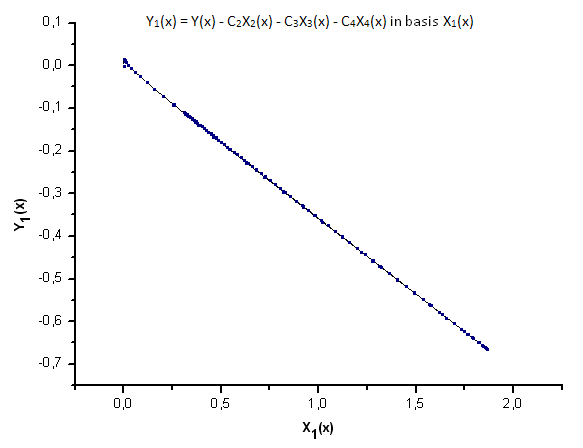
Fig. 23. Representación de la función Y1(x) sobre la base de X1(x)

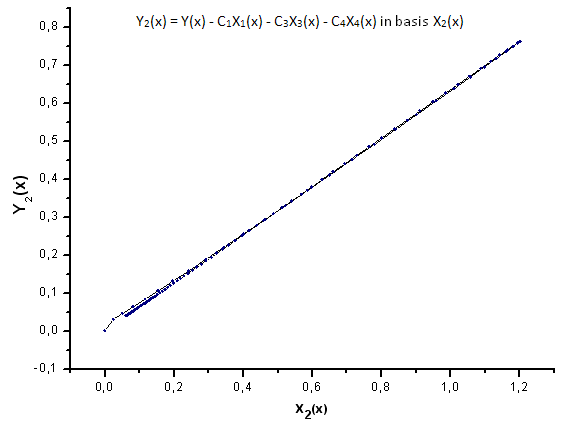
Fig. 24. Representación de la función Y2(x) sobre la base de X2(x)

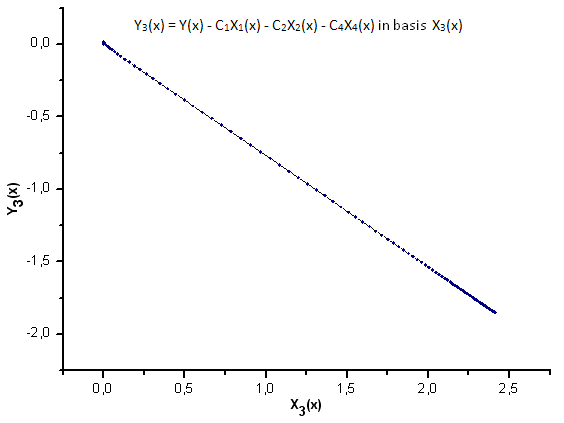
Fig. 25. Representación de la función Y3(x) sobre la base de X3(x)

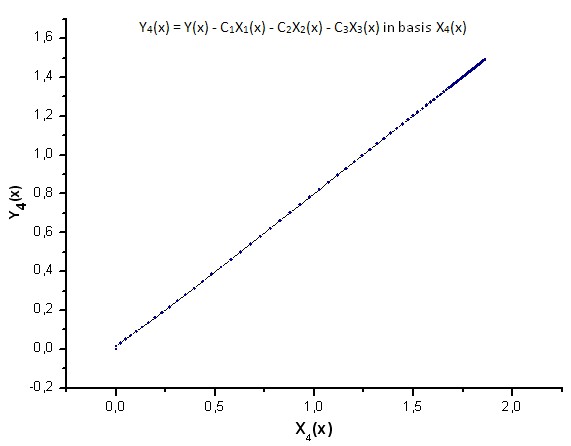
Fig. 26. Representación de la función Y4(x) sobre la base de X4(x)

 

4. Si parece un gato... puede que no lo sea

La familia de las distribuciones q-gausianas descansa en el corazón de la mecánica estadística no extensiva y era lógico esperar que apareciera en el teorema central del límite generalizado. Las consideraciones entrópicas han servido como argumento principal a su favor [26].

No obstante, el artículo [18, presentación] mostró que distribuciones como la q-gausiana no son universales, y por tanto plantean dudas sobre su función especial como distribuciones límite.

Por ejemplo, la función (solución analítica de uno de los problemas):

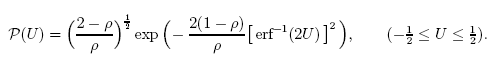
puede describirse con precisión usando la distribución q-gausiana.

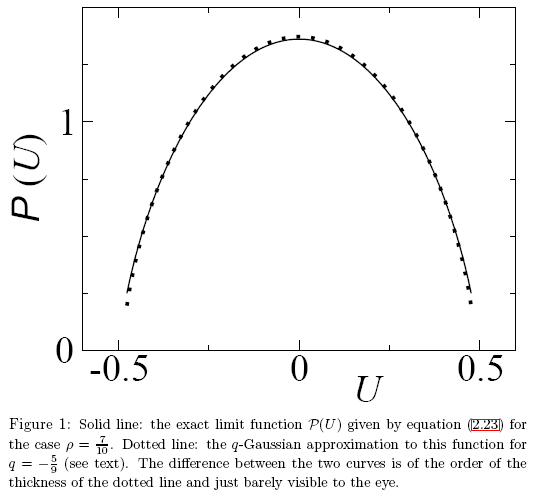
Fig. 27. Un ejemplo del artículo "Un apunte sobre las distribuciones q-gausianas y no gausianas en la mecánica estadística"

En este caso, las funciones analíticamente distintas tienen valores numéricos similares y las diferencias son, por tanto, escasamente visibles al ojo. Es necesario un método preciso de identificación de la función. Este problema puede resolverse adecuadamente usando el método de las coordenadas Eigen.

Vamos a revisar un ejemplo del desarrollo de las coordenadas Eigen de la función P(U) y a mostrar qué es exactamente lo que la hace distinta de la q-gausiana. Las funciones parecen muy similares a simple vista (Fig. 27).

Generamos una señal (100 valores de la función P(U)) y la "proyectamos" sobre el sistema de coordenadas Eigen de la función P2(x) trazada en la Sección 3.2.

El script Hilhorst-Schehr-problem.mq5 calcula la función P(U) y construye las series de datos que se guardan en el archivo MQL5\Files\test-data.csv. Estos datos son analizados por EC_Example3_Test.mq5.

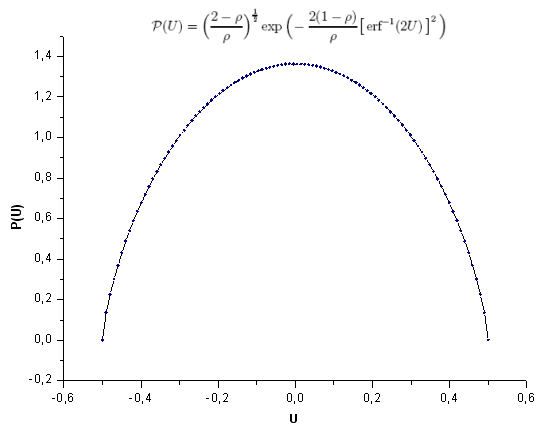
Fig. 28. Función modelo P(U), 100 puntos

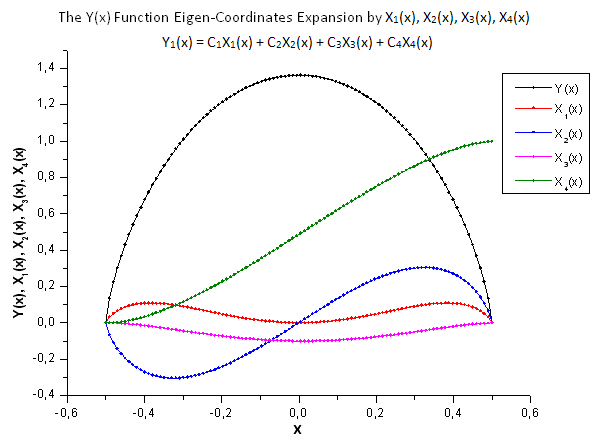
Fig. 29. Forma general de la función Y(x) y de las coordenadas Eigen X1(x), X2(x), X3(x) y X4(x)

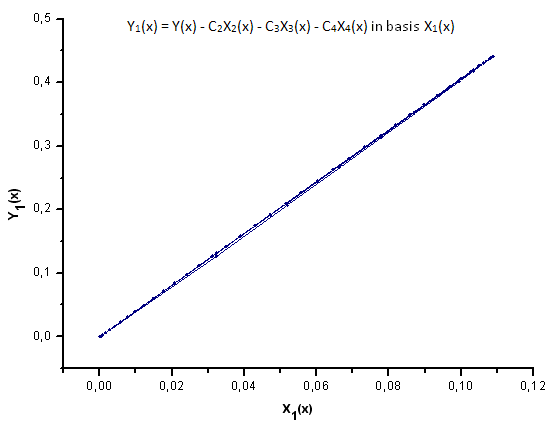
Fig. 30. Representación de la función Y1(x) sobre la base de X1(x)

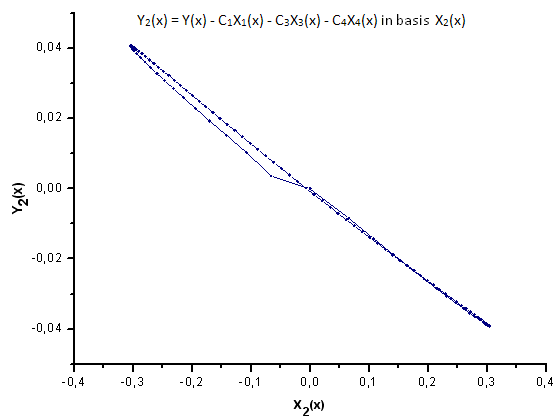
Fig. 31. Representación de la función Y2(x) sobre la base de X2(x)

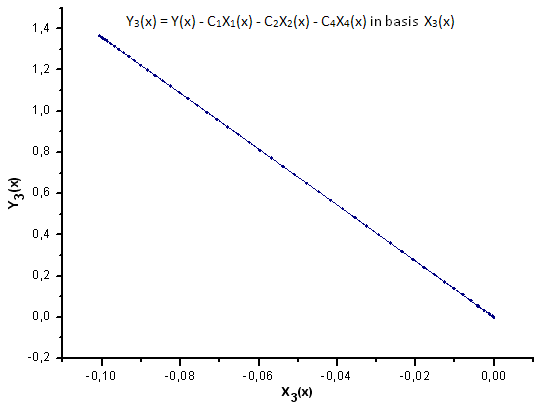
Fig. 32. Representación de la función Y3(x) sobre la base de X3(x)

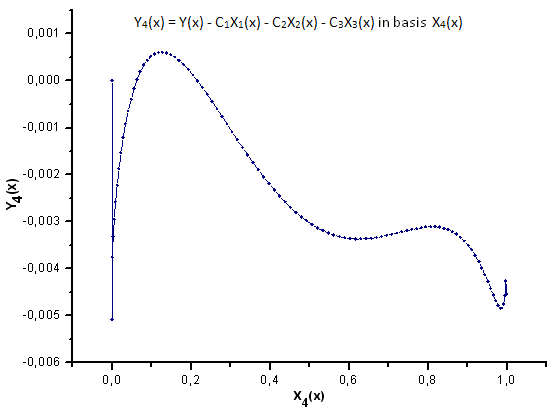
Fig. 33. Representación de la función Y4(x) sobre la base de X4(x)

Como sugieren las Fig. 30-33, las funciones P2(x) y P(U) son muy similares en términos de coordenadas X1(x), X2(x) y X3(x), ya que uno puede apreciar una buena dependencia lineal entre Xi(x) e Yi(x). Puede apreciarse una diferencia considerable en el componente X4(x) (Fig. 33).

La ausencia de dependencia lineal para el componente de X4(x) demuestra que el conjunto de datos generados por P(U), a pesar de resultar similar a la distribución q-gausiana, no es en realidad este tipo de distribución.

Podemos ver de otra forma estas funciones (Figuras 34-37) trazando Xi(x) e Yi(x) conjuntamente.

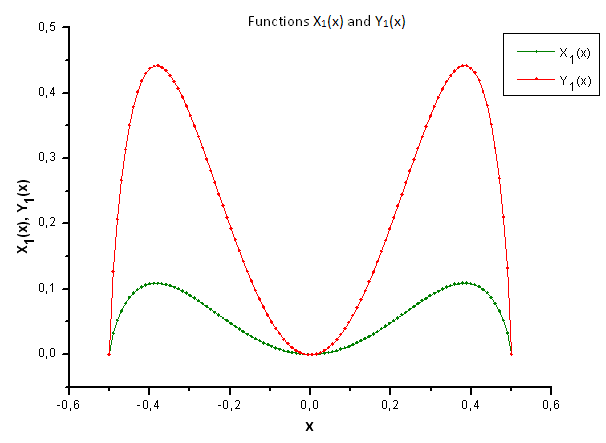
Fig. 34. Forma general de las funciones X1(x) e Y1(x)

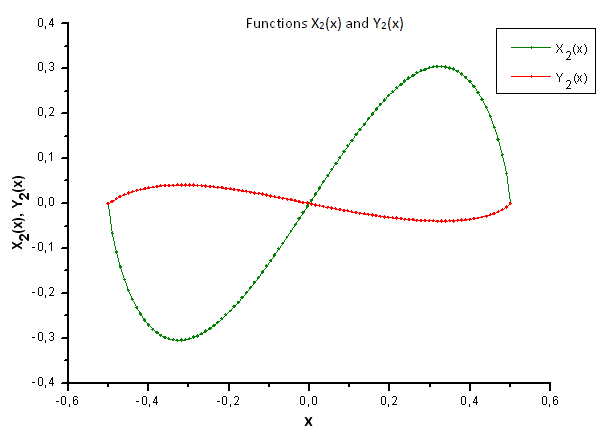
Fig. 35. Forma general de las funciones X2(x) e Y2(x)

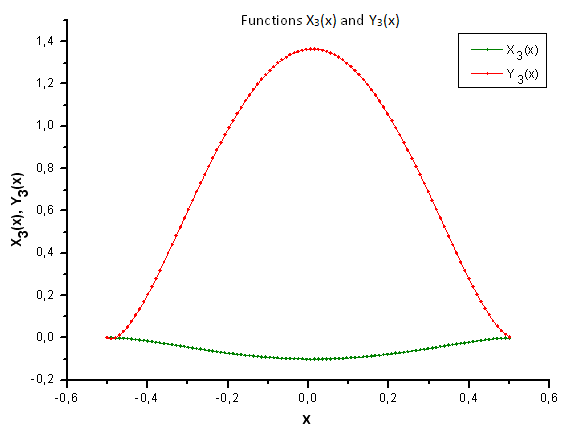
Fig. 36. Forma general de las funciones X3(x) e Y3(x)

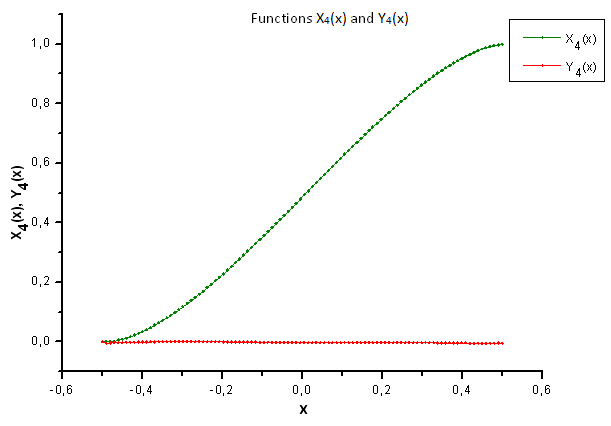
Fig. 37. Forma general de las funciones X4(x) e Y4(x)

Como sugiere la Fig. 37, la diferencia estructural en el componente X4(x) se ha hecho más evidente al proyectar los datos generados por la función P(U) sobre las coordenadas Eigen de la función P2(x). De este modo, podemos decir que los datos experimentales no se corresponden con los de la función P2(x).

Los cálculos mostrados más abajo (EC_Example3_test) apoyan este hecho:

2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1  0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2  0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3  -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4  0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994

También ha desvirtuado las relaciones entre los parámetros.

 

Conclusión

El método de las coordenadas Eigen es una herramienta única para el análisis de las propiedades de las relaciones funcionales, permitiendo simplificar considerablemente el análisis e interpretación de los datos.

El concepto detrás de este método es el uso de conjuntos de datos experimentales {xi,yi} para construir nuevas funciones que se correspondan con el modelo propuesto. La forma del desarrollo del operador se determina por la estructura de la ecuación diferencial que es satisfecha por la función que sirve como "candidata" para la descripción de los datos. Si la función es nativa, los desarrollos de la función calculados usando los datos {xi,yi}, tendrán una forma linear sobre la base de las coordenadas Eigen. Las desviaciones de la linealidad en la base de las coordenadas Eigen de la "función candidata" sugieren que los datos {xi,yi} no pueden ser generados por dicha función y el modelo construido no es el adecuado.

En algunos casos complejos, la función candidata y la función nativa pueden parecer muy similares hasta tal punto que una gran parte de los desarrollos calculados resultarán ser lineales. No obstante, el método de las coordenadas Eigen nos permite identificar la diferencia entre estas funciones, advirtiéndonos de su presencia al desvirtuar la linealidad del desarrollo. El ejemplo de Hilhorst y Schehr ha servido como muestra de la diferencia que existe en el miembro del último desarrollo al proyectar sobre X4(x).

Esta información pueden ser también útil al trabajar con una ecuación diferencial (Sección 3.2) que es satisfecha por la función P2(x). El miembro en cuestión corresponde a la parte lineal relativa a P2(x). Puede que no sea tan interesante en caso de una descripción fenomenológica de los datos experimentales ("buscamos una solución del tipo q-gausiana"). Sin embargo, si el modelo se basa en ecuaciones diferenciales (Fig. 3), puede comprenderse mejor el papel de cada uno de los mecanismos considerados en los modelos de procesos físicos.

 

Bibliografía

1. C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
2. C. Tsallis, "Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
3. C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
4. Europhysics News "Special Issue: Nonextensive Statistical Mechanics: New Trends, New Perspectives", Vol. 36 No. 6 (November-December 2005).
5. M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
6. Constantino Tsallis, the Official Website Nonextensive Statistical Mechanics and Thermodynamics.
7. Chumak, O.V. "Entropy and Fractals in Data Analysis", М.-Izhevsk: RDC "Regular and Chaotic Dynamics", Institute for Computer Research, 2011. - 164 p.
8. Qiuping A. Wang, "Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
9. Qiuping A. Wang, "Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory", Entropy, 5(2003).
10. Lisa Borland, "Long-Range Memory and Nonextensivity in Financial Markets", Europhysics News 36, 228-231 (2005)
11. T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
12. S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-Law Distributions in Economics: A Nonextensive Statistical Approach", Proceedings of SPIE (2005) Volume: 5848, Publisher: SPIE, Pages: 151-164, (preprint)
13. R Hanel, S Thurner, "Derivation of Power-Law Distributions within Standard Statistical Mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Issue: 2-4, Publisher: Elsevier, Pages: 260-268. (preprint)
14. A K Rajagopal, Sumiyoshi Abe, "Statistical Mechanical Foundations of Power-Law Distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Issue: 1-4, Pages: 19 (preprint)
15. T. Kaizoji, "An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
16. V. Gontis, J. Ruseckas, A. Kononovičius, "A Long-Range Memory Stochastic Model of the Return in Financial Markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
17. H.E. Roman, M. Porto, "Self-Generated Power-Law Tails in Probability Distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Issue: 3 Pt 2, Pages: 036-128.
18. H. J. Hilhorst, G. Schehr, "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" (2007, preprint, presentation).
19. D. J. Hudson, "Lectures on Elementary Statistics and Probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
20. D. J. Hudson, "Statistics Lectures II : Maximum Likelihood and Least Squares Theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
21. R. R. Nigmatullin, "Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
22. R.R. Nigmatullin, "Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method", Physica A: Statistical Mechanics and its Applications Volume 285, Issues 3–4, 1 October 2000, pp. 547–565.
23. C. Antonini "q-Gaussians in Finance" (2010).
24. C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
25. L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical Indications of a q-Generalised Central Limit Theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
26. T. Dauxois, "Non-Gaussian Distributions under Scrutiny", J. Stat. Mech. (2007) N08001. (preprint)