Kapsamlı Olmayan İstatistiksel Dağılımların Yapısal Analizine Öz-Koordinatlar Yönteminin Uygulanması
140
0
İçindekiler
- Giriş
- 1. Ekonometride Q-Gauss
- 2. Öz-Koordinatlar
- 3. Kapsamlı Olmayan Olasılık Dağılımları
- 4. Bir kediye benziyorsa... bir kedi olmayabilir
- Sonuç
- Referanslar
- Ek. Q-Gauss ile SP500 günlük getirilerinin analizi
Giriş
1988'de, Constantino Tsallis, Boltzmann-Gibbs-Shannon istatistiksel mekaniğinin genelleştirilmesini önerdi [1] ve burada kapsamlı olmayan bir entropi kavramı sundu.
Entropinin genelleştirilmesinin önemli bir sonucu, yeni istatistiksel mekanikte (Q-Üstel ve Q-Gauss) kilit rol oynayan yeni dağılım türlerinin [2] varlığı olarak ortaya çıktı:
Bu dağılım türlerinin, uzun aralıklı bellek içeren sistemlerde, uzun aralıklı kuvvetlere sahip sistemlerde ve güçlü bir şekilde ilişkili sistemlerde çok sayıda deneysel veriyi tanımlamak için kullanılabileceği tespit edildi.
Entropi, bilgi ile yakından ilişkilidir [7]. Bilgi teorisine dayalı istatistiksel mekaniğin genelleştirilmesi [8-9]'da sunulmuştur. Kapsamlı olmayan yeni istatistiksel mekaniğin ekonometri için çok faydalı olduğu kanıtlandı [10-17]. Örneğin, Q-Gauss dağılımı, finansal enstrüman fiyat teklifi artışlarının dağılımlarının geniş kanatlarını (kuyruklarını) iyi tanımlar (q~1,5). Bununla birlikte, finansal zaman serilerinin artışlarının çoğu dağılımı, daha büyük ölçeklerde (aylar, yıllar) normal dağılımlara (q=1) dönüşür [10].
Doğal olarak, istatistiksel mekaniğin bu şekilde genelleştirilmesinin, q-Gauss dağılımları için merkezi limit teoreminin bir analoguyla sonuçlanması bekleniyordu. Ancak bunun yanlış olduğu [18]'de gösterilmiştir - Güçlü bir şekilde ilişkili rastgele değişkenlerin toplamının limit dağılımı, analitik olarak q-Gauss'tan farklıdır.
Ancak, başka tür bir sorun ortaya çıktı: Bulunan kesin çözümün sayısal değerlerinin Q-Gauss'a çok yakın olduğu ortaya çıktı ("sayısal olarak benzer, analitik olarak farklı"). Fonksiyonlar arasındaki farkları analiz etmek ve Q-Gauss dağılımının en iyi parametrelerini elde etmek için [18]'de bir seri açılımı kullanılmıştır. Bu fonksiyonların ilişkileri, sistemin yayılmazlık derecesini karakterize eden q parametresinde kuvvet açılımına yol açtı.
Uygulamalı istatistiklerin majör sorunu, istatistiksel hipotezleri kabul etme sorunudur. Modern uygulamalı istatistik yöntemlerini kullanarak mümkün olandan daha fazlasını görmeye izin verecek özel bir araç (elektron mikroskobu gibi bir şey) gerektiren [19-20] çözümünün uzun zamandır imkansız olduğu düşünülüyordu.
[21]'de tanıtılan öz-koordinatlar yöntemi, daha derin bir düzeye ulaşmamızı sağlar - Fonksiyonel ilişkilerin yapısal özelliklerinin analizi. Bu çok ince yöntem, çeşitli sorunları çözmek için kullanılabilir. Yukarıdaki kapsamlı olmayan dağılımlara karşılık gelen fonksiyonların operatör açılımları [22]'de gösterilmiştir.
Bu makale öz-koordinatlar yöntemini ve pratik kullanım örneklerini ele alacaktır. Yöntemin özünün anlaşılması için büyük önem taşıyan birçok formül içerir. Tüm hesaplamaları tekrarladıktan sonra, ilgilendiğiniz fonksiyonlar için fonksiyon açılımlarını kendi başınıza çizebileceksiniz.
1. Ekonometride Q-Gauss
Q-Gauss dağılımı ekonometride çok önemli bir rol oynar [4,10-17].
Mevcut araştırma düzeyi hakkında genel bir fikir edinmek için, Dr. Claudio Antonini'nin "Finansta q-Gauss" [23] ve "Finansta q-Gauss Dağılımı Kullanımı" [24] adlı çalışmalarına başvurulabilir.
Ana sonuçları kısaca özetleyelim.
Şek. 1. Bilim metodolojisi (Slayt 4 "Finansta q-Gauss Dağılımı Kullanımı")
Finansal zaman serilerinin ana özellikleri Şekil 2'de gösterilmiştir:
Şek. 2. Finansal zaman serilerinin özellikleri (Slayt 3 "Finansta q-Gauss Dağılımı Kullanımı")
Finansal zaman serilerini tanımlamak için kullanılan birçok teorik model Q-Gauss dağılımına yol açar:
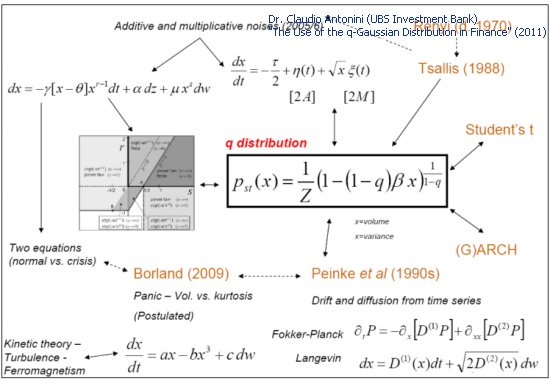
Şek. 3. Teorik modeller ve Q-Gauss (Slayt 27 "Finansta Q-Gauss Dağılımı Kullanımı")
Q-Gauss dağılımı, fiyat teklifi dağılımlarının fenomenolojik açıklaması için de kullanılır:
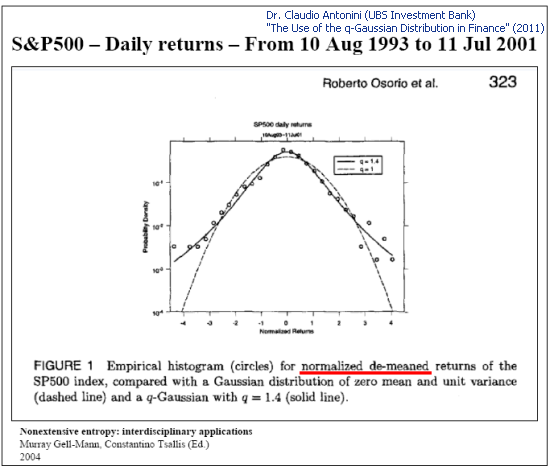
Şek. 4. S&P 500 günlük getirilerinin örnek analizi (Slayt 8 "Finansta q-Gauss Dağılımı Kullanımı")
Gerçek verilerle çalışmak, bir işlev tanımlama sorunu yaratır:
Şek. 5. Dağılım işlevi tanımlama sorunu (Slayt 14 "Finansta q-Gauss"
Dr. Claudio Antonini'nin her iki makalesi de yeterli fiziksel süreç modelleri oluşturmak için işlevlerin doğru tanımlanmasının önemini vurgulamaktadır:
Şek. 6. "Finansta q-Gauss" ve "Finansta q-Gauss Dağılımı Kullanımı" (Dr. Claudio Antonini, 2010, 2011) bölümlerinden çıkarılan sonuçlar
- q-Gaussian Stock Price Dynamics, (Michael English, 2008)
- q-Gaussian European Options (Michael English, 2008)
- q-Gaussian Random Deviates & Distribution, (Michael English, 2008)
- q-Gaussian Portfolios (Michael English, 2008)
- q-Gaussian Risk Measures (Michael English, 2008)
- Expected Value & Value at Risk for Lognormal Asset (Michael English, 2008)
2. Öz-Koordinatlar
Öz-koordinat açılımı aşağıdaki gibidir:
Burada, C1…CN sabitler ve X1(t),..,XN(t) "öz-koordinatlardır".
Bu tür doğrusal açılımlar çok elverişlidir ve genellikle veri analizinde kullanılır. Örneğin, logaritmik ölçekte üstel bir işlev düz bir çizgiye dönüşür (eğimi doğrusal regresyon kullanılarak kolayca hesaplanabilir). Böylece işlev parametrelerinin belirlenmesi için doğrusal olmayan optimizasyona (uydurma) gerek kalmaz.
Ancak, logaritmik ölçek, daha karmaşık işlevlerle (örneğin iki üstelin toplamı) uğraşırken çok az yardımcı olacaktır - İşlev, düz bir çizgi olarak görünmeyecektir. Ve işlev katsayılarını belirlemek için doğrusal olmayan bir optimizasyon gerekecektir.
Deneysel verilerin, tümü farklı fiziksel süreç modellerine karşılık gelen çeşitli işlevler kullanılarak eşit derecede iyi açıklanabileceği durumlar vardır. Peki hangi işlevin seçilmesi gerekir? Hangisi deneysel verilerin dışında gerçekliğin daha yeterli bir resmini sağlayacaktır?
Doğru işlev tanımlaması, karmaşık sistemlerin (örneğin finansal zaman serileri) analizi için çok önemlidir - Her dağılım belirli bir fiziksel sürece karşılık gelir; yeterli bir model seçerek karmaşık sistemlerin dinamiklerini ve genel özelliklerini daha iyi anlayabileceğiz.
Uygulamalı istatistikler [19, 20], yanlış bir istatistiksel hipotezi reddetmenize izin veren herhangi bir kriter olmadığını belirtir. Öz-koordinatlar yöntemi bu soruna tamamen açıklık getiriyor (hipotez kabulü).
Deneysel verilerin tanımlanması için kullanılan işlev, belirli bir diferansiyel denklemin çözümü olarak görülebilir. Biçimi, öz-koordinat açılımının yapısını belirler.
Öz-koordinat açılımının özgün bir özelliği, Y(t) fonksiyonu tarafından oluşturulan tüm verilerin, Y(t) fonksiyonunun X1(t)..XN(t) öz-koordinatları temelinde yapıda doğrusal olmasıdır. Başka herhangi bir F(t) işlevi tarafından oluşturulan veriler, bu temelde artık düz bir çizgi olarak görünmeyecektir (F(t) işlevinin öz-koordinatları temelinde doğrusal görüneceklerdir).
Bu gerçek, işlevlerin doğru bir şekilde tanımlanmasına izin verir; böylece istatistiksel hipotezlerle çalışılmasını büyük ölçüde kolaylaştırır.
2.1. Öz-Koordinatlar Yöntemi
Yöntemin arka planındaki kavram, Xk(t) öz-koordinatlarını Y(t) işlevine dayalı operatörler şeklinde oluşturmaktır.
Bu, Xk(t) öz-koordinatlarının integral konvolüsyonlar şeklini aldığı ve açılımın Y(t) fonksiyonu tarafından sağlanan diferansiyel denklemin yapısı tarafından belirlendiği matematiksel analiz kullanılarak yapılabilir. Ayrıca, C1 katsayılarını belirleme sorunu.. CN ortaya çıkar.
Ortogonal taban açılımında (ör. Fourier dönüşüm katsayıları belirlenirken) vektör bazında izdüşümü alınarak açılım katsayıları hesaplanır ve taban fonksiyonların ortogonalliğinden dolayı istenen sonuç elde edilir.
X1(t)… XN(t)'nin ortogonalliği hakkında bilgi olmadığı için bu bizim durumumuz için uygun değildir.
2.2. En Küçük Kareler Yöntemi Kullanılarak Açılım Katsayılarının Hesaplanması
Ck katsayıları en küçük kareler yöntemi kullanılarak hesaplanabilir. Bu sorun, bir doğrusal denklem sistemini çözmeye indirgenir.
Farz edelim ki:
Neredeyse her 
ölçümü için bir 
hatası vardır:
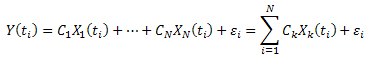
Karesi alınmış sapmaların toplamını en aza indirin:
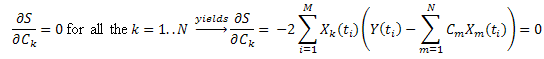
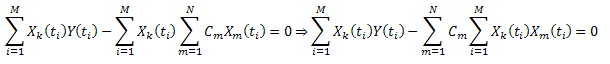
Notasyonla tanışın: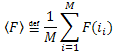 
, şu şekilde yazılabilir:
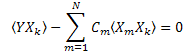
Böylece, C1...CN (k=1..N)'de bir doğrusal denklem sistemi elde ederiz:
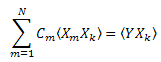
"Korelasyon" matrisi simetriktir: 
.
Bazı durumlarda, öz-koordinat açılımı integral formda daha uygun görünebilir:
Bu, hataların etkisini (ortalama alma nedeniyle) azaltmaya izin verir, ancak ek hesaplamalar gerektirir.
2.3. R(x) Fonksiyon Açılımı Örneği
Aşağıdaki fonksiyonun öz-koordinat açılımına bir göz atalım:
Bu işlev, birkaç istatistiksel dağılım üretir [21]:
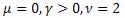- Normal (Gauss) dağılım,
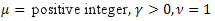- Poisson dağılımı,
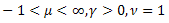- Gama dağılımı,
- 
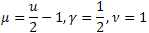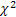dağılımı;
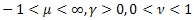- Özel bir durum olarak Weibull dağılımını içeren Schtauffer dağılımı 
.
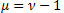Ek olarak, gevşeme süreçlerini tanımlamak için de çok uygundur:
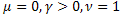- olağan üstel işlev,
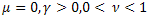- uzatılmış üstel işlev,
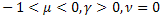- güç gevşeme işlevi.
R(x)'in x'eye göre türevini aldıktan sonra:
Her iki tarafı da x ile çarpın:
'ü dönüştürün:
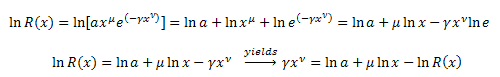
Denklemde yerine koyun:
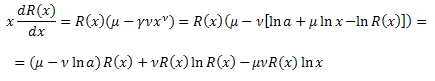
R(x) fonksiyonu için diferansiyel denklemi elde ederiz:
[xm,x] aralığı üzerinden x'e göre her iki tarafın da integralini alın:
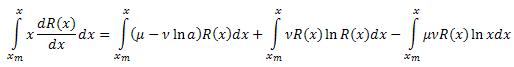
Denklemin sol tarafının bölümlere göre integralini alın:
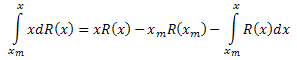
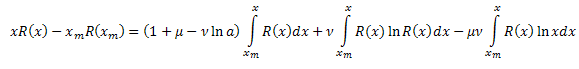
Sonuç olarak, elimizde şunlar var:
Burada:
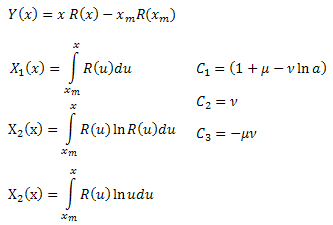
katsayılarını hesaplayarak, 
işlev parametrelerini belirleyebiliriz. Dördüncü parametre 
, R(x) formülünden türetilebilir.
2.4. Uygulama
Açılım katsayılarının hesaplanması, doğrusal denklem sisteminin çözülmesini gerektirir. Matrislerle çalışmanın kolaylık sağlaması için bu, ayrı bir CMatrix sınıfı (CMatrix.mqh dosyası) olarak düzenlenebilir. Bu sınıfın yöntemlerini kullanarak matris parametrelerini, matris öğe değerlerini ayarlayabilir ve Gauss yöntemini kullanarak doğrusal denklem sistemini çözebilirsiniz.
//+------------------------------------------------------------------+ //| CMatrix class | //+------------------------------------------------------------------+ class CMatrix { double m_matrix[]; int m_rows; int m_columns; public: void SetSize(int nrows,int ncolumns); double Get(int i,int j); void Set(int i,int j,double val); void GaussSolve(double &v[]); void Test(); };
R(x) işlevinin öz-koordinatlarını ve parametrelerini hesaplayan script dosyasının (EC_Example1.mq5) bir örneğini verelim.
//+------------------------------------------------------------------+ //| EC_Example1.mq5 | //| Copyright 2012, MetaQuotes Software Corp. | //| https://www.mql5.com | //+------------------------------------------------------------------+ #property copyright "Copyright 2012, MetaQuotes Software Corp." #property link "https://www.mql5.com" #property version "1.00" #include <CMatrix.mqh> //+------------------------------------------------------------------+ //| CECCalculator | //+------------------------------------------------------------------+ class CECCalculator { protected: int m_size; //--- x[i] double m_x[]; //--- y[i] double m_y[]; //--- matrix CMatrix m_matrix; //--- Y[i] double m_ec_y[]; //--- eigen-coordinates X1[i],X2[i],X3[i] double m_ec_x1[]; double m_ec_x2[]; double m_ec_x3[]; //--- coefficients C1,C2,C3 double m_ec_coefs[]; //--- function f1=Y-C2*X2-C3*X3 double m_f1[]; //--- function f2=Y-C1*X1-C3*X3 double m_f2[]; //--- function f3=Y-C1*X1-C2*X2 double m_f3[]; private: //--- function for data generation double R(double x,double a,double mu,double gamma,double nu); //--- calculation of the integral double Integrate(double &x[],double &y[],int ind); //--- calculation of the function Y(x) void CalcY(double &y[]); //--- calculation of the function X1(x) void CalcX1(double &x1[]); //--- calculation of the function X2(x) void CalcX2(double &x2[]); //--- calculation of the function X3(x) void CalcX3(double &x3[]); //--- calculation of the correlator double Correlator(int ind1,int ind2); public: //--- method for generating the test function data set x[i],y[i] void GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu); //--- loading data from the file bool LoadData(string filename); //--- saving data into the file bool SaveData(string filename); //--- saving the calculation results void SaveResults(string filename); //--- calculation of the eigen-coordinates void CalcEigenCoordinates(); //--- calculation of the linear expansion coefficients void CalcEigenCoefficients(); //--- calculation of the function parameters void CalculateParameters(); //--- calculation of the functions f1,f2,f3 void CalculatePlotFunctions(); }; //+------------------------------------------------------------------+ //| Function R(x) | //+------------------------------------------------------------------+ double CECCalculator::R(double x,double a,double mu,double gamma,double nu) { return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x))))); } //+-----------------------------------------------------------------------+ //| Method for generating the data set x[i],y[i] of the test function R(x)| //+-----------------------------------------------------------------------+ void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu) { if(size<=0) return; if(x1>=x2) return; m_size=size; ArrayResize(m_x,m_size); ArrayResize(m_y,m_size); double delta=(x2-x1)/(m_size-1); //--- for(int i=0; i<m_size; i++) { m_x[i]=x1+i*delta; m_y[i]=R(m_x[i],a,mu,gamma,nu); } }; //+------------------------------------------------------------------+ //| Method for loading data from the .CSV file | //+------------------------------------------------------------------+ bool CECCalculator::LoadData(string filename) { int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } m_size=0; while(!FileIsEnding(filehandle)) { string str=FileReadString(filehandle); if(str!="") { string astr[]; StringSplit(str,';',astr); if(ArraySize(astr)==2) { ArrayResize(m_x,m_size+1); ArrayResize(m_y,m_size+1); m_x[m_size]=StringToDouble(astr[0]); m_y[m_size]=StringToDouble(astr[1]); m_size++; } else { m_size=0; return(false); } } } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Method for saving data into the .CSV file | //+------------------------------------------------------------------+ bool CECCalculator::SaveData(string filename) { if(m_size==0) return(false); if(ArraySize(m_x)!=ArraySize(m_y)) return(false); if(ArraySize(m_x)==0) return(false); int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r'); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename,", error",GetLastError()); return(false); } for(int i=0; i<ArraySize(m_x); i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); return(true); } //+------------------------------------------------------------------+ //| Method for the calculation of the integral | //+------------------------------------------------------------------+ double CECCalculator::Integrate(double &x[],double &y[],int ind) { double sum=0; for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5; return(sum); } //+------------------------------------------------------------------+ //| Method for the calculation of the function Y(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; }; //+------------------------------------------------------------------+ //| Method for the calculation of the function X1(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the function X2(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i])); ArrayResize(x2,m_size); for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the function X3(x) | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i])); ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| Method for the calculation of the eigen-coordinates | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoordinates() { CalcY(m_ec_y); CalcX1(m_ec_x1); CalcX2(m_ec_x2); CalcX3(m_ec_x3); } //+------------------------------------------------------------------+ //| Method for the calculation of the correlator | //+------------------------------------------------------------------+ double CECCalculator::Correlator(int ind1,int ind2) { if(m_size==0) return(0); if(ind1<=0 || ind1>4) return(0); if(ind2<=0 || ind2>4) return(0); //--- double arr1[]; double arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); //--- switch(ind1) { case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break; } switch(ind2) { case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break; case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break; case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break; case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break; } //--- double sum=0; for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i]; } sum=sum/m_size; return(sum); }; //+------------------------------------------------------------------+ //| Method for the calculation of the linear expansion coefficients | //+------------------------------------------------------------------+ void CECCalculator::CalcEigenCoefficients() { //--- setting the matrix size 3x4 m_matrix.SetSize(3,4); //--- calculation of the correlation matrix for(int i=3; i>=1; i--) { string s=""; for(int j=1; j<=4; j++) { double corr=Correlator(i,j); m_matrix.Set(i,j,corr); s=s+" "+DoubleToString(m_matrix.Get(i,j)); } Print(i," ",s); } //--- solving the system of the linear equations m_matrix.GaussSolve(m_ec_coefs); //--- displaying the solution - the obtained coefficients C1,..CN for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]); }; //+--------------------------------------------------------------------+ //| Method for the calculation of the function parameters a,mu,nu,gamma| //+--------------------------------------------------------------------+ void CECCalculator::CalculateParameters() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- calculate a double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1])); //--- calculate mu double mu=-m_ec_coefs[2]/m_ec_coefs[1]; //--- calculate nu double nu=m_ec_coefs[1]; //--- calculate gamma double arr1[],arr2[]; ArrayResize(arr1,m_size); ArrayResize(arr2,m_size); double corr1=0; double corr2=0; for(int i=0; i<m_size; i++) { arr1[i]=MathPow(m_x[i],nu); arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]); corr1+=arr1[i]*arr2[i]; corr2+=arr1[i]*arr1[i]; } double gamma=-corr1/corr2; //--- Print("a=",a); Print("mu=",mu); Print("nu=",nu); Print("gamma=",gamma); }; //+------------------------------------------------------------------+ //| Method for the calculation of the functions | //| f1=Y-C2*X2-C3*X3 | //| f2=Y-C1*X1-C3*X3 | //| f3=Y-C1*X1-C2*X2 | //+------------------------------------------------------------------+ void CECCalculator::CalculatePlotFunctions() { if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;} //--- ArrayResize(m_f1,m_size); ArrayResize(m_f2,m_size); ArrayResize(m_f3,m_size); //--- for(int i=0; i<m_size; i++) { //--- plot function f1=Y-C2*X2-C3*X3 m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f2=Y-C1*X1-C3*X3 m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i]; //--- plot function f3=Y-C1*X1-C2*X2 m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i]; } } //+------------------------------------------------------------------+ //| Method for saving the calculation results | //+------------------------------------------------------------------+ void CECCalculator::SaveResults(string filename) { if(m_size==0) return; int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI); if(filehandle==INVALID_HANDLE) { Alert("Error in open of file ",filename," for writing, error",GetLastError()); return; } for(int i=0; i<m_size; i++) { string s=DoubleToString(m_x[i],8)+";"; s+=DoubleToString(m_y[i],8)+";"; s+=DoubleToString(m_ec_y[i],8)+";"; s+=DoubleToString(m_ec_x1[i],8)+";"; s+=DoubleToString(m_f1[i],8)+";"; s+=DoubleToString(m_ec_x2[i],8)+";"; s+=DoubleToString(m_f2[i],8)+";"; s+=DoubleToString(m_ec_x3[i],8)+";"; s+=DoubleToString(m_f3[i],8)+";"; s+="\r"; FileWriteString(filehandle,s); } FileClose(filehandle); } //+------------------------------------------------------------------+ //| Script program start function | //+------------------------------------------------------------------+ void OnStart() { CECCalculator ec; //--- model function data preparation ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3); //--- saving into the file ec.SaveData("ex1.csv"); //--- calculation of the eigen-coordinates ec.CalcEigenCoordinates(); //--- calculation of the coefficients ec.CalcEigenCoefficients(); //--- calculation of the parameters ec.CalculateParameters(); //--- calculation of the functions f1,f2,f3 ec.CalculatePlotFunctions(); //--- saving the results into the file ec.SaveResults("ex1-results.csv"); }
2.5. R(x) Modeli Fonksiyon Hesaplama Sonuçları
Model verisi olarak [0,25,15,25] aralığında R(x) işlevinin 100 değerini üreteceğiz.
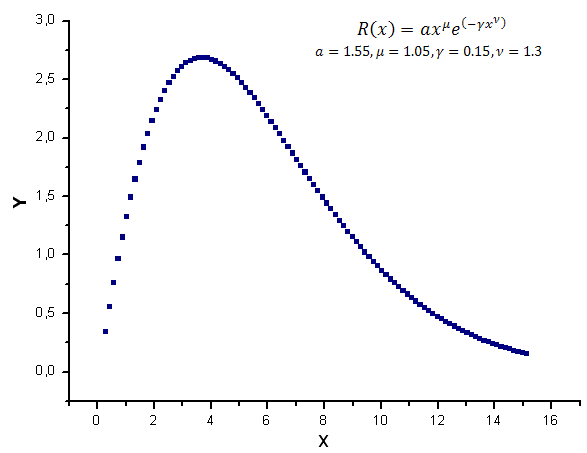
Şek. 7. Hesaplamalar için kullanılan model fonksiyonu
Bu veriler, Y(x) fonksiyonunu ve onun X1(x), X2(x) ve X3(x) fonksiyonlarındaki açılımını çizmek için temel sağlar.
Şekil 8'de, Y(x) fonksiyonu ve onun X1(x), X2(x) ve X3(x) "öz-koordinatları" gösterilmiştir.
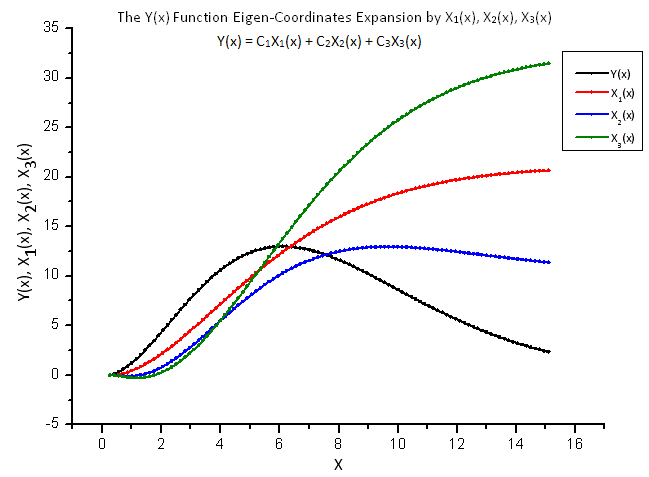öz koordinatlarının genel biçimi
Şek. 8. Y(x) fonksiyonunun ve X1(x), X2(x) ve X3(x) öz-koordinatlarının genel biçimi
X1(x), X2(x) ve X3(x) operatörlerinin integral yapısından kaynaklanan bu fonksiyonların düzgünlüğüne dikkat edin.
Y(x), X1(x), X2(x) ve X3(x) fonksiyonlarının hesaplanmasından sonra korelasyon matrisi oluşturulur, daha sonra C1, C2 ve C3 katsayıları için denklemler çözülür ve R(x) işlev parametreleri şu elde edilen değerler temel alınarak hesaplanır:
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1 221.03637620 148.53278281 305.48547011 101.93843241 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2 148.53278281 101.63995012 202.85142688 74.19784681 2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3 305.48547011 202.85142688 429.09345292 127.82779760
Şimdi hesaplanan açılımın doğrusallığını kontrol edeceğiz. Bunun için 3 fonksiyonu hesaplamamız gerekiyor:
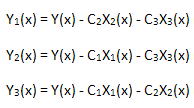
her birinin, X1(x), X2(x) ve X3(x) öz-koordinatlarının temelinde izdüşümü alınır:
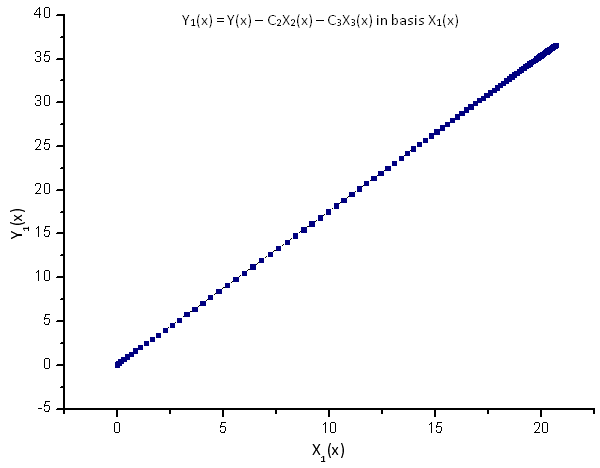
Şek. 9. Y1(x) fonksiyonunun X1(x) temelinde temsili
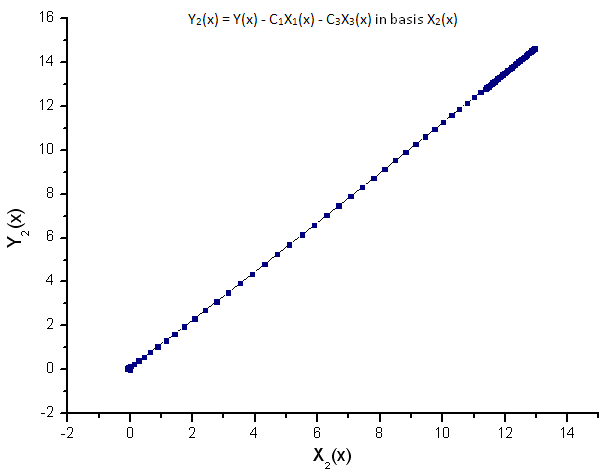
Şek. 10. Y2(x) fonksiyonunun X2(x) temelinde temsili
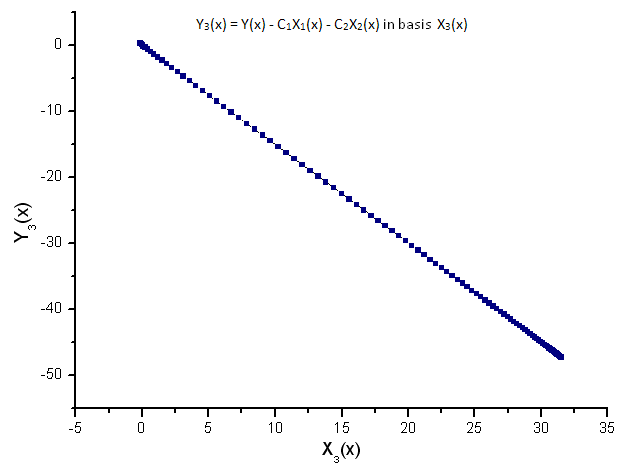
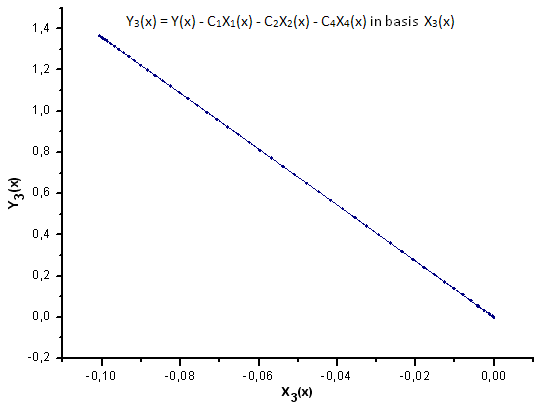
Şek. 11. Y3(x) fonksiyonunun X3(x) temelinde temsili
Çizilen fonksiyonların doğrusal bağımlılığı, Şek. 7'deki veri serisinin kesinlikle R(x) fonksiyonuna karşılık geldiğini göstermektedir.
R(x) öz-koordinatlarında temsil edilen herhangi bir başka fonksiyon (biçim olarak benzer olsa dahi) artık doğrusal bir biçime sahip olmayacaktır. Bu gerçek, fonksiyonları tanımlamamızı sağlar.
Nokta sayısı 10000'e yükseltilirse (aynı aralık korunarak) model işlev parametrelerinin sayısal değerlerinin hesaplanmasının doğruluğu iyileştirilebilir:
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1 225.47846911 151.22066473 311.86134419 104.65062550 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2 151.22066473 103.30005101 206.66297964 76.03285182 2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3 311.86134419 206.66297964 438.35625824 131.91955339
Bu durumda, işlev parametreleri daha doğru hesaplanmıştır.
2.6. Gürültü Etkisi
Gerçek deneysel veriler her zaman gürültü içerir.
ECCCalculator sınıfının GenerateData() yönteminde şunu değiştiririz:
m_y[i]=R(m_x[i],a,mu,gamma,nu);
ile
m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;
maksimum işlev değerinin yaklaşık %10'u olan rastgele bir parazit ekleyerek.
EC_Example1-noise.mq5 script dosyası sonucu aşağıdaki gibidir:
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1 254.45082565 185.19087989 354.25574000 125.17343164 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2 185.19087989 136.81028987 254.92996885 97.14705491 2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3 354.25574000 254.92996885 501.76021715 159.49440494
Rastgele bir gürültü içeren model fonksiyonunun grafiği Şek. 12'de gösterilmiştir.
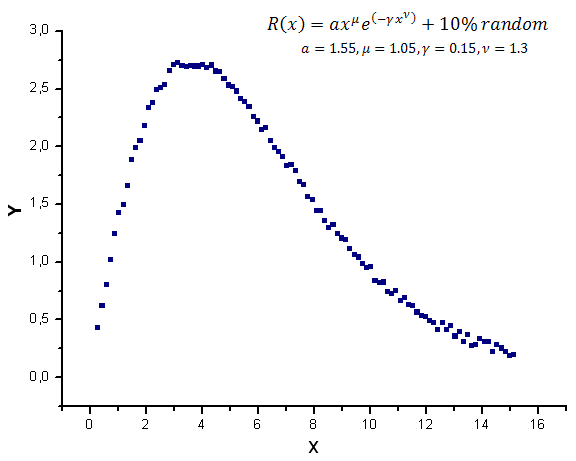
Şek. 12. Hesaplamalar için kullanılan gürültü içeren model fonksiyonu
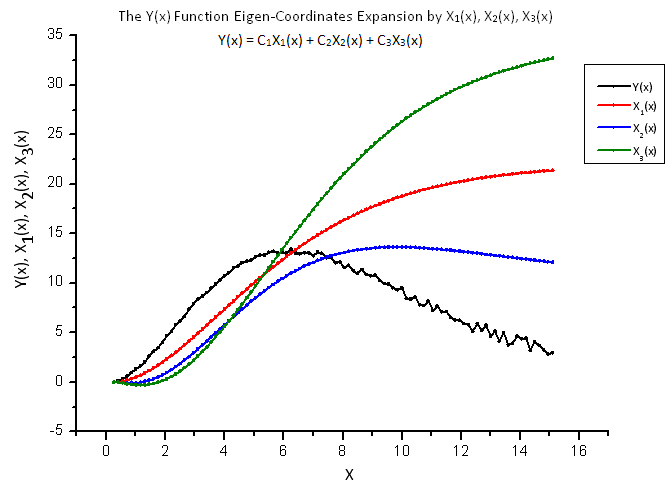
Şek. 13. Y(x) fonksiyonunun ve X1(x), X2(x) ve X3(x) öz-koordinatlarının genel biçimi
X1(x), X2(x) ve X3(x) fonksiyonları "öz-koordinatlar" olarak işlev görürken yine de düz görünür, ancak doğrusal kombinasyonları olarak çizilen Y(x) farklı görünür (Şek. 13).
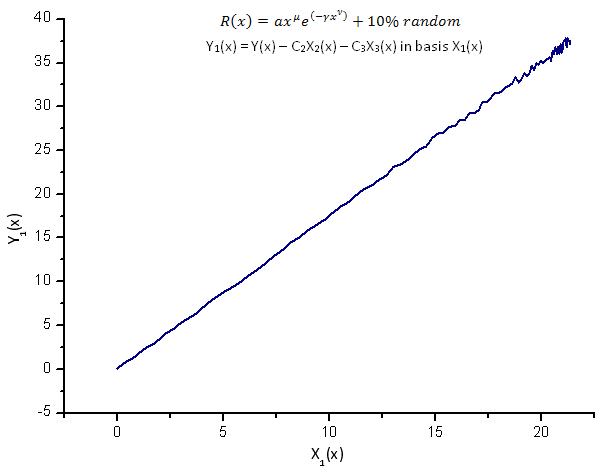
Şek. 14. Y1(x) fonksiyonunun X1(x) temelinde temsili
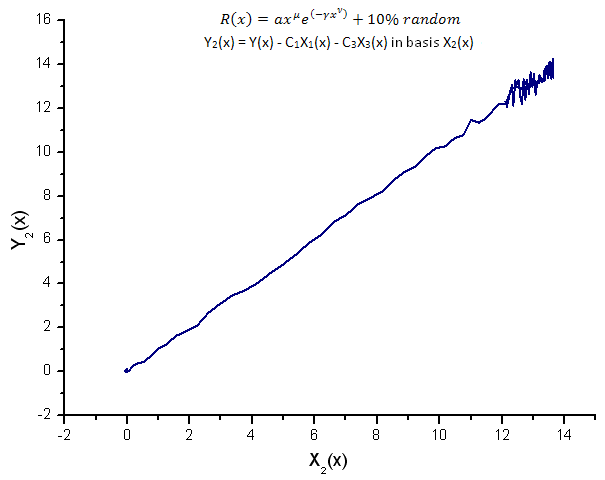
Şek. 15. Y2(x) fonksiyonunun X2(x) temelinde temsili
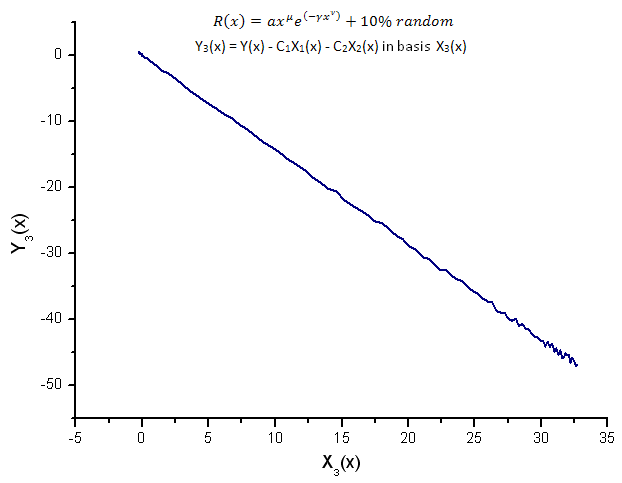
Şek. 16. Y3(x) fonksiyonunun X3(x) temelinde temsili
Y1(x),Y2(x) ve Y3(x) fonksiyonlarının öz-koordinatlar temelinde temsili (Şekil 8-10) hala doğrusal bir biçime sahiptir, ancak gürültünün varlığından dolayı düz çizgi etrafındaki dalgalanmalar fark edilebilir. Bu, sinyal/gürültünün minimum hale geldiği daha büyük X'lere göre en belirgindir.
Burada gürültü bileşenleri düz çizginin her iki tarafında yer alır ve bu durumda integral öz-koordinat açılımını kullanmak uygundur (Bölüm 2.2).
3. Kapsamlı Olmayan Olasılık Dağılımları
İstatistiksel mekaniğin genelleştirilmesi, dağılımlarla sonuçlanır [2, 22]:
Burada; 
, 
.
q-Gauss dağılımı, P2(x) fonksiyonunun özel bir durumudur.
3.1. P1(x) Fonksiyonu Öz-Koordinatları Açılımı
P1(x)'in türevini alırız:
Ortaya çıkan diferansiyel denklem şu şekildedir:
[xm,x] aralığı üzerinden integral alın:
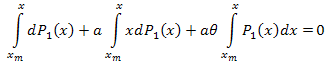
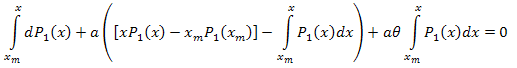
Böylece:
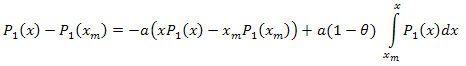
Öz-koordinat açılımı aşağıdaki gibidir:
Burada:
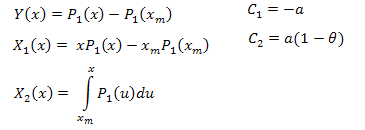
Hesaplamalar için fonksiyonlar aşağıda belirtildiği gibidir (EC_Example2.mq5):
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); //--- Y=P(x)-P(xm) for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=x*P(x)-xm*P(xm) for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=Integrate(P1(x)) for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i); }
Bu kez korelasyon matrisi boyutu 2x3'tür; P1(x) fonksiyonunun a ve teta parametrelerinin değerleri С1 ve C2 katsayılarına göre belirlenir. B parametresinin sayısal değeri, normalizasyon gerekliliğinden elde edilebilir.
Aşağıda, x [0,10] aralığı üzerinde P1(x,1,0,5,2) model fonksiyonu hesaplama sonucu yer almaktadır; kullanılan nokta sayısı 1000'dir:
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1 0.15420524 0.48808959 -0.32145543 2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2 0.48808959 1.79668322 -1.14307410P1(x) fonksiyonu ve öz-koordinat açılımı Şekil 17-20'de gösterilmiştir.
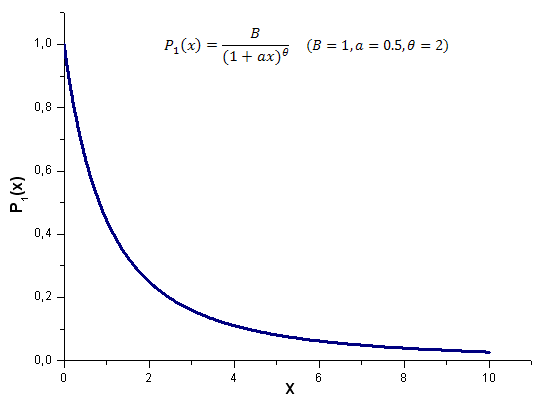
Şek. 17. Hesaplamalar için kullanılan model fonksiyonu P1(x, 1, 0,5, 2), 1000 nokta
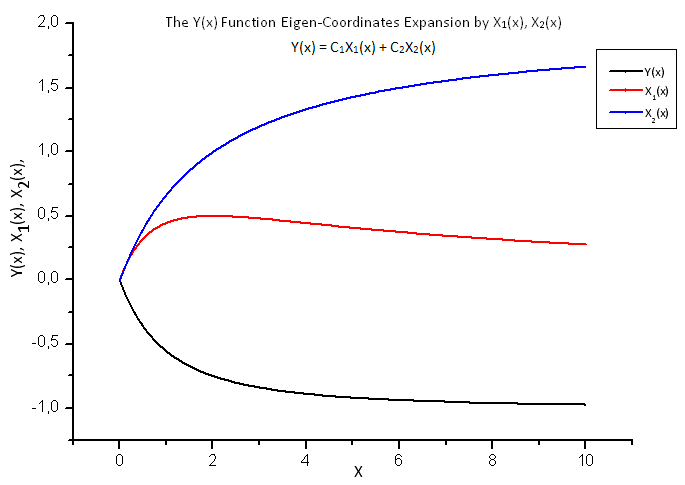
Şek. 18. Y(x) fonksiyonunun ve X1(x) ve X2(x) öz-koordinatlarının genel biçimi
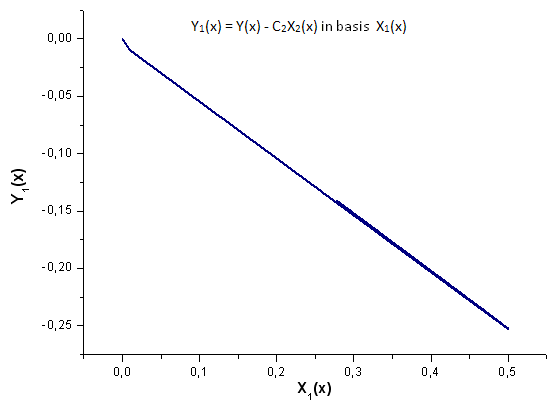
Şek. 19. Y1(x) fonksiyonunun X1(x) temelinde temsili
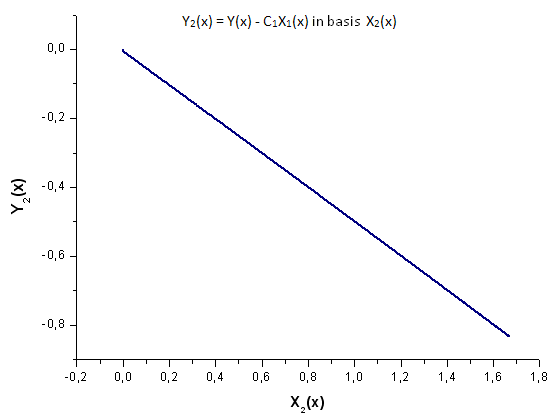
Şek. 20. Y2(x) fonksiyonunun X2(x) temelinde temsili
Şekil 19'a tam olarak bir göz atın. Grafiğin en başında ve üçte ikisinde doğrusal bağımlılıkta hafif bir bozulma vardır.
Bu, hesaplanan açılımın özellikleriyle ilişkilidir - X1(x), integral yapısında değildir.
3.2. P2(x) Fonksiyonu Öz-Koordinatları Açılımı
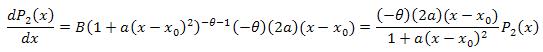
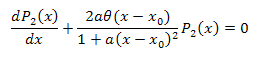
Diferansiyel denklem:
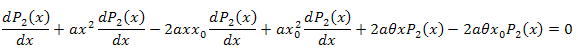
[xm,x] aralığı üzerinden x'e göre integralini alırız:
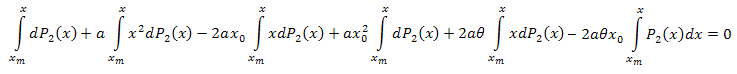
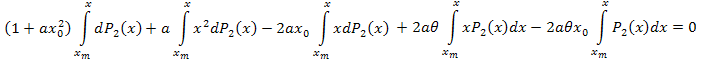
Parçalara göre integralini alarak şunu elde ederiz:
Basitleştirin:
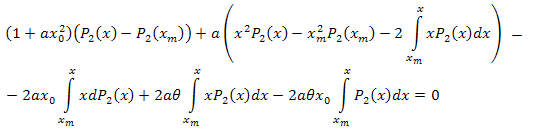
Cebirsel işlemlerden sonra şunu elde ederiz:
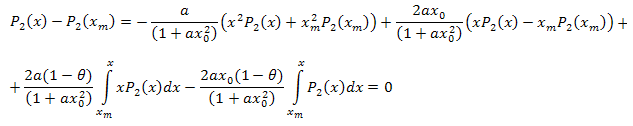
Dolayısıyla, ortaya çıkan açılım şu şekildedir:
Burada:
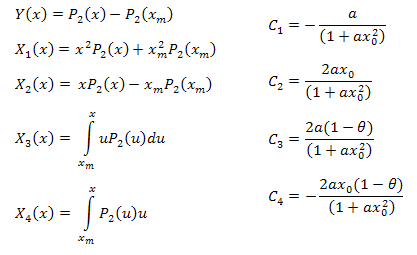
İşlev parametreleri aşağıdaki formüller kullanılarak hesaplanabilir:
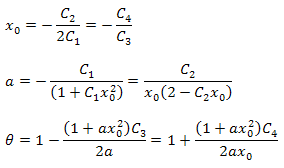
Ortaya çıkan açılımda parametreler arasında ek bir ilişki olduğuna dikkat edilmelidir. Bu gerçek, analiz için seçilen fonksiyonun doğruluğunu doğrulamak için kullanılabilir. Bu ilişkiler, P2(x) fonksiyonuna kesin olarak karşılık gelen veriler için her zaman doğrudur.
B parametresinin sayısal değeri, normalizasyon gerekliliğinden elde edilebilir.
Öz-koordinatların hesaplanmasına yönelik fonksiyonlar aşağıdaki gibidir (EC_Example3.mq5):
//+------------------------------------------------------------------+ //| CalcY | //+------------------------------------------------------------------+ void CECCalculator::CalcY(double &y[]) { if(m_size==0) return; ArrayResize(y,m_size); for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0]; }; //+------------------------------------------------------------------+ //| CalcX1 | //+------------------------------------------------------------------+ void CECCalculator::CalcX1(double &x1[]) { if(m_size==0) return; ArrayResize(x1,m_size); //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm) for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX2 | //+------------------------------------------------------------------+ void CECCalculator::CalcX2(double &x2[]) { if(m_size==0) return; ArrayResize(x2,m_size); //--- X2=(x)*P2(x)-(xm)*P2(xm) for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0]; } //+------------------------------------------------------------------+ //| CalcX3 | //+------------------------------------------------------------------+ void CECCalculator::CalcX3(double &x3[]) { if(m_size==0) return; double tmp[]; ArrayResize(tmp,m_size); for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i]; //--- X3=Integrate(X*P2(x)) ArrayResize(x3,m_size); for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i); } //+------------------------------------------------------------------+ //| CalcX4 | //+------------------------------------------------------------------+ void CECCalculator::CalcX4(double &x4[]) { if(m_size==0) return; //--- X4=Integrate(P2(x)) ArrayResize(x4,m_size); for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i); }
Aşağıda P2(x) model fonksiyonu hesaplama sonucu (B=1, a=0,5, teta=2, x0=1) verilmiştir; kullanılan nokta sayısı 1000'dir:
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1 1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2 0.60684314 0.37995888 0.55974145 0.58899739 0.06731011 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3 1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224 2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4 1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168P2(x) fonksiyonu ve öz-koordinat açılımı Şekil 21-26'da gösterilmiştir.
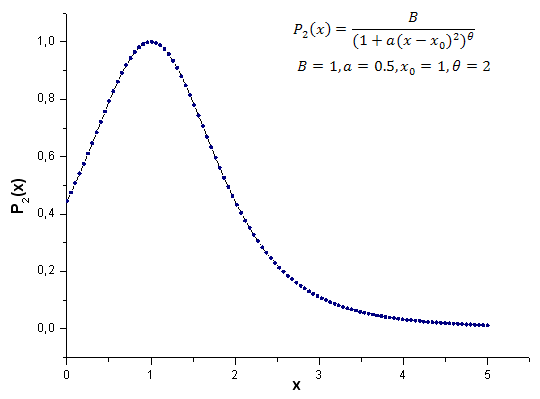
Şek. 21. Hesaplamalar için kullanılan model fonksiyonu P2(x,1,0,5,2,1), 100 nokta
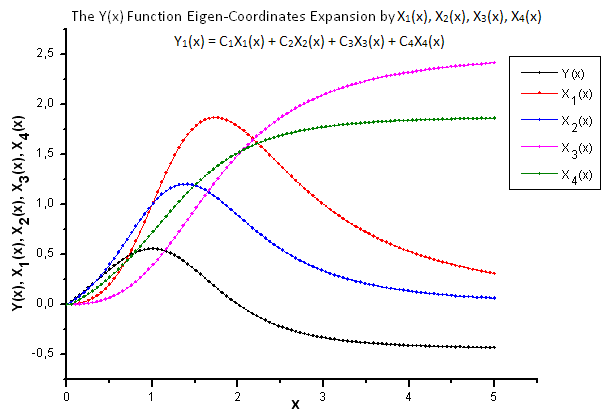
Şek. 22. Y(x) fonksiyonunun ve X1(x), X2(x), X3(x) ve X4(x) öz-koordinatlarının genel biçimi
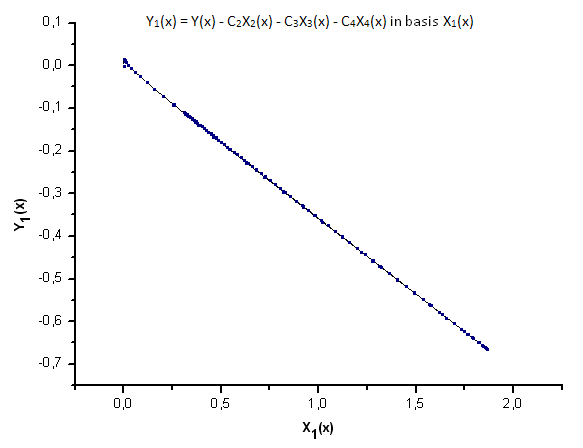
Şek. 23. Y1(x) fonksiyonunun X1(x) temelinde temsili
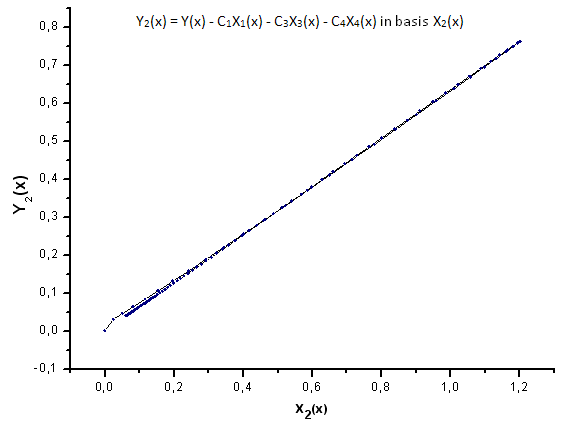
Şek. 24. Y2(x) fonksiyonunun X2(x) temelinde temsili
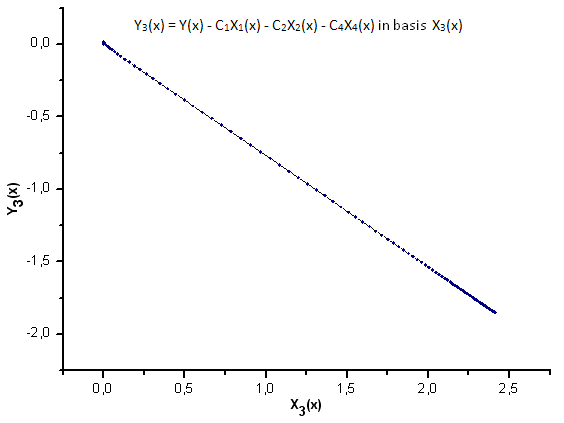
Şek. 25. Y3(x) fonksiyonunun X3(x) temelinde temsili
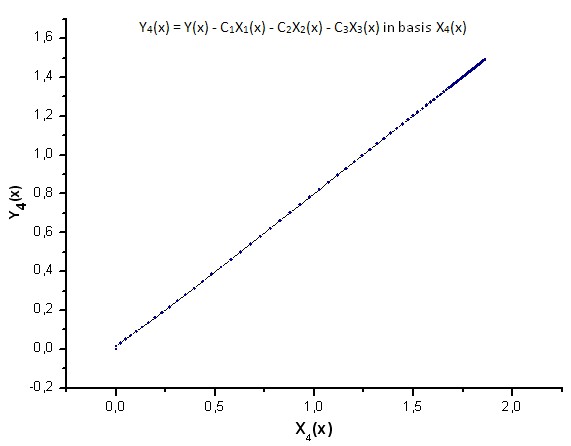
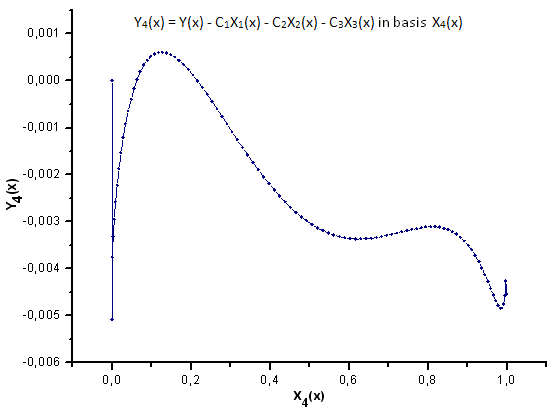
Şek. 26. Y4(x) fonksiyonunun X4(x) temelinde temsili
4. Bir Kediye Benziyorsa... Bir Kedi Olmayabilir
q-Gauss dağılımları ailesi, kapsamlı olmayan istatistiksel mekaniğin tam kalbinde yer alır ve bu nedenle, genelleştirilmiş merkezi limit teoreminde ortaya çıkmasını beklemek doğaldır. Entropik düşünceler, onun lehine ana argüman olarak hizmet etmiştir [26].
Ancak, [18, makale] sunumu, q-Gauss gibi dağılımların, evrensel olmadığını, dolayısıyla limit dağılımları olarak özel rolleri konusunda şüphe uyandırdığını göstermiştir.
Örneğin, fonksiyon (sorunlardan birinin analitik çözümü):
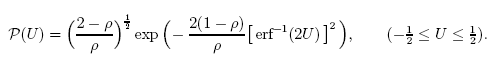
q-Gauss dağılımı kullanılarak çok doğru bir şekilde tanımlanabilir.
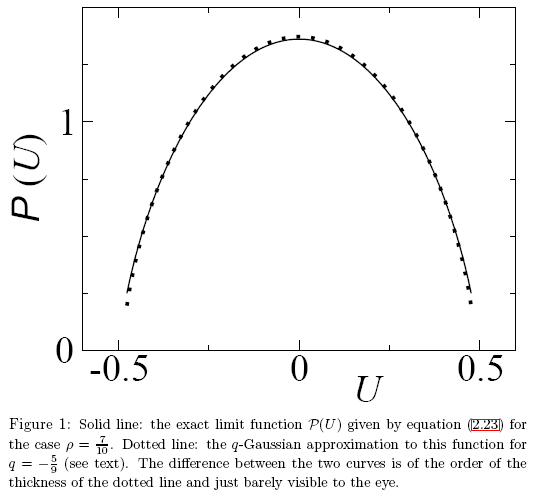
Şek. 27. "İstatistiksel Mekanikte q-Gauss Olan ve Gauss Olmayan Üzerine Bir Not" makalesinden bir örnek
Bu durumda, analitik olarak farklı fonksiyonlar benzer sayısal değerlere sahiptir ve bu nedenle farklılıklar gözle zar zor görülebilir. Doğru bir fonksiyon tanımlama yöntemi gereklidir. Bu sorun, öz-koordinatlar yöntemi kullanılarak uygun bir şekilde çözülebilir.
P(U) fonksiyonunun öz-koordinatları açılımının bir örneğini gözden geçirelim ve onu q-Gauss'dan tam olarak neyin farklı kıldığını gösterelim. Fonksiyonlar, göze çok benzer görünmektedir (Şek. 27).
Bir sinyal üretiyoruz (P(U) fonksiyonunun 100 değeri) ve onu Bölüm 3.2'de çizilen P2(x) fonksiyonunun öz-koordinatları sistemine "yansıtıyoruz".
Hilhorst-Schehr-problem.mq5 script dosyası, P(U) fonksiyonunu hesaplar ve MQL5\Files\test-data.csv dosyasına kaydedilen veri serilerini oluşturur. Bu veriler, EC_Example3_Test.mq5 ile analiz edilir.
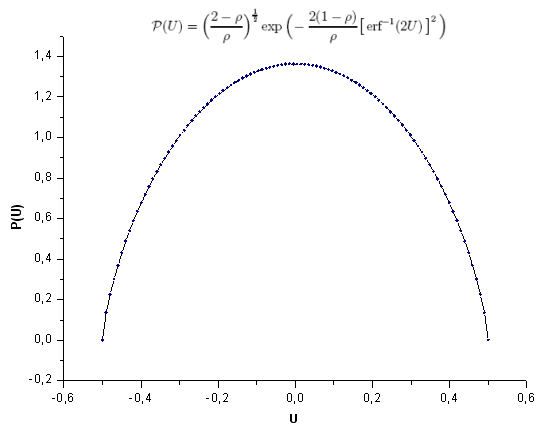
Şek. 28. Model fonksiyonu P(U), 100 nokta
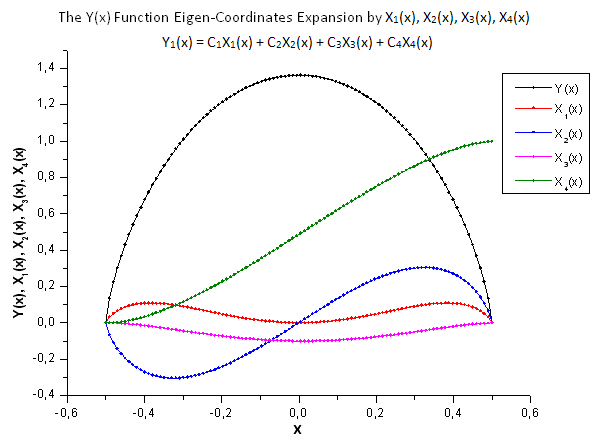
Şek. 29. Y(x) fonksiyonunun ve X1(x), X2(x), X3(x) ve X4(x) öz-koordinatlarının genel biçimi
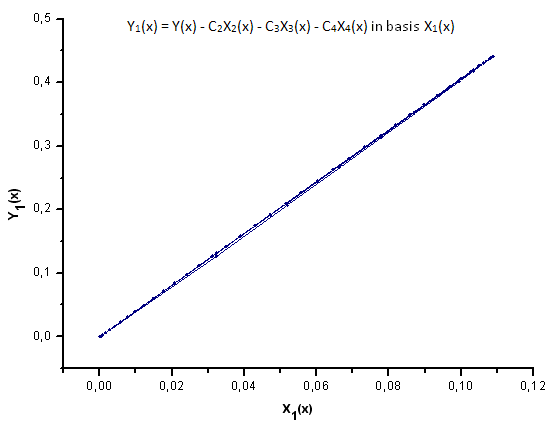
Şek. 30. Y1(x) fonksiyonunun X1(x) temelinde temsili
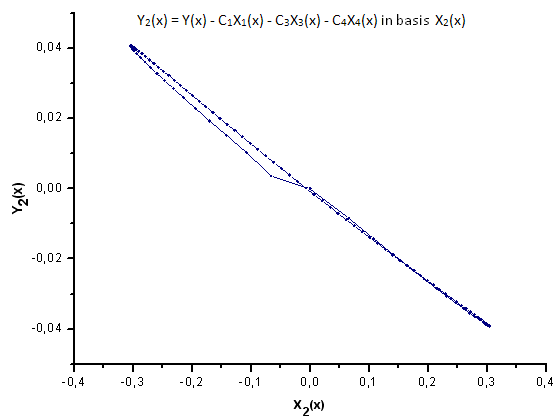
Şek. 31. Y2(x) fonksiyonunun X2(x) temelinde temsili
Şek. 32. Y3(x) fonksiyonunun X3(x) temelinde temsili
Şek. 33. Y4(x) fonksiyonunun X4(x) temelinde temsili
Şek. 30-33'te gösterildiği gibi, P2(x) ve P(U) fonksiyonları X1(x), X2(x) ve X3(x) koordinatları açısından çok benzerdir - Xi(x) ve Yi(x) arasında iyi bir doğrusal bağımlılık olduğu gözlemlenebilir. X4(x) bileşeninde önemli bir fark görülebilir (Şek. 33).
X4(x) bileşeni için doğrusal bağımlılığın olmaması, P(U) tarafından üretilen veri kümesinin, q-Gauss dağılımına benzer görünmesine rağmen, aslında q-Gauss dağılımı olmadığını kanıtlamaktadır.
Xi(x) ve Yi(x)'i birlikte çizerek fonksiyonlara (Şekil 34-37) farklı bir şekilde bakabiliriz.
Şek. 34. X1(x) ve Y1(x) fonksiyonlarının genel biçimi
Şek. 35. X2(x) ve Y2(x) fonksiyonlarının genel biçimi
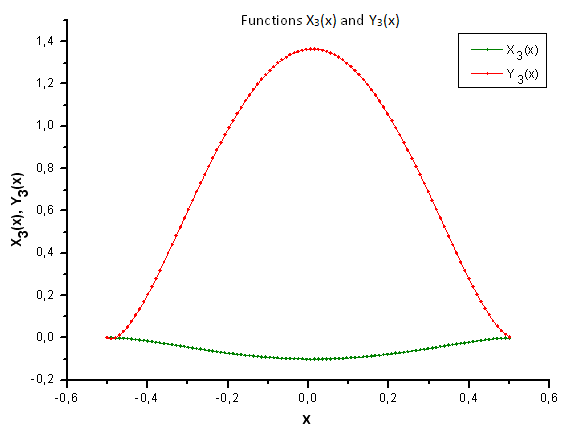
Şek. 36. X3(x) ve Y3(x) fonksiyonlarının genel biçimi
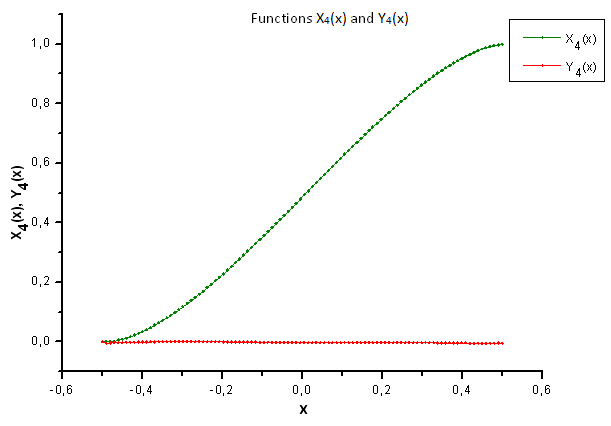
Şek. 37. X4(x) ve Y4(x) fonksiyonlarının genel biçimi
Şekil 37'de gösterildiği gibi, X4(x) bileşenindeki yapısal farklılık, P(U) fonksiyonu tarafından üretilen verileri P2(x) fonksiyonunun öz-koordinatlarına yansıtırken belirgin hale gelmiştir. Böylece, deneysel verilerin P2(x) fonksiyonuna karşılık gelmediğini kesin olarak söyleyebiliriz.
Aşağıda belirtilen hesaplama (EC_Example3_test) bu gerçek lehindedir:
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1 0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2 0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3 -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437 2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4 0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994
Ayrıca bu, parametreler arasındaki ilişkileri de bozmuştur.
Sonuç
Öz-koordinatlar yöntemi, verilerin analizini ve yorumlanmasını büyük ölçüde basitleştirmeye olanak tanıyan, fonksiyonel ilişkilerin yapısal özelliklerinin analizi için benzersiz bir araçtır.
Bu yöntemin arka planındaki kavram, önerilen modele karşılık gelen yeni fonksiyonlar oluşturmak için {xi,yi} deneysel veri kümelerini kullanmaktır. Operatör açılımlarının biçimi, verilerin tanımlanması için bir "aday" olarak işlev gören fonksiyon tarafından karşılanan diferansiyel denklemin yapısı tarafından belirlenir. Fonksiyon yerel ise, {xi,yi} verileri kullanılarak hesaplanan fonksiyon açılımları, öz-koordinatlar temelinde doğrusal bir biçim alacaktır. "Aday fonksiyon"un öz-koordinatları temelinde doğrusallıktan sapmalar, {xi,yi} verilerinin verilen fonksiyon tarafından üretilemediğini ve oluşturulan modelin uygun olmadığını göstermektedir.
Bazı karmaşık durumlarda, aday fonksiyon ve yerel fonksiyon o kadar benzer görünebilir ki, hesaplanan açılımların daha büyük bir kısmının doğrusal olduğu ortaya çıkar. Bununla birlikte, öz-koordinatlar yöntemi, açılımın bozulmuş doğrusallığı ile varlığının bilinmesini sağlayan bu fonksiyonlar arasındaki farkı tanımlamamıza olanak tanır - Hilhorst ve Schehr örneği, X4(x) üzerinde izdüşüm alınırken son açılım öğesinde belirgin hale gelen farkın bir örneklemesi olarak işlev görmüştür.
Bu bilgi ayrıca, P2(x) fonksiyonu tarafından karşılanan bir diferansiyel denklemle (Bölüm 3.2) ilgilenirken de faydalı olabilir - Söz konusu öğe, P2(x)'ye göre doğrusal kısma karşılık gelir. Bu, deneysel verilerin fenomenolojik açıklaması durumunda çok ilginç olmayabilir ("q-Gauss biçiminde bir çözüm arıyoruz"). Ancak, model diferansiyel denklemlere dayanıyorsa (Şek. 3), fiziksel süreç modellerinde dikkate alınan mekanizmaların her birinin rolü daha iyi anlaşılabilir.
Referanslar
- C. Tsallis, "Possible Generalization of Boltzmann-Gibbs Statistics", Journal of Statistical Physics, Vol. 52, Nos. 1/2, 1988.
- C. Tsallis, "Nonextensive Statistics: Theoretical, Experimental and Computational Evidences and Connections". Brazilian Journal of Physics, (1999) vol. 29. p.1.
- C. Tsallis, "Some Comments on Boltzmann-Gibbs Statistical Mechanics", Chaos, Solitons & Fractals Volume 6, 1995, pp. 539–559.
- Europhysics News "Special Issue: Nonextensive Statistical Mechanics: New Trends, New Perspectives", Vol. 36 No. 6 (November-December 2005).
- M. Gell-Mann, C. Tsallis, "Nonextensive Entropy: Interdisciplinary Applications", Oxford University Press, 15.04.2004, 422 p.
- Constantino Tsallis, the Official Website Nonextensive Statistical Mechanics and Thermodynamics.
- Chumak, O.V. "Entropy and Fractals in Data Analysis", М.-Izhevsk: RDC "Regular and Chaotic Dynamics", Institute for Computer Research, 2011. - 164 p.
- Qiuping A. Wang, "Incomplete Statistics and Nonextensive Generalizations of Statistical Mechanics", Chaos, Solitons and Fractals, 12(2001)1431-1437.
- Qiuping A. Wang, "Extensive Generalization of Statistical Mechanics Based on Incomplete Information Theory", Entropy, 5(2003).
- Lisa Borland, "Long-Range Memory and Nonextensivity in Financial Markets", Europhysics News 36, 228-231 (2005)
- T. S. Biró, R. Rosenfeld, "Microscopic Origin of Non-Gaussian Distributions of Financial Returns", Physica A: Statistical Mechanics and its Applications, Vol. 387, Nr. 7 (Mar 1, 2008) , p. 1603-1612 (preprint).
- S. M. D. Queiros, C. Anteneodo, C. Tsallis, "Power-Law Distributions in Economics: A Nonextensive Statistical Approach", Proceedings of SPIE (2005) Volume: 5848, Publisher: SPIE, Pages: 151-164, (preprint)
- R Hanel, S Thurner, "Derivation of Power-Law Distributions within Standard Statistical Mechanics", Physica A: Statistical Mechanics and its Applications (2005), Volume: 351, Issue: 2-4, Publisher: Elsevier, Pages: 260-268. (preprint)
- A K Rajagopal, Sumiyoshi Abe, "Statistical Mechanical Foundations of Power-Law Distributions", Physica D: Nonlinear Phenomena (2003), Volume: 193, Issue: 1-4, Pages: 19 (preprint)
- T. Kaizoji, "An Interacting-Agent Model of Financial Markets from the Viewpoint of Nonextensive Statistical Mechanics", Physica A: Statistical Mechanics and its Applications, Vol. 370, N. 1 (Oct 1, 2006) , p. 109-113. (preprint)
- V. Gontis, J. Ruseckas, A. Kononovičius, "A Long-Range Memory Stochastic Model of the Return in Financial Markets", Physica A: Statistical Mechanics and its Applications 389 (2010) 100-106. (preprint)
- H.E. Roman, M. Porto, "Self-Generated Power-Law Tails in Probability Distributions", Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, Issue: 3 Pt 2, Pages: 036-128.
- H. J. Hilhorst, G. Schehr, "A Note on q-Gaussians and Non-Gaussians in Statistical Mechanics" (2007, preprint, presentation).
- D. J. Hudson, "Lectures on Elementary Statistics and Probability", CERN-63-29, Geneva : CERN, 1963. - 101 p.
- D. J. Hudson, "Statistics Lectures II : Maximum Likelihood and Least Squares Theory", CERN-64-18. - Geneva : CERN, 1964. - 115 p.
- R. R. Nigmatullin, "Eigen-Coordinates: New Method of Analytical Functions Identification in Experimental Measurements", Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
- R.R. Nigmatullin, "Recognition of Nonextensive Statistical Distributions by the Eigencoordinates Method", Physica A: Statistical Mechanics and its Applications Volume 285, Issues 3–4, 1 October 2000, pp. 547–565.
- C. Antonini "q-Gaussians in Finance" (2010).
- C. Antonini, "The Use of the q-Gaussian Distribution in Finance" (2011).
- L. G. Moyano, C. Tsallis, M. Gell-Mann, "Numerical Indications of a q-Generalised Central Limit Theorem", Europhysics Letters 73, 813-819, 2006, (preprint).
- T. Dauxois, "Non-Gaussian Distributions under Scrutiny", J. Stat. Mech. (2007) N08001. (preprint)
Ek. Q-Gauss ile SP500 günlük getirilerinin analizi
SP500 günlük getirilerine (P2(x) fonksiyonu) başarılı q-Gauss yaklaşımının klasik örneğini (Şek. 4) ele alalım.
Şuradaki günlük verileri kullandık: http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500/
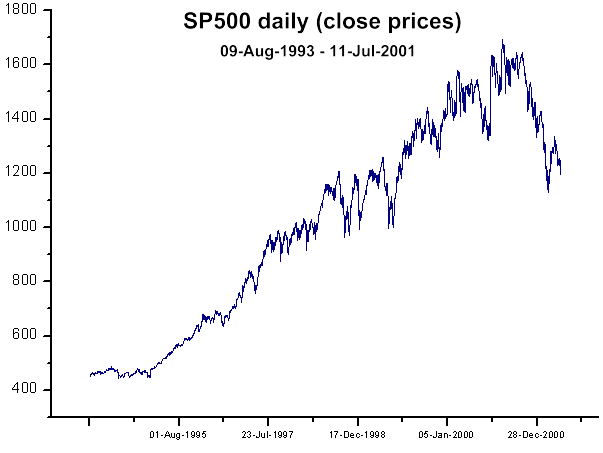
Şek. 38. SP500 kapanış fiyatları (günlük)
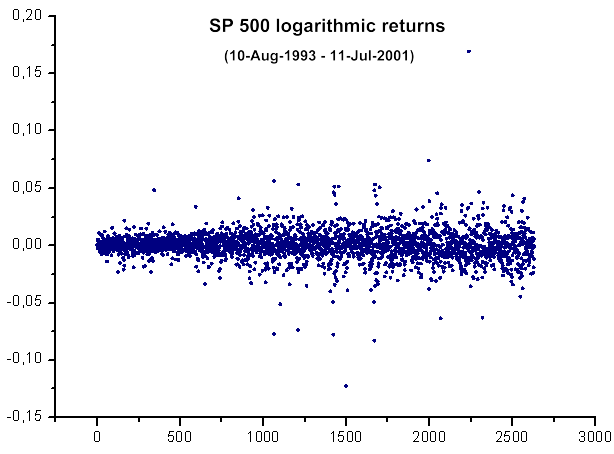
Şek. 39. SP500 logaritmik getirileri
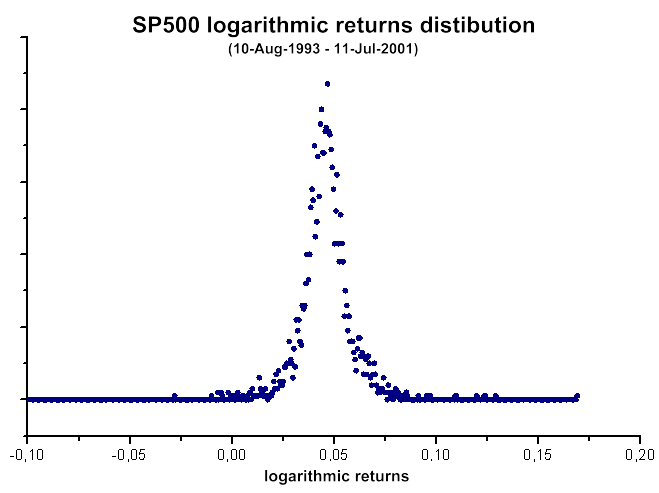
Şek. 40. SP500 logaritmik getiri dağılımı
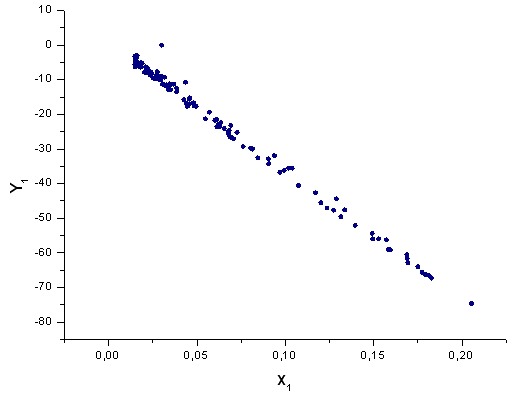
Şek. 41. Y1(x) fonksiyonunun X1(x) temelinde temsili
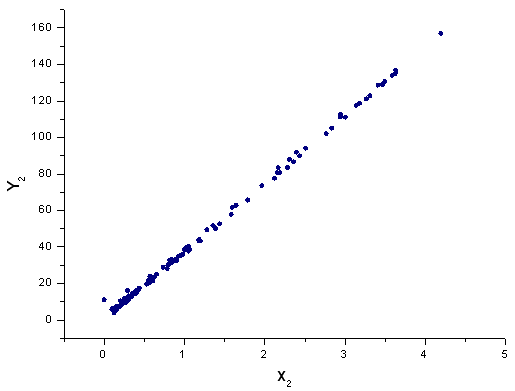
Şek. 42. X2(x) temelinde Y2(x) fonksiyonu
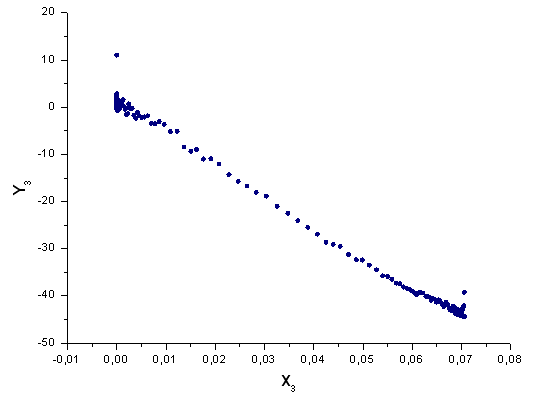
Şek. 43. X3(x) temelinde Y3(x) fonksiyonu
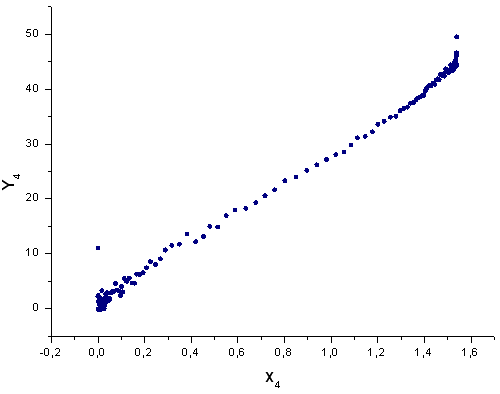
Şek. 44. X4(x) temelinde Y4(x) fonksiyonu
Analizin terminalinizde nasıl gerçekleştirileceğini görmek için SP500-data.csv dosyası \Files\ klasörüne yerleştirilmelidir.
Bunun ardından, iki script dosyası başlatmanız gerekir:
- CalcDistr_SP500.mq5 (dağılımı hesaplar).
- q-gaussian-SP500.mq5 (öz-koordinatlar analizi)
2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: theta=1.770125768485269 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: theta=1.864132228192338 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: a=2798.166930885822 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: a=8676.207867097581 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2: x0=0.04567518783335043 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1: x0=0.0512505923716428 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C1=-364.7131366394939 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C2=37.38352859698793 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C3=-630.3207508306047 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) C4=28.79001868944634 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 1 0.00177913 0.03169294 0.00089521 0.02099064 0.57597695 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 2 0.03169294 0.59791579 0.01177430 0.28437712 11.55900584 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 3 0.00089521 0.01177430 0.00193200 0.04269286 0.12501732 2012.06.29 20:01:19 q-gaussian-SP500 (EURUSD,D1) 4 0.02099064 0.28437712 0.04269286 0.94465120 3.26179090 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) checking distibution cnt=2632.0 n=2632 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632 2012.06.29 20:01:09 CalcDistr_SP500 (EURUSD,D1) Total data=2633
Öz-koordinatlar yöntemiyle elde edilen tahmini q değeri (q=1+1/teta): q~1,55
Kitapta bildirilen değer (Şek. 4) q~1,4.
Sonuç: Genel olarak, bu verilerin q-gauss fonksiyonu ile tanımlanabileceği görülebilir. Bu, kitapta bildirilen q-gauss kullanılarak yapılan başarılı yorumlamayı açıklamaktadır.
MetaQuotes Ltd tarafından Rusçadan çevrilmiştir.
Orijinal makale: https://www.mql5.com/ru/articles/412
Ampirik Mod Ayrıştırma Yöntemine Giriş
Algoritmik ticaret makaleniz için 200 USD kazanın!
MetaTrader Mobil Terminalinde MetaQuotes Kimliği
Bilinmeyen Olasılık Yoğunluk Fonksiyonunun Çekirdek Yoğunluk Tahmini
- Ücretsiz alım-satım uygulamaları
- İşlem kopyalama için 8.000'den fazla sinyal
- Finansal piyasaları keşfetmek için ekonomik haberler
Gizlilik ve Veri Koruma Politikasını ve MQL5.com Kullanım Şartlarını kabul edersiniz