MetaTrader 5 / Experts
English Русский 中文 Español Deutsch 日本語 Português 한국어 Italiano Türkçe
Application de la méthode des coordonnées propres à l'analyse structurelle de distributions statistiques non extensives

Application de la méthode des coordonnées propres à l'analyse structurelle de distributions statistiques non extensives

MetaTrader 5 — Experts | 12 janvier 2022, 17:15
136 1
MetaQuotes
MetaQuotes

Contenu


Introduction

En 1988, Constantino Tsallis a proposé la généralisation de la mécanique statistique de Boltzmann-Gibbs-Shannon [1] où il a présenté une notion de entropie non extensive.

Une conséquence importante de la généralisation de l'entropie semble être l'existence de nouveaux types de distribution [2] jouant le rôle clé dans la nouvelle mécanique statistique (Q-Exponentielle et Q-Gaussienne) :

distributions statistiques non extensives

Il a été constaté que ces types de distribution peuvent être utilisés pour décrire de nombreuses données expérimentales dans des systèmes à mémoire à longue portée, des systèmes avec des forces de longue portée et des systèmes fortement corrélés.

L'entropie est étroitement liée à l'information [7]. La généralisation de la mécanique statistique basée sur la théorie de l'information a été présentée dans [8-9]. Une nouvelle mécanique statistique non extensive s'est avérée très utile pour l'économétrie [10-17]. Par exemple, la Q-Gaussian distribution décrit bien les larges ailes (queues) des distributions d'incréments de cotations d'instruments financiers (q~1,5). Cela dit, la plupart des distributions d'incréments de séries chronologiques financières se transforment en distributions normales (q=1) à plus grande échelle (mois, années) [10].

On s'attendait naturellement à ce qu'une telle généralisation de la mécanique statistique aboutisse à un analogue du théorème central limite pour les distributions q-gaussiennes. Mais cela s'est avéré faux dans [18] - la distribution limite de la somme des variables aléatoires fortement corrélées est analytiquement différente des q-gaussiennes.

Cependant, un problème d'un autre genre est apparu : il s'est avéré que les valeurs numériques de la solution exacte trouvée étaient très proches du Q-Gaussien (« numériquement similaire, analytiquement différent »). Pour analyser les différences entre les fonctions et obtenir les meilleurs paramètres de la distribution Q-gaussienne, une expansion en série a été utilisée dans [18]. Les relations de ces fonctions ont conduit à une expansion en puissance du paramètre q caractérisant le degré de non-extensivité du système.

Le problème majeur des statistiques appliquées est le problème de l'acceptation des hypothèses statistiques. Il a longtemps été considéré comme impossible à résoudre [19-20] nécessitant un outil spécial (quelque chose comme un microscope électronique) qui permettrait de voir plus que ce qui est possible en utilisant les méthodes de la statistique appliquée moderne.

La méthode des coordonnées propres introduite dans [21] nous permet d'atteindre un niveau plus profond - l'analyse des propriétés structurelles des relations fonctionnelles. Cette méthode très fine peut être utilisée pour résoudre une variété de problèmes. Les développements d'opérateurs de fonctions correspondant aux distributions non extensives ci-dessus ont été démontrés dans [22].

Cet article traitera de la méthode des coordonnées propres et d'exemples de son utilisation pratique. Il contient de nombreuses formules qui sont d'une grande importance pour comprendre l'essence de la méthode. Après avoir répété tous les calculs, vous serez en mesure de tracer vous-même les développements de fonctions pour les fonctions qui vous intéressent.

1. Les Q-Gaussiens en économétrie

La distribution Q-Gaussienne joue un rôle très important en économétrie [4,10-17].

Pour avoir une idée générale du niveau actuel de la recherche, on peut se référer aux travaux du Dr. Claudio Antonini « q-gaussiennes en finance » [23] et « L'utilisation de la distribution q-gaussienne en finance » [24].

Présentons brièvement les principaux résultats.

Fig. 1. Méthodologie scientifique (diapositive 4 « L'utilisation de la distribution q-gaussienne en finance »)

Fig. 1. Méthodologie scientifique (diapositive 4 « L'utilisation de la distribution q-gaussienne en finance »)

Les principales particularités des séries chronologiques financières sont présentées à la figure 2 :

Fig. 2. Propriétés des séries chronologiques financières (diapositive 3 « L'utilisation de la distribution q-gaussienne en finance »)

Fig. 2. Propriétés des séries chronologiques financières (diapositive 3 « L'utilisation de la distribution q-gaussienne en finance »)

De nombreux modèles théoriques utilisés pour décrire les séries chronologiques financières conduisent à la distribution Q-Gaussienne :

Fig. 3. Modèles théoriques et Q-Gaussien (diapositive 27 « L'utilisation de la distribution q-gaussienne en finance »)

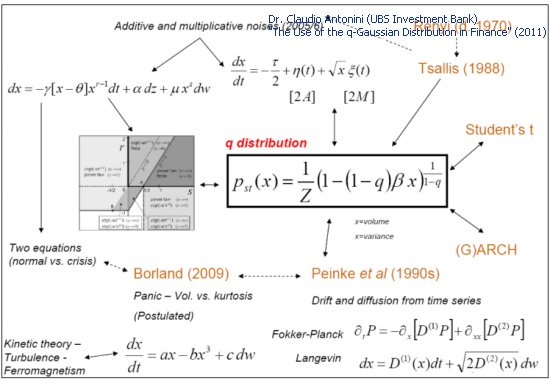
Fig. 3. Modèles théoriques et Q-Gaussien (diapositive 27 « L'utilisation de la distribution q-gaussienne en finance »)

La distribution Q-gaussienne est également utilisée pour la description phénoménologique des distributions de cotations :

Fig. 4. Exemple d'analyse des rendements quotidiens du S&P 500 (diapositive 8 « L'utilisation de la distribution q-gaussienne en finance »)

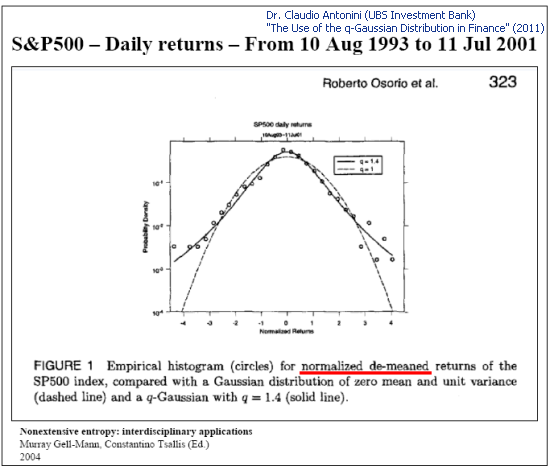
Fig. 4. Exemple d'analyse des rendements quotidiens du S&P 500 (diapositive 8 « L'utilisation de la distribution q-gaussienne en finance »)

Travailler avec des données réelles pose un problème d'identification des fonctions :

Fig. 5. Le problème de l'identification des fonctions de distribution (diapositive 14 « q-gaussiennes en finance »)

Fig. 5. Le problème de l'identification des fonctions de distribution (diapositive 14 « q-gaussiennes en finance »)

Les deux articles du Dr. Claudio Antonini souligne l'importance d'une identification correcte des fonctions pour construire des modèles adéquats de processus physiques :

Fig. 6. Conclusions tirées de « q-Gaussiens en finance » et « L'utilisation de la distribution q-gaussienne en finance » (Dr. Claudio Antonini, 2010, 2011)

Fig. 6. Conclusions tirées dans « q-Gaussiens en finance » et « L'utilisation de la distribution q-gaussienne en finance » (Dr. Claudio Antonini, 2010, 2011)

Exemples d'utilisation des statistiques q-gaussiennes en finance (feuilles de calcul + fichiers MathCad) :


2. Coordonnées propres

Le développement des coordonnées propres est le suivant :

où C1…CN sont des constantes et X1(t),..,XN(t) sont les « coordonnées propres ».

De telles expansions linéaires sont très pratiques et souvent utilisées dans l'analyse de données. Par exemple, une fonction exponentielle sur une échelle logarithmique se transforme en une ligne droite (sa pente peut facilement être calculée à l'aide de la régression linéaire). Il n'est donc pas nécessaire de procéder à une optimisation non linéaire (ajustement) pour déterminer les paramètres de la fonction.

L'échelle logarithmique ne sera cependant pas d'une grande aide dans le cas de fonctions plus complexes (par exemple la somme de deux exposants) - la fonction n'apparaîtra pas comme une ligne droite. Et une optimisation non linéaire sera nécessaire pour déterminer les coefficients de la fonction.

Il existe des cas où les données expérimentales peuvent être tout aussi bien expliquées à l'aide de plusieurs fonctions, qui correspondent toutes à différents modèles de processus physiques. Quelle fonction choisir ? Laquelle fournira une image plus adéquate de la réalité en dehors des données expérimentales ?

L'identification correcte des fonctions est vitale pour l'analyse des systèmes complexes (par exemple, les séries chronologiques financières) - chaque distribution correspond à un certain processus physique et nous serons en mesure de mieux comprendre la dynamique et les propriétés générales des systèmes complexes en ayant choisi un modèle adéquat.

Selon la statistique appliquée [19, 20], il n'existe pas de critère permettant de rejeter une hypothèse statistique erronée. La méthode des coordonnées propres jette une toute nouvelle lumière sur ce problème (acceptation de l'hypothèse).

La fonction utilisée pour la description des données expérimentales peut être considérée comme une solution à une certaine équation différentielle. Sa forme détermine la structure de l'expansion des coordonnées propres.

Une caractéristique particulière de l'expansion des coordonnées propres est que toutes les données générées par la fonction Y(t) ont une structure linéaire dans la base des coordonnées propres X1(t)..XN(t) de la fonction Y(t). Les données générées par toute autre fonction F(t) n'apparaîtront plus dans cette base comme une ligne droite (elles apparaîtront linéaires dans la base des coordonnées propres de la fonction F(t)).

Ce fait permet d'identifier avec précision les fonctions, facilitant ainsi grandement le travail avec des hypothèses statistiques.


2.1. La méthode des coordonnées propres

Le concept de cette méthode consiste à construire les coordonnées propres Xk(t) sous la forme d'opérateurs basés sur la fonction Y(t).

Cela peut se faire à l'aide d'une analyse mathématique dans laquelle les coordonnées propres Xk(t) prennent la forme de convolutions intégrales et l'expansion est déterminée par la structure de l'équation différentielle qui est satisfaite par la fonction Y(t). En outre, un problème de détermination des coefficients C1.. CN apparaît.

Dans l'expansion de base orthogonale (par exemple lors de la détermination des coefficients de transformée de Fourier), les coefficients d'expansion sont calculés en projetant le vecteur sur la base et le résultat souhaité est obtenu grâce à l'orthogonalité des fonctions de base.

Cela ne convient pas dans notre cas car il n'y a aucune information sur l'orthogonalité de X1(t)… XN(t).


2.2. Calcul des coefficients d'expansion par la méthode des moindres carrés

Les coefficients Ck peuvent être calculés par la méthode des moindres carrés. Ce problème se réduit à la résolution d'un système d'équations linéaires.

Supposons que :

Expansion des coordonnées propres

Pour pratiquement chaque mesure de il y a une erreur :

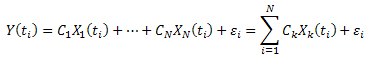
Minimiser la somme des écarts au carré :


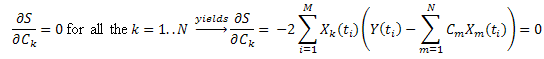
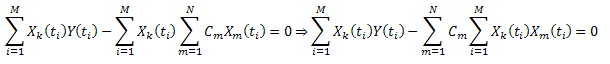
En introduisant la notation : 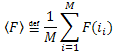moyenne, on peut l'écrire comme suit :

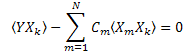
Ainsi, nous obtenons un système d'équations linéaires dans C1...CN (k=1..N):

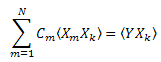
La matrice de « corrélation » est symétrique : .

Dans certains cas, l'expansion des coordonnées propres peut sembler plus pratique sous forme intégrale :

Elle permet de réduire l'impact des erreurs (dues au calcul de la moyenne) mais nécessite des calculs supplémentaires.


2.3. Un exemple d'extension de la fonction R(x)

Examinons l'expansion des coordonnées propres de la fonction suivante :

Cette fonction génère plusieurs distributions statistiques [21] :

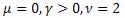  1. - la distribution normale (gaussienne) ;
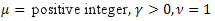  2. - la distribution de Poisson ;
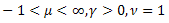  3. - la distribution gamma ;
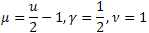  4. - la 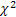distribution ;
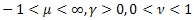  5. - La distribution de Schtauffer qui inclut la distribution de Weibull comme cas particulier .

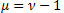De plus, elle est également bien adaptée à la description des processus de relaxation :

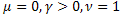  1. - la fonction exponentielle ordinaire ;
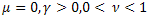  2. - la fonction exponentielle étirée ;
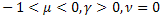  3. - la fonction de relaxation de la puissance.

Ayant différentié R(x) par rapport à x, nous avons :


Multipliez les deux côtés par x :

Transformer :

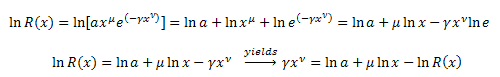
Substituer dans l'équation :

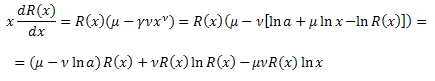
On obtient l'équation différentielle pour la fonction R(x) :

Intégrer les deux côtés par rapport à x sur l'intervalle [xm,x] :


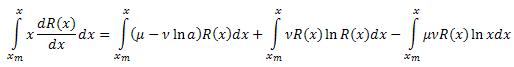
Intégrez le côté gauche de l'équation par parties :

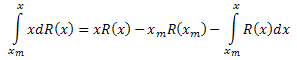
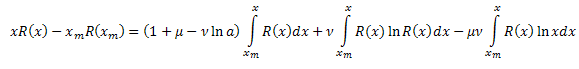
En conséquence, nous avons :

où :

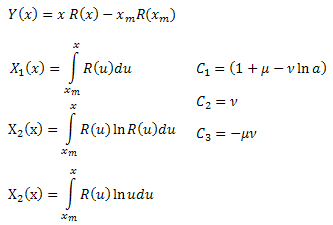
En calculant les coefficients , nous pouvons déterminer les paramètres de la fonction . Le quatrième paramètre peut être dérivé de la formule pour R(x).


2.4. Mise en œuvre

Le calcul des coefficients d'expansion nécessite de résoudre le système d'équations linéaires. Pour faciliter le travail avec les matrices, elle peut être organisée comme une classe séparée CMatrix (le fichier CMatrix.mqh). En utilisant les méthodes de cette classe, vous pouvez définir des paramètres de matrice, des valeurs d'élément de matrice et résoudre le système d'équations linéaires en utilisant la méthode gaussienne.

//+------------------------------------------------------------------+
//| CMatrix class                                                    |
//+------------------------------------------------------------------+
class CMatrix
  {
   double            m_matrix[];
   int               m_rows;
   int               m_columns;
public:
   void              SetSize(int nrows,int ncolumns);
   double            Get(int i,int j);
   void              Set(int i,int j,double val);
   void              GaussSolve(double &v[]);
   void              Test();
  };

Donnons un exemple du script (EC_Example1.mq5) qui calcule les coordonnées propres et les paramètres de la fonction R(x).

//+------------------------------------------------------------------+
//|                                                  EC_Example1.mq5 |
//|                        Copyright 2012, MetaQuotes Software Corp. |
//|                                              https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Copyright 2012, MetaQuotes Software Corp."
#property link      "https://www.mql5.com"
#property version   "1.00"
#include <CMatrix.mqh>
//+------------------------------------------------------------------+
//| CECCalculator                                                    |
//+------------------------------------------------------------------+
class CECCalculator
  {
protected:
   int               m_size;
   //--- x[i]
   double            m_x[];
   //--- y[i]
   double            m_y[];
   //--- matrix
   CMatrix           m_matrix;
   //--- Y[i]
   double            m_ec_y[];
   //--- eigen-coordinates X1[i],X2[i],X3[i]
   double            m_ec_x1[];
   double            m_ec_x2[];
   double            m_ec_x3[];
   //--- coefficients C1,C2,C3
   double            m_ec_coefs[];
   //--- function f1=Y-C2*X2-C3*X3
   double            m_f1[];
   //--- function f2=Y-C1*X1-C3*X3
   double            m_f2[];
   //--- function f3=Y-C1*X1-C2*X2
   double            m_f3[];
private:
   //--- function for data generation
   double            R(double x,double a,double mu,double gamma,double nu);
   //--- calculation of the integral
   double            Integrate(double &x[],double &y[],int ind);
   //--- calculation of the function Y(x)
   void              CalcY(double &y[]);
   //--- calculation of the function X1(x)
   void              CalcX1(double &x1[]);
   //--- calculation of the function X2(x)
   void              CalcX2(double &x2[]);
   //--- calculation of the function X3(x)
   void              CalcX3(double &x3[]);
   //--- calculation of the correlator
   double            Correlator(int ind1,int ind2);
public:
   //--- method for generating the test function data set x[i],y[i]
   void              GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu);
   //--- loading data from the file
   bool              LoadData(string filename);
   //--- saving data into the file
   bool              SaveData(string filename);
   //--- saving the calculation results
   void              SaveResults(string filename);
   //--- calculation of the eigen-coordinates
   void              CalcEigenCoordinates();
   //--- calculation of the linear expansion coefficients
   void              CalcEigenCoefficients();
   //--- calculation of the function parameters
   void              CalculateParameters();
   //--- calculation of the functions f1,f2,f3
   void              CalculatePlotFunctions();
  };
//+------------------------------------------------------------------+
//| Function R(x)                                                    |
//+------------------------------------------------------------------+
double CECCalculator::R(double x,double a,double mu,double gamma,double nu)
  {
   return(a*MathExp(mu*MathLog(MathAbs(x)))*MathExp(-gamma*MathExp(nu*MathLog(MathAbs(x)))));
  }
//+-----------------------------------------------------------------------+
//| Method for generating the data set x[i],y[i] of the test function R(x)|
//+-----------------------------------------------------------------------+
void CECCalculator::GenerateData(int size,double x1,double x2,double a,double mu,double gamma,double nu)
  {
   if(size<=0) return;
   if(x1>=x2) return;
   m_size=size;
   ArrayResize(m_x,m_size);
   ArrayResize(m_y,m_size);
   double delta=(x2-x1)/(m_size-1);
//---
   for(int i=0; i<m_size; i++)
     {
      m_x[i]=x1+i*delta;
      m_y[i]=R(m_x[i],a,mu,gamma,nu);
     }
  };
//+------------------------------------------------------------------+
//| Method for loading data from the .CSV file                       |
//+------------------------------------------------------------------+
bool CECCalculator::LoadData(string filename)
  {
   int filehandle=FileOpen(filename,FILE_CSV|FILE_READ|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   m_size=0;
   while(!FileIsEnding(filehandle))
     {
      string str=FileReadString(filehandle);
      if(str!="")
        {
         string astr[];
         StringSplit(str,';',astr);
         if(ArraySize(astr)==2)
           {
            ArrayResize(m_x,m_size+1);
            ArrayResize(m_y,m_size+1);
            m_x[m_size]=StringToDouble(astr[0]);
            m_y[m_size]=StringToDouble(astr[1]);
            m_size++;
           }
         else
           {
            m_size=0;
            return(false);
           }
        }
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for saving data into the .CSV file                        |
//+------------------------------------------------------------------+
bool CECCalculator::SaveData(string filename)
  {
   if(m_size==0) return(false);
   if(ArraySize(m_x)!=ArraySize(m_y)) return(false);
   if(ArraySize(m_x)==0) return(false);
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI,'\r');
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename,", error",GetLastError());
      return(false);
     }
   for(int i=0; i<ArraySize(m_x); i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
   return(true);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the integral                       |
//+------------------------------------------------------------------+
double CECCalculator::Integrate(double &x[],double &y[],int ind)
  {
   double sum=0;
   for(int i=0; i<ind-1; i++) sum+=(x[i+1]-x[i])*(y[i+1]+y[i])*0.5;
   return(sum);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function Y(x)                  |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the function X1(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   for(int i=0; i<m_size; i++) x1[i]=Integrate(m_x,m_y,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X2(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_y[i]));
   ArrayResize(x2,m_size);
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the function X3(x)                 |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_y[i]*MathLog(MathAbs(m_x[i]));
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the eigen-coordinates              |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoordinates()
  {
   CalcY(m_ec_y);
   CalcX1(m_ec_x1);
   CalcX2(m_ec_x2);
   CalcX3(m_ec_x3);
  }
//+------------------------------------------------------------------+
//| Method for the calculation of the correlator                     |
//+------------------------------------------------------------------+
double CECCalculator::Correlator(int ind1,int ind2)
  {
   if(m_size==0) return(0);
   if(ind1<=0 || ind1>4) return(0);
   if(ind2<=0 || ind2>4) return(0);
//---
   double arr1[];
   double arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
//---
   switch(ind1)
     {
      case 1: ArrayCopy(arr1,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr1,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr1,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr1,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
   switch(ind2)
     {
      case 1: ArrayCopy(arr2,m_ec_x1,0,0,WHOLE_ARRAY); break;
      case 2: ArrayCopy(arr2,m_ec_x2,0,0,WHOLE_ARRAY); break;
      case 3: ArrayCopy(arr2,m_ec_x3,0,0,WHOLE_ARRAY); break;
      case 4: ArrayCopy(arr2,m_ec_y,0,0,WHOLE_ARRAY); break;
     }
//---
   double sum=0;
   for(int i=0; i<m_size; i++) { sum+=arr1[i]*arr2[i];  }
   sum=sum/m_size;
   return(sum);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the linear expansion coefficients  |
//+------------------------------------------------------------------+
void CECCalculator::CalcEigenCoefficients()
  {
//--- setting the matrix size 3x4
   m_matrix.SetSize(3,4);
//--- calculation of the correlation matrix 
   for(int i=3; i>=1; i--)
     {
      string s="";
      for(int j=1; j<=4; j++)
        {
         double corr=Correlator(i,j);
         m_matrix.Set(i,j,corr);
         s=s+" "+DoubleToString(m_matrix.Get(i,j));
        }
      Print(i," ",s);
     }
//--- solving the system of the linear equations
   m_matrix.GaussSolve(m_ec_coefs);
//--- displaying the solution - the obtained coefficients C1,..CN 
   for(int i=ArraySize(m_ec_coefs)-1; i>=0; i--) Print("C",i+1,"=",m_ec_coefs[i]);
  };
//+--------------------------------------------------------------------+
//| Method for the calculation of the function parameters a,mu,nu,gamma|
//+--------------------------------------------------------------------+
void CECCalculator::CalculateParameters()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//--- calculate a
   double a=MathExp((1-m_ec_coefs[0])/m_ec_coefs[1]-m_ec_coefs[2]/(m_ec_coefs[1]*m_ec_coefs[1]));
//--- calculate mu
   double mu=-m_ec_coefs[2]/m_ec_coefs[1];
//--- calculate nu
   double nu=m_ec_coefs[1];
//--- calculate gamma
   double arr1[],arr2[];
   ArrayResize(arr1,m_size);
   ArrayResize(arr2,m_size);
   double corr1=0;
   double corr2=0;
   for(int i=0; i<m_size; i++)
     {
      arr1[i]=MathPow(m_x[i],nu);
      arr2[i]=MathLog(MathAbs(m_y[i]))-MathLog(a)-mu*MathLog(m_x[i]);
      corr1+=arr1[i]*arr2[i];
      corr2+=arr1[i]*arr1[i];
     }
   double gamma=-corr1/corr2;
//---
   Print("a=",a);
   Print("mu=",mu);
   Print("nu=",nu);
   Print("gamma=",gamma);
  };
//+------------------------------------------------------------------+
//| Method for the calculation of the functions                      |
//| f1=Y-C2*X2-C3*X3                                                 |
//| f2=Y-C1*X1-C3*X3                                                 |
//| f3=Y-C1*X1-C2*X2                                                 |
//+------------------------------------------------------------------+
void CECCalculator::CalculatePlotFunctions()
  {
   if(ArraySize(m_ec_coefs)==0) {Print("Coefficients are not calculated!"); return;}
//---
   ArrayResize(m_f1,m_size);
   ArrayResize(m_f2,m_size);
   ArrayResize(m_f3,m_size);
//---
   for(int i=0; i<m_size; i++)
     {
      //--- plot function f1=Y-C2*X2-C3*X3
      m_f1[i]=m_ec_y[i]-m_ec_coefs[1]*m_ec_x2[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f2=Y-C1*X1-C3*X3
      m_f2[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[2]*m_ec_x3[i];
      //--- plot function f3=Y-C1*X1-C2*X2
      m_f3[i]=m_ec_y[i]-m_ec_coefs[0]*m_ec_x1[i]-m_ec_coefs[1]*m_ec_x2[i];
     }
  }
//+------------------------------------------------------------------+
//| Method for saving the calculation results                        |
//+------------------------------------------------------------------+
void CECCalculator::SaveResults(string filename)
  {
   if(m_size==0) return;
   int filehandle=FileOpen(filename,FILE_WRITE|FILE_CSV|FILE_ANSI);
   if(filehandle==INVALID_HANDLE)
     {
      Alert("Error in open of file ",filename," for writing, error",GetLastError());
      return;
     }
   for(int i=0; i<m_size; i++)
     {
      string s=DoubleToString(m_x[i],8)+";";
      s+=DoubleToString(m_y[i],8)+";";
      s+=DoubleToString(m_ec_y[i],8)+";";
      s+=DoubleToString(m_ec_x1[i],8)+";";
      s+=DoubleToString(m_f1[i],8)+";";
      s+=DoubleToString(m_ec_x2[i],8)+";";
      s+=DoubleToString(m_f2[i],8)+";";
      s+=DoubleToString(m_ec_x3[i],8)+";";
      s+=DoubleToString(m_f3[i],8)+";";
      s+="\r";
      FileWriteString(filehandle,s);
     }
   FileClose(filehandle);
  }
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   CECCalculator ec;
//--- model function data preparation
   ec.GenerateData(100,0.25,15.25,1.55,1.05,0.15,1.3);
//--- saving into the file
   ec.SaveData("ex1.csv");
//--- calculation of the eigen-coordinates
   ec.CalcEigenCoordinates();
//--- calculation of the coefficients
   ec.CalcEigenCoefficients();
//--- calculation of the parameters
   ec.CalculateParameters();
//--- calculation of the functions f1,f2,f3
   ec.CalculatePlotFunctions();
//--- saving the results into the file
   ec.SaveResults("ex1-results.csv");
  }

2.5. Résultats du calcul de la fonction modèle R(x)

Nous allons générer 100 valeurs de la fonction R(x) sur l'intervalle [0,25 ;15,25] comme données du modèle.

Fig. 7. Fonction du modèle utilisée pour les calculs

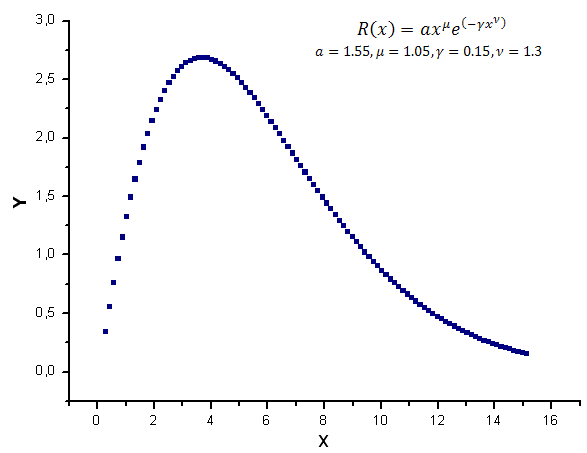
Fig. 7. Fonction du modèle utilisée pour les calculs

Ces données permettent de tracer la fonction Y(x) et son développement dans les fonctions X1(x), X2(x) and X3(x).

La figure 8 montre la fonction Y(x) et ses « coordonnées propres » X1(x), X2(x) and X3(x).

Fig. 8. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x) et X3(x)

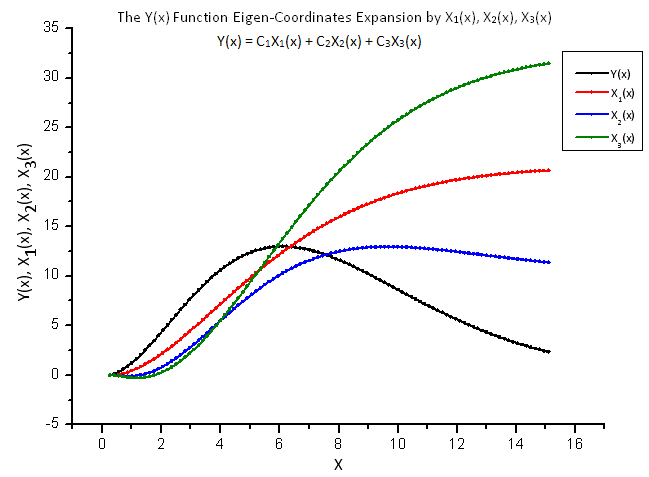
Fig. 8. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x) et X3(x)

Notez le caractère lisse de ces fonctions résultant de la nature intégrale des opérateurs X1(x), X2(x) and X3(x).

Après le calcul des fonctions Y(x), X1(x), X2(x) and X3(x), la matrice de corrélation est construite, puis les équations des coefficients C1, C2 and C3 sont résolues et les paramètres de la fonction R(x) sont calculés sur la base des valeurs obtenues :

2012.06.21 14:20:28 ec_example1 (EURUSD,H1) gamma=0.2769402213886906
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) nu=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) mu=1.328595266178149
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) a=1.637687667818532
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C1=1.772838639779728
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C2=1.126643424450548
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) C3=-1.496853120395737
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 1  221.03637620 148.53278281 305.48547011 101.93843241
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 2  148.53278281 101.63995012 202.85142688 74.19784681
2012.06.21 14:20:28 ec_example1 (EURUSD,H1) 3  305.48547011 202.85142688 429.09345292 127.82779760

Nous allons maintenant vérifier la linéarité de l'expansion calculée. Pour ce faire, nous devons calculer 3 fonctions :

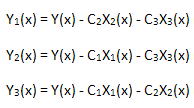
dont chacune est projetée sur sa base des coordonnées propres X1(x), X2(x) and X3(x):

Fig. 9. Représentation de la fonction Y1(x) dans la base X1(x)

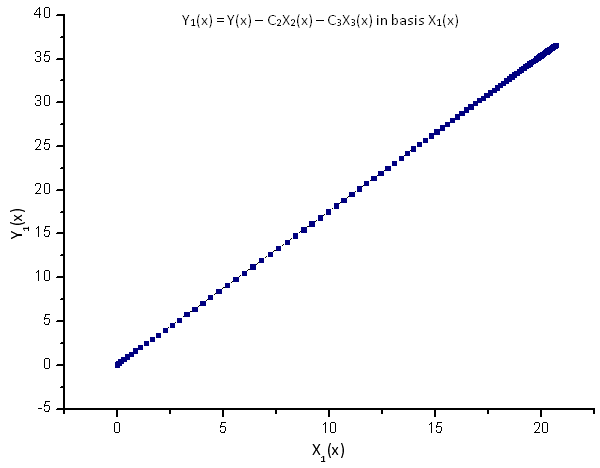
Fig. 9. Représentation de la fonction Y1(x) dans la base X1(x)

Fig. 10. Représentation de la fonction Y2(x) dans la base X2(x)

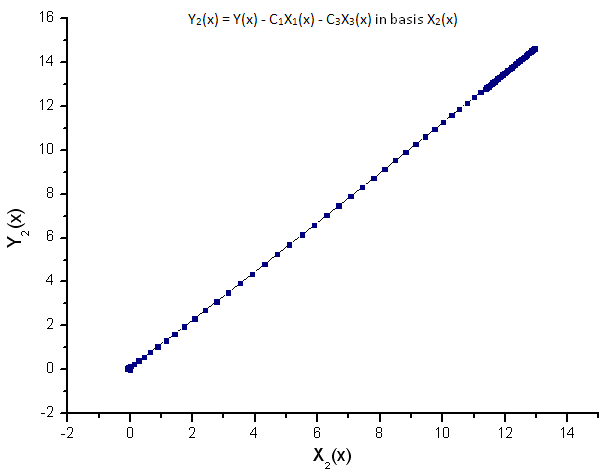
Fig. 10. Représentation de la fonction Y2(x) dans la base X2(x)

Fig. 11. Représentation de la fonction Y3(x) dans la base X3(x)

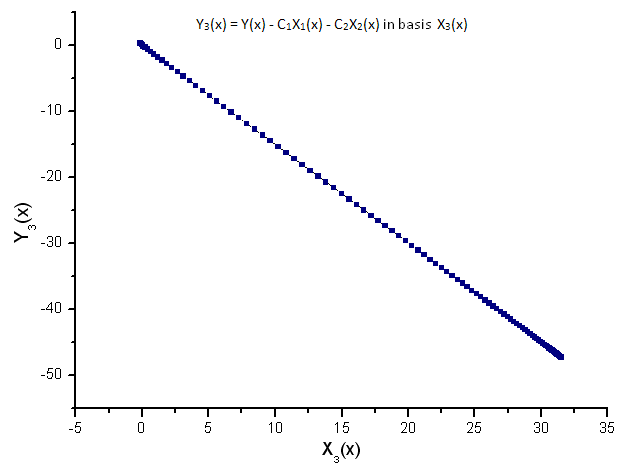
Fig. 11. Représentation de la fonction Y3(x) dans la base X3(x)

La dépendance linéaire des fonctions tracées suggère que la série de données de la figure 7 correspond strictement à la fonction R(x).

Toute autre fonction (même de forme similaire) représentée dans les coordonnées propres R(x) n'aura plus une forme linéaire. Ce fait nous permet d'identifier des fonctions.

La précision du calcul des valeurs numériques des paramètres de la fonction du modèle peut être améliorée, si le nombre de points est augmenté à 10000 (tout en gardant le même intervalle) :

2012.06.21 14:22:18 ec_example1 (EURUSD,H1) gamma=0.1508739336762316
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) nu=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) mu=1.052364487161627
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) a=1.550281229466634
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C1=1.483135479113404
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C2=1.298316173744703
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) C3=-1.36630183435649
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 1  225.47846911 151.22066473 311.86134419 104.65062550
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 2  151.22066473 103.30005101 206.66297964 76.03285182
2012.06.21 14:22:18 ec_example1 (EURUSD,H1) 3  311.86134419 206.66297964 438.35625824 131.91955339

Dans ce cas, les paramètres de la fonction ont été calculés avec plus de précision.


2.6. Effet de bruit

Les données expérimentales réelles contiennent toujours du bruit.

Dans la méthode GenerateData() de la classe ECCCalculator, on remplace :

m_y[i]=R(m_x[i],a,mu,gamma,nu);

avec

m_y[i]=R(m_x[i],a,mu,gamma,nu)+0.25*MathRand()/32767.0;

l'ajout d'un bruit aléatoire, soit environ 10 % de la valeur maximale de la fonction.

Le résultat du script EC_Example1-noise.mq5 est le suivant :

2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) gamma=0.4013079343855266
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) nu=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) mu=1.403541951457922
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) a=2.017238416806171
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C1=1.707774107235756
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C2=0.9915044018913447
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) C3=-1.391618023109698
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 1  254.45082565 185.19087989 354.25574000 125.17343164
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 2  185.19087989 136.81028987 254.92996885 97.14705491
2012.06.21 14:24:30 EC_Example1-noise (EURUSD,H1) 3  354.25574000 254.92996885 501.76021715 159.49440494

Le graphique de la fonction du modèle avec un bruit aléatoire est illustré à la Fig. 12.

Fig. 12. Fonction modèle avec bruit utilisée pour les calculs

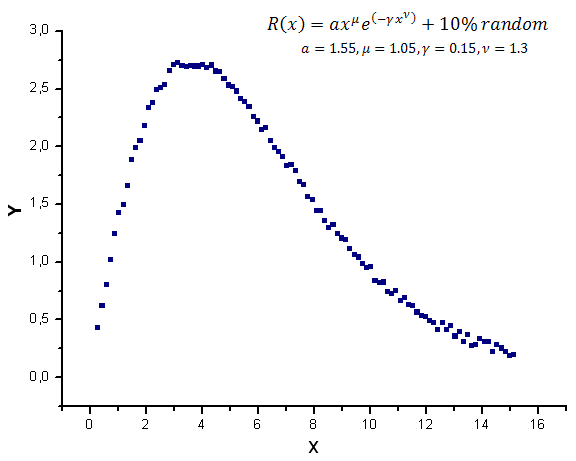
Fig. 12. Fonction de modèle avec bruit utilisée pour les calculs

Fig. 13. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x) et X3(x)

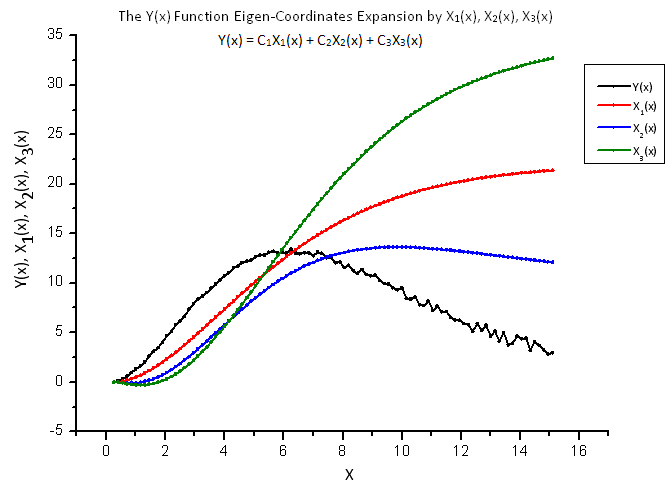
Fig. 13. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x) et X3(x)

Les fonctions X1(x), X2(x) and X3(x) servant de « coordonnées propres » semblent toujours lisses, mais le Y(x) tracé car leur combinaison linéaire semble être différent (Fig. 13).

Fig. 14. Représentation de la fonction Y1(x) dans la base X1(x)

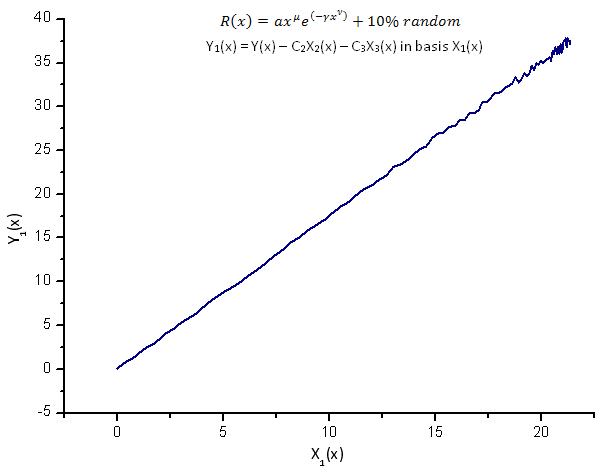
Fig. 14. Représentation de la fonction Y1(x) dans la base X1(x)

Fig. 15. Représentation de la fonction Y2(x) dans la base X2(x)

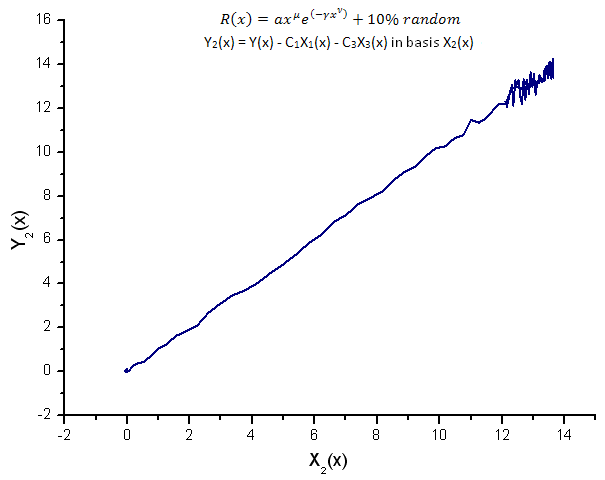
Fig. 15. Représentation de la fonction Y2(x) dans la base X2(x)

Fig. 16. Représentation de la fonction Y3(x) dans la base X3(x)

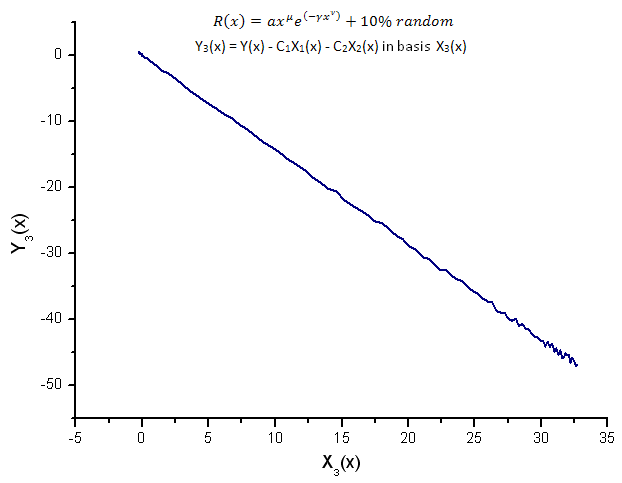
Fig. 16. Représentation de la fonction Y3(x) dans la base X3(x)

La représentation des fonctions Y1(x),Y2(x) and Y3(x) dans la base des coordonnées propres (Figures 8-10) a toujours une forme linéaire mais on peut noter des fluctuations autour de la ligne droite dues à la présence de bruit. Il est plus prononcé en ce qui concerne les grands X où le signal/bruit devient minimal.

Ici, les composantes du bruit se trouvent de part et d'autre de la ligne droite et, dans ce cas, il est donc pratique d'utiliser l'expansion intégrale des coordonnées propres (section 2.2).

 

3. Distributions de probabilité non extensives

La généralisation de la mécanique statistique aboutit aux distributions [2, 22] :

où , .

La distribution q-gaussienne est un cas particulier de la fonction P2(x).


3.1. L'expansion des coordonnées propres de la fonction P1(x)

Nous différencions P1(x):

L'équation différentielle qui en résulte est la suivante :

Intégrer sur l'intervalle [xm,x]:

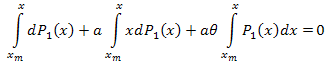
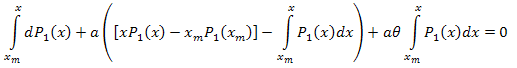
Ainsi :

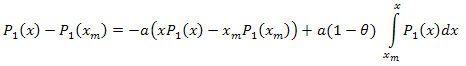
Le développement des coordonnées propres est le suivant :

où :

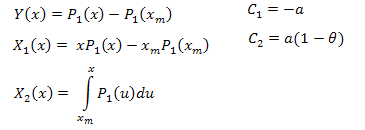
Les fonctions de calcul sont présentées ci-dessous (EC_Example2.mq5) :

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
//--- Y=P(x)-P(xm)
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
//--- X1=x*P(x)-xm*P(xm)
   for(int i=0; i<m_size; i++) x1[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
//--- X2=Integrate(P1(x)) 
   for(int i=0; i<m_size; i++) x2[i]=Integrate(m_x,m_y,i);
  }

Cette fois, la taille de la matrice de corrélation est de 2x3 ; les valeurs des paramètres a et thêta de la fonction P1(x) sont déterminées en fonction des coefficients С1 et C2. La valeur numérique du paramètre B peut être obtenue à partir de l'exigence de normalisation.

Voici le résultat du calcul de la fonction modèle P1(x,1,0.5,2) sur l'intervalle x [0,10] ; le nombre de points utilisés est de 1000 :

2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) theta=1.986651299600245
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) a=0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C1=-0.5056083906174813
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) C2=-0.4988591756915261
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 1  0.15420524 0.48808959 -0.32145543
2012.06.21 14:26:02 EC_Example2 (EURUSD,H1) 2  0.48808959 1.79668322 -1.14307410
La fonction P1(x) et son expansion des coordonnées propres sont illustrées dans les figures 17-20.

Fig. 17. Fonction modèle P1(x, 1, 0,5, 2) utilisée pour les calculs, 1000 points

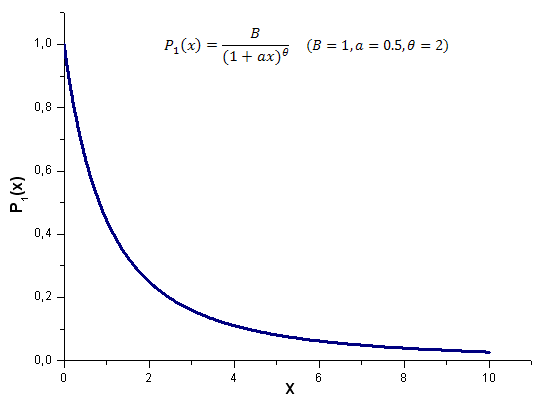
Fig. 17. Fonction modèle P1(x, 1, 0,5, 2) utilisée pour les calculs, 1000 points

Fig. 18. Forme générale de la fonction Y(x) et des coordonnées propres X1(x) et X2(x)

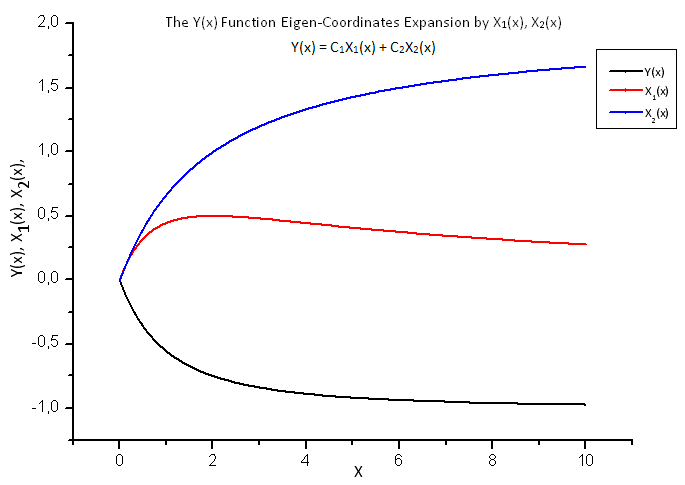
Fig. 18. Forme générale de la fonction Y(x) et des coordonnées propres X1(x) et X2(x)

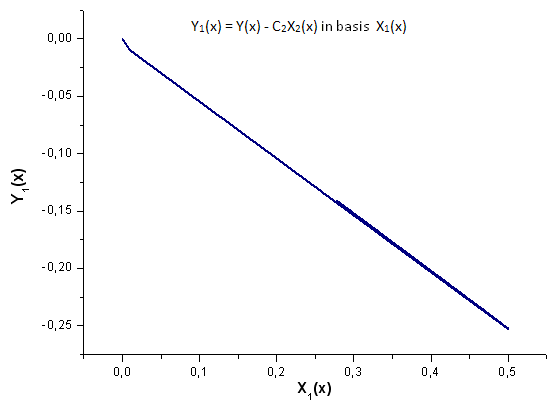
Fig. 19. Représentation de la fonction Y1(x) dans la base X1(x)

Fig. 19. Représentation de la fonction Y1(x) dans la base X1(x)

Fig. 20. Représentation de la fonction Y2(x) dans la base X2(x)

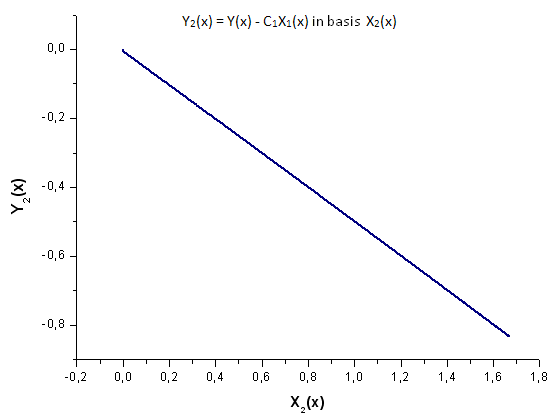
20. Représentation de la fonction Y2(x) dans la base X2(x)

Observez attentivement la Fig. 19. Il y a une légère distorsion de la dépendance linéaire au tout début et dans le deuxième tiers du graphique.

Ceci est lié aux particularités de l'expansion calculée - X1(x) n'est pas de nature intégrale.


3.2. L'expansion des coordonnées propres de la fonction P2(x

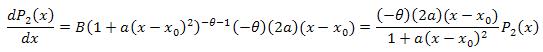
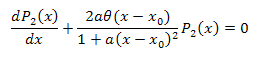
L'équation différentielle :

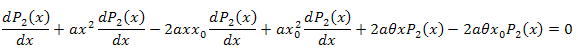
Nous intégrons par rapport à x sur l'intervalle [xm,x] :

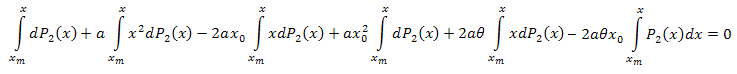
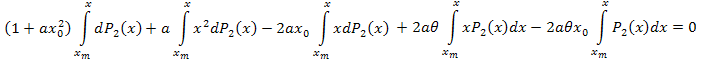
En intégrant par parties, on a :

Simplifier :

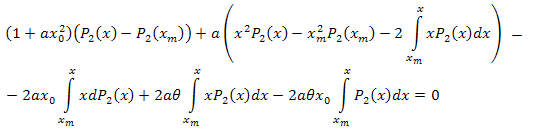
En suivant les manipulations algébriques, on obtient :

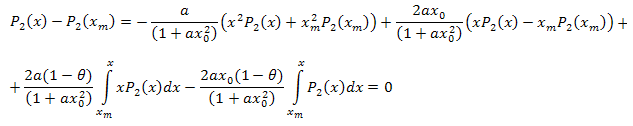
Ainsi, l'expansion résultante est la suivante :

où :

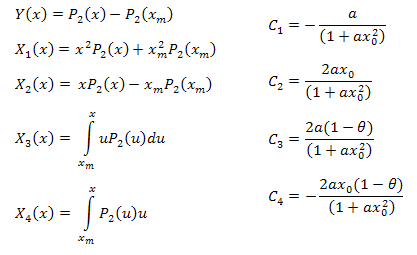
Les paramètres de la fonction peuvent être calculés à l'aide des formules ci-dessous :

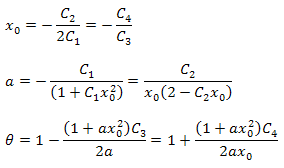
Il convient de noter qu'il existe une relation supplémentaire entre les paramètres dans l'expansion résultante. Ce fait peut être utilisé pour vérifier l'exactitude de la fonction sélectionnée pour l'analyse. Ces relations sont toujours vraies pour les données correspondant strictement à la fonction P2(x).

La valeur numérique du paramètre B peut être obtenue à partir de l'exigence de normalisation.

Les fonctions de calcul des coordonnées propres sont les suivantes (EC_Example3.mq5) :

//+------------------------------------------------------------------+
//| CalcY                                                            |
//+------------------------------------------------------------------+
void CECCalculator::CalcY(double &y[])
  {
   if(m_size==0) return;
   ArrayResize(y,m_size);
   for(int i=0; i<m_size; i++) y[i]=m_y[i]-m_y[0];
  };
//+------------------------------------------------------------------+
//| CalcX1                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX1(double &x1[])
  {
   if(m_size==0) return;
   ArrayResize(x1,m_size);
   //--- X1=(x^2)*P2(x)+(xm)^2*P2(xm)
   for(int i=0; i<m_size; i++) x1[i]=(m_x[i]*m_x[i])*m_y[i]+(m_x[0]*m_x[0])*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX2                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX2(double &x2[])
  {
   if(m_size==0) return;
   ArrayResize(x2,m_size);
   //--- X2=(x)*P2(x)-(xm)*P2(xm)
   for(int i=0; i<m_size; i++) x2[i]=m_x[i]*m_y[i]-m_x[0]*m_y[0];
  }
//+------------------------------------------------------------------+
//| CalcX3                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX3(double &x3[])
  {
   if(m_size==0) return;
   double tmp[];
   ArrayResize(tmp,m_size);
   for(int i=0; i<m_size; i++) tmp[i]=m_x[i]*m_y[i];
   //--- X3=Integrate(X*P2(x)) 
   ArrayResize(x3,m_size);
   for(int i=0; i<m_size; i++) x3[i]=Integrate(m_x,tmp,i);  
  }
//+------------------------------------------------------------------+
//| CalcX4                                                           |
//+------------------------------------------------------------------+
void CECCalculator::CalcX4(double &x4[])
  {
   if(m_size==0) return;
   //--- X4=Integrate(P2(x))
   ArrayResize(x4,m_size);
   for(int i=0; i<m_size; i++) x4[i]=Integrate(m_x,m_y,i);
  }

Voici le résultat du calcul de la fonction modèle P2(x) (B=1, a=0.5, theta=2, x0=1) ; le nombre de points utilisés est de 1000 :

2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: theta=2.260782711057654
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: theta=2.076195813531546
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: a=0.4557937139014854
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: a=0.4977821155774935
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2: x0=1.043759816231049
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1: x0=0.8909465007003451
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C1=-0.3567992171618368
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C2=0.6357780279659221
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C3=-0.7679716475618039
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) C4=0.8015779457297644
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 1  1.11765877 0.60684314 1.34789126 1.28971267 -0.01429928
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 2  0.60684314 0.37995888 0.55974145 0.58899739 0.06731011
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 3  1.34789126 0.55974145 3.00225771 2.54531927 -0.39043224
2012.06.21 14:27:47 EC_Example3 (EURUSD,H1) 4  1.28971267 0.58899739 2.54531927 2.20595917 -0.27218168
La fonction P2(x) et son expansion des coordonnées propres sont illustrées aux Figures 21-26.

Fig. 21. Fonction modèle P2(x,1,0,5,2,1) utilisée pour les calculs, 100 points

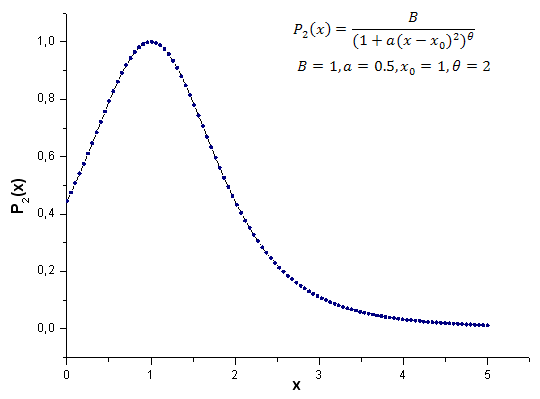
Fig. 21. Fonction de modèle P2(x,1,0,5,2,1) utilisée pour les calculs, 100 points

Fig. 22. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x), X3(x) et X4(x)

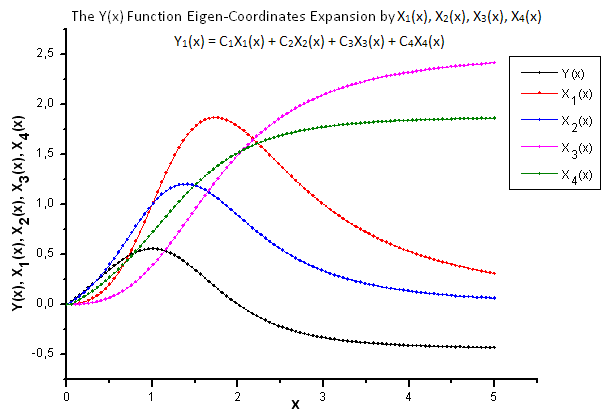
Fig. 22. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x), X3(x) et X4(x)

Fig. 23. Représentation de la fonction Y1(x) dans la base X1(x)

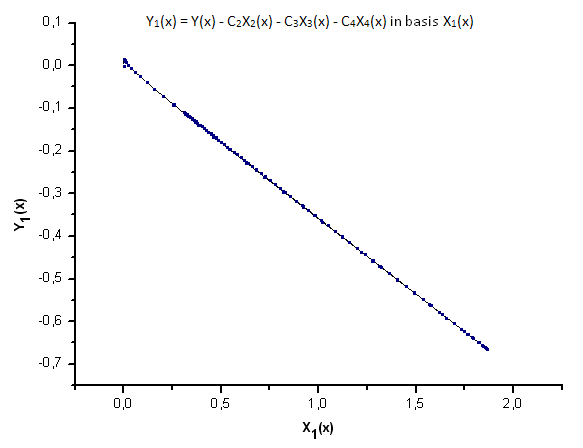
Fig. 23. Représentation de la fonction Y1(x) dans la base X1(x)

Fig. 24. Représentation de la fonction Y2(x) dans la base X2(x)

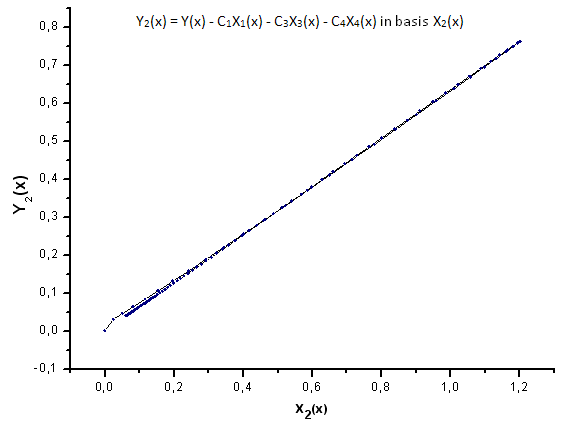
Fig. 24. Représentation de la fonction Y2(x) dans la base X2(x)

Fig. 25. Représentation de la fonction Y3(x) dans la base X3(x)

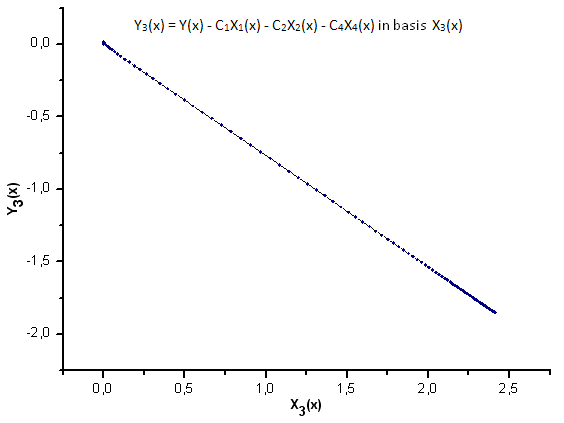
Fig. 25. Représentation de la fonction Y3(x) dans la base X3(x)

Fig. 26. Représentation de la fonction Y4(x) dans la base X4(x)

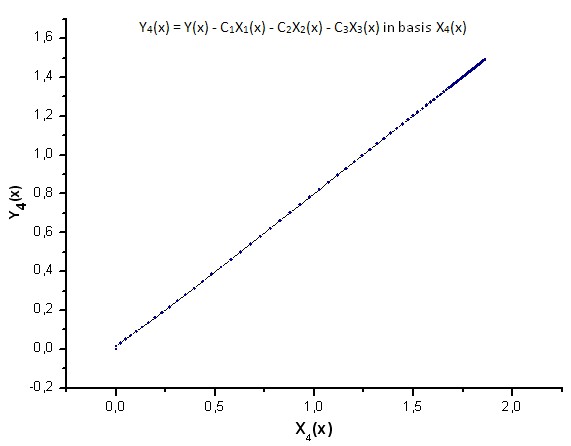
Fig. 26. Représentation de la fonction Y4(x) dans la base X4(x)


4. Si ça ressemble à un chat... Ce n'est peut-être pas un chat

La famille des distributions q-gaussiennes est au cœur même de la mécanique statistique non extensive et il était donc naturel de s'attendre à ce qu'elle apparaisse dans le théorème central limite généralisé. Les considérations entropiques ont été le principal argument en sa faveur [26].

Cependant, l'article [18, presentation] a montré que les distributions, telles que la q-gaussienne, ne sont pas universelles, mettant ainsi en doute leur rôle particulier en tant que distributions limites.

Par exemple, la fonction (solution analytique à l'un des problèmes) :

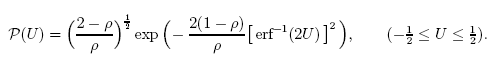
peut être décrit très précisément en utilisant la distribution q-gaussienne.

Fig. 27. Un exemple tiré de l'article « Une note sur les q-gaussiens et les non-gaussiens en mécanique statistique »

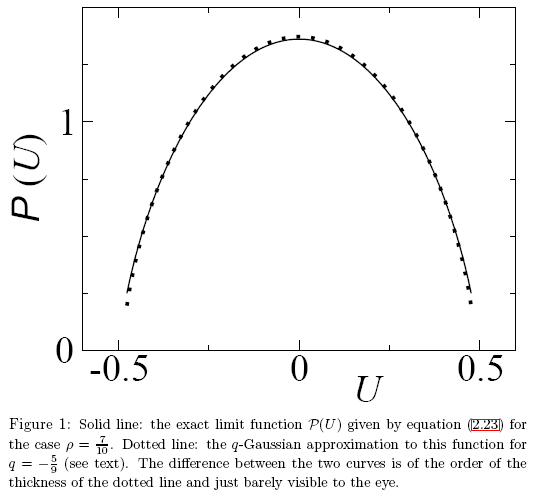
Fig. 27. Un exemple tiré de l'article « Une note sur les q-gaussiens et les non-gaussiens en mécanique statistique »

Dans ce cas, des fonctions analytiquement différentes ont des valeurs numériques similaires et les différences sont donc à peine visibles à l'œil nu. Une méthode précise d'identification des fonctions est nécessaire. Ce problème peut être résolu de manière satisfaisante en utilisant la méthode des coordonnées propres.

Examinons un exemple d'expansion des coordonnées propres de la fonction P(U) et montrons ce qui la différencie exactement de la q-gaussienne. Les fonctions semblent très similaires à celles de l'œil (Fig. 27).

Nous générons un signal (100 valeurs de la fonction P(U)) et le « projetons » sur le système des coordonnées propres de la fonction P2(x) tracé dans la section 3.2.

Le script Hilhorst-Schehr-problem.mq5 calcule la fonction P(U) et construit des séries de données qui sont enregistrées dans le fichier MQL5\Files\test-data.csv. Ces données sont analysées par EC_Example3_Test.mq5.

Fig. 28. Fonction modèle P(U), 100 points

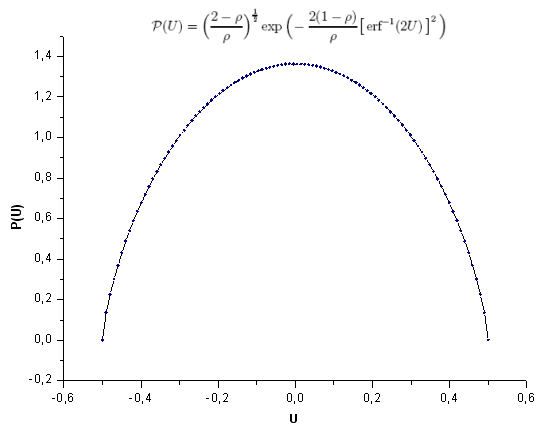
Fig. 28. Fonction modèle P(U), 100 points

Fig. 29. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x), X3(x) et X4(x)

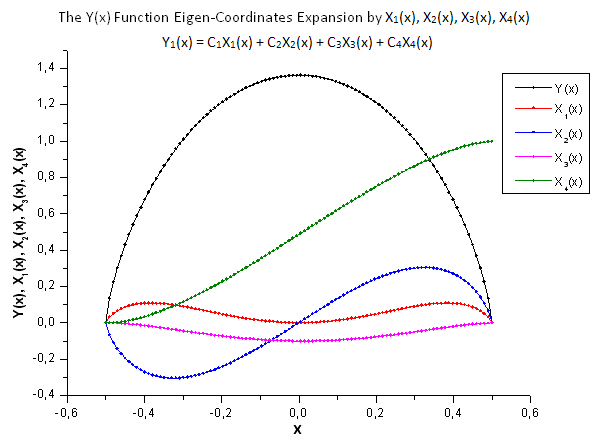
Fig. 29. Forme générale de la fonction Y(x) et des coordonnées propres X1(x), X2(x), X3(x) et X4(x)

Fig. 30. Représentation de la fonction Y1(x) dans la base X1(x)

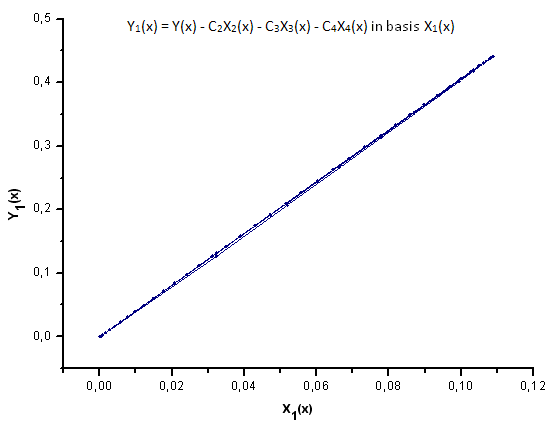
Fig. 30. Représentation de la fonction Y1(x) dans la base X1(x)

Fig. 31. Représentation de la fonction Y2(x) dans la base X2(x)

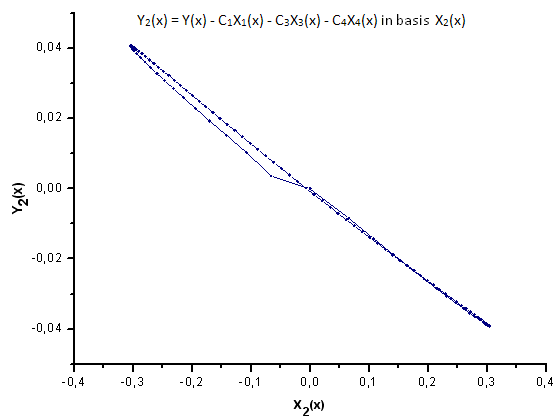
Fig. 31. Représentation de la fonction Y2(x) dans la base X2(x)

Fig. 32. Représentation de la fonction Y3(x) dans la base X3(x)

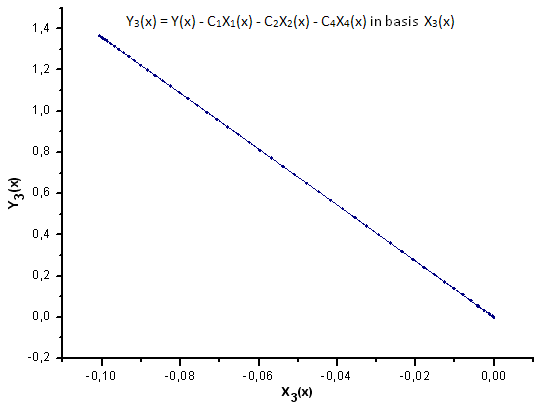
Fig. 32. Représentation de la fonction Y3(x) dans la base X3(x)

Fig. 33. Représentation de la fonction Y4(x) dans la base X4(x)

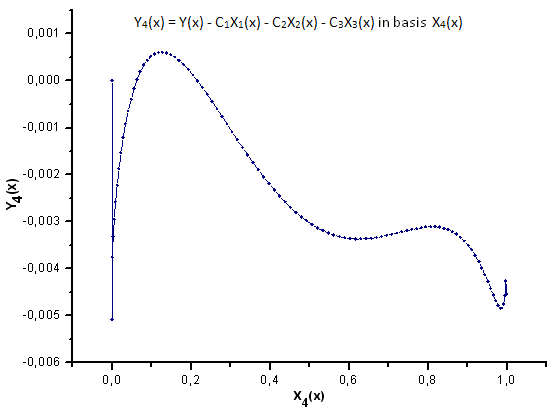
Fig. 33. Représentation de la fonction Y4(x) dans la base X4(x)


Comme le suggèrent les Fig. 30-33, les fonctions P2(x) et P(U) sont très similaires en termes de coordonnées X1(x), X2(x) et X3(x) - on peut observer une bonne dépendance linéaire entre Xi(x) et Yi(x). Une différence significative peut être observée dans la composante X4(x) (Fig. 33).

L'absence de dépendance linéaire pour la composante X4(x) prouve que l'ensemble de données généré par P(U), bien qu'apparaissant similaire à la distribution q-gaussienne, n'est en fait pas la q-gaussienne.

On peut porter un regard différent sur les fonctions (figures 34-37) en traçant ensemble Xi(x) et Yi(x).

Fig. 34. Forme générale des fonctions X1(x) et Y1(x)

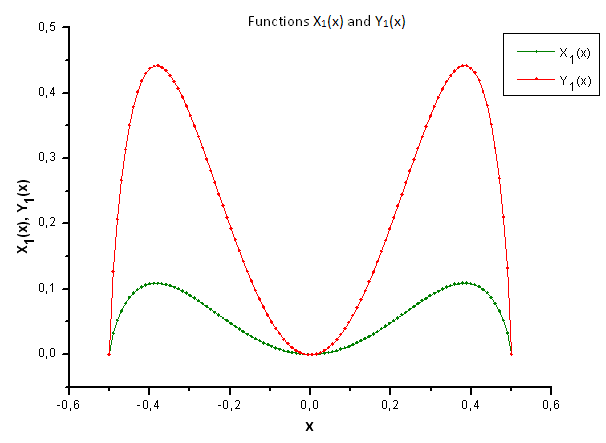
Fig. 34. Forme générale des fonctions X1(x) et Y1(x)

Fig. 35. Forme générale des fonctions X2(x) et Y2(x)

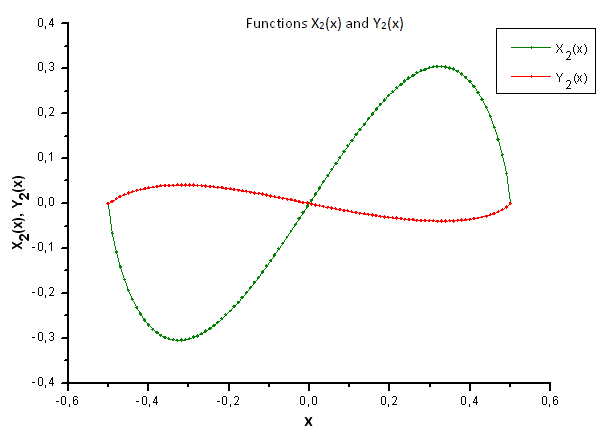
Fig. 35. Forme générale des fonctions X2(x) et Y2(x)

Fig. 36. Forme générale des fonctions X3(x) et Y3(x)

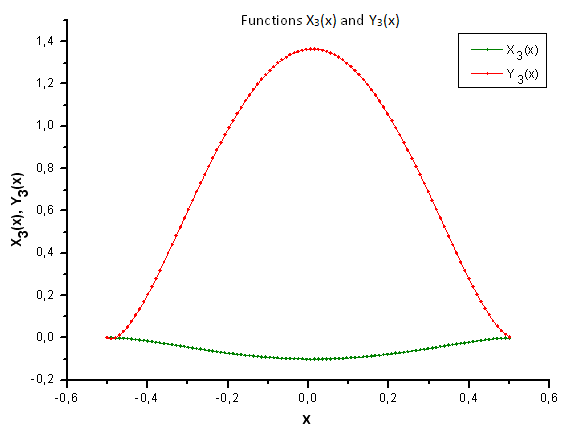
Fig. 36. Forme générale des fonctions X3(x) et Y3(x)

Fig. 37. Forme générale des fonctions X4(x) et Y4(x)

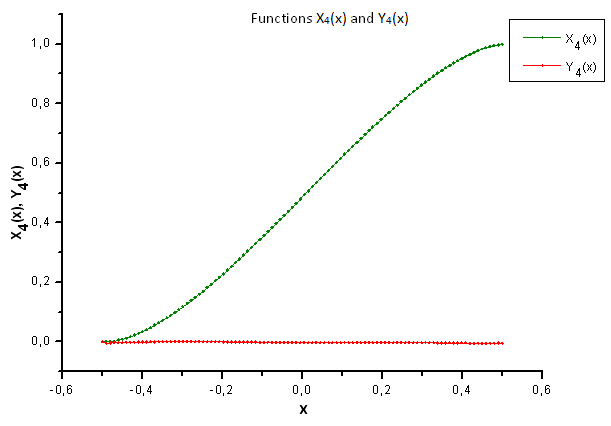
Fig. 37. Forme générale des fonctions X4(x) et Y4(x)

Comme le suggère la figure 37, la différence structurelle de la composante X4(x) est devenue apparente lorsque l'on projette les données générées par la fonction P(U) sur les coordonnées propres de la fonction P2(x). Ainsi, nous pouvons affirmer avec certitude que les données expérimentales ne correspondent pas à la fonction P2(x).

Le calcul présenté ci-dessous (EC_Example3_test) va dans ce sens :

2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: theta=1.034054797050629
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: theta=-0.6736146397139184
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: a=199.3574440289263
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: a=-4.052181367572913
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2: x0=-0.0003278538628371299
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1: x0=0.0161122975924721
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C1=4.056448634458822
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C2=-0.1307174151339552
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C3=-13.57786363975563
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) C4=-0.004451555043369697
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 1  0.00465975 0.00000000 -0.00218260 0.02762761 0.04841405
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 2  0.00000000 0.04841405 -0.00048835 0.06788438 0.00000001
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 3  -0.00218260 -0.00048835 0.00436149 -0.02811625 -0.06788437
2012.06.21 14:29:35 EC_Example3_test (EURUSD,H1) 4  0.02762761 0.06788438 -0.02811625 0.35379820 0.48337994

Cela a également altéré les relations entre les paramètres.


Conclusion

La méthode des coordonnées propres est un outil unique pour l'analyse des propriétés structurelles des relations fonctionnelles permettant de simplifier considérablement l'analyse et l'interprétation des données.

Le concept derrière cette méthode est d'utiliser des ensembles de données expérimentales {xi,yi} pour construire de nouvelles fonctions correspondant au modèle proposé. La forme des développements d'opérateurs est déterminée par la structure de l'équation différentielle qui est satisfaite par la fonction servant de « candida t» à la description des données. Si la fonction est native, les développements de la fonction calculés à partir des données {xi,yi}, prendront, dans la base des coordonnées propres, une forme linéaire. Les déviations de la linéarité dans la base des coordonnées propres de la « fonction candidate » suggèrent que les données {xi,yi} n'ont pas pu être générées par la fonction donnée et que le modèle construit n'est pas approprié.

Dans certains cas compliqués, la fonction candidate et la fonction native peuvent sembler similaires dans la mesure où une grande partie des expansions calculées s'avère être linéaire. Néanmoins, la méthode des coordonnées propres nous permet d'identifier la différence entre ces fonctions qui fait connaître sa présence par une linéarité altérée du développement - l'exemple de Hilhorst et Schehr a servi d'illustration de la différence qui devient apparente dans le dernier membre du développement lors de la projection sur X4(x).

Cette information peut également être utile lorsqu'on traite une équation différentielle (section 3.2) qui est satisfaite par la fonction P2(x - le membre en question correspond à la partie linéaire par rapport à P2(x). Elle peut ne pas être aussi intéressante dans le cas d'une description phénoménologique des données expérimentales (« nous cherchons une solution sous la forme de la q-Gaussienne »). Cependant, si le modèle est basé sur des équations différentielles (Fig. 3), le rôle de chacun des mécanismes pris en considération dans les modèles de processus physiques peut être mieux compris.


Références

  1. C. Tsallis, « de Généralisation possible de Boltzmann-Gibbs Statistiques », Journal of Physics statistique, Vol. 52, nos. 1/2, 1988.
  2. C. Tsallis, « Statistiques non extensives : Preuves et liens théoriques, expérimentaux et informatiques ». Journal brésilien de physique, (1999) vol. 29. p.1.
  3. C. Tsallis, « Quelques commentaires sur la mécanique statistique de Boltzmann-Gibbs » , Chaos, Solitons & Fractals Volume 6, 1995, pp. 539-559.
  4. Europhysics News « Numéro spécial : Mécanique statistique non extensive : Nouvelles tendances, nouvelles perspectives », Vol. 36 No. 6 (novembre-décembre 2005).
  5. M. Gell-Mann, C. Tsallis,« Entropie non étendue : Applications interdisciplinaires », Oxford University Press, 15.04.2004, 422 p.
  6. Constantino Tsallis, le site officiel Mécanique statistique et thermodynamique non extensive.
  7. Chumak, O.V. » Entropie et fractales dans l'analyse des données », М.-Izhevsk : RDC « Dynamique Régulière et Chaotique », Institut de Recherche Informatique, 2011. - 164 p.
  8. Qiuping A. Wang, « Statistiques incomplètes et généralisations non extensives de la mécanique statistique », Chaos, solitons et fractales, 12(2001)1431-1437.
  9. Qiuping A. Wang, « Généralisation extensive de la mécanique statistique basée sur la théorie de l'information incomplète », Entropy, 5(2003).
  10. Lisa Borland, « Mémoire à longue portée et non-extensivité sur les marchés financiers », Europhysics News 36, 228-231 (2005)
  11. T. S. Biró, R. Rosenfeld, « Origine microscopique des distributions non gaussiennes des rendements financiers », Physica A : Mécanique statistique et ses applications, vol. 387, n° 7 (1 mars 2008) , p. 1603-1612 (preprint).
  12. S. M. D. Queiros, C. Anteneodo, C. Tsallis, « Distributions de la loi du pouvoir en économie : Une approche statistique non extensive », Actes de la SPIE (2005) Volume : Editeur 5848, Editeur : 151-164, (preprint)
  13. R Hanel, S Thurner, « Dérivation des distributions puissance-loi dans le cadre de la mécanique statistique standard », Physica A : Mécanique statistique et ses applications (2005), Volume : 351, numéro : 2-4, Editeur : Elsevier, Pages : 260-268. (preprint)
  14. A K Rajagopal, Sumiyoshi Abe, « Fondements statistico-mécaniques des distributions de puissance- loi », Physica D : Phénomènes non linéaires (2003), Volume : 193, numéro : 1-4, Pages : 19 (preprint)
  15. T. Kaizoji, « Un modèle de marchés financiers à agents interactifs du point de vue de la mécanique statistique non extensive », Physica A : Mécanique statistique et ses applications, vol. 370, N. 1 (1er octobre 2006) , p. 109-113. (preprint)
  16. V. Gontis, J. Ruseckas, A. Kononovičius, « Un modèle stochastique de mémoire à long terme du rendement des marchés financiers », Physica A : Mécanique statistique et ses applications 389 (2010) 100-106. (preprint)
  17. H.E. Roman, M. Porto, « Queues de puissance auto-générées dans les distributions de probabilités », Physical Review E - Statistical, Nonlinear and Soft Matter Physics (2001), Volume: 63, numéro : 3 Pt 2, Pages : 036-128.
  18. H. J. Hilhorst, G. Schehr, « Note sur l'utilisation des q-gaussiens et des non-gaussiens en mécanique statistique » (2007, preprint, présentation).
  19. D. J. Hudson, « Lectures sur les statistiques et probabilités élémentaires », CERN-63-29, Geneva : CERN, 1963. - 101 p.
  20. D. J. Hudson, « Conférences sur les statistiques II : Théorie du maximum de vraisemblance et des moindres carrés », CERN-64-18. - Genève : CERN, 1964. - 115 p.
  21. R. R. Nigmatullin, « Coordonnées propres : Nouvelle méthode d'identification des fonctions analytiques dans les mesures expérimentales », Applied Magnetic Resonance Volume 14, Number 4 (1998), 601-633.
  22. R.R. Nigmatullin, « Reconnaissance de distributions statistiques non extensives par la méthode des coordonnées propres », Physica A : La mécanique statistique et ses applications Volume 285, numéros 3-4, 1er octobre 2000, pp. 547-565.
  23. C. Antonini « q-Gaussiens en finance » (2010).
  24. C. Antonini, « L'utilisation de la distribution q-gaussienne en finance » (2011).
  25. L. G. Moyano, C. Tsallis, M. Gell-Mann, « Indications numériques d'un théorème limite central généralisé de q », Europhysics Letters 73, 813-819, 2006, (preprint).
  26. T. Dauxois, « Distributions non gaussiennes sous surveillance », J. Stat. Méca. (2007) N08001. (preprint)

Annexe. Analyse des rendements quotidiens du SP500 à l'aide de la méthode Q-Gaussienne

Considérons l'exemple classique (Fig. 4) d'une approche q-gaussienne réussie des rendements quotidiens SP500 (fonction P2(x)).

Nous avons utilisé les données quotidiennes de : http://wikiposit.org/w?filter=Finance/Futures/Indices/S__and__P%20500/

Fig. 38. Cours de clôture du SP500 (quotidien)

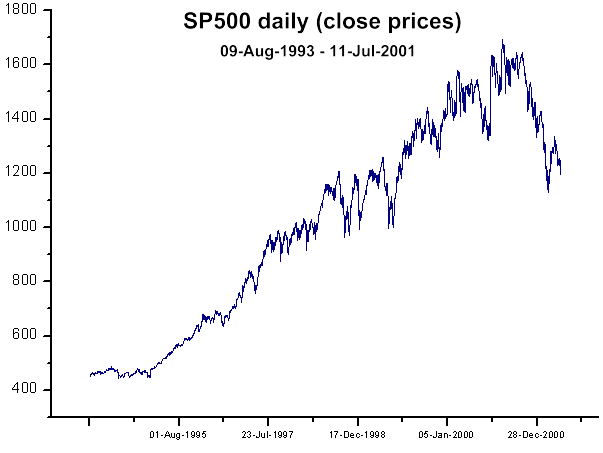
Fig. 38. Cours de clôture du SP500 (quotidien)

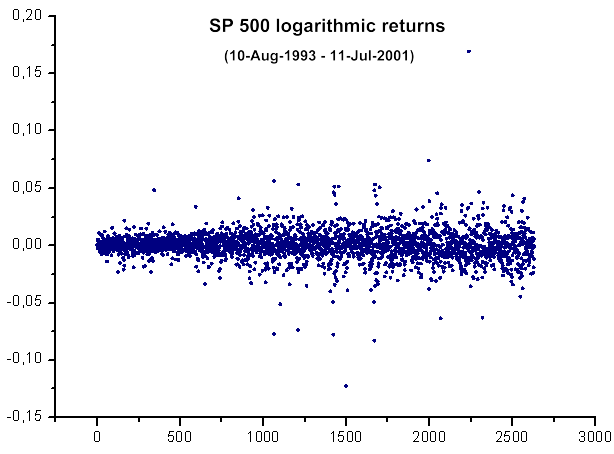
Fig. 39. Rendements logarithmiques SP500

Fig. 39. Rendements logarithmiques SP500

Fig. 40. Distribution des rendements logarithmiques SP500

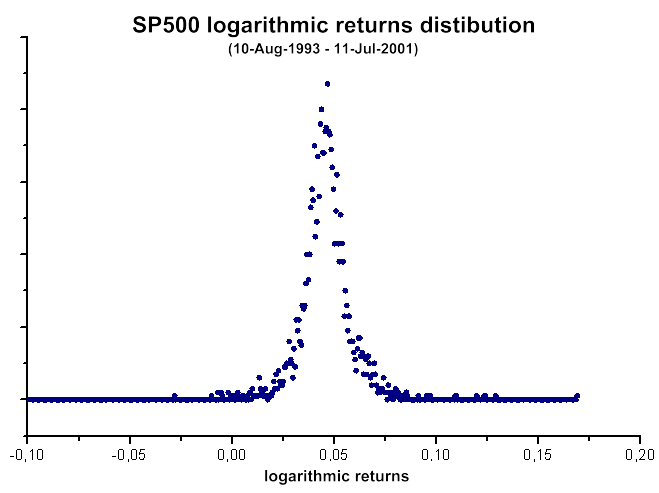
40. Distribution des rendements logarithmiques SP500

Fig. 41. La fonction Y1(x) dans la base X1(x)

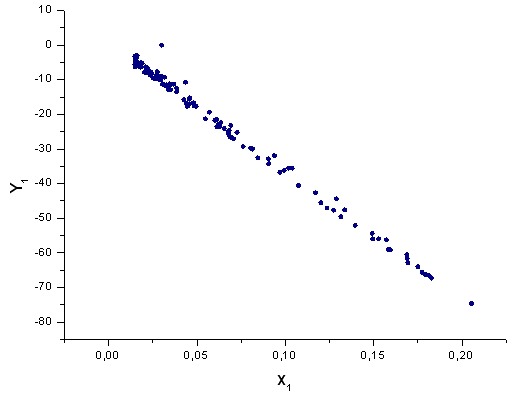
Fig. 41. La fonction Y1(x) dans la base X1(x)

Fig. 42. La fonction Y2(x) dans la base X2(x)

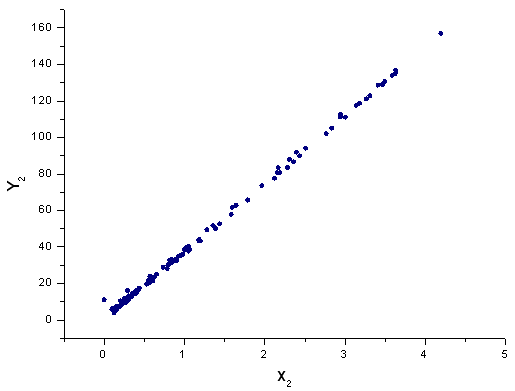
Fig. 42. La fonction Y2(x) dans la base X2(x)

Fig. 43. La fonction Y3(x) dans la base X3(x)

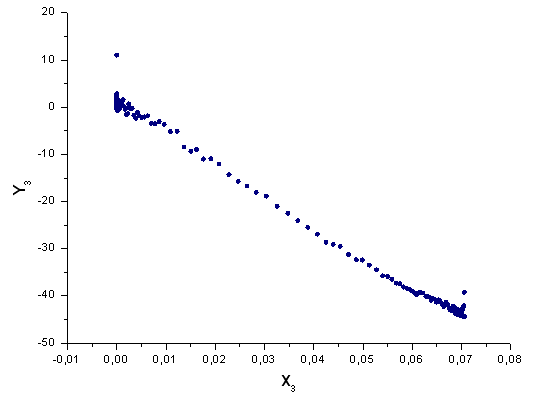
Fig. 43. La fonction Y3(x) dans la base X3(x)

Fig. 44. La fonction Y4(x) dans la base X4(x)

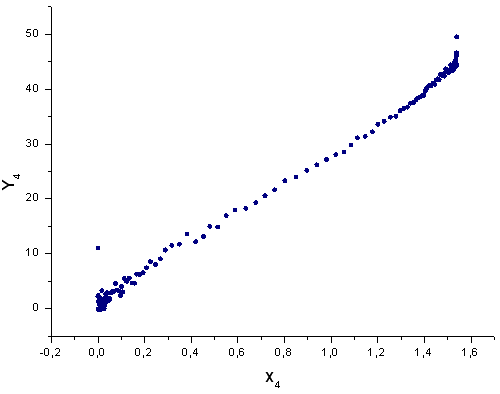
Fig. 44. La fonction Y4(x) dans la base X4(x)

Pour voir comment effectuer l'analyse dans votre terminal, le fichier SP500-data.csv doit être placé dans le dossier \Files\.

Après cela, vous devez lancer deux scripts :

  1. CalcDistr_SP500.mq5 (il calcule la distribution).
  2. q-gaussian-SP500.mq5 (analyse des coordonnées propres)
Les résultats sont :
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: theta=1.770125768485269
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: theta=1.864132228192338
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: a=2798.166930885822
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: a=8676.207867097581
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2: x0=0.04567518783335043
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1: x0=0.0512505923716428
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C1=-364.7131366394939
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C2=37.38352859698793
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C3=-630.3207508306047
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    C4=28.79001868944634
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    1  0.00177913 0.03169294 0.00089521 0.02099064 0.57597695
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    2  0.03169294 0.59791579 0.01177430 0.28437712 11.55900584
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    3  0.00089521 0.01177430 0.00193200 0.04269286 0.12501732
2012.06.29 20:01:19    q-gaussian-SP500 (EURUSD,D1)    4  0.02099064 0.28437712 0.04269286 0.94465120 3.26179090
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    checking distibution cnt=2632.0 n=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Min=-0.1229089015984444 Max=0.1690557338964631 range=0.2919646354949075 size=2632
2012.06.29 20:01:09    CalcDistr_SP500 (EURUSD,D1)    Total data=2633

La valeur estimée de q, obtenue par la méthode des coordonnées propres (q=1+1/thêta) : q~1,55

La valeur, rapportée dans le livre (Fig. 4) q~1.4.

Conclusion : De manière générale, on peut voir que ces données peuvent être décrites par une fonction q-gaussienne. Il explique l'interprétation réussie à l'aide du q-gaussien, rapportée dans le livre.


Traduit du russe par MetaQuotes Ltd.
Article original : https://www.mql5.com/ru/articles/412

Fichiers joints |
Télécharger ZIP
cmatrix.mqh (4.1 KB)
ec_example1.mq5 (13.89 KB)
ec_example1-noise.mq5 (13.97 KB)
ec_example2.mq5 (12 KB)
ec_example3.mq5 (14.94 KB)
hilhorst-schehr-problem.mq5 (4.03 KB)
ec_example3_test.mq5 (15.07 KB)
Avertissement: Tous les droits sur ces documents sont réservés par MetaQuotes Ltd. La copie ou la réimpression de ces documents, en tout ou en partie, est interdite.

Autres articles par cet auteur

Derniers commentaires | Aller à la discussion (1)
Bou Islam
Bou Islam | 22 sept. 2022 à 10:37
Good 
Introduction à la méthode de décomposition en modes empiriques Introduction à la méthode de décomposition en modes empiriques
Cet article a pour but de familiariser le lecteur avec la méthode de décomposition empirique des modes (EMD). C’est la partie fondamentale de la transformée de Hilbert-Huang et est destinée à l’analyse des données issues des processus non stationnaires et non linéaires. Cet article présente également une mise en œuvre logicielle possible de cette méthode ainsi qu’un bref examen de ses particularités et donne quelques exemples simples de son utilisation.
Nouveau système de publication d’articles sur MQL5.community Nouveau système de publication d’articles sur MQL5.community
Nous vous présentons un nouveau système de publication d’articles sur MQL5.community. Dans le nouveau système, nous avons essayé de rendre l'ensemble du processus de rédaction d'un article clair et confortable en le décomposant en plusieurs étapes. À chaque étape, nous vous donnerons des conseils et des recommandations utiles, une sorte de distillation de l’expérience de rédaction d’articles. Nous espérons que cet article contribuera à répondre à bon nombre de vos questions. Vous êtes invités à nous envoyer de nouveaux documents intéressants qui vous rendront populaire parmi les visiteurs de la MQL5.community.
ID MetaQuotes dans le terminal mobile MetaTrader ID MetaQuotes dans le terminal mobile MetaTrader
Les appareils Android et iOS nous offrent de nombreuses fonctionnalités que nous ne connaissons même pas. L'une de ces fonctionnalités est les notifications push qui nous permettent de recevoir des messages personnels, quel que soit notre numéro de téléphone ou notre opérateur de réseau mobile. Le terminal mobile MetaTrader peut déjà recevoir de tels messages directement de votre robot de trading. Vous ne devez connaître que l'ID MetaQuotes de votre appareil. Plus de 9 000 000 de terminaux mobiles l'ont déjà reçu.
Estimation de la densité de noyau de la fonction de densité de probabilité inconnue Estimation de la densité de noyau de la fonction de densité de probabilité inconnue
L'article traite de la création d'un programme permettant d'estimer la densité à noyau de la fonction de densité de probabilité inconnue. La méthode d'estimation de la densité du noyau a été choisie pour exécuter la tâche. L'article contient les codes sources de la mise en œuvre logicielle de la méthode, des exemples d'utilisation et des illustrations.