
Uma Introdução à Lógica Fuzzy
Introdução
A teoria matemática dos conjuntos difusos (fuzzy sets) e da lógica fuzzy, também conhecida como lógica nebulosa ou difusa, tiveram origem em 1965. Seu fundador foi o professor Lotfi Zadeh, da Universidade de Berkeley, que fez a primeira introdução de ambos os conceitos em seu artigo "Fuzzy Sets" no periódico Information and Control. Este instrumento matemático permitiu introduzir os conceitos difusos,que qualquer pessoa poderia usar, na ciência exata, tal como a matemática, lançando as bases para fundamentar novos métodos de resolução de problemas baseados nas técnicas de Soft computing. Todas estas inovações, quando utilizadas corretamente, podem facilitar muito o processo de resolução de problemas de classificação, a criação de sistemas especialistas, bem como a construção de redes neurais.
No entanto, a aplicação prática da lógica fuzzy não para por aí, na verdade, este instrumento matemático tornou-se predominantemente utilizado na teoria de controle e automação. Isto ainda pode ser ligada ao aparecimento de um novo conceito - modelo fuzzy. O modelo difuso (fuzzy) é um caso particular de um modelo matemático.
1. A Teoria por trás dos Conjuntos Fuzzy e da Lógica Fuzzy
De certa forma, a nova teoria de Lotfi Zadeh expandiu os limites da lógica matemática e da teoria dos conjuntos que são familiares a nós. A lógica matemática é capaz de operar apenas com dados estritamente formais, e os membros do objeto para um determinado conjunto é definido somente por dois conceitos, portanto, o termo "associação" tem um valor discreto que pode ter dois significados:
- "1" - se o objeto pertence a um conjunto;
- "0" - se o objeto não pertence a um conjunto.
Em sua teoria dos conjuntos fuzzy, Lotfi Zadeh passou do conceito distinto de "pertinência" e introduziu um novo termo - "grau de pertinência", ao passo que o termo "conjunto", utilizado anteriormente, foi substituído pelo "conjunto fuzzy".
1.1. Termos e definições Básicas
Definição 1. O conjunto fuzzy ![]() sobre o conjunto universal
sobre o conjunto universal ![]() é um conjunto de pares
é um conjunto de pares ![]() , onde
, onde ![]() é o grau de pertinência do elemento
é o grau de pertinência do elemento ![]() para os conjuntos fuzzy.
para os conjuntos fuzzy.
Definição 2. Grau de pertinência é um número dentro do intervalo [0, 1]. Quanto maior o grau de pertinência, maior será a correspondência do elemento de um conjunto universal às propriedades de um conjunto fuzzy. Assim, se o grau de pertinência é igual a 0, então, o elemento dado não corresponde ao conjunto, e, pelo contrário, se o grau é igual a 1, ele torna-se totalmente correspondente. Estes dois casos são extremos, e sem outras opções, eles seriam encaminhados a um conjunto regular. A presença de todas as outras opções é uma diferença fundamental de um conjunto fuzzy.
Definição 3. A função de pertinência é uma função que permite calcular o grau de pertinência de um elemento aleatório do conjunto universal para um conjunto fuzzy. Consequentemente, os domínios das funções de pertinência devem estar dentro do intervalo [0, 1]. Na maioria dos casos, a função de pertinência é uma função monótona contínua.
Definição 4. A variável linguística é uma variável cujos valores são palavras ou combinações de palavras em uma linguagem natural ou artificial. Os conjuntos fuzzy, em particular, são compostos de variáveis linguísticas. Ao definir um conjunto fuzzy, a quantidade e a natureza das variáveis fuzzy são subjetivas para cada tarefa individual.
Definição 5. O conjunto de termos é um conjunto de todos os valores possíveis, que uma variável linguística é capaz de receber.
Definição 6. O termo pode ser qualquer elemento de um conjunto de termos (term set). Na teoria dos conjuntos fuzzy um termo é formalizado por um conjunto difuso através da função de pertinência. A função de pertinência para cada termo é muito individual e muitas vezes única. Os métodos de construção dessas funções podem ser variados: direto, indireto e de frequências relativas. Estes são muitas vezes baseados em pontos específicos da função de pertinência e nas evidências empíricas de um especialista deste campo.
Exemplo:
Vamos definir uma variável linguística chamado "Idade" (Age). Por definição, "Idade" é um período, um passo para o desenvolvimento e crescimento de um ser humano, animal, vegetal. O valor mínimo desta variável é 0, o que significa que um homem não tem sequer um ano de idade. Ela está configurada com um valor máximo de até 80. Dependendo da idade da pessoa, podemos dar-lhe a seguinte avaliação: "recém-nascido", "jovem", "meia-idade", "velho", "sênior" etc. Esta lista pode acomodar um número bastante grande de itens. Ela será um conjunto de termos para a nossa variável linguística e seus elementos serão os termos.
A figura abaixo mostra um exemplo da variável fuzzy "Idade", que tem apenas três termos definidos: "Jovem", "Meia-idade,", "Velho". Cada um desses termos tem a sua própria função de pertinência.
Vamos olhar para o caso quando alguém é de 30 anos de idade, que na figura irá corresponder a linha perpendicular traçada do ponto (30, 0). Esta linha irá cruzar as três funções de pertinência nos seguintes pontos:
- (30, 0) - o ponto de interseção do gráfico "Idade 30" e o gráfico "Velho".
- (30; 0,29) - o ponto de intersecção do gráfico "Idade 30" e o gráfico "Meia-idade".
- (30, 0,027) - o ponto de interseção do gráfico "Idade 30" e o gráfico "Jovem".
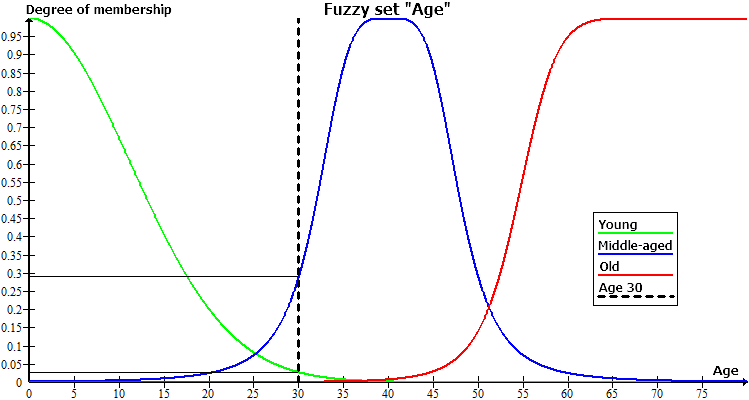
A partir das coordenadas desses três pontos, podemos fazer uma conclusão de que um homem de 30 anos de idade não pode ser chamado de velho, e na escolha entre os termos jovem e meia-idade, a segunda iria prevalecer. O grau de associação com o termo "Meia-idade" é igual a 0,29, o que é bastante pequeno, e, de fato, para um homem de 30 anos um outro termo "Jovem" caberia consideravelmente melhor.
Definição 7. Defuzzificação é um procedimento de conversão de um conjunto fuzzy em um número específico. Atualmente há mais de vinte métodos disponíveis, e os seus resultados são significativamente diferentes uns dos outros. Por favor, note que até agora os melhores resultados são alcançados usando o método Centro de gravidade de defuzzificação.
1.2. Lógica Fuzzy
A lógica fuzzy - É uma síntese da lógica tradicional aristotélica para o caso quando a veracidade é marcada como uma variável linguística. A lógica fuzzy, equivalente a lógica clássica, possui a suas próprias operações de lógica fuzzy em conjuntos fuzzy definidos. Há as mesmas operações para os conjuntos fuzzy, bem como para os conjuntos comuns, apenas o seu cálculo que é, de longe, bem mais difícil. Devemos também observar que a composição dos conjuntos fuzzy constituem como um conjunto fuzzy.
As particularidades principais da lógica fuzzy, que se diferenciam da lógica clássica, são a proximidade máxima para a reflexão da realidade e o alto nível de subjetividade, o que pode levar a erros significativos com cálculos.
Modelo fuzzy - é um modelo matemático cujo o cálculo é baseado na lógica fuzzy. A construção de tais modelos é aplicável quando o objeto de estudo tem uma formalização fraca e sua descrição matemática exata é complexa demais ou simplesmente não conhecida. A qualidade dos valores de saída destes modelos (modelo de erro) dependem diretamente apenas do especialista que criou este modelo. A melhor opção para minimizar os erros é desenhar o modelo mais completo e abrangente e, posteriormente, ajusta-lo com a aprendizagem de máquina em um grande conjunto de treinamento.
O progresso de um modelo de construção pode ser dividido em três fases principais:
- Definição de características de entrada e saída de um modelo.
- Construção de uma base de conhecimento.
- Selecionar um dos métodos de inferência fuzzy.
A primeira etapa afeta diretamente os dois seguintes e determina o futuro da operação do modelo. A base de conhecimento ou, às vezes chamado de, base de regras - é um conjunto de regras do tipo fuzzy: "se, então" que definem a relação entre as entradas e saídas do objeto examinado. O número de regras no sistema não é limitado e é determinado também pelo especialista. O formato generalizado de regras fuzzy é a seguinte:
Se condição da regra, então conclusão da regra.
Condição da regra descreve o estado atual do objeto, e a conclusão da regra - como esta condição afeta o objeto. A visão geral das condições e conclusões não podem ser selecionados porque eles são determinados por uma inferência fuzzy.
Cada regra no sistema tem o seu peso - esta característica define a importância da regra no modelo. Os fatores de ponderação são atribuídos a uma regra dentro do intervalo [0, 1]. Em muitos exemplos com modelos fuzzy, que podem ser encontrados na literatura relevante, os dados de peso não estão especificados, mas isso não significa que eles não se encontram presentes. Na verdade, em tal caso, para cada regra da base de regra, o peso é fixo e igual a 1. Não pode haver dois tipos de termos e conclusões para cada regra:
- simples - inclui uma variável fuzzy;
- complexa - inclui diversas variáveis fuzzy.
Dependendo da base de conhecimento criada, o sistema de inferência fuzzy é determinada por um modelo. A Inferência lógica fuzzy é uma entrada de conclusão na forma de um conjunto fuzzy correspondente ao valor atual das entradas com uso da base de conhecimento e operações difusas. Os dois principais tipos de inferência fuzzy são os métodos Mamdani e Sugeno.
1.3. Inferência Fuzzy do tipo Mamdani
De acordo com o algoritmo de Mamdani, a inferência fuzzy é executada utilizando a base difusa de conhecimento:
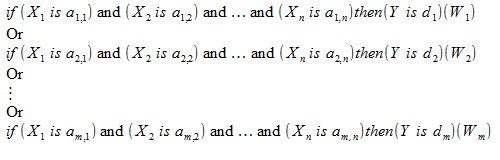
Os valores das variáveis de entrada e saída na base de conhecimento são constituídas por conjuntos fuzzy.
Essa base de conhecimento também pode ser escrita como:
![]()
onde se aplica o seguinte:
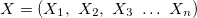 — vetor de variáveis de entrada;
— vetor de variáveis de entrada;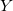 — variável de saída;
— variável de saída;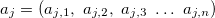 — vetor de variáveis de entrada na j-ésima regra, j = 0,1,2...m;
— vetor de variáveis de entrada na j-ésima regra, j = 0,1,2...m;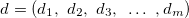 — vetor de valores para a variável de saída;
— vetor de valores para a variável de saída;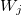 — peso da j-ésima regra, j = 0,1,2...m.
— peso da j-ésima regra, j = 0,1,2...m.
Vamos introduzir uma nova designação: ![]() — a função de pertinência de entrada fuzzy ou a variável de saída v para os termos difusos t.
— a função de pertinência de entrada fuzzy ou a variável de saída v para os termos difusos t.
O grau de pertinência do vetor de entrada para os termos difusos ![]() é calculado a partir da base de conhecimento do seguinte modo:
é calculado a partir da base de conhecimento do seguinte modo:
![]() — Esta função irá caracterizar o resultado do trabalho da j-ésima regra a partir da base de conhecimentos;
— Esta função irá caracterizar o resultado do trabalho da j-ésima regra a partir da base de conhecimentos;
onde ![]() — a operação S-norma (t-norma), ou seja, do conjunto de implementações das operações lógicas OR (AND). As seguintes implementações são utilizadas com maior frequência: para a operação OR - encontrando a máxima e para as operações de AND - encontrando a mínima.
— a operação S-norma (t-norma), ou seja, do conjunto de implementações das operações lógicas OR (AND). As seguintes implementações são utilizadas com maior frequência: para a operação OR - encontrando a máxima e para as operações de AND - encontrando a mínima.
Depois de encontrar ![]() para
para ![]() obtemos m novas funções de pertinência, que em conjunto irão formar um novo conjunto fuzzy (difuso ou nebuloso), denotamos como
obtemos m novas funções de pertinência, que em conjunto irão formar um novo conjunto fuzzy (difuso ou nebuloso), denotamos como ![]() , correspondente ao vetor de entrada
, correspondente ao vetor de entrada ![]() .
.
![]()
Uma característica especial deste conjunto fuzzy é que o seu conjunto universal é um termo-conjunto da variável de saída ![]() .
.
Em seguida, é necessário fazer o seguinte:
- "cortar" a função de pertinência
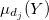 no nível
no nível 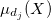 ;
; - combinar os conjuntos fuzzy obtidos.
Em outras palavras, usamos os termos da lógica fuzzy para produzir uma implicação e agregação de condições. Existem duas maneiras de modelar a implicação: encontrar o mínimo ou o produto dos conjuntos, a agregação, - encontrando o máximo ou a soma dos conjuntos.
Depois disso, vamos obter o conjunto fuzzy resultante, cuja defuzzificação nos dará a saída exata do sistema.
1.4. Inferência Fuzzy do Tipo Sugeno
De acordo com o algoritmo do tipo Sugeno, a inferência fuzzy é executada pela base difusa de conhecimento:
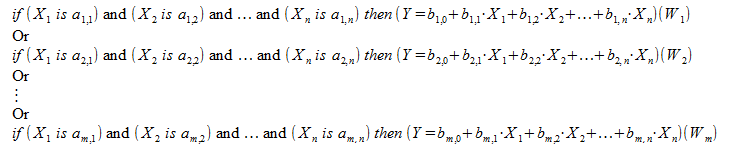
A base de conhecimento Sugeno é semelhante à base de conhecimento de Mamdani, com exceção das regras finais ![]() , que não são definidos pelos termos fuzzy, mas por uma função linear a partir das entradas:
, que não são definidos pelos termos fuzzy, mas por uma função linear a partir das entradas:
![]()
As regras da base de conhecimento Sugeno podem ser encaminhadas por uma espécie de comutadores de uma lei linear de "entrada - saída" para o outro, também linear. Os limites dos subdomínios são difusos, portanto, várias leis lineares de vários graus podem ser executadas simultaneamente.
Essa base de conhecimento também pode ser escrita como:
![]()
onde se aplica o seguinte:
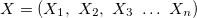 — vetor de variáveis de entrada.
— vetor de variáveis de entrada.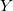 — variável de saída.
— variável de saída.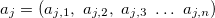 — vetor de variáveis de entrada na j-ésima regra, j = 0,1,2...m.
— vetor de variáveis de entrada na j-ésima regra, j = 0,1,2...m.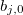 — coeficiente de termos livres na função linear para o valor de saída na j-ésima regra, j = 0,1,2...m.
— coeficiente de termos livres na função linear para o valor de saída na j-ésima regra, j = 0,1,2...m.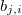 — coeficiente do i-ésimo termo na função linear para o valor de saída na j-ésima regra, j = 0,1,2...m, i = 0,1,2...n.
— coeficiente do i-ésimo termo na função linear para o valor de saída na j-ésima regra, j = 0,1,2...m, i = 0,1,2...n.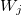 — peso da j-ésima regra, j = 0,1,2...m.
— peso da j-ésima regra, j = 0,1,2...m.
Vamos introduzir uma nova designação: ![]() — a função de pertinência de entrada fuzzy ou a variável de saída v para os termos difusos t.
— a função de pertinência de entrada fuzzy ou a variável de saída v para os termos difusos t.
O grau de pertinência do vetor de entrada para os termos difusos ![]() é calculado a partir da base de conhecimento do seguinte modo:
é calculado a partir da base de conhecimento do seguinte modo:
![]() — Esta função irá caracterizar o resultado do trabalho da j-ésima regra a partir da base de conhecimentos;
— Esta função irá caracterizar o resultado do trabalho da j-ésima regra a partir da base de conhecimentos;
onde ![]() — a operação S-norma (t-norma), ou seja, do conjunto de implementações das operações lógicas OR (AND). Na inferência fuzzy de Sugeno a seguinte implementação de normas triangulares são mais frequentemente utilizadas: OR probabilístico como a s-norma e produção como a t-norma.
— a operação S-norma (t-norma), ou seja, do conjunto de implementações das operações lógicas OR (AND). Na inferência fuzzy de Sugeno a seguinte implementação de normas triangulares são mais frequentemente utilizadas: OR probabilístico como a s-norma e produção como a t-norma.
Depois de encontrar ![]() para
para ![]() obtemos m novas funções de pertinência, que em conjunto irão formar um novo conjunto fuzzy (difuso ou nebuloso), denotamos como
obtemos m novas funções de pertinência, que em conjunto irão formar um novo conjunto fuzzy (difuso ou nebuloso), denotamos como ![]() , correspondente ao vetor de entrada
, correspondente ao vetor de entrada ![]() .
.
![]()
Por favor, note que, em contraste com o resultado da saída de Mamdani, o conjunto fuzzy acima mencionado é o conjunto fuzzy normal de primeira ordem. Ele é baseado no conjunto de números precisos. O valor do resultado ![]() é definido como uma superposição de dependências lineares realizadas no ponto
é definido como uma superposição de dependências lineares realizadas no ponto ![]() do espaço fatorial de dimensão n. Por esta razão, um conjunto difuso
do espaço fatorial de dimensão n. Por esta razão, um conjunto difuso ![]() é defuzzificado, calculando a média ou a soma ponderada.
é defuzzificado, calculando a média ou a soma ponderada.
2. Biblioteca da Lógica Fuzzy FuzzyNet
Na prática, o processo de criação e operação pode ser uma tarefa difícil, mesmo com um modelo fuzzy muito simples envolvido. No entanto, existem muitas ferramentas de software e bibliotecas diferentes, podendo simplifica-la. Como exemplo, vamos dar uma olhada nos scripts de teste da Biblioteca FuzzyNet para MQL5 sobre como criar e operar com dois modelos fuzzy.
2.1. Criando Sistemas do Tipo Mamdani
O primeiro exemplo é o script Tips_Sample_Mamdani.mq5 da biblioteca FuzzyNet para MQL5. Ele implementa um modelo fuzzy para calcular a gorjeta, que um visitante prefere deixar baseado em seu/sua avaliação do serviço e da qualidade do alimento. Este sistema possui duas entradas de lógica difusa, uma saída, a base de conhecimento consiste de três regras utilizando o sistema de saída lógico do tipo Mamdani.
Os parâmetros de entrada são variáveis difusas comida e serviço, ambas as variáveis são medidas em uma escala de 0 a 10 - estes são os seus valores mínimos e máximos. A variável "alimento" consiste de dois termos: "rançoso","delicioso". A variável "serviço" será composta de três termos difusos: pobre, boa, excelente.
Na saída obtemos a variável fuzzy "gorjetas". Vamos definir um intervalo de valores para as gorjetas entre 5% a 30% do valor da conta e introduzir três termos: "barato","médio","generoso" para esta variável.
A base do sistema de conhecimento conterá três regras:
- Se (o serviço for pobre) ou (a comida rançosa), em seguida, as gorjetas serão baratas.
- Se (o serviço é bom), em seguida, as gorjetas serão médias.
- Se (o serviço é excelente) ou (a comida é deliciosa), em seguida, as gorjetas serão generosas.
Agora que temos uma idéia geral sobre o sistema, vamos dar uma olhada para o processo de sua criação:
- Nós vamos incluir o arquivo MamdaniFuzzySystem.mqh da biblioteca FuzzyNet para MQL5:
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>Esse arquivo permite criar os sistemas do tipo Mamdani e operar com eles. - Agora nós podemos criar um sistema de Mamdani vazio e preenchê-lo:
MamdaniFuzzySystem *fsTips=new MamdaniFuzzySystem(); - Vamos criar a primeira variável de entrada "serviço". Ao criar as variáveis difusas como um parâmetro para o construtor, em primeiro lugar, o nome de uma variável é indicado na linha, seguido pelo seu valor mínimo e máximo.
FuzzyVariable *fvService=new FuzzyVariable("service",0.0,10.0);
- Nós adicionamos os termos difusos a ele. O construtor de termos difusos utiliza nomes na string como primeiro parâmetro e sua correspondente função de pertinência como segundo parâmetro.
fvService.Terms().Add(new FuzzyTerm("poor", new TriangularMembershipFunction(-5.0, 0.0, 5.0))); fvService.Terms().Add(new FuzzyTerm("good", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvService.Terms().Add(new FuzzyTerm("excellent", new TriangularMembershipFunction(5.0, 10.0, 15.0)));
Neste exemplo as funções de pertinência são apresentadas como uma função triangular para todos os termos. - Agora, a variável fuzzy já formada é adicionada ao nosso sistema:
fsTips.Input().Add(fvService);
- Da mesma forma, vamos implementar uma segunda entrada para a variável "alimento", mas os termos para essa variável terá uma função de pertinência trapezoidal.
FuzzyVariable *fvFood=new FuzzyVariable("food",0.0,10.0); fvFood.Terms().Add(new FuzzyTerm("rancid", new TrapezoidMembershipFunction(0.0, 0.0, 1.0, 3.0))); fvFood.Terms().Add(new FuzzyTerm("delicious", new TrapezoidMembershipFunction(7.0, 9.0, 10.0, 10.0))); fsTips.Input().Add(fvFood);
- Uma vez que o sistema possui uma inferência Mamdani, os seus valores de entrada e saída serão determinados pelos mesmos métodos. Portanto, da mesma forma, nós criamos uma saída semelhante:
FuzzyVariable *fvTips=new FuzzyVariable("tips",0.0,30.0); fvTips.Terms().Add(new FuzzyTerm("cheap", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvTips.Terms().Add(new FuzzyTerm("average", new TriangularMembershipFunction(10.0, 15.0, 20.0))); fvTips.Terms().Add(new FuzzyTerm("generous", new TriangularMembershipFunction(20.0, 25.0, 30.0))); fsTips.Output().Add(fvTips);
- Vamos criar as regras difusas, que em conjunto irão apresentar a base de conhecimento para o nosso sistema. Para criar uma regra, é necessário chamar o método ParseRule a partir do objeto, que apresenta o nosso sistema, e como uma opção para dar-lhe uma representação simples de strings de regras fuzzy:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is cheap)"); MamdaniFuzzyRule *rule2 = fsTips.ParseRule("if (service is good) then (tips is average)"); MamdaniFuzzyRule *rule3 = fsTips.ParseRule("if (service is excellent) or (food is delicious) then (tips is generous)");
As escritas das regras fuzzy são estritamente digitadas, não permite o uso de palavras não-chave. As palavras-chave são: "if", "then", "is", "and", "or", "not", "(", ")", "slightly", "somewhat", "very", "extremely". As últimas quatro palavras-chave são os quantificadores linguísticos. Além disso, todos os nomes de variáveis, termos e funções disponíveis no seu sistema estão incluídos na lista de palavras-chave. A importância dos termos fuzzy ou das funções lineares de Sugeno são elevadas ou reduzidas com os quantificadores linguísticos. A seguinte implementação dos quantificadores linguísticos se aplicam a seguir:
- "slightly" ou "apenas" - substitui o resultado da sua condição pela sua raiz cúbica. Reduz muito valor.
- "somewhat" ou "um pouco" - substitui o resultado da condição por sua raiz quadrada. Reduz o valor.
- "very" ou "muito" - traz o resultado da condição para o segundo nível. Aumenta o valor.
- "extremely" ou "extremamente" - traz o resultado da condição para o terceiro nível. Aumenta muito valor.
- "slightly" ou "apenas" - substitui o resultado da sua condição pela sua raiz cúbica. Reduz muito valor.
- A etapa restante é para adicionar regras para o sistema:
fsTips.Rules().Add(rule1); fsTips.Rules().Add(rule2); fsTips.Rules().Add(rule3);
Agora nós temos um modelo pré-fabricado para o cálculo de gorjetas com base no sistema de inferência fuzzy de Mamdani.
2.2. Criando Sistemas do Tipo Sugeno
Como um exemplo da implementação do sistema do tipo Sugeno, nós vamos usar um script para medir o controle necessário de um sistema de controle de velocidade em um carro. Este script é descrito no arquivo Cruise_Control_Sample_Sugeno.mq5 na Biblioteca FuzzyNet para MQL5 e serve como um dos exemplos de aplicação de modelos fuzzy para resolver os problemas de controle automático.
A lógica fuzzy é usada principalmente para tarefas unidimensionais equivalentes em sistemas de controle e automático (ACS). A definição destas metas pode ser descrito da seguinte forma: um objeto em um determinado ponto no tempo ![]() está num estado "A", e durante o período de tempo
está num estado "A", e durante o período de tempo ![]() ela tem que atingir uma condição "B". Para resolver tarefas semelhantes, a estrutura geral é dividida em
ela tem que atingir uma condição "B". Para resolver tarefas semelhantes, a estrutura geral é dividida em ![]() partes, um intervalo de tempo igual a
partes, um intervalo de tempo igual a ![]() é localizado, e em seguida, o sistema de controle automático gerencia ele em todos os pontos
é localizado, e em seguida, o sistema de controle automático gerencia ele em todos os pontos ![]() , onde i = 0,1,2,...n.
, onde i = 0,1,2,...n.
Vários controladores PID podem lidar facilmente com essa tarefa, mas eles têm uma desvantagem, já que eles não são capazes de trabalhar com um controle "suave". Em outras palavras, se você construir um sistema de controle de velocidade de um carro baseado no controlador PID, com uma mudança de velocidade o sistema vai se ajustar à velocidade desejada, no entanto, saltos e solavancos podem ocorrer no processo. Do ponto de vista de um ser humano, o controlador fuzzy pode executar mais suave e com mais conforto.
Torna-se evidente que na saída do nosso controlador fuzzy haverá uma alteração da velocidade necessária em forma de aceleração, e na entrada estará um erro e acontecerá a primeira derivada do erro. O erro é o desvio atual do estado desejado. Em outras palavras, o sistema de entrada vai receber a informação seguinte:
- a diferença entre a velocidade do veículo no momento atual e a velocidade definida no sistema de controle de velocidade;
- a rapidez com que essa diferença diminui (aumenta).
Assim, o primeiro parâmetro de entrada do "erro de velocidade" vai variar de -20 a 20 km/h, possuindo três termos "mais devagar" (slower), "zero", "mais rápido" (faster). Todos os três termos terá uma função de associação triangular. A segunda entrada - "SpeedErrorDot" varia de -5 a 5, e opera os termos fuzzy "mais devagar" (slower), "zero", "mais rápido" (faster), também com uma função de associação triangular.
Desde que o nosso modelo tenha um sistema de inferência de Sugeno, o valor de saída da "aceleração" não terá um valor máximo e mínimo, e em vez de termos fuzzy haverá combinações lineares das variáveis de entrada, o que também possuem nomes: "zero", "mais rápido", "mais devagar", "func". Vamos descrever todas as quatro combinações lineares. Para isso, nós denotamos as variáveis SpeedError como ![]() , SpeedErrorDot como
, SpeedErrorDot como ![]() e Acelerate como
e Acelerate como ![]() para obter as seguintes equações:
para obter as seguintes equações:
- zero:
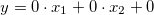 ;
; - faster:
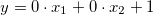 ;
; - slower:
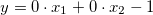 ;
; - func:
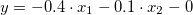 .
.
A base deste sistema de conhecimento será composto de nove regras:
- Se o (erro de velocidade for mais lento), e (a derivada do erro de velocidade for mais lenta), a aceleração é mais rápida.
- Se o (erro de velocidade for mais lento), e (a derivada do erro de velocidade for zero), a aceleração é mais rápida.
- Se o (erro de velocidade for mais lento), e (a derivada do erro de velocidade for mais rápida), a aceleração é zero.
- Se o (erro de velocidade for zero), e (a derivada do erro de velocidade for mais lenta), a aceleração é mais rápida.
- Se o (erro de velocidade for zero), e (a derivada do erro de velocidade for zero), a aceleração é func.
- Se o (erro de velocidade for zero), e (a derivada do erro de velocidade for mais rápida), a aceleração é mais lenta.
- Se o (erro de velocidade for mais rápido), e (a derivada do erro de velocidade for mais lenta), a aceleração é mais rápida.
- Se o (erro de velocidade for mais rápido), e (a derivada do erro de velocidade for zero), a aceleração é mais lenta.
- Se o (erro de velocidade for mais rápido), e (a derivada do erro de velocidade for mais elevada), a aceleração é mais lenta.
Vamos descrever o curso do sistema de criação:
- Nós incluímos o arquivo SugenoFuzzySystem.mqh da biblioteca FuzzyNet para MQL5:
#include <Math\FuzzyNet\SugenoFuzzySystem.mqh>Esse arquivo permite criar sistemas do tipo Sugeno e trabalhar com eles. - Agora nós podemos criar um sistema de Sugeno vazio e proceder com seu preenchimento:
SugenoFuzzySystem *fsCruiseControl=new SugenoFuzzySystem(); - As variáveis de entrada para o sistema de Sugeno são criadas da mesma forma que para o sistema do tipo Mandani.
Vamos criar a variável "SpeedError" e adicioná-la ao sistema:
FuzzyVariable *fvSpeedError=new FuzzyVariable("SpeedError",-20.0,20.0); fvSpeedError.Terms().Add(new FuzzyTerm("slower",new TriangularMembershipFunction(-35.0,-20.0,-5.0))); fvSpeedError.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-15.0, -0.0, 15.0))); fvSpeedError.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(5.0, 20.0, 35.0)));
Vamos criar a variável "SpeedErrorDot" e também adicioná-la ao sistema:
FuzzyVariable *fvSpeedErrorDot=new FuzzyVariable("SpeedErrorDot",-5.0,5.0); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("slower", new TriangularMembershipFunction(-9.0, -5.0, -1.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-4.0, -0.0, 4.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(1.0, 5.0, 9.0)));
- Vamos criar a variável fuzzy do tipo Sugeno que será a saída do sistema. Ao criar uma variável fuzzy o construtor aceita o seu nome como único parâmetro. Funções lineares podem ser adicionadas a ele, mas em primeiro lugar, essas funções precisam ser determinadas, e para isso precisamos de uma array de coeficientes do tipo double.
A formação de uma função linear é conduzida da seguinte forma: cada variável de entrada, terá uma quantidade desconhecida de uma equação com coeficientes obtidos a partir do array de coeficientes. Desta forma, os coeficientes de uma matriz devem ser colocados na mesma ordem em que foram registadas as variáveis de entrada. Assim, para a primeira variável de entrada, o coeficiente de índice 0, é aplicável, para o segundo - índice 1 etc. Portanto, o comprimento de um conjunto de coeficientes deve ser maior do que uma unidade ou um número igual de variáveis de entrada. Se os comprimentos são iguais, então o coeficiente de um termo livre é igual a zero, caso contrário, o seu valor será igual ao último elemento do array.
Há duas variáveis de entrada no nosso sistema, de modo que o comprimento dos arrays de coeficientes não devem ser superior a três. Nós vamos anunciar todas os quatro arrays, com base em sua informação que formarão as funções descritas acima e adicioná-las a uma variável fuzzy do tipo Sugeno e, em seguida, incluí-las no sistema:SugenoVariable *svAccelerate=new SugenoVariable("Accelerate"); double coeff1[3]={0.0,0.0,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("zero",coeff1)); double coeff2[3]={0.0,0.0,1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("faster",coeff2)); double coeff3[3]={0.0,0.0,-1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("slower",coeff3)); double coeff4[3]={-0.04,-0.1,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("func",coeff4)); fsCruiseControl.Output().Add(svAccelerate);
- Respectivamente com o sistema Mamdani, nós vamos criar nove regras fuzzy:
SugenoFuzzyRule *rule1 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule2 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is zero) then (Accelerate is faster)"); SugenoFuzzyRule *rule3 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is faster) then (Accelerate is zero)"); SugenoFuzzyRule *rule4 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule5 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is zero) then (Accelerate is func)"); SugenoFuzzyRule *rule6 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is faster) then (Accelerate is slower)"); SugenoFuzzyRule *rule7 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule8 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is zero) then (Accelerate is slower)"); SugenoFuzzyRule *rule9 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is faster) then (Accelerate is slower)");
- Vamos adicioná-las ao nosso sistema:
fsCruiseControl.Rules().Add(rule1); fsCruiseControl.Rules().Add(rule2); fsCruiseControl.Rules().Add(rule3); fsCruiseControl.Rules().Add(rule4); fsCruiseControl.Rules().Add(rule5); fsCruiseControl.Rules().Add(rule6); fsCruiseControl.Rules().Add(rule7); fsCruiseControl.Rules().Add(rule8); fsCruiseControl.Rules().Add(rule9);
2.3. Cálculo dos sistemas do tipo Mamdani e Sugeno
A variável fuzzy e o seu valor devem ser enviados para a entrada de um sistema fuzzy. Como mencionado acima, as variáveis fuzzy tomam os valores dos seus conjuntos de termos. Por conseguinte, o resultado do cálculo do sistema irá depender das funções de pertinência que correspondem aos termos aplicados na entrada com as variáveis de entrada fuzzy. No entanto, na maioria dos casos, as variáveis fuzzy são enviadas para o sistema de entrada em forma de simples valores numéricos, que são destinados a obter os mesmos resultados precisos sobre a forma de saída. Neste caso, verifica-se que o termo fuzzy não possui declaração aparente e sua função de pertinência é representada como uma função de pertinência constante. Os sistemas escritos usando a biblioteca FuzzyNet são projetados para operar em um caso tão particular.
O que exatamente precisa ser enviado para a entrada do sistema e de que forma é que vamos obter os resultados a partir dele?
O número de variáveis de entrada para os sistemas fuzzy não são limitados, cada entrada deve tomar alguns valores, por isso, precisamos ter uma lista que irá armazenar os valores para cada entrada. Um objeto complexo com dois campos deve ser o elemento desta lista: primeiro campo - variável fuzzy, segundo campo - Tipo do valor numérico double. No arquivo Dictionary.mqh, tomado a partir da biblioteca FuzzyNet do MQL5, a classe Dictionary_Obj_Double é implementada permitindo criar tais objetos.
Vamos formar uma lista de entrada para o nosso sistema do tipo Mamdani:
CList *in=new CList; Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double; p_od_Service.SetAll(fvService, Service); p_od_Food.SetAll(fvFood, Food); in.Add(p_od_Service); in.Add(p_od_Food);
Aqui Service e Food - são dois parâmetros de entrada do tipo double.
Nos exemplos descritos acima, ambos os sistemas de Sugeno e Mamdani possuem apenas uma saída, embora, em geral, o mesmo que com entradas, não existem restrições para a sua quantidade. A estrutura de entrada e saída não tem quaisquer diferenças.
A saída para sistemas do tipo Mamdani:
CList *result=new CList; Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;
Agora, para cada sistema, vamos chamar a função Calculate que assume um parâmetro - uma lista de entradas, e retorna uma lista de saídas. De acordo com o índice 0 na lista, vamos obter o valor de saída do sistema, que é representado como um objeto da classe Dictionary_Obj_Double. Usando para isso os métodos objeto Chave e Valor podemos obter uma variável e, respectivamente, o seu resultado.
Nós vamos fazer um cálculo para o sistema de Mamdani e exibir o número recebido em uma variável fuzzy de saída fvTips:
result=fsTips.Calculate(in); p_od_Tips=result.GetNodeAtIndex(0); Alert("Tips, %: ",p_od_Tips.Value());
Vamos fazer o mesmo com o sistema do tipo Sugeno:
CList *in=new CList; Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double; p_od_Error.SetAll(fvSpeedError,Speed_Error); p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot); in.Add(p_od_Error); in.Add(p_od_ErrorDot); CList *result=new CList; Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double; result=fsCruiseControl.Calculate(in); p_od_Accelerate=result.GetNodeAtIndex(0); Alert("Accelerate, %: ",p_od_Accelerate.Value()*100);
Conclusão
Para mais informações sobre os scripts descritos acima, bem como para criar seu modelo fuzzy, faça o download da bibliotecaa FuzzyNet para MQL5 ou MQL4. É essencial compreender que a construção de modelos fuzzy "ao vivo" é uma tarefa desafiadora, mesmo com o auxílio de bibliotecas auxiliares. Além disso, cada modelo terminado requer controles obrigatórios completos e ajustes.
Lista de Referências e Links
- http://www.bindichen.co.uk/post/AI/mamdani-fuzzy-model.html — Modelo fuzzy de Mamdani.
- http://www.bindichen.co.uk/post/AI/takagi-sugeno-fuzzy-model.html — Modelo fuzzy de Sugeno.
- http://reference.wolfram.com/applications/fuzzylogic/DemonstrationNotebooks/5.html — Controle lógico de fuzzy.
- http://plato.stanford.edu/entries/logic-fuzzy — Introdução a lógica Fuzzy.
- Lotfi A. Zadeh. Conjuntos fuzzy e suas aplicações
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/1991
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
 Uma Visão Sobre o Indicador Accumulation-Distribution e Onde Conseguilo
Uma Visão Sobre o Indicador Accumulation-Distribution e Onde Conseguilo
 Kit do Trader: Biblioteca Drag Trade
Kit do Trader: Biblioteca Drag Trade
 MetaTrader 4 no Linux
MetaTrader 4 no Linux
 Barras sintéticas - Uma Nova Dimensão para Exibição de Informações Gráficas dos Preços
Barras sintéticas - Uma Nova Dimensão para Exibição de Informações Gráficas dos Preços
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
oi
quando atualizei o metatrader para a versão 2342
todas as amostras com a biblioteca de lógica fuzzy
erro de retorno "fundição incorreta de ponteiros" em MQL5\Include\Math\Fuzzy\RuleParser.mqh Linha 712
Por favor, ajude a corrigir o erro
Muito obrigado
leia minha postagem anterior.
Olá
Obrigado por sua resposta
O verdadeiro autor é Dmitry Kalyuzhny, mas ele codificou essa biblioteca em .Net
Mas talvez outra pessoa tenha alterado o código para mql
Vejo que o autor deste artigo é Дмитрий Калюжный
mas não consegui encontrar o perfil de Дмитрий Калюжный no mql5
Poderia me ajudar a entrar em contato ou corrigir esse bug?
Muito obrigado
Foi publicado o novo artigo An Introduction to Fuzzy Logic (Introdução à lógica difusa ):
Autor: MetaQuotes Software Corp.
Hi
Quando atualizei o Metatrader para a versão 2342
todos os exemplos com a biblioteca de lógica difusa
retornam o erro "incorrect casting of pointers" na linha 712 do arquivo MQL5\Include\Math\Fuzzy\RuleParser.mqh
Por favor, ajude a corrigir o erro
Muito obrigado
oi
Obrigado por sua reprodução
O verdadeiro autor é Dmitry Kalyuzhny, mas ele codificou essa biblioteca em .Net
Mas talvez outra pessoa tenha alterado o código para mql
Vejo que o autor deste artigo é Дмитрий Калюжный
mas não consegui encontrar o perfil do Дмитрий Калюжный no mql5
Poderia me ajudar a entrar em contato ou corrigir esse bug?
Muito obrigado
Se ninguém ajudar neste tópico, você poderá usar o Freelance, por exemplo.
Olá, pessoal,
Tenho uma pergunta sobre os "quantificadores linguísticos": " ligeiramente", "um pouco", "muito", "extremamente"...
Qual é o uso correto deles na função ParseRule?
Se eu tentar algo assim:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is very cheap)");...recebo este erro: "A parte da conclusão da regra deve estar no formato: 'variable is term'"
Onde eu teria que colocar o 'very' na string acima?
Agradeceria muito a ajuda!
Obrigado!