
Einführung in die Theorie der Fuzzylogik
Einleitung
Die mathematische Theorie der unscharfen Mengen (fuzzy sets) und die Fuzzylogik (fuzzy logic) nehmen ihren Anfang 1965. Als Gründungsvater dieser Theorie gilt Professor Lotfi Zadeh aus der Universität von Kalifornien, Berkeley. In seinem Artikel über Fuzzy-Sets im Magazin "Information and Control" führte er beide Begriffe ein. Das mathematische Mittel ermöglichte es, in solch eine strikte Wissenschaft wie Mathematik unscharfe (verschwommene) Begriffe einzuführen, die jeder nutzen kann, und schuf Voraussetzungen für grundlegend neue Lösungen, und zwar Soft-Computing. Diese Neuerungen können bei der richtigen Anwendung den Prozess der Klassifizierung, Erstellung von Expertensystemen und Entwicklung von neuronalen Netzen.
Die praktische Anwendung der Fuzzylogik beschränkt sich aber darauf nicht. In der Tat ist dieses mathematische Mittel in der Theorie der automatischen Steuerung besonders verbreitet. Damit kann man auch die Entstehung eines weiteren Begriffs verbinden, und zwar geht es um das unscharfe Modell. Das unscharfe Modell ist ein Sonderfall des mathematischen Modells.
1. Theorie der unscharfen Mengen und der Fuzzylogik
Die neue Theorie von Lotfi A. Zadeh läuft über die gewohnten Grenzen der mathematischen Logik und der Mengentheorie hinaus. Die mathematische Logik kennt nur strikt formalisierte Daten, und die Zugehörigkeit eines Objektes zu einer Menge wird nur durch zwei Begriffe bestimmt, d.h. diese "Zugehörigkeit" ist ein diskreter Wert, der nur zwei Werte annehmen kann:
- "1" — wenn das Objekt zu einer oder anderen Menge gehört;
- "0" — wenn das Objekt zu keiner Menge gehört.
Lotfi Zadeh verzichtet in seiner Theorie unscharfer Mengen auf einen diskreten Begriff der "Zugehörigkeit" und führt einen neuen Begriff des "Grades der Zugehörigkeit" ein, und die geläufigen "Mengen" werden durch "unscharfe Mengen" ersetzt.
1.1. Grundbegriffe und Definitionen
Definition 1. Als eine unscharfe Menge (fuzzy set) ![]() in der universellen Menge
in der universellen Menge ![]() wird die Gesamtheit der Paare
wird die Gesamtheit der Paare ![]() bezeichnet, wo
bezeichnet, wo ![]() den Grad der Zugehörigkeit eines Elements zu einer
den Grad der Zugehörigkeit eines Elements zu einer ![]() unscharfen Menge beschreibt.
unscharfen Menge beschreibt.
Definition 2. Der Grad der Zugehörigkeit ist eine Zahl aus dem Zahlenbereich [0, 1]. Je höher der Grad der Zugehörigkeit ist, in desto höherem Maße entspricht das Element der universellen Menge den Eigenschaften der gegebenen Fuzzy-Menge. Wenn der Grad der Zugehörigkeit gleich Null ist, entspricht dieses Element der Menge absolut nicht; sollte dieser Wert gleich 1 sein, kann man von einer vollständigen Entsprechung sprechen. Diese zwei Zustände sind Grenzwerte und gäbe es keine weiteren Varianten, wäre dies eine gewöhnliche Menge. Der Hauptunterschied einer Fuzzy-Menge von scharfen Mengen besteht gerade darin, dass es weitere Varianten gibt.
Definition 3. Als Zugehörigkeitsfunktion (membership function) wird die Funktion bezeichnet, anhand deren man den Grad der Zugehörigkeit eines Elements der universellen Menge zu einer unscharfen Menge berechnen kann. Demzufolge müssen die Werte der Funktion im Bereich [0, 1] liegen. In den meisten Fällen stellt die Zugehörigkeitsfunktion eine kontinuierliche Funktion dar.
Definition 4. Als linguistische (unscharfe) Variable (linguistic variable) wird die Variable bezeichnet, deren Wert Wörter oder Wortgruppen einer natürlichen oder einer künstlichen Sprache sein können. Gerade aus linguistischen Variablen bestehen unscharfe Mengen. Bei der Bestimmung einer Fuzzy-Menge sind die Anzahl und die Art unscharfer Variablen für jede einzelne Aufgabe subjektiv.
Definition 5. Als Term-Menge (term set) wird eine Menge aller möglichen Werte genannt, die die linguistische Variable annehmen kann.
Definition Nr.6. Als Term (term) wird jedes Element einer Term-Menge genannt. In der Theorie unscharfer Mengen werden Terme durch Fuzzy-Mengen mithilfe der Zugehörigkeitsfunktion formalisiert. Die Zugehörigkeitsfunktion ist für jeden Term individuell und häufig einmalig. Es gibt verschiedene Methoden, diese Funktionen zu konstruieren: direkte, indirekte und Methoden relativer Häufigkeiten. Oft beruhen diese auf den Punkten der Zugehörigkeitsfunktion oder auf empirischen Daten eines Experten aus diesem Bereich.
Beispiel:
Definieren wir eine linguistische Variable mit dem Namen "Alter". Nach der Definition bedeutet "Alter" eine Periode bzw. Stufe in der Entwicklung und dem Wachstum eines Menschen, Tieres, einer Pflanze usw. Der niedrigste Wert dieser Variablen beträgt Null, d.h. man ist nicht einmal ein Jahr alt. Als höchsten Wert setzen wir 80. Je nach Alter kann man einen Menschen als "neugeboren", "jung", "mittleren Alters", "älter", "alt" usw. bezeichnen. Diese Liste kann viele Elementen enthalten. Sie stellt eine Term-Menge dar, und ihre Elemente sind Terme.
Auf der Abbildung unten ist die Variable "Alter" als Beispiel angeführt, die Term-Menge besteht für diese Variable aus drei Termen: "Jung", "Mittleren Alters", "Alt". Jeder Term hat seine Zugehörigkeitsfunktion.
Schauen wir uns den Fall an, wo man 30 Jahre alt ist. Auf der Abbildung entspricht dies dem Lot vom Punkt (30, 0). Diese Gerade schneidet alle drei Zugehörigkeitsfunktionen in den Punkten:
- (30, 0) — Schnittpunkt der Grafik "30 Jahre alt" und der Grafik "Alt".
- (30, 0.29) — Schnittpunkt der Grafik "30 Jahre alt" und der Grafik "Mittleren Alters".
- (30, 0.027) — Schnittpunkt der Grafik "30 Jahre alt" und der Grafik "Jung".
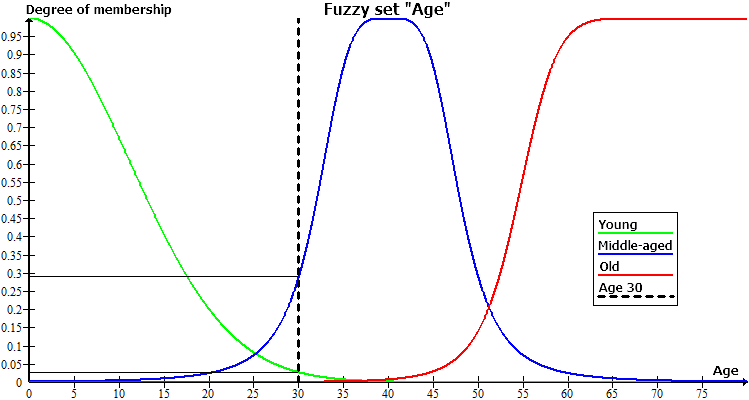
Aus den Koordinaten dieser Punkte lässt sich die Schlussfolgerung ziehen, dass man einen 30-jährigen Menschen auf keinem Fall alt nennen kann, und sollte man sich zwischen "Jung" und "Mittleren Alters" entscheiden, dann würde eher die letzte Variante stimmen. Der Zugehörigkeitsgrad zum Term "Mittleren Alters" ist gleich 0.29, was ein relativ niedriger Wert ist, und für einen 30-jährigen würde ein anderer Term, z.B. "Jung" besser passen.
Definition 7. Der Begriff Defuzzifizierung (defuzzification) beschreibt den Vorgang, bei dem eine Fuzzy-Menge in einen scharfen Wert umgewandelt wird. Heutzutage gibt es über 20 Methoden der Defuzzifizierung. Dabei können sich ihre Ergebnisse von einander wesentlich unterscheiden. Es ist zu betonen, dass die besten Ergebnisse mit der Defuzzifizierung nach der Schwerpunktmethode (center of gravity) erzielt werden können.
1.2. Fuzzy-Logik
Die Fuzzylogik ist eine Verallgemeinerung der traditionellen aristotelischen Logik, wenn die Wahrheit als linguistische Variable betrachtet wird. Genauso wie in der klassischen Logik gibt es in der Fuzzylogik unscharfe logische Operationen mit Fuzzy-Mengen. Für unscharfe Mengen gelten die gleichen Operationen wie für reguläre Mengen, die Berechnungen sehen allerdings viel komplizierter aus. Man muss auch hervorheben, dass eine Komposition von Fuzzy-Mengen eine Fuzzy-Menge ist.
Die Fuzzylogik unterscheidet sich von der klassischen Logik hauptsächlich dadurch, dass sie möglichst nah an der Realität ist und einen hohen Subjektivitätsgrad aufweist, was zu erheblichen Ungenauigkeiten und Fehlern bei Berechnungen führen kann.
Als Fuzzy-Modell bezeichnet man ein mathematisches Modell, dem die Fuzzylogik zugrunde liegt. Solche Modelle werden in dem Fall erstellt, wenn das Objekt wenig formalisiert ist und seine genaue mathematische Beschreibung zu kompliziert oder einfach unbekannt ist. Die Qualität der Ausganswerten solcher Modelle (Modellfehler) ist nur von dem Experten direkt abhängig, der das Modell erstellt und eingestellt hat. Um Fehler zu minimieren wäre es am besten, ein umfassendes Modell mithilfe von Methoden des maschinellen Lernens anhand einer großen Stichprobe zu erstellen und einzustellen.
Der Aufbau eines Modells besteht aus drei Schritten:
- Eingangs- und Ausgangsparameter des Modells bestimmen.
- Aufbau einer Wissensbank.
- Auswahl einer Inferenzmethode.
Vom ersten Schritt hängen die weiteren zwei ab. Der erste Schritt bestimmt, wie das Modell in der Zukunft funktionieren wird. Die Wissensbank oder mit anderen Worten die Regelbasis umfasst unscharfe Regeln vom Typ: "wenn, dann", die den Zusammenhang zwischen den Eingangs- und Ausgangsgrößen bestimmen. Die Anzahl an Regeln im System ist unbegrenzt und wird auch vom Experten bestimmt. Ein allgemeines Format unscharfer Regeln sieht folgendermaßen aus:
Wenn Bedingung (Prämisse) der Regel, dann Konklusion.
Die Prämisse charakterisiert den aktuellen Zustand des Objekts und die Konklusion — wie diese Prämisse das Objekt beeinflussen wird. Es gibt keine allgemeine Form von Prämissen und Konklusionen, denn diese werden durch die unscharfe Inferenz bestimmt.
Jede Regel hat ihr eigenes Gewicht im System. Dieser Parameter charakterisiert die Gewichtung der Regel im Modell. Die Regeln können zwischen 0 und 1 gewichtet werden. In vielen Beispielen für Fuzzy-Modelle, die in Fachliteratur zu finden sind, ist diese Gewichtung nicht angegeben. Dies bedeutet aber nicht, dass sie nicht existiert. In der Wirklichkeit ist diese Gewichtung für jede Regel aus der Wissensbank festgelegt und ist gleich 1. Es kann zwei Typen von Prämissen und Konklusionen für jede Regel geben:
- einfache — Typ mit einer unscharfen Variablen;
- komplexe — Typ mit mehreren unscharfen Variablen.
In Hinblick auf die erstellte Regelung wird die Interferenz definiert. Als Fuzzy-Inferenz bezeichnet man eine Konklusion in Form einer Fuzzy-Menge, die den aktuellen Eingangsgrößen entspricht, unter Verwendung einer unscharfen Regelbasis und unscharfen Operationen. Zu den zwei Grundtypen der Interferenz gehören die vom Typ Mamdani und die vom Typ Sugeno.
1.3. Unscharfe Inferenz von Mamdani
Unscharfe Inferenz nach dem Mamdani-Algorithmus:
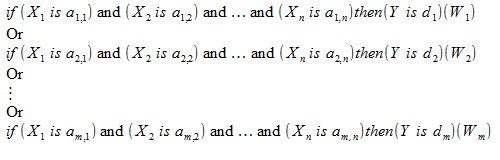
Die Werte der Eingangsvariablen und der Ausgangvariablen werden durch Fuzzy-Mengen gesetzt.
Diese Wissensbank kann folgendermaßen notiert werden:
![]()
wobei:
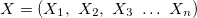 — Vektor der Eingangsvariablen;
— Vektor der Eingangsvariablen;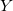 — Ausgangsvariable;
— Ausgangsvariable;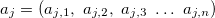 — Vektor der Eingangsvariablen in der j-en Regel, j=0,1,2...m;
— Vektor der Eingangsvariablen in der j-en Regel, j=0,1,2...m;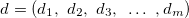 — Vektor der Ausgangsvariablen;
— Vektor der Ausgangsvariablen;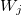 — Gewicht der j-en Regel, j=0,1,2...m.
— Gewicht der j-en Regel, j=0,1,2...m.
Führen wir eine neue Bezeichnung ein: ![]() — Zugehörigkeitsfunktion einer unscharfen Eingangs- oder Ausgangsvariablen v zum unscharfen Term t.
— Zugehörigkeitsfunktion einer unscharfen Eingangs- oder Ausgangsvariablen v zum unscharfen Term t.
Der Zugehörigkeitsgrad des Eingansvektors zu unscharfen Termen ![]() aus der Wissensbank wird folgendermaßen berechnet:
aus der Wissensbank wird folgendermaßen berechnet:
![]() — diese Funktion wird das Ergebnis der j-en Regel aus der Wissensbank charakterisieren;
— diese Funktion wird das Ergebnis der j-en Regel aus der Wissensbank charakterisieren;
wobei ![]() — Operation aus der s-Norm (t-Norm) ist, d.h. aus der Implementierungsmenge der logischen Operation ODER (UND). Besonders häufig werden die folgenden Implementierungen verwendet: für ODER — Maximum finden; für UND — Minimum finden.
— Operation aus der s-Norm (t-Norm) ist, d.h. aus der Implementierungsmenge der logischen Operation ODER (UND). Besonders häufig werden die folgenden Implementierungen verwendet: für ODER — Maximum finden; für UND — Minimum finden.
Nach dem ![]() für
für ![]() gefunden wurde, bekommen wir m neue Zugehörigkeitsfunktionen, die eine neue Fuzzy-Menge bilden, nennen wir diese
gefunden wurde, bekommen wir m neue Zugehörigkeitsfunktionen, die eine neue Fuzzy-Menge bilden, nennen wir diese ![]() , die dem Eingangsvektor
, die dem Eingangsvektor ![]() entspricht.
entspricht.
![]()
Die Besonderheit dieser Fuzzy-Menge besteht darin, dass die Term-Menge der Ausgangsvariablen ![]() für diese als eine universelle Menge gilt.
für diese als eine universelle Menge gilt.
Weiter muss man:
- die Zugehörigkeitsfunktionen
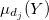 an der Ebene
an der Ebene 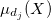 "schneiden";
"schneiden"; - die Fuzzy-Mengen vereinen.
Wenn wir uns der Fachbegriffe der Fuzzylogik bedienen, muss man die Implikation und Aggregation der Bedingungen vornehmen. Die Implikation kann mithilfe von zwei Methoden modelliert werden: durch das Finden des Minimums oder des Produkts der Mengen, Aggregation — Finden des Maximums oder der Summe der Mengen.
Als Ergebnis bekommen wir eine Fuzzy-Menge, deren Defuzzifizierung uns einen genauen Output gibt.
1.4. Unscharfe Inferenz nach Sugeno
Die unscharfe Inferenz nach dem Algorithmus von Sugeno wird nach der unscharfen Datenbank ausgeführt:
Die Wissensbank von Sugeno ist der von Mamdani gleich außer der Inferenzen ![]() , die nicht durch unscharfe Terme, sondern durch eine lineare Funktion von den Inpunts gesetzt werden:
, die nicht durch unscharfe Terme, sondern durch eine lineare Funktion von den Inpunts gesetzt werden:
![]()
Die Regeln in der Sugeno-Regelung schalten quasi zwischen dem linearen Gesetzt "Input-Output" und einem anderen (auch linear) um. Grenzen der Unterbereiche sind verschwommen, d.h. mehrere lineare Gesetze (aber unterschiedlichen Grades) können gleichzeitig vollzogen werden.
Diese Wissensbank kann folgendermaßen notiert werden:
![]()
wobei:
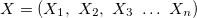 — Vektor der Eingangsvariablen.
— Vektor der Eingangsvariablen.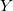 — Ausgangsvariable.
— Ausgangsvariable.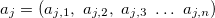 — Vektor der Eingangsvariablen in der j-en Regel, j=0,1,2...m.
— Vektor der Eingangsvariablen in der j-en Regel, j=0,1,2...m.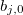 — Koeffizient bei einem absoluten Glied in der linearen Funktion für den Output in der j-en Regel, j=0,1,2...m.
— Koeffizient bei einem absoluten Glied in der linearen Funktion für den Output in der j-en Regel, j=0,1,2...m.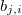 — Koeffizient bei dem i-en Glied in der linearen Funktion für den Output in der j-en Regel, j=0,1,2...m, i=0,1,2...n.
— Koeffizient bei dem i-en Glied in der linearen Funktion für den Output in der j-en Regel, j=0,1,2...m, i=0,1,2...n.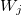 — Gewicht der j-en Regel, j=0,1,2...m.
— Gewicht der j-en Regel, j=0,1,2...m.
Führen wir eine neue Bezeichnung ein: ![]() — Zugehörigkeitsfunktion einer unscharfen Eingangs- oder Ausgangsvariablen v zum unscharfen Term t.
— Zugehörigkeitsfunktion einer unscharfen Eingangs- oder Ausgangsvariablen v zum unscharfen Term t.
Der Zugehörigkeitsgrad des Eingansvektors zu unscharfen Termen ![]() aus der Wissensbank wird folgendermaßen berechnet:
aus der Wissensbank wird folgendermaßen berechnet:
![]() — diese Funktion wird das Ergebnis der j-en Regel aus der Wissensbank charakterisieren;
— diese Funktion wird das Ergebnis der j-en Regel aus der Wissensbank charakterisieren;
wobei ![]() — Operation aus der s-Norm (t-Norm) ist, d.h. aus der Implementierungsmenge der logischen Operation ODER (UND). In der Inferenz nach Sugeno werden am häufigsten die folgenden Implementierungen der Dreiecksnormen verwendet: probabilistische ODER als eine s-Norm und das Produkt als eine t-Norm.
— Operation aus der s-Norm (t-Norm) ist, d.h. aus der Implementierungsmenge der logischen Operation ODER (UND). In der Inferenz nach Sugeno werden am häufigsten die folgenden Implementierungen der Dreiecksnormen verwendet: probabilistische ODER als eine s-Norm und das Produkt als eine t-Norm.
Nach dem ![]() für
für ![]() gefunden wurde, bekommen wir m neue Zugehörigkeitsfunktionen, die eine neue Fuzzy-Menge bilden, nennen wir diese
gefunden wurde, bekommen wir m neue Zugehörigkeitsfunktionen, die eine neue Fuzzy-Menge bilden, nennen wir diese ![]() , die dem Eingangsvektor
, die dem Eingangsvektor ![]() entspricht.
entspricht.
![]()
Im Vergleich zu Mamdani-Inferenz ist die oben angeführte Fuzzy-Menge eine einfache Fuzzy-Menge ersten Grades. Sie wird durch eine Menge scharfer Werte definiert. Das Ergebnis des Outputs wird als eine ![]() Superposition linearen Abhängigkeiten im Punkt
Superposition linearen Abhängigkeiten im Punkt ![]() eines n-dimensionalen Faktorraums bezeichnet. Hierfür wird die Fuzzy-Menge
eines n-dimensionalen Faktorraums bezeichnet. Hierfür wird die Fuzzy-Menge ![]() deffuziert, indem man das gewichtete arithmetische Mittel oder die gewichtete Summe findet.
deffuziert, indem man das gewichtete arithmetische Mittel oder die gewichtete Summe findet.
2. FuzzyNet - Bibliothek der Fuzzylogik
In der Praxis ist es relativ kompliziert, auch ein einfaches Fuzzy-Modell zu erstellen und mit dieser zu arbeiten. Es gibt aber vielfältige Programme und Bibliotheken, die diese Aufgabe erleichtern. Schauen wir uns die Erstellung und Arbeit mit zwei Fuzzy-Modellen anhand der Testskripte aus der FuzzyNet-Bibliothek für MQL5 an.
2.1. Systeme vom Typ Mamdani entwerfen
Erstes Beispiel: das Skript Tips_Sample_Mamdani.mq5 aus der FuzzyNet-Bibliothek für MQL5. In diesem Beispiel wird ein Fuzzy-Modell für die Berechnung des Trinkgeldes je nach der Qualität der Bedienung und des Essens umgesetzt. Dieses System besteht aus zwei unscharfen Eingangsparameter, einer Regelung aus drei Regeln und einer Inferenz nach Mamdani.
Als Eingangsparameter dienen die Fuzzy-Variablen "Essen" (food) und "Bedienung" (service); die beiden Variablen werden von 0 bis 10 bewertet — dies sind der minimale und der maximale Werte. Die Variable "Essen" besteht aus zwei Termen: "schlecht" (rancid) und "lecker" (delicious). Die Variable "Bedienung" besteht aus drei unscharfen Termen: "schlecht" (poor), "gut" (good) und "ausgezeichnet" (excellent).
Ausgegeben wird eine unscharfe Variable "Trinkgeld" (tips). Legen wir den Bereich für Trinkgeld in Höhe von 5% bis 30% vom Gesamtbetrag fest und bestimmen wir drei Terme für diese Variable: "wenig" (cheap), "wie üblich" (average), "gut" (generous).
Die Regelung besteht aus drei Regeln:
- Wenn (schlechte Bedienung) oder (schlechtes Essen), dann wenig Trinkgeld.
- Wenn (gute Bedienung), dann Trinkgeld wie üblich.
- Wenn (ausgezeichnete Bedienung) oder (leckeres Essen), dann gutes Trinkgeld.
Nun haben wir eine allgemeine Vorstellung vom System. Schauen wir uns die Erstellung genauer an:
- Fügen wir die MamdaniFuzzySystem.mqh-Datei aus der FuzzyNet-Bibliothek für MQL5 ein:
#include <Math\FuzzyNet\MamdaniFuzzySystem.mqh>Diese Datei ermöglicht es, Systeme vom Typ Mamdani zu erstellen und mit diesen zu arbeiten. - Jetzt können wir ein leeres Mamdani-System erstellen und es mit Inhalten füllen:
MamdaniFuzzySystem *fsTips=new MamdaniFuzzySystem(); - Erstellen wir die erste Eingangsvariable "Bedienung". Bei der Erstellung unscharfer Variablen wird zuerst der Name der Variablen als eine Zeile und dann ihre niedrigster und höchster Werte angegeben.
FuzzyVariable *fvService=new FuzzyVariable("service",0.0,10.0);
- Fügen wir die unscharfen Terme hinzu. Der Fuzzy-Regler legt den Namen als eine Zeile als ersten Parameter und eine entsprechende Zugehörigkeitsfunktion als zweiten Parameter fest.
fvService.Terms().Add(new FuzzyTerm("poor", new TriangularMembershipFunction(-5.0, 0.0, 5.0))); fvService.Terms().Add(new FuzzyTerm("good", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvService.Terms().Add(new FuzzyTerm("excellent", new TriangularMembershipFunction(5.0, 10.0, 15.0)));
Die Zugehörigkeitsfunktionen stellen für jeden Term in diesem Beispiel eine Dreiecksfunktion dar. - Fügen wir die fertige und geformte unscharfe Variable unserem System hinzu:
fsTips.Input().Add(fvService);
- Das zweite Input wird für das System mit der Variablen "Essen" umgesetzt. Die Terme haben für diese Variable eine trapezförmige Zugehörigkeitsfunktion.
FuzzyVariable *fvFood=new FuzzyVariable("food",0.0,10.0); fvFood.Terms().Add(new FuzzyTerm("rancid", new TrapezoidMembershipFunction(0.0, 0.0, 1.0, 3.0))); fvFood.Terms().Add(new FuzzyTerm("delicious", new TrapezoidMembershipFunction(7.0, 9.0, 10.0, 10.0))); fsTips.Input().Add(fvFood);
- Das System hat die Inferenz vom Typ Mamdani, so werden die Eingangs- und Ausgangsgrößen nach einer und dergleichen Methode definiert. Nach gleichem Schema erstellen wir die Ausgabe:
FuzzyVariable *fvTips=new FuzzyVariable("tips",0.0,30.0); fvTips.Terms().Add(new FuzzyTerm("cheap", new TriangularMembershipFunction(0.0, 5.0, 10.0))); fvTips.Terms().Add(new FuzzyTerm("average", new TriangularMembershipFunction(10.0, 15.0, 20.0))); fvTips.Terms().Add(new FuzzyTerm("generous", new TriangularMembershipFunction(20.0, 25.0, 30.0))); fsTips.Output().Add(fvTips);
- Erstellen wir unscharfe Regeln, die die Wissensbank des Systems bilden werden. Für die Erstellung einer Regel muss man die ParseRule Methode von dem Objekt aufrufen, das unser System repräsentiert, und ihm eine einfache String-Repräsentation der unscharfen Regel als Parameter übergeben:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is cheap)"); MamdaniFuzzyRule *rule2 = fsTips.ParseRule("if (service is good) then (tips is average)"); MamdaniFuzzyRule *rule3 = fsTips.ParseRule("if (service is excellent) or (food is delicious) then (tips is generous)");
Das Schreiben unscharfer Regeln ist strikt festgelegt und lässt nur Schlüsselwörter zu. Als Schlüsselwörter gelten: "if", "then", "is", "and", "or", "not", "(" , ")", "slightly", "somewhat", "very" und "extremely". Die letzten vier Schlüsselwörter sind linguistische Quantoren. Zu Schlüsselwörtern zählen auch die Namen aller Variablen, Termini und Funktionen, die es in Ihrem System gibt. Linguistische Quantoren steigern oder senken die Gewichtung unscharfer Terme oder linearer Sugeno-Funktionen. Umsetzung linguistischer Quantoren:
- "slightly" — "kaum", ersetzt das Ergebnis der Bedingung durch ihre Kubikwurzel. Erheblich senkt die Gewichtung.
- "somewhat" — "zum Teil", ersetzt das Ergebnis der Bedingung durch ihre Quadratwurzel. Senkt die Gewictung.
- "very" — "sehr", erhebt das Ergebnis der Bedingung ins Quadrat. Erhöht die Gewichtung.
- "extremely" — "höchst", erhebt das Ergebnis der Bedingung in die dritte Potenz. Wesentlich erhöht die Gewichtung.
- "slightly" — "kaum", ersetzt das Ergebnis der Bedingung durch ihre Kubikwurzel. Erheblich senkt die Gewichtung.
- Es bleibt nur die Regeln dem System hinzuzufügen:
fsTips.Rules().Add(rule1); fsTips.Rules().Add(rule2); fsTips.Rules().Add(rule3);
Nun ist das Modell zur Berechnung des Trinkgeldes nach der Mamdani-Inferenz fertig.
2.2. Systeme vom Typ Sugeno auslegen
Die Auslegung eines Systems vom Typ Sugeno kann man am Skript zur Berechnung der Steuerung eines Tempomats erläutern. Das Skript ist in der Datei Cruise_Control_Sample_Sugeno.mq5 der FuzzyNet Bibliothek für MQL5 beschrieben und ist eines der Bespiele für die Anwendung unscharfer Modelle bei der Problemlösung der automatischen Steuerung.
Besonders häufig wird die Fuzzylogik gerade für solche eindimensionalen Aufgaben in den automatischen Steuerungssystemen verwendet. Die Aufgabe lautet: irgendein Objekt befindet sich in einem Moment der Zeit ![]() im Zustand "A", es wird benötigt, dass er innerhalb der Zeit
im Zustand "A", es wird benötigt, dass er innerhalb der Zeit ![]() den Zustand "B" einnimmt. Um diese Aufgabe zu lösen, wird das Zeitintervall in
den Zustand "B" einnimmt. Um diese Aufgabe zu lösen, wird das Zeitintervall in ![]() Abschnitte aufgeteilt. Man findet einen Zeitschritt, der
Abschnitte aufgeteilt. Man findet einen Zeitschritt, der ![]() gleich ist, anschließend setzt das automatische Steuerungssystem dies in jedem Punkt
gleich ist, anschließend setzt das automatische Steuerungssystem dies in jedem Punkt ![]() um, wo i=0,1,2...n.
um, wo i=0,1,2...n.
Diese Aufgabe können unterschiedliche PID-Regler meistern, sie weisen aber einen wesentlichen Nachteil auf: sie können keine "gleichmäßige" Steuerung gewährleisten. Das heißt, wenn man den Tempomat aufgrund eines PID-Reglers bildet, stellt das System bei der Veränderung der Geschwindigkeit zwar die gewünschte Geschwindigkeit ein, dabei kann es aber zu Rucken kommen. Ein Fuzzy-Regler kann diese Aufgabe gleichmäßiger und aus der Perspektive des Kunden bequemer ausführen.
Der Fuzzy-Regler wird die notwendige Geschwindigkeitsänderung als Beschleunigung ausgeben, eingegeben werden der Fehler und die erste Variable des Fehlers. Als Fehler gilt die Abweichung des aktuellen Zustands vom gewünschten. Anders gesagt, werden die folgenden Daten ins System eingegeben:
- Differenz zwischen der Geschwindigkeit in dem Moment und der Geschwindigkeit, die im Tempomat eingestellt wurde;
- wie schnell sich die Differenz verkleinert (vergrößert).
Der Wert des erstes Eingangsparameters "Geschwindigkeitsfehler" (SpeedError) wird zwischen -20 und 20 km/h liegen und drei Terme haben: "gesunken" (slower), "blieb unverändert" (zero), "gestiegen" (faster). Alle drei Terme haben eine Dreiecksfunktion der Zugehörigkeit. Der zweite Eingangsparameter — "Variable nach Geschwindigkeitsfehler" (SpeedErrorDot) mit dem Wertebereich -5 5 und unscharfen Termen "gesunken" (slower), "unverändert" (zero), "gestiegen" (faster), auch mit einer Dreiecksfunktion der Zugehörigkeit.
Da das Model eine Sugeno-Inferenz hat, hat der Ausgabewert "Beschleunigung" (Accelerate) weder den maximalen noch den minimalen Wert und statt Fuzzy-Terme gibt es lineare Kombinationen der Eingangsvariablen, die die Namen: "unverändert lassen" (zero), "erhöhen" (faster), "senken" (slower), "einhalten" (func) haben werden. Erweitern wir alle vier linearen Kombinationen. Dafür bezeichnen wir die Variable SpeedError als ![]() , SpeedErrorDot als
, SpeedErrorDot als ![]() und Accelerate als
und Accelerate als ![]() , dann bekommen wir folgende Gleichungen:
, dann bekommen wir folgende Gleichungen:
- zero:
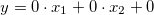 ;
; - faster:
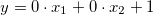 ;
; - slower:
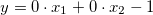 ;
; - func:
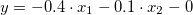 .
.
Die Regelung dieses Systems wird aus neun Regeln bestehen:
- Wenn der (Geschwindigkeitsfehler gesunken) und die (Variable gesunken) sind, dann die Beschleunigung erhöhen.
- Wenn der (Fehler gesunken) ist und die (Variable unverändert) blieb, dann die Beschleunigung erhöhen.
- Wenn der (Fehler gesunken) und die (Variable gestiegen) sind, dann die Beschleunigung unverändert lassen.
- Wenn der (Fehler unverändert) blieb und die (Variable gesunken) sind, dann die Beschleunigung erhöhen.
- Wenn der (Fehler unverändert) und die (Variable unverändert) blieben, dann die Beschleunigung einhalten.
- Wenn der (Fehler unverändert) blieb und die (Variable gestiegen) ist, dann die Beschleunigung senken.
- Wenn der (Fehler gestiegen) und die (Variable gesunken) sind, dann die Beschleunigung erhöhen.
- Wenn der (Fehler gestiegen) ist und die (Variable unverändert) blieb, dann die Beschleunigung senken.
- Wenn der (Fehler gestiegen) und die (Variable gestiegen) sind, dann die Beschleunigung senken.
Schauen wir uns den Verlauf genauer an:
- Fügen wir die Datei SugenoFuzzySystem.mqh aus der FuzzyNet Bibliothek für MQL5 ein:
#include <Math\FuzzyNet\SugenoFuzzySystem.mqh>Diese Datei lässt Systeme vom Typ Sugeno erstellen und mit diesen arbeiten. - Jetzt können wir ein "leeres" Sugeno-System erstellen und dieses mit Inhalten füllen:
SugenoFuzzySystem *fsCruiseControl=new SugenoFuzzySystem(); - Die Eingangsvariablen werden für das Sugeno-System genauso wie für das Mamdani-System erstellt.
Erstellen wir die Variable "Geschwindigkeitsfehler" und fügen wir diese dem System hinzu:
FuzzyVariable *fvSpeedError=new FuzzyVariable("SpeedError",-20.0,20.0); fvSpeedError.Terms().Add(new FuzzyTerm("slower",new TriangularMembershipFunction(-35.0,-20.0,-5.0))); fvSpeedError.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-15.0, -0.0, 15.0))); fvSpeedError.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(5.0, 20.0, 35.0)));
Erstellen wir die Variable "Änderung des Geschwindigkeitsfehlers" und fügen wir diese ebenso dem System hinzu:
FuzzyVariable *fvSpeedErrorDot=new FuzzyVariable("SpeedErrorDot",-5.0,5.0); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("slower", new TriangularMembershipFunction(-9.0, -5.0, -1.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("zero", new TriangularMembershipFunction(-4.0, -0.0, 4.0))); fvSpeedErrorDot.Terms().Add(new FuzzyTerm("faster", new TriangularMembershipFunction(1.0, 5.0, 9.0)));
- Erstellen wir eine unscharfe Variable vom Typ Sugeno, die als Output für das System gelten wird. Bei der Erstellung einer unscharfen Variablen akzeptiert der Konstruktor nur einen Parameter - ihren Namen. Danach kann man lineare Funktionen hinzufügen, zunächst müssen aber diese definiert werden. Dafür wird das Array der Koeffizienten vom Typ double benötigt.
Die lineare Funktion wird folgendermaßen realisiert: jede Eingangsvariable ist die Unbekannte der Gleichung mit einem Koeffizient aus dem Koeffizienten-Array. Die Koeffizienten müssen im Array in der Reihenfolge platziert werden, in der die Eingangsvariablen eingegeben wurden. Der Index des Koeffizienten bei der ersten Eingangsvariablen beträgt 0, bei der zweiten — 1 usw. Aus diesem Grund muss das Arrays der Koeffizienten um 1 länger oder der Anzahl der Eingabevariablen gleich sein. Wenn die Längen gleich sind, wird der Koeffizient bei einem absoluten Glied Null betragen, sonst wird er dem letzten Element des Arrays gleich sein.
Wir haben zwei Eingabevariablen in unserem System, deswegen dürfen die Arrays nicht länger als drei sein. Deklarieren wir alle vier Arrays, konstruieren wir die oben beschriebenen Funktionen und fügen wir diese der Variablen vom Typ Sugeno hinzu:SugenoVariable *svAccelerate=new SugenoVariable("Accelerate"); double coeff1[3]={0.0,0.0,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("zero",coeff1)); double coeff2[3]={0.0,0.0,1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("faster",coeff2)); double coeff3[3]={0.0,0.0,-1.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("slower",coeff3)); double coeff4[3]={-0.04,-0.1,0.0}; svAccelerate.Functions().Add(fsCruiseControl.CreateSugenoFunction("func",coeff4)); fsCruiseControl.Output().Add(svAccelerate);
- Analog zum System von Mamdani erstellen wir alle neun unscharfe Regeln:
SugenoFuzzyRule *rule1 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule2 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is zero) then (Accelerate is faster)"); SugenoFuzzyRule *rule3 = fsCruiseControl.ParseRule("if (SpeedError is slower) and (SpeedErrorDot is faster) then (Accelerate is zero)"); SugenoFuzzyRule *rule4 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule5 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is zero) then (Accelerate is func)"); SugenoFuzzyRule *rule6 = fsCruiseControl.ParseRule("if (SpeedError is zero) and (SpeedErrorDot is faster) then (Accelerate is slower)"); SugenoFuzzyRule *rule7 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is slower) then (Accelerate is faster)"); SugenoFuzzyRule *rule8 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is zero) then (Accelerate is slower)"); SugenoFuzzyRule *rule9 = fsCruiseControl.ParseRule("if (SpeedError is faster) and (SpeedErrorDot is faster) then (Accelerate is slower)");
- Fügen wir diese unserem System hinzu:
fsCruiseControl.Rules().Add(rule1); fsCruiseControl.Rules().Add(rule2); fsCruiseControl.Rules().Add(rule3); fsCruiseControl.Rules().Add(rule4); fsCruiseControl.Rules().Add(rule5); fsCruiseControl.Rules().Add(rule6); fsCruiseControl.Rules().Add(rule7); fsCruiseControl.Rules().Add(rule8); fsCruiseControl.Rules().Add(rule9);
2.3. Berechnung der Systeme von Mamdani und Sugeno
Zum Input eines unscharfen Systems muss eine unscharfe Variable und ihr Wert geschickt werden. Wie bereits oben erwähnt wurde, nehmen unscharfe Variablen Werte aus ihren Term-Mengen an. Demzufolge hängt das Berechnungsergebnis von der Zugehörigkeitsfunktionen ab, die den Termen bei der Eingabe entsprechen. In den meisten Fällen schickt man aber zur Ausgabe unscharfe Variablen als einfache Zahlenwerte und will ein genaues Ergebnis in der gleichen Form bekommen. In diesem Fall ergibt es sich, dass der unscharfe Term keine offensichtliche Deklarierung hat und seine Zugehörigkeitsfunktion als eine konstante Zugehärigkeitsfunktion dargestellt wird. Gerade mit diesem Sonderfall haben die Systeme zu tun, die anhand der FuzzyNet Bibliothek geschrieben wurden.
Was genau muss zur Eingabe des Systems geschickt werden und in welcher Form bekommen wir das Ergebnis?
Die Zahl der Eingangsvariablen ist für unscharfe Systeme unbegrenzt, jede Ausgabe muss einen Wert annehmen, deswegen müssen wir eine Liste haben, in der Werte für jede Ausgabe gespeichert werden. Zu Elementen dieser Liste gehört ein komplexes Objekt mit zwei Feldern: erstes Feld — eine Fuzzy-Variable, zweites Feld — Zahlenwerte vom Typ double. In der Datei Dictionary.mqh aus der FuzzyNet Bibliothek in MQL5 wurde die Klasse Dictionary_Obj_Double umgesetzt, mit der man solche Objekte erstellen kann.
Erstellen wir die Eingangsliste für das System vom Typ Mamdani:
CList *in=new CList; Dictionary_Obj_Double *p_od_Service=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_Food=new Dictionary_Obj_Double; p_od_Service.SetAll(fvService, Service); p_od_Food.SetAll(fvFood, Food); in.Add(p_od_Service); in.Add(p_od_Food);
Service und Food sind hier zwei Ausgangsparameter vom Typ double.
In den oben beschriebenen Beispielen haben beide Systeme (Mamdani und Sugeno) nur eine Ausgabe. Im Allgemeinen ist die Zahl der Ausgaben und Eingaben unbegrenzt. Eingabe und Ausgabe unterscheiden sich nicht voneinander.
Ausgabe für das System vom Typ Mamdani:
CList *result=new CList; Dictionary_Obj_Double *p_od_Tips=new Dictionary_Obj_Double;
Nun rufen wir die Calculate Funktion für jedes System auf, die nur einen Parameter — die Eingabeliste empfängt und die Ausgabeliste liefert. Nach dem Index 0 erhalten wir den Output-Wert, der als ein Objekt der Klasse Dictionary_Obj_Double darstellt. Wenn man Key und Value für dieses Objekt nutzt, kann man eine Variable und ihr Ergebnis bekommen.
Machen wir Berechnungen für das Mamdani-System und zeigen wir die Zahl bei der unscharfen Ausgangsvariablen fvTips auf dem Bildschirm an:
result=fsTips.Calculate(in); p_od_Tips=result.GetNodeAtIndex(0); Alert("Tips, %: ",p_od_Tips.Value());
Unternehmen wir das gleiche für das System vom Typ Sugeno:
CList *in=new CList; Dictionary_Obj_Double *p_od_Error=new Dictionary_Obj_Double; Dictionary_Obj_Double *p_od_ErrorDot=new Dictionary_Obj_Double; p_od_Error.SetAll(fvSpeedError,Speed_Error); p_od_ErrorDot.SetAll(fvSpeedErrorDot,Speed_ErrorDot); in.Add(p_od_Error); in.Add(p_od_ErrorDot); CList *result=new CList; Dictionary_Obj_Double *p_od_Accelerate=new Dictionary_Obj_Double; result=fsCruiseControl.Calculate(in); p_od_Accelerate=result.GetNodeAtIndex(0); Alert("Accelerate, %: ",p_od_Accelerate.Value()*100);
Fazit
Mehr über die oben beschriebenen Skripte erfahren sowie ein eigenes unscharfes Modell erstellen können Sie, indem Sie die FuzzyNet Bibliothek für MQL5 oder MQL4 herunterladen. Man muss sich im Klaren sein, dass der Aufbau funktionierender Fuzzy-Modelle kompliziert ist, auch wenn man sich dabei Bibliotheken bedient, und jedes fertige Modell sorgfältig überprüft und eingestellt werden muss.
Quellenangabe
- Technische Anwendungen von Fuzzy-Systemen
- Mathias Bank. Fuzzy-Logik
- Fuzzy-Logik in Theorie und Praxis
- Fuzzy-Regler
- R. Mikut, S. Böhlmann, B. Cuno, J. Jäkel, A. Kroll,T. Rauschenbach, B.-M. Pfeiffer, T. Slawinski. Fuzzy-Logik und Fuzzy Control - Begriffe und Definitionen
Übersetzt aus dem Russischen von MetaQuotes Ltd.
Originalartikel: https://www.mql5.com/ru/articles/1991
Warnung: Alle Rechte sind von MetaQuotes Ltd. vorbehalten. Kopieren oder Vervielfältigen untersagt.
 Atypisches Automatisiertes Trading
Atypisches Automatisiertes Trading
 Praktische Implementierung digitaler Filter in MQL5 für Anfänger
Praktische Implementierung digitaler Filter in MQL5 für Anfänger
 Test Visualisierung: Kontostand Charts
Test Visualisierung: Kontostand Charts
 MQL5: Analyse und Umgang mit Berichten der US-Warenterminhandelsaufsichtsbehörde (US-Warenterminhandelsaufsichtsbehörde , CFTC) in MetaTrader 5
MQL5: Analyse und Umgang mit Berichten der US-Warenterminhandelsaufsichtsbehörde (US-Warenterminhandelsaufsichtsbehörde , CFTC) in MetaTrader 5
- Freie Handelsapplikationen
- Über 8.000 Signale zum Kopieren
- Wirtschaftsnachrichten für die Lage an den Finanzmärkte
Sie stimmen der Website-Richtlinie und den Nutzungsbedingungen zu.
Hallo
als ich Metatrader auf Build 2342 aktualisiert habe
alle Beispiele mit Fuzzy-Logik-Bibliothek
Rückgabefehler "incorrect casting of pointers" in MQL5\Include\Math\Fuzzy\RuleParser.mqh Zeile 712
Bitte helfen Sie, den Fehler zu beheben
vielen Dank
Lesen Sie meinen vorherigen Beitrag.
Hallo
danke für deine Antwort
der eigentliche Autor ist Dmitry Kalyuzhny, aber er hat diese Bibliothek in .Net kodiert.
Aber vielleicht hat jemand anderes den Code in mql geändert
ich sehe der Autor dieses Artikels ist Дмитрий Калюжный
aber ich konnte Дмитрий Калюжный Profil auf mql5 nicht finden.
Würden Sie mir bitte helfen, Kontakt aufzunehmen oder diesen Fehler zu beheben
vielen Dank
Der neue Artikel An Introduction to Fuzzy Logic wurde veröffentlicht:
Autor: MetaQuotes Software Corp.
Hallo
als ich Metatrader auf Build 2342 aktualisiert habe
alle Beispiele mit Fuzzy-Logik-Bibliothek
geben den Fehler "incorrect casting of pointers" in MQL5\Include\Math\Fuzzy\RuleParser.mqh Zeile 712 zurück
Bitte helfen Sie, den Fehler zu beheben
vielen Dank
Hallo
danke für die Wiederholung
der eigentliche Autor ist Dmitry Kalyuzhny, aber er hat diese Bibliothek in .Net programmiert
Aber vielleicht hat jemand anderes den Code in mql geändert
ich sehe der Autor dieses Artikels ist Дмитрий Калюжный
aber ich konnte Дмитрий Калюжный Profil auf mql5 nicht finden
Würden Sie mir bitte helfen, diesen Fehler zu kontaktieren oder zu beheben
vielen Dank
Wenn niemand auf diesem Thread hilft, so können Sie Freelance zum Beispiel verwenden.
Hallo Leute,
ich habe eine Frage zu den 'linguistischen Quantoren': " etwas", "etwas", "sehr", "extrem"...
Was ist die korrekte Verwendung dieser Quantoren in der ParseRule-Funktion?
Wenn ich etwas wie dieses versuche:
MamdaniFuzzyRule *rule1 = fsTips.ParseRule("if (service is poor) or (food is rancid) then (tips is very cheap)");...erhalte ich diesen Fehler: "Der Schlussteil der Regel sollte in der Form sein: 'variable is term'"
Wo müsste ich das 'very' in der obigen Zeichenkette platzieren?
Für Hilfe wäre ich sehr dankbar!
Vielen Dank!