Análise espectral singular unidimensional

Introdução

Os mercados financeiros caracterizam-se por elevada volatilidade e processos dinâmicos complexos, o que torna o prognóstico e a identificação de padrões tarefas extremamente desafiadoras. A análise espectral singular (SSA) é um método eficaz de análise de séries temporais que possibilita representar a estrutura complexa da série sob a forma de uma decomposição em componentes simples, como tendência, oscilações sazonais (periódicas) e ruído. Baseado em álgebra linear, o método SSA dispensa hipóteses de estacionariedade, o que o torna uma ferramenta universal para investigar a estrutura de séries temporais. 

Contudo, o amplo uso de teoria de álgebra vetorial e matricial na literatura sobre SSA cria um nível de entrada bastante alto, o que pode dificultar a compreensão do tema por leitores sem preparação específica e impedi-los de perceber todas as sutilezas e vantagens desse método de análise. Este artigo busca apresentar de forma acessível e clara os fundamentos teóricos do SSA (sem eles o método se torna uma "caixa-preta") assim como oferecer uma implementação prática dos conceitos descritos. 

É necessário esclarecer que o termo SSA deve ser entendido como um conjunto inteiro de métodos de análise, porém todos se baseiam na aplicação sequencial de quatro etapas:

• transformação da série temporal em matriz de trajetória (matriz de Hankel),
• decomposição da matriz de trajetória em soma de matrizes elementares de posto um,
• agrupamento das matrizes elementares,
• reconstrução (recuperação) da série temporal.

Examinemos com mais detalhes cada uma dessas etapas.

Construção da matriz de trajetória

A ideia principal consiste em transformar a série temporal em uma matriz que reflita sua estrutura em um espaço multidimensional. Isso é feito para revelar dependências ocultas entre valores sequenciais da série. A matriz de trajetória é construída da seguinte maneira. Toma-se uma amostra unidimensional da série temporal de tamanho N e transforma-se em um conjunto de K vetores (K = N – L + 1) por meio da composição de subamostras deslizantes de tamanho L (comprimento da janela). Os vetores resultantes de comprimento L (x1,x2,...,xL,{x2,x3,...,xL+1}e assim por diante), são dispostos nas colunas da matriz de trajetória X.

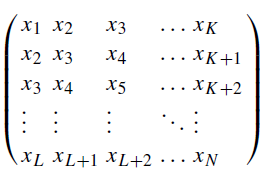
Fig.1 Matriz de trajetória X

Aqui o parâmetro L define a profundidade da análise. Normalmente ele é fixado como N/2.

Decomposição da matriz de trajetória em soma de matrizes de posto um

Após construir a matriz de trajetória, realiza-se a sua decomposição. Quando essa decomposição é o valor singular (SVD) da matriz de trajetória, o método recebe o nome de básico (Basic-SSA).

Com a decomposição singular formam-se as chamadas tríades próprias (√λi, Ui, Vi), onde

• σi = √λi — os valores singulares iguais à raiz dos autovalores da matriz XX',
• Ui — vetores singulares à esquerda,
• Vi — vetores singulares à direita,
• i — quantidade de valores singulares, igual ao posto da matriz de trajetória X.

Os valores singulares σi indicam o peso de cada componente; valores grandes correspondem a padrões importantes (tendência, ciclos), e valores pequenos correspondem a ruído.

Assim, por meio da decomposição SVD, a matriz de trajetória pode ser representada como a soma de matrizes elementares Xi de posto um:

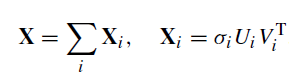
As matrizes de posto um são "tijolos" a partir dos quais se constroem matrizes mais complexas.

Esclareçamos o conceito de posto de matriz no contexto do método SSA. O SSA visa extrair o sinal determinístico de uma série temporal. Sequências determinísticas, como exponencial, polinômio ou senoide, caracterizam-se por posto finito. Isso ocorre porque satisfazem relações lineares recorrentes (LRR) e suas matrizes de trajetória contêm um número limitado de vetores linearmente independentes. Por exemplo, a matriz de trajetória de uma sequência exponencial tem posto 1 (apenas um vetor linearmente independente), a de uma senoide tem posto 2, a de um polinômio de grau k tem posto k+1 e assim por diante.

Script Rank que demonstra o conceito de posto de séries determinísticas:

//+------------------------------------------------------------------+
//|                                                         Rank.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs

input int         N  = 100;                // N - length of generated time series
input int         L  = 30;                 // L - window length
input int         T  = 22;                 // T - period length of sine function
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   matrix X=matrix::Zeros(L,N-L+1);
   vector x_exp= vector::Zeros(N);
   vector x_sinus= vector::Zeros(N);
   vector x_polynom= vector::Zeros(N);
   for(int t=0; t <N; t++)
     {
      x_exp[t] = MathPow(1.01,t);           // 1. Экспоненциальная последовательность: x_t = 1.01^t
      x_sinus[t] = MathSin(2*M_PI*t/T);     // 2. Синусоида: x_t = sin(2 * pi * t / T)
      x_polynom[t] =  1 + t+ MathPow(t,2);  // 3. Полином степени 2: x_t = 1 + t + t^2
     }
   trajectory_matrix(x_exp,L,X);
   Print("Rank Exponential sequence = ",Rank_SVD(X));
   trajectory_matrix(x_sinus,L,X);
   Print("Rank Sinus sequence = ",Rank_SVD(X));
   trajectory_matrix(x_polynom,L,X);
   Print("Rank Polynom sequence = ",Rank_SVD(X));
  }
//+------------------------------------------------------------------+
//| Траекторная матрица X                                            |
//+------------------------------------------------------------------+
void trajectory_matrix(vector & series,int window_length, matrix & X)
  {
   int N_ = (int)series.Size();
   int L_ = window_length;
   int K = N_ - L_ + 1;
   X=matrix::Zeros(L_,K);
   for(int i=0; i <L_;  i++)
     {
      for(int j=0; j <K;  j++)
        {
         X[i,j] = series[i+j];
        }
     }
  }
//+------------------------------------------------------------------+
//|Finds the rank of a matrix using SVD                              |
//+------------------------------------------------------------------+
int Rank_SVD(matrix & X)
  {
   vector sv;
   matrix U,V;
   double tol = 1e-8;  // Порог для ненулевых значений
   X.SingularValueDecompositionDC(SVDZ_N,sv,U,V);
   double threshold = tol * sv.Max();
   int rank=0;
   for(int i=0; i<(int)sv.Size(); i++)
     {
      if(sv[i] > threshold)
         rank++;
     }
   return rank;
  }
//+------------------------------------------------------------------+

Séries temporais reais, como preços de mercado, não são sequências de posto finito devido à presença de ruído, o que as torna séries de posto completo = min(L, K). Todavia, se a série for a soma de um sinal determinístico de posto finito e de ruído, o SSA consegue isolar aproximadamente esse sinal. Em seguida, a previsão é realizada apenas para a componente determinística e o ruído é descartado. Para isso, a matriz de trajetória (X) é decomposta em matrizes elementares de posto 1, das quais se formam matrizes mais complexas correspondentes ao sinal determinístico útil. Nessa ideia reside o cerne do método SSA.

Agrupamento

Na etapa de agrupamento, as matrizes elementares de posto um são reunidas em grupos que são interpretados como diferentes componentes da série (tendência, sazonalidade, ruído). Um dos métodos mais difundidos consiste em agrupar as matrizes com base na proximidade dos valores singulares da matriz X. Depois de definidas m grupos I não sobrepostos, a decomposição da matriz de trajetória X pode ser escrita da seguinte forma:

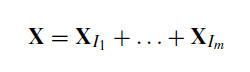
Por exemplo:

• Itrend = , para a tendência,
• Iseasonal = {2,3}, para a sazonalidade,
• Inoise = {4....,i}, para o ruído,
  onde i = quantidade de valores singulares.

A representação gráfica dos vetores singulares à esquerda é útil para avaliar visualmente a presença de sinal determinístico. Por exemplo, se a série temporal contiver uma tendência, o vetor singular correspondente exibirá uma trajetória suavemente variável. Havendo uma componente periódica, um par de vetores singulares (já que o sinal periódico tem posto 2) lembrará senóides. Vetores singulares visualmente semelhantes a ruído branco gaussiano e associados a valores singulares pequenos correspondem à componente de ruído. Essas características permitem agrupar as componentes com base na análise visual dos vetores singulares.

Recuperação (reconstrução) da série temporal

O passo seguinte consiste em converter cada matriz agrupada obtida em uma nova série temporal de comprimento N utilizando a média diagonal (diagonal averaging):

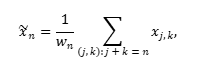
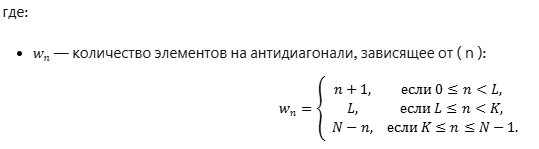
a, xj,k, elementos da matriz agrupada (ou elementar).

A série temporal reconstruída dessa forma representará ou a tendência ou a componente periódica. A soma dessas séries constitui um modelo não paramétrico da série temporal original, que depende do comprimento da janela L e do modo de agrupamento das matrizes elementares. A soma de todas as séries reconstruídas (incluindo o ruído) recompõe integralmente a série temporal original.

Previsão

A previsão dos valores da série temporal gi para M passos à frente no método SSA é realizada com base na série reconstruída, utilizando a fórmula de recorrência linear:

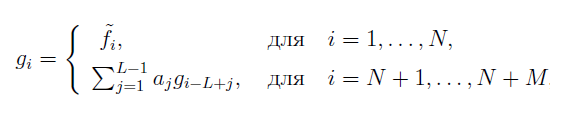
onde:

• aj  — coeficientes da relação de recorrência LRR (Linear Recurrence Relation),
• fi — valores da série reconstruída.

O vetor de coeficientes aj  é determinado com base nos vetores singulares Ui:

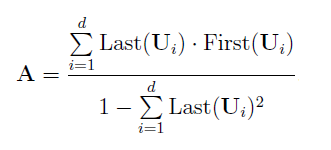
onde:

• First : as primeiras L − 1 coordenadas do vetor singular Ui,
• Last : a última coordenada do vetor singular Ui,
• d — quantidade de vetores singulares escolhidos que representam o sinal útil
  

Toeplitz-SSA

Existe ainda uma variante do SSA que se diferencia da abordagem tradicional. Ao contrário do Basic-SSA, que utiliza a matriz de trajetória baseada na janela deslizante da série temporal, o Toeplitz-SSA constrói uma matriz de autocovariância com estrutura de Toeplitz (daí o nome do método). Em seguida é realizada a decomposição SVD dessa matriz de autocovariância. O procedimento de agrupamento, a média diagonal, a obtenção dos coeficientes LRR e a previsão ocorrem exatamente da mesma forma que no Basic-SSA.

Toeplitz-SSA é mais adequado para a análise de séries temporais estacionárias, pois apresenta erro de previsão menor em comparação com o método básico. No entanto, para séries não estacionárias, o SSA clássico demonstra resultados melhores. Como nos mercados financeiros lidamos com processos não estacionários, decidi limitar esta matéria apenas ao algoritmo básico.

Exemplo de análise Basic-SSA

Passemos da teoria à implementação prática dos conceitos descritos em MQL5. Para isso foi preparado um script que gera quatro séries temporais sintéticas:

• senoide + ruído branco gaussiano,
• tendência linear + senoide + ruído branco gaussiano,
• caminhada aleatória gaussiana simétrica, ruído branco gaussiano.
  

Essas séries possuem as seguintes características:

• A primeira série é estacionária, com componente periódica.
• A segunda série é não estacionária, com tendência determinística e componente periódica.
• A terceira é uma série não estacionária com tendência estocástica.
• A quarta é ruído branco estacionário.
  
  

Esses modelos cobrem parcialmente o espectro de séries temporais encontradas em tarefas reais.

O script gera, conforme a escolha, uma série sintética e executa sequencialmente as etapas que analisamos acima, além de exibir no monitor os seguintes gráficos:

• dados gerados,
• valores singulares relativos (fração da variância de cada tríade singular),
• os dois primeiros vetores singulares,
• o diagrama de dispersão dos dois primeiros vetores singulares,
• a série de dados + sua reconstrução + previsão,
• a reconstrução + previsão utilizando a função MQL5SingularSpectrumAnalysisForecast.
  
  

O gráfico dos valores singulares espectrais relativos (fração do quadrado do valor singular sobre a soma dos quadrados de todos os valores singulares σi^2/∑ σj^2 — fig.2) permite determinar o tipo de componentes presentes na série temporal e escolher a quantidade de tríades singulares para reconstrução do sinal. Normalmente escolhem-se as componentes até o ponto de queda acentuada (o chamado "cotovelo" no gráfico).

Para uma componente periódica, devem aparecer dois valores singulares próximos em magnitude. Pode também haver um platô seguido de queda, o que indica a presença de várias componentes harmônicas (senoides com diferentes frequências), após as quais surge o ruído.

Um decaimento suave dos valores do espectro indica ausência de sinal determinístico.

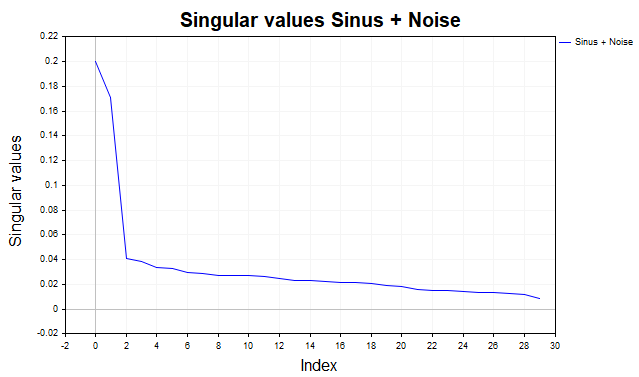
Fig.2 Especro relativo, sinus+noise

Aqui vale mencionar uma limitação do SSA, que consiste na incapacidade de distinguir uma tendência estocástica de uma determinística. Por exemplo, para uma série de caminhada aleatória teremos apenas uma componente expressiva, que responde pela tendência. Mas todos sabemos que essa tendência é aleatória e imprevisível. Especialmente para verificar esse caso, incluí no conjunto de dados um exemplo de caminhada aleatória.

Depois de identificar vários dos maiores valores singulares, é útil analisar os gráficos dos vetores singulares à esquerda correspondentes (fig.3). Para um sinal periódico misturado com ruído, os dois primeiros vetores singulares associados aos maiores valores singulares geralmente apresentam uma forma próxima à de uma senoide ou cossenoide, refletindo a natureza periódica do sinal.

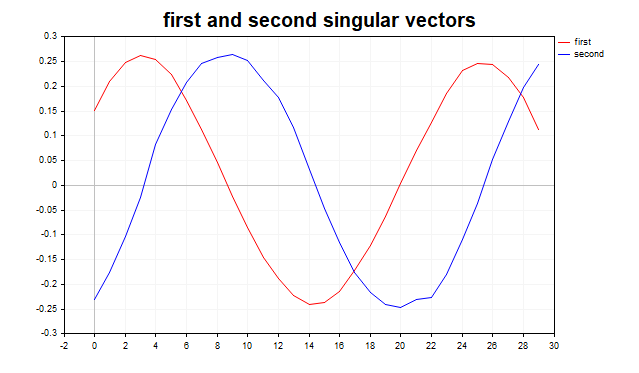
Fig.3 Os dois primeiros vetores singulares, sinus+noise

Além disso, é possível construir um gráfico de dispersão para o par de vetores singulares, onde no eixo (x) se coloca, por exemplo, o primeiro vetor singular (U1), e no eixo (y), o segundo (U2). (fig.4)

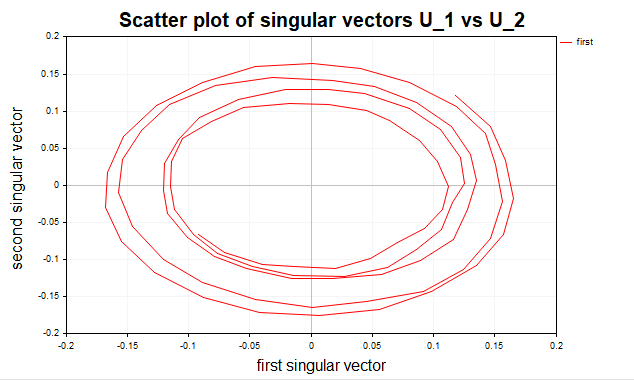
Fig.4 Diagrama de dispersão dos dois primeiros vetores singulares, sinus+noise

Se os dados contiverem componentes cíclicas, o diagrama de dispersão frequentemente assume a forma de uma elipse ou circunferência, o que confirma o caráter senoidal do sinal. Isso ocorre porque o par de vetores singulares associado à componente periódica corresponde a duas harmônicas ortogonais (por exemplo, seno e cosseno). Se os pontos no gráfico de dispersão formarem uma nuvem caótica sem estrutura geométrica nítida, isso indica ausência de uma componente periódica ou determinística expressiva.

Na fig.5 é apresentada a série sintética sinus+noise, sua reconstrução e a previsão para 100 passos à frente. Visualmente é difícil determinar a presença de um sinal periódico nos dados originais devido ao forte ruído, porém o SSA isola de forma eficaz a componente periódica. Naturalmente, este é um exemplo muito simples, e em dados financeiros reais um quadro tão claro raramente ocorre. Ainda assim, o SSA oferece uma excelente oportunidade para confirmar ou refutar a hipótese da presença de ciclos nos preços.

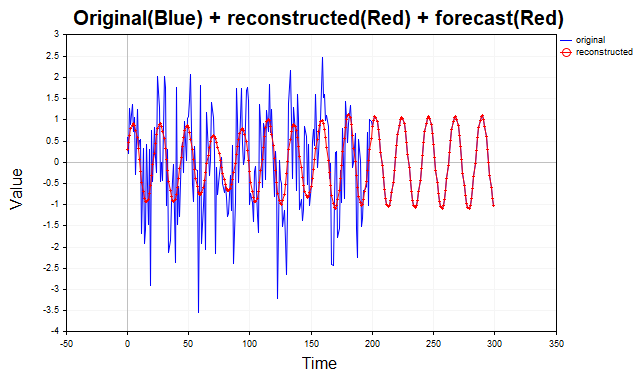
Fig.5 Previsão da série sinus+noise

Implementação do SSA em MQL5

Vamos nos deter nas implementações já existentes de SSA em MQL5. Na distribuição do terminal há a função SingularSpectrumAnalysisForecast, localizada na seção Métodos de matrizes e vetores\OpenBLAS. Pela descrição dessa função, não ficou totalmente claro para mim qual variante de SSA exatamente está implementada.

Inicialmente eu supunha que se tratava de uma variante Toeplitz-SSA, baseada na decomposição da matriz de autocovariância. Porém, como os resultados de previsão e reconstrução da série obtidos pelo script Basic-SSA e pela função SingularSpectrumAnalysisForecast coincidiram completamente, então provavelmente trata-se mesmo da implementação do algoritmo básico. Como exemplo, apresento o gráfico de previsão da série trend+sinus+noise pelas três principais componentes (fig.6). A série analisada consiste em 200 valores, e a previsão é feita para 100 passos à frente.

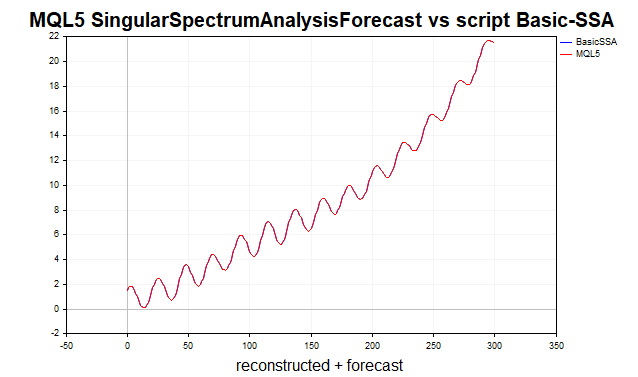
Fig.6 Série de reconstrução e previsão MQL5 vs BasicSSA

Para a decomposição da matriz de trajetória utilizei a função SingularValueDecompositionDC da mesma seção OpenBLAS, já que os desenvolvedores posicionam o algoritmo "dividir para conquistar" (divide and conquer)^ como o mais rápido entre os demais algoritmos de SVD. É muito conveniente que essa função permita calcular tanto matrizes singulares completas quanto truncadas.

Código do script Basic-SSA:

//+------------------------------------------------------------------+
//|                                                    Basic-SSA.mq5 |
//|                                                           Eugene |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Eugene"
#property link      "https://www.mql5.com"
#property version   "1.00"
#property script_show_inputs
#include <Math\Stat\Stat.mqh>
#include <Graphics\Graphic.mqh>

enum SimpleData
  {
   SinusPlusNoise,
   Trend_Sinus_Noise,
   RandomWalk,
   WhiteNoise,
  };

input int         L  = 30;                 // L - window length
input int         N  = 200;                // N - length of generated time series
input int         T  = 22;                 // T - period length of sine function
input int         fs = 100;                // fs - forecast horizon
input int         r_ = 2;                  // r - singular components
input SimpleData  sd = SinusPlusNoise;     // Data
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
   int err;
   vector x = vector::Zeros(N); // time series
   double x_array[];
   double original_series[];
//------------1. Данные --------------------
//------------------ sinus + noise ---------
   if(sd == SinusPlusNoise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] = MathSin(2*M_PI*(i+1)/T) + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//------------------trend + sinus + noise ----
   if(sd == Trend_Sinus_Noise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] =  0.05 * i + MathSin(2*M_PI*(i+1)/T) + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//-------------- random walk -----------------
   if(sd == RandomWalk)
     {
      x[0]=100;
      for(int i=1; i <N;  i++)
        {
         x[i] = x[i-1] + MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1);
     }
//-------------- white noise -----------------
   if(sd == WhiteNoise)
     {
      for(int i=0; i <N;  i++)
        {
         x[i] = MathRandomNormal(0,1,err);
        }
      VectortoArray(x,x_array);
      ArrayCopy(original_series,x_array,0,0,WHOLE_ARRAY);
      PlotGraphic(x_array,5,1); // график белого шума
     }
//------------2. Траекторная матрица -------------------
   matrix X;
   trajectory_matrix(x,L,X);
//-------------3. Cингулярное разложение (SVD) ----
   matrix U, V;
   vector singular_values;
   X.SingularValueDecompositionDC(SVDZ_A,singular_values,U,V);
   V = V.Transpose();
   double total_variance;
   vector powv = singular_values*singular_values;
   total_variance = powv.Sum();
   VectortoArray(powv/total_variance,x_array);
   PlotGraphic(x_array,5,2); // График  сингулярного спектра
   double x_1[],x_2[];
   VectortoArray(U.Col(0),x_1);
   VectortoArray(U.Col(1),x_2);
   PlotGraphic(x_1,x_2,5,3); // график первых двух сингулярных векторов
   PlotGraphic(x_1,x_2,5,4); // диаграмма рассеяния первых двух сингулярных векторов
//---------- 4. Реконструкция временного ряда----
   int K = N - L + 1;
   matrix X_i = matrix::Zeros(L,K);
   matrix Ui = matrix::Zeros(L,1);
   matrix Vi = matrix::Zeros(1,K);
   vector x_tilde;
   vector recon_series = vector::Zeros(N);
   for(int i=0; i<r_;i++)
     {
      Ui.Col(U.Col(i),0);
      Vi.Row(V.Col(i),0);
      X_i = (Ui.MatMul(Vi))*singular_values[i];  // матрицы ранга один
      diagonal_averaging(X_i,x_tilde);
      recon_series = recon_series + x_tilde;     // реконструированный ряд
     }
   double recon[];
   VectortoArray(recon_series,recon);

//------------5. Вектор коэффициентов LRR   --------------------
   matrix U_r = U;
   U_r.Resize(L,r_);              // r левых сингулярных векторов
   vector a = vector::Zeros(L-1); // вектор а коэффициентов LRR
   double denom =0;
   vector u_k;
   double last;
   for(int k=0; k<r_;k++)
     {
      u_k = U_r.Col(k);           //  k-ый сингулярный вектор
      last = u_k[L-1];
      u_k.Resize(L-1);
      a = a + last*u_k;
      denom = denom + MathPow(last,2);
     }
   denom = 1 - denom;
   a = a/denom;                   // вектор а коэффициентов LRR

//----------------- 6. Прогноз с использованием LRR-коэффициентов -----------
   int forecast_steps = fs;
   double forecast[];
   ArrayResize(forecast,forecast_steps);
   double fi[];
   ArrayCopy(fi,recon,0,N-L+1,L-1);
   for(int i=0;i<forecast_steps;i++)
     {
      double sum = 0.0;
      for(int j = 0; j < L-1; j++)
        {
         sum += a[j] * fi[j];
        }
      forecast[i]= sum;  // Прогноз
      // Обновляем fi
      ArrayCopy(fi, fi, 0, 1, ArraySize(fi)-1); // Сдвигаем влево
      fi[L-2] = forecast[i];                    // Добавляем новое значение
     }

   double originalplusforecast[];
   ArrayResize(originalplusforecast,N+forecast_steps);
   ArrayCopy(originalplusforecast,original_series,0,0,WHOLE_ARRAY);
   ArrayCopy(originalplusforecast,forecast,N,0,WHOLE_ARRAY);

   double reconstructedplusforecast[];
   ArrayResize(reconstructedplusforecast,N+forecast_steps);
   ArrayCopy(reconstructedplusforecast,recon,0,0,WHOLE_ARRAY);
   ArrayCopy(reconstructedplusforecast,forecast,N,0,WHOLE_ARRAY);
   PlotGraphic(originalplusforecast,reconstructedplusforecast,15,5);

//----реконструированные данные и прогноз по функции SingularSpectrumAnalysisForecast
   vector MQLreconforecast;
   x.SingularSpectrumAnalysisForecast(L,r_,forecast_steps,MQLreconforecast);
   double MQL_RF[];
   VectortoArray(MQLreconforecast,MQL_RF);
   PlotGraphic(reconstructedplusforecast,MQL_RF,10,6);
  }

//+------------------------------------------------------------------+
//| Plot Graphic                                                     |
//+------------------------------------------------------------------+
void PlotGraphic(double &data[], int sec, int n_graph)
  {
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0,CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS);

   if(ObjectFind(0,"Graphic")<0)
      graphic.Create(0,"Graphic",0,0,0,int(width),int(height));
   else
      graphic.Attach(0,"Graphic");

   string st;
   if(sd == SinusPlusNoise)
     {
      st = "Sinus + Noise";
     }
   if(sd == Trend_Sinus_Noise)
     {
      st = "Trend + Sinus + Noise";
     }
   if(sd == RandomWalk)
     {
      st = "Random Walk";
     }
   if(sd == WhiteNoise)
     {
      st = "White Noise ";
     }

   if(n_graph==1) // график данных
     {
      CCurve *curve = graphic.CurveAdd(data,ColorToARGB(clrRed,255),CURVE_LINES,st);
      graphic.XAxis().Name("Series " + st);
      graphic.BackgroundMain(st);
     }
   if(n_graph==2) // график сингулярных значений (relative_variance = sigma_i^2/Sum Sigma_j^2)
     {
      CCurve *curve = graphic.CurveAdd(data,ColorToARGB(clrBlue,255),CURVE_LINES,st);
      graphic.XAxis().Name("Index ");
      graphic.YAxis().Name("Singular values ");
      graphic.BackgroundMain("Singular values " + st);
     }
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack,255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec*1000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
   ChartRedraw(0);
  }

//+------------------------------------------------------------------+
//| Plot Graphic                                                     |
//+------------------------------------------------------------------+
void PlotGraphic(double &data1[],double &data2[], int sec,int n_graph)
  {
   ChartSetInteger(0,CHART_SHOW,false);
   CGraphic graphic;
   ulong width = ChartGetInteger(0,CHART_WIDTH_IN_PIXELS);
   ulong height = ChartGetInteger(0,CHART_HEIGHT_IN_PIXELS);

   if(ObjectFind(0,"Graphic")<0)
      graphic.Create(0,"Graphic",0,0,0,int(width),int(height));
   else
      graphic.Attach(0,"Graphic");

   if(n_graph==3)
     {
      CCurve *curve =  graphic.CurveAdd(data1,ColorToARGB(clrRed,255),CURVE_LINES,"first");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrBlue,255),CURVE_LINES,"second");
      graphic.XAxis().Name(" ");
      graphic.BackgroundMain("first and second singular vectors");
     }
   if(n_graph==4) // scatter plot of singular vectors
     {
      CCurve *curve =  graphic.CurveAdd(data1,data2,ColorToARGB(clrRed,255),CURVE_LINES,"first");
      graphic.XAxis().Name("first singular vector");
      graphic.YAxis().Name("second singular vector");
      graphic.BackgroundMain("Scatter plot of singular vectors U_1 vs U_2");
     }

   if(n_graph==5) // график данных плюс прогноз
     {
      CCurve *curve = graphic.CurveAdd(data1,ColorToARGB(clrBlue,255),CURVE_LINES,"original");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrRed,255),CURVE_POINTS_AND_LINES,"reconstructed");
      graphic.XAxis().Name("Time ");
      graphic.YAxis().Name("Value ");
      graphic.BackgroundMain("Original(Blue) + reconstructed(Red) + forecast(Red) ");
      curve1.PointsSize(3);
     }

// график сравнения прогноза функции MQL5 SingularSpectrumAnalysisForecast с прогнозом Basic-SSA
   if(n_graph==6)
     {
      CCurve *curve = graphic.CurveAdd(data1,ColorToARGB(clrBlue,255),CURVE_LINES,"BasicSSA");
      CCurve *curve1 = graphic.CurveAdd(data2,ColorToARGB(clrRed,255),CURVE_LINES,"MQL5");
      graphic.XAxis().Name("reconstructed + forecast ");
      graphic.BackgroundMain(" MQL5 SingularSpectrumAnalysisForecast vs script Basic-SSA ");
      curve1.PointsSize(3);
     }
   graphic.XAxis().NameSize(18);
   graphic.YAxis().NameSize(18);
   graphic.BackgroundMainColor(ColorToARGB(clrBlack,255));
   graphic.BackgroundMainSize(24);
   graphic.CurvePlotAll();
   graphic.Update();
   Sleep(sec*1000);
   ChartSetInteger(0,CHART_SHOW,true);
   graphic.Destroy();
   ChartRedraw(0);
  }

//+------------------------------------------------------------------+
//| Копируем вектор в массив                                         |
//+------------------------------------------------------------------+
void VectortoArray(vector &v, double &array[])
  {
   int v_size = (int)v.Size();
   ArrayResize(array,v_size);
   for(int i=0; i<v_size; i++)
     {
      array[i]   =  v[i];
     }
  }
//+------------------------------------------------------------------+
//| Траекторная матрица X                                            |
//+------------------------------------------------------------------+
void trajectory_matrix(vector & series,int window_length, matrix & X)
  {
   int N_ = (int)series.Size();
   int L_ = window_length;
   int K = N_ - L_ + 1;
   X=matrix::Zeros(L_,K);
   for(int i=0; i <L_;  i++)
     {
      for(int j=0; j <K;  j++)
        {
         X[i,j] = series[i+j];
        }
     }
  }
//+-------------------------------------------------------------------+
//| Диагональное усреднение матрицы                                   |
//| Вход: Xi - матрица L x K (элементарная матрица i-ой компоненты)   |
//| Выход: x_tilde - восстановленный временной ряд                    |
//+-------------------------------------------------------------------+
void diagonal_averaging(matrix &Xi,vector &x_tilde)
  {
   int L_ = (int)Xi.Rows();
   int K  = (int)Xi.Cols();
   int N_ = L_ + K - 1; // Длина исходного временного ряда

   x_tilde = vector::Zeros(N_);
   double total; // Сумма элементов на антидиагонали
   int w_n;      // Количество элементов на антидиагонали
   int k;
   for(int n=0; n < N_; n++)
     {
      total = 0;
      w_n = 0;
      for(int j=0; j <L_; j++)
        {
         k = n - j ; // Индекс столбца: n = j + k ---> k = n - j
         if(k >= 0 && k < K) // Проверка, что индекс в пределах матрицы
           {
            total = total + Xi[j, k];
            w_n = w_n + 1;
           }
        }
      x_tilde[n] = total / w_n; // Усреднение
     }
  }
//+------------------------------------------------------------------+

Considerações finais

Neste artigo examinamos os fundamentos da análise espectral singular (SSA), um método que utiliza a decomposição singular (SVD) da matriz de trajetória para detectar estruturas ocultas nos dados. Mostramos como o SSA separa de forma eficaz uma série temporal em componentes interpretáveis (como tendência, sazonalidade e ruído) garantindo sua reconstrução e previsão.

No entanto, o método possui limitações, em particular a incapacidade de distinguir de forma confiável tendências determinísticas e estocásticas, como a caminhada gaussiana aleatória. Ao mesmo tempo, vale notar que o SSA não tem como objetivo uma classificação estatística rígida das tendências; sua força está na decomposição flexível e na capacidade de destacar a estrutura dos dados, tarefa que realiza com sucesso.

A aplicação do SSA não se limita à análise de séries temporais unidimensionais. O método permite trabalhar com dados multidimensionais, e com base nele é possível construir um indicador de descontinuidade (change-point detection) para detectar mudanças bruscas no comportamento de instrumentos financeiros. Essas direções representam perspectivas para pesquisas futuras, já que compreender com precisão a natureza dos dados é fundamental para a identificação de padrões de mercado.