Por favor, explique meu obstáculo. Acontece que o HSIC mostrará a dependência para qualquer função clássica Y=F(X1, X2, ...)?
Provavelmente não para nenhum deles, porque a dependência pode ser muito fraca (devido a um forte ruído, por exemplo) e, portanto, pode não ser detectada. Mas, em geral, se houver algo significativo nos dados, o teste o detectará.
Peguei dados de uma natureza diferente.
// Y são as barras do símbolo, X1 são as barras antes de Y, X2 são as barras antes de X1. bool Fill( double &X1[], double &X2[], double &Y[], const int Size = 1000, const datetime Time = 0, const string Symb = NULL ) { int Pos = iBarShift(Symb, PERIOD_CURRENT, Time ? Time : TimeCurrent()); return((CopyClose(Symb, PERIOD_CURRENT, Pos, Size, Y) == Size) && (CopyClose(Symb, PERIOD_CURRENT, Pos += Size, Size, X1) == Size) && (CopyClose(Symb, PERIOD_CURRENT, Pos += Size, Size, X2) == Size)); }
No script de reorganização proposto, fiz essa substituição.
if (SData == Nonlinear_dependence){ /* double x1 []; MathRandomUniform(-5,5,data_,x1); double x2 []; MathRandomUniform(-5,5,data_,x2); double NormD[]; MathRandomNormal(0,0.1,data_,NormD); double y[]; ArrayResize(y,data_); for (int i=0;i<data_;i++){ y[i] = pow(x1[i],2)*cos(M_PI*x2[i]) + NormD[i]; // Y = X1^2 * cos(pi*X2) + Noise } */ double x1[], x2[], y[]; Fill(x1, x2, y, data_);
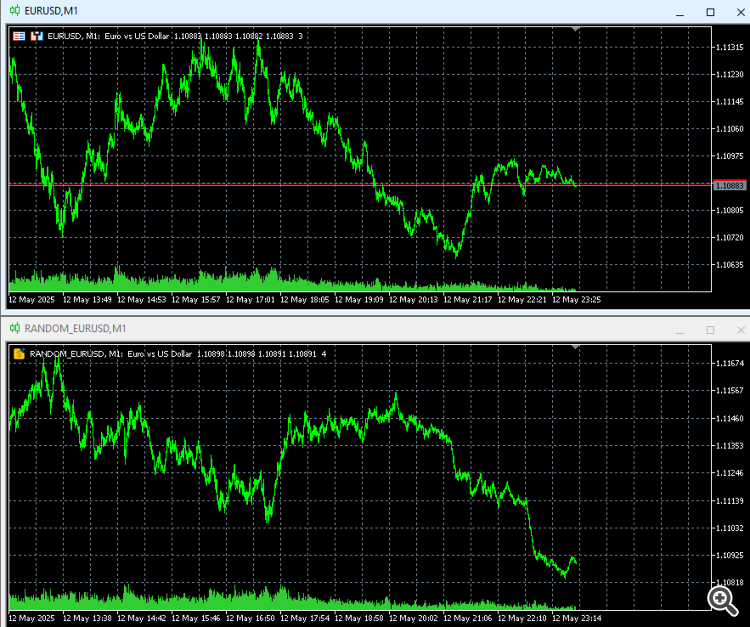
Os resultados são para EURUSD.
Test6 (EURUSD,M1) Коэффициент корреляции (X1, Y) = 0.3757 Test6 (EURUSD,M1) Коэффициент корреляции (X2, Y) = -0.4280 Test6 (EURUSD,M1) ----------------Nonlinear_dependence------------- Test6 (EURUSD,M1) Время выполнения: 12.688 seconds Test6 (EURUSD,M1) ----------------------------------- Test6 (EURUSD,M1) Number observations 1000 Test6 (EURUSD,M1) HSIC: 0.01050641 Test6 (EURUSD,M1) p-value: 0.0000 Test6 (EURUSD,M1) Critical value: 0.0010 Test6 (EURUSD,M1) Отвергаем H0: Наблюдения зависимы
Em seguida, criei um símbolo personalizado com base em incrementos aleatórios e o executei nele.
Test6 (RANDOM_EURUSD,M1) Коэффициент корреляции (X1, Y) = -0.6103 Test6 (RANDOM_EURUSD,M1) Коэффициент корреляции (X2, Y) = -0.4954 Test6 (RANDOM_EURUSD,M1) ----------------Nonlinear_dependence------------- Test6 (RANDOM_EURUSD,M1) Время выполнения: 12.656 seconds Test6 (RANDOM_EURUSD,M1) ----------------------------------- Test6 (RANDOM_EURUSD,M1) Number observations 1000 Test6 (RANDOM_EURUSD,M1) HSIC: 0.00900188 Test6 (RANDOM_EURUSD,M1) p-value: 0.0000 Test6 (RANDOM_EURUSD,M1) Critical value: 0.0009 Test6 (RANDOM_EURUSD,M1) Отвергаем H0: Наблюдения зависимы
Por que há dependência no segundo caso? Em termos gerais, supostamente há uma dependência entre três vetores, que são somas cumulativas de uma variável aleatória.
...
Por que há uma dependência no segundo caso? Em termos gerais, supostamente há uma dependência entre três vetores que são somas cumulativas de uma variável aleatória.
Ela (a dependência) está definitivamente presente, porque um PRNG bastante simples é usado (presumo que você use um padrão, você pode verificar isso com o vórtice de Mersenne, por exemplo).
Outra questão é quão forte é a dependência. Não tenho certeza disso e peço ao autor que explique como interpretar corretamente as métricas obtidas.
Obteve dados de uma natureza diferente.
No script de rearranjo proposto, fiz essa substituição.
Resultados em EURUSD.
Em seguida, criei um símbolo personalizado com base em incrementos aleatórios e o executei.
Por que há uma dependência no segundo caso? Em termos gerais, supostamente há uma dependência entre três vetores, que são somas cumulativas de uma variável aleatória.
Obteve dados de uma natureza diferente.
No script de rearranjo proposto, fiz essa substituição.
Resultados em EURUSD.
Em seguida, criei um símbolo personalizado com base em incrementos aleatórios e o executei.
Por que há uma dependência no segundo caso? Em termos gerais, supostamente há uma dependência entre três vetores, que são somas cumulativas de uma variável aleatória.
Definitivamente, ela (a dependência) existe, pois usa um PRNG bastante simples (presumo que você use um padrão, você pode verificar isso no Mersenne's Vortex, por exemplo).
Outra questão é a intensidade da dependência. Estou um pouco confuso com isso e peço ao autor que explique como interpretar corretamente as métricas obtidas.
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso
Novo artigo Critério de Independência de Hilbert-Schmidt (HSIC) foi publicado:
A principal tarefa do trader ao trabalhar com cotações de instrumentos financeiros é a criação de um sistema de negociação (EA) com expectativa matemática positiva. Ao projetar esses sistemas, frequentemente se assume que existem dependências ocultas nos dados utilizados para aprendizado e posterior negociação. No entanto, a questão da verificação estatística dessa suposição geralmente não é considerada. Acredita-se que uma resposta indireta possa ser obtida por meio dos resultados de testes em dados fora da amostra (out-of-sample).
Enquanto isso, uma resposta estatisticamente fundamentada à questão da existência de relação entre os atributos e a variável-alvo tem importância fundamental. Uma resposta positiva dá confiança na viabilidade do uso de modelos preditivos, enquanto uma resposta negativa leva a refletir: o que exatamente o algoritmo está tentando prever?
Na estatística matemática, a questão da existência ou ausência de ligação probabilística entre variáveis aleatórias é respondida pelos critérios de independência. Um desses critérios é o teste estatístico HSIC — um poderoso método não paramétrico desenvolvido em 2005 pelo estatístico Arthur Gretton.
Diferentemente do coeficiente de correlação, que identifica apenas relações lineares, o HSIC é capaz de detectar tanto dependências lineares quanto não lineares. Graças a isso, ele é amplamente utilizado em aprendizado de máquina para seleção de atributos, análise de relações de causa e efeito e outras tarefas. Neste artigo, vamos analisar o princípio de funcionamento do HSIC e implementá-lo no ambiente MQL5.
Autor: Evgeniy Chernish