Redes neurais em trading: Detecção de anomalias no domínio da frequência (Conclusão)
Introdução
No artigo anterior, conhecemos o inovador framework CATCH, projetado para detectar anomalias em séries temporais multidimensionais. O método de análise de dados no domínio da frequência, proposto pelos autores do framework, permite identificar não apenas anomalias pontuais sob a forma de valores atípicos e mudanças abruptas, mas também padrões mais complexos e ocultos, que escapam aos métodos tradicionais. O framework CATCH utiliza a transformada de Fourier para realizar a transição da representação temporal dos dados para sua forma espectral, o que abre novas possibilidades para o estudo detalhado das características da sequência analisada.
Uma das principais vantagens do CATCH é o uso do patching em frequência. Em vez de analisar todo o espectro de uma só vez, o modelo o divide em fragmentos individuais correspondentes a determinadas faixas de frequência. Esse método permite observar tanto as tendências globais quanto as particularidades locais típicas dos componentes de alta frequência. Graças a essa abordagem, é possível destacar e classificar diferentes tipos de anomalias com alto grau de precisão, sejam picos de curta duração ou desvios mais complexos em nível de subsequência. Essa divisão espectral possibilita um estudo mais detalhado da estrutura da série temporal.
Uma parte essencial do framework é o módulo adaptativo responsável pela análise das inter-relações entre os diversos canais de dados. Esse componente, que implementa o princípio da atenção mascarada, ajuda o sistema a concentrar-se nas correlações mais significativas, eliminando a influência de fatores ruidosos e dados irrelevantes. Tal mecanismo contribui para o aprimoramento da reconstrução do comportamento normal e aumenta significativamente a robustez do modelo em ambientes de mercado voláteis. Diferentemente dos métodos tradicionais, que analisam os canais separadamente, o CATCH permite levar em consideração suas interdependências complexas, o que é especialmente relevante ao lidar com dados financeiros, onde o movimento em um mercado pode influenciar outros segmentos.
Na etapa final do funcionamento do CATCH ocorre a reconstrução da série temporal original. Após a análise detalhada no domínio da frequência e a identificação das possíveis anomalias, o sistema executa a transformada inversa, retornando os dados à sua forma temporal habitual. A diferença entre os valores originais e a série reconstruída serve como um indicador confiável de desvios, permitindo reagir prontamente às mudanças na dinâmica do mercado.
A visualização autoral do framework CATCH é apresentada a seguir.
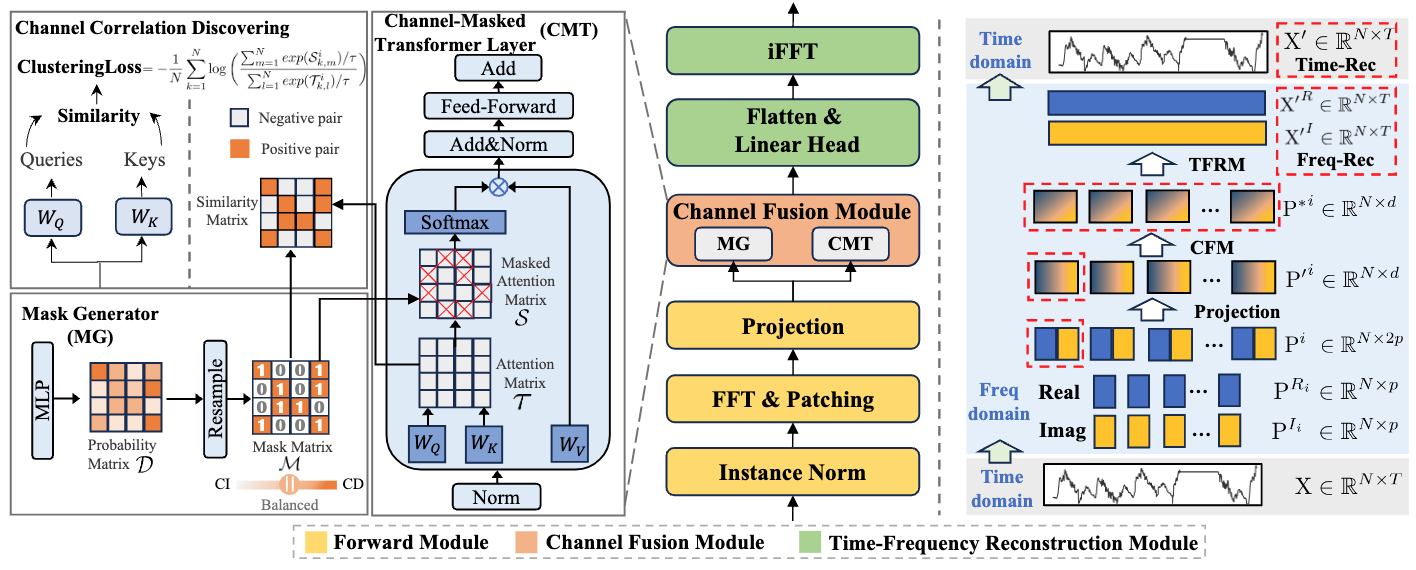
Na parte prática do artigo anterior, iniciamos a implementação da nossa própria versão das abordagens propostas utilizando MQL5, em particular, foi implementada uma camada convolucional para trabalhar com valores complexos. Além disso, analisamos a implementação das propagações para frente e reversa do módulo de atenção mascarada para grandezas complexas no lado do contexto OpenCL. Hoje, damos continuidade a esse trabalho.
Objeto de atenção mascarada para valores complexos
No artigo anterior, examinamos os kernels MaskAttentionComplex e MaskAttentionGradientsComplex, nos quais foram implementados os algoritmos de propagação para frente e propagação reversa do mecanismo de atenção mascarada no domínio das grandezas complexas. Continuamos o trabalho iniciado. Hoje, estruturaremos o funcionamento do módulo de atenção mascarada no lado do programa principal. Para isso, criamos um novo objeto chamado CNeuronComplexMVMHMaskAttention, cuja estrutura é apresentada abaixo.
class CNeuronComplexMVMHMaskAttention : public CNeuronBaseOCL { protected: uint iWindow; uint iWindowKey; uint iHeads; uint iUnits; uint iVariables; //--- CNeuronComplexConvOCL cQKV; CNeuronBaseOCL cQ; CNeuronBaseOCL cKV; CNeuronConvOCL cMask; CNeuronBaseOCL cMHAttentionOut; CNeuronComplexConvOCL cPooling; CNeuronBaseOCL cResidual; CNeuronComplexConvOCL cFeedForward[2]; //--- virtual bool AttentionOut(void); virtual bool AttentionInsideGradients(void); virtual bool SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out, int dimension, bool normilize = true, int shift_in1 = 0, int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f) override; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; public: CNeuronComplexMVMHMaskAttention(void) {}; ~CNeuronComplexMVMHMaskAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronComplexMVMHMaskAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Como se pode observar, a estrutura apresentada do novo objeto é bastante padrão para módulos de atenção, em suas diversas variações que já criamos repetidas vezes em nossa biblioteca. No entanto, há uma particularidade associada ao uso de grandezas complexas. Supõe-se que os dados brutos alimentem esse objeto já no formato de valores complexos, portanto, omitimos a etapa de transformação dos dados. E, para a formação das entidades Query, Key e Value, utilizamos a camada convolucional de trabalho com grandezas complexas que implementamos anteriormente. Mas vamos por partes.
Todos os objetos internos são declarados estaticamente, o que nos permite deixar vazios o construtor e o destrutor da classe. A inicialização dos objetos declarados e herdados é realizada no método Init. Nos parâmetros desse método, recebemos um conjunto de constantes que permitem definir de forma inequívoca a arquitetura do objeto criado. Sua estrutura é bastante comum para esse tipo de componente.
bool CNeuronComplexMVMHMaskAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { //--- if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count * variables, optimization_type, batch)) return false;
No corpo do método, chamamos imediatamente o método homônimo da classe base, na qual já está implementado o algoritmo de inicialização dos objetos herdados e das interfaces. Em seguida, armazenamos nas variáveis internas as constantes de arquitetura do modelo recebidas do programa externo.
iWindow = window; iWindowKey = MathMax(window_key, 1); iUnits = units_count; iHeads = MathMax(heads, 1); iVariables = variables;
Em seguida, passamos a trabalhar com os novos objetos declarados. O primeiro a ser inicializado é o objeto responsável pela geração da matriz de mascaramento.
Aqui vale destacar que os autores do framework propuseram um módulo de geração de máscara baseado em uma projeção treinável dos dados brutos. Nesse processo, é utilizado o mecanismo de atenção multicabeça, em que cada cabeça possui sua própria máscara exclusiva.
Outro ponto igualmente importante é que a atenção não é aplicada a toda a sequência do espectro de frequências. Os autores do framework CATCH sugerem usar a atenção apenas dentro de patches individuais, que correspondem a um mesmo fragmento de frequência, mas pertencem a diferentes sequências unitárias.
Além disso, na saída do objeto gerador de máscara, devemos obter uma representação probabilística da influência de cada canal, expressa em valores reais.
Para atender a essas restrições, em nossa implementação utilizamos uma camada convolucional comum com o dobro do tamanho da janela (para cobrir a janela de valores complexos) e um número de filtros igual ao vetor de mascaramento de um único elemento da sequência.
uint index = 0; if(!cMask.Init(0, index, OpenCL, 2 * iWindow, 2 * iWindow, iVariables * iHeads, iUnits, iVariables, optimization, iBatch)) return false; cMask.SetActivationFunction(SIGMOID); CBufferFloat *temp = cMask.GetWeightsConv(); if(!temp || !temp.Fill(0)) return false;
A fim de manter os resultados do objeto dentro do intervalo de valores necessário, utilizamos uma função de ativação sigmoide.
Observe que, durante a inicialização do objeto, preenchemos a matriz de parâmetros treináveis com valores nulos. Isso nos permite, na etapa inicial, atribuir a todos os elementos uma máscara de influência uniforme no nível de "0.5". No decorrer do treinamento, os pesos serão ajustados, modificando a máscara de dependência entre os canais.
O próximo passo é inicializar o objeto responsável pela geração das entidades Query, Key e Value. Aqui, utilizamos uma camada convolucional complexa, pois tanto na entrada quanto na saída do objeto esperamos obter valores complexos.
index++; if(!cQKV.Init(0, index, OpenCL, iWindow, iWindow, 3 * iWindowKey * iHeads, iUnits, iVariables, optimization, iBatch)) return false; cQKV.SetActivationFunction(None);
O tensor geral dessas três entidades será dividido em duas partes, isolando a entidade Query em uma matriz separada. Para isso, inicializamos dois objetos adicionais.
index++; if(!cQ.Init(0, index, OpenCL, 2 * iWindowKey * iHeads * iVariables * iUnits, optimization, iBatch)) return false; cQ.SetActivationFunction(None); index++; if(!cKV.Init(0, index, OpenCL, 2 * cQ.Neurons(), optimization, iBatch)) return false; cKV.SetActivationFunction(None);
Logo em seguida, inicializamos também o objeto destinado ao armazenamento dos resultados da atenção multicabeça.
index++; if(!cMHAttentionOut.Init(0, index, OpenCL, cQ.Neurons(), optimization, iBatch)) return false; cMHAttentionOut.SetActivationFunction(None);
Adicionamos ainda uma camada convolucional complexa para reduzir a dimensionalidade dos resultados da atenção.
index++; if(!cPooling.Init(0, index, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, iVariables, optimization, iBatch)) return false; cPooling.SetActivationFunction(None);
De forma análoga à arquitetura clássica do Transformer, adicionamos uma camada para a preservação das conexões residuais.
index++; if(!cResidual.Init(0, index, OpenCL, cPooling.Neurons(), optimization, iBatch)) return false; cResidual.SetActivationFunction(None);
Em seguida, incluímos duas camadas convolucionais complexas do módulo FeedForward.
index++; if(!cFeedForward[0].Init(0, index, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, iVariables, optimization, iBatch)) return false; cFeedForward[0].SetActivationFunction(LReLU); index++; if(!cFeedForward[1].Init(0, index, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, iVariables, optimization, iBatch)) return false; cFeedForward[1].SetActivationFunction(None); SetActivationFunction(None); //--- return true; }
Após isso, concluímos o método de inicialização do objeto, retornando previamente o resultado lógico da execução das operações para o programa chamador.
A próxima etapa será a construção do algoritmo de propagação para frente dentro do método feedForward.
bool CNeuronComplexMVMHMaskAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
Nos parâmetros desse método, recebemos um ponteiro para o objeto de dados brutos, cuja validade verificamos de imediato.
Para aumentar a estabilidade do processo de treinamento, normalizamos os dados obtidos.
if(!NeuronOCL.SwapOutputs()) return false; if(!SumAndNormilize(NeuronOCL.getPrevOutput(), NeuronOCL.getPrevOutput(), NeuronOCL.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Aqui é importante observar que os dados brutos recebidos são representados por grandezas complexas. Por esse motivo, o método de soma e normalização dos dados foi redefinido para operar com esse tipo de valor. O código completo desse método pode ser consultado no anexo.
Após a normalização, os dados brutos são utilizados para gerar os tensores de mascaramento e as entidades Query, Key e Value.
if(!cMask.FeedForward(NeuronOCL)) return false; if(!cQKV.FeedForward(NeuronOCL)) return false;
O tensor geral das entidades geradas é dividido em dois conjuntos separados.
if(!NeuronOCL.SwapOutputs()) return false; if(!DeConcat(cQ.getOutput(), cKV.getOutput(), cQKV.getOutput(), 2 * iWindowKey * iHeads, 4 * iWindowKey * iHeads, iUnits * iVariables)) return false;
Em seguida, todos os dados preparados são enviados ao kernel de propagação para frente do mecanismo de atenção mascarada. Essa operação é realizada dentro de um método específico chamado AttentionOut.
if(!AttentionOut()) return false;
Depois, reduzimos a dimensionalidade dos resultados da atenção multicabeça e somamos os valores obtidos aos dados originais, criando as conexões residuais.
if(!cPooling.FeedForward(cMHAttentionOut.AsObject())) return false; if(!SumAndNormilize(NeuronOCL.getOutput(), cPooling.getOutput(), cResidual.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Em seguida, os dados são processados por duas camadas convolucionais do módulo FeedForward.
if(!cFeedForward[0].FeedForward(cResidual.AsObject())) return false; if(!cFeedForward[1].FeedForward(cFeedForward[0].AsObject())) return false;
Mais uma vez, adicionamos as conexões residuais. O resultado dessa operação é armazenado no buffer herdado da interface de troca de dados com outras camadas neurais do modelo.
if(!SumAndNormilize(cResidual.getOutput(), cFeedForward[1].getOutput(), getOutput(), iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
Após isso, concluímos o método, retornando o resultado lógico da execução das operações para o programa chamador.
Vale dedicar algumas palavras ao método AttentionOut, no qual é feita a colocação na fila de execução do kernel de atenção mascarada multicabeça MaskAttentionComplex. Ultimamente, temos abordado com pouca frequência os algoritmos dos métodos de enfileiramento de kernels em programas OpenCL. Isso é compreensível, pois o algoritmo de enfileiramento de um kernel para execução é bastante padronizado. E não há necessidade de descrever as mesmas operações repetidas vezes. No entanto, neste caso há um detalhe específico relacionado ao funcionamento do framework CATCH.
Como mencionado anteriormente, os autores do framework CATCH propõem que as operações de atenção mascarada sejam realizadas estritamente entre os elementos de um mesmo intervalo de frequência pertencentes a diferentes sequências unitárias. Em termos simples, pegamos patches idênticos de diferentes sequências unitárias e analisamos suas dependências. Isso permite identificar de forma independente as correlações entre diferentes sequências unitárias em distintas frequências, separadamente para tendências de longo prazo e separadamente para tendências de curto prazo. Contudo, não levamos essa particularidade em consideração ao criar o kernel unificado de atenção mascarada.
Mesmo assim, temos a possibilidade de estruturar o processo necessário controlando o espaço de tarefas no enfileiramento do kernel para execução. Para começar, vejamos a dimensionalidade dos dados brutos recebidos na entrada do objeto. Obtemos dados segmentados de uma sequência multidimensional, que podem ser representados como um tensor tridimensional {Variável, Segmento, Dimensão}. Em seguida, ao formar as entidades para a atenção multicabeça, os resultados da geração de cada uma podem ser representados como um tensor de quatro dimensões {Variável, Segmento, Cabeça, Dimensão}.
Aqui é importante observar que o algoritmo de atenção multicabeça que construímos realiza uma análise independente para cada cabeça de atenção. Portanto, se combinarmos as dimensões dos segmentos e das cabeças de atenção, tratando cada segmento como uma cabeça independente, obteremos uma análise das dependências entre os mesmos segmentos de diferentes sequências unitárias, exatamente o que é necessário para o funcionamento do framework CATCH.
O método AttentionOut não possui parâmetros. No bloco de controle desse método, verificamos apenas a validade do ponteiro para o objeto que trabalha com o contexto OpenCL.
bool CNeuronComplexMVMHMaskAttention::AttentionOut(void) { if(!OpenCL) return false;
Em seguida, declaramos os arrays que definem o espaço de tarefas para o enfileiramento do kernel na fila de execução. Conforme discutido anteriormente, como dimensão das sequências indicamos a quantidade de sequências unitárias presentes nos dados analisados. Já para o número de cabeças, especificamos o produto entre a quantidade definida de cabeças de atenção e o número de segmentos em cada sequência.
uint global_work_offset[3] = {0}; uint global_work_size[3] = {iVariables/*Q units*/, iVariables/*K units*/, iHeads * iUnits/*Heads*/}; uint local_work_size[3] = {1, iVariables, 1};
Logo após, agrupamos os fluxos de operações em grupos de trabalho conforme a segunda dimensão do espaço de tarefas.
Em seguida, passamos, nos parâmetros do kernel, os ponteiros para os buffers de dados necessários.
ResetLastError(); int kernel = def_k_MaskAttentionComplex; if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_q, cQ.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_kv, cKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_scores, cMask.getPrevOutIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_out, cMHAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_masks, cMask.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Aqui aproveitamos que as dimensões da matriz de coeficientes de atenção e da máscara dos canais são iguais. Essa coincidência nos permitiu não criar um buffer adicional para o armazenamento temporário dos coeficientes de atenção, já que essa função será desempenhada pelo buffer livre do objeto responsável pela geração da matriz de mascaramento.
Depois, transmitimos ao kernel os parâmetros necessários.
if(!OpenCL.SetArgument(kernel, def_k_maskattcom_dimension, (int)iWindowKey)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_maskattcom_heads_kv, (int)(iHeads * iUnits))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
E novamente, ao definir o número de cabeças de atenção para as entidades Key e Value, utilizamos o produto entre a quantidade de cabeças de atenção especificada pelo usuário e o comprimento da sequência.
Por fim, colocamos o kernel na fila de execução.
if(!OpenCL.Execute(kernel, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
Concluímos, então, o método, retornando previamente o resultado lógico da execução das operações para o programa chamador.
Após finalizar o trabalho com os algoritmos de propagação para frente, passamos à construção dos processos de propagação reversa. O primeiro passo é criar o método de distribuição dos gradientes do erro entre todos os objetos internos, de acordo com sua influência sobre o resultado do funcionamento do modelo calcInputGradients.
bool CNeuronComplexMVMHMaskAttention::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Nos parâmetros do método, recebemos novamente o mesmo objeto de dados brutos utilizado durante a propagação para frente. Desta vez, porém, devemos transmitir a ele o gradiente do erro, conforme a influência dos dados brutos. E, logo de início, verificamos a validade do ponteiro recebido.
Neste estágio, o buffer das interfaces externas do nosso objeto contém o gradiente do erro recebido da camada subsequente. Seus valores foram obtidos sem levar em conta a correção pela derivada da função de ativação utilizada, pois intencionalmente indicamos a ausência dessa função durante a inicialização do objeto. Isso foi feito para garantir maior liberdade na escolha das funções de ativação dos objetos internos. Agora, corrigimos o gradiente do erro recebido aplicando a derivada da função de ativação da última camada convolucional do módulo FeedForward, transmitindo a ela os valores ajustados.
if(!DeActivation(cFeedForward[1].getOutput(), cFeedForward[1].getGradient(), Gradient, cFeedForward[1].Activation())) return false;
Em seguida, propagamos o gradiente do erro pelos níveis inferiores do módulo até o objeto das conexões residuais, que se encontra logo após o módulo de atenção.
if(!cFeedForward[0].calcHiddenGradients(cFeedForward[1].AsObject())) return false; if(!cResidual.calcHiddenGradients(cFeedForward[0].AsObject())) return false;
Para o objeto das conexões residuais, também especificamos a ausência de uma função de ativação. Assim, repetimos o procedimento de correção pela derivada da função de ativação da camada de redução de dimensão dos resultados da atenção multicabeça.
if(!DeActivation(cPooling.getOutput(), cPooling.getGradient(), cResidual.getGradient(), cPooling.Activation()) || !DeActivation(cPooling.getOutput(), cPooling.getPrevOutput(), Gradient, cPooling.Activation()) || !SumAndNormilize(cPooling.getGradient(), cPooling.getPrevOutput(), cPooling.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
No entanto, aqui é importante observar que o objeto das conexões residuais contém apenas o gradiente do erro referente à linha principal do módulo FeedForward. Precisamos adicionar também as informações provenientes do ramo das conexões residuais. Por isso, novamente corrigimos o gradiente do erro a partir do buffer das interfaces externas, mas desta vez utilizando a derivada da função de ativação da camada convolucional responsável pela redução da dimensionalidade dos resultados da atenção multicabeça.
Vale destacar que o uso repetido dos dados do buffer das interfaces externas não implica em distorção dupla. No primeiro caso, os resultados da correção foram armazenados no buffer da última camada do módulo FeedForward, enquanto os dados originais permaneceram inalterados no buffer das interfaces. Agora, os resultados das operações são gravados no buffer da camada de projeção, sem modificar os dados originais, que ainda serão utilizados novamente durante a transmissão dos valores pelo ramo das conexões residuais até o nível dos dados brutos.
Após a correção dos valores, somamos as informações provenientes dos dois fluxos de dados. Em seguida, distribuímos o gradiente do erro entre as cabeças de atenção.
if(!cMHAttentionOut.calcHiddenGradients(cPooling.AsObject())) return false; if(!AttentionInsideGradients()) return false;
Chamamos então o método responsável pela distribuição do gradiente do erro através do processo de atenção AttentionInsideGradients. Não entraremos aqui em uma análise detalhada do algoritmo desse método, deixando-a para estudo independente. Seu código completo está apresentado no anexo. Entretanto, é importante ressaltar que o espaço de tarefas e os parâmetros de enfileiramento do kernel para execução devem corresponder à metodologia proposta para a propagação para frente.
Na etapa seguinte, unificamos os gradientes de erro de todas as entidades em um único tensor.
if(!Concat(cQ.getGradient(), cKV.getGradient(), cQKV.getGradient(), 2 * iWindowKey * iHeads, 4 * iWindowKey * iHeads, iUnits * iVariables)) return false;
Depois disso, propagamos o erro até o nível dos dados brutos, aplicando previamente a correção pela derivada da respectiva função de ativação.
if(!DeActivation(cQKV.getOutput(), cQKV.getPrevOutput(), cQKV.getGradient(), cQKV.Activation()) || !prevLayer.calcHiddenGradients(cQKV.AsObject())) return false;
Entretanto, esse é apenas um dos fluxos de informação. Adicionamos aos valores obtidos os dados do fluxo de informação das conexões residuais, previamente corrigidos pela derivada da função de ativação do objeto de dados brutos.
Nesse caso, utilizamos dados tanto do módulo FeedForward quanto do buffer das interfaces externas.
if(!DeActivation(prevLayer.getOutput(),cResidual.getPrevOutput(),cResidual.getGradient(),prevLayer.Activation()) || !SumAndNormilize(prevLayer.getGradient(), cResidual.getPrevOutput(), cResidual.getPrevOutput(), iWindow, false, 0, 0, 0, 1)) return false; if(!DeActivation(prevLayer.getOutput(), cResidual.getGradient(), Gradient, prevLayer.Activation()) || !SumAndNormilize(cResidual.getGradient(), cResidual.getPrevOutput(), cResidual.getPrevOutput(), iWindow, false, 0, 0, 0, 1)) return false;
Aqui vale lembrar que os dados brutos também foram usados para a geração da matriz de mascaramento. Portanto, adicionamos aos dados já reunidos o gradiente do erro correspondente a esse fluxo de informação.
if(!DeActivation(cMask.getOutput(), cMask.getGradient(), cMask.getGradient(), cMask.Activation()) || !prevLayer.calcHiddenGradients(cMask.AsObject()) || !SumAndNormilize(prevLayer.getGradient(), cResidual.getPrevOutput(), prevLayer.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; //--- return true; }
Agora, reunimos no nível dos dados brutos o gradiente do erro de todos os fluxos de informação e podemos encerrar o método, retornando o resultado lógico da execução das operações para o programa chamador.
O método de otimização dos parâmetros do objeto deixaremos para estudo independente. Seu algoritmo é bastante simples, nele são apenas chamados os métodos homônimos dos objetos internos. O código completo do método está apresentado no anexo, onde também é possível encontrar o código integral do objeto e de todos os seus métodos. Seguimos agora para a próxima etapa do trabalho.
Montando o framework CATCH
Pode-se dizer que até este ponto realizamos um extenso trabalho preparatório, durante o qual foram construídos objetos individuais, e agora iremos reuni-los em uma estrutura unificada do framework CATCH. Os algoritmos de funcionamento serão estruturados dentro do objeto CNeuronCATCH, cuja composição é apresentada a seguir.
class CNeuronCATCH : public CNeuronTransposeOCL { protected: CNeuronTransposeOCL cTranspose; CNeuronBaseOCL caFreqIn[2]; CNeuronBaseOCL cFreqConcat; CNeuronComplexConvOCL caProjection[2]; CNeuronComplexMVMHMaskAttention caChannelFusion[2]; CNeuronComplexConvOCL caLinearHead[2]; CNeuronBaseOCL caFreqOut[2]; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, uint variables, bool reverse = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; public: CNeuronCATCH(void) {}; ~CNeuronCATCH(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint time_step, uint variables, uint window, uint step, uint window_key, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronCATCH; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Na estrutura apresentada, observamos uma quantidade considerável de objetos internos, cada um desempenhando sua função dentro do complexo algoritmo do framework. Falaremos sobre suas finalidades ao longo da construção dos métodos da nova classe. Por ora, vale observar que todos os objetos são declarados de forma estática, o que nos permite deixar o construtor e o destrutor da classe vazios. A inicialização de todos os objetos é realizada no método Init.
bool CNeuronCATCH::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint time_step, uint variables, uint window, uint step, uint window_key, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, variables, time_step, optimization_type, batch)) return false;
Nos parâmetros desse método, recebemos um conjunto de constantes que permitem definir de maneira inequívoca a arquitetura do objeto em inicialização. Algumas dessas constantes indicam a dimensionalidade dos dados brutos, enquanto outras determinam a estrutura dos fluxos internos de informação. Por exemplo, em time_step e variables são definidos, respectivamente, o número de passos de tempo e o número de sequências unitárias na série temporal multidimensional dos dados brutos. Já os parâmetros window e step indicam as configurações de segmentação do espectro de frequência. Por sua vez, window_key e heads, como é fácil deduzir, representam os principais parâmetros do módulo de atenção.
No corpo do método, como de costume, chamamos imediatamente o método homônimo da classe-pai. Desta vez, utilizamos como classe-pai o objeto de transposição de dados, e, como você deve ter percebido, essa escolha não é aleatória. O objeto espera receber na entrada uma série temporal multidimensional representada sob a forma de uma matriz, na qual cada linha corresponde a um vetor que descreve o estado do ambiente em um determinado passo de tempo. No entanto, o framework CATCH é construído com base na análise do espectro de frequência de sequências unitárias individuais. Para facilitar o trabalho com essas sequências, precisamos transpor o tensor recebido, retornando os dados à sua forma original na saída. Essa última operação será realizada pelos recursos do objeto-pai, o que é refletido nos parâmetros que lhe são passados.
Para converter a série temporal ao domínio da frequência, planejamos utilizar o algoritmo da Transformada Rápida de Fourier. Contudo, esse algoritmo funciona corretamente apenas com sequências cujo comprimento seja uma potência de 2. Ainda assim, podemos aumentar a dimensão de qualquer sequência completando-a com valores nulos, o que não afetará o resultado. Portanto, precisamos determinar o valor mais próximo adequado.
//--- Calculate FFT size int power = int(MathLog(time_step) / M_LN2); if(power <= 0) return false; if(MathPow(2, power) != time_step) power++; uint FreqUinits = uint(MathPow(2, power));
Em seguida, definimos a quantidade de segmentos de acordo com os parâmetros de segmentação estabelecidos.
if(window <= 0 || step <= 0) return false; int Segments = int((FreqUinits - int(window) + step - 1) / step); if(Segments <= 0) return false;
Com isso, concluímos o trabalho preparatório e passamos à inicialização dos objetos internos. O primeiro é a camada de transposição dos dados brutos. Acredito que os parâmetros de sua inicialização não suscitam dúvidas.
uint index = 0; if(!cTranspose.Init(0, index, OpenCL, time_step, variables, optimization, iBatch)) return false;
Depois, criamos dois buffers de dados para registrar as partes real e imaginária do espectro de frequência após a decomposição de Fourier.
for(uint i = 0; i < caFreqIn.Size(); i++) { index++; if(!caFreqIn[i].Init(0, index, OpenCL, FreqUinits * variables, optimization, iBatch)) return false; caFreqIn[i].SetActivationFunction(None); }
Adicionamos, então, o objeto de concatenação dos dados do espectro de frequência.
index++; if(!cFreqConcat.Init(0, index, OpenCL, 2 * FreqUinits * variables, optimization, iBatch)) return false; cFreqConcat.SetActivationFunction(None);
Para o processo de segmentação do espectro de frequência, utilizamos uma camada convolucional capaz de operar com grandezas complexas, especificando nela os parâmetros necessários.
index++; if(!caProjection[0].Init(0, index, OpenCL, window, step, 2 * window, Segments, variables, optimization, iBatch)) return false; caProjection[0].SetActivationFunction(LReLU);
Uma segunda camada convolucional finaliza a criação das incorporações (embeddings) dos nossos patches.
index++; if(!caProjection[1].Init(0, index, OpenCL,2*window,2*window,window_key, Segments, variables, optimization, iBatch)) return false; caProjection[1].SetActivationFunction(TANH);
A análise das interdependências entre os espectros de frequência das diferentes sequências unitárias é realizada por meio de dois módulos de atenção aplicados em sequência. O primeiro trabalha diretamente com as incorporações (embeddings) dos patches criados.
index++; if(!caChannelFusion[0].Init(0, index, OpenCL,window_key,window_key,heads,Segments, variables, optimization, iBatch)) return false;
Já a arquitetura da segunda camada, responsável pela atenção mascarada intercanal, varia conforme a quantidade de segmentos. Se o número de segmentos for múltiplo de 2, é realizado o agrupamento em pares, a fim de detectar dependências de nível hierárquico mais elevado.
index++; if(Segments % 2 == 0) { if(!caChannelFusion[1].Init(0, index, OpenCL, 2 * window_key, window_key, heads, Segments / 2, variables, optimization, iBatch)) return false; } else if(!caChannelFusion[1].Init(0, index, OpenCL, window_key, window_key, heads, Segments, variables, optimization, iBatch)) return false;
Caso contrário, repetimos a arquitetura da camada de atenção anterior.
A dimensionalidade do tensor resultante do processamento pelos módulos de atenção é reduzida ao nível do comprimento do espectro de frequência dos dados brutos, utilizando duas camadas convolucionais de projeção aplicadas em sequência.
index++; if(!caLinearHead[0].Init(0, index, OpenCL, window_key, window_key, window, Segments, variables, optimization, iBatch)) return false; caLinearHead[0].SetActivationFunction(LReLU); index++; if(!caLinearHead[1].Init(0, index, OpenCL, window * Segments, window * Segments, FreqUinits, variables, 1, optimization, iBatch)) return false; caLinearHead[ 1 ].SetActivationFunction(None);
A primeira camada altera a dimensionalidade dos segmentos, enquanto a segunda ajusta o comprimento das sequências unitárias.
Adicionamos também dois objetos para separar as partes real e imaginária do espectro de frequência antes da aplicação do algoritmo da transformada inversa de Fourier.
for(uint i = 0; i < caFreqOut.Size(); i++) { index++; if(!caFreqOut[i].Init(0, index, OpenCL, FreqUinits * variables, optimization, iBatch)) return false; caFreqOut[i].SetActivationFunction(None); } //--- return true; }
Neste ponto, concluímos a inicialização de todos os objetos internos e podemos encerrar o método, retornando o resultado lógico da execução das operações ao programa chamador.
Em seguida, passamos à construção do processo de propagação para frente no método feedForward. Como mencionado anteriormente, nos parâmetros do método recebemos um ponteiro para o objeto de dados brutos, que contém o tensor da série temporal multidimensional.
bool CNeuronCATCH::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cTranspose.FeedForward(NeuronOCL)) return false;
Os dados recebidos são primeiramente transpostos para facilitar o processamento das sequências unitárias e, em seguida, transformados para o domínio da frequência utilizando o algoritmo da Transformada Rápida de Fourier.
if(!FFT(cTranspose.getOutput(), NULL, caFreqIn[0].getOutput(), caFreqIn[1].getOutput(), iCount, false)) return false;
Os resultados da transformação no domínio da frequência são concatenados em um único tensor.
if(!Concat(caFreqIn[0].getOutput(), caFreqIn[1].getOutput(), cFreqConcat.getOutput(), 1, 1, caFreqIn[0].Neurons())) return false;
Depois disso, realizamos o patching do espectro de frequência e a incorporação (embedding) dos dados utilizando duas camadas convolucionais de projeção.
CNeuronBaseOCL *neuron = cFreqConcat.AsObject(); for(uint i = 0; i < caProjection.Size(); i++) { if(!caProjection[i].FeedForward(neuron)) return false; neuron = caProjection[i].AsObject(); }
A etapa seguinte consiste em buscar as interdependências por meio da análise dos dados pelos módulos de atenção mascarada intercanal.
for(uint i = 0; i < caChannelFusion.Size(); i++) { if(!caChannelFusion[i].FeedForward(neuron)) return false; neuron = caChannelFusion[i].AsObject(); }
Em seguida, retornamos os dados à dimensionalidade original do espectro de frequência.
for(uint i = 0; i < caLinearHead.Size(); i++) { if(!caLinearHead[i].FeedForward(neuron)) return false; neuron = caLinearHead[i].AsObject(); }
Depois disso, separamos as partes real e imaginária do espectro de frequência em objetos distintos.
if(!DeConcat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), neuron.getOutput(), 1, 1, caFreqOut[0].Neurons())) return false; if(!FFT(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caFreqOut[0].getPrevOutput(), caFreqOut[1].getPrevOutput(), iCount, true)) return false;
Em seguida, executamos a transformada inversa de Fourier, que converte os dados do domínio da frequência de volta à representação de série temporal. No entanto, é importante considerar que o resultado da transformada inversa de Fourier gera uma série temporal cuja dimensão é uma potência de 2, o que pode diferir da dimensão da série temporal analisada. Por isso, descartamos os valores excedentes por meio da desconcatenação do tensor.
if(!DeConcat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caFreqOut[0].getPrevOutput(), iWindow, caFreqOut[0].Neurons() / iCount - iWindow, iCount)) return false;
Aos valores obtidos, adicionamos as conexões residuais provenientes dos dados brutos transpostos, normalizamos os resultados e realizamos a transformação inversa para retornar os dados à forma original da série temporal.
if(!SumAndNormilize(caFreqOut[0].getOutput(),cTranspose.getOutput(),caFreqOut[0].getOutput(),iWindow,true,0,0,0,1)) return false; //--- return CNeuronTransposeOCL::feedForward(caFreqOut[0].AsObject()); }
Com isso, encerra-se o funcionamento do método de propagação para frente, e o resultado lógico das operações é retornado ao programa chamador.
A próxima etapa do nosso trabalho é a construção dos processos de propagação reversa do novo objeto. E aqui, atenção especial deve ser dada ao método de distribuição do erro entre todos os componentes do processo, de acordo com sua contribuição para o resultado final, o método calcInputGradients.
bool CNeuronCATCH::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
Nos parâmetros do método, recebemos um ponteiro para o objeto de dados brutos e, imediatamente, verificamos a validade do ponteiro recebido. A necessidade desse ponto de controle já foi discutida diversas vezes anteriormente.
Em seguida, transpondo o gradiente do erro recebido da camada subsequente para a representação das sequências unitárias.
if(!CNeuronTransposeOCL::calcInputGradients(caFreqOut[1].AsObject())) return false; if(!SumAndNormilize(caFreqOut[1].getGradient(),caFreqOut[1].getGradient(),cTranspose.getPrevOutput(), iWindow,false,0,0,0,0.5f)) return false;
Imediatamente copiamos os valores obtidos para o buffer livre do objeto de transposição dos dados brutos, o que corresponde ao fluxo das conexões residuais.
Vale lembrar que a dimensionalidade dos resultados da transformada inversa de Fourier pode exceder o comprimento esperado da série temporal. Durante a propagação para frente, descartamos os valores excedentes. Aqui é importante observar que, ao realizar a propagação direta, complementamos a série temporal analisada com valores nulos até o tamanho exigido. Portanto, na parte descartada dos resultados da transformada inversa de Fourier, esperamos obter os mesmos valores nulos. Assim, para que o treinamento do modelo seja coerente, o gradiente do erro dessa parte descartada deve ser indicado com o sinal invertido em relação ao resultado obtido anteriormente.
if((caFreqOut[0].Neurons() - iWindow) > 0) if(!SumAndNormilize(caFreqOut[1].getOutput(), caFreqOut[1].getOutput(), caFreqOut[1].getOutput(), 1, false, 0, 0, 0, -0.5f)) return false;
Concatenamos os gradientes de erro dos dois blocos em um único tensor.
if(!Concat(caFreqOut[1].getGradient(), caFreqOut[1].getOutput(), caFreqOut[0].getGradient(), iWindow, caFreqOut[0].Neurons() - iWindow, iCount)) return false;
Dessa forma, obtemos o gradiente do erro da parte real do sinal reconstruído. Mas ainda há a parte imaginária. Aqui, é importante recordar que, com a transformada inversa de Fourier, reconstruímos a série temporal a partir de sua representação no domínio da frequência. A própria série temporal é composta por valores reais, cuja parte imaginária é igual a zero. Consequentemente, a abordagem para determinar o gradiente do erro da parte imaginária é idêntica àquela aplicada à parte descartada da componente real, invertemos o sinal dos resultados obtidos anteriormente.
if(!SumAndNormilize(caFreqOut[1].getPrevOutput(), caFreqOut[1].getPrevOutput(), caFreqOut[1].getGradient(), 1, false, 0, 0, 0, -0.5f)) return false;
Agora podemos, com a ajuda da Transformada Rápida de Fourier, converter os gradientes de erro para o domínio da frequência.
if(!FFT(caFreqOut[0].getGradient(), caFreqOut[1].getGradient(), caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), iCount, false)) return false;
Em seguida, concatenamos os resultados obtidos em um único tensor, combinando as partes real e imaginária das grandezas complexas.
if(!Concat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caLinearHead[1].getGradient(), 1, 1, caFreqOut[0].Neurons())) return false;
Depois disso, conduzimos o gradiente do erro sequencialmente através de todos os objetos internos, começando pelos objetos de projeção final dos módulos de atenção.
if(!caLinearHead[0].calcHiddenGradients(caLinearHead[1].AsObject())) return false;
Através dos módulos de atenção, propagamos o gradiente do erro até as camadas convolucionais responsáveis pelas incorporações (embeddings).
CObject *neuron = caLinearHead[0].AsObject(); for(int i = int(caChannelFusion.Size()) - 1; i >= 0; i--) { if(!caChannelFusion[i].calcHiddenGradients(neuron)) return false; neuron = caChannelFusion[i].AsObject(); }
Em seguida, continuamos até o nível dos dados concatenados do espectro de frequência dos dados brutos.
for(int i = int(caProjection.Size()) - 1; i >= 0; i--) { if(!caProjection[i].calcHiddenGradients(neuron)) return false; neuron = caProjection[i].AsObject(); } //--- if(!cFreqConcat.calcHiddenGradients(neuron)) return false;
Nesse ponto, separamos o resultado obtido nas partes real e imaginária.
if(!DeConcat(caFreqIn[0].getGradient(), caFreqIn[1].getGradient(), cFreqConcat.getGradient(), 1, 1, caFreqIn[0].Neurons())) return false;
Em seguida, utilizando a transformada inversa de Fourier, retornamos o gradiente do erro para a representação da série temporal.
if(!FFT(caFreqIn[0].getGradient(), caFreqIn[1].getGradient(), caFreqIn[0].getPrevOutput(), caFreqIn[1].getPrevOutput(), iCount, false)) return false;
Selecionamos apenas a parte relevante dos dados, correspondente à série temporal original.
if(!DeConcat(cTranspose.getGradient(), caFreqIn[0].getGradient(), caFreqIn[0].getPrevOutput(), iWindow, caFreqIn[0].Neurons() / iCount - iWindow, iCount)) return false; //--- if(!SumAndNormilize(cTranspose.getGradient(),cTranspose.getPrevOutput(),cTranspose.getGradient(),iWindow, false,0,0,0,1.0f)) return false;
Por fim, somamos os resultados aos dados previamente armazenados das conexões residuais.
No término do método, transpondo os gradientes do erro para a representação dos dados brutos e, se necessário, aplicamos a correção pela derivada da função de ativação do objeto de dados brutos.
if(!prevLayer.calcHiddenGradients(cTranspose.AsObject())) return false; if(prevLayer.Activation() != None) { if(!DeActivation(prevLayer.getOutput(), prevLayer.getGradient(), prevLayer.getGradient(), prevLayer.Activation())) return false; } //--- return true; }
O resultado lógico da execução das operações é retornado ao programa chamador, encerrando assim o funcionamento do método.
Com isso, concluímos a análise dos algoritmos de construção da nossa própria visão das abordagens propostas pelos autores do framework CATCH. O código completo de todos os objetos e seus respectivos métodos pode ser consultado no anexo deste artigo.
Arquitetura das modelos
Após detalharmos os algoritmos de implementação da nossa versão das abordagens apresentadas, vale comentar um pouco sobre a arquitetura das modelos treináveis. Assim como no trabalho anterior, treinaremos três modelos: o Codificador (Encoder) do estado do ambiente, o Ator (Actor) e o modelo de previsão de probabilidades da direção do movimento futuro. As abordagens do framework CATCH são implementadas no Codificador responsável pela descrição do estado analisado do ambiente. E, graças ao fato de que praticamente todo o framework foi reunido em um único objeto, a arquitetura da modelo torna-se visualmente simples.
bool CreateDescriptions(CArrayObj *&encoder, CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Primeiro, como de costume, utilizamos uma camada totalmente conectada para registrar os dados brutos, seguida por um objeto de normalização em lote (batch normalization). Nessa etapa, ocorre o processamento inicial da série temporal multidimensional recebida e o alinhamento das sequências unitárias para uma forma comparável.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Em seguida, aplicamos o nosso módulo CATCH. Nele, realizamos a segmentação do espectro de frequência em blocos de 8 elementos, com um passo de 1. Isso nos permite analisar com mais profundidade as interdependências ao longo de todo o espectro de frequência dos dados brutos.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCATCH; prev_count=descr.count = HistoryBars; { int temp[]={BarDescr,8,32,4}; // Variables, Frequency window, Key Size, Heads if(ArrayCopy(descr.windows, temp) < (int)temp.Size()) return false; } descr.step=1; int prev_out=descr.windows[0]; descr.batch = 1e4; descr.optimization=ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Os dados resultantes são ajustados para um intervalo estreito de valores normalizados.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; descr.window_out = BarDescr; descr.layers = 1; descr.activation = TANH; if(!encoder.Add(descr)) { delete descr; return false; }
Depois, restituímos sua distribuição original por meio de uma camada de normalização inversa.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = HistoryBars * BarDescr; descr.layers = 1; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
As arquiteturas do Ator e do modelo de previsão das probabilidades da direção do movimento futuro foram transferidas do trabalho anterior praticamente sem alterações. Recomendo que você as estude de forma independente. O código completo está disponível no anexo, onde também se encontram os programas de interação com o ambiente e de treinamento das modelos, que foram mantidos sem qualquer modificação.
Testes
Realizamos um trabalho bastante extenso na implementação, em MQL5, das abordagens propostas no âmbito do framework CATCH e na integração delas às modelos treináveis. Chegou, então, o momento decisivo, verificar a eficácia das soluções implementadas em dados históricos reais. Isso permitirá avaliar os pontos fortes e fracos das abordagens desenvolvidas, bem como identificar o potencial para futuras otimizações.
Para o treinamento da modelo, compilamos um conjunto de dados de aprendizado a partir de passagens aleatórias no testador de estratégias do MetaTrader 5. Como base, foram utilizados dados históricos do par de moedas EURUSD, no timeframe M1, cobrindo todo o ano de 2024.
O teste das modelos treinadas foi realizado utilizando dados históricos do período de janeiro a março de 2025. Todos os parâmetros do experimento foram mantidos inalterados, o que garante a objetividade dos resultados obtidos e possibilita uma avaliação independente da eficácia da estratégia. Essa abordagem assegura que a modelo não esteja apenas memorizando as características do conjunto de treinamento, mas que de fato demonstre capacidade de adaptação a novas condições de mercado.
A seguir, são apresentados os resultados dos testes.
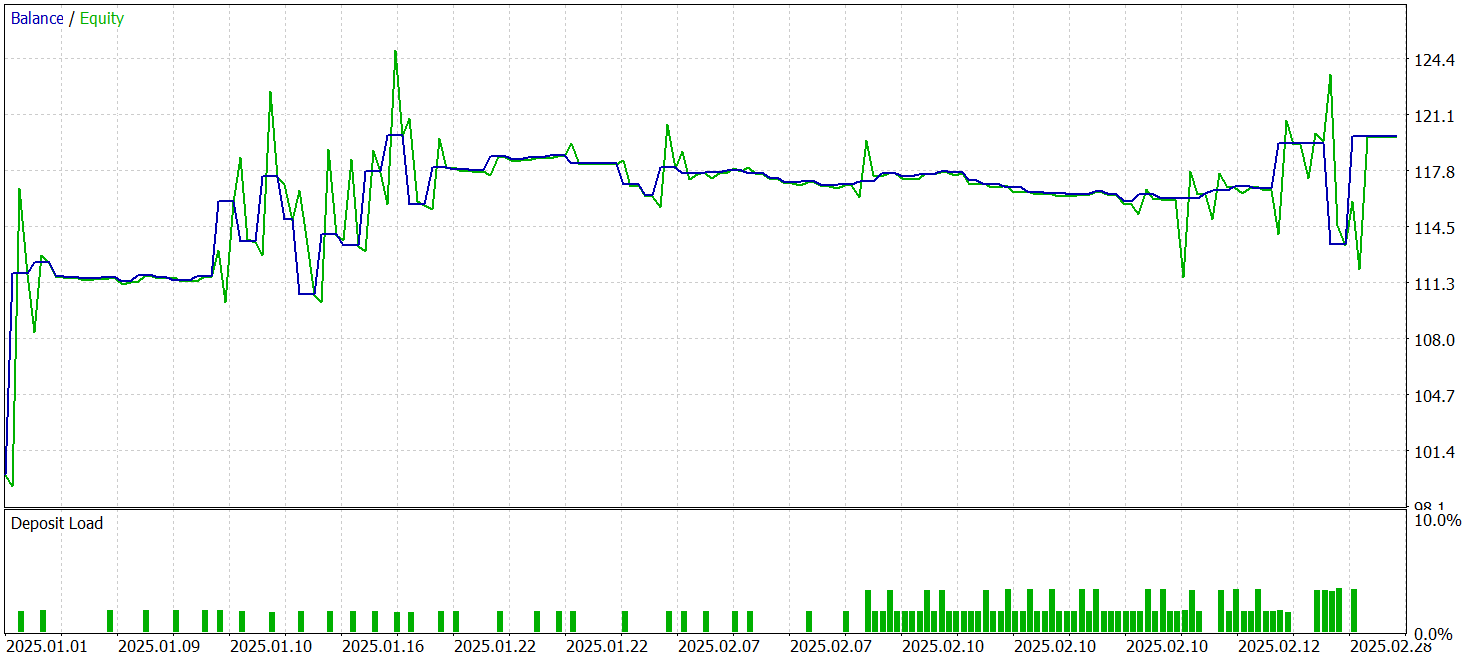
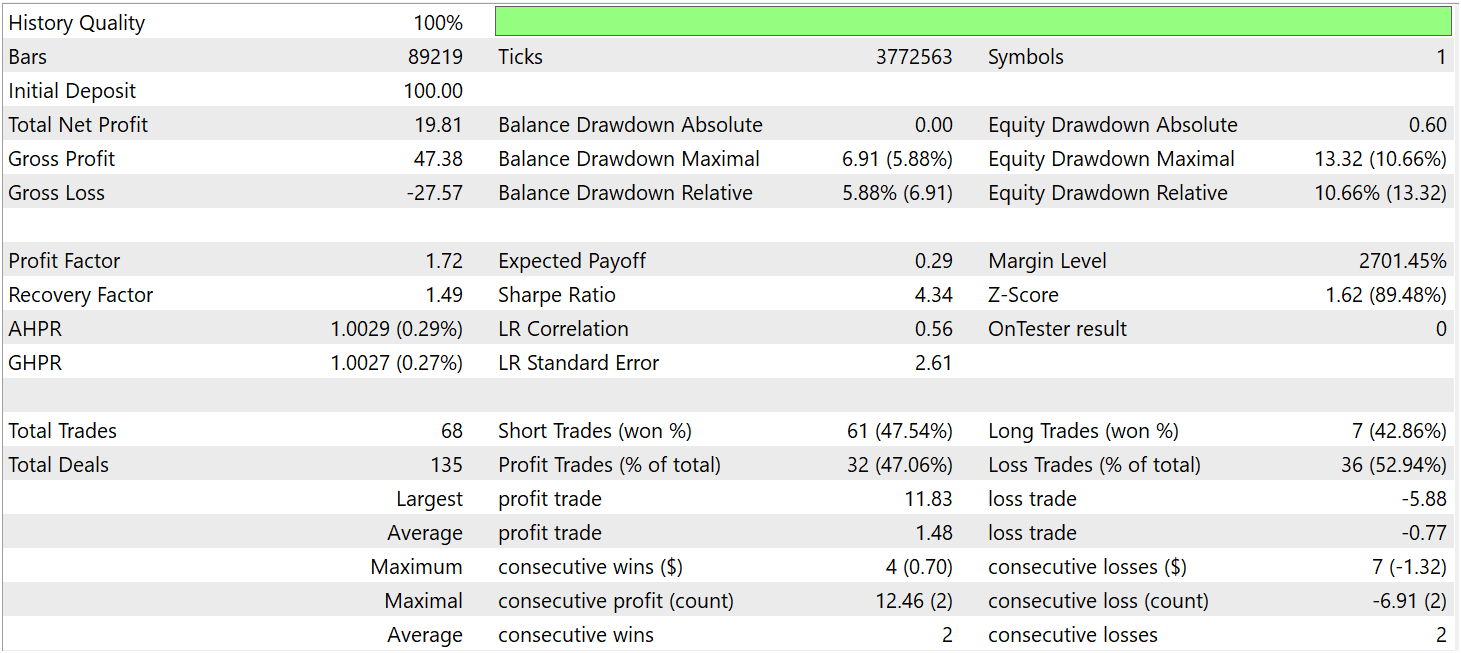
Durante o período de teste, o modelo executou 68 operações, das quais apenas 32 foram encerradas com lucro, representando pouco mais de 47%. Ao mesmo tempo, a média das operações lucrativas foi quase duas vezes superior à média das operações com prejuízo. Como resultado, ao longo do período analisado, a modelo conseguiu gerar lucro, registrando um profit factor de 1,72.
Considerações finais
Ao longo destas duas partes do artigo, conhecemos os fundamentos teóricos do framework CATCH, que representa uma abordagem inovadora ao combinar a transformada de Fourier e o mecanismo de patching em frequência para detectar anomalias em séries temporais multidimensionais. Sua principal vantagem está na capacidade de identificar padrões complexos que permanecem invisíveis quando analisados exclusivamente no domínio temporal.
O uso da representação em frequência permite uma compreensão mais profunda da estrutura da dinâmica de mercado, enquanto o mecanismo de patching em frequência confere flexibilidade à análise, ajudando o modelo a se adaptar às condições variáveis do ambiente analisado. Diferentemente dos métodos clássicos, o CATCH não se limita à detecção de picos de preço e valores atípicos, mas possibilita reconhecer dependências ocultas.
Na parte prática, implementamos nossa própria versão das abordagens propostas utilizando MQL5, treinamos a modelo e realizamos testes com dados históricos reais. Os resultados obtidos indicam um potencial promissor, embora ainda existam questões em aberto relacionadas à otimização futura.
Referências
- CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching
- Outros artigos da série
Programas utilizados neste artigo:
| # | Nome | Tipo | Descrição |
|---|---|---|---|
| 1 | Research.mq5 | Expert Advisor | EA para coleta de exemplos pelo método ExORL |
| 2 | ResearchRealORL.mq5 | Expert Advisor | EA para coleta de exemplos utilizando o método Real-ORL |
| 3 | Study.mq5 | Expert Advisor | EA para treinamento de modelos |
| 4 | Test.mq5 | Expert Advisor | EA para teste de modelo |
| 5 | Trajectory.mqh | Biblioteca de classe | Estrutura para descrição do estado do sistema e arquitetura dos modelos |
| 6 | NeuroNet.mqh | Biblioteca de classe | Biblioteca de classes para criação de redes neurais |
| 7 | NeuroNet.cl | Biblioteca | Biblioteca de código para programas OpenCL |
Traduzido do russo pela MetaQuotes Ltd.
Artigo original: https://www.mql5.com/ru/articles/17675
Aviso: Todos os direitos sobre esses materiais pertencem à MetaQuotes Ltd. É proibida a reimpressão total ou parcial.
Esse artigo foi escrito por um usuário do site e reflete seu ponto de vista pessoal. A MetaQuotes Ltd. não se responsabiliza pela precisão das informações apresentadas nem pelas possíveis consequências decorrentes do uso das soluções, estratégias ou recomendações descritas.
 Critérios de tendência. Conclusão
Critérios de tendência. Conclusão
 Redes neurais em trading: Ator–Diretor–Crítico (Conclusão)
Redes neurais em trading: Ator–Diretor–Crítico (Conclusão)
 Reimaginando Estratégias Clássicas (Parte 13): Minimizando o Atraso em Cruzamentos de Médias Móveis
Reimaginando Estratégias Clássicas (Parte 13): Minimizando o Atraso em Cruzamentos de Médias Móveis
- Aplicativos de negociação gratuitos
- 8 000+ sinais para cópia
- Notícias econômicas para análise dos mercados financeiros
Você concorda com a política do site e com os termos de uso