Redes neurais em trading: Identificação de anomalias no domínio da frequência (CATCH)

Introdução

Os mercados financeiros modernos operam em tempo real, onde a cada segundo são processados volumes gigantescos de dados. Cotações de ações, taxas de câmbio, volumes de negociação, taxas de juros, tudo isso forma séries temporais complexas e multivariadas. A análise desses dados é criticamente importante para traders e investidores. Ela ajuda a prever movimentos futuros do mercado e a identificar padrões ocultos.

Uma das principais tarefas da análise de séries temporais é a detecção de anomalias. Saltos inesperados de preços, mudanças bruscas de liquidez, atividades de negociação suspeitas podem sinalizar manipulações de mercado ou negociação com informação privilegiada. Se não forem percebidas a tempo, as consequências podem ser catastróficas, desde grandes prejuízos até o colapso de instituições financeiras inteiras.

As anomalias podem ser de dois tipos: pontuais e na forma de subsequências. As anomalias pontuais são valores atípicos abruptos, por exemplo, um aumento súbito no volume de negociações de uma única ação. Elas são facilmente detectadas com o uso de métodos padrão. Já as anomalias de subsequência são mais complexas; são mudanças que parecem normais, mas violam os padrões de mercado habituais. Por exemplo, um deslocamento de longo prazo na correlação entre ações, ou um crescimento de preço anormalmente suave em um mercado instável. Essas anomalias são especialmente importantes, pois podem indicar riscos ocultos.

Uma das abordagens mais eficazes para sua detecção é a transferência dos dados para o domínio da frequência. Nessa representação, diferentes tipos de anomalias se manifestam em faixas de frequência específicas. Por exemplo, picos de volatilidade de curto prazo afetam componentes de alta frequência, enquanto mudanças globais de tendência impactam componentes de baixa frequência. No entanto, os métodos padrão frequentemente perdem detalhes importantes, especialmente nas altas frequências, onde se escondem sinais pouco perceptíveis, mas criticamente importantes.

Também é importante considerar as relações entre diferentes ativos de mercado. Por exemplo, se os futuros de petróleo caem drasticamente, mas as ações de empresas petrolíferas permanecem estáveis, isso pode ser um sinal de inconsistência no mercado. Contudo, os modelos clássicos ou ignoram essas inter-relações, ou as consideram de forma excessivamente rígida, o que reduz a precisão das previsões.

Uma das soluções para os problemas mencionados foi proposta no trabalho "CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching". Seus autores apresentaram um novo framework CATCH, que utiliza a transformada de Fourier para analisar dados de mercado no domínio da frequência. Com o objetivo de melhorar a detecção de anomalias complexas, os autores do framework desenvolveram um mecanismo de patching de frequência, que ajuda a modelar o comportamento normal dos ativos com alta precisão. Um módulo adaptativo de inter-relações permite identificar automaticamente correlações importantes entre instrumentos de mercado, ignorando o ruído.

Algoritmo CATCH

A arquitetura CATCH consiste em três módulos-chave:

• Forward Module,
• Channel Fusion Module (CFM),
• Time-Frequency Reconstruction Module (TFRM).

Essa arquitetura foi desenvolvida levando em consideração a necessidade de uma análise detalhada das características temporais e de frequência dos dados, bem como a identificação de padrões ocultos entre os canais. Essa abordagem permite detectar anomalias de forma eficaz mesmo em séries temporais multidimensionais complexas.

A primeira etapa do processamento de dados é o Forward Module. Ele inclui a normalização dos dados, a transformação da série temporal para o domínio da frequência por meio da transformada rápida de Fourier (FFT), e, em seguida, a divisão em fragmentos de frequência (patches). A transformada de Fourier permite representar os dados temporais na forma de funções trigonométricas ortogonais, preservando as partes real e imaginária do espectro de frequência da série temporal analisada.

Em seguida, é realizada a divisão em L patches de frequência de tamanho P com passo S. O patching é aplicado aos dados das partes real e imaginária do espectro de frequência com os mesmos parâmetros; após isso, os dados são concatenados, unificando as partes real e imaginária do espectro de cada segmento em um único tensor.

Na etapa seguinte, os patches são transferidos para o espaço latente por meio de uma camada de projeção:

Esse processo desempenha um papel importante, pois permite reduzir a dimensionalidade dos dados, mantendo ao mesmo tempo as características mais relevantes para a análise posterior. Graças a isso, é possível melhorar a capacidade de generalização do modelo e aumentar a precisão da detecção de anomalias.

Em seguida, é utilizado o Channel Fusion Module (CFM), que identifica as interdependências entre os canais em cada faixa de frequência. Para isso, é aplicado o mecanismo Channel-Masked Transformer (CMT). Aqui, a máscara de canais M é criada com o auxílio do Mask Generator (MG). O MG constrói matrizes probabilísticas D, que posteriormente são binarizadas por meio de reamostragem de Bernoulli. Dessa forma, valores altos em D resultam em unidades em M, indicando a existência de uma relação entre os canais.

O CMT processa os patches levando em consideração a atenção mascarada, que pode ser representada pelas seguintes expressões matemáticas:

Para alcançar uma otimização eficaz no contexto da geração de máscaras e do ajuste dos mecanismos de atenção, é importante desenvolver objetivos de otimização claros que permitam aumentar a qualidade das máscaras obtidas. Nesse caso, o aspecto-chave é o aumento explícito dos coeficientes de atenção entre os canais relevantes, que foram determinados com o auxílio da máscara. Isso permite alinhar o mecanismo de atenção com a correlação de canais mais atual e otimizada, o que, por sua vez, contribui para a melhoria da qualidade do modelo.

Uma das vantagens mais importantes dessa abordagem é a possibilidade de evitar efeitos negativos que surgem quando canais irrelevantes são incluídos no processo de atenção. O mecanismo mascarado, levando em conta o ajuste das conexões, foca de forma eficaz a atenção nos canais mais significativos, minimizando a influência de ruídos e distorções. Esse tipo de abordagem permite alcançar a estabilidade do mecanismo de atenção, o que aumenta significativamente a precisão e a eficiência do modelo em condições de dados variáveis.

O próximo passo é a otimização iterativa do gerador de máscaras, voltada para o refinamento mais preciso das correlações entre os canais. Esse processo inclui o ajuste do mecanismo de atenção na camada do Transformer mascarado no recorte por canais, o que permite capturar e processar de forma completa todas as possíveis inter-relações entre os canais.

Para a otimização do mecanismo de mascaramento, os autores do framework propõem o uso da função de perda ClusteringLoss:

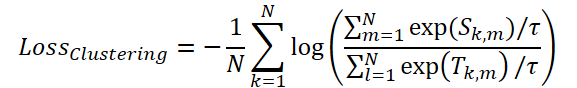
Na etapa final, o Time-Frequency Reconstruction Module (TFRM) executa a transformada inversa de Fourier (iFFT) para a reconstrução da série temporal:

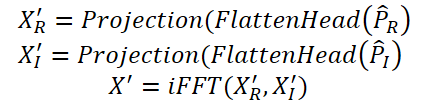
As anomalias são identificadas com base no erro de reconstrução.

Graças ao uso de uma análise de dados abrangente, baseada em características temporais e de frequência, o modelo CATCH assegura uma identificação confiável de anomalias.

A visualização autoral do framework CATCH é apresentada a seguir.

Implementação com MQL5

Após a análise dos aspectos teóricos do framework CATCH, passamos para a parte prática do nosso artigo, na qual implementamos nossa própria visão das abordagens propostas utilizando MQL5.

Antes de tudo, é necessário dar atenção especial ao fato de que, nesse framework, praticamente todas as operações são realizadas no domínio da frequência dos dados analisados. Essa é uma característica-chave que define a abordagem de processamento dos dados e a escolha dos métodos matemáticos.

Como é sabido, a representação de um sinal no domínio da frequência é realizada utilizando números complexos. Consequentemente, para o funcionamento correto do sistema, é necessário garantir um processamento eficiente de dados complexos, incluindo operações aritméticas.

Uma tarefa semelhante já havia sido parcialmente resolvida por nós durante o desenvolvimento do framework ATFNet. Naquela ocasião, foram estabelecidos os princípios de processamento de dados espectrais e definidos os enfoques metodológicos, que agora podem ser utilizados na criação da solução atual. Esses desenvolvimentos nos permitem simplificar significativamente a implementação das funções principais.

Camada convolucional de dados complexos

Iniciaremos nosso trabalho com o desenvolvimento de uma camada convolucional para operar com valores complexos. Como mostra a prática, camadas convolucionais são uma das ferramentas mais eficazes para o processamento de sequências multidimensionais. É justamente por essa razão que damos prioridade à construção desse componente.

Como de costume, inicialmente construiremos os algoritmos de funcionamento do novo objeto no lado do OpenCL-contexto. A transferência de todas as operações-chave para o nível da GPU nos permite alcançar o máximo paralelismo, o que é criticamente importante no processamento de dados multidimensionais. Diferentemente dos cálculos sequenciais na CPU, aqui cada núcleo da GPU executa parte da tarefa geral, o que resulta em uma aceleração significativa do funcionamento do modelo, tanto durante o processo de treinamento quanto durante a utilização em massa.

As operações de propagação para frente serão implementadas no kernel FeedForwardComplexConv. Nos parâmetros desse kernel são passados ponteiros para três buffers de dados e uma série de constantes que determinam a estrutura dos dados.

É importante chamar atenção especial para o fato de que todos os buffers de dados utilizam o tipo vetorial float2. Essa escolha se deve à necessidade de um processamento eficiente de números complexos, nos quais cada valor é representado por um par de componentes, a parte real e a parte imaginária.

O uso de float2 nos oferece várias vantagens importantes:

• Otimização do carregamento e do salvamento de dados: graças à representação vetorial, podemos ler simultaneamente dos buffers e gravar neles dois valores de uma só vez, o que reduz o número de operações de leitura e escrita.
• Aceleração por hardware: OpenCL fornece suporte em nível de hardware para o trabalho com tipos vetoriais, o que permite acelerar a execução de operações aritméticas.
• Representação uniforme dos dados: o uso de float2 torna o código mais legível e lógico, pois cada variável corresponde explicitamente a um número complexo.

__kernel void FeedForwardComplexConv(__global const float2 *matrix_w,
                                     __global const float2 *matrix_i,
                                     __global float2 *matrix_o,
                                     const int inputs,
                                     const int step,
                                     const int window_in,
                                     const int activation
                                    )
  {
   const size_t i = get_global_id(0);
   const size_t units = get_global_size(0);
   const size_t out = get_global_id(1);
   const size_t w_out = get_global_size(1);
   const size_t var = get_global_id(2);
   const size_t variables = get_global_size(2);

O funcionamento desse kernel é projetado para um espaço de tarefas tridimensional. Na primeira dimensão, indicamos a quantidade de elementos da sequência. Na segunda, o número de filtros. Já a terceira dimensão do espaço de tarefas indica o número de sequências unitárias independentes no tensor geral dos dados de entrada. No corpo do kernel, identificamos imediatamente o fluxo atual de operações no espaço de tarefas em todas as dimensões. Os valores obtidos são armazenados em constantes locais.

Em seguida, com base nos resultados da identificação do fluxo de operações, determinamos os deslocamentos nos buffers de dados. Essa operação é completamente idêntica ao algoritmo utilizado na camada convolucional de valores reais criada anteriormente, o que se tornou possível graças ao uso de um tipo de dado vetorial para representar grandezas complexas.

int w_in = window_in;
int shift_out = w_out * (i + units * var);
int shift_in = step * i + inputs * var;
int shift = (w_in + 1) * (out + var * w_out);
int stop = (w_in <= (inputs - shift_in) ? w_in : (inputs - shift_in)) + inputs * var;

Com isso, a etapa preparatória é concluída, e passamos diretamente à operação de convolução. Nesse caso, os dados de entrada e os parâmetros treináveis dos filtros são grandezas complexas. O resultado das operações também será representado como um valor complexo. Todas as operações matemáticas serão realizadas utilizando as funções previamente criadas de operações básicas com números complexos.

Inicialmente, declaramos uma variável local para o armazenamento temporário dos resultados intermediários e transferimos para ela o valor do elemento de viés treinável.

   float2 sum = ComplexMul((float2)(1, 0), matrix_w[shift + w_in]);
#pragma unroll
   for(int k = 0; k <= stop; k ++)
      sum += IsNaNOrInf2(ComplexMul(matrix_i[shift_in + k], matrix_w[shift + k]), (float2)0);

Em seguida, organizamos o laço de multiplicação do vetor de dados de entrada pelo vetor correspondente do filtro, com a soma dos resultados na variável local.

Depois disso, resta apenas aplicar a função de ativação necessária e salvar o valor obtido no buffer de resultados.

   switch(activation)
     {
      case 0:
         sum = ComplexTanh(sum);
         break;
      case 1:
         sum = ComplexDiv((float2)(1, 0), (float2)(1, 0) + ComplexExp(-sum));
         break;
      case 2:
         if(sum.x < 0)
           {
            sum.x *= 0.01f;
            sum.y *= 0.01f;
           }
         break;
      default:
         break;
     }
   matrix_o[out + shift_out] = sum;
  }

No próximo passo, passamos à construção dos algoritmos de propagação reversa. Consideremos o kernel de distribuição do gradiente de erro CalcHiddenGradientComplexConv. Aqui utilizamos a mesma abordagem de representação de números complexos na forma de uma grandeza vetorial. Ao mesmo tempo, nos parâmetros do método adicionamos buffers dos gradientes de erro nos níveis correspondentes das operações.

__kernel void CalcHiddenGradientComplexConv(__global const float2 * matrix_w,
                                            __global const float2 * matrix_g,
                                            __global const float2 * matrix_o,
                                            __global float2 * matrix_ig,
                                            const int outputs,
                                            const int step,
                                            const int window_in,
                                            const int window_out,
                                            const int activation,
                                            const int shift_out
                                           )
  {
   const size_t i = get_global_id(0);
   const size_t inputs = get_global_size(0);
   const size_t var = get_global_id(1);
   const size_t variables = get_global_size(1);

Vale a pena observar que o objetivo desta operação é transferir o gradiente do erro para o nível dos dados de entrada de acordo com sua influência no resultado do funcionamento do modelo. Isso foi o que determinou as mudanças no espaço de tarefas de execução do kernel. Na nossa implementação, utilizamos um espaço de tarefas bidimensional. A primeira dimensão indica o elemento na sequência dos dados de entrada, enquanto a segunda indica a sequência unitária do conjunto multivariado.

No corpo do kernel, assim como anteriormente, primeiro identificamos o fluxo atual de operações em todas as dimensões do espaço de tarefas. Os valores obtidos são armazenados na forma de constantes locais.

Em seguida, determinamos os deslocamentos nos buffers de dados. Aqui é importante notar que um elemento dos dados de entrada, dependendo do passo utilizado na janela de convolução, pode participar de várias operações de convolução. Consequentemente, precisamos agregar o gradiente do erro de todas essas operações. Para isso, definimos os limites dos intervalos nos quais o gradiente do erro será acumulado.

float2 sum = (float2)0;
float2 out = matrix_o[i];
int start = i - window_in + step;
start = max((start - start % step) / step, 0) + var * inputs;
int stop = (i + step - 1) / step;
if(stop > (outputs / window_out))
   stop = outputs / window_out;
stop += var * outputs;

Após a conclusão do trabalho preparatório, organizamos um laço de passagem pelos intervalos previamente definidos com o passo especificado e somamos os gradientes do erro levando em consideração os coeficientes de peso correspondentes.

#pragma unroll
   for(int h = 0; h < window_out; h ++)
     {
      for(int k = start; k < stop; k++)
        {
         int shift_g = k * window_out + h;
         int shift_w = (stop - k - 1) * step + i % step + h * (window_in + 1);
         if(shift_g >= outputs || shift_w >= (window_in + 1) * window_out)
            break;
         sum += ComplexMul(matrix_g[shift_out + shift_g], matrix_w[shift_w]);
        }
     }
   sum = IsNaNOrInf2(sum, (float2)0);

O valor obtido é então ajustado pela derivada da função de ativação dos dados de entrada.

   switch(activation)
     {
      case 0:
         sum = ComplexMul(sum, (float2)1.0f - ComplexMul(out, out));
         break;
      case 1:
         sum = ComplexMul(sum, ComplexMul(out, (float2)1.0f - out));
         break;
      case 2:
         if(out.x < 0.0f)
           {
            sum.x *= 0.01f;
            sum.y *= 0.01f;
           }
         break;
      default:
         break;
     }
   matrix_ig[i] = sum;
  }

O resultado das operações é armazenado no elemento correspondente do buffer global de dados.

O código completo dos kernels apresentados acima pode ser encontrado no anexo do artigo. No mesmo local, também está disponível o código completo dos kernels de otimização dos parâmetros treináveis dos filtros, que proponho deixar para estudo independente. E nós seguimos para a organização dos processos no lado do programa principal.

Aqui criamos um novo objeto CNeuronComplexConvOCL, cuja estrutura é apresentada abaixo.

class CNeuronComplexConvOCL    :  public CNeuronConvOCL
  {
protected:
   //---
   virtual bool      feedForward(CNeuronBaseOCL *NeuronOCL);
   virtual bool      updateInputWeights(CNeuronBaseOCL *NeuronOCL);
   virtual bool      calcInputGradients(CNeuronBaseOCL *NeuronOCL);

public:
                     CNeuronComplexConvOCL(void)   {  activation = None;   }
                    ~CNeuronComplexConvOCL(void) {};
   virtual bool      Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                          uint window, uint step, uint window_out, 
                          uint units_count, uint variables, 
                          ENUM_OPTIMIZATION optimization_type, uint batch);
   //---
   virtual int       Type(void)   const   {  return defNeuronComplexConvOCL;   }
  };

É bastante natural que o objeto da camada convolucional de valores reais seja utilizado como classe pai. Isso nos permite aproveitar integralmente a infraestrutura da classe pai, incluindo objetos internos e interfaces. Ainda assim, algumas correções no funcionamento dos métodos herdados precisarão ser realizadas.

Antes de tudo, naturalmente, trata-se dos métodos de propagação para frente e de propagação reversa. Nós os sobrescrevemos para trabalhar com os novos kernels OpenCL-do programa, cujos algoritmos foram descritos acima. O algoritmo de enfileiramento desses kernels para execução permanece padrão. Por isso, não vamos nos deter em uma análise detalhada desses métodos. Vamos deixá-los para estudo independente; o código completo está disponível no anexo.

No entanto, dedicaremos algum tempo à análise do algoritmo do método de inicialização do novo objeto, pois o trabalho com grandezas complexas leva a mudanças nos buffers de dados. Aqui vale destacar que, embora o MQL5 suporte o trabalho com grandezas complexas, não introduzimos novos objetos de buffer de dados. Apenas aumentamos o tamanho dos já existentes. Isso torna nossa solução mais universal e não exige a introdução de modificações complexas no funcionamento dos métodos.

A estrutura dos parâmetros do método de inicialização é totalmente herdada da classe pai.

bool CNeuronComplexConvOCL::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl,
                                 uint window, uint step, uint window_out, 
                                 uint units_count, uint variables, 
                                 ENUM_OPTIMIZATION optimization_type, uint batch)
  {
   if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * units_count * window_out * variables,
                                                                         optimization_type, batch))
      return false;

No corpo do método, inicialmente chamamos o método homônimo da camada totalmente conectada, que é a classe pai de todos os objetos de camadas neurais da nossa biblioteca, incluindo a camada convolucional. Não podemos utilizar o método homônimo da classe pai direta devido à incompatibilidade dos tamanhos dos buffers de dados.

Observe que, ao definir o tamanho do objeto criado pelos meios do método da classe pai, indicamos um tamanho de camada duas vezes maior que o valor calculado. Como não é difícil perceber, isso se deve à necessidade de armazenar as partes real e imaginária de uma grandeza complexa.

Em seguida, salvamos as constantes da arquitetura do objeto em variáveis internas.

iWindow = (int)window;
iStep = MathMax(step, 1);
activation = None;
iWindowOut = window_out;
iVariables = variables;

No próximo passo, passamos à inicialização dos buffers de dados herdados. Primeiro, verificamos sua atualidade e, se necessário, criamos um novo objeto de buffer dos parâmetros treináveis.

if(CheckPointer(WeightsConv) == POINTER_INVALID)
  {
   WeightsConv = new CBufferFloat();
   if(CheckPointer(WeightsConv) == POINTER_INVALID)
      return false;
  }

Ao definir o tamanho do buffer dos parâmetros treináveis, é preciso considerar que aqui também utilizamos grandezas complexas. Portanto, aumentamos o tamanho do buffer em duas vezes em relação ao valor calculado.

int count = (int)(2 * (iWindow + 1) * iWindowOut * iVariables);
if(!WeightsConv.Reserve(count))
   return false;

E inicializamos o buffer com valores aleatórios.

float k = (float)(1 / sqrt(iWindow + 1));
for(int i = 0; i < count; i++)
  {
   if(!WeightsConv.Add((GenerateWeight() * 2 * k - k)*WeightsMultiplier))
    return false;
  }
if(!WeightsConv.BufferCreate(OpenCL))
   return false;

Depois disso, dependendo do método de otimização dos parâmetros, inicializamos a quantidade necessária de buffers para armazenar os dados dos momentos da otimização dos parâmetros. A inicialização inicial desses buffers é realizada com valores nulos.

   if(optimization == SGD)
     {
      if(CheckPointer(DeltaWeightsConv) == POINTER_INVALID)
        {
         DeltaWeightsConv = new CBufferFloat();
         if(CheckPointer(DeltaWeightsConv) == POINTER_INVALID)
            return false;
        }
      if(!DeltaWeightsConv.BufferInit(count, 0.0))
         return false;
      if(!DeltaWeightsConv.BufferCreate(OpenCL))
         return false;
     }
   else
     {
      if(CheckPointer(FirstMomentumConv) == POINTER_INVALID)
        {
         FirstMomentumConv = new CBufferFloat();
         if(CheckPointer(FirstMomentumConv) == POINTER_INVALID)
            return false;
        }
      if(!FirstMomentumConv.BufferInit(count, 0.0))
         return false;
      if(!FirstMomentumConv.BufferCreate(OpenCL))
         return false;
      //---
      if(CheckPointer(SecondMomentumConv) == POINTER_INVALID)
        {
         SecondMomentumConv = new CBufferFloat();
         if(CheckPointer(SecondMomentumConv) == POINTER_INVALID)
            return false;
        }
      if(!SecondMomentumConv.BufferInit(count, 0.0))
         return false;
      if(!SecondMomentumConv.BufferCreate(OpenCL))
         return false;
     }
//---
   return true;
  }

Após isso, concluímos a execução do método, retornando o resultado lógico da execução das operações para o programa chamador.

Com isso, encerramos a análise dos algoritmos de organização do funcionamento do objeto da camada convolucional para trabalho com grandezas complexas. O código completo desse objeto e de todos os seus métodos é apresentado no anexo do artigo.

Objeto de atenção mascarada para grandezas complexas

O próximo bloco, bastante amplo, do nosso trabalho será a criação do objeto de atenção mascarada para grandezas complexas, que servirá de base para o Channel Fusion Module.

Anteriormente, já criamos objetos de atenção mascarada que trabalham com grandezas reais. Agora, precisamos construir o algoritmo de funcionamento com grandezas complexas e, naturalmente, adicionar algumas particularidades do framework CATCH.

Como sempre, iniciamos o trabalho com o novo objeto a partir da construção dos processos no lado do contexto OpenCL. O algoritmo de propagação para frente será implementado no kernel MaskAttentionComplex. Nos parâmetros do kernel, iremos passar ponteiros para cinco buffers de dados e duas constantes que definem a estrutura dos dados analisados. Como está prevista a operação com grandezas complexas, os buffers destinados à transferência dos dados de entrada e à obtenção dos resultados receberam o tipo vetorial float2. No entanto, o buffer da matriz de mascaramento e dos coeficientes de atenção continua a conter números reais, pois representa uma distribuição probabilística.

__kernel void MaskAttentionComplex(__global const float2 *q,
                                   __global const float2 *kv,
                                   __global float2 *scores,
                                   __global const float *masks,
                                   __global float2 *out,
                                   const int dimension,
                                   const int heads_kv
                                  )
  {
//--- init
   const int q_id = get_global_id(0);
   const int k = get_local_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int kunits = get_local_size(1);
   const int heads = get_global_size(2);

O funcionamento do kernel é previsto em um espaço de tarefas tridimensional. A primeira dimensão é responsável pela dimensionalidade do tensor Query e indica a quantidade de elementos analisados. A segunda dimensão indica a dimensionalidade do tensor Key, isto é, a quantidade de elementos para a busca de dependências. Nessa dimensão, agrupamos os fluxos em grupos de trabalho. E a terceira dimensão indica o número de cabeças de atenção. No corpo do kernel, identificamos imediatamente o fluxo em todas as dimensões do espaço de tarefas e armazenamos os valores obtidos em constantes locais.

Com base nesses dados constantes, determinamos os deslocamentos em todos os buffers de dados.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h);
   const int shift_k = dimension * (2 *  heads_kv * k + h_kv);
   const int shift_v = dimension * (2 *  heads_kv * k + heads_kv + h_kv);
   const int shift_s = kunits * (q_id *  heads + h) + k;

E, imediatamente, salvamos o valor da máscara em uma variável local.

   const float mask = IsNaNOrInf(masks[shift_s], 0);

Aqui é importante observar que, na entrada do kernel, esperamos um tensor de mascaramento levando em consideração as cabeças de atenção. Em outras palavras, cada cabeça de atenção possui sua própria matriz de mascaramento de canais.

Em seguida, declaramos um array na memória local do contexto OpenCL, que será utilizado para a troca de dados dentro do grupo de trabalho.

   const uint ls = min((uint)kunits, (uint)LOCAL_ARRAY_SIZE);
   float2 koef = (float2)(fmax((float)sqrt((float)dimension), (float)1), 0);
   __local float2 temp[LOCAL_ARRAY_SIZE];

Com isso, concluímos o trabalho preparatório e passamos diretamente ao processo de cálculos. Inicialmente, precisamos determinar os coeficientes de atenção. Para isso, organizamos um laço de multiplicação dos vetores correspondentes Query e Key. O valor exponencial do produto obtido é multiplicado pela máscara.

//--- Score
   float score = 0;
   float2 score2 = (float2)0;
   if(ComplexAbs(mask) >= 0.01)
     {
      for(int d = 0; d < dimension; d++)
         score2 = IsNaNOrInf2(ComplexMul(q[shift_q + d], kv[shift_k + d]), (float2)0);
      score = IsNaNOrInf(ComplexAbs(ComplexExp(ComplexDiv(score, koef))) * mask, 0);
     }

Observe que essa operação é realizada apenas no caso em que o coeficiente de mascaramento é maior ou igual ao valor limite. Dessa forma, excluímos a influência de canais não relevantes.

Em seguida, precisamos normalizar os valores obtidos, convertendo-os para uma medida probabilística por meio da função SoftMax. Para isso, organizamos o processo de soma dos valores obtidos dentro do grupo de trabalho. Inicialmente, organizamos um laço de soma parcial dos valores nos elementos do array local.

//--- sum of exp
#pragma unroll
   for(int i = 0; i < kunits; i += ls)
     {
      if(k >= i && k < (i + ls))
         temp[k % ls].x = (i == 0 ? 0 : temp[k % ls].x) + score;
      barrier(CLK_LOCAL_MEM_FENCE);
     }

E depois somamos os valores dos elementos do nosso array.

   uint count = ls;
#pragma unroll
   do
     {
      count = (count + 1) / 2;
      if(k < ls)
         temp[k].x += (k < count && (k + count) < kunits ? temp[k + count].x : 0);
      if(k + count < ls)
         temp[k + count].x = 0;
      barrier(CLK_LOCAL_MEM_FENCE);
     }
   while(count > 1);

Como resultado da execução de todas as iterações dos laços, no primeiro elemento do array local fica armazenada a soma de todos os valores dentro do grupo de trabalho. Agora, precisamos dividir o valor do coeficiente de atenção obtido em cada fluxo de operações pelo valor total calculado, para obter a representação normalizada desejada. O resultado das operações é armazenado no elemento correspondente do buffer global.

//--- score
   if(temp[0].x > 0)
      score = score / temp[0].x;
   scores[shift_s] = score;

Agora resta determinar a representação final do elemento analisado levando em consideração a influência dos demais canais. Para isso, precisamos multiplicar o vetor dos coeficientes de atenção obtidos pela matriz Value. Esse processo é dificultado pela necessidade de executar as operações em fluxos paralelos do grupo de trabalho, já que cada fluxo contém apenas um coeficiente de atenção. Por isso, criamos todo um sistema de laços. O laço externo percorre os elementos da linha correspondente da matriz Value.

//--- out
#pragma unroll
   for(int d = 0; d < dimension; d++)
     {
      float2 val = (score > 0 ? ComplexMul(kv[shift_v + d], (float2)(score,0)) : (float2)0);

E, no corpo do laço, salvamos imediatamente em uma variável local o valor atual do buffer global de dados multiplicado pelo coeficiente de atenção correspondente. No entanto, com o objetivo de reduzir a quantidade de operações custosas de acesso à memória global, essa operação é realizada apenas quando existe um coeficiente de atenção maior que "0". Caso contrário, podemos inicializar a variável com valor zero sem recorrer ao buffer global de dados.

Em seguida, precisamos somar os valores obtidos nos fluxos paralelos de operações do grupo de trabalho. Aqui organizamos um processo análogo à soma dos coeficientes de atenção. Primeiro, somamos os valores individuais nos elementos do array local.

#pragma unroll
      for(int i = 0; i < kunits; i += ls)
        {
         if(k >= i && k < (i + ls))
            temp[k % ls] = (i == 0 ? (float2)0 : temp[k % ls]) + val;
         barrier(CLK_LOCAL_MEM_FENCE);
        }

E depois somamos os valores dos elementos do array local.

      uint count = ls;
#pragma unroll
      do
        {
         count = (count + 1) / 2;
         if(k < ls)
            temp[k] += (k < count && (k + count) < kunits ? temp[k + count] : (float2)0);
         if((k + count) < ls)
            temp[k + count] = (float2)0;
         barrier(CLK_LOCAL_MEM_FENCE);
        }
      while(count > 1);

Para armazenar o valor obtido no buffer global de dados, é suficiente utilizar um único fluxo de execução.

      //---
      if(k == 0)
         out[shift_q + d] = temp[0];
      barrier(CLK_LOCAL_MEM_FENCE);
     }
  }

Aqui realizamos obrigatoriamente a sincronização do trabalho dos fluxos do grupo de trabalho e passamos para a próxima iteração do laço.

Após a execução bem-sucedida de todas as iterações do sistema de laços, concluímos a execução do kernel.

O próximo estágio do nosso trabalho é a construção do processo de distribuição do gradiente de erro por meio das operações de atenção mascarada para grandezas complexas. Esse processo é implementado no kernel MaskAttentionGradientsComplex.

__kernel void MaskAttentionGradientsComplex(__global const float2 *q, __global float2 *q_g,
                                            __global const float2 *kv, __global float2 *kv_g,
                                            __global const float *scores,
                                            __global const float *mask, __global float *mask_g,
                                            __global const float2 *gradient,
                                            const int kunits, const int heads_kv
                                           )
  {
//--- init
   const int q_id = get_global_id(0);
   const int d = get_global_id(1);
   const int h = get_global_id(2);
   const int qunits = get_global_size(0);
   const int dimension = get_global_size(1);
   const int heads = get_global_size(2);

A estrutura dos parâmetros do kernel, em grande parte, lembra o kernel de propagação para frente. Apenas adicionamos buffers globais de dados dos gradientes de erro correspondentes. No entanto, alteramos ligeiramente a estrutura do espaço de tarefas. Continua sendo utilizado um espaço de tarefas tridimensional, porém agora a segunda dimensão indica a dimensionalidade dos vetores internos, e não há mais a união dos fluxos em grupos de trabalho.

No corpo do kernel, identificamos o fluxo atual de operações em todas as dimensões do espaço de tarefas, salvando os valores obtidos em constantes locais. Assim como anteriormente, utilizamos esses valores para determinar os deslocamentos nos buffers globais de dados.

   const int h_kv = h % heads_kv;
   const int shift_q = dimension * (q_id * heads + h) + d;
   const int shift_s = (q_id * heads + h) * kunits;
   const int shift_g = h * dimension + d;
   float2 koef = (float2)(fmax(sqrt((float)dimension), (float)1), 0);

Após a conclusão do trabalho preparatório, passamos diretamente à coleta dos gradientes de erro. Inicialmente, determinamos o erro no nível do tensor Value.

Aqui é importante lembrar que o tensor Value é utilizado para gerar todos os elementos da sequência resultante por meio da multiplicação pela matriz dos coeficientes de atenção. Consequentemente, transferimos os gradientes de erro dos resultados da atenção para o nível do tensor Value, levando em consideração os coeficientes de atenção correspondentes. Para isso, organizamos um sistema de laços.

//--- Calculating Value's gradients
   int step_score = kunits * heads;
   if(h < heads_kv)
     {
#pragma unroll
      for(int v = q_id; v < kunits; v += qunits)
        {
         float2 grad = (float2)0;
         for(int hq = h; hq < heads; hq += heads_kv)
           {
            int shift_score = hq * kunits + v;
            for(int g = 0; g < qunits; g++)
              {
               float sc = IsNaNOrInf(scores[shift_score + g * step_score], 0);
               if(sc > 0)
                  grad += ComplexMul(gradient[shift_g + dimension * (hq - h + g  * heads)],
                                     (float2)(sc, 0));
              }
           }
         int shift_v = dimension * (2 *  heads_kv * v + heads_kv + h) + d;
         kv_g[shift_v] = grad;
        }
     }

No próximo passo, precisamos distribuir o gradiente de erro até o nível do tensor Query. É evidente que cada elemento desse tensor influencia apenas um elemento no tensor de resultados. Portanto, podemos armazenar o valor do gradiente de erro correspondente em uma variável local, reduzindo a quantidade de acessos à memória global.

//--- Calculating Query's gradients
   float2 grad = 0;
   float2 out_g = IsNaNOrInf2(gradient[shift_g + q_id * dimension], (float2)0);
   int shift_val = (heads_kv + h_kv) * dimension + d;
   int shift_key = h_kv * dimension + d;
#pragma unroll
   for(int k = 0; (k < kunits && ComplexAbs(out_g) != 0); k++)
     {
      float2 sc_g = 0;
      float2 sc = (float2)(scores[shift_s + k], 0);
      for(int v = 0; v < kunits; v++)
         sc_g += IsNaNOrInf2(ComplexMul(
                                ComplexMul((float2)(scores[shift_s + v], 0),
                                           out_g * kv[shift_val + 2 * v * heads_kv * dimension]),
                                ((float2)(k == v, 0) - sc)), (float2)0);
      float m = mask[shift_s + k];
      mask_g[shift_s + k] = IsNaNOrInf(sc.x / m * sc_g.x + sc.y / m * sc_g.y, 0);
      grad += IsNaNOrInf2(ComplexMul(sc_g, kv[shift_key + 2*k*heads_kv*dimension]), (float2)0);
     }
   q_g[shift_q] = IsNaNOrInf2(ComplexDiv(grad, koef), (float2)0);

No entanto, durante a formação do valor resultante, ocorre interação com diversos valores dos tensores Key e Value. Para obter o valor de erro necessário, inicialmente propagamos o gradiente até a matriz dos coeficientes de atenção e somente depois o transferimos para o tensor Query.

Observe que, nesse mesmo momento, também transferimos o gradiente de erro para a matriz de mascaramento dos canais.

Na etapa final, de forma análoga, transferimos o gradiente de erro para o nível do tensor Key. O algoritmo praticamente repete por completo a distribuição do gradiente de erro para o nível Query, com a diferença de que, neste caso, nos movemos ao longo da coluna da matriz de atenção.

//--- Calculating Key's gradients
   if(h < heads_kv)
     {
#pragma unroll
      for(int k = q_id; k < kunits; k += qunits)
        {
         int shift_k = dimension * (2 *  heads_kv * k + h_kv) + d;
         grad = 0;
         for(int hq = h; hq < heads; hq++)
           {
            int shift_score = hq * kunits + k;
            float2 val = IsNaNOrInf2(kv[shift_k + heads_kv * dimension], (float2)0);
            for(int scr = 0; scr < qunits; scr++)
              {
               float2 sc_g = (float2)0;
               int shift_sc = scr * kunits * heads;
               float2 sc = (float2)(IsNaNOrInf(scores[shift_sc + k], 0), 0);
               if(ComplexAbs(sc) == 0)
                  continue;
               for(int v = 0; v < kunits; v++)
                  sc_g += IsNaNOrInf2(
                             ComplexMul(
                                ComplexMul((float2)(scores[shift_sc + v], 0),
                                           gradient[shift_g + scr * dimension]),
                                ComplexMul(val, ((float2)(k == v, 0) - sc))),
                             (float2)0);
               grad += IsNaNOrInf2(ComplexMul(sc_g, q[shift_q + scr * dimension]), (float2)0);
              }
           }
         kv_g[shift_k] = IsNaNOrInf2(ComplexDiv(grad, koef), (float2)0);
        }
     }
  }

Com isso, concluímos a análise dos algoritmos de construção dos processos de atenção mascarada no domínio de valores complexos no lado do contexto OpenCL. O código completo dos kernels apresentados pode ser consultado no anexo.

O próximo estágio do nosso trabalho será a implementação dos algoritmos de mascaramento da atenção para valores complexos no lado do programa principal. Porém, falaremos sobre isso já no próximo artigo.

Considerações finais

Nós nos familiarizamos com os aspectos teóricos do framework CATCH, que combina a transformada de Fourier e o mecanismo de patching de frequência para a detecção de anomalias em séries temporais multidimensionais. Sua principal vantagem é a capacidade de identificar padrões complexos de mercado que permanecem imperceptíveis quando a análise é realizada apenas no domínio do tempo.

O uso da representação em frequência permite compreender de forma mais profunda a dinâmica do mercado, enquanto o mecanismo de patching de frequência adapta a análise às condições em constante mudança. Além disso, CATCH leva em consideração as inter-relações entre ativos, o que o torna mais sensível a anomalias sistêmicas do mercado. Diferentemente dos métodos tradicionais, ele não apenas registra saltos evidentes e valores atípicos, mas também reconhece dependências complexas e ocultas, que podem antecipar mudanças nas tendências de mercado.

Na parte prática, foi iniciado o trabalho de implementação, por meio do MQL5, de uma visão própria das abordagens propostas pelos autores do framework. No próximo artigo, daremos continuidade ao trabalho iniciado, ao final do qual avaliaremos a eficácia das soluções implementadas com base em dados históricos reais.

Referências

• CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching
• Outros artigos da série

Programas utilizados no artigo

#	Nome	Tipo	Descrição
1	Research.mq5	EA	EA de coleta de exemplos
2	ResearchRealORL.mq5	EA	EA de coleta de exemplos pelo método Real-ORL
3	Study.mq5	EA	EA para treinamento de modelos
4	Test.mq5	EA	EA para teste de modelo
5	Trajectory.mqh	Biblioteca de classe	Estrutura de descrição do estado do sistema e da arquitetura dos modelos
6	NeuroNet.mqh	Biblioteca de classe	Biblioteca de classes para criação de redes neurais
7	NeuroNet.cl	Biblioteca	Biblioteca de código OpenCL-programas