Нейросети в трейдинге: Выявление аномалий в частотной области (Окончание)
Введение
В предыдущей статье мы познакомились с инновационным фреймворком CATCH, предназначенным для обнаружения аномалий в многомерных временных рядах. Предложенный авторами фреймворка метод анализа данных в частотной области позволяет не только выявлять точечные аномалии в виде выбросов и резких изменений, но и обнаруживать более сложные, скрытые паттерны, ускользающие от традиционных подходов. Фреймворк CATCH использует преобразование Фурье для перехода от временного представления данных к их спектральному виду, что открывает новые возможности для детального изучения характеристик анализируемой последовательности.
Одним из важнейших преимуществ CATCH является использование частотного патчинга. Вместо того, чтобы анализировать весь спектр целиком, модель разбивает его на отдельные фрагменты, соответствующие определённому диапазону частот. Этот метод позволяет рассматривать как глобальные тренды, так и локальные особенности, характерные для высокочастотных компонент. Благодаря такому подходу, можно с высокой точностью выделять и классифицировать различные аномалии. Будь то кратковременные всплески, или более сложные отклонения на уровне подпоследовательностей. Подобное разбиение спектра даёт возможность более детально изучать структуру временного ряда.
Значимой частью фреймворка является адаптивный модуль, отвечающий за анализ взаимосвязей между различными каналами данных. Этот компонент, реализующий принцип маскированного внимания, помогает системе сосредоточиться на наиболее значимых корреляциях, исключая влияние шумовых факторов и нерелевантных данных. Такой механизм способствует улучшению качества реконструкции нормального поведения и значительно повышает устойчивость модели в условиях изменчивой рыночной среды. В отличие от традиционных методов, которые анализируют каналы по отдельности, CATCH позволяет учитывать их сложные взаимосвязи. Это особенно важно при работе с финансовыми данными, где движение на одном рынке может оказывать влияние на другие сегменты.
На завершающем этапе работы CATCH происходит восстановление исходного временного ряда. После детального анализа в частотной области и выявления потенциальных аномалий, система выполняет обратное преобразование, возвращая данные в привычное временное представление. Разница между исходными значениями и восстановленным рядом служит надежным индикатором отклонений, позволяющим своевременно реагировать на изменения в рыночной динамике.
Авторская визуализация фреймворка CATCH представлена ниже.
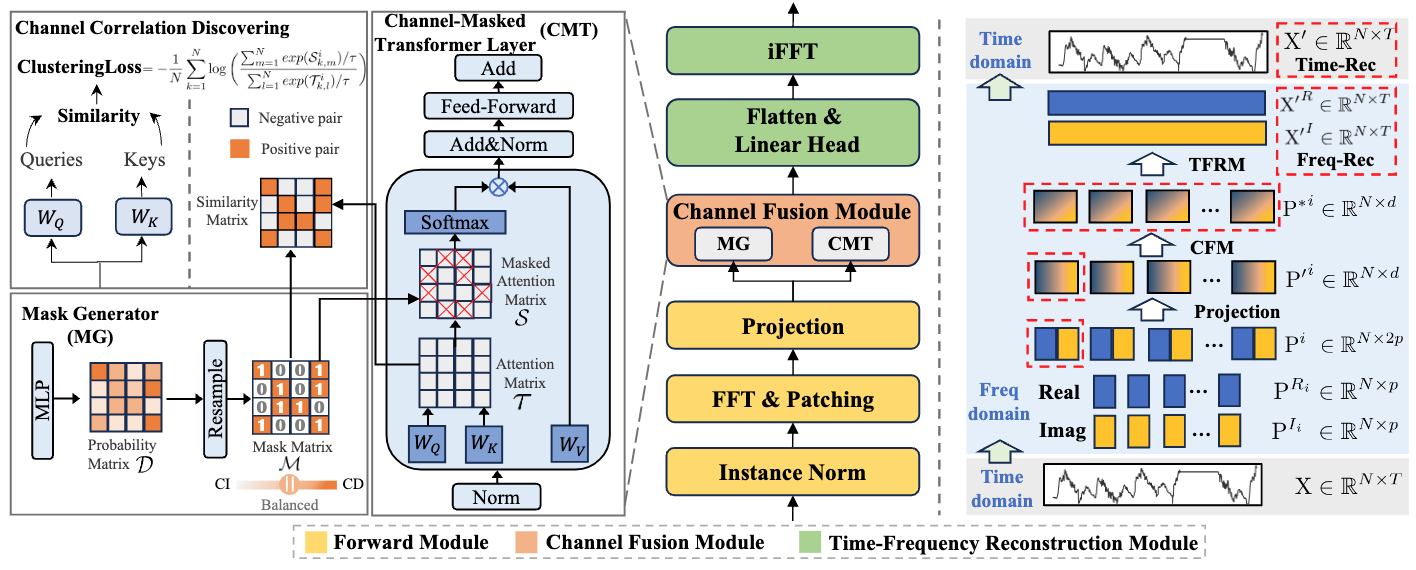
В практической части предыдущей статьи была начата работа по имплементации собственного видения предложенных подходов средствами MQL5, в частности, был реализован сверточный слой работы с комплексными значениями. А так же мы рассмотрели реализацию прямого и обратного проходов модуля маскированного внимания к комплексным величинам на стороне OpenCL-контекста. Сегодня мы продолжаем начатую работу.
Объект маскированного внимания к комплексным значениям
В предыдущей статье мы рассмотрели кернелы MaskAttentionComplex и MaskAttentionGradientsComplex, в которых реализованы алгоритмы прямого и обратного проходов механизма маскированного внимания в области комплексных величин. Продолжаем начатую работу. И сегодня мы организуем работу модуля маскированного внимания на стороне основной программы. С этой целью создаем новый объект CNeuronComplexMVMHMaskAttention, структура которого представлена ниже.
class CNeuronComplexMVMHMaskAttention : public CNeuronBaseOCL { protected: uint iWindow; uint iWindowKey; uint iHeads; uint iUnits; uint iVariables; //--- CNeuronComplexConvOCL cQKV; CNeuronBaseOCL cQ; CNeuronBaseOCL cKV; CNeuronConvOCL cMask; CNeuronBaseOCL cMHAttentionOut; CNeuronComplexConvOCL cPooling; CNeuronBaseOCL cResidual; CNeuronComplexConvOCL cFeedForward[2]; //--- virtual bool AttentionOut(void); virtual bool AttentionInsideGradients(void); virtual bool SumAndNormilize(CBufferFloat *tensor1, CBufferFloat *tensor2, CBufferFloat *out, int dimension, bool normilize = true, int shift_in1 = 0, int shift_in2 = 0, int shift_out = 0, float multiplyer = 0.5f) override; //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; public: CNeuronComplexMVMHMaskAttention(void) {}; ~CNeuronComplexMVMHMaskAttention(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) const { return defNeuronComplexMVMHMaskAttention; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
Как можно заметить, представленная структура нового объекта довольно стандартна для модулей внимания, различные варианты которых мы уже не раз создавали в нашей библиотеке. Однако, есть особенность, связанная с использованием комплексных величин. Предполагается, что на вход данного объекта подаются исходные данные уже в виде комплексных значений, поэтому мы опускаем этап преобразования данных. А для формирования сущностей Query, Key и Value используем ранее созданный сверточный слой работы с комплексными величинами. Но обо всем по порядку.
Все внутренние объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. А инициализация объявленных и унаследованных объектов осуществляется в методе Init. В параметрах данного метода получаем ряд констант, позволяющих однозначно определить архитектуру создаваемого объекта. Их структура довольно обычна для подобных объектов.
bool CNeuronComplexMVMHMaskAttention::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint window, uint window_key, uint heads, uint units_count, uint variables, ENUM_OPTIMIZATION optimization_type, uint batch) { //--- if(!CNeuronBaseOCL::Init(numOutputs, myIndex, open_cl, 2 * window * units_count * variables, optimization_type, batch)) return false;
В теле метода сразу вызываем одноименный метод родительского класса, в котором уже реализован алгоритм инициализации унаследованных объектов и интерфейсов. После чего, сохраним полученные от внешней программы константы архитектуры модели во внутренние переменные.
iWindow = window; iWindowKey = MathMax(window_key, 1); iUnits = units_count; iHeads = MathMax(heads, 1); iVariables = variables;
Далее переходим к работе с вновь объявленными объектами. И первым инициализируем объект генерации матрицы маскирования.
Здесь следует обратить внимание, что авторами фреймворка предложен модуль генерации маски на основе обучаемой проекции исходных данных. При этом используется многоголовое внимание с уникальной маской для каждой головы.
Еще один немаловажный момент — внимание осуществляется не ко всей последовательности частотного спектра. Авторы фреймворка CATCH предлагают использовать внимание только в рамках отдельных патчей, относящихся к одному фрагменту частот, но разных унитарных последовательностей.
Ну и, конечно, на выходе объекта генерации маски мы должны получить вероятностное представление влияния отдельных каналов в виде действительных значений.
Для удовлетворения указанных ограничений, в своей реализации мы используем обычный сверточный слой с удвоенным размером окна (для охвата окна комплексных значений) и числом фильтров, равным вектору маскирования для одного элемента последовательности.
uint index = 0; if(!cMask.Init(0, index, OpenCL, 2 * iWindow, 2 * iWindow, iVariables * iHeads, iUnits, iVariables, optimization, iBatch)) return false; cMask.SetActivationFunction(SIGMOID); CBufferFloat *temp = cMask.GetWeightsConv(); if(!temp || !temp.Fill(0)) return false;
С целью поддержания результатов работы объекта в необходимом диапазоне значений, мы используем сигмовидную функцию активации.
Обратите внимание, что при инициализации объекта мы заполняем матрицу обучаемых параметров нулевыми значениями. Это позволит нам на начальном этапе присвоить всем элементам равную маску влияния на уровне "0.5". В процессе обучения веса будут корректироваться, изменяя маску зависимости между каналами.
Следующим инициализируем объект генерации сущностей Query, Key и Value. Здесь мы уже используем комплексный сверточный слой, так как на входе и выходе объекта ожидаем получить комплексные значения.
index++; if(!cQKV.Init(0, index, OpenCL, iWindow, iWindow, 3 * iWindowKey * iHeads, iUnits, iVariables, optimization, iBatch)) return false; cQKV.SetActivationFunction(None);
Общий тензор трех сущностей мы разделим на 2 составляющие, выделим сущность Query в отдельную матрицу. Для этого инициализируем 2 дополнительных объекта.
index++; if(!cQ.Init(0, index, OpenCL, 2 * iWindowKey * iHeads * iVariables * iUnits, optimization, iBatch)) return false; cQ.SetActivationFunction(None); index++; if(!cKV.Init(0, index, OpenCL, 2 * cQ.Neurons(), optimization, iBatch)) return false; cKV.SetActivationFunction(None);
Тут же инициализируем объект хранения результатов многоголового внимания.
index++; if(!cMHAttentionOut.Init(0, index, OpenCL, cQ.Neurons(), optimization, iBatch)) return false; cMHAttentionOut.SetActivationFunction(None);
И добавим комплексный сверточный слой для понижения размерности результатов внимания.
index++; if(!cPooling.Init(0, index, OpenCL, iWindowKey * iHeads, iWindowKey * iHeads, iWindow, iUnits, iVariables, optimization, iBatch)) return false; cPooling.SetActivationFunction(None);
Аналогично классической архитектуре Transformer, добавим слой сохранения остаточных связей.
index++; if(!cResidual.Init(0, index, OpenCL, cPooling.Neurons(), optimization, iBatch)) return false; cResidual.SetActivationFunction(None);
А за ним 2 комплексных сверточных слоя модуля FeedForward.
index++; if(!cFeedForward[0].Init(0, index, OpenCL, iWindow, iWindow, 4 * iWindow, iUnits, iVariables, optimization, iBatch)) return false; cFeedForward[0].SetActivationFunction(LReLU); index++; if(!cFeedForward[1].Init(0, index, OpenCL, 4 * iWindow, 4 * iWindow, iWindow, iUnits, iVariables, optimization, iBatch)) return false; cFeedForward[1].SetActivationFunction(None); SetActivationFunction(None); //--- return true; }
После чего, завершаем работу метода инициализации объекта, предварительно вернув логический результат выполнения операций вызывающей программе.
Следующим этапом будет построение алгоритма прямого прохода в рамках метода feedForward.
bool CNeuronComplexMVMHMaskAttention::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!NeuronOCL) return false;
В параметрах данного метода получаем указатель на объект исходных данных, актуальность которого мы сразу проверяем.
Для повышения стабильности процесса обучения, мы нормализуем полученные данные.
if(!NeuronOCL.SwapOutputs()) return false; if(!SumAndNormilize(NeuronOCL.getPrevOutput(), NeuronOCL.getPrevOutput(), NeuronOCL.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Здесь стоит отметить, что получаемые исходные данные представлены комплексными величинами. Поэтому метод суммирования и нормализации данных был переопределен для работы с таковыми. С полным его кодом можно ознакомиться во вложении.
После нормализации, исходные данные используются для генерации тензоров маскирования и сущностей Query, Key, Value.
if(!cMask.FeedForward(NeuronOCL)) return false; if(!cQKV.FeedForward(NeuronOCL)) return false;
Общий тензор сгенерированных сущностей разделяем на 2 отдельных.
if(!NeuronOCL.SwapOutputs()) return false; if(!DeConcat(cQ.getOutput(), cKV.getOutput(), cQKV.getOutput(), 2 * iWindowKey * iHeads, 4 * iWindowKey * iHeads, iUnits * iVariables)) return false;
После передаем все подготовленные данные в кернел прямого прохода маскированного внимания. Данная операция осуществляется в рамках отдельного метода AttentionOut.
if(!AttentionOut()) return false;
Затем понижаем размерность результатов многоголового внимания и суммируем полученные значения с исходными данными, создавая остаточные связи.
if(!cPooling.FeedForward(cMHAttentionOut.AsObject())) return false; if(!SumAndNormilize(NeuronOCL.getOutput(), cPooling.getOutput(), cResidual.getOutput(), iWindow, true, 0, 0, 0, 1)) return false;
Далее проводим данные через 2 сверточных слоя модуля FeedForward.
if(!cFeedForward[0].FeedForward(cResidual.AsObject())) return false; if(!cFeedForward[1].FeedForward(cFeedForward[0].AsObject())) return false;
И снова добавляем остаточные связи. А результат операции сохраняем в унаследованном буфере интерфейса обмена данными с другими нейронными слоями модели.
if(!SumAndNormilize(cResidual.getOutput(), cFeedForward[1].getOutput(), getOutput(), iWindow, true, 0, 0, 0, 1)) return false; //--- return true; }
После чего, завершаем работу метода, вернув логический результат выполнения операций вызывающей программе.
Несколько слов стоит сказать о методе AttentionOut, в котором осуществляется постановка в очередь выполнения кернела многоголового маскированного внимания MaskAttentionComplex. В последнее время мы редко рассматриваем алгоритмы методов постановки кернелов OpenCL-программы в очередь выполнения. Это и понятно. Алгоритм постановки кернела в очередь выполнения довольно стандартный. И нет необходимости каждый раз описывать одни и те же операции. Но в данном случае есть нюанс, связанный с работой фреймворка CATCH.
Как было сказано выше, авторы фреймворка CATCH предлагают осуществлять операции маскированного внимания строго между элементами одного диапазона частот разных унитарных последовательностей. Попросту мы берем одинаковые патчи от разных унитарных последовательностей и анализируем их зависимости. Это позволяет независимо выявлять зависимости различных унитарных последовательностей на разных частотах: отдельно долгосрочные тренды, отдельно краткосрочные тенденции. Однако, мы не учли эту особенность, создавая унифицированный кернел маскированного внимания.
Тем не менее, у нас есть возможность организовать необходимый процесс путем управления пространством задач постановки кернела в очередь выполнения. Для начала давайте посмотрим на размерность исходных данных, получаемых на вход объекта. Мы получаем сегментированные данные многомерной последовательности, которые можно представить в виде трехмерного тензора {Variable, Segment, Dimension}. Далее, при формировании сущностей для многоголового внимания, результаты генерации каждой можно представить уже в виде четырехмерного тензора {Variable, Segment, Head, Dimension}.
Здесь стоит обратить внимание, что построенный нами алгоритм многоголового внимания осуществляет независимый анализ отдельных голов внимания. Следовательно, если мы объединим размерности сегментов и голов внимания, представив каждый сегмент в качестве независимой головы внимания, то получим анализ зависимостей между одинаковыми сегментами различных унитарных последовательностей. Что и требуется для организации фреймворка CATCH.
Метод AttentionOut не содержит параметров. А в блоке контролей данного метода мы проверяем лишь актуальность указателя на объект работы с OpenCL-контекстом.
bool CNeuronComplexMVMHMaskAttention::AttentionOut(void) { if(!OpenCL) return false;
Далее объявляем массивы указания пространства задач постановки кернела в очередь выполнения. Как обсуждалось выше, в качестве размерности последовательностей мы указываем количество унитарных последовательностей в анализируемых данных. А для количества голов, указываем произведение заданного количество голов внимания на количество сегментов в каждой последовательности.
uint global_work_offset[3] = {0}; uint global_work_size[3] = {iVariables/*Q units*/, iVariables/*K units*/, iHeads * iUnits/*Heads*/}; uint local_work_size[3] = {1, iVariables, 1};
Тут же объединяем потоки операций в рабочие группы по второму измерению пространства задач.
Затем, в параметрах кернела, передаем указатели на необходимые буферы данных.
ResetLastError(); int kernel = def_k_MaskAttentionComplex; if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_q, cQ.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_kv, cKV.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_scores, cMask.getPrevOutIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_out, cMHAttentionOut.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgumentBuffer(kernel, def_k_maskattcom_masks, cMask.getOutputIndex())) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
Здесь мы воспользуемся равенством размеров матрицы коэффициентов внимания и маскирования каналов. Это обстоятельство позволило не создавать дополнительный буфер для временного хранения коэффициентов внимания. Его роль выполнит свободный буфер объекта генерации матрицы маскирования.
Далее, передадим в кернел необходимы параметры.
if(!OpenCL.SetArgument(kernel, def_k_maskattcom_dimension, (int)iWindowKey)) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; } if(!OpenCL.SetArgument(kernel, def_k_maskattcom_heads_kv, (int)(iHeads * iUnits))) { printf("Error of set parameter kernel %s: %d; line %d", __FUNCTION__, GetLastError(), __LINE__); return false; }
И тут мы снова, в качестве количества голов внимания, для сущностей Key и Value указываем произведение заданного пользователем количества голов внимания на длину последовательности.
В завершении, ставим кернел в очередь выполнения.
if(!OpenCL.Execute(kernel, 3, global_work_offset, global_work_size, local_work_size)) { printf("Error of execution kernel %s: %d", __FUNCTION__, GetLastError()); return false; } //--- return true; }
И завершаем работу метода, предварительно вернув логический результат выполнения операций вызывающей программе.
После завершения работы с алгоритмами прямого прохода, переходим к построению процессов обратного прохода. И первым создадим метод распределения градиентов ошибки между всеми внутренними объектами, в соответствии с их влиянием на итоговый результат работы модели calcInputGradients.
bool CNeuronComplexMVMHMaskAttention::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
В параметрах метода получаем на тот же объект исходных данных, который использовали при прямом проходе. Только на этот раз нам предстоит передать в него градиент ошибки, в соответствии с влиянием исходных данных. И сразу проверяем актуальность полученного указателя.
На данном этапе в буфере внешних интерфейсов нашего объекта содержится градиент ошибки, полученный от последующего слоя. Его значения получены без учета корректировки на производную используемой функции активации. Ведь мы намеренно указали её отсутствие при инициализации объекта. Это сделано для создания дополнительных свобод в выборе функций активации внутренних объектов. И сейчас мы корректируем полученный градиент ошибки на производную функции активации последнего сверточного слоя модуля FeedForward с передачей ему полученных значений.
if(!DeActivation(cFeedForward[1].getOutput(), cFeedForward[1].getGradient(), Gradient, cFeedForward[1].Activation())) return false;
А затем опускаем градиент ошибки по слоям модуля до уровня объекта остаточных связей после модуля внимания.
if(!cFeedForward[0].calcHiddenGradients(cFeedForward[1].AsObject())) return false; if(!cResidual.calcHiddenGradients(cFeedForward[0].AsObject())) return false;
Для объекта остаточных связей мы так же указали отсутствие функции активации. И теперь повторим процедуру корректировки на производную функции активации слоя масштабирования результатов многоголового внимания.
if(!DeActivation(cPooling.getOutput(), cPooling.getGradient(), cResidual.getGradient(), cPooling.Activation()) || !DeActivation(cPooling.getOutput(), cPooling.getPrevOutput(), Gradient, cPooling.Activation()) || !SumAndNormilize(cPooling.getGradient(), cPooling.getPrevOutput(), cPooling.getGradient(), iWindow, false, 0, 0, 0, 1)) return false;
Однако здесь следует обратить внимание, что в объекте остаточных связей содержится градиент ошибки только по магистрали модуля FeedForward. Нам же необходимо добавить данные и магистрали остаточных связей. Поэтому мы снова корректируем градиент ошибки из буфера внешних интерфейсов, но уже на производную функции активации сверточного слоя масштабирования результатов многоголового внимания.
Хочу отметить, что повторное использование данных из буфера внешних интерфейсов не означает их двойное искажение. В первом случае результаты корректировки мы сохранили в буфере последнего слоя модуля FeedForward, а в буфере интерфейсов данные остались в первоначальном виде. И сейчас результаты операций записываются в буфер слоя проекции без изменения исходных данных, которые мы ещё раз будем использовать при передаче значений по магистрали остаточных связей на уровень исходных данных.
После корректировки значений, мы суммируем информацию двух информационных потоков. А затем распределяем градиент ошибки по головам внимания.
if(!cMHAttentionOut.calcHiddenGradients(cPooling.AsObject())) return false; if(!AttentionInsideGradients()) return false;
И вызываем метод распределения градиента ошибки сквозь процесс внимания AttentionInsideGradients. Мы не будем останавливаться на подробном рассмотрении алгоритма указанного метода. Оставим для самостоятельного изучения. Полный его код представлен во вложении. Но следует обратить внимание, что пространство задач и параметры постановки кернела в очередь выполнения должны соответствовать методологии, предложенной для прямого прохода.
На следующем этапе мы объединяем градиенты ошибки всех сущностей в единый тензор.
if(!Concat(cQ.getGradient(), cKV.getGradient(), cQKV.getGradient(), 2 * iWindowKey * iHeads, 4 * iWindowKey * iHeads, iUnits * iVariables)) return false;
После чего, спускаем ошибку до уровня исходных данных, предварительно скорректировав на производную соответствующей функции активации.
if(!DeActivation(cQKV.getOutput(), cQKV.getPrevOutput(), cQKV.getGradient(), cQKV.Activation()) || !prevLayer.calcHiddenGradients(cQKV.AsObject())) return false;
Однако, это лишь один информационный поток. Добавим к полученным значениям данные информационного потока остаточных связей, предварительно скорректировав их на производную функции активации объекта исходных данных.
В данном случае мы используем данные ка от модуля FeedForward, так и из буфера внешних интерфейсов.
if(!DeActivation(prevLayer.getOutput(),cResidual.getPrevOutput(),cResidual.getGradient(),prevLayer.Activation()) || !SumAndNormilize(prevLayer.getGradient(), cResidual.getPrevOutput(), cResidual.getPrevOutput(), iWindow, false, 0, 0, 0, 1)) return false; if(!DeActivation(prevLayer.getOutput(), cResidual.getGradient(), Gradient, prevLayer.Activation()) || !SumAndNormilize(cResidual.getGradient(), cResidual.getPrevOutput(), cResidual.getPrevOutput(), iWindow, false, 0, 0, 0, 1)) return false;
Здесь следует вспомнить, что исходные данные так же использовались и для генерации матрицы маскирования. Следовательно, добавим к ранее собранным данным и градиент ошибки по данному информационному потоку.
if(!DeActivation(cMask.getOutput(), cMask.getGradient(), cMask.getGradient(), cMask.Activation()) || !prevLayer.calcHiddenGradients(cMask.AsObject()) || !SumAndNormilize(prevLayer.getGradient(), cResidual.getPrevOutput(), prevLayer.getGradient(), iWindow, false, 0, 0, 0, 1)) return false; //--- return true; }
Вот теперь мы собрали на уровне исходных данных градиент ошибки по всем информационным потокам и можем завершить работу метода, вернув логический результат работы вызывающей программе.
Метод оптимизации параметров объекта я предлагаю оставить для самостоятельного изучения. Его алгоритм довольно прост, в нем лишь вызываются одноименные методы внутренних объектов. Полный код метода представлен во вложении. Там же вы найдете полный код представленного объекта и всех его методов. А мы переходим к следующему этапу нашей работы.
Собираем фреймворк CATCH
Можно сказать, что до этого была проведена большая подготовительная работа, в ходе которой были построены отдельные объекты, и теперь мы соберем их в единую структуру фреймворка CATCH. Алгоритмы его работы будут построены в рамках объекта CNeuronCATCH, структура которого представлена ниже.
class CNeuronCATCH : public CNeuronTransposeOCL { protected: CNeuronTransposeOCL cTranspose; CNeuronBaseOCL caFreqIn[2]; CNeuronBaseOCL cFreqConcat; CNeuronComplexConvOCL caProjection[2]; CNeuronComplexMVMHMaskAttention caChannelFusion[2]; CNeuronComplexConvOCL caLinearHead[2]; CNeuronBaseOCL caFreqOut[2]; //--- virtual bool FFT(CBufferFloat *inp_re, CBufferFloat *inp_im, CBufferFloat *out_re, CBufferFloat *out_im, uint variables, bool reverse = false); //--- virtual bool feedForward(CNeuronBaseOCL *NeuronOCL) override; virtual bool updateInputWeights(CNeuronBaseOCL *NeuronOCL) override; virtual bool calcInputGradients(CNeuronBaseOCL *prevLayer) override; public: CNeuronCATCH(void) {}; ~CNeuronCATCH(void) {}; //--- virtual bool Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint time_step, uint variables, uint window, uint step, uint window_key, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch); //--- virtual int Type(void) override const { return defNeuronCATCH; } //--- virtual bool Save(int const file_handle) override; virtual bool Load(int const file_handle) override; //--- virtual bool WeightsUpdate(CNeuronBaseOCL *source, float tau) override; virtual void SetOpenCL(COpenCLMy *obj) override; };
В представленной структуре мы видим довольно большое количество внутренних объектов, каждый из которых выполняет свою роль в сложном алгоритме фреймворка. Но об их назначении мы поговорим в процессе построения методов нового класса. А сейчас отметим, что все объекты объявлены статично, что позволяет нам оставить пустыми конструктор и деструктор класса. Инициализация всех объектов осуществляется в методе Init.
bool CNeuronCATCH::Init(uint numOutputs, uint myIndex, COpenCLMy *open_cl, uint time_step, uint variables, uint window, uint step, uint window_key, uint heads, ENUM_OPTIMIZATION optimization_type, uint batch) { if(!CNeuronTransposeOCL::Init(numOutputs, myIndex, open_cl, variables, time_step, optimization_type, batch)) return false;
В параметрах данного метода получаем ряд констант, позволяющих однозначно определить архитектуру инициализируемого объекта. Одни из них указывают размерность исходных данных. Другие определяют структуру внутренних информационных потоков. К примеру, в time_step и variables задается количество временных шагов и унитарных последовательностей в многомерном временном ряде исходных данных. А window и step укажут на параметры сегментирования частотного спектра. В то же время window_key и heads, как не сложно догадаться, являются основными параметрами модуля внимания.
В теле метода, как обычно, сразу вызываем одноименный метод родительского класса. На этот раз, в качестве родительского мы используем объект транспонирования данных, и, как вы догадались, этот выбор не случаен. На вход объект ожидаем получать многомерный временной ряд в виде матрицы, каждая строка которой представляет вектор описания состояния окружающей среды на одном временном шаге. Однако, фреймворк CATCH строится на анализе частотного спектра отдельных унитарных последовательностей. Для удобства работы с унитарными последовательностями нам придется транспонировать полученный тензор, а на выходе вернуть данные в исходное представление. Последнюю операцию мы планируем выполнять средствами родительского объекта, что и отражается в передаваемых ему параметрах.
Для преобразования временного ряда в частотную область, мы планируем использовать алгоритм быстрого преобразования Фурье. Однако этот алгоритм корректно работает только с последовательностями, длина которых является степенью числа 2. Тем не менее, мы можем увеличить размерность любой последовательности, дополнив её нулевыми значениями, что не окажет влияния на результат. Однако, нам необходимо определить ближайшее нужное значение.
//--- Calculate FFT size int power = int(MathLog(time_step) / M_LN2); if(power <= 0) return false; if(MathPow(2, power) != time_step) power++; uint FreqUinits = uint(MathPow(2, power));
А затем, определим количество сегментов в соответствии с заданными параметрами сегментирования.
if(window <= 0 || step <= 0) return false; int Segments = int((FreqUinits - int(window) + step - 1) / step); if(Segments <= 0) return false;
На этом подготовительная работа завершена, и мы переходим к инициализации внутренних объектов. Первым идет слой транспонирования исходных данных. Думаю, параметры его инициализации не вызывают вопросов.
uint index = 0; if(!cTranspose.Init(0, index, OpenCL, time_step, variables, optimization, iBatch)) return false;
Затем, создадим 2 буфера данных для записи действительной и мнимой частей частотного спектра после разложения Фурье.
for(uint i = 0; i < caFreqIn.Size(); i++) { index++; if(!caFreqIn[i].Init(0, index, OpenCL, FreqUinits * variables, optimization, iBatch)) return false; caFreqIn[i].SetActivationFunction(None); }
И добавим объект конкатенации данных частотного спектра.
index++; if(!cFreqConcat.Init(0, index, OpenCL, 2 * FreqUinits * variables, optimization, iBatch)) return false; cFreqConcat.SetActivationFunction(None);
Для сегментирования частотного спектра, мы воспользуемся сверточным слоем работы с комплексными величинами, указав ему необходимые параметры.
index++; if(!caProjection[0].Init(0, index, OpenCL, window, step, 2 * window, Segments, variables, optimization, iBatch)) return false; caProjection[0].SetActivationFunction(LReLU);
А второй сверточный слой завершит работу по созданию эмбедингов наших патчей.
index++; if(!caProjection[1].Init(0, index, OpenCL,2*window,2*window,window_key, Segments, variables, optimization, iBatch)) return false; caProjection[1].SetActivationFunction(TANH);
Анализ взаимозависимостей между частотными спектрами отдельных унитарных последовательностей выполняется двумя последовательными модулями внимания. При чем первый работает непосредственно с созданными эмбедингами патчей.
index++; if(!caChannelFusion[0].Init(0, index, OpenCL,window_key,window_key,heads,Segments, variables, optimization, iBatch)) return false;
А вот архитектура второго слоя межканального маскированного внимания варьируется от количества сегментов. Если их число кратно 2, то осуществляется попарное объединение сегментов для поиска взаимозависимостей более высокого ранга.
index++; if(Segments % 2 == 0) { if(!caChannelFusion[1].Init(0, index, OpenCL, 2 * window_key, window_key, heads, Segments / 2, variables, optimization, iBatch)) return false; } else if(!caChannelFusion[1].Init(0, index, OpenCL, window_key, window_key, heads, Segments, variables, optimization, iBatch)) return false;
В противном случае, повторяем архитектуру предыдущего слоя внимания.
Размерность тензора, получаемого по результатам работы модулей внимания, мы понижаем до уровня длины частотного спектра исходных данных с помощью 2 последовательных сверточных слоев проекции.
index++; if(!caLinearHead[0].Init(0, index, OpenCL, window_key, window_key, window, Segments, variables, optimization, iBatch)) return false; caLinearHead[0].SetActivationFunction(LReLU); index++; if(!caLinearHead[1].Init(0, index, OpenCL, window * Segments, window * Segments, FreqUinits, variables, 1, optimization, iBatch)) return false; caLinearHead[ 1 ].SetActivationFunction(None);
Первый слой изменяет размерность сегментов, а второй корректирует длину унитарных последовательностей.
И добавим 2 объекта для разделения действительной и мнимой части частотного спектра перед применением алгоритма обратного преобразования Фурье.
for(uint i = 0; i < caFreqOut.Size(); i++) { index++; if(!caFreqOut[i].Init(0, index, OpenCL, FreqUinits * variables, optimization, iBatch)) return false; caFreqOut[i].SetActivationFunction(None); } //--- return true; }
На данном этапе мы провели инициализацию всех внутренних объектов и можем завершить работу метода, вернув логический результат выполнения операций вызывающей программе.
Далее переходим к построению процесса прямого прохода в методе feedForward. Как было сказано выше, в параметрах метода получаем указатель на объект исходных данных, содержащий тензор многомерного временного ряда.
bool CNeuronCATCH::feedForward(CNeuronBaseOCL *NeuronOCL) { if(!cTranspose.FeedForward(NeuronOCL)) return false;
Полученные данные сначала транспонируем для удобства обработки унитарных последовательностей, после чего, перенесем их в область частотного представления с помощью алгоритма быстрого преобразования Фурье.
if(!FFT(cTranspose.getOutput(), NULL, caFreqIn[0].getOutput(), caFreqIn[1].getOutput(), iCount, false)) return false;
Результаты частотной трансформации конкатенируем в единый тензор.
if(!Concat(caFreqIn[0].getOutput(), caFreqIn[1].getOutput(), cFreqConcat.getOutput(), 1, 1, caFreqIn[0].Neurons())) return false;
После чего, осуществляем патчинг частотного спектра и эмбединг данных с помощью двух сверточных слоев проекции.
CNeuronBaseOCL *neuron = cFreqConcat.AsObject(); for(uint i = 0; i < caProjection.Size(); i++) { if(!caProjection[i].FeedForward(neuron)) return false; neuron = caProjection[i].AsObject(); }
Следующим этапом идет поиск взаимозависимостей путем анализа данных модулями межканального маскированного внимания.
for(uint i = 0; i < caChannelFusion.Size(); i++) { if(!caChannelFusion[i].FeedForward(neuron)) return false; neuron = caChannelFusion[i].AsObject(); }
И возвращаем данные в размерность исходного частотного спектра.
for(uint i = 0; i < caLinearHead.Size(); i++) { if(!caLinearHead[i].FeedForward(neuron)) return false; neuron = caLinearHead[i].AsObject(); }
Далее, мы разделяем действительную и мнимую часть частотного спектра в отдельные объекты.
if(!DeConcat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), neuron.getOutput(), 1, 1, caFreqOut[0].Neurons())) return false; if(!FFT(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caFreqOut[0].getPrevOutput(), caFreqOut[1].getPrevOutput(), iCount, true)) return false;
После чего, выполняем обратное преобразования Фурье, что возвращает данные из частотного спектра в представление временной последовательности. Однако, здесь следует учесть, что в результате обратного преобразования Фурье, мы получаем временной ряд с размерностью равной степени числа 2. А это может отличаться от размерности анализируемого временного ряда, поэтому мы отбрасываем лишние значения путем деконкатенации тензора.
if(!DeConcat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caFreqOut[0].getPrevOutput(), iWindow, caFreqOut[0].Neurons() / iCount - iWindow, iCount)) return false;
К полученным значениям добавляем остаточные связи от транспонированных исходных данных с последующей нормализацией результатов. И выполняем обратную трансформацию данных в представление исходного временного ряда.
if(!SumAndNormilize(caFreqOut[0].getOutput(),cTranspose.getOutput(),caFreqOut[0].getOutput(),iWindow,true,0,0,0,1)) return false; //--- return CNeuronTransposeOCL::feedForward(caFreqOut[0].AsObject()); }
На этом завершается работа метода прямого прохода, а логический результат выполнения операций возвращаем вызывающей программе.
Следующим этапом нашей работы является построение процессов обратного прохода нашего нового объекта. И здесь особое внимание следует уделить методу распределения ошибки между всеми участниками процесса, в соответствии с их вкладом в общий результат calcInputGradients.
bool CNeuronCATCH::calcInputGradients(CNeuronBaseOCL *prevLayer) { if(!prevLayer) return false;
В параметрах метода получаем указатель на объект исходных данных и сразу проверяем актуальность полученного указателя. Необходимость такой точки контроля уже не раз обсуждалась ранее.
Далее транспонируем градиент ошибки, полученный от последующего слоя в представление унитарных последовательностей.
if(!CNeuronTransposeOCL::calcInputGradients(caFreqOut[1].AsObject())) return false; if(!SumAndNormilize(caFreqOut[1].getGradient(),caFreqOut[1].getGradient(),cTranspose.getPrevOutput(), iWindow,false,0,0,0,0.5f)) return false;
И разу скопируем полученные значения в свободный буфер объекта транспонирования исходных данных, что подразумевается потоком остаточных связей.
Далее следует вспомнить, что размерность результатов обратного преобразования Фурье может превышать длину ожидаемого временного ряда. В рамках прямого прохода мы отбрасывали лишние значения. Здесь следует обратить внимание, что при осуществлении прямого прохода, мы дополняли нулевыми значениями анализируемый временной ряд до требуемого размера. Следовательно, в отброшенной части результатов обратного преобразования Фурье мы ожидаем получить аналогичные нулевые значения. Таким образом, для корректного обучения модели, в качестве градиента ошибки отброшенной части корректно указать полученный ранее результат с обратным знаком.
if((caFreqOut[0].Neurons() - iWindow) > 0) if(!SumAndNormilize(caFreqOut[1].getOutput(), caFreqOut[1].getOutput(), caFreqOut[1].getOutput(), 1, false, 0, 0, 0, -0.5f)) return false;
Конкатенируем градиенты ошибки двух блоков в единый тензор.
if(!Concat(caFreqOut[1].getGradient(), caFreqOut[1].getOutput(), caFreqOut[0].getGradient(), iWindow, caFreqOut[0].Neurons() - iWindow, iCount)) return false;
Таким образом, мы получили градиент ошибки действительной части восстановленного сигнала. Но у нас еще есть мнимая часть. Здесь следует вспомнить, что обратным преобразованием Фурье мы восстанавливали временной ряд из его частотного представления. Сам по себе временной ряд представляется действительными значениями, мнимая часть которых равна нулю. Следовательно, подход к определению градиента ошибки мнимой части идентичен отброшенной части действительной части, — меняем знак ранее полученных результатов.
if(!SumAndNormilize(caFreqOut[1].getPrevOutput(), caFreqOut[1].getPrevOutput(), caFreqOut[1].getGradient(), 1, false, 0, 0, 0, -0.5f)) return false;
Теперь мы можем с помощью быстрого преобразования Фурье перевести градиенты ошибки в частотную область.
if(!FFT(caFreqOut[0].getGradient(), caFreqOut[1].getGradient(), caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), iCount, false)) return false;
И конкатенируем полученные результаты в единый тензор, совмещая действительную и мнимую часть комплексных величин.
if(!Concat(caFreqOut[0].getOutput(), caFreqOut[1].getOutput(), caLinearHead[1].getGradient(), 1, 1, caFreqOut[0].Neurons())) return false;
Далее, последовательно проводим градиент ошибки через все внутренние объекты. Сначала через объекты финальной проекции для модулей внимания.
if(!caLinearHead[0].calcHiddenGradients(caLinearHead[1].AsObject())) return false;
Через модули внимания опускаем градиент ошибки до сверточных слоев эмбединга.
CObject *neuron = caLinearHead[0].AsObject(); for(int i = int(caChannelFusion.Size()) - 1; i >= 0; i--) { if(!caChannelFusion[i].calcHiddenGradients(neuron)) return false; neuron = caChannelFusion[i].AsObject(); }
И далее, до уровня конкатенированных данных частотного спектра исходных данных.
for(int i = int(caProjection.Size()) - 1; i >= 0; i--) { if(!caProjection[i].calcHiddenGradients(neuron)) return false; neuron = caProjection[i].AsObject(); } //--- if(!cFreqConcat.calcHiddenGradients(neuron)) return false;
Здесь мы разделяем полученный результат на действительную и мнимую части.
if(!DeConcat(caFreqIn[0].getGradient(), caFreqIn[1].getGradient(), cFreqConcat.getGradient(), 1, 1, caFreqIn[0].Neurons())) return false;
А затем, с помощью обратного преобразования Фурье, возвращаем градиент ошибки в представление временного ряда.
if(!FFT(caFreqIn[0].getGradient(), caFreqIn[1].getGradient(), caFreqIn[0].getPrevOutput(), caFreqIn[1].getPrevOutput(), iCount, false)) return false;
Здесь мы выделяем только актуальную часть данных, релевантную для исходных данных.
if(!DeConcat(cTranspose.getGradient(), caFreqIn[0].getGradient(), caFreqIn[0].getPrevOutput(), iWindow, caFreqIn[0].Neurons() / iCount - iWindow, iCount)) return false; //--- if(!SumAndNormilize(cTranspose.getGradient(),cTranspose.getPrevOutput(),cTranspose.getGradient(),iWindow, false,0,0,0,1.0f)) return false;
И суммируем с ранее сохраненными данными остаточных связей.
В завершении работы метода, транспонируем градиенты ошибки в представление исходных данных и, при необходимости, корректируем на производную функции активации объекта исходных данных.
if(!prevLayer.calcHiddenGradients(cTranspose.AsObject())) return false; if(prevLayer.Activation() != None) { if(!DeActivation(prevLayer.getOutput(), prevLayer.getGradient(), prevLayer.getGradient(), prevLayer.Activation())) return false; } //--- return true; }
Логический результат выполнения операций возвращаем вызывающей программе и завершаем работу метода.
На этом мы завершаем рассмотрение алгоритмов построения собственного видения подходов, предложенных авторами фреймворка CATCH. С полным кодом всех рассмотренных объектов и их методов вы можете ознакомиться во вложении к статье.
Архитектура моделей
После рассмотрения алгоритмов реализации собственного видения предложенных подходов, несколько слов скажем об архитектуре обучаемых моделей. Аналогично предыдущей работе, мы будем обучать 3 модели: Энкодер состояния окружающей среды, Актер и прогнозная модель вероятностей направления предстоящего движения. Подходы фреймворка CATCH имплементируем в Энкодер описания анализируемого состояния окружающей среды. И благодаря тому, что практически весь фреймворк собран в одном объекте, архитектура модели становится визуально простой.
bool CreateDescriptions(CArrayObj *&encoder, CArrayObj *&actor, CArrayObj *&probability) { //--- CLayerDescription *descr; //--- if(!encoder) { encoder = new CArrayObj(); if(!encoder) return false; } if(!actor) { actor = new CArrayObj(); if(!actor) return false; } if(!probability) { probability = new CArrayObj(); if(!probability) return false; } //--- Encoder encoder.Clear(); //--- Input layer if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBaseOCL; int prev_count = descr.count = (HistoryBars * BarDescr); descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Первым, как обычно, мы используем полносвязный слой для записи "сырых" исходных данных, за которым следует объект пакетной нормализации данных. В нем осуществляется первичная обработка получаемого многомерного временного ряда и приведение унитарных последовательностей в сопоставимый вид.
//--- layer 1 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronBatchNormOCL; descr.count = prev_count; descr.batch = 1e4; descr.activation = None; descr.optimization = ADAM; if(!encoder.Add(descr)) { delete descr; return false; }
Далее используем наш модуль CATCH. В нем мы используем сегментацию частотного спектра по 8 элементов с шагом 1. Это позволит нам более детально проанализировать взаимозависимости на всем протяжении частотного спектра исходных данных.
//--- layer 2 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronCATCH; prev_count=descr.count = HistoryBars; { int temp[]={BarDescr,8,32,4}; // Variables, Frequency window, Key Size, Heads if(ArrayCopy(descr.windows, temp) < (int)temp.Size()) return false; } descr.step=1; int prev_out=descr.windows[0]; descr.batch = 1e4; descr.optimization=ADAM; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Полученные данные скорректируем в узкий диапазон нормированных значений.
//--- layer 3 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronConvOCL; descr.count = HistoryBars; descr.window = BarDescr; descr.step = BarDescr; descr.window_out = BarDescr; descr.layers = 1; descr.activation = TANH; if(!encoder.Add(descr)) { delete descr; return false; }
И вернем их распределение исходных данных с помощью слоя обратной нормализации.
//--- layer 4 if(!(descr = new CLayerDescription())) return false; descr.type = defNeuronRevInDenormOCL; descr.count = HistoryBars * BarDescr; descr.layers = 1; descr.activation = None; if(!encoder.Add(descr)) { delete descr; return false; }
Архитектуры Актера и прогнозной модели вероятностей направления предстоящего движения перенесены из предыдущей работы практически без изменений. С ними я предлагаю вам ознакомиться самостоятельно. Их полный код представлен во вложении. Там же вы найдете программы взаимодействия с окружающей средой и обучения моделей, которые перенесены без каких-либо корректировок.
Тестирование
Мы провели довольно объемную работу по реализации подходов, предложенных в рамках фреймворка CATCH, средствами MQL5 и их интеграции в обучаемые модели. И пришло время решающего этапа — проверки эффективности внедрённых решений на реальных исторических данных. Это позволит оценить сильные и слабые стороны реализованных подходов, а также определить потенциал дальнейшей оптимизации.
Для обучения модели мы собрали обучающую выборку из случайных проходов в тестере стратегий MetaTrader 5. В качестве базы использовались исторические данные валютной пары EURUSD, таймфрейм M1 за весь 2024 год.
Тестирование обученных моделей осуществлялось на исторических данных за период Января-Март 2025 года. При этом все параметры эксперимента сохранялись неизменными, что обеспечивает объективность полученных результатов и позволяет провести независимую оценку эффективности стратегии. Такой подход гарантирует, что модель не просто запоминает характеристики обучающего набора данных, а действительно демонстрирует способность адаптироваться к новым рыночным условиям.
Ниже представлены результаты тестирования.
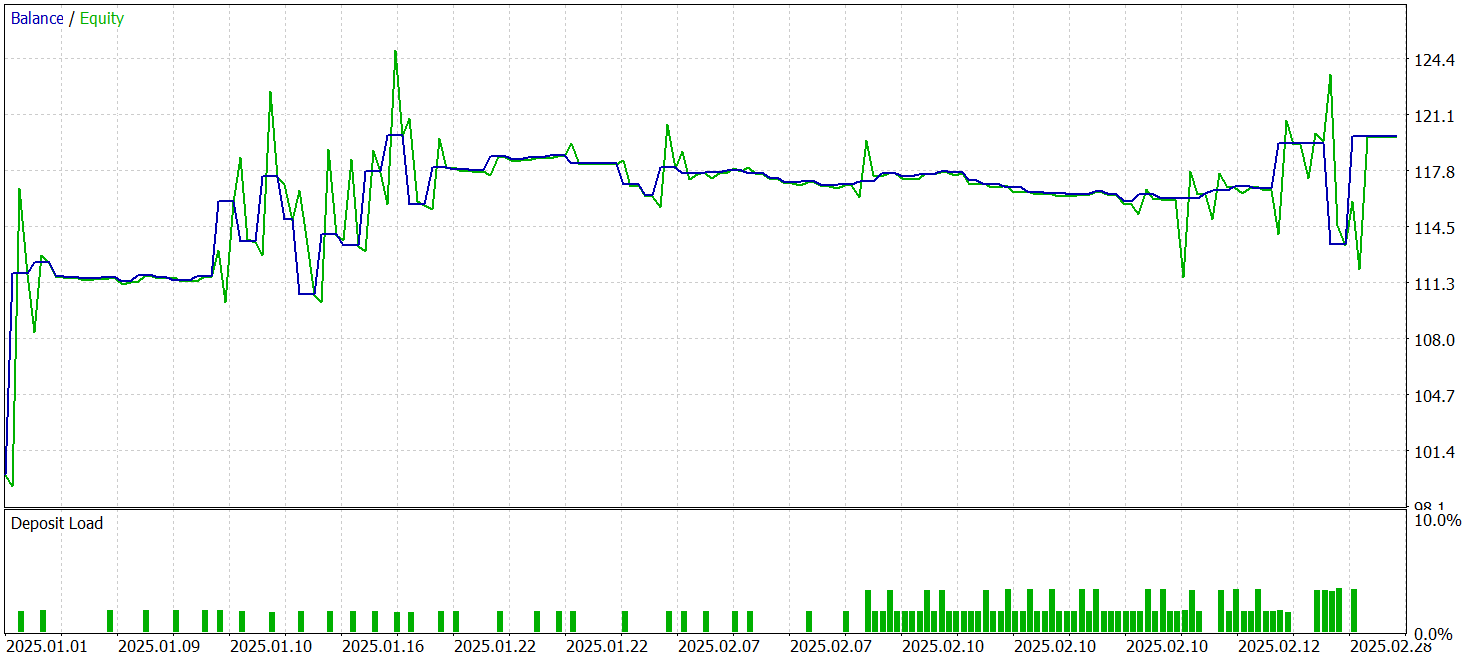
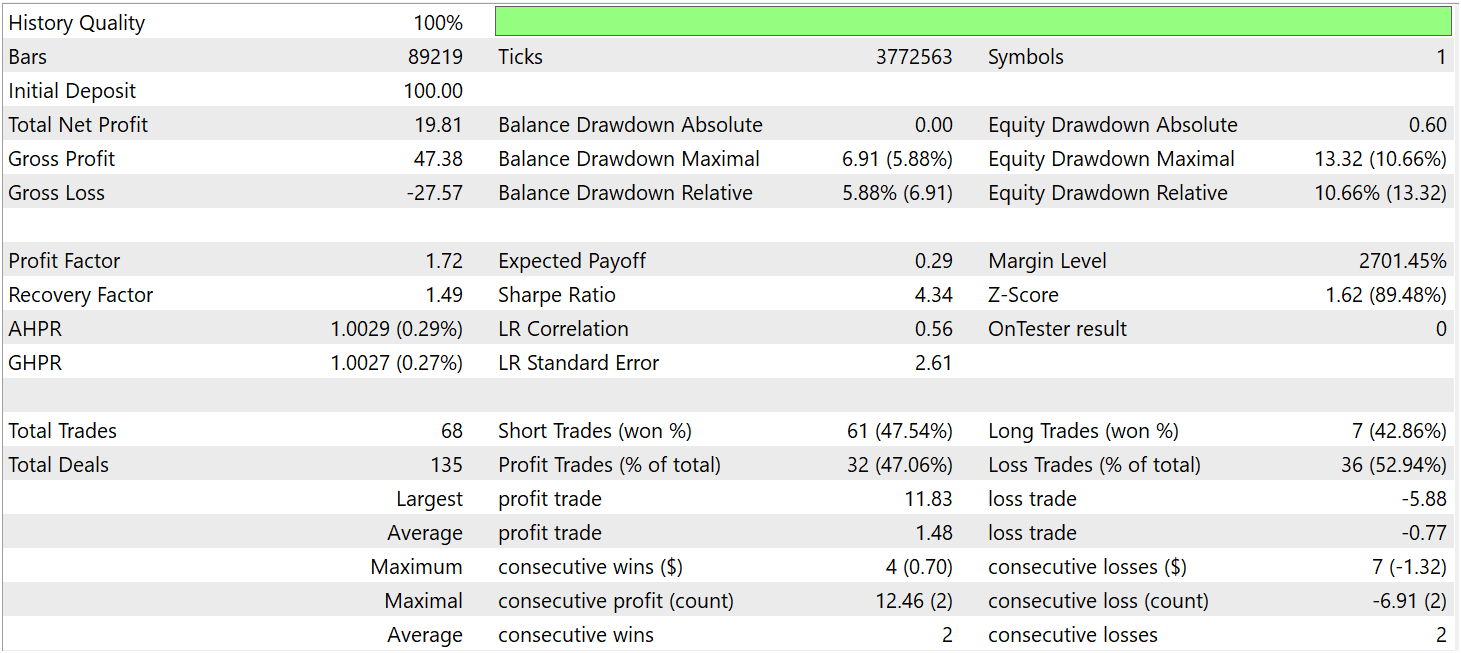
За период тестирования модель совершила 68 торговых операций и 32 из них было закрыто с прибылью, что составило чуть более 47%. При этом, средняя прибыльная сделка почти в 2 раза превышает аналогичный показатель убыточных операций. В итоге, за период тестирования модель смогла получить прибыль, зафиксировав показатель профит-фактор на уровне 1.72.
Заключение
На протяжении двух статей мы познакомились с теоретическими аспектами фреймворка CATCH, который представляет собой инновационный подход, объединяющий преобразование Фурье и механизм частотного патчинга, для обнаружения аномалий в многомерных временных рядах. Его главное преимущество заключается в способности выявлять сложные закономерности, которые остаются незаметными при анализе исключительно во временной области.
Использование частотного представления позволяет глубже проникнуть в структуру рыночной динамики. А механизм частотного патчинга обеспечивает гибкость анализа, помогая адаптировать модель к изменяющимся условиям анализируемой среды. В отличие от классических методов, CATCH не ограничивается фиксацией резких ценовых скачков и выбросов, а позволяет распознавать скрытые зависимости.
В практической части мы реализовали собственное видение предложенных подходов средствами MQL5, обучили модель и провели её тестирование на реальных исторических данных. Полученные результаты свидетельствуют о наличии потенциала, однако, остаются открытыми вопросы дальнейшей оптимизации.
Ссылки
- CATCH: Channel-Aware multivariate Time Series Anomaly Detection via Frequency Patching
- Другие статьи серии
Программы, используемые в статье
| # | Имя | Тип | Описание |
|---|---|---|---|
| 1 | Research.mq5 | Советник | Советник сбора примеров |
| 2 | ResearchRealORL.mq5 | Советник | Советник сбора примеров методом Real-ORL |
| 3 | Study.mq5 | Советник | Советник обучения моделей |
| 4 | Test.mq5 | Советник | Советник для тестирования модели |
| 5 | Trajectory.mqh | Библиотека класса | Структура описания состояния системы и архитектуры моделей |
| 6 | NeuroNet.mqh | Библиотека класса | Библиотека классов для создания нейронной сети |
| 7 | NeuroNet.cl | Библиотека | Библиотека кода OpenCL-программы |
Предупреждение: все права на данные материалы принадлежат MetaQuotes Ltd. Полная или частичная перепечатка запрещена.
Данная статья написана пользователем сайта и отражает его личную точку зрения. Компания MetaQuotes Ltd не несет ответственности за достоверность представленной информации, а также за возможные последствия использования описанных решений, стратегий или рекомендаций.
 Оптимизация нейробоидами — Neuroboids Optimization Algorithm 2 (NOA2)
Оптимизация нейробоидами — Neuroboids Optimization Algorithm 2 (NOA2)
 Разработка трендовых торговых стратегий на основе машинного обучения
Разработка трендовых торговых стратегий на основе машинного обучения
 Создание торговой панели администратора на MQL5 (Часть II): Повышение оперативности реагирования и быстрого обмена сообщениями
Создание торговой панели администратора на MQL5 (Часть II): Повышение оперативности реагирования и быстрого обмена сообщениями
 Своп-арбитраж на Форекс: Собираем синтетический портфель и создаем стабильный своп-поток
Своп-арбитраж на Форекс: Собираем синтетический портфель и создаем стабильный своп-поток
- Бесплатные приложения для трейдинга
- 8 000+ сигналов для копирования
- Экономические новости для анализа финансовых рынков
Вы принимаете политику сайта и условия использования