Do básico ao intermediário: Ponto Flutuante

Introdução

O conteúdo exposto aqui, visa e tem como objetivo, pura e simplesmente a didática. De modo algum deve ser encarado como uma aplicação final, onde o objetivo não seja o estudo dos conceitos aqui mostrados.

No artigo anterior Do básico ao intermediário: Definições (II), falamos como as macros são importantes, e como podemos fazer um bom uso das mesmas. Isto com o objetivo de tornar nosso código ainda mais legível.

Pois bem, com base em tudo que já foi visto até agora. Já temos material suficiente e também meios adequados para explicar uma coisa. Como os números de ponto flutuante funcionam. Sei que muitos acreditam que valores do tipo double ou do tipo float, são a melhor escolha em diversos tipos de situação. Porém, existe um problema envolvido neste tipo de número, que poucas, se não quase ninguém fora do círculo da programação realmente compreende.

E como este tipo de número é muito utilizado aqui no MQL5, por conta de que trabalhamos com informações, onde o ponto flutuante, é quase um consenso. É preciso entender de maneira bastante clara, como este tipo de valor é trabalhado pela CPU.

E por que estou dizendo isto? É claro que números com valores fracionados, como por exemplo 2.5 são sempre muito bem compreendidos. Já que ninguém irá confundir este tipo de valor com um outro valor qualquer. Porém, meu caro leitor, quando se trata de computação, as coisas não são bem assim. Os números em ponto flutuante, são de fato, algo bastante útil em diversas situações. Porém, eles não devem ser considerados ou entendidos da mesma forma que números inteiros.

Basicamente, muitos de vocês, devem estar acostumados em lidar com ponto flutuante em dois tipos de notação. A cientifica, onde escrevemos os valores como, por exemplo 1-e2 e a mais comum que é o aritmético, onde escrevemos os valores como 0.01. Ambos valores são iguais em grandeza, porém escritos de forma diferente. Assim como também existe a forma fracionária de escrever este mesmo valor que seria 1/100.

Note que em todos os casos estamos falando do mesmo valor. Mas apesar disto, programas, ou linguagens de programação diferentes, lidam com estes valores de forma diferente.

Um pouco da história

No início da computação, números de ponto flutuante, como são atualmente conhecidos. Não existiam, ou melhor dizendo, não existia uma forma padronizada de lidar com eles. Cada programador, cada sistema operacional, ou até mesmo cada programa, lidava com este tipo de número de maneira muito particular e pessoal.

Durante os anos entre 1960 e 1970, não existia forma de um programa, conversar com outro a ponto de conseguir compartilhar e tornar a fatoração de tais valores mais rápidos. Pensa só, em pleno início da era espacial, onde tais números seria de suma importância. NÃO ERA POSSIVEL, calcular valores de ponto flutuante nos computadores da época. E quando tal possibilidade existia. Não era possível dividir a tarefa entre mais computadores a fim de efetuar os cálculos de maneira mais rápida.

Então a IBM, que era quem tinha quase a totalidade do mercado, começou a propor uma forma de representar este tipo de valor. Mas o mercado nem sempre aceita o que lhe é proposto. Então outros fabricantes, criaram suas próprias maneiras de representar tais valores. Era um verdadeiro CAOS. Até que em um dado momento o instituto de engenheiros elétricos e eletrônicos ( IEEE ) começou a colocar ordem na casa, estabelecendo assim, o que é conhecido como padrão IEEE 754. No final deste artigo, em referências, irei deixar alguns links para quem tiver interesse em se aprofundar no assunto.

O primeiro padrão estabelecido foi o IEEE 754-1985 como uma forma de tentar resolver a questão toda. Hoje já utilizamos um padrão bem mais atual, mas tudo baseado naquele padrão estabelecido inicialmente.

Um detalhe importante: Apesar de existir este padrão, a fim de normalizar e permitir uma fatoração distribuída. Existem casos em que este padrão não é utilizado. Sendo a computação, ou melhor dizendo, a fatoração, efetuada seguindo outros critérios, dos quais não iremos ver aqui. Pois fogem completamente do assunto. Já que o MQL5, faz uso, assim como diversas outras linguagens, deste mesmo padrão IEEE 754.

Ok, no começo a CPU não conseguia lidar com este tipo de cálculo. Sendo que existia uma CPU, que era conhecida na época como FPU, apenas para este objetivo. Esta FPU era comprada a parte, já que o custo da mesma, nem sempre compensa a sua utilização. Um exemplo de FPU seria o 80387. E sim, não escrevi errado. O modelo de fato se parece muito com o conhecido 80386, conhecido popularmente como 386. Mas isto era mais uma questão de marketing da Intel. Isto para diferenciar a CPU que seria o 80386, da FPU que seria o 80387. O computador conseguia trabalhar somente com a CPU. Mas não somente com a FPU. Já que esta era voltada apenas para efetuar os cálculos de ponto flutuante.

Bem, mas qual o problema do ponto flutuante? Por que um artigo apenas para falar sobre isto? O motivo, é que sem entender como o ponto flutuante funciona. Você pode acabar cometendo uma série de erros. Não devido a uma programação deficiente. Mas sim, por imaginar que os cálculos feitos, devem ser levados ao pé da letra. Quando na verdade, o simples fato de utilizar o padrão IEEE 754, gera um erro potencial no valor final que estaria sendo calculado.

Isto parece ser um absurdo. Já que computadores, são máquinas que sempre deveria nos apresentar valores precisos. Falar que existe um erro, no resultado de uma operação. Não parece ser algo de fato palpável e tão pouco aceitável. Já que o objetivo é operar no mercado de capitais, usando tais dados. E se os nossos cálculos estiverem errados. Podemos estar perdendo dinheiro, mesmo quando tudo indica que deveríamos estar é ganhando. E é justamente por conta disto, que este artigo é importante.

Existem uma série de coisas relacionadas ao ponto flutuante, que para o que iremos fazer, não tem muita importância. Mas existe uma coisa que é muito importante, e que faz toda a diferença. Que é o arredondamento.

Sei que muitos dizem, ou mesmo batem no peito dizendo: 

Mas eu não faço arredondamento em meus cálculos. Eles são sempre exatos e precisos.

Mas é justamente esta ideia, que ao meu entender, mostra uma completa e total falta de entendimento sobre programação, que fazem as pessoas imaginarem algo, quando na verdade as coisas não são bem como parece. O arredondamento, não precisa ser feito pelo programador. Ele simplesmente existe. Independentemente de o programador querer ou não o efetuar. Por isto é importante que você veja as referências que irei deixar no final do artigo. Já que esta questão do ponto flutuante, não é algo que poderia ser explicado em um simples artigo. Lembre-se: Existem profissionais, trabalhando nisto, desde os primórdios da computação.

O que iremos ver aqui, é outro tipo de coisa, muito mais simples e voltada justamente a entender o que seria o tipo double ou float. Já que todos os demais tipos, são bem mais simples e foram explicados nos artigos anteriores.

Representação de um ponto flutuante

Ok, aqui vamos falar do tipo realmente utilizado no MQL5. Neste tipo, basicamente seguimos o que é proposto pelo IEEE 754. Tendo dois formatos, ou melhor dizendo: Duas precisões diferentes. E sim, o correto quando falamos em ponto flutuante, é dizer precisão e não formato, e tão pouco número de bits envolvidos. Mas para não tornar a coisa muito confusa, já que por si só pode ser bem confusa para muitos. Iremos aqui utilizar o termo número de bits. Apenas para permitir uma melhor compreensão por parte da grande maioria, além de tornar mais simples a explicação que será dada. Pois acredito, que não estou falando com engenheiros ou pessoas deste calibre, com um amplo e vasto conhecimento sobre eletrônica ou desenvolvimento de chips. Mas sim com pessoas interessadas e sedentas por conhecimento a respeito de programação em MQL5.

Pois bem, para começar vamos ver um código bem simples. No entanto, mesmo sendo simples, para conseguir entender, é necessário, que você tenha assimilado o conhecimento presente nos artigos anteriores. Então vamos a ele.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

Código 01

Bem, meu caro leitor, este código é muito interessante, além de ser bastante curioso e divertido de brincar com ele. Apesar de tudo, aqui estamos fazendo apenas a primeira parte do que realmente queremos e iremos fazer.

Preste atenção. Na linha quatro dizemos qual o tipo de valor que estaremos usando como ponto flutuante. Podemos dizer que queremos o tipo double ou float. A diferença entre um e o outro é justamente a precisão que cada um nos permite obter. Porém antes de entramos nestes detalhes, vamos entender o que este código está fazendo.

Muito bem, feita a declaração do tipo, podemos usar uma união para criar uma forma de ler a memória. Para isto, usamos a linha oito. Já dentro da união, usamos a linha 10 para criar uma variável e a linha 11 para um array de compartilhamento. Este tipo de coisa foi visto e explicado em artigos anteriores. Veja os mesmos para mais detalhes, caso não esteja entendendo o que está ocorrendo aqui. E qual o propósito da criação desta união.

Já a linha mais importante aqui para nós, é justamente a linha 14. Pois é nela que declaramos o valor que queremos visualizar. Já a linha 16, apenas irá nos fornecer a forma de mostrar o conteúdo da memória. Como é o nosso atual desejo. Já que queremos entender como um valor em ponto flutuante é representado na memória a ponto de o computador conseguir compreender o mesmo.

Muito bem, quando executado, este código 01 irá nos apresentar o seguinte resultado mostrado na imagem abaixo.

Imagem 01

Hum. Que coisa estranha é está, que estamos vendo como representação hexadecimal? Bem meu caro leitor, está é a forma como o computador, usando a norma IEEE 754, enxerga um valor em ponto flutuante. Um detalhe importante, este valor está sendo escrito como um valor seguindo o modelo Little Endian. Em outro momento iremos falar mais sobre o que este modelo representa. Mas por hora, você precisa entender apenas o seguinte. Este valor hexadecimal está escrito ao contrário. Devendo ser lido da direita para a esquerda.

Bem, de qualquer forma, talvez você não esteja acreditando. Então podemos fazer uso de um outro programa, só para tornar isto claro. Assim vamos utilizar um editor hexadecimal. O HxD é um editor simples e gratuito. Se você digitar os valores mostrados no campo hexadecimal da imagem 01. Selecionar as mesmas e olhar qual o valor que está sendo representado ali, irá ver uma imagem parecida com a vista logo abaixo.

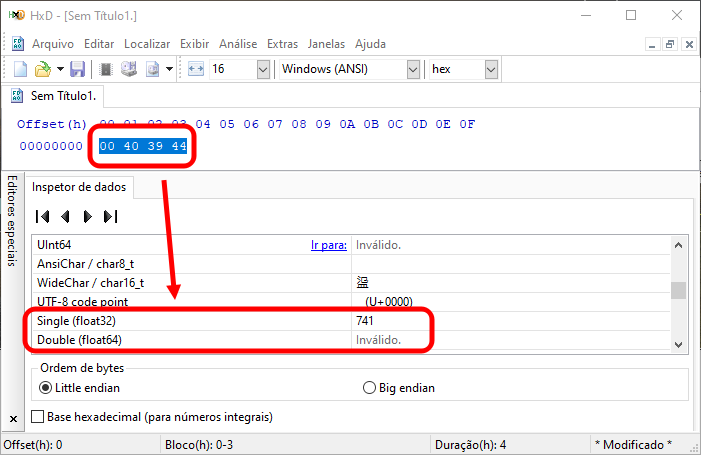
Imagem 02

Note que de fato, temos o valor esperado, podendo ser visualizado ali. Porém, eu em particular, gosto de utilizar uma extensão da minha plataforma de desenvolvimento para ver este tipo de coisa. Isto para evitar precisar ter diversos programas instalados na máquina. Se bem que o HxD não precisa ser instalado. De qualquer forma, o que podemos ver é mostrado na imagem logo abaixo.

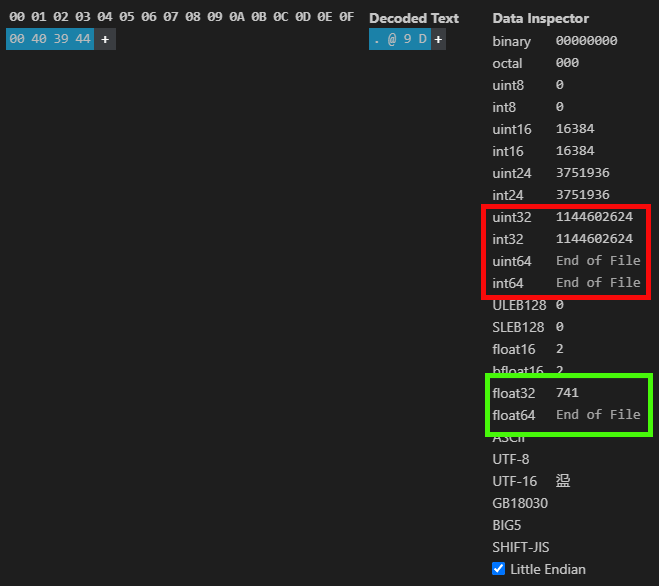
Imagem 03

Este tipo de informação que está sendo vista aqui, também pode ser visto, tanto no MetaTrader 5, quanto também no HxD. Porém, quero que você observe o que estou mostrando nesta imagem 03. Note que um mesmo valor em ponto flutuante representa um outro valor em inteiro. Mas porque disto? O motivo, é que para o computador, tanto faz se é inteiro ou outro tipo qualquer, para ele não faz diferença. Porém para nós, e para o compilador, um tipo ou outro, pode fazer com que tenhamos uma resposta plausível e uma completamente estranha sendo fornecida.

Mas este caso, que vimos neste código 01, é um exemplo simples. Vamos mudar o código 01, para um exemplo um pouco diferente. Este é visto logo abaixo.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

Código 02

Muito bem, este código 02, parece ser mais complicado. Porém ele é tão simples como o código 01. Só que nele temos a oportunidade de dizer algumas coisas extras, sobre como o ponto flutuante será apresentado a nós. Isto por que, devido a linha quatro, podemos selecionar se queremos usar um tipo com precisão simples, ou precisão dupla. Mas o código sendo executado, como mostrado acima, teremos como resposta o que é visto logo abaixo.

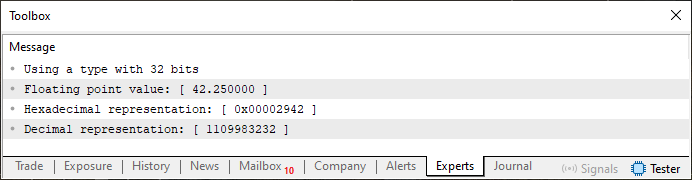
Imagem 04

E da mesma forma que foi visto antes. Temos ao usar os valores informados e vistos na imagem 04, o resultado que é visto na imagem logo na sequência.

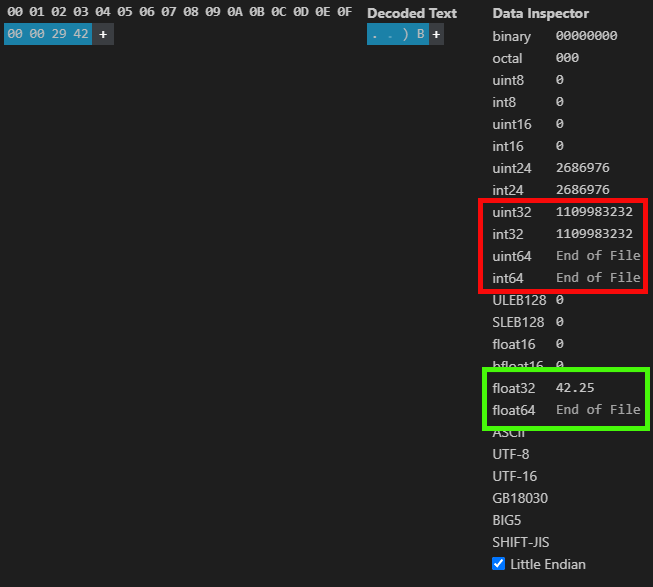
Imagem 05

Ou seja, de fato existe algo acontecendo aqui. Mas como este sistema IEEE 754 funciona? Bem, meu caro leitor, para explicar isto, precisamos recorrer a uma visualização mais interna do próprio sistema. Tentarei não complicar a coisa toda. Já que isto acabaria por destruir qualquer tentativa de explicar e de você compreender o que se passa aqui. Mas, basicamente, e atualmente, temos dois formatos IEEE 754. Uma para precisão simples, onde usamos 32 bits e um outro para precisão dupla, onde usamos 64 bits. A diferença entre um e outro, não está no fato de um ser mais exato que o outro. A diferença está no range que podemos utilizar. Por isto, o termo precisão, muitas vezes é um tanto quanto enganador. Sendo assim prefiro não utilizar este termo. Apesar de ele ser o termo correto a ser adotado.

Na imagem logo abaixo, você pode observar os dois tipos que são definidos pelo padrão.

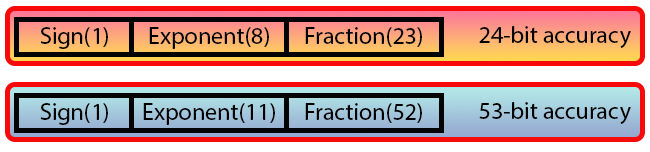
Imagem 06

Mas espere um pouco. Você não disse que usamos 32 bits para um tipo e 64 para outro? Mas aqui parece que estamos utilizando algo que não tem muito sentido. O que são todos estes dados, e valores, que podemos ver na imagem 06? Bem, esta é a forma como um valor em ponto flutuante é representado pela norma IEEE 754. Aqui cada um dos valores que você pode observar, são BITS. Note que temos unidades com largura diferente da usual. Visto até aqui. Porém, isto não nos impede de entender tal sistema. Se bem, que o mesmo seria mais simples de ser explicado, se fosse utilizado C ou C++. Isto por que no MQL5, não temos meios de nomear bit a bit. Coisa que é possível ser feita no C ou C++. Porém, podemos utilizar macros e definições para conseguir aproximar do que seria feito em C ou C++.

Então vou tentar explicar isto, ainda neste artigo. Se não der, irei montar um outro artigo para permitir uma explicação adequada. Não quero explicar a coisa de maneira superficial. Quero que você, meu caro leitor, de fato consiga compreender que tipo de problema existe, quando utilizamos ponto flutuante nos nossos códigos. Pois vejo muita gente, afirmar e acreditar que podemos calcular coisas, que na verdade não podemos. Pois existe um pequeno desvio, entre o resultado esperado e o resultado calculado. Gerando assim problemas quando não estamos devidamente preparados para eles.

Vamos começar entendendo o seguinte: Se você somar a quantidade de bits mostradas na imagem 06. Irá notar que o primeiro formato contém 32 bits e o seguindo 64 bits. As questões se iniciam por este ponto. Então para simplificar, vamos focar em apenas um dos formatos. Já que a diferença entre um e outro é com relação ao valor usado no ajuste. Mas iremos falar sobre isto depois.

O bit que na imagem 06 é o Sign é o bit de sinal. Ou seja, é ele que diz se um valor é negativo ou positivo. Assim como acontece nos tipos inteiros. Onde o bit mais à esquerda nos diz se o valor é negativo ou se ele é positivo.

Bem seguindo este bit Sign, temos oito bits, com o nome de Exponent. Este valor gera um bias de 127. Que codifica o expoente. Já no caso de uma precisão dupla, temos onze bits, que gera um bias de 1023. Veja que apesar do nome precisão dupla, o bias é muito maior.

Mas a parte que interessa de fato é o que vem logo depois. Que é o campo Fraction. Este campo é o que gera a precisão do valor que será representado. Note que no caso de 32 bits, temos 23 bits neste campo, nos dados uma precisão de 24 bits. E no caso da precisão dupla, temos 52 bits neste campo, nos dando uma precisão de 53 bits. Novamente o valor é mais que o dobro do anterior. E por conta disto, mais uma vez este termo, precisão dupla é um tanto quanto enganador.

Mas se você procurar se aprofundar nesta questão dos números em ponto flutuante, irá ver que este campo, que aqui chamamos de Fraction, é conhecido como mantissa. Sendo está a parte interessante da criação dos valores em ponto flutuante.

Existe uma série de coisas envolvidas aqui. Mas para tornar as coisas agradáveis, já que muitos podem acabar desanimando ao ver certos detalhes envolvidos. Vamos a um exemplo prático. No código 01, usamos na linha 14, o valor 741. E o transformamos em um valor de ponto flutuante. No caso um valor de 32 bits. Ou seja, precisão simples. Assim, podemos usar o modelo em laranja da imagem 06. Quero que você procure focar no que será mostrado para entender este modelo simples primeiro.

Bem, para começar, precisamos transformar este valor 741 em binário. Para fazer isto, podemos usar de diversos meios. Porém, o que muitos acham mais simples, é justamente utilizar a divisão por dois. Um detalhe, se você não sabe como converter um número em binário. Não se preocupe, já que este primeiro valor é mais simples. Será fácil entender como fazer isto. Na imagem 07, vista logo abaixo, vemos como isto é feito.

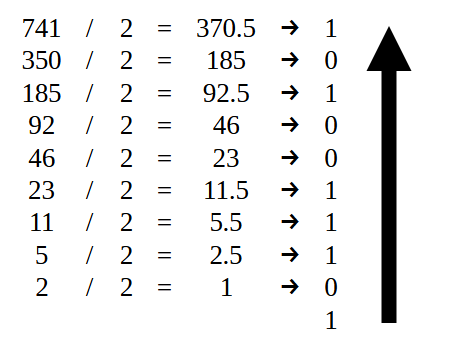
Imagem 07

Uma vez feito as divisões, temos no final uma serie de zeros e uns. Mas para que o valor seja corretamente escrito, precisamos fazer a escrita conforme é mostrada pela seta. Com isto temos o que é visto na imagem abaixo.

Imagem 08

Ok, esta é a primeira parte. Conseguir chegar nesta imagem 08. Uma vez feito isto, podemos partir para a segunda fase. Que é justamente transformar este valor binário em um valor de ponto flutuante. Agora preste atenção, pois este é o caso mais simples que existe. Porém precisa ser muito bem entendido para se conseguir entender casos mais complicados.

Precisamos criar a nossa mantissa, ou seja, a parte fracionária. Para fazer isto, precisamos deslocar a virgula que está na extrema direita, de forma implícita para a esquerda. Isto de forma que tenhamos apenas um bit com o valor igual a um a esquerda. Isto irá gerar o que é visto na imagem abaixo.

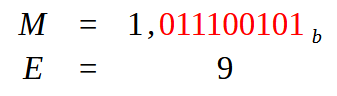
Imagem 09

Agora veja o seguinte: M é o que seria a nossa mantissa, ou seja a parte fracionária do ponto flutuante. Já E seria o nosso expoente. Mas de onde surgiu este valor igual a nove? Bem ele surge do fato de que temos nove valores em vermelho na mantissa. Mas este valor nove ainda precisa ser trabalhado. E é aqui onde surge a terceira fase da transformação. Pois dependendo da escolha que venhamos a fazer, iremos trabalhar este valor nove de uma forma ou de outra. Gerando assim valores diferentes. Isto para representar o ponto flutuante em termos de informação hexadecimal.

Mas antes de vermos o que iremos fazer com este valor nove. Vamos entender como a parte fracionária do ponto flutuante foi será criada.

Lembra que temos 23 bits para um valor de precisão simples e 52 bits para um valor de precisão dupla? Mas que a precisão era de 24 bits para a precisão simples e 53 para a precisão dupla. Pois bem, aquele um que você pode observar em preto na imagem 09. É justamente o bit extra que surge aqui. Ou seja, ele NÃO ESTÁ PRESENTE. Mas está implícito no campo Fraction. Com isto temos o campo Fraction criado da seguinte maneira:

Imagem 10

A quantidade de zeros em verde nesta imagem 10, depende da quantidade de bits no campo Fraction. Mas existirá tantos zeros quantos os necessários para preencher todo o restante do campo. Assim, já temos a parte fracionária do valor em ponto flutuante. Nos falta a parte do expoente. Já que o valor é positivo temos o campo Sign será igual a zero. Para criar a parte do expoente precisamos olhar para o tipo de precisão que estamos utilizando. Caso seja uma precisão simples iremos somar o valor E visto na imagem 09. Que no caso é nove, com o valor de bias, que no caso seria 127. Com isto temos o valor de 136. Esta operação é mostrada na imagem logo abaixo.

Imagem 11

Agora finalmente podemos montar o valor de precisão simples para representar 741 em formato de ponto flutuante. Este valor é mostrado logo abaixo.

Imagem 12

Separando estes bits da imagem 12 a fim de construir a representação em hexadecimal, temos o que é visto na imagem 13 logo na sequência.

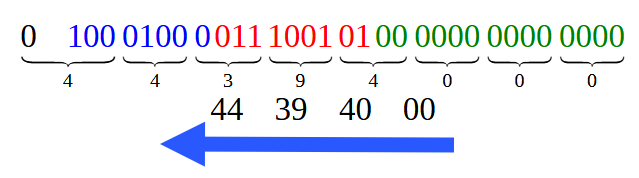
Imagem 13

Note que cada um deste valores em hexadecimal, vistos nesta imagem 13 são os mesmos que podemos visualizar na imagem 01. Porém você deve lembrar de os ler conforme a indicação da seta. Isto por conta de um detalhe que iremos ver em outro artigo futuro. Bem, este é o caso mais simples de todos. Porém neste artigo vimos um outro caso um pouco mais complicado. Se é que podemos dizer assim. Que é o caso visto no código 02, onde temos de fato um valor com ponto decimal. E nesta situação como deveremos proceder?

Bem, meu caro leitor, quando temos um ponto decimal sendo utilizado no valor numérico, a coisa é um pouco diferente. Mas nem tanto. A verdade, neste caso precisamos dividir o que seria a etapa de conversão em binário em duas partes. Uma para a parte a esquerda do ponto decimal e a outra para a parte a direita do ponto decimal. Parece complicado não é mesmo? Mas na prática é bem simples e direto. Bastando para isto que você preste atenção ao que está fazendo.

Para começar a parte que estiver à ESQUERDA do ponto decimal, deverá ser feita como na imagem 07. Ou seja, temos que usar apenas o valor 42, como é visto logo abaixo.

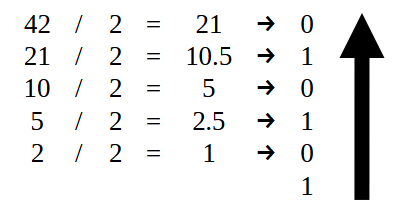
Imagem 14

Já a parte que estiver à DIREITA do ponto decimal, deverá ser feita conforme pode ser visto na imagem 15. Ou seja, os 0.25, agora iremos converter em binário a parte decimal do valor que está no código 02.

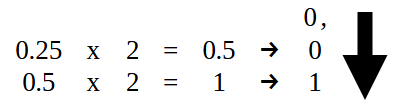
Imagem 15

Isto resulta no que é a representação logo abaixo do valor 42.25 em binário.

Imagem 16

Preste muita, mas muita atenção ao fato de que nesta imagem 16, JÁ TEMOS UMA VIRGULA, sendo indicada ali. Isto irá mudar ligeiramente o que será feito nos próximos passos. Basicamente o que seria o passo que foi visto na imagem 09, onde procuramos o valor da mantissa e do expoente. Como aqui na imagem 16, já temos uma virgula, sendo indicada, tudo que precisamos é deslocar ela de forma a poder termos apenas e somente um único bit com o valor um na extrema esquerda. Da mesma forma que ocorreu na imagem 09. Com isto temos o seguinte resultado, visto na imagem logo na sequência.

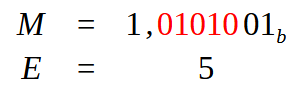
Imagem 17

Note que aqui na imagem 17, os valores em vermelho são exatamente os que foram necessários deslocarmos a fim de conseguir levar a virgula para a posição correta. Com isto temos que o valor de ajuste para o expoente será igual a cinco. Assim como também já temos o valor da mantissa, que é usada para gerar a parte do campo Fraction. Então calculando o valor para uma precisão simples, temos o que é mostrado logo abaixo.

Imagem 18

Observe que o valor hexadecimal que foi encontrado, é exatamente o valor mostrado na imagem 04. Lembrando é claro que você precisa ler ele seguindo a seta, em grupos de dois em dois. Ok, mas será que teríamos o mesmo resultado se fosse utilizado a precisão dupla? Ou seja, se fizéssemos com que a linha quatro do código 02, não fosse um comentário, a ponto de que aquela diretiva fosse utilizada. Estaríamos utilizando 64 bits ao invés de 32 bits. Fazendo assim a utilização da precisão dupla no sistema.

Então neste caso, teríamos o mesmo dado que vemos na imagem 18? Bem, seria mais ou menos isto meu caro leitor. Na verdade, a parte fracionária se manteria, claro que precisaríamos adicionar mais zeros, a fim de preencher os demais bits para completar os 52 bits que a parte fracionaria exigiria neste caso. Porém a parte do expoente seria bem diferente. Isto por conta do fato de que ao invés de utilizar 127 para ajustar o expoente, precisaríamos utilizar o valor de 1023. Assim a única parte que seria visivelmente modificada na imagem 18. É justamente a parte vista em azul. Para tornar isto mais claro, veja na imagem abaixo como seria a representação do valor no caso de utilizarmos a precisão dupla.

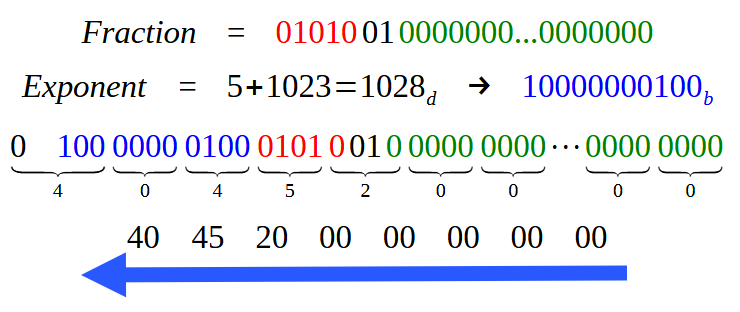
Imagem 19

E para comprovar se está ou não correta esta nossa estimativa. Executamos o código 02, com a mudança proposta e o resultado é o que podemos visualizar logo abaixo.

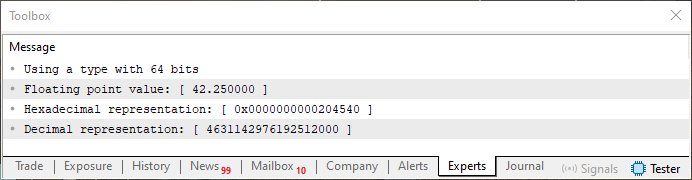
Imagem 20

Considerações finais

Neste artigo, que é apenas uma breve introdução o que seria pontos flutuantes. Vimos como um ponto flutuante é representado dentro da memória. E como podemos trabalhar com este tipo de valor. Sei que neste momento você pode estar um tanto quanto confuso a respeito de diversas coisas sobre pontos flutuantes meu caro leitor. Não é para menos. Eu mesmo no começo, demorei algum tempo para conseguir compreender como este tipo de dado era criado. Mas principalmente como efetuar cálculos usando tais informações. Apesar de que, não é o meu objetivo primário aqui. Quem sabe em um momento futuro, eu possa explicar como os cálculos usando ponto flutuantes acontecem. Pois é algo de fato muito interessante. Ainda mais utilizando o padrão IEEE 754.

Claro que existem outros formatos e maneira de representar números que contém ponto decimal. Porém, como o MQL5, assim como diversas outras linguagens de programação, fazem uso do que foi visto aqui neste artigo. É bom que você procure entender e estudar com calma este tipo de dado. Já que ele muitas das vezes não representam exatamente o valor que estamos calculando. E sugiro que você veja as referências que estou postando e procure estudar como é feito o arredondamento para valores em ponto flutuante. Pois existem regras para isto. Não sendo feito de qualquer maneira.

No entanto, isto fica como sendo algo que cada um deverá procurar saber. Já que com base no que foi mostrado aqui, já poderemos trabalhar com este tipo de valor. Sendo estas partes extras, como saber como o arredondamento é feito, e quais valores podem ou não ser representados aqui. É algo necessário apenas para quem realmente deseja uma boa precisão e exatidão nos valores usados nas suas aplicações. Coisa que aqui, não será de fato necessária.

Referências:

• IEEE 754
• Trabalho com modelos ONNX nos formatos float16 e float8