Do básico ao intermediário: Filas, Listas e Árvores (VIII)

Introdução

No artigo anterior Do básico ao intermediário: Filas, Listas e Árvores (VII), foi explicado um de tantas formas possíveis de implementarmos um mecanismo de exclusão de um node em uma árvore. Aquele tipo de coisa precisa ser muito bem compreendido para que possamos trabalhar com árvores com diferentes objetivos. Como foi mencionado no artigo anterior, existem outras maneiras de se implementar o mecanismo de exclusão. Porém, aquele que foi mostrado ali, ao meu ver é um dos mais simples, que não fazem uso de um modelo onde utilizamos a recursividade. O fato de não utilizarmos, ou de você tomar o cuidado de não utilizar a recursividade, no mecanismo de exclusão, se deve justamente ao fato de que, se for necessário excluir diversos elementos na árvore. E estes elementos vierem a se encontrar em um node bem profundo na árvore. A recursividade, irá gerar um custo computacional considerável. Já que para chegar em cada elemento, precisaremos empilhar diversas chamadas e depois as desempilhar. E isto acaba tomando muito tempo, degradando assim a performance dos mecanismos envolvidos na construção e manutenção da árvore.

Ok, entender isto que foi explicado, é algo realmente necessário. Isto por que, de uma maneira muito parecida, o mecanismo de busca, precisa ser muito bem pensado. Isto para evitar que tenhamos o mesmo problema de degradação da performance da árvore. Porém, e esta é a parte que complica tudo. Existe um outro problema. O balanceamento da árvore. Entender esta questão referente ao balanceamento é tão, ou talvez até mais importante do que entender os próprios mecanismos que estão, ou precisarão ser implementados.

Então neste artigo iremos entender o que seria este tal balanceamento, e por que ele é tão importante. Mas também vamos começar a entender, já que isto será visto em um outro artigo, na prática, porque as vezes não podemos, ou não devemos balancear a árvore. Mesmo que isto venha a nós causar um certo desequilíbrio durante o uso de algumas operações que venhamos a fazer na árvore. E quando me refiro a desequilíbrio, estou querendo mencionar o fato de que, as vezes as operações serão executadas rapidamente, enquanto em outros momentos ela pode vir a demorar um pouco mais. De qualquer forma, vamos iniciar o que será o tópico principal deste artigo.

Filas, listas e árvores (VIII)

Diferente das filas e listas, uma árvore nos permite fazer algo, que de outra maneira seria bem mais complexo. Quando começamos estávamos terminamos de falar sobre o assunto listas, mencionei que seria muito bom se pudéssemos pesquisar em uma lista ordenada de modo a acelerar a própria pesquisa. Pois bem, para conseguir fazer isto, precisaríamos ter meios de dividir a lista no meio, a cada ciclo envolvido na pesquisa. Isto faria com que a pesquisa ocorresse no menor tempo possível. Porém ao montarmos esta mesma lista, com o objetivo de a dividir ao meio a cada ciclo da pesquisa, acabávamos construindo algo diferente da lista. Este algo recebeu a denominação de árvore.

Porém existe uma questão, que nos faz retornar a ideia original, lá nas listas. A questão em si, refere-se ao fato de qual seria, ou melhor dizendo, como seria feita a escolha do elemento que ficaria no ponto central da lista. Onde toda a pesquisa iria se iniciar. Pois bem, parece ser algo simples de ser feito, não é mesmo meu caro leitor? Já que se uma lista contém, por exemplo, 100 elementos, deveríamos utilizar o elemento 50. Pois este seria o ponto em que a lista seria dividida ao meio.

Porém, na prática as coisas não são tão simples assim, e acabamos tendo algo conhecido como problema de balanceamento. E isto tem uma referência bastante fácil de entender. Pois se trata de algo similar ao visto na imagem logo abaixo.

Imagem 01

Uma balança de dois pratos, como esta que estamos vendo na imagem 01, representa exatamente o problema que temos aqui. Caso um dos lados esteja mais pesado do que o outro lado. A balança irá pender para aquele lado. E considerando o fato de que, cada elemento presente em uma árvore tem o mesmo peso. Se um dos lados, contiver mais elementos, teremos este lado pendendo a balança em sua direção. Agora pense no seguinte fato. Quando mais a balança estiver inclinada em uma direção, maior o tempo gasto ou necessário para que algo seja feito naquele lado da balança. Visto que temos um número maior de elementos presentes ali. Este tipo de coisa degrada bastante qualquer tipo de operação que venha a ser feita em uma árvore. Existe um outro problema aqui, mas este iremos falar depois a respeito dele. Por hora vamos focar na questão da balança.

Ok, acho que consegui compreender a ideia. Porém não consigo entender uma coisa. Se estamos adicionando elementos em uma árvore, não podemos dizer onde estes elementos deverão ficar? Isto evitaria o desbalanceamento, ou pelo menos minimizaria o problema.

De certa forma, meu caro leitor, na teoria, sim, poderíamos dizer onde cada elemento deveria ficar. Porém na prática, isto é bem mais complicado do talvez você tenha imaginado. Para começar, até o momento temos trabalhado com elementos do tipo discreto. Isto objetivando a didática nos artigos. Porém na prática, o conteúdo que irá de fato existir em uma árvore, é bem mais complexo. Podendo assumir um grau gigantesco de complexidade.

Dentro de uma árvore real, os elementos NÃO SERÃO DO TIPO DISCRETOS, eles serão registros, ou estruturas de dados.

Agora você talvez esteja começando a entender o qual complicado a coisa começa a se tornar. Um exemplo simples, que poderia ser imaginado como sendo uma árvore, seria um banco de dados SQL. Na verdade ele é um pouco mais complicado do que isto. Mas serve como forma podermos exemplificar as coisas de modo que você possa imaginar que tipo de coisa estaria em uma árvore.

Vamos supor o seguinte cenário: Você tem uma quantidade de registros em formato SQL, onde temos uma ID, e alguns dados relacionados. Assim você decide que irá utilizar a ID para pesquisar dentro do banco de dados SQL. Se este banco de dados contiver 1.000.000 elementos presentes nele, você na pior das hipóteses precisará analisar os 1.000.000 elementos para encontrar o elemento procurado. Porém considerando que você esteja utilizando uma árvore perfeitamente balanceada para efetuar a procura, irá precisar ler no máximo 20 elementos para encontrar o elemento procurado. O que? Como assim? Que tipo de matemática maluca é esta que você está utilizando para precisar olhar no máximo 20 elementos para encontrar 1 dentro de um conjunto de 1.000.000 elementos. Cara me explica esta mágica, pois eu também quero saber como fazer isto.

Não é mágica, meu caro leitor, é matemática. Para entender, por que desta queda vertiginosa no número de elementos a ser observado a fim de encontrar um específico. Você precisa entender a própria natureza do balanceamento.

Supondo que você esteja utilizando um node que pode se ligar a dois outros. Assim como tem sido feito nos códigos até este momento. Isto faz com que cada camada, venha a ter um número de nodes correspondente a equação mostrada logo abaixo.

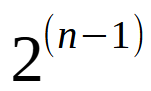
Imagem 02

Onde n representa a cada em questão. Por exemplo, na camada 1, teríamos apenas um node possível. Na camada 5, poderíamos ter 16 nodes possíveis. E assim por diante. De uma forma geral, esta expressão vista na imagem 02, pode ser remodelada de forma a se criar a expressão logo abaixo.

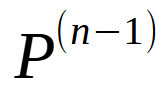
Imagem 03

Aqui P representa o número de ramos que pode sair de cada node. Por exemplo, se nossa árvore tivesse nodes, que poderia se ligar a outros 5 nodes, a expressão seria escrita como mostrado logo abaixo.

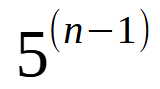
Imagem 04

Logo você percebe que a velocidade de acesso aumenta bastante. Porém isto tem um custo, que é a forma de você selecionar qual ramo deverá ser utilizado. Então vamos voltar ao nosso caso mais simples, onde temos apenas dois ramos para cada node. Neste caso com no máximo 20 camadas poderíamos manter os tais 1.000.000 elementos. Porém a quantidade de camadas a serem utilizadas, será sempre um fator menor que o número n usado na expressão. E o motivo para isto, é muito simples, já que o número de elementos em uma camada, será sempre somado como o número de elementos das camadas anteriores. Ou seja, na prática, iremos de fato precisar de 19 camadas para comportar os tais 1.000.000 elementos. Isto considerando uma árvore bem balanceada. Quem gosta de química, deve já ter entendido a ideia. Onde cada camada eletrônica somente pode comportar um dado número de elétrons. E para saber em que camada a ligação se deu, você precisará distribuir os elétrons de maneira adequada.

Ok, acho que conseguir entender agora, por que precisamos de tão poucas analises para encontrar o elemento desejado. De fato, sempre imaginei porque alguém iria perder tanto tempo implementando uma árvore, se no final isto apenas me parecia, uma pura bobagem. Mas vendo estes números, agora consigo entender a motivação.

De fato, meu caro leitor, muitas vezes, usamos algo menos adequado, justamente por falta de conhecimento. Mas quando entendemos as coisas, passamos a compreender a motivação para o desenvolvimento das mesmas. E desta maneira, finalmente você agora, consegue entender porque o balanceamento é tão importante em diversas situações.

Assim como o método de exclusão, que foi visto no artigo anterior, contém suas variações. Os métodos de balanceamento, também tem suas variações. Admito que escolher um para mostrar aqui no artigo, foi algo um tanto quanto difícil de ser feito. Já que a escolha do algoritmo a ser implementado, depende do motivo, ou melhor dizendo, do momento pelo qual você deseja balancear a árvore. Existe um algoritmo bons e bastante simples que permitem efetua o balanceamento conforme os elementos vão sendo inseridos na árvore. Apesar de ele ser muito fácil de implementar, o mesmo não é adequado para o propósito do artigo. Existem outros um tanto mais elaborado e com objetivos bastante interessantes. Então meu caro leitor, o que será mostrado aqui, é apenas uma entre tantas alternativas distintas e possíveis de serem efetuadas.

Mas para que tenhamos um algoritmo adequado para ser estudado aqui no artigo. Irei promover algumas mudanças no código da árvore que estamos modelando. Assim será mais simples focarmos apenas no algoritmo de balanceamento. Já que o objetivo aqui, será justamente focar neste algoritmo. Se todo o código fosse colocado junto, muito provavelmente você que esteja iniciando e querendo aprender como as coisas funcionam iria ficar um tanto quanto perdido em meio a tantas coisas juntas. Assim sendo o código no qual iremos trabalhar pode ser visto logo abaixo.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. //+------------------------------------------------------------------+
004. template <typename T>
005. class C_TreeNode
006. {
007.     private :
008. //+----------------+
009.         T           info;
010.         C_TreeNode  *left,
011.                     *right;
012. //+----------------+
013.     public  :
014. //+----------------+
015.         C_TreeNode(T arg)
016.             :left(NULL),
017.             right(NULL),
018.             info(arg)
019.         {}
020. //+----------------+
021.         void SetLeft(C_TreeNode *ptr) { left = ptr; }
022. //+----------------+
023.         void SetRight(C_TreeNode *ptr) { right = ptr; }
024. //+----------------+
025.         T GetInfo(void) const { return info; }
026. //+----------------+
027.         C_TreeNode *GetLeft(void) const { return left; }
028. //+----------------+
029.         C_TreeNode *GetRight(void) const { return right; }
030. //+----------------+
031. };
032. //+------------------------------------------------------------------+
033. #define C_TreeNode C_TreeNode<T>
034. template <typename T>
035. class C_Tree
036. {
037. //+----------------+
038.     #define def_InfoToString(A) (A != NULL ? StringFormat("%d ", (*A).GetInfo()) : "")
039.     enum E_SEQ {eInOrder, ePreOrder, ePostOrder, eDestroy};
040. //+----------------+
041.     private :
042.         C_TreeNode *root;
043.         string      m_szInfo;
044. //+----------------+
045.         C_TreeNode *Insert(C_TreeNode *ptr, T info)
046.         {
047.             if (ptr == NULL)
048.                 return new C_TreeNode(info);
049. 
050.             if (info < (*ptr).GetInfo()) (*ptr).SetLeft(Insert((*ptr).GetLeft(), info));
051.             else (*ptr).SetRight(Insert((*ptr).GetRight(), info));
052. 
053.             return ptr;
054.         }
055. //+----------------+
056.         void Extra(C_TreeNode *ptr, const E_SEQ type)
057.         {
058.             if (ptr == NULL) return;
059. 
060.             switch (type)
061.             {
062.                 case eInOrder   :
063.                 case ePostOrder :
064.                 case eDestroy   :
065.                     Extra((*ptr).GetLeft(), type);
066.                     if (type == eInOrder) break;
067.                     Extra((*ptr).GetRight(), type);
068.             }
069.             m_szInfo += def_InfoToString(ptr);
070.             switch (type)
071.             {
072.                 case ePreOrder  :
073.                     Extra((*ptr).GetLeft(), type);
074.                 case eInOrder   :
075.                     Extra((*ptr).GetRight(), type);
076.                     break;
077.                 case eDestroy   :
078.                     delete ptr;
079.             }
080.         }
081. //+----------------+
082.     public  :
083. //+----------------+
084.         C_Tree()
085.             :root(NULL)
086.         {}
087. //+----------------+
088.         ~C_Tree()
089.         {
090.             Extra(root, eDestroy);
091.         }
092. //+----------------+
093.         void Store(T info)
094.         {
095.             if (root == NULL) root = Insert(root, info);
096.             else Insert(root, info);
097.         }
098. //+----------------+
099.         string In_Order(void)
100.         {
101.             m_szInfo = "In Order: ";
102.             Extra(root, eInOrder);
103.             
104.             return m_szInfo;
105.         }
106. //+----------------+
107.         string Pre_Order(void)
108.         {
109.             m_szInfo = "Pre Order: ";
110.             Extra(root, ePreOrder);
111. 
112.             return m_szInfo;
113.         }
114. //+----------------+
115.         string Post_Order(void)
116.         {
117.             m_szInfo = "Post Order: ";
118.             Extra(root, ePostOrder);
119. 
120.             return m_szInfo;
121.         }
122. //+----------------+
123.     #undef def_InfoToString
124. //+----------------+
125. };
126. #undef C_TreeNode
127. //+------------------------------------------------------------------+
128. void OnStart(void)
129. {
130.     C_Tree <int> Tree;
131. 
132.     Tree.Store(10);
133.     Tree.Store(-6);
134.     Tree.Store(47);
135.     Tree.Store(35);
136.     Tree.Store(51);
137.     Tree.Store(90);
138.     Tree.Store(85);
139.     Tree.Store(40);
140. 
141.     Print(Tree.In_Order());
142.     Print(Tree.Pre_Order());
143.     Print(Tree.Post_Order());
144. }
145. //+------------------------------------------------------------------+

Código 01

Neste código 01, você pode notar que removi algumas partes a fim de tornar o código mais adequado. Ao mesmo tempo, também foram feitos alguns pequenos ajustes no código. A fim de o deixar o mais enxuto quanto foi possível fazer. De qualquer forma o resultado final é o que você pode observar na imagem logo abaixo.

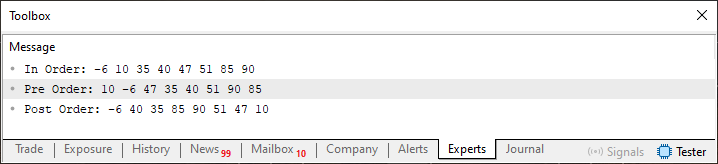
Imagem 05

Agora com base no conhecimento demonstrado no artigo anterior, você claramente irá conseguir olhar esta imagem 05 e pensar em como a árvore se encontra construída. É extremamente importante que você consiga fazer isto. Caso contrário, o que será visto e implementado a seguir não fará sentido algum. Mas independente disto, você claramente consegue notar que esta árvore, mostrada na imagem 05 está desbalanceada. A pergunta é: O quanto ela está desbalanceada?

Bem esta é a parte interessante e divertida deste artigo. Pois para saber o quanto esta árvore está desbalanceada, você primeira precisa saber como ela se encontra construída. Porém, mesmo sem saber disto, podemos implementar algum código com objetivo de descobrir o quanto a árvore está desbalanceada. Fazer isto, é algo bem simples e direto. Tudo que precisamos fazer é navegar até a folha mais distante da raiz. Primeiro por um ramo, seja ele o esquerda ou direto. Depois pelo outro ramo. Se a árvore estiver perfeitamente balanceada, ambas distâncias serão iguais. Assim se subtrairmos a quantidade de camadas, entre a raiz e a folha mais distante, termos um valor. Que será zero caso a árvore esteja balanceada, ou um valor qualquer, caso ela esteja desbalanceada. Para verificar isto, vamos utilizar o código logo abaixo.

001. //+------------------------------------------------------------------+
002. #property copyright "Daniel Jose"
003. //+------------------------------------------------------------------+
004. template <typename T>
005. class C_TreeNode
006. {
007.     private :
008. //+----------------+
009.         T           info;
010.         C_TreeNode  *left,
011.                     *right;
012. //+----------------+
013.     public  :
014. //+----------------+
015.         C_TreeNode(T arg)
016.             :left(NULL),
017.             right(NULL),
018.             info(arg)
019.         {}
020. //+----------------+
021.         void SetLeft(C_TreeNode *ptr) { left = ptr; }
022. //+----------------+
023.         void SetRight(C_TreeNode *ptr) { right = ptr; }
024. //+----------------+
025.         T GetInfo(void) const { return info; }
026. //+----------------+
027.         C_TreeNode *GetLeft(void) const { return left; }
028. //+----------------+
029.         C_TreeNode *GetRight(void) const { return right; }
030. //+----------------+
031. };
032. //+------------------------------------------------------------------+
033. #define C_TreeNode C_TreeNode<T>
034. template <typename T>
035. class C_Tree
036. {
037. //+----------------+
038.     #define def_InfoToString(A) (A != NULL ? StringFormat("%d ", (*A).GetInfo()) : "")
039.     enum E_SEQ {eInOrder, ePreOrder, ePostOrder, eDestroy};
040. //+----------------+
041.     private :
042.         C_TreeNode *root;
043.         string      m_szInfo;
044. //+----------------+
045.         int countL(C_TreeNode *ptr)
046.         {
047.             int count = 0;
048. 
049.             while ((*ptr).GetLeft() != NULL)
050.             {
051.                 ptr = (*ptr).GetLeft();
052.                 count++;
053.                 if (((*ptr).GetLeft() == NULL) && ((*ptr).GetRight() != NULL)) while ((*ptr).GetRight() != NULL)
054.                 {
055.                     ptr = (*ptr).GetRight();
056.                     count++;
057.                 }
058.             }
059. 
060.             return count;
061.         }
062. //+----------------+
063.         int countR(C_TreeNode *ptr)
064.         {
065.             int count = 0;
066. 
067.             while ((*ptr).GetRight() != NULL)
068.             {
069.                 ptr = (*ptr).GetRight();
070.                 count++;
071.                 if (((*ptr).GetRight() == NULL) && ((*ptr).GetLeft() != NULL)) while ((*ptr).GetLeft() != NULL)
072.                 {
073.                     ptr = (*ptr).GetLeft();
074.                     count++;
075.                 }
076.             }
077. 
078.             return count;
079.         }
080. //+----------------+
081.         C_TreeNode *Insert(C_TreeNode *ptr, T info)
082.         {
083.             if (ptr == NULL)
084.                 return new C_TreeNode(info);
085. 
086.             if (info < (*ptr).GetInfo()) (*ptr).SetLeft(Insert((*ptr).GetLeft(), info));
087.             else (*ptr).SetRight(Insert((*ptr).GetRight(), info));
088. 
089.             return ptr;
090.         }
091. //+----------------+
092.         void Seq(C_TreeNode *ptr, const E_SEQ type)
093.         {
094.             if (ptr == NULL) return;
095. 
096.             switch (type)
097.             {
098.                 case eInOrder   :
099.                 case ePostOrder :
100.                 case eDestroy   :
101.                     Seq((*ptr).GetLeft(), type);
102.                     if (type == eInOrder) break;
103.                     Seq((*ptr).GetRight(), type);
104.             }
105.             m_szInfo += def_InfoToString(ptr);
106.             switch (type)
107.             {
108.                 case ePreOrder  :
109.                     Seq((*ptr).GetLeft(), type);
110.                 case eInOrder   :
111.                     Seq((*ptr).GetRight(), type);
112.                     break;
113.                 case eDestroy   :
114.                     delete ptr;
115.             }
116.         }
117. //+----------------+
118.     public  :
119. //+----------------+
120.         C_Tree()
121.             :root(NULL)
122.         {}
123. //+----------------+
124.         ~C_Tree()
125.         {
126.             Seq(root, eDestroy);
127.         }
128. //+----------------+
129.         void Store(T info)
130.         {
131.             if (root == NULL) root = Insert(root, info);
132.             else Insert(root, info);
133.         }
134. //+----------------+
135.         void CheckBalance(void)
136.         {
137.             Print("Balance: ", countR(root) - countL(root));
138.         }
139. //+----------------+
140.         string In_Order(void)
141.         {
142.             m_szInfo = "In Order: ";
143.             Seq(root, eInOrder);
144.             
145.             return m_szInfo;
146.         }
147. //+----------------+
148.         string Pre_Order(void)
149.         {
150.             m_szInfo = "Pre Order: ";
151.             Seq(root, ePreOrder);
152. 
153.             return m_szInfo;
154.         }
155. //+----------------+
156.         string Post_Order(void)
157.         {
158.             m_szInfo = "Post Order: ";
159.             Seq(root, ePostOrder);
160. 
161.             return m_szInfo;
162.         }
163. //+----------------+
164.     #undef def_InfoToString
165. //+----------------+
166. };
167. #undef C_TreeNode
168. //+------------------------------------------------------------------+
169. void OnStart(void)
170. {
171.     C_Tree <int> Tree;
172. 
173.     Tree.Store(10);
174.     Tree.Store(-6);
175.     Tree.Store(47);
176.     Tree.Store(35);
177.     Tree.Store(51);
178.     Tree.Store(90);
179.     Tree.Store(85);
180.     Tree.Store(40);
181. 
182.     Print(Tree.In_Order());
183.     Print(Tree.Pre_Order());
184.     Print(Tree.Post_Order());
185.     
186.     Tree.CheckBalance();
187. }
188. //+------------------------------------------------------------------+

Código 02

Ao executar este código 02, você irá ver o resultado mostrado logo abaixo.

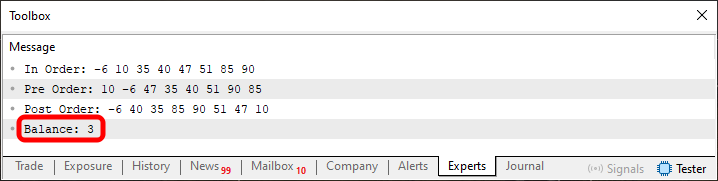
Imagem 06

Note que estou destacando uma informação aqui, na imagem 06. Esta representa exatamente o valor de balanço da árvore. Como o valor é positivo, temos uma árvore cujo ramo da direita é maior que o ramo da esquerda. No caso, o ramo da direita contém três camadas a mais que o ramo da esquerda. E é isto que esta informação destacada, está nos dizendo. Mas como eu posso ter certeza de que você não está me enganando? Bem, meu caro leitor, no artigo anterior expliquei como você pode transformar estas informações vistas na imagem 05 e 06 em uma árvore. Faça isto e você saberá como o código conseguiu saber em quantas camadas a árvore está desbalanceada. Somente assim, este código 02, passará a fazer sentido para você. Como quero que você procure estudar os artigos, não vou mostrar a imagem da árvore que estas imagens 05 e 06 mostram como a árvore está construída.

Muito bem, agora voltando ao código, podemos observar, que para fazer esta contabilidade, utilizamos duas funções. Uma está implementada na linha 45 e a outra na linha 63. A única diferença entre elas é qual o ramo iremos iniciar nossa busca. Como ambas são muito parecidas, podemos unir as mesmas em um código comum. Este é visto no fragmento logo abaixo.

                   .
                   .
                   .
044. //+----------------+
045.         int countLayers(C_TreeNode *ptr, const bool branchR)
046.         {
047.             int count = 0;
048. 
049.             while ((branchR ? (*ptr).GetRight() : (*ptr).GetLeft()) != NULL)
050.             {
051.                 ptr = (branchR ? (*ptr).GetRight() : (*ptr).GetLeft());
052.                 count++;
053.                 if (((branchR?(*ptr).GetRight():(*ptr).GetLeft())==NULL)&&((branchR?(*ptr).GetLeft():(*ptr).GetRight())!= NULL)) while((branchR?(*ptr).GetLeft():(*ptr).GetRight())!= NULL)
054.                 {
055.                     ptr = (branchR ? (*ptr).GetLeft() : (*ptr).GetRight());
056.                     count++;
057.                 }
058.             }
059. 
060.             return count;
061.         }
062. //+----------------+
                   .
                   .
                   .
116. //+----------------+
117.         void CheckBalance(void)
118.         {
119.             Print("Balance: ", countLayers(root, true) - countLayers(root, false));
120.         }
121. //+----------------+
                   .
                   .
                   .

Fragmento 01

Como todo o restante do código permanece inalterado não vejo motivo em ficar repetindo ele a todo momento. Assim vendo apenas estas partes que forma modificadas ficará mais simples focarmos no que realmente importa. Ok, a contabilidade de balanceamento está sendo executado. Agora vem a pergunta: No que isto irá nos ajudar aqui? Bem, isto que fizemos até aqui, foi apenas uma parte do que realmente precisamos fazer. Como agora você já sabe que temos como contabilizar cada camada a fim de conhecer o balanceamento da árvore. Podemos começar a trabalhar na questão do próprio balanceamento. A questão agora é como podemos balancear a árvore? Bem para isto existem diversos meios possíveis. Cada qual com sua vantagem e desvantagem. Aqui iremos fazer um balanceamento por rotação.

O balanceamento por rotação é relativamente simples. Já que dependendo da forma como a árvore vai ficando desbalanceada ela naturalmente irá começar a pender para um dos lados. Então a ideia é, sempre que ela começar a pender para um dos lados, iremos compensar isto, girando algum ramo para uma outra posição, seja para a direita, seja para a esquerda. Mas, e é isto que é importante que você venha a entender. Quando estamos falando de gira o ramo para uma outra posição, estamos dizendo que parte da árvore será modificada, mantendo a própria simetria de construção. Ou seja, os elementos de maior valor ainda assim irão se manter de um lado e os elementos de menor valor irão se manter do outro lado.

Para deixar as coisas mais claras em sua mente, meu caro leitor, veja a imagem logo abaixo.

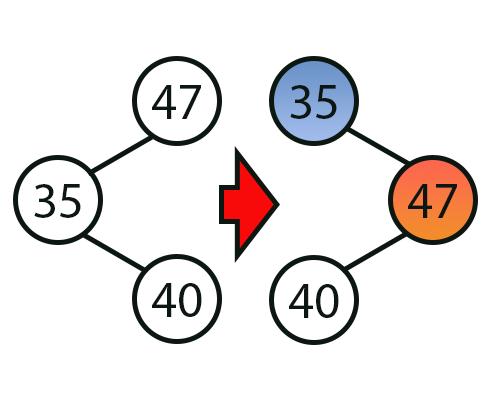
Imagem 07

A grande sacada aqui, meu caro leitor, e que você precisa compreender é que quando fazemos a rotação do node, iremos manter um mesmo padrão de análise. Isto quando formos fazer a navegação dentro da árvore. Ou seja, apesar do valor 35 ter mudado de lugar com o valor 47, a estrutura em si não mudou. Mas conforme vamos fazendo isto, em algum momento iremos fazer com que a raiz da árvore mude de um node para outro mais adequado. E quando isto ocorrer, a árvore que estava desbalanceada passará a ficar balanceada.

Mas espere um pouco aí. Antes que venhamos a implementar o código de rotação, estou um tanto quanto preocupado com relação a uma coisa aqui. Supondo que tenhamos uma árvore, que irá ter por exemplo 30 camadas, isto quando ela estiver perfeitamente balanceada. E estamos falando de uma árvore que imagino ser bem rasa, por assim dizer. Se precisarmos a cada rodada de adicionar um novo elemento tivermos de navegar por toda a árvore a fim de saber se ela está ou não pendendo para um sentido, a fim de ficar desbalanceada. Acabamos ficando um tanto quanto lentos. Isto por que, toda vez que tivermos de verificar o balanço da árvore, teremos de executar esta função vista no fragmento 01, no mínimo duas vezes. E ao meu entender, isto não parece muito adequado. Então meu amigo autor, mesmo que o código venha a ficar um pouco mais complexo. Será que não teria uma forma de sermos mais eficientes nesta questão do desbalanceamento? Isto de forma o próprio node venha a saber o quanto desbalanceado a árvore estaria?

Hum, deixe-me pensar um pouco. Sim, meu caro leitor, este seu questionamento é algo realmente bastante válido. E sim, existe de fato uma forma de tornar as coisas um pouco mais simples, por assim dizer. Mas para isto, precisaremos promover algumas mudanças. No entanto, ainda assim, espero que você tenha entendido qual será o plano a ser efetuado. De qualquer forma, vamos fazer o seguinte: Como aqui o objetivo é a didática, podemos adicionar uma variável extra no node. Isto a fim de contabilizar o quanto ele está desbalanceado. Mesmo que não venhamos ficar ajustando-o a todo momento. Será bem mais rápido saber se a árvore precisará ou não ser desbalanceada. E quando for preciso, iremos fazer isto de maneira o mais eficiente possível. Então a primeira coisa a ser feita é modificar a classe C_TreeNode, como mostrado no fragmento abaixo. Iremos trabalhar com fragmentos para facilitar a compreensão do que será feito.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. template <typename T>
05. class C_TreeNode
06. {
07.     private :
08. //+----------------+
09.         T           info;
10.         C_TreeNode  *left,
11.                     *right;
12.         int         prof;
13. //+----------------+
14.     public  :
15. //+----------------+
16.         C_TreeNode(T arg)
17.             :left(NULL),
18.             right(NULL),
19.             info(arg),
20.             prof(1)
21.         {}
22. //+----------------+
23.         void SetLeft(C_TreeNode *ptr) { left = ptr; }
24. //+----------------+
25.         void SetRight(C_TreeNode *ptr) { right = ptr; }
26. //+----------------+
27.         void SetProf(const int arg) { prof = arg; }
28. //+----------------+
29.         int GetProf(void) { return prof; }
30. //+----------------+
31.         T GetInfo(void) const { return info; }
32. //+----------------+
33.         C_TreeNode *GetLeft(void) const { return left; }
34. //+----------------+
35.         C_TreeNode *GetRight(void) const { return right; }
36. //+----------------+
37. };
38. //+------------------------------------------------------------------+
                   .
                   .
                   .

Fragmento 02

Ok, agora temos uma nova variável dentro da classe C_TreeNode. Esta variável, é previamente ajustada na linha 20. Porém este valor no qual estaremos inicializando esta variável, tem uma peculiaridade, que irei dizer depois, pois neste momento, não faria sentido em mencionar algo curioso que acontece quando mudamos o valor nesta linha 20.

Muito bem, a próxima coisa a implementarmos será uma forma de contabilizar qual é a profundidade que o node se encontra na árvore. Isto seria o equivalente ao que foi feito no fragmento 01. Porém, agora iremos fazer isto de uma forma muito mais eficiente. Para cumprir tal objetivo, usaremos o fragmento mostrado logo abaixo.

                   .
                   .
                   .
50. //+----------------+
51.         int WhatProf(C_TreeNode *ptr)
52.         {
53.             C_TreeNode *p1, *p2;
54. 
55.             p1 = (*ptr).GetLeft();
56.             p2 = (*ptr).GetRight();
57. 
58.             if (p1 && p2)
59.                 return MathMax((*p1).GetProf(), (*p2).GetProf()) + 1;
60.             return  (p1 && (p2 == NULL) ? (*p1).GetProf() : (*p2).GetProf()) + 1;
61.         }
62. //+----------------+
                   .
                   .
                   .

Fragmento 03

Beleza, note que esta função vista no fragmento estará nos retornando um valor, baseado no valor que estiver no node. Voltaremos a falar disto depois. Assim sendo, para saber se a árvore está ou não desbalanceada, precisaremos implementar um outro código. Porém, diferente do que foi feito antes, agora NÃO IREMOS FOCAR NA ÁRVORE E SIM NO NODE. Isto por que se o node estiver balanceado, a própria árvore também estará. Para fazer esta contabilização, iremos utilizar a função vista no fragmento logo abaixo.

                   .
                   .
                   .
62. //+----------------+
63.         int BalanceFactor(C_TreeNode *ptr)
64.         {
65.             C_TreeNode *p1, *p2;
66. 
67.             p1 = (*ptr).GetLeft();
68.             p2 = (*ptr).GetRight();
69. 
70.             if (p1 && p2) return ((*p1).GetProf() - (*p2).GetProf());
71.             return (p1 && (p2 == NULL) ? (*p1).GetProf() : -(*p2).GetProf());
72.         }
73. //+----------------+
                   .
                   .
                   .

Fragmento 04

Agora preste atenção meu caro leitor. Esta função vista no fragmento 04 irá retornar um valor que irá nos ajudar a estabelecer que tipo de rotação precisaremos fazer no node. Dependendo da maneira como o node esteja desajustado, precisaremos fazer uma entre quatro tipos diferentes de rotação. O código de cada uma destas rotações é visto logo abaixo.

                   .
                   .
                   .
073. //+----------------+
074.         C_TreeNode *Rotation_R(C_TreeNode *ptr)
075.         {
076.             C_TreeNode *p1;
077.             
078.             p1 = (*ptr).GetRight();
079.             (*ptr).SetRight((*p1).GetLeft());
080.             (*p1).SetLeft(ptr);
081. 
082.             return p1;
083.         }
084. //+----------------+
085.         C_TreeNode *Rotation_L(C_TreeNode *ptr)
086.         {
087.             C_TreeNode *p1;
088.             
089.             p1 = (*ptr).GetLeft();
090.             (*ptr).SetLeft((*p1).GetRight());
091.             (*p1).SetRight(ptr);
092. 
093.             return p1;
094.         }
095. //+----------------+
096.         C_TreeNode *Rotation_2R(C_TreeNode *ptr)
097.         {
098.             C_TreeNode *p1, *p2;
099. 
100.             p1 = (*ptr).GetRight();
101.             p2 = (*p1).GetLeft();
102.             (*ptr).SetRight((*p2).GetLeft());
103.             (*p1).SetLeft((*p2).GetRight());
104.             (*p2).SetLeft(ptr);
105.             (*p2).SetRight(p1);
106. 
107.             return p2;
108.         }
109. //+----------------+
110.         C_TreeNode *Rotation_2L(C_TreeNode *ptr)
111.         {
112.             C_TreeNode *p1, *p2;
113. 
114.             p1 = (*ptr).GetLeft();
115.             p2 = (*p1).GetRight();
116.             (*ptr).SetLeft((*p2).GetRight());
117.             (*p1).SetRight((*p2).GetLeft());
118.             (*p2).SetRight(ptr);
119.             (*p2).SetLeft(p1);
120. 
121.             return p2;
122.         }
123. //+----------------+
                   .
                   .
                   .

Fragmento 05

Muito bem, para entender este fragmento 05, vamos usar algumas imagens, que pode ser vista logo abaixo.

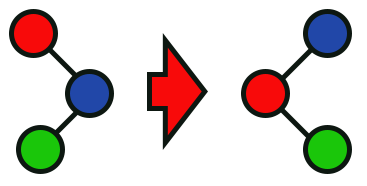
Imagem 08

Nesta imagem 08, você pode ver o que será efetuado pela função implementada na linha 74.

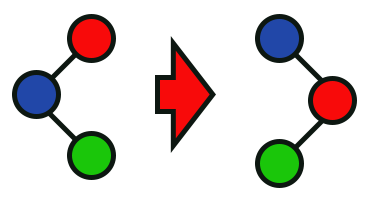
Imagem 09

Nesta imagem 09, podemos observar o que será feito quando a função da linha 85 for executada.

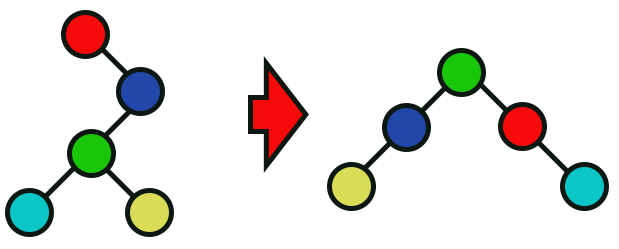
Imagem 10

Agora, já nesta imagem 10, podemos observar o que será executado na árvore, quando a função da linha 96 for executada.

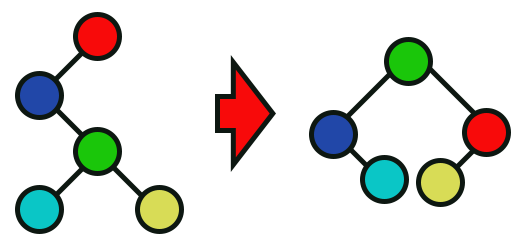
Imagem 11

E finalmente, nesta imagem 11, podemos claramente observar o que será feito pela função presente na linha 110. Em todos estes casos, o circulo vermelho é o node que está sendo passado como argumento para as funções vistas no fragmento 05.

Sei que isto parece como aquelas instruções para resolver um cubo mágico. Mas apesar de parecer algo bem estranho à primeira vista, estas quatro imagens vistas acima, conseguem de fato tornar uma árvore que originalmente seria totalmente desbalanceada em uma árvore perfeitamente balanceada. Com um detalhe: O próprio algoritmo irá tentar fazer com que todas as camadas fiquem completas. Isto é algo bem surpreendente, considerando o nível de simplicidade envolvida aqui.

Ok, mas como o código irá conseguir fazer com que a árvore venha a ser balanceada? Até agora não vi absolutamente nada que venha a tornar isto possível. Pois bem, meu caro leitor, agora vem o pulo do gato. Isto por que iremos precisar fazer uma pequena modificação no código responsável por inserir dados na árvore. Lembrando que até o presente momento, removemos temporariamente o código responsável por excluir elementos da árvore. Isto por que, quero que você entenda muito bem como a árvore irá ser balanceada, conforme iremos mexendo nela.

                   .
                   .
                   .
123. //+----------------+
124.         C_TreeNode *Insert(C_TreeNode *ptr, T info)
125.         {
126.             if (ptr == NULL)
127.                 return new C_TreeNode(info);
128. 
129.             if (info < (*ptr).GetInfo()) (*ptr).SetLeft(Insert((*ptr).GetLeft(), info));
130.             else (*ptr).SetRight(Insert((*ptr).GetRight(), info));
131. 
132.             (*ptr).SetProf(WhatProf(ptr));
133.             if ((BalanceFactor(ptr) == 2) && (BalanceFactor((*ptr).GetLeft()) == 1)) ptr = Rotation_L(ptr);
134.             else if ((BalanceFactor(ptr) == -2) && (BalanceFactor((*ptr).GetRight()) == -1)) ptr = Rotation_R(ptr);
135.             else if ((BalanceFactor(ptr) == -2) && (BalanceFactor((*ptr).GetRight()) == 1)) ptr = Rotation_2R(ptr);
136.             else if ((BalanceFactor(ptr) == 2) && (BalanceFactor((*ptr).GetLeft()) == -1)) ptr = Rotation_2L(ptr);
137. 
138.             return ptr;
139.         }
140. //+----------------+
                   .
                   .
                   .
177. //+----------------+
178.         void Store(T info)
179.         {
180.             root = Insert(root, info);
181.         }
182. //+----------------+
                   .
                   .
                   .
211. //+------------------------------------------------------------------+
212. void OnStart(void)
213. {
214.     C_Tree <int> Tree;
215. 
216.     Tree.Store(10);
217.     Tree.Store(-6);
218.     Tree.Store(47);
219.     Tree.Store(35);
220.     Tree.Store(51);
221.     Tree.Store(90);
222.     Tree.Store(85);
223.     Tree.Store(40);
224. 
225.     Print(Tree.In_Order());
226.     Print(Tree.Pre_Order());
227.     Print(Tree.Post_Order());
228. }
229. //+------------------------------------------------------------------+

Fragmento 06

Agora observe o que fizemos de mudança no código de inclusão de novos elementos na árvore. Note que conforme a árvore for sendo criada, a raiz dela poderá mudar. Por conta disto na linha 180, modificamos o processo de ajuste da raiz. Mas o que eu quero que você de fato tente entender, é justamente o que está sendo feito entre as linhas 132 até a linha 136. Pois é ali que estaremos ajustando e verificando como a árvore está sendo montada. É impressionante o nível de simplicidade do que está sendo feito aqui. Tanto que nem vou me dar ao trabalho de explicar o funcionamento deste fragmento de código. Só quero que você o observe e o admire. Pois isto é realmente muito belo. E não, não foi eu quem desenvolveu este algoritmo. Este algoritmo é conhecido como árvore AVL, em homenagem aos pesquisadores e matemáticos que propuseram este tipo de abordagem. São eles Adelson-Velsky e Landis que em 1962, publicaram o conceito que vocês podem ver, sendo implementado aqui em MQL5 puro.

Mas antes de terminarmos, quero chamar a sua atenção a um detalhe aqui, meu caro leitor. Lembra de uma coisa que mencionei lá no fragmento 02, na linha 20? Pois bem, se o código for compilado com a linha 20 indicado que a propriedade do node irá iniciar em um. Teremos o que você pode ver na imagem logo abaixo.

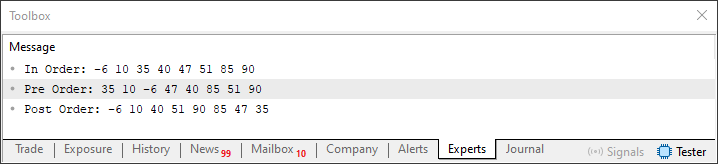
Imagem 12

Agora preste atenção ao seguinte ponto, pois esta é a parte maluca neste algoritmo. Se você modificar aquela mesma linha 20, vista no fragmento 02, para que a propriedade de profundidade se inicie em zero e não em um. Esta árvore que você pode observar, sendo modelada na imagem 12, irá ficar diferente. Então fazendo só e tão somente, esta única modificação no código, que você terá no anexo. O resultado será o que pode ser observado logo abaixo.

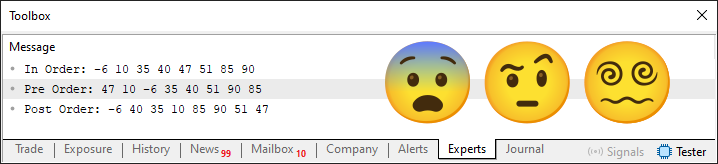
Imagem 13

Isto de fato é algo muito doido. E por conta disto, foi que decidi mostrar justamente este algoritmo aqui no artigo.

Ok, agora que você já sabe como a árvore vai sendo modificada conforme novos elementos vão sendo adicionados a ela. Que tal vermos o que seria uma proposta de código responsável por excluir elementos da árvore poderia vir a ser implementado? Pois bem, esta minha proposta, pode ser visualizada no fragmento logo abaixo.

142. //+----------------+
143.         C_TreeNode *Erase(C_TreeNode *ptr, T info)
144.         {
145.             C_TreeNode *tmp;
146.             int         i;
147. 
148.             if (((*ptr).GetLeft() == NULL) && ((*ptr).GetRight() == NULL))
149.             {
150.                 delete ptr;
151.                 return NULL;
152.             }
153.             if ((*ptr).GetInfo() < info) (*ptr).SetRight(Erase((*ptr).GetRight(), info)); else
154.             if ((*ptr).GetInfo() > info) (*ptr).SetLeft(Erase((*ptr).GetLeft(), info)); else
155.             {
156.                 if ((*ptr).GetLeft() != NULL)
157.                 {
158.                     tmp = (*ptr).GetLeft();
159.                     while ((*tmp).GetRight() != NULL) tmp = (*tmp).GetRight();
160.                     (*ptr).SetInfo((*tmp).GetInfo());
161.                     (*ptr).SetLeft(Erase((*ptr).GetLeft(), (*tmp).GetInfo()));
162.                 }else
163.                 {
164.                     tmp = (*ptr).GetRight();
165.                     while ((*tmp).GetLeft() != NULL) tmp = (*tmp).GetLeft();
166.                     (*ptr).SetInfo((*tmp).GetInfo());
167.                     (*ptr).SetRight(Erase((*ptr).GetRight(), (*tmp).GetInfo()));
168.                 }
169.             }
170.             i = BalanceFactor(ptr);
171.             if (i > 1) ptr = (BalanceFactor((*ptr).GetLeft()) >= 0 ? Rotation_L(ptr) : Rotation_2L(ptr)); 
172.             else if (i < -1) ptr = (BalanceFactor((*ptr).GetRight()) <= 0 ? Rotation_R(ptr) : Rotation_2R(ptr)); 
173. 
174.             return ptr;
175.         }
176. //+----------------+
                   .
                   .
                   .
242. //+----------------+
243.         void DeleteNode(const T info)
244.         {
245.             root = Erase(root, info);
246.         }
247. //+----------------+
                   .
                   .
                   .
252. //+------------------------------------------------------------------+
253. void OnStart(void)
254. {
255.     C_Tree <int> Tree;
256. 
257.     Tree.Store(10);
258.     Tree.Store(-6);
259.     Tree.Store(47);
260.     Tree.Store(35);
261.     Tree.Store(51);
262.     Tree.Store(90);
263.     Tree.Store(85);
264.     Tree.Store(40);
265. 
266.     Print(Tree.In_Order());
267.     Print(Tree.Pre_Order());
268.     Print(Tree.Post_Order());
269. 
270.     Tree.DeleteNode(10);
271.     Tree.DeleteNode(-6);
272.     Print("-----------");
273.     Print(Tree.In_Order());
274.     Print(Tree.Pre_Order());
275.     Print(Tree.Post_Order());
276. }
277. //+------------------------------------------------------------------+

Fragmento 07

É claro que algumas outras partes do código passaram por alguns ajustes, para evitar de ele quebrar quando tentarmos remover algum node. Porém, como são pequenos ajustes, e você terá o código na íntegra no anexo, para poder estudar como o mesmo funciona. Não acho necessário, mostrar e tão pouco explicar os ajustes que foram feitos. No entanto, quero que você observe e veja que nas linhas 270 e 271 estamos removendo completamente o que seria o ramo esquerdo da árvore. Sem que venhamos a fazer um balanceamento da árvore, não teremos nenhum tipo de elemento presente no ramo esquerdo. Isto partindo da raiz. Porém, como estaremos fazendo um novo balanceando a árvore, o resultado é um pouco diferente. No caso ele pode ser observado na imagem logo abaixo.

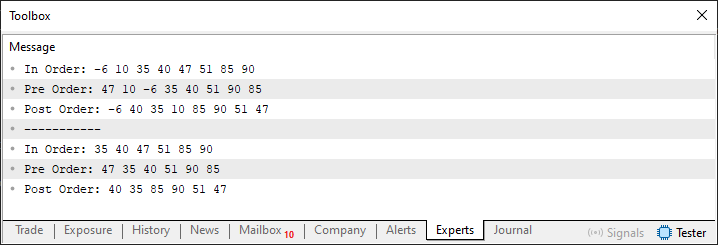
Imagem 14

Considerações finais

Neste artigo, fizemos a demonstração do que seria um algoritmo de balanceamento de uma árvore. Tal mecanismo visto neste artigo é apenas um entre diversos algoritmos possíveis de serem implementados. E mesmo este algoritmo mostrado aqui, é apenas o que seria a minha proposta para implementar o mesmo. Existem forma mais ou menos elaboradas de se fazer o mesmo tipo de implementação, isto visando ter um desempenho melhor, ou um balanceamento mais adequado. Porém, o que realmente importa aqui, é que você consiga compreender a importância e como poderia ser feito o balanceamento de uma árvore. A forma de fazer isto pouco importa. Desde que você consiga entender que este balanceamento pode melhor ou prejudicar de alguma forma a parte referente a pesquisa que será feita na árvore.

Esta parte referente a pesquisa, ou estudo utilizando uma árvore. É algo muito interessante. Porém vamos ver isto em um outro momento. Já que por hora acredito que você precise de um tempo para realmente assimilar tudo que foi visto e feito até este momento. Assim, no próximo artigo, iremos tratar de um outro assunto. Dando assim tempo para que você estude com calma este material visto até aqui.

Além do mais, precisamos ver outras coisas que tornarão a implementação de árvores algo bem mais simples é fácil. Coisa que será necessário quando formos falar sobre trabalhos de pesquisa na mesma.

Arquivo MQ5	Descrição
Code 01	Árvore simples
Code 02	Árvore simples
Code 03	Árvore simples
Code 04	Árvore simples