初級から中級まで：浮動小数点

はじめに

前回の「初級から中級まで：定義(II)」では、マクロの重要性と、それを効果的に使ってコードをより読みやすくする方法について解説しました。

さて、これまでに議論した内容を踏まえれば、浮動小数点数がどのように動作するかを説明するための十分な材料と適切な道具が揃ったことになります。多くの人は、状況によってdoubleやfloatの値が最適だと考えています。しかし、この型の値には、多くの人にとって、特にプログラマー以外の人にとっては理解しにくい問題があります。

そして、このような値はMQL5でも広く使われており、浮動小数点がほぼ標準となっている情報を扱う際には、この型の値がCPUによってどのように処理されるかをしっかり理解することが必要です。

なぜこう言うのかというと、2.5のような小数点付きの数は理解しやすく、他の値と混同されることはほとんどないからです。しかし、計算の話になると事情はそう単純ではありません。実際、浮動小数点数は多くの状況で非常に便利です。しかし、それらを整数と同じように扱ったり、同じように理解したりしてはいけません。

基本的に、多くの方は浮動小数点数を2種類の表記で扱ったことがあるかもしれません。一つは、1-e2のように値を表す科学的表記法で、もうひとつは0.01のようなより一般的な算術表記です。両者の値は大きさとしては同じですが、表記方法が異なります。同様に、同じ値を1/100のような分数表記で示すこともできます。

いずれの場合も、私たちが扱っている値は同じものです。ただし、異なるプログラムやプログラミング言語では、これらの値の扱い方が異なることに注意してください。

簡単な歴史

コンピューターが誕生した当初には、今日私たちが知るような浮動小数点数は存在していませんでした。正確には、浮動小数点数を扱う標準化された方法が存在しなかったのです。プログラマーやオペレーティングシステム、さらにはプログラムごとに、この型の数値の扱い方は非常に特有で個別のものでした。

1960～1970年代には、あるプログラムが他のプログラムと情報をやり取りして、このような値の計算を高速化する方法は存在しませんでした。想像してみてください。宇宙開発初期の頃、こうした数値が極めて重要であった時代に、当時のコンピュータで浮動小数点数を計算することは不可能でした。さらに、計算能力が得られるようになったとしても、多数のコンピュータに計算を分散させて高速化することも不可能でした。

その後、当時ほぼ市場を独占していたIBMが、このような値を表現する方法を提供し始めました。しかし、市場は提供されたものを必ずしも受け入れるわけではありません。そこで、他のメーカーも独自の方法で値を表現しました。その結果、本当に混沌とした状態になりました。やがて、IEEE (Institute of Electrical and Electronics Engineers)が介入し、現在のIEEE 754標準として知られる規格を制定することで整理されました。詳しく知りたい方のために、記事末の「リンク」欄に参考情報を掲載しています。

最初に制定された規格はIEEE 754-1985（英語）で、この問題全体を解決する試みでした。現在はより最新の標準が使われていますが、基本的には当初の方式に基づいています。

重要な点として、この標準は分散計算や数値の正規化を可能にすることを目的としていますが、標準が使われない場合や、他の原理で計算（厳密には分解）がおこなわれる場合もあります。これについては本稿の範囲外です。MQL5などの言語は、このIEEE 754標準を採用しています。

初期のCPUには浮動小数点計算能力がなかったため、FPU (Floating Point Unit)と呼ばれる専用プロセッサが別途存在しました。当時のFPUは単独で購入する必要があり、そのコストが常に使用に見合うわけではありませんでした。例として、FPUのモデル80387が挙げられます。いいえ、誤記ではありません。本質的に、このモデルは有名な80386、一般的には386と呼ばれるCPUに非常によく似ています。これは、IntelがCPU (80386)とFPU (80387)を区別するためのマーケティング的な命名でした。コンピュータは中央処理装置(CPU)だけで動作できますが、FPU単体では動作できません。FPUは浮動小数点計算専用に設計されているためです。

では、浮動小数点数にどのような問題があるのでしょうか。なぜこの記事全体がこのテーマに割かれているのでしょうか。その理由は、浮動小数点表現の仕組みを理解していないと、多くの誤りを犯す可能性があるということです。これはプログラミング技術の未熟さによるものではなく、計算結果を文字通りに受け取るべきだという考え方が誤っているためです。IEEE 754標準を使用している時点で、計算結果には潜在的な誤差が含まれることがあります。

一見すると不合理に思えるかもしれません。コンピュータは常に正確な値を返す機械であるはずだからです。しかし、特に金融市場でこうしたデータを用いて取引する場合、計算結果に誤差が含まれることは重大な問題になります。計算が誤っていれば、利益が見込める場合でも損失が発生する可能性があるからです。このため、浮動小数点数の理解は重要です。

浮動小数点に関連する側面の中には、本稿の目的においてそれほど重要でないものもあります。しかし、もうひとつ非常に重要で決定的なものがあります。それは丸めです。

多くの人は次のように言ったり、自慢したりします。 

私は計算で丸めを使わない。常に正確で誤差はない。

しかし、この考え方はプログラミングに対する完全な誤解を示しています。丸めはプログラマーが自らおこなう必要があるわけではありません。丸めは、プログラマーの意図に関わらず存在するものです。そのため、ここで紹介するリンク先の資料を必ず読むことが重要です。浮動小数点数の問題は、一つの記事だけで説明できるものではありません。覚えておいてください。このテーマは、コンピュータ技術の発展初期から多くの専門家が取り組んできた分野です。

ここでは、より単純な話に焦点を当てます。doubleやfloatが具体的に何であるかを理解することを目的とします。その他のデータ型は比較的簡単であり、前回の記事ですでに説明済みです。

浮動小数点数の表現

ここでは、実際にMQL5で使用されている型について解説します。この型では基本的にIEEE 754規格に従っています。この規格では、2つのフォーマット、より正確に言えば2つの精度が定められています。そして、浮動小数点数について話す場合、「フォーマット」や「使用ビット数」ではなく「精度」という用語を使うのが正しいです。しかし、これは多くの人にとってやや混乱を招く可能性があるため、ここでは「ビット数」という用語を用います。これはあくまで、読者がより理解しやすくするためと、以降の説明を簡単にするためです。私は、電子工学やチップ設計の広範な知識を持つ技術者や専門家に向けて話しているのではなく、MQL5言語のプログラミングに興味があり、知識を深めたいと考えている人々に向けて解説していることをご理解ください。

では、まず非常に簡単なコードを見てみましょう。しかし、単純に見えるこのコードを完全に理解するためには、これまでの連載記事で得た知識が必要です。それでは始めましょう。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

コード01

このコードは非常に興味深く、また実験してみるととても面白いものです。ただし、ここで実装しているのは、私たちが本当にやりたいことのうちの最初の部分に過ぎません。

注意してください。4行目では、どの型の値を浮動小数点数として使用するかを指定しています。double型かfloat型のどちらかを指定することができます。両者の違いは、それぞれが提供できる精度にあります。しかし、その詳細に入る前に、このコードが何をしているのかを理解しておきましょう。

型を宣言した後、メモリを読み取る方法を作るためにunionを使用します。そのために8行目を使います。unionの中では、10行目で変数を作成し、11行目で共有アクセス用の配列を作成します。これと似た構造については、前回の記事ですでに説明済みです。ここで何がおこなわれているのか、なぜこのunionを作るのか理解できない場合は、前の記事を参照してください。

ここで私たちにとって最も重要なのは14行目です。ここで表示したい値を設定しています。そして16行目は、メモリの内容を表示する方法を提供しています。これは現在の私たちの目的、つまりコンピュータが浮動小数点値を解釈する前に、メモリ内でどのように表現されているかを理解することに直結しています。

コード01を実行すると、下の画像に示すような結果が提供されます。

図01

うーん…この奇妙な16進数表現は一体何でしょうか。これはまさにコンピュータが浮動小数点値を解釈する方法であり、IEEE 754標準に従っています。重要な点として、この値はリトルエンディアン形式で表記されていることに注意してください。この形式については後ほど詳しく解説します。しかし今のところ理解しておくべきことは、この16進数の値は逆順に記録されており、右から左へ読み取る必要があるということです。

とはいえ、おそらく信じられないと思います。そこで、別のプログラムを使って確認してみましょう。ここでは16進エディタを使用します。HxDは最も簡単で無料の選択肢の一つです。図01の16進数フィールドに示された値を入力し、それをハイライトしてどの値が表現されているかを確認すると、下に示すようなイメージを見ることができます。

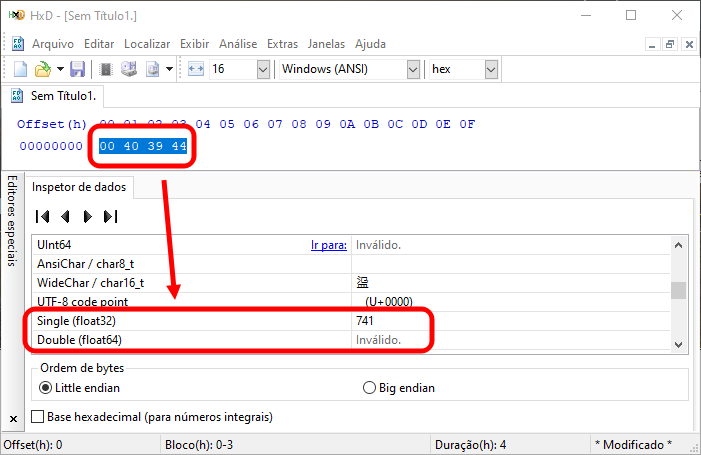
図02

注意してください。実際には、可視化できる期待される値があります。しかし、私自身はこのようなものを見る際には、開発環境の拡張機能を使うことを好みます。これにより、コンピュータにさまざまなプログラムをインストールする必要がなくなります。ただし、公平に言うと、HxDはインストールを必要としません。いずれにしても、私たちが確認できる内容は、以下の図の通りです。

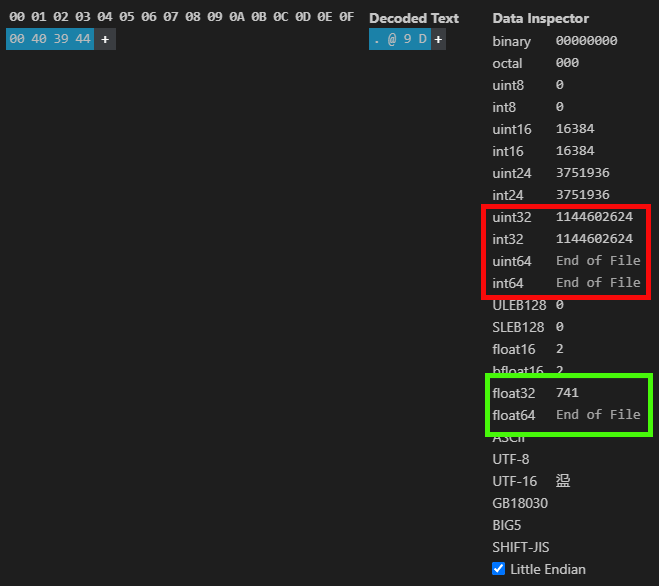
図03

ここで示したような情報は、MetaTrader 5でもHxDでも得ることができます。しかし、図03で私が示している内容をよく見てください。同じ浮動小数点値が、整数として表現すると異なる値になることに気づくでしょう。しかし、なぜそうなるのでしょうか。その理由は、コンピュータにとって、値が整数として表現されているか他の型として表現されているかは関係がないということです。コンピュータにとっては何の違いもありません。しかし、私たちやコンパイラにとっては基本的な問題です。データ型によって、合理的な結果が得られるか、それともまったく予期しない結果になるかが決まるのです。

とはいえ、先ほどコード01で考えた例は、単純なケースに過ぎません。ここで、コード01を少し異なる例に置き換えてみましょう。以下に示します。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

コード02

コード02はより複雑に見えるかもしれません。しかし、実際にはコード01と同じくらい単純です。ただし、ここでは浮動小数点値の表示に関して、いくつか追加のポイントを議論する機会があります。これは、4行目のおかげで可能になります。そこでは、単精度(float)型を使うのか、倍精度(double)型を使うのかを選択できるのです。しかし、上記のようにコードを実行すると、以下に示す結果が得られます。

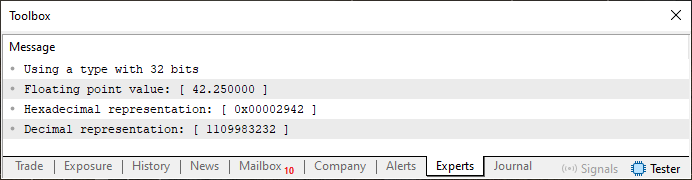
図04

そして、先ほど見たのと同じように、図04に示された指定値を使用すると、次の図に示される結果が得られます。

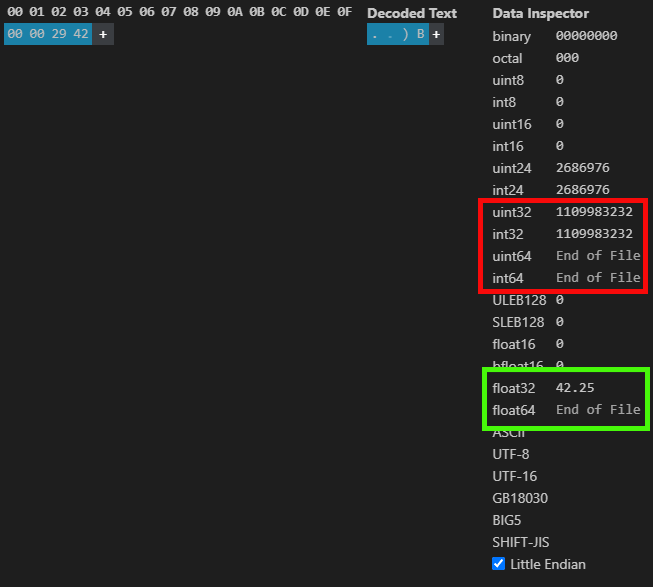
図05

つまり、ここでは確かに何かが起こっているのです。では、IEEE 754システムはどのように機能するのでしょうか。これを説明するために、システム自体の内部構造を少し掘り下げて見ていく必要があります。あまり複雑にしすぎないよう努めます。なぜなら、複雑にしてしまうと説明の試み自体が無意味になり、理解の妨げとなるからです。

当初から、そして現在も、IEEE 754には2つの形式があります。ひとつは単精度（32ビットを使用）、もうひとつは倍精度（64ビットを使用）です。両者の違いは「どちらがより正確か」ということではなく、扱える値の範囲にあります。したがって、「精度」という言葉はしばしば誤解を招きます。正しい用語であるとはいえ、私が好んで使わない理由はそこにあります。

下の図では、この標準で定義されている2種類の型を確認することができます。

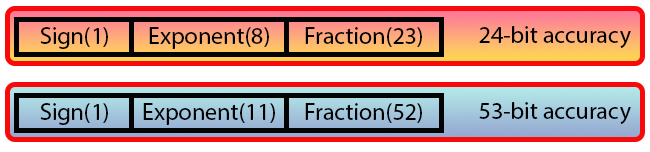
図06

「ちょっと待って…片方は32ビットでもう片方は64ビットを使うって言っていませんでしたか。図06ではどう見ても意味が分からないものが使われています。これらのデータや値はいったい何ですか。」

これがIEEE 754標準に従って浮動小数点数が表現される方法です。ここで見える値はそれぞれ1ビットです。これまでに見てきたものとは異なる幅で区切られているのに気づくと思います。しかし、それでもシステム自体を理解するうえで問題はありません。もっとも、CやC++の言語を使えば説明はさらに簡単になるでしょう。なぜならMQL5ではビット単位で名前を付けることができないからです。CやC++では可能ですが、MQL5ではできません。ただし、マクロや定義を利用することでこれらの言語に近づけることはできます。

そこで、この説明をこの記事の中で試みます。もしうまくいかなければ、改めて別の記事で正しく説明するつもりです。単なる表面的な説明にとどめたくありません。読者の皆さんに、本当に浮動小数点をコードで扱う際にどこに問題があるのかを理解してほしいのです。というのも、多くの人が、実際には不可能な計算を可能だと思い込み、信じ込んでいるのを見かけるからです。これは期待される結果と実際の結果の間にわずかなずれがあるためであり、事前に理解していないと問題を引き起こす可能性があります。

まず次のことから始めましょう。図06に示されたビット数を数えてみると、最初の形式は32ビット、次の形式は64ビットで構成されていることが分かります。ここから疑問が生じ始めるわけです。したがって、簡単にするために1つの形式に絞って考えましょう。両者の違いは調整時に使われる値に関係していますが、それについては後ほど触れます。

図06で「Sign」と示されたビットは符号ビットです。これはその値が負なのか正なのかを示します。整数型と同様に、一番左のビットが数が負か正かを教えてくれるのです。

次に符号ビット(Sign)に続くのは8ビットの「Exponent」です。この値は127というバイアスを生成し、それによって指数を符号化します。倍精度(double)の場合は11ビットが使われ、これにより1023というバイアスが作られます。「倍精度」という名前が付いてはいますが、ここでのバイアス値は大幅に大きくなることに注意してください。

しかし私たちにとって最も重要なのは、この指数の直後にあるフィールドです。これは「Fraction」と呼ばれ、提示される値の精度を決定します。32ビット（単精度）の場合、このフィールドは23ビットを持ち、これにより24ビットの精度が得られます。一方、倍精度では52ビットを持ち、53ビットの精度を実現します。ここでも前者の倍以上となるため、「倍精度」という言葉はやはり多少誤解を招きます。

さらに浮動小数点数の問題を掘り下げると、この「Fraction」と呼んだフィールドはしばしば「仮数」と呼ばれていることに気づくでしょう。仮数部こそが浮動小数点数の形成において鍵となる部分なのです。

ここには多くの要素が関わってきますが、あまりに技術的な細部を見せすぎると多くの人が興味を失ってしまうかもしれません。そこで説明をより楽しめるように、実際的な例に進みましょう。コード01では、14行目で741という値を浮動小数点に変換しました。この場合、32ビットの値、すなわち単精度フォーマットに変換しています。したがって、図06のオレンジ色の図式を使うことができます。ここではまず、このシンプルなモデルを理解できるよう集中してみてください。

最初のステップは741を2進数に変換することです。その方法はいくつかありますが、最も分かりやすいのは2で割っていくやり方です。もし2進数への変換方法を知らなくても心配いりません。この最初の値はとても単純なので、すぐに理解できるでしょう。図07はその方法を示しています

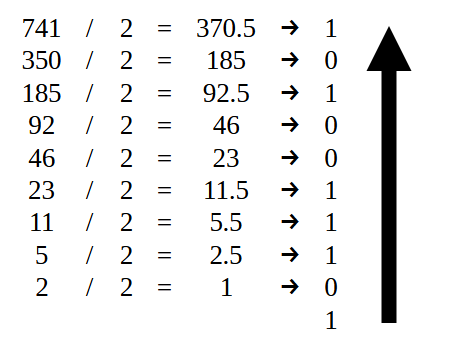
図07

すべての割り算を終えると、0と1の並びが得られます。しかし、値を正しく表記するためには矢印で示された順序で並べなければなりません。その結果が次の図に示されます。

図08

さて、図08に示されているものを得るのが最初のステップです。これが終わったら次のステップに進めます。それは、この2進数の値を浮動小数点数に変換することです。ここで注意が必要です。というのも、これは可能な限り最も単純なケースだからです。しかし、この単純なケースをよく理解することが、後でより複雑なケースを扱えるようになるために必要なのです。

次におこなうのは仮数、つまり小数部分を作ることです。そのためには、右端にある小数点を左へ移動させ、値が1のビットが1つだけ残るようにします。この変換をおこなうと、次の図のようになります。

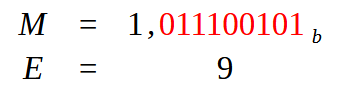
図09

ここで次の点を確認しましょう。Mは「仮数」と呼ばれる部分であり、浮動小数点数の小数部分です。Eは指数になります。では、この値9はどこから来たのでしょうか。これは仮数に赤く示された値が9個あるためです。しかし、この値9はまだ処理する必要があります。ここから変換の第3段階が始まります。どのアプローチを取るかによって、この値9の処理方法が異なり、それによって生成される値も異なります。これは浮動小数点数を16進数で表現するために必要な手順です。

ただし、この9をどう扱うかを考える前に、浮動小数点数の小数部分がどのように形成されるかを理解しておきましょう。

覚えていると思いますが、単精度では23ビット、倍精度では52ビットのFractionフィールドがありました。そして精度は単精度で24ビット、倍精度で53ビットになるのでした。では、この図09で黒く強調された値1のビットはどうでしょうか。これはFractionフィールドには存在しない、しかし「暗黙のビット」として仮定される追加の1です。つまり、Fractionフィールドは次のように構成されます。

図10

図10にある緑の0の数はFractionフィールドのビット数に依存します。残りを埋めるのに必要なだけの0が入ります。これで浮動小数点数の小数部分ができました。あとは指数部分を形成するだけです。値が正なのでSignフィールドは0になります。指数部分を作るためには、使用する精度の種類を考慮しなければなりません。単精度の場合、図09に示されたEの値（この場合は9）をバイアス値127に加えます。その結果136という値になります。この計算は次の図に示されています。

図11

これでようやく、741という数を浮動小数点形式で表す単精度値を構成できます。その値は次の図に示されています。

図12

さらに、この図12のビットを分割して16進数表現を作ると、図13のようになります。

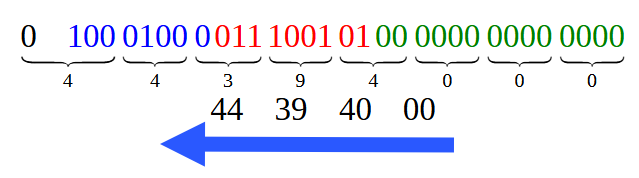
図13

図13に示された16進数の各値が図01で見たものと一致していることに注目してください。ただし、矢印で示された順序で読み取る必要があることを忘れないでください。  これは別の記事で扱う予定の特徴に関係しています。さて、これが最も単純なケースでした。しかしこの記事ではもうひとつ、少し複雑なケースについても扱いました。コード02で検討したケースです。ここでは本質的に小数点を含む値を扱います。この場合はどうすればよいのでしょうか。

実は、小数点を含む数値を扱う場合もそれほど大きくは変わりません。この場合は、2進数変換のステップを2つに分ければよいのです。ひとつは小数点より左側、もうひとつは右側です。複雑に思えるかもしれませんが、実際には非常に単純かつ論理的です。ただ、何をしているのかに注意を払う必要があります。

まず、小数点より左側の部分は図07に示された方法で変換します。つまり値42だけを使います。その結果が次の図です。

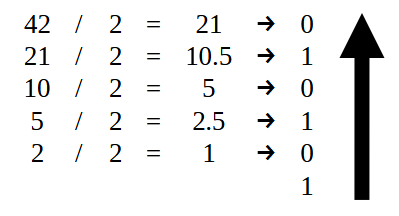
図14

次に、小数点より右側の部分を図15のように変換します。つまり0.25を取り、コード02で指定された値の小数部分を2進数に変換するのです。

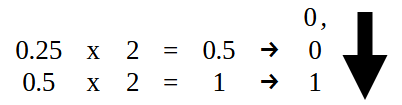
図15

これにより、42.25という数を2進数で表したものが次に示されます。

図16

図16ではすでに小数点があることに注目してください。これは次のステップ、つまり図09でおこなった仮数と指数の決定に影響します。すでに小数点が示されているので、左端に値1のビットが1つだけ残るようにシフトするだけでよいのです。図09と全く同じです。その結果が次の図になります。

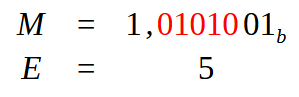
図17

図17で赤く示されている値は、小数点を正しい位置に持ってくるためにシフトされる部分です。したがって、指数を設定する値は5になります。またFractionフィールドを形成するための仮数もすでに得られています。単精度で計算すると次の結果になります。

図18

求められた16進数値が図04に示された値と完全に一致していることに注意してください。もちろん、矢印の方向に従い2バイトごとに読む必要があります。さて、もし倍精度を使った場合はどうなるでしょうか。つまり、コード02の4行目をこのディレクティブが適用されるようにアンコメントして、32ビットではなく64ビットを使用する、すなわちシステムに倍精度を適用する場合です。

この場合、図18と同じ結果になるでしょうか。実際のところ、ほぼ同じになります。小数部分は変わりません。ただし、倍精度では52ビットをすべて埋める必要があるため、Fractionフィールドに0を追加する必要があります。しかし指数は完全に異なります。なぜなら、単精度では127ですが、倍精度では1023になるからです。したがって、図18で見える青い指数部分だけが見た目で異なることになります。より分かりやすくするために、倍精度での値の入力がどのように見えるかを次の図に示します。

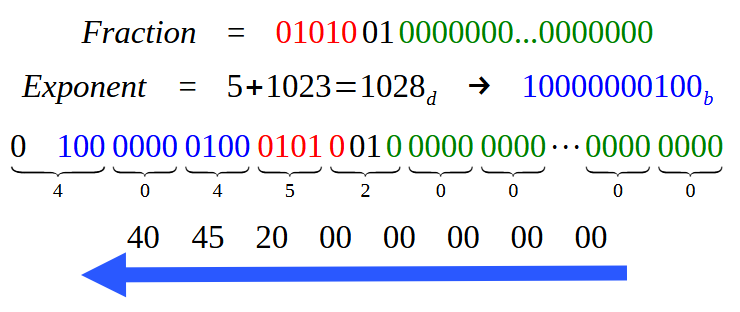
図19

そして、この見積りが正しいかどうかを確認するために、提案した変更を加えた状態でコード02を実行します。結果は以下のとおりになります。

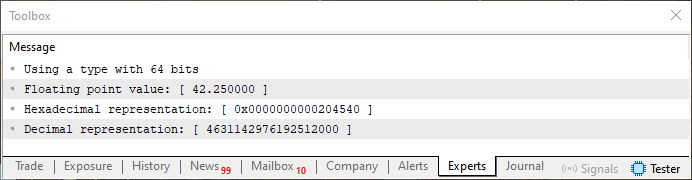
図20

最終的な考察

本記事では、浮動小数点値に関する簡単な入門として、メモリ上でのこの型の数値の表現方法や、この型の値をどのように扱うかについて考察しました。読者の皆さんにとっては、浮動小数点値に関するさまざまな側面に少し戸惑いを感じるかもしれません。そしてこれは驚くべきことではありません。私自身、この型のデータがどのように作られるのか、特にこのデータを用いてどのように計算をおこなうのかを理解するのに多くの時間を費やしました。ここでの主な目的は計算方法を詳しく説明することではありませんが、将来的には浮動小数点数を用いた計算方法を解説できるかもしれません。IEEE 754標準の観点から考えると、これは非常に興味深いテーマです。

もちろん、小数点を含む数値を表す他の形式や方法も存在します。しかし、MQL5は多くのプログラミング言語と同様に、本記事で扱った形式を使用しているため、この型のデータについて慎重に学習することをお勧めします。結局のところ、こうした数値はしばしば、私たちが計算していると考えている値を正確には表していないことがあります。そして、浮動小数点値の丸め方については、明確なルールがあるため、下記のリンクを参照して学習することをお勧めします。これは決して無意味ではありません。

ただし、最終的な判断は読者に委ねられます。本記事で取り上げた内容に基づけば、すでに浮動小数点数を用いて十分に作業することは可能です。しかし、丸め規則や表現可能・不可能な値のリストなどの追加的な側面は、高い精度や正確な値の使用を追求する場合にのみ必要です。今回の記事では必須ではありません。

リンク

• IEEE 754
• float16およびfloat8形式のONNXモデルを扱う