从基础到中级：浮点数

概述

在上一篇文章“从基础到中级：定义（二） ”中，我们讨论了宏的重要性以及如何有效地使用它们来使我们的代码更具可读性。

好吧，考虑到我们到目前为止讨论的一切，我们现在有足够的材料和足够的工具来解释浮点数是如何工作的。我知道很多人认为在不同的情况下，双精度或浮点值是最佳选择。然而，这种类型的值有一个问题，很少有人理解，尤其是那些非程序员。

由于这些值在 MQL5 中被广泛使用，并且我们处理的信息几乎是浮点数的共识，因此有必要很好地了解 CPU 是如何处理这类值的。

为什么这么说呢？很明显，像 2.5 这样的小数总是很容易理解的，因为没有人会把这类值与其他值混淆。但是，亲爱的读者，说到计算，事情并没有那么简单。事实上，浮点数在许多情况下都非常有用。然而，它们不应被视为或理解为整数。

基本上，你们中的许多人可能习惯于用两种类型的符号处理浮点数：一种是科学符号，我们记下 1-e2 这样的值，另一种是更常见的算术符号，我们记录 0.01 这样的值。这两个值的大小相等，但表示方法不同。同样，也有一种分数方式来记录相同的值，该值等于 1/100。

请注意，在所有情况下，我们谈论的都是相同的值。然而，不同的程序或编程语言对这些值的处理方式不同。

简史

在计算的早期，我们今天所知道的浮点数并不存在。或者更确切地说，没有标准化的方法来处理它们。每个程序员、每个操作系统，甚至每个程序都以非常具体和个性化的方式处理这类数字。

在 20 世纪 60 年代和 70 年代，一个程序无法与另一个程序交互以共享和加速这些值的分解。试想一下：在太空时代的初期，当这些数字至关重要时，在当时操作的计算机上计算浮点值是不可能的。即使有了这样的能力，也不可能将任务分配给大量计算机以加快计算速度。

随后，当时几乎控制了整个市场的 IBM 开始提供一种方式来表示这些值。但市场并不总是接受它所提供的东西。因此，其他制造商也开发了自己的方式以表示这些值。这真是一片混乱。直到某个时候，电气电子工程师协会 (IEEE) 开始通过建立现在称为 IEEE 754 的标准来清理一切。在本文的最后，在“链接”部分，我将为那些想更深入地研究这个主题的人留下一些链接。

第一个建立的标准是 IEEE 754-1985 ，旨在解决整个问题。如今，我们使用的是一个更新的标准，但它是基于最初建立的相同方案。

一个重要的细节是：尽管存在旨在规范化和实现分布式因式分解的标准，但在某些情况下，该标准没有被使用，计算 —— 或者更确切地说，分解 —— 是根据其他原则进行的，我们在这里不会考虑这些原则，因为它们完全超出了本主题的范围。这是因为 MQL5 与其他几种语言一样，使用了 IEEE 754 标准。

最初，CPU 无法处理这种类型的计算，因此有一个单独的处理器，当时称为 FPU，专门用于此目的。该 FPU 是单独购买的，因为其成本并不总是证明其使用是合理的。型号 80387 可以作为 FPU 的一个例子。是的，这不是打字错误。本质上，该模型与著名的 80386（通常称为 386）非常相似。但这更多的是英特尔的一种营销解决方案，以区分 CPU（80386）和 FPU（80387）。计算机只能与中央处理器一起工作，而不能单独与 FPU 一起工作，因为后者仅用于执行浮点计算。

好的，但这个浮点数有什么问题吗？为什么整篇文章只讨论这个主题？原因是，如果你不了解浮点数表示是如何工作的，你可能会犯很多错误。不是因为编程不好，而是因为所执行的计算应该按字面意思进行，而使用 IEEE 754 标准的事实已经在计算的最终值中产生了潜在的误差。

这似乎很荒谬，因为计算机是必须始终为我们提供准确值的机器。说操作结果包含错误并不严重，这是不可接受的，尤其是当我们的目标是使用这些数据在金融市场上进行交易时。如果我们的计算有误，我们可能会亏损，即使一切都指向盈利的可能性。正是由于这个原因，这篇文章很重要。

在我们要做的框架内，有许多与浮点数相关的方面并不那么重要。但还有一件事非常重要和关键，那就是舍入。

我知道很多人说，甚至吹嘘，声称： 

我在计算中不使用舍入。它们总是准确且无错误的。

但在我看来，这个特殊的想法表明了对编程的完全和彻底的误解，这导致人们做出错误的假设，而事实上一切都不一样。舍入不一定必须由程序员完成。它只是存在而不管程序员是否愿意。因此，请务必阅读我在本文末尾留下的链接上的材料。我这样做是因为浮点数的问题无法在一篇文章中解释。记住：从计算技术发展的一开始，就有专家在研究这个话题。

在这里，我们将研究另一种类型的东西，它要简单得多，并且专注于准确理解 double 或 float 是什么，因为所有其他数据类型都要简单得得多，在前面的文章中已经解释过了。

浮点数的表示

因此，在这里我们将讨论 MQL5 中实际使用的类型。在这种类型中，我们基本上遵循 IEEE 754 规范，该规范提供了两种格式，或者更确切地说，两种精度。是的，当我们谈论浮点数时，使用“精度”一词而不是“格式”或“所涉及的位数”是正确的。但为了不使事情复杂化，因为这可能会让许多人感到困惑，我们在这里使用“位数”一词，但这只是为了让大多数读者更好地理解材料并简化进一步的解释。我相信，我不是在向在电子和芯片设计领域拥有广泛而全面知识的工程师或专家发表演讲，而是向那些对 MQL5 语言编程感兴趣并渴望知识的人发表演讲。

首先，让我们来看一个非常简单的代码。然而，尽管它很简单，但您需要从本系列前几篇文章中获得的所有知识才能完全理解它。让我们开始吧。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

代码 01

好吧，亲爱的读者，这段代码很有趣，而且很好奇，很有趣。尽管如此，我们在这里只实施了我们真正想要和将要做的第一部分。

请注意：在第四个字符串中，我们指定将使用哪种类型的值作为浮点数。我们可以指定我们需要 double 或 float 类型。它们之间的区别在于它们各自能让你获得的精度。但在我们深入了解更多细节之前，让我们先弄清楚这段代码的作用。

因此，在声明类型后，我们可以使用联合来创建一种读取内存的方法。为了做到这一点，我们使用了第 8 行代码。在联合内部，我们使用第 10 行代码创建一个变量，使用第11 行创建一个共享访问数组。类似的结构已在之前的文章中讨论和解释过。如果您不清楚这里发生了什么以及创建这个联合的目的是什么，请阅读它们以获取更多信息。

对于我们来说，这里最重要的代码是第 14 行，因为我们在其中设置了我们想要可视化的值。而第 16 行只是提供了一种显示内存内容的方法，这也是我们现在的目标，因为我们想了解浮点值在内存中是如何表示的，直到计算机可以解释它。

因此，执行后，代码 01 将为我们提供下图所示的结果。

图 01

唔...我们目前看到的这种奇怪的十六进制格式的表示是什么？好吧，我亲爱的读者，这正是计算机解释浮点值的方式，遵循 IEEE 754 标准。一个重要的细节是：此值以小端格式（Little Endian）格式表示。稍后我们将详细讨论这种格式是什么。但现在，您只需要了解以下内容：这个十六进制值是以相反的顺序记录的，必须从右向左读取。

好吧，无论如何，你可能不相信。因此，我们可以使用另一个程序来澄清这一点。让我们使用十六进制编辑器。HxD 是最简单且免费的选项之一。如果您输入图 01 的十六进制字段中显示的值，突出显示它们并查看那里代表什么值，您将看到类似于下面显示的图像。

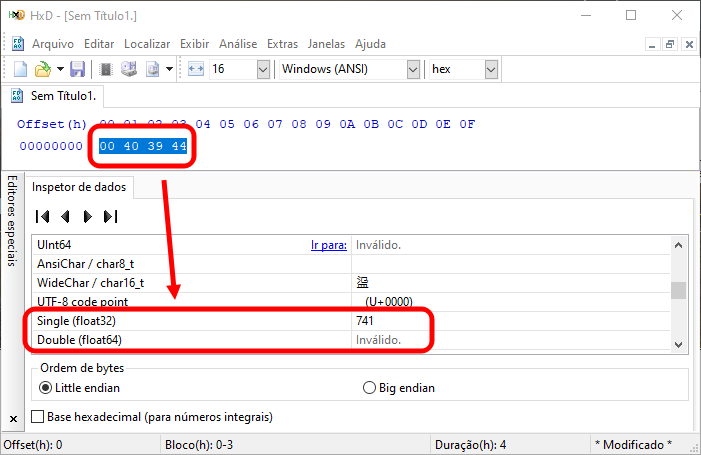
图 02

请注意，我们实际上有一个可以可视化的预期值。然而，我个人更喜欢使用我的开发环境的扩展来查看这些东西，这样可以避免在计算机上安装很多不同的程序。不过，公平地说，我要指出的是，HxD 不需要安装。无论如何，我们可以看到如下图所示的情况。

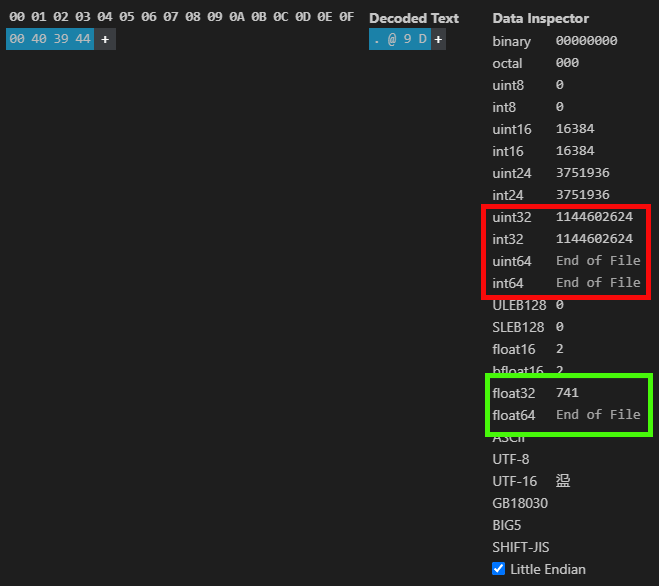
图 03

此处提供的信息可在 MetaTrader 5 和 HxD 中获得。但我希望您仔细看看我在图 03 中展示的内容。请注意，相同的浮点值以整数表示时是不同的值。但为什么会这样呢？原因是，对于计算机来说，一个值是用整数还是其他类型表示并不重要 —— 这对计算机来说没有任何区别。然而，对于我们和编译器来说，这是至关重要的 —— 数据类型会影响我们是否得到合理的结果或完全出乎意料的结果。

尽管如此，我们刚才在代码 01 中考虑的例子只是一个简单的例子。让我们用稍微不同的示例替换代码 01，如下所示。

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

代码 02

很好，代码 02 可能看起来更复杂。然而，它就像代码 01 一样简单，但这里我们有机会讨论有关浮点值显示的一些额外要点。这要归功于第 4 行代码，我们可以选择是否要使用单精度（浮点）或双精度类型。但是，当执行如上所示的代码时，我们将得到如下所示的答案。

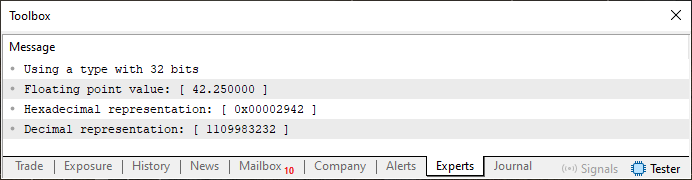
图 04

正如我们之前看到的，使用图 04 中所示的指定值，我们得到下图所示的结果：

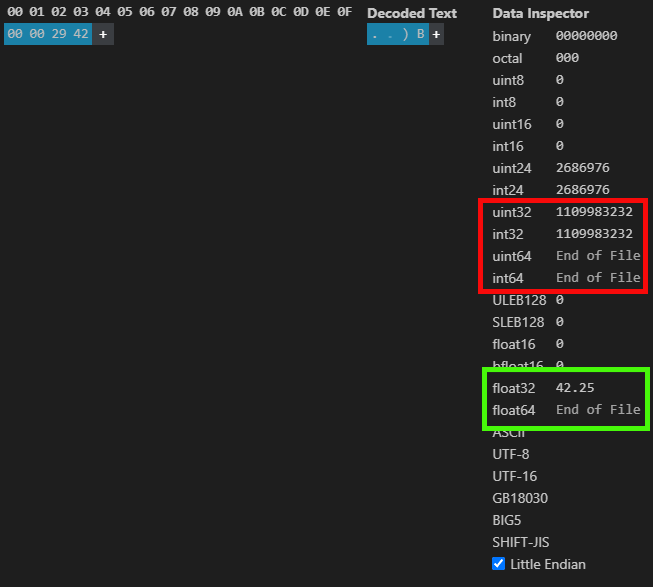
图 05

换句话说，这里确实发生了一些事情。但是 IEEE 754 系统是如何工作的呢？亲爱的读者，为了解释这一点，我们应该更深入地研究系统本身的内部结构。我会尽量不把事情复杂化太多，因为最终它会否定任何解释正在发生的事情并帮助弄清楚一切的尝试。

最初（目前）有两种 IEEE 754 格式：一种用于单精度（使用 32 位），另一种用于双精度（使用 64 位）。它们之间的区别不在于一个比另一个更精确；差异在于工作范围内的值。因此，“精确度”一词常常会产生误导。这就是为什么我宁愿不使用它的原因，即使它被认为是正确的。

在下图中，您可以看到标准定义的两种类型：

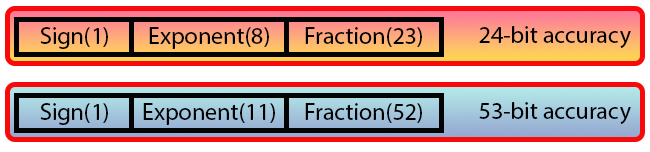
图片 06

“等一下...您不是说过我们对一种类型使用 32 位，对另一种类型使用 64 位吗？但这里似乎使用了一些毫无意义的东西。我们在图 06 中看到的这些数据和值是什么？”

嗯，这是根据 IEEE 754 标准表示浮点值的方式。这里，您看到的每个值都是一个位。请注意，我们有一些宽度不寻常的块，与我们迄今为止看到的不同。然而，这并不妨碍我们理解系统本身。尽管如果我们使用 C 或 C++ 语言，解释可能会更简单。这是因为在 MQL5 中我们没有办法一次命名一个位，而这可以在 C 或 C++ 中完成。然而，我们可以使用宏和定义来更接近这些语言中正在做的事情。

因此，我将在本文中对此进行解释。如果不成功，我会单独写一篇文章来正确解释一切。我不想把自己局限于一个粗略的解释。亲爱的读者，我希望你真正理解在我们的代码中使用浮点值时的问题是什么。因为我看到有多少人声称，甚至真诚地相信，有可能进行实际上不可能的计算。这是因为预期结果和实际结果之间存在轻微差异，如果我们不做好准备，可能会导致问题。

让我们从以下内容开始：如果你把图 06 中显示的位数加起来，你会注意到第一种格式包含 32 位，第二种格式包含 64 位。这就是问题开始出现的地方。因此，为了简化，让我们只关注其中一种格式，因为它们之间的差异与调整过程中使用的值有关。但我们稍后再谈论这个。

图 06 中表示为符号的位是符号位。也就是说，它表示该值是负数还是正数，就像整数类型一样，最左边的位告诉我们该数字是负数还是正数。

因此，符号位（Sign）后面紧跟着八位，称为指数。该值生成一个等于 127 的所谓偏差，它对指数进行编码。对于双精度（double）的情况，使用 11 位，因此产生 1023 的偏差。请注意，尽管名称为“双精度”，但这里的偏差值要高得多。

但对我们来说，最重要的部分是紧随指数之后的部分。这个字段称为分数。它决定了将呈现的值的准确性。请注意，在 32 位（单精度）的情况下，该字段包含 23 位，因此精度为 24 位。而在双精度的情况下，该字段包含 52 位，因此精度为 53 位。同样，该值是前一个值的两倍多，因此，“双精度”一词再次具有误导性。

但是，如果你更深入地研究浮点数的问题，你会发现我们在这里称之为分数的字段通常被称为尾数。尾数是浮点数形成的关键部分。

这里涉及很多方面，但由于许多人在看到太多技术细节后可能会失去兴趣，为了使这个过程更加愉快，让我们继续举一个实际的例子。在代码 01 中的第 14 行中，我们使用了值 741 并将其转换为浮点值。在这种情况下，为 32 位值，即单精度格式。因此，我们可以使用图 06 中的橙色方案。我希望你试着专注于将要展示的内容，这样你就可以首先理解这个简单的模型。

因此，首先我们要将 741 的值转换为二进制格式。为此，可以使用各种方法。然而，对于大多数人来说最容易理解的是就是除以 2。让我注意一下，如果你不知道如何将一个数字转换为二进制，不要担心，因为第一个值很简单。并且很容易理解如何去做。下面的图 07 演示了如何完成此操作。

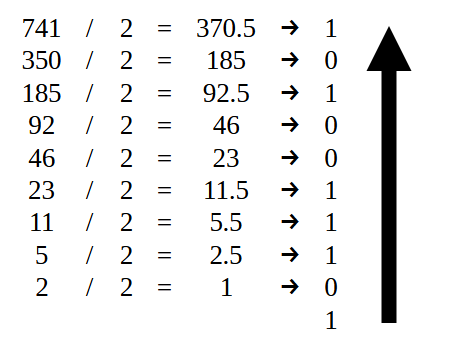
图 07

所有除法完成后，我们得到了一系列 0 和 1 的序列。但为了正确记录值，必须按照箭头所示的顺序记录。于是我们得到了下图所示的结果。

图 08

好的，得到和图 08一样的效果就是第一部分。完成此操作后，我们可以继续进行第二步，即将此二进制值转换为浮点值。现在要小心，因为这是最简单的情况。然而，必须很好地理解它，以便以后能够处理更复杂的情况。

我们需要创建尾数，即小数部分。为此，我们需要将最右侧的点向左移动。这样，我们就只剩下一位，其值等于 1。这种转换将产生下图所示的结果。

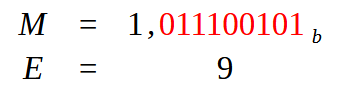
图 09

现在让我们看看以下内容：M 是所谓的尾数，即浮点数的小数部分。E 将是我们的指数。但是这个 “9” 的值是从哪里来的呢？嗯，这是因为尾数中有 9 个红色值。但 9 这个值仍需处理，这就是转换的第三阶段的开始。根据我们选择的方法，我们将以某种方式处理这个值 9，从而生成不同的值。这对于以十六进制格式表示浮点数是必要的。

但在考虑如何处理值 9 之前，让我们先弄清楚浮点数的小数部分是如何形成的。

还记得单精度值有 23 位，双精度值有 52 位吗？而单精度的精度为 24 位，双精度的精度为 53 位，不是吗？因此，图 09 上以黑色突出显示的这个值为 1 的位就是出现的额外位。也就是说，它不存在，但在小数字段中隐含。因此，小数字段的形成如下：

图 10

图 10 中的绿色零的数量取决于小数字段中的位数。将有尽可能多的 0 来填充字段的其余部分。所以，现在我们有浮点值的小数部分。它仍然构成指数的一部分。由于该值为正数，因此符号字段将为 0。为了形成指数部分，必须考虑所使用的精度类型。如果这是单精度，我们将图 09 中显示的 E 值（在本例中为 9）添加到偏差值中，对于这种类型，偏差值是 127。结果，我们得到的值为 136。该操作如下图所示。

图 11

现在，我们终于可以生成一个单精度值来以浮点格式表示数字 741。该值如下所示。

图 12

将图 12 中的位除以十六进制表示形式，我们得到图 13 所示的内容。

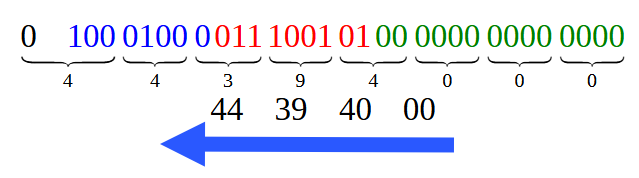
图 13

请注意，图 13 中显示的每个十六进制值与我们在图 01 中看到的值相匹配。但是，您应该记住按照箭头指示的顺序读取它们。  这与我们将在未来的另一篇文章中讨论的一个特性有关。好的，这是最简单的情况。但在本文中，我们还考虑了另一种情况，如果可以这么说的话，这种情况稍微复杂一些。这是在代码 02 中考虑的情况，其中我们基本上有一个小数点的值。那么在这种情况下我们应该怎么做呢？

好吧，亲爱的读者，当在数值中使用小数点时，情况会有些不同，但差别不大。事实上，在这种情况下，我们应该将二进制转换步骤分为两部分：一部分 —— 用于小数点左边的部分，另一部分 —— 用于小数点右边的部分。看起来很复杂，对吧？但实际上，一切都很简单，很有逻辑，你只需要注意你在做什么。

首先，小数点左边的部分应该按照图 07 所示进行转换。也就是说，我们应该只使用值 42，如下所示。

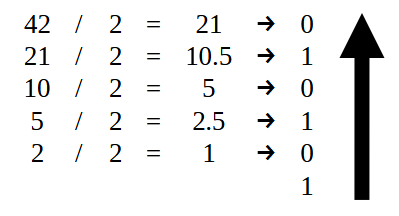
图 14

但小数点右边的部分应该按照图 15 所示进行转换。也就是说，我们取 0.25，并将代码 02 中指定的值的小数部分转换为二进制格式。

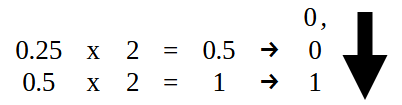
图 15

其结果如下：以二进制格式表示数字 42.25，如下所示。

图 16

请密切注意，我们在图 16 中已经有一个点。这将在一定程度上改变我们在接下来的步骤中要做的事情 —— 事实上，这将是图 09 所示的阶段，我们确定了尾数和指数的值。由于我们已经有了图 16 中所示的小数点，我们需要做的就是对其进行偏移，以便最左边的位置只剩下一位值为 1 的位。与图 09 完全相同。因此，我们得到了下图所示的结果。

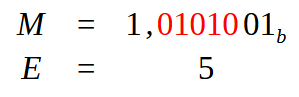
图 17

请注意，在图 17 中，用红色突出显示的值正是为了使点处于正确位置而需要偏置的值。因此，设置指数的值将为 5。我们也已经有了尾数值，用于形成小数字段。计算单精度值后，我们得到如下所示的结果。

图 18

请注意，找到的十六进制值与图 04 中显示的值完全匹配。当然，请记住，应该按照箭头方向读取，以两个字节为一组。好吧，但如果我们使用双精度，我们会得到相同的结果吗？也就是说，如果代码 02 中的第 4 行取消注释以应用此指令，我们将使用 64 位而不是 32 位，从而在系统中应用双精度。

这样的话，我们会得到和图 18 一样的数据吗？好吧，亲爱的读者，我们得到的结果几乎是一样的。事实上，小数部分将保持不变。当然，我们必须添加更多的零来填充双精度格式的小数部分字段所需的全部 52 位。但是，指数将完全不同，因为我们将使用 1023，而不是 127（单精度）。因此，图 18 中唯一在视觉上不同的部分是表示指数的蓝色区域。为了更清楚地说明这一点，请看下图，它显示了使用双精度时数值条目的外观。

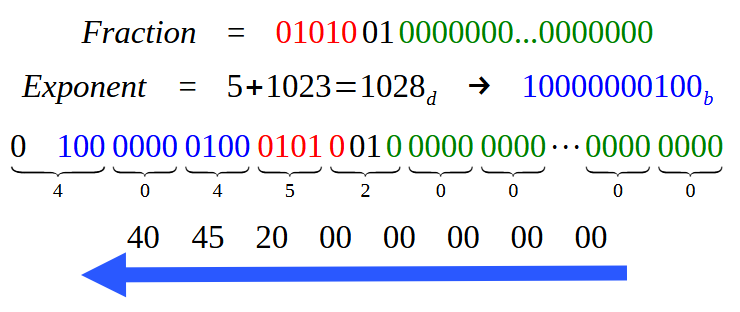
图 19

为了检查我们的估计是否正确，我们运行带有建议更改的代码 02。结果如下所示。

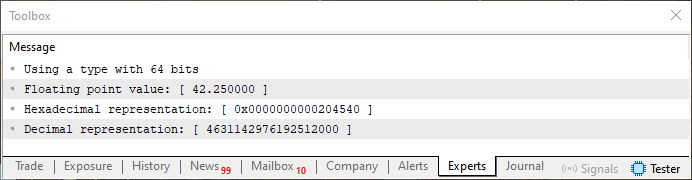
图 20

最后的探讨

在这篇简要介绍浮点值主题的文章中，我们探讨了如何在内存中表示这样的数字，以及如何使用这种类型的值。我知道，亲爱的读者，在这一点上，你可能会对浮点值的各个方面感到有点困惑。这并不奇怪。我自己花了很多时间来弄清楚这类数据是如何创建的，尤其是如何使用这些数据进行计算。虽然这不是我在这里的主要目标，但谁知道呢，也许将来我能够解释如何使用浮点数进行计算。这确实是一个非常有趣的话题，尤其是通过 IEEE 754 标准的视角。

当然，还有其他格式和方法来表示包含小数点的数字。然而，由于 MQL5 与许多其他编程语言一样，使用本文所讨论的格式，我们建议您仔细研究此类数据。毕竟，这些数字往往并不完全代表我们认为我们正在计算的值。我建议你看看下面的链接，学习如何对浮点值进行舍入，因为这有明确的规则，而且不是无缘无故的。

当然，这仍由您决定。根据我们在这里的考虑，使用浮点数已经完全可以的了。但是，其他方面，如舍入规则和可能表示或可能不表示的值列表，只对那些努力提高应用中使用的值的准确性和正确性的人来说是必要的。这在目前的文章中不是强制性的。

链接：

• IEEE 754
• 使用 float16 和 float8 格式的 ONNX 模型