От начального до среднего уровня: Плавающая точка

Введение

В предыдущей статье «От начального до среднего уровня: Определения (II)», мы говорили о том, насколько важны макросы, и как мы можем эффективно их использовать, чтобы сделать наш код еще более читабельным.

Что ж, учитывая все, рассмотренное ранее, у нас теперь достаточно материала и адекватных средств, чтобы объяснить, как работают числа с плавающей точкой. Я знаю, многие считают, что значения double или float являются наилучшим выбором в различных ситуациях. Однако, с этим типом значений связана одна проблема, которую очень мало кто понимает, особенно за пределами программистских кругов.

И поскольку такие значения широко используются в MQL5, и мы работаем с информацией, где плавающая точка является практически консенсусом, необходимо очень хорошо понимать, как этот тип значений обрабатывается CPU.

Для чего же я это говорю? Понятно, что дробные числа, такие как 2,5, всегда очень просты для понимания, поскольку никто не спутает этот тип значений ни с каким другим. Но, мой дорогой читатель, когда дело касается вычислений, все обстоит не так просто. На самом деле, числа с плавающей точкой весьма полезны в ряде ситуаций. Однако, их не следует рассматривать или понимать так же, как целые числа.

По сути, многие из вас, должно быть, привыкли иметь дело с числами с плавающей точкой в двух типах записи: научной, где мы записываем значения, например, как 1-e2, и более распространенной, арифметической, где мы записываем значения как 0,01. Оба значения равны по величине, но записываются по-разному. Точно так же существует и дробный способ записи этого же значения, который будет равен 1/100.

Обратите внимание, что во всех случаях речь идет об одном и том же значении. Но несмотря на это, разные программы или языки программирования обрабатывают эти значения по-разному.

Немного истории

На заре вычислительной техники чисел с плавающей точкой в том виде, в каком мы их знаем сегодня, не существовало, или, скорее, не существовало стандартизированного способа их обработки. Каждый программист, каждая операционная система и даже каждая программа обращались с этим типом чисел очень специфическим и индивидуальным образом.

В период с 1960 по 1970 год не было возможности взаимодействия одной программы с другой с целью совместного использования и ускорения факторизации таких значений. Только представьте: в самом начале космической эры, когда такие цифры имели бы первостепенное значение, БЫЛО НЕВОЗМОЖНО вычислять значения с плавающей точкой на компьютерах того времени. А даже когда такая возможность появилась, было невозможно разделить задачу между большим количеством компьютеров, чтобы ускорить вычисления.

Тогда IBM, которая в то время контролировала почти весь рынок, начала предлагать способ представления такого рода значений. Но рынок не всегда принимает то, что ему предлагают. Поэтому другие производители разработали свои собственные способы представления таких значений. Это был настоящий ХАОС. Пока в какой-то момент Институт инженеров по электротехнике и электронике (IEEE) не начал наводить порядок, установив то, что сейчас известно как стандарт IEEE 754. В конце этой статьи, в разделе «Ссылки», я оставлю несколько ссылок для тех, кто захочет углубиться в эту тему.

Первым установленным стандартом стал IEEE 754-1985, как попытка решить весь этот вопрос. Сегодня мы используем гораздо более современный стандарт, но он основан на той же, изначально установленной схеме.

Важная деталь: несмотря на существование этого стандарта, предназначенного для нормализации и обеспечения возможности распределённой факторизации, существуют случаи, когда данный стандарт не используется, и вычисления — или, точнее, факторизация — производятся по другим принципам, которые мы здесь рассматривать не будем, так как они полностью выходят за рамки темы. Это связано с тем, что MQL5, как и несколько других языков, использует именно этот стандарт IEEE 754.

Изначально центральный процессор не справлялся с таким типом вычислений, поэтому существовал отдельный процессор, известный в то время как FPU, предназначенный исключительно для этой цели. Данный FPU приобретался отдельно, так как его стоимость не всегда оправдывала его применение. Примером FPU может служить модель 80387. И да, это не опечатка. По сути, эта модель очень похожа на известную 80386, обычно называемую 386. Но это было скорее маркетинговым решением Intel, чтобы отличить центральный процессор CPU (80386) от блока FPU (80387). Компьютер мог работать только с центральным процессором, но не с одним только блоком FPU, поскольку последний был предназначен только для выполнения вычислений с плавающей точкой.

Хорошо, но в чем же проблема этой плавающей точки? Почему целая статья посвящена только этой теме? Причина в том, что, не понимая, как работает представление чисел с плавающей точкой, можно совершить ряд ошибок. Не из-за плохого программирования, а из-за представления о том, что выполняемые вычисления следует воспринимать буквально, тогда как сам факт использования стандарта IEEE 754 уже создает потенциальную погрешность в конечном вычисляемом значении.

Это может показаться абсурдным, ведь компьютеры — это машины, которые всегда должны предоставлять нам точные значения. Говорить о том, что результат операции содержит ошибку, несерьезно, более того — неприемлемо. Особенно когда нашей целью является торговля на финансовом рынке с использованием таких данных. Если наши расчеты неверны, мы можем терять деньги, даже если все будет указывать на вероятность получения прибыли. И именно по этой причине данная статья имеет важное значение.

Существует ряд аспектов, связанных с плавающей точкой, которые не так важны в рамках того, что мы собираемся делать. Но есть одна вещь, которая очень важна и имеет решающее значение, — это округление.

Я знаю, что многие говорят или даже хвастаются, утверждая: 

Я НЕ использую округление в своих вычислениях. Они всегда точные и безошибочные.

Но именно эта идея, на мой взгляд, демонстрирует полное и абсолютное непонимание программирования, которое приводит людей к ложным предположениям, тогда как на самом деле все обстоит иначе. Округление вовсе не обязательно должно выполняться программистом. Оно просто существует — независимо от того, хочет того программист или нет. Поэтому важно, чтобы вы ознакомились с материалами по ссылкам, которые я оставлю в конце, поскольку вопрос чисел с плавающей точкой невозможно объяснить в одной статье. Помните: есть специалисты, работающие над этой темой с самого начала развития вычислительной техники.

Здесь мы рассмотрим другой тип вещей, гораздо более простой и ориентированный именно на понимание того, что такое double или float, поскольку все остальные типы данных куда проще, и уже были объяснены в предыдущих статьях.

Представление числа с плавающей точкой

Итак, здесь мы поговорим о типе, который действительно используется в MQL5. В этом типе мы в основном следуем спецификации IEEE 754, которая предусматривает два формата — или, точнее сказать, две точности. И да, когда мы говорим о числах с плавающей точкой, правильно использовать термин «точность», а не «формат» или «количество задействованных бит». Но чтобы не усложнять, так как это может быть довольно запутанно для многих людей, здесь мы будем использовать термин «количество бит», но лишь для того, чтобы большая часть читателей смогла лучше понять материал, и чтобы упросить дальнейшие объяснения. Полагаю, что я обращаюсь не к инженерам или специалистам, обладающим обширными и всеобъемлющими знаниями в области электроники и разработки микросхем, а скорее к людям, интересующимся программированием на языке MQL5 и жаждущими знаний.

Ну что ж, для начала давайте рассмотрим очень простой код. Однако, несмотря на всю его простоту, для полного понимания вам понадобятся все знания, почерпнутые из предыдущих статей серии. Итак, приступим.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. #define typeFloating float
05. //+----------------+
06. void OnStart(void)
07. {
08.     union un_1
09.     {
10.         typeFloating v;
11.         uchar arr[sizeof(typeFloating)];
12.     }info;
13. 
14.     info.v = 741;
15. 
16.     PrintFormat("Floating point value: [ %f ] Hexadecimal representation: [ %s ]", info.v, ArrayToHexadecimal(info.arr));
17. }
18. //+------------------------------------------------------------------+
19. string ArrayToHexadecimal(const uchar &arr[])
20. {
21.     const string szChars = "0123456789ABCDEF";
22.     string sz = "0x";
23. 
24.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
25.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
26. 
27.     return sz;
28. }
29. //+------------------------------------------------------------------+

Код 01

Что ж, мой дорогой читатель, этот код довольно интересен, помимо того, что с ним довольно любопытно и весело экспериментировать. Несмотря на это, здесь мы реализуем только первую часть того, что на самом деле хотим и будем делать.

Обратите внимание: в четвертой строке мы указываем, какой тип значения будем использовать в качестве числа с плавающей точкой. Мы можем указать, что нам нужен тип double или float. Разница между ними заключается именно в точности, которую каждый из них позволяет получить. Но прежде чем углубляться в подробности, давайте разберемся, что делает этот код.

Итак, после объявления типа мы можем использовать объединение (union) для создания способа чтения памяти. Для этого мы используем строку восемь. Уже внутри объединения, мы используем строку 10 для создания переменной и строку 11 для создания массива общего доступа. Подобные конструкции уже рассматривались и объяснялись в предыдущих статьях. Пожалуйста, ознакомьтесь с ними для получения более подробной информации, если вам не ясно, что здесь происходит, и какова цель создания этого объединения.

Для нас самой важной строкой здесь является строка 14, поскольку именно в ней мы задаем значение, которое хотим визуализировать. А строка 16 просто предоставляет способ отобразить содержимое памяти, что сейчас и является нашей целью, поскольку мы хотим понять, как значение с плавающей точкой представлено в памяти до момента, когда компьютер сможет его интерпретировать.

Итак, после выполнения код 01 предоставит нам результат, показанный на изображении ниже.

Рисунок 01

Хм... Что это за странное представление в шестнадцатеричном формате, которое мы сейчас видим? Что ж, мой дорогой читатель, это именно тот способ, с помощью которого компьютер — следуя стандарту IEEE 754 — интерпретирует значение с плавающей точкой. Важная деталь: это значение записывается как значение в формате Little Endian. Позже мы еще поговорим подробнее о том, что представляет собой этот формат. Но сейчас вам просто нужно понять следующее: это шестнадцатеричное значение записано в обратном порядке и должно читаться справа налево.

Ну, в любом случае, вероятно, вы в это не верите. Поэтому мы можем использовать другую программу, чтобы прояснить это. Давайте воспользуемся шестнадцатеричным редактором. HxD — один из самых простых и бесплатных вариантов. Если вы введете значения, показанные в шестнадцатеричном поле изображения 01, выделите их и посмотрите, какое значение там представлено, то увидите изображение, похожее на то, что показано ниже.

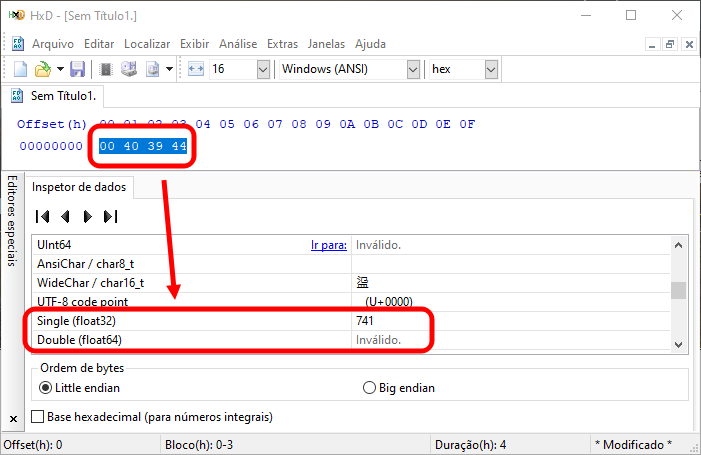
Рисунок 02

Обратите внимание, что на самом деле у нас есть ожидаемое значение, которое можно визуализировать. Однако, лично я предпочитаю использовать расширение моей среды разработки для просмотра подобных вещей — это позволяет избежать установки на компьютер множества разных программ. Хотя, справедливости ради, отмечу, что HxD не требует установки. В любом случае, то, что мы можем увидеть, показано на следующем рисунке.

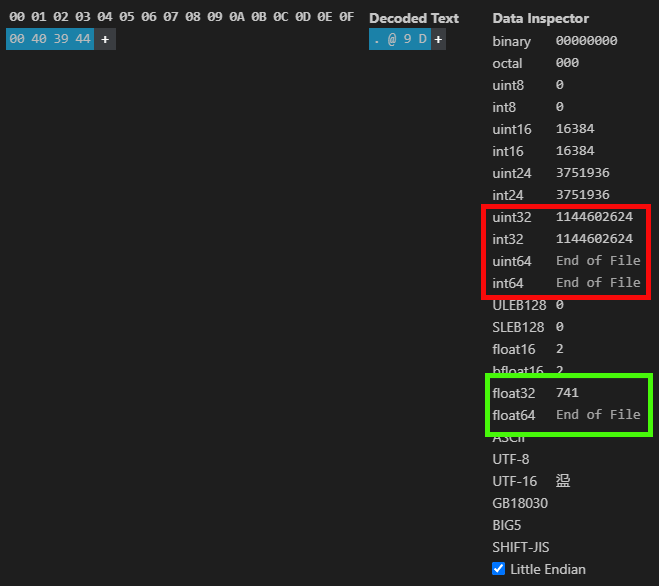
Рисунок 03

Такую информацию, которая приведена здесь, можно получить как в MetaTrader 5, так и в HxD. Но я хочу, чтобы вы внимательно посмотрели на то, что я показываю на изображении 03. Обратите внимание, что то же самое значение с плавающей точкой представляет собой другое значение в виде целого числа. Но почему этак происходит? Причина в том, что для компьютера неважно, представлено ли значение целым числом или любым другим типом — для него нет никакой разницы. Однако для нас и для компилятора это принципиально — тип данных влияет на то, получим ли мы разумный результат или что-то совершенно неожиданное.

Тем не менее, пример, который мы только что рассмотрели в коде 01, — это всего лишь простой случай. Давайте заменим код 01 на немного другой пример, который можно увидеть чуть ниже.

01. //+------------------------------------------------------------------+
02. #property copyright "Daniel Jose"
03. //+------------------------------------------------------------------+
04. // #define Floating_64Bits
05. //+----------------+
06. #ifdef Floating_64Bits
07.     #define typeFloating double
08. #else
09.     #define typeFloating float
10. #endif
11. //+----------------+
12. void OnStart(void)
13. {
14.     union un_1
15.     {
16.         typeFloating v;
17. #ifdef Floating_64Bits
18.         ulong integer;
19. #else
20.         uint integer;
21. #endif
22.         uchar arr[sizeof(typeFloating)];
23.     }info;
24. 
25.     info.v = 42.25;
26. 
27.     PrintFormat("Using a type with %d bits\nFloating point value: [ %f ]\nHexadecimal representation: [ %s ]\nDecimal representation: [ %I64u ]",
28. #ifdef Floating_64Bits
29.         64,
30. #else
31.         32,
32. #endif
33.         info.v, ArrayToHexadecimal(info.arr), info.integer);
34. }
35. //+------------------------------------------------------------------+
36. string ArrayToHexadecimal(const uchar &arr[])
37. {
38.     const string szChars = "0123456789ABCDEF";
39.     string sz = "0x";
40. 
41.     for (uchar c = 0; c < (uchar)arr.Size(); c++)
42.         sz = StringFormat("%s%c%c", sz, szChars[(uchar)((arr[c] >> 4) & 0xF)], szChars[(uchar)(arr[c] & 0xF)]);
43. 
44.     return sz;
45. }
46. //+------------------------------------------------------------------+

Код 02

Очень хорошо, код 02 может показаться более сложным. Однако он так же прост, как и код 01, просто здесь у нас есть возможность обсудить несколько дополнительных моментов, касающихся отображения значений с плавающей точкой. Это возможно, благодаря строке 4, где мы можем выбрать, хотим ли мы использовать тип с одинарной (float) или двойной (double) точностью. Но при выполнении кода, который показан выше, мы получим ответ, представленный ниже.

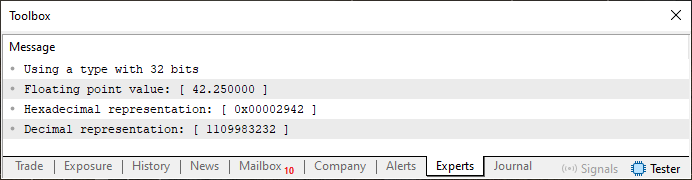
Рисунок 04

И точно также, как мы видели ранее, используя указанные значения, отображенные на рисунке 04, мы получаем результат, показанный на следующем изображении:

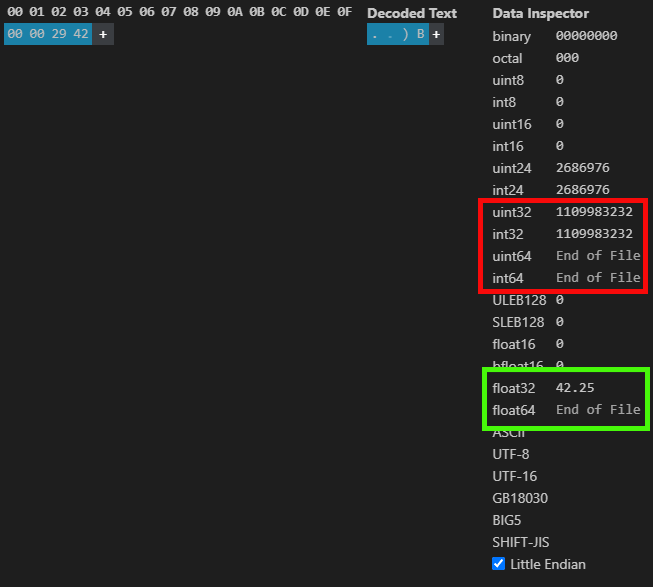
Рисунок 05

То есть, действительно, здесь что-то происходит. Но как работает система IEEE 754? Что ж, дорогой читатель, чтобы объяснить это, нам нужно заглянуть глубже во внутреннее устройство самой системы. Я постараюсь не усложнять слишком сильно, поскольку в итоге это может свести на нет любую попытку объяснить происходящее и помочь во всем разобраться.

Изначально — и в настоящее время — существует два формата IEEE 754: один для одинарной точности (где используется 32 бита) и другой для двойной точности (где используется 64 бита). Разница между ними не в том, что один точнее другого; разница заключается в диапазоне значений, с которым можно работать. Поэтому термин «точность» зачастую может вводить в заблуждение. Именно по этой причине я предпочитаю его не использовать, хотя он и считается корректным.

На изображении ниже вы можете увидеть два типа, определенные стандартом:

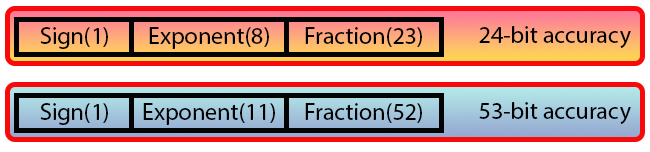
Изображение 06

"Подожди-ка... Разве ты не говорил, что мы используем 32 бита для одного типа и 64 – для другого? Но здесь, похоже, используется нечто, вовсе не имеющее смысла. Что это за данные и значения, которые мы видим на изображении 06?"

Хорошо, это и есть способ, которым значение с плавающей точкой представляется по стандарту IEEE 754. Здесь каждое из значений, которые вы видите, является БИТОМ. Обратите внимание, что у нас есть блоки с необычной шириной, отличной от той, которую мы видели до сих пор. Однако, это не мешает нам понять саму систему. Хотя объяснения могли бы быть проще, если бы мы использовали языки C или C++. Это связано с тем, что в MQL5 у нас нет возможности именовать биты по одному — то, что можно сделать в C или C++. Однако, мы можем использовать макросы и определения, чтобы приблизиться к тому, что делается в этих языках.

Поэтому, я попытаюсь объяснить это уже в этой статье. Если не получится — сделаю отдельную статью, чтобы объяснить все как следует. Я не хочу ограничиваться лишь поверхностным объяснением. Я хочу, чтобы вы, дорогой читатель, действительно поняли,в чем заключается проблема при использовании значений с плавающей точкой в наших кодах. Потому что я вижу, как многие утверждают и даже искренне верят, что можно производить вычисления, которые на самом деле невозможны. Все из-за того, что между ожидаемым и фактическим результатом возникает небольшое расхождение, которое может вызвать проблемы, если мы к этом не готовы.

Давайте начнем со следующего: если вы сложите количество бит, показанное на изображении 06, вы заметите, что первый формат содержит 32 бита, а второй — 64 бита. Именно здесь и начинают возникать вопросы. Поэтому, для упрощения давайте сосредоточимся только на одном из форматов, поскольку разница между ними связана со значением, используемым при корректировке. Но об этом мы поговорим позже.

Бит, обозначенный на изображении 06 как Sign, — это знаковый бит. То есть, именно он указывает, является ли значение отрицательным или положительным, так же, как это происходит в целочисленных типах, где самый левый бит сообщает нам, отрицательное это число или положительное.

Итак, сразу после знакового бита (Sign) идут восемь битов, называемых экспонентой (Exponent). Это значение генерирует так называемое смещение (bias), равное 127, которое кодирует показатель степени. В случае с двойной точностью (double) используется одиннадцать бит, что создает bias 1023. Обратите внимание, что, несмотря на название «двойная точность», значение смещения здесь существенно выше.

Но самая важная для нас часть, это та, что идет сразу после показателя степени. Это поле называется Fraction. Именно оно определяет точность значения, которое будет представлено. Обратите внимание, что в случае 32-х бит (одинарная точность), это поле содержит 23 бита, что дает точность в 24 бита. А в случае двойной точности у нас в этом поле 52 бита, что дает точность в 53 бита. Опять же, значение более чем вдвое превышает предыдущее, и по этой причине термин «двойная точность» снова несколько вводит в заблуждение.

Но если вы углубитесь в вопрос чисел с плавающей точкой, вы увидите, что поле, которое мы здесь называем Fraction, часто называют мантиссой. Именно мантисса и представляет собой ключевую часть в формировании чисел с плавающей точкой.

Здесь задействовано много аспектов, но чтобы сделать процесс более приятным — ведь многие могут потерять интерес, увидев слишком много технических деталей — давайте перейдем к практическому примеру. В коде 01 в строке 14 мы использовали значение 741 и преобразовали его в значение с плавающей точкой. В данном случае, в 32-битное значение, то есть, в формат одинарной точности. Поэтому, мы можем использовать оранжевую схему с рисунка 06. Я хочу, чтобы вы постарались сосредоточиться на том, что будет показано, чтобы сначала понять эту простую модель.

Итак, для начала, нам нужно преобразовать значение 741 в двоичный формат. Для этого можно использовать различные способы. Однако, самый понятный для большинства — это деление на два. Отмечу: если вы не знаете, как преобразовать число в двоичную систему, не волнуйтесь, так как это первое значение достаточно простое, и будет легко понять, как это делается. На изображении 07, представленном ниже, можно увидеть, как это выполняется.

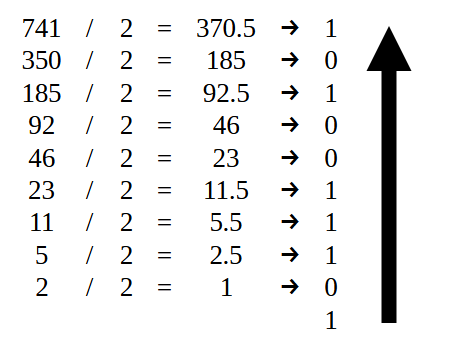
Рисунок 07

После того, как все деления выполнены, в итоге у нас получается последовательность нулей и единиц. Но чтобы значение было записано правильно, нам нужно записать его в том порядке, как показано стрелкой. В результате мы получаем то, что показано на изображении ниже.

Изображение 08

Хорошо, это первая часть — получить то же, что на изображении 08. Как только это будет сделано, мы можем перейти ко второму этапу, который заключается в преобразовании этого двоичного значения в значение с плавающей точкой. А теперь будьте внимательны, потому что это самый простой случай из возможных. Однако, необходимо очень хорошо его понимать, чтобы впоследствии суметь разобраться в более сложных ситуациях.

Нам нужно создать нашу мантиссу, то есть дробную часть. Для этого нам необходимо сдвинуть запятую, которая находится в крайнем правом положении, влево. Таким образом, чтобы слева у нас остался только один бит со значением, равным единице. Это преобразование приведет к тому, что вы видите на рисунке ниже.

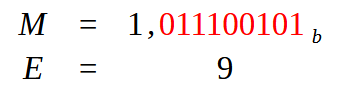
Изображение 09

Теперь посмотрим на следующее: M — это то, что называют мантиссой, то есть дробной частью числа с плавающей точкой. E – будет нашей экспонентой (показателем степени). Но откуда взялось это значение, равное девяти? Ну, оно возникает из-за того, что у нас есть девять красных значений в мантиссе. Но над этим значением 9 еще нужно поработать. И именно здесь начинается третий этап преобразования. В зависимости от того, какой подход мы выберем, мы будем обрабатывать это значение 9 тем или иным образом, генерируя тем самым разные значения. Это необходимо для представления числа с плавающей точкой в шестнадцатеричном формате.

Но прежде чем рассматривать, что делать со значением 9, давайте разберемся, как формируется дробная часть числа с плавающей точкой.

Помните, что у нас есть 23 бита для значения одинарной точности и 52 бита для значения двойной точности? И при этом точность составляет 24 бита для одинарной точности и 53 бита для двойной? Так вот, этот самый бит со значением 1, что выделен черным на изображении 09, — это и есть тот дополнительный бит, который появляется. То есть, он НЕ ПРИСУТСТВУЕТ, но подразумевается в поле Fraction. Таким образом, поле Fraction формируется следующим образом:

Рисунок 10

Количество зеленых нулей на изображении 10 зависит от количества бит в поле Fraction. Будет столько нулей, сколько необходимо для заполнения всей оставшейся части поля. Итак, теперь у нас есть дробная часть значения с плавающей точкой. Осталось сформировать часть экспоненты. Поскольку значение положительное, то поле Sign будет равно нулю. Чтобы сформировать часть экспоненты, нам нужно учитывать используемый тип точности. Если это одинарная точность, мы добавляем значение E, показанное на рисунке 09 (которое в данном случае равно девяти), к значению bias, которое для этого типа составляет 127. В результате получаем значение 136. Эта операция показана на рисунке ниже.

Рисунок 11

Теперь, наконец, мы можем сформировать значение одинарной точности для представления числа 741 в формате с плавающей точкой. Это значение показано чуть ниже.

Рисунок 12

Разделив биты с изображения 12, для построения шестнадцатеричного представления, мы получаем то, что изображено на рисунке 13.

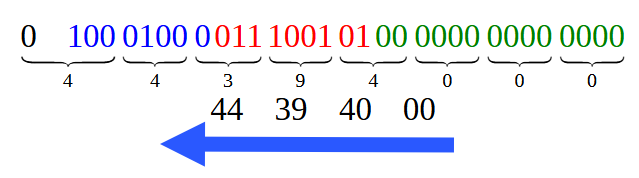
Рисунок 13

Обратите внимание, что каждое из шестнадцатеричных значений, показанных на рисунке 13, совпадает с тем, что мы видим на изображении 01. Однако, вы должны помнить, что читать их нужно в порядке, указанном стрелкой, — это связано с одной особенностью, которую мы рассмотрим в другой, будущей статье. Хорошо, это был самый простой случай из всех. Но в этой статье мы также рассмотрели другой случай, немного сложнее — если можно так выразиться — это случай, рассматриваемый в коде 02, где у нас, по сути, есть значение с десятичной точкой. И как нам следует действовать в этой ситуации?

Что ж, мой дорогой читатель, когда в числовом значении используется десятичная точка, все обстоит немного иначе, но не сильно. Правда в том, что в этом случае нам нужно разделить этап преобразования в двоичный формат на две части: одну — для части слева от десятичной точки, и другую — для части справа от нее. Кажется сложным, не так ли? Но на практике все довольно просто и логично, просто нужно быть внимательными к тому, что делаете.

Для начала, ту часть, которая находится СЛЕВА от десятичной точки, следует преобразовать так, как на рисунке 07. То есть, мы должны использовать только значение 42, как показано ниже.

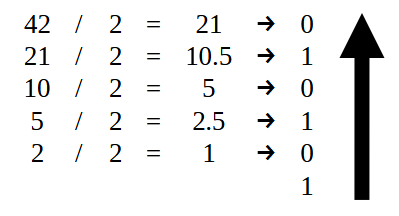
Рисунок 14

А вот часть, которая находится СПРАВА от десятичной точки, должна быть преобразована так, как показано на рисунке 15. То есть, мы берем 0,25 — и будем преобразовывать в двоичный формат десятичную часть значения, указанного в коде 02.

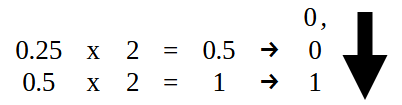
Рисунок 15

Это приводит к следующему — представлению числа 42.25 в двоичном формате, показанном сразу ниже.

Рисунок 16

Обратите очень пристальное внимание на тот факт, что на изображении 16 У НАС УЖЕ УКАЗАНА ЗАПЯТАЯ. Это немного изменит то, что мы будем делать на следующих этапах — по сути, это будет этап, показанный на рисунке 09, где мы определяли значение мантиссы и экспоненты. Поскольку у нас уже есть десятичная точка, обозначенная здесь, на рисунке 16, все, что нам нужно сделать, это сместить ее так, чтобы остался только один бит со значением 1 в крайней левой позиции. Точно так же, как на рисунке 09. В результате, мы получаем следующее, что показано на изображении ниже.

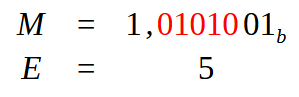
Рисунок 17

Обратите внимание, что на изображении 17 значения, выделенные красным цветом, — это именно те, которые нужно было сместить, чтобы запятая заняла правильное положение. Таким образом, значение для настройки экспоненты будет равно пяти. Также у нас уже есть значение мантиссы, которое используется для формирования поля Fraction. Выполнив вычисления значения для одинарной точности, мы получаем то, что показано чуть ниже.

Рисунок 18

Обратите внимание, что найденное шестнадцатеричное значение в точности совпадает со значением, показанным на изображении 04. Конечно, напоминаю, что читать его нужно по направлению стрелки, группами по два байта. Хорошо, но получили ли бы мы тот же результат, если бы использовали двойную точность? То есть, если бы строка 4 в коде 02 была незакомментирована, чтобы эта директива применялась, мы бы использовали 64 бита вместо 32, тем самым применяя в системе двойную точность.

В таком случае получим ли мы те же данные, что и на изображении 18? Что ж, мы получим примерно то же самое, мой дорогой читатель. В действительности дробная часть останется прежней — конечно, нам придется добавить больше нулей, чтобы заполнить все 52 бита, необходимые для поля дробной части в формате двойной точности. Однако экспонета будет совершенно другой, поскольку вместо значения 127 (для одинарной точности) мы будем использовать значение 1023. Таким образом, единственная часть, которая будет визуально отличаться на изображении 18, — это синяя область, обозначающая экспоненту. Чтобы сделать это более наглядным, посмотрите на следующее изображение, где показано, как будет выглядеть запись значения при использовании двойной точности.

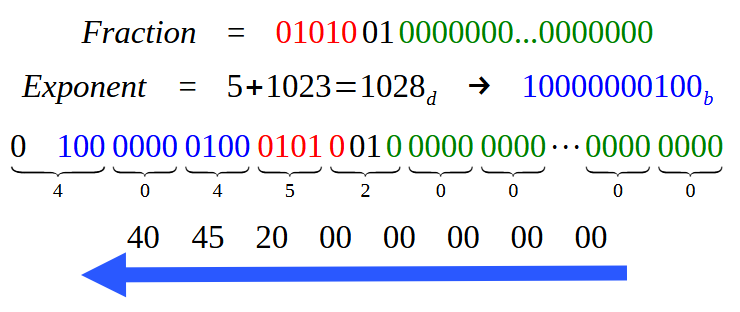
Рисунок 19

И чтобы проверить, верна ли наша оценка, мы запускаем код 02 с предложенным изменением, и результат получится таким, как показано ниже.

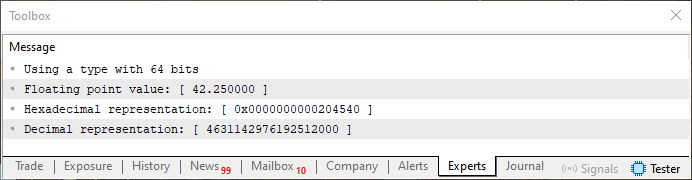
Рисунок 20

Заключительные соображения

В этой статье, которая представляет собой краткое введение в тему значений с плавающей точкой, мы рассмотрели, как такое число представлено в памяти, и как можно работать с этим типом значений. Я знаю, что на данный момент вы, мой дорогой читатель, можете быть немного озадачены различными аспектами, касающимися значений с плавающей точкой. И это неудивительно. Сам я потратил немало времени, чтобы разобраться, как создается этот тип данных, но особенно — как выполнять вычисления с использованием этих данных. Хотя это и не является моей главной целью здесь, кто знает, возможно, в будущем я смогу объяснить, как выполнять вычисления с использованием чисел с плавающей точкой. Это действительно очень увлекательная тема для рассмотрения, особенно через призму стандарта IEEE 754.

Разумеется, существуют и другие форматы и способы представления чисел, содержащих десятичную точку. Однако, поскольку MQL5, как и многие другие языки программирования, использует именно тот формат, что рассматривался в этой статье, желательно, чтобы вы вдумчиво отнеслись к изучению этого типа данных. Ведь зачастую такие числа не представляют точно то значение, которое, как нам кажется, мы вычисляем. И я предлагаю вам просмотреть ссылки, оставленные ниже, и изучить, как выполняется округление значений с плавающей точкой, потому что для этого есть четкие правила, и это не делается просто так.

Тем не менее, это уже остается на ваше усмотрение. На основе того, что мы рассмотрели здесь, уже вполне можно работать с числами с плавающей точкой. А вот дополнительные аспекты — такие как правила округления и список значений, которые могут или не могут быть представлены — необходимы только тем, кто стремится к высокой точности и правильности значений, используемых в своих приложениях. А это не является обязательным в рамках текущей статьи.

Ссылки:

• 754
• Работа с моделями ONNX в форматах float16 и float8