Funcionalidades do Assistente MQL5 que você precisa conhecer (Parte 31): Escolha da função de perda

Introdução

O Assistente MQL5 pode servir como um campo de testes para uma ampla variedade de ideias. Algumas delas já foram abordadas nesta série. De tempos em tempos, encontramos sinais personalizados que podem ser implementados de diferentes formas. Vimos um exemplo disso nos dois artigos sobre taxas de aprendizado, bem como no artigo anterior sobre normalização em lote. Como já discutido, cada um desses aspectos do aprendizado de máquina pode representar mais de um possível sinal personalizado. O mesmo se aplica à função de perda, devido à existência de múltiplos formatos.

Não há um único método para comparar o resultado de um teste com o valor-alvo. No ENUM_LOSS_FUNCTION são oferecidas 14 opções de enumeração, e essa lista não é exaustiva. Isso significa que cada uma delas representa uma abordagem distinta para o aprendizado de máquina? Talvez não, mas o ponto central é que há diferenças que frequentemente exigem uma escolha criteriosa da função de perda, dependendo da natureza da rede ou do algoritmo em treinamento.

No entanto, além da função de perda, também podemos considerar o uso de ENUM_REGRESSION_METRIC. No entanto, essa abordagem, mais relacionada à estatística, não se aplica bem aqui, pois é mais adequada como métrica para avaliar o desempenho do próprio algoritmo de aprendizado de máquina após o treinamento. Dessa forma, esse conjunto de métricas será especialmente útil quando o resultado final tiver mais de uma dimensão. Contudo, nesta discussão, o foco principal é a função objetivo.

A escolha da medida de perda adequada é essencial, pois as redes neurais (nosso algoritmo de aprendizado de máquina para este artigo) podem se enquadrar na categoria de regressão (ao contrário da classificação) ou ser utilizadas no aprendizado supervisionado (em oposição ao aprendizado não supervisionado). Além disso, paradigmas como o aprendizado por reforço podem exigir uma abordagem multifacetada para o uso e a aplicação da função de perda.

Assim, as funções de perda podem ser aplicadas de várias maneiras, não apenas porque existem muitos formatos, mas também porque há diversos tipos de tarefas (redes neurais) que precisam ser resolvidas. Ao abordar esses problemas ou durante o processo de aprendizado, a função de perda serve, em primeiro lugar, para quantificar o quão distantes os parâmetros testados estão do valor-alvo esperado (aprendizado supervisionado).

No caso da função de perda, sempre fica claro intuitivamente que ela é projetada para o aprendizado supervisionado. No entanto, a questão sobre qual seria a função de perda ideal para o aprendizado não supervisionado pode parecer inadequada. Ainda assim, mesmo em condições não supervisionadas, como mapas de Kohonen ou clustering, sempre há necessidade de uma métrica padronizada para medir lacunas ou distâncias em dados multidimensionais, e a função de perda pode preencher essa lacuna.

Visão geral das funções de perda

O MQL5 oferece até 14 métodos diferentes para quantificar a função de perda, e todos eles serão examinados antes de analisarmos exemplos de aplicação. Para nossos propósitos, a perda é usada para denotar o gradiente de perda, e os resultados esperados são vetores, não valores escalares. Além disso, não será fornecido o código MQL5 que implementa essas fórmulas, pois TODOS eles são executados por meio de funções vetoriais embutidas. Abaixo está um script simples para testar diferentes funções de perda:

#property  script_show_inputs
input ENUM_LOSS_FUNCTION __loss = LOSS_HUBER;
//+------------------------------------------------------------------+
//| Script program start function                                    |
//+------------------------------------------------------------------+
void OnStart()
  {
//---
      vector _a = {1.0, 2.0, 4.0};
      vector _b = {4.0, 12.0, 36.0 };
      
      vector _loss = _a.LossGradient(_b,__loss); 
      
      printf(__FUNCSIG__+" for: "+EnumToString(__loss));
      Print(" loss gradient is: ",_loss);
      PrintFormat(" while loss is: %.5f. ",_a.Loss(_b,__loss));
  }
//+------------------------------------------------------------------+

Primeiramente, o erro quadrático médio (MSE). Essa é uma função de perda amplamente utilizada para medir o quadrado da diferença entre os valores previstos e os valores-alvo, determinando assim a magnitude do erro. Isso garante que o erro seja sempre positivo (o foco está na magnitude) e "pune" significativamente erros grandes devido à elevação ao quadrado. A interpretação também se torna mais suave, pois o erro está sempre expresso em unidades da variável-alvo. A fórmula é apresentada a seguir:

onde

• n — a dimensionalidade da variável-alvo e da variável comparada. Normalmente, essas variáveis têm formato vetorial.
• i — índice interno no espaço vetorial
• y^ — vetor de saída ou previsão
• y — vetor-alvo

Entre os pontos positivos dessa função, estão sua sensibilidade a erros grandes e sua boa adaptabilidade a métodos de otimização baseados em descida de gradiente, devido ao gradiente suave. A principal desvantagem é sua sensibilidade a valores atípicos.

A próxima função é o erro absoluto médio (MAE) (loss-mean-absolute-error). Assim como o MSE, essa é outra função de perda comum que foca no erro de magnitude, sem considerar a direção. A diferença em relação ao MSE é que ele não atribui peso adicional a valores grandes, pois não há elevação ao quadrado. Como a elevação ao quadrado não é utilizada, as unidades do erro correspondem às unidades do vetor-alvo, tornando a interpretação mais simples do que no caso do MSE. Sua fórmula, semelhante à apresentada anteriormente, tem o seguinte formato:

onde

• n, i, y e y^ representam os mesmos valores definidos no MSE acima.

As principais vantagens do MAE são sua menor sensibilidade a valores atípicos e a erros grandes, uma vez que não há elevação ao quadrado, e a facilidade de manter as unidades-alvo, o que simplifica a interpretação. No entanto, seu comportamento em relação ao gradiente não é tão suave quanto o do MSE, pois, ao ser diferenciado, o valor de saída assume um dos seguintes valores: +1,0, -1,0 ou zero. A alternância desses valores dificulta a convergência do processo de aprendizado, que ocorre de maneira mais suave no MSE. Isso pode ser problemático, especialmente em ambientes de regressão. Além disso, o fato de tratar todos os erros como iguais pode dificultar o processo de convergência.

Isso nos leva à entropia cruzada categórica (categorical cross entropy). Essa função permite medir, em um espaço estritamente multidimensional, a diferença entre a distribuição de probabilidades prevista e a real. Enquanto usamos MAE e MSE como saídas vetoriais no algoritmo de função de perda do MQL5 (pois as diferenças individuais não são somadas), elas também podem ser representadas como escalares, conforme mostrado em suas fórmulas. Por outro lado, a entropia cruzada categórica (Categorical Cross Entropy, CCE) sempre gera um resultado multidimensional. Sua fórmula é dada por:

onde

• N — número de classes ou dimensão do vetor de pontos de dados
• y — valor real ou valor-alvo
• p — valor previsto ou saída da rede
• log — logaritmo natural

A CCE é, por natureza, um classificador, e não um regressor, sendo especialmente adequada para casos em que mais de uma classe é utilizada na categorização de um conjunto de dados durante o aprendizado. Suas principais áreas de aplicação incluem gráficos e processamento de imagens, mas isso não impede que busquemos formas de aplicá-la à negociação. No entanto, é importante notar que a CCE funciona melhor quando combinada com uma ativação que faça com que todas as probabilidades somem exatamente 1. Esse método é bem adequado para encontrar distribuições de probabilidade das diferentes classes analisadas para um determinado ponto de dados. O componente logarítmico "pune" previsões erradas com alta confiança mais severamente do que previsões menos confiantes. Isso está diretamente relacionado à prática de codificação one-hot, na qual os valores-alvo são sempre normalizados, atribuindo peso total (normalmente 1,0) à classe correta, enquanto todas as outras recebem um peso de zero. A CCE fornece gradientes suaves durante a otimização e incentiva os modelos a se tornarem mais confiantes em suas previsões, devido ao efeito penalizador mencionado anteriormente no caso de previsões incorretas. Durante o treinamento em populações desbalanceadas entre diferentes classes, é possível aplicar ajustes de pesos para equilibrar as condições de aprendizado. No entanto, existe o risco de overfitting quando há um número excessivo de classes, por isso é essencial ter cautela ao determinar quantas classes o modelo deve avaliar.

O próximo método é a entropia cruzada binária (binary cross entropy, BCE), que está intimamente relacionada à CCE. Ela também quantifica a discrepância entre a previsão e o valor-alvo, mas em um cenário binário, ao contrário da CCE, que é mais eficaz ao lidar com múltiplas classes. Sua saída está no intervalo de 0,0 a 1,0 e é definida pela seguinte fórmula:

onde

• N, como nas funções de perda anteriores, representa o tamanho da amostra.
• y — valor previsto
• p — valor da previsão
• log — logaritmo natural

No caso da BCE, as duas classes consideradas são frequentemente chamadas de positiva e negativa. Assim, a saída da BCE é interpretada como a probabilidade de um determinado ponto de dados pertencer à classe positiva, com esse valor variando entre 0,0 e 1,0. Para isso, a função de ativação mais adequada para a BCE costuma ser a sigmoide, que impõe um limite rígido às probabilidades geradas. O tipo de dado vetorial do MQL5, usado para funções de ativação embutidas, retorna um vetor que deve conter duas probabilidades: uma para a classe positiva e outra para a negativa.

A divergência de Kullback-Leibler (Kullback-Leibler Divergence, KLD) é outro algoritmo interessante para função de perda, semelhante aos métodos de separação vetorial que discutimos anteriormente. Sua fórmula é dada por:

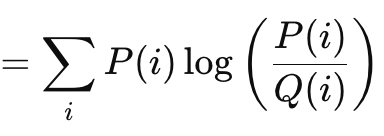
onde

• P — probabilidade prevista
• Q — probabilidade real

Seus valores de saída variam de 0, indicando ausência de divergência, até o infinito. Esses valores positivos são um indicador claro de quão distante a previsão está da "verdade". Como mostrado na fórmula acima, a soma só é relevante no cálculo da saída escalar. A implementação vetorial incorporada no MQL5 fornece uma saída vetorial, o que é mais conveniente e necessário para calcular deltas e, consequentemente, gradientes durante a propagação reversa. A divergência de Kullback-Leibler baseia-se na teoria da informação e tem sido amplamente utilizada no aprendizado por reforço devido à sua flexibilidade, bem como em autocodificadores variacionais. Entre seus pontos negativos, incluem-se assimetria, sensibilidade a valores nulos e dificuldades de interpretação, devido ao caráter não diretamente relacionado de seus valores de saída. A sensibilidade a zeros é importante, pois, se um dos valores de probabilidade for zero, o outro pode se tornar infinito automaticamente. Além disso, a assimetria não apenas dificulta a correta interpretação das probabilidades, mas também complica o aprendizado por transferência (transfer learning), pois a probabilidade P condicional a K não é a mesma que a probabilidade de K condicional a P. As somas das probabilidades direta e inversa não resultam em um valor fixo. Em alguns casos, podem ser infinitas; em outros, não.

Isso nos leva ao coeficiente cosseno (cosine similarity), que, ao contrário das métricas de diferença vetorial que analisamos até agora, considera a direção. Sua fórmula é dada por:

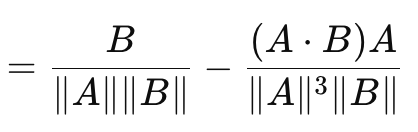
onde

• A.B — produto escalar entre dois vetores
• ||A|| e ||B|| — suas magnitudes ou normas

A fórmula acima se refere ao gradiente da função de perda em relação ao vetor A. A fórmula correspondente ao vetor B é uma inversa separada e, ao ser somada à similaridade cosseno entre A e B, não resulta em uma constante fixa ou arbitrária. Por esse motivo, a similaridade cosseno não é uma métrica verdadeira, pois não satisfaz a desigualdade triangular (triangle of inequality). (A similaridade cosseno entre A e B somada à similaridade cosseno entre B e C nem sempre é maior ou igual à similaridade cosseno entre A e C). Sua principal vantagem é a invariância de escala, pois o valor retornado não depende da magnitude dos vetores considerados. Isso pode ser essencial quando a direção é mais relevante do que a magnitude. Além disso, esse método requer menos recursos computacionais do que outros, o que é um fator crítico ao trabalhar com redes muito profundas ou transformadores — ou ambos! Esse método tem sido amplamente aplicado a dados multidimensionais, como incorporações de texto em grandes modelos de linguagem, em que a direção inferida (ou significado) é uma métrica mais relevante do que os valores individuais de cada componente vetorial. No entanto, suas limitações incluem o fato de não ser adequado para todas as tarefas, especialmente aquelas em que a magnitude dos vetores desempenha um papel importante no processo de aprendizado. Além disso, se um dos vetores tiver norma zero (onde todos os valores são zero), a similaridade cosseno será indefinida. Por fim, a incapacidade de ser usada como uma métrica real devido à violação da desigualdade triangular pode ser uma limitação crítica em certos contextos. Exemplos onde isso se torna fundamental incluem aprendizado profundo geométrico, redes neurais baseadas em grafos e funções de perda comparativas em redes siamesas. Em cada um desses casos, a magnitude é mais importante que a direção. No entanto, ao aplicar a similaridade cosseno no MQL5, é essencial observar que o valor retornado refere-se especificamente à similaridade cosseno, pois essa métrica é mais relevante para aprendizado de máquina. Isso equivale à distância do cosseno do ângulo, obtida subtraindo-se a similaridade cosseno de 1.

A função de gradiente de perda de Poisson é adequada para a modelagem de dados contáveis ou discretos. Ela se assemelha à forma como as funções de perda mencionadas anteriormente são implementadas por meio de funções vetoriais embutidas no tipo de dado vetorial. Sua fórmula é dada por:

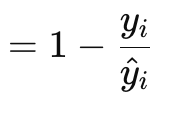
onde

• y — valor-alvo do vetor (no índice i)
• y^ — valor previsto

Os valores do gradiente são retornados no formato vetorial, pois esse formato é muito mais adequado para a propagação reversa. Eles também correspondem às derivadas de primeira ordem da função escalar original de Poisson, resultando na seguinte fórmula:

onde

• os componentes são os mesmos da fórmula do gradiente.

O tipo de dados discretos que os traders podem alimentar na rede neural nesse caso pode incluir tipos de barras de preço ou informações sobre se as barras anteriores foram de alta (bullish), de baixa (bearish) ou neutras (flat). No entanto, suas aplicações vão além da contagem de dados; por exemplo, uma rede neural pode ser treinada para analisar padrões de barras de candles extraídos de um histórico recente e prever quantas velas de um determinado tipo são esperadas em uma amostra padrão de, digamos, 10 barras de preço futuras. Seus coeficientes são fáceis de interpretar, pois representam relações logarítmicas de taxas e estão bem alinhados com a regressão de Poisson. Isso significa que a análise pós-treinamento pode ser facilmente realizada por meio da regressão de Poisson. Essa característica também garante que as previsões de contagem sejam sempre positivas (não negativas). Por outro lado, essa função tem algumas limitações, incluindo o pressuposto de que a variância e a média são sempre iguais ou muito próximas. Se essa suposição não se sustentar, a função de perda pode não funcionar corretamente. Além disso, ela é sensível a valores atípicos, especialmente quando há uma grande quantidade de entradas. O uso do logaritmo natural pode resultar em valores inválidos ou NaN (não numéricos). Outro ponto importante é que sua aplicação é restrita a dados contáveis e positivos, o que significa que não pode ser utilizada em situações que exigem previsões contínuas e negativas, como a previsão de variações de preços.

A função de gradiente de perda de Huber (Huber gradient-loss function) conclui nossa análise das capacidades do MQL5 em relação ao tipo de dado vetorial. Existem outras classes que não abordamos, como o logaritmo do cosseno hiperbólico (logarithm of hyperbolic cosine), a perda de dobradiça categórica (categorical hinge), a perda de dobradiça quadrática (squared hinge), a perda de dobradiça (hinge), o erro quadrático médio logarítmico (mean-squared logarithmic error) e o erro percentual absoluto médio (mean absolute percentage error). Essas funções não afetam diretamente se a rede neural é um regressor ou um classificador, o que é um fator importante para nós, por isso as ignoramos. No entanto, a perda de Huber é calculada pela seguinte fórmula:

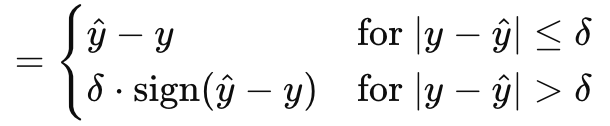
onde

• y^ — valor previsto
• y — valor-alvo
• Delta — parâmetro que define o ponto em que a relação muda de linear para quadrática.

O gradiente, assim como a própria função de perda de Huber, pode ser calculado de duas maneiras, dependendo de como o valor-alvo é comparado à previsão. Trata-se de uma função parcialmente linear e parcialmente quadrática, que mede a diferença entre os valores-alvo e previstos ao ajustar os parâmetros de entrada. Ela é amplamente utilizada na regressão robusta (robust regression), pois combina o melhor do MAE e do MSE, sendo menos sensível a valores atípicos e mais estável que o MAE em pequenas variações. Por ser totalmente diferenciável, a perda de Huber é ideal para descida de gradiente e pode ser facilmente ajustada por meio do parâmetro delta: valores menores de delta fazem com que a função se comporte como o MAE, enquanto valores maiores a aproximam do MSE. Isso permite controlar o equilíbrio entre robustez e sensibilidade. Por outro lado, embora a perda de Huber seja relativamente mais complexa, calcular e definir o valor ideal de delta pode ser um desafio. Dado isso, a implementação no MQL5 não revela como o valor de delta é computado nas funções embutidas de Huber loss e gradiente de Huber loss. Apesar de poder ser combinada com diferentes funções de ativação, a ativação linear é frequentemente recomendada como a opção mais adequada.

Funções de perda para modelos de regressão

Então, qual desses algoritmos de perda é mais adequado para redes de regressão? A resposta: MSE, MAE e Huber Loss. Redes de regressão são caracterizadas por seu objetivo de prever valores numéricos contínuos, em vez de rótulos categóricos ou dados discretos. Isso significa que a camada de saída dessas redes normalmente retorna números reais que podem cobrir uma ampla faixa de valores. A natureza das tarefas de regressão exige minimizar grandes desvios entre os valores previstos e os valores reais durante a otimização, ao contrário das redes de classificação, onde há um número conhecido e geralmente pequeno de classes de saída.

Isso nos leva ao MSE. Como mencionado anteriormente, ele impõe penalidades quadráticas para erros maiores, o que significa que direciona a descida de gradiente e a otimização para desvios menores, algo essencial para a eficiência de redes de regressão. Além disso, sua suavidade e facilidade de diferenciação o tornam uma escolha natural para lidar com dados contínuos processados por redes de regressão.

No entanto, redes de regressão também são altamente suscetíveis a valores atípicos, exigindo uma função de perda que seja suficientemente robusta para lidar com esses desvios. É aqui que entra o MAE. Diferente do MSE, que penaliza erros ao quadrado, o MAE aplica penalidades lineares, tornando-o menos sensível a valores atípicos. Além disso, sua medida de erro fornece uma estimativa confiável do erro médio, o que pode ser útil em conjuntos de dados ruidosos.

Por fim, argumenta-se que redes de regressão precisam de um mecanismo de equilíbrio ou compromisso entre sensibilidade a pequenos erros e robustez. Esses dois atributos são precisamente os que a função de perda de Huber fornece, além de oferecer suavidade suficiente para facilitar a diferenciação ao longo de todo o processo de otimização.

Se todas essas três funções de perda "ideais" forem adotadas, qual seria a melhor escolha de funções de ativação para redes de regressão? As recomendações oficiais apontam para a ativação linear e a ativação identidade (identity activation), sendo que esta última preserva a magnitude da saída da rede para capturar a máxima variabilidade dos dados. Os principais argumentos a favor dessas duas abordagens são a natureza irrestrita de suas saídas, garantindo que não haja perda de dados durante a propagação para frente e o treinamento da rede. Pessoalmente, sou um defensor das saídas limitadas, por isso preferiria usar Soft-Sign e TANH, pois ambas permitem valores reais negativos e positivos, mas dentro de uma faixa restrita de -1,0 a +1,0. Acredito que saídas limitadas são importantes porque ajudam a evitar problemas com gradientes explosivos e gradientes desaparecendo durante a propagação reversa, o que representa um dos principais desafios no treinamento de redes neurais.

Funções de perda para modelos de classificação

E quanto às redes neurais de classificação? Como ocorre a escolha das funções de perda e ativação nesse caso? Bem, o processo de tomada de decisão aqui não é muito diferente: essencialmente, observamos as características principais da rede, e elas determinam nossa escolha.

As redes de classificação são projetadas para prever rótulos de classe individuais a partir de um conjunto predefinido de categorias possíveis. Essas redes geram probabilidades que indicam a chance de cada classe ser a correta, sendo que o objetivo principal é maximizar a precisão dessas previsões minimizando as perdas. Dessa forma, a escolha da função de perda desempenha um papel fundamental no treinamento da rede para distinguir e identificar classes corretamente. Com base nessas características essenciais, há um consenso de que a entropia cruzada categórica (Categorical Cross Entropy, CCE) e a entropia cruzada binária (Binary Cross Entropy, BCE) são as duas funções de perda mais adequadas para redes de classificação dentro do conjunto de enumerações do MQL5.

A BCE classifica os dados em duas categorias possíveis, mas, frequentemente, o número de previsões que precisa ser feito é maior do que apenas duas. O tamanho do lote (batch) afeta a norma do vetor de gradiente. Assim, o valor em cada índice do vetor de gradiente será a derivada parcial da função de perda BCE, conforme indicado anteriormente na fórmula geral, e esses valores serão utilizados na propagação reversa. No entanto, os valores de saída da rede representarão as probabilidades do chamado "classe positiva", conforme mencionado anteriormente, e existirão para cada valor previsto no vetor de saída.

A BCE é apropriada para redes de classificação porque as probabilidades são facilmente interpretáveis, já que indicam diretamente a associação com a classe positiva. Ela é sensível às diferentes probabilidades de cada saída, pois foca na maximização da verossimilhança logarítmica das classes corretas dentro do lote. Como pode ser diferenciada não como uma constante, mas como uma variável, isso facilita significativamente o cálculo do gradiente de maneira suave e eficiente durante a propagação reversa.

A CCE expande a BCE, permitindo a classificação de mais de duas categorias, e a norma ou o tamanho do vetor de saída sempre corresponde ao número de classes, cada uma com uma probabilidade associada. Isso difere da BCE, onde poderíamos fazer previsões, por exemplo, para 5 valores, e cada um deles teria um estado binário (verdadeiro ou falso). Na CCE, a dimensão da saída inclui um prefixo correspondente ao número da classe. Como mencionado anteriormente, a codificação one-hot é útil para normalizar os vetores-alvo antes de medir as discrepâncias nas previsões.

A forma ideal de ativação para esse tipo de abordagem seria, portanto, qualquer função que mapeie saídas dentro do intervalo de 0,0 a +1,0. Entre elas, estão Softmax, Sigmoid e Hard Sigmoid.

Testes

Realizaremos dois conjuntos de testes: um para um MLP regressivo e outro para um classificador. O objetivo do teste é demonstrar a implementação no MQL5 e sua aplicação como um EA, explorando a relação entre funções de perda e funções de ativação. Os resultados apresentados não devem ser interpretados como uma recomendação para uso em contas reais. Encorajamos os leitores a realizarem seus próprios testes em dados reais de ticks do seu broker ao longo de períodos prolongados, caso considerem a estratégia de negociação adequada. A implantação em condições reais deve ser realizada apenas após uma validação cruzada ou testes diretos que forneçam resultados satisfatórios.

Portanto, testaremos o par GBPCHF no timeframe diário ao longo do ano de 2023. Para construir nossa rede de regressão, utilizaremos a classe Cmlp, que apresentamos no artigo anterior. Como nossas entradas serão variações percentuais de preço (e não pontos), testaremos a ativação TANH em conjunto com a função de perda de Huber para avaliar a aplicabilidade da estratégia ao trading. As condições personalizadas para ordens de compra e venda são implementadas no MQL5 da seguinte forma:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalRegr::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] < 0.0)
   {  result = int(round(100.0*(fabs(_out[0])/(fabs(_out[0])+fabs(m_close.GetData(StartIndex()) - m_close.GetData(StartIndex()+1))))));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

Além disso, realizamos um teste simultâneo do EA em dados históricos, treinando a rede a cada nova barra de preço. Essa é outra decisão-chave, que pode ser facilmente ajustada para realizar o treinamento a cada 6 meses ou em um período predefinido mais longo, evitando que a rede se sobreajuste a variações de curto prazo. Essa rede regressora possui três camadas no formato 4-7-1 (onde os números representam os tamanhos das camadas), o que significa que as últimas quatro variações de preço são utilizadas como entradas, enquanto a única saída prevista é a próxima variação de preço.

A execução dos testes com o par GBPCHF ao longo de 2023 no timeframe diário nos fornece o seguinte relatório:

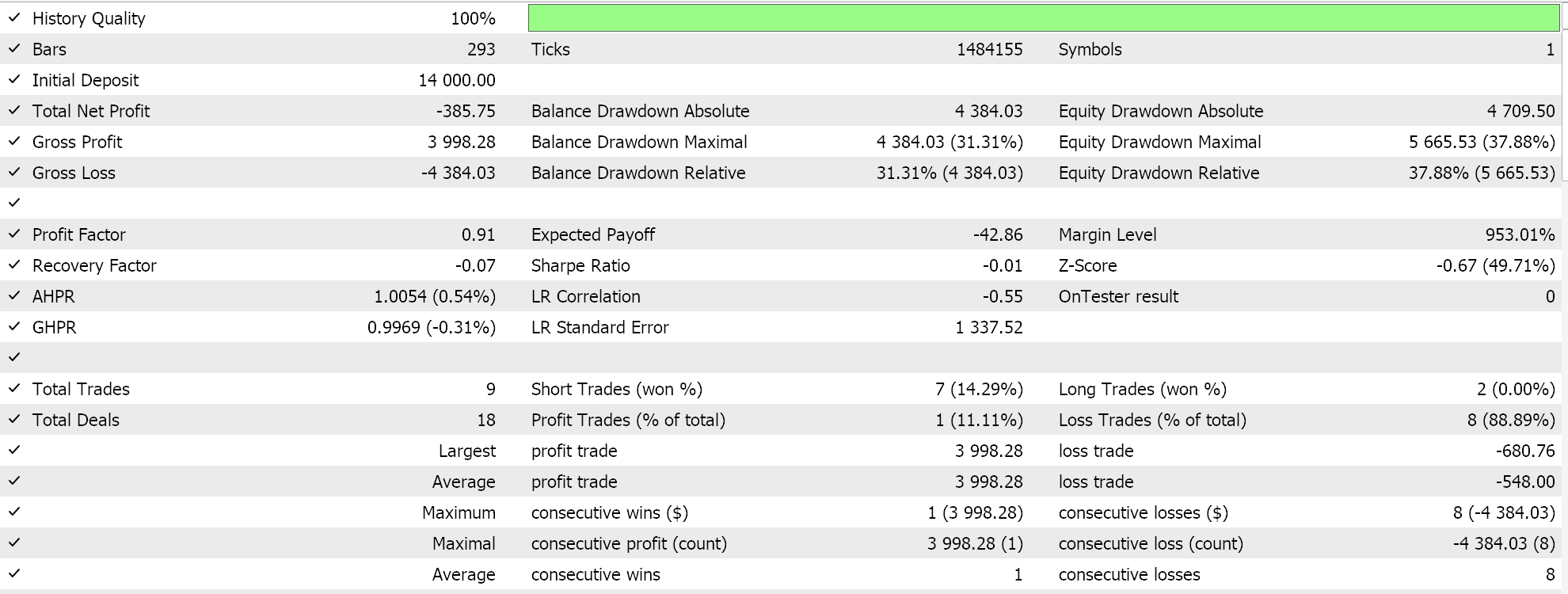
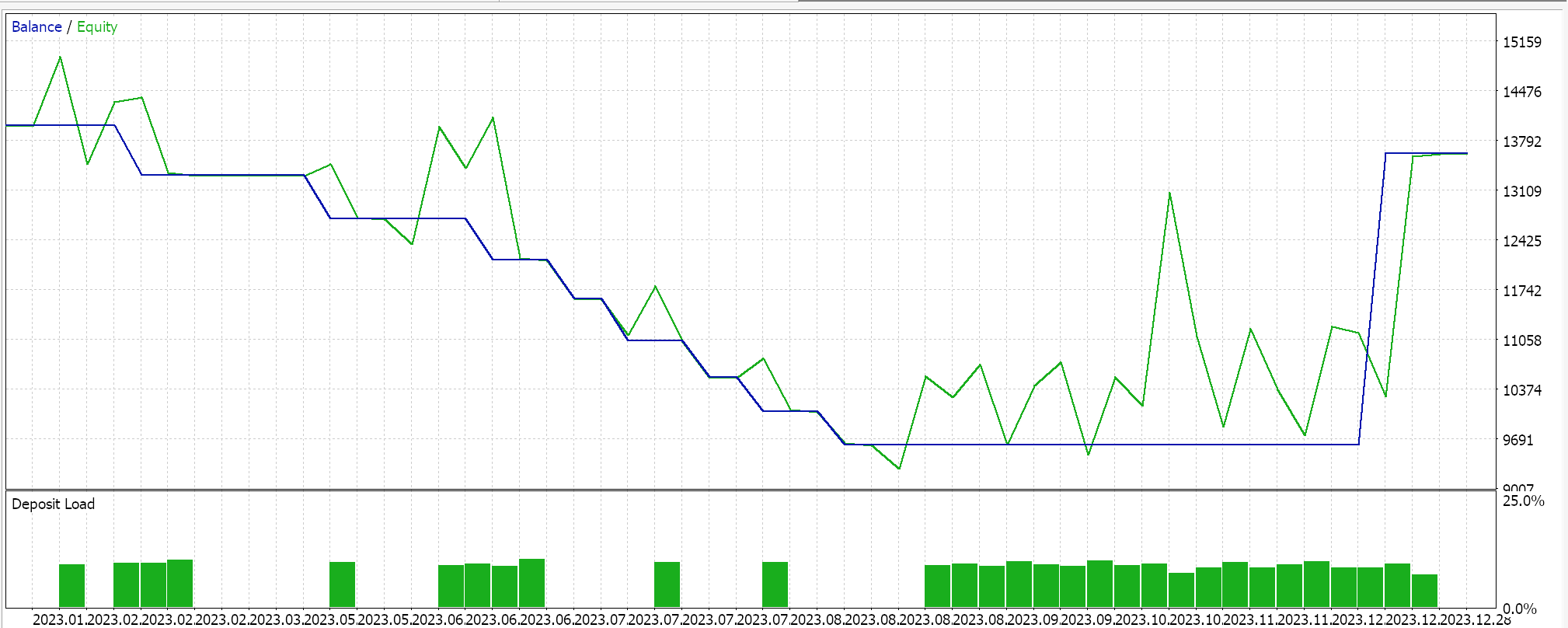
Para a rede classificador, continuamos utilizando a classe Cmlp como base, mas, neste caso, nossas entradas são as classificações dos três últimos pontos de preço. Esses dados são alimentados em uma rede MLP 3-6-3, que também consiste em apenas três camadas. Como estamos analisando três classificações possíveis e utilizando a CCE como função de perda, a camada de saída também precisa ter um tamanho 3 para representar um vetor de probabilidades. A geração das condições de compra e venda é implementada no MQL5 da seguinte forma:

//+------------------------------------------------------------------+
//| "Voting" that price will grow.                                   |
//+------------------------------------------------------------------+
int CSignalClas::LongCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[2] > _out[1] && _out[2] > _out[0])
   {  result = int(round(100.0 * _out[2]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[2],  result);return(0);
   return(result);
}
//+------------------------------------------------------------------+
//| "Voting" that price will fall.                                   |
//+------------------------------------------------------------------+
int CSignalClas::ShortCondition(void)
{  int result = 0;
   vector _out;
   GetOutput(_out);
   m_close.Refresh(-1);
   if(_out[0] > _out[1] && _out[0] > _out[2])
   {  result = int(round(100.0 * _out[0]));
   }
//printf(__FUNCSIG__ + " output is: %.5f,  and result is: %i", _out[0],  result);return(0);
   return(result);
}

Testes semelhantes foram conduzidos para o EA classificador, resultando nos seguintes dados:

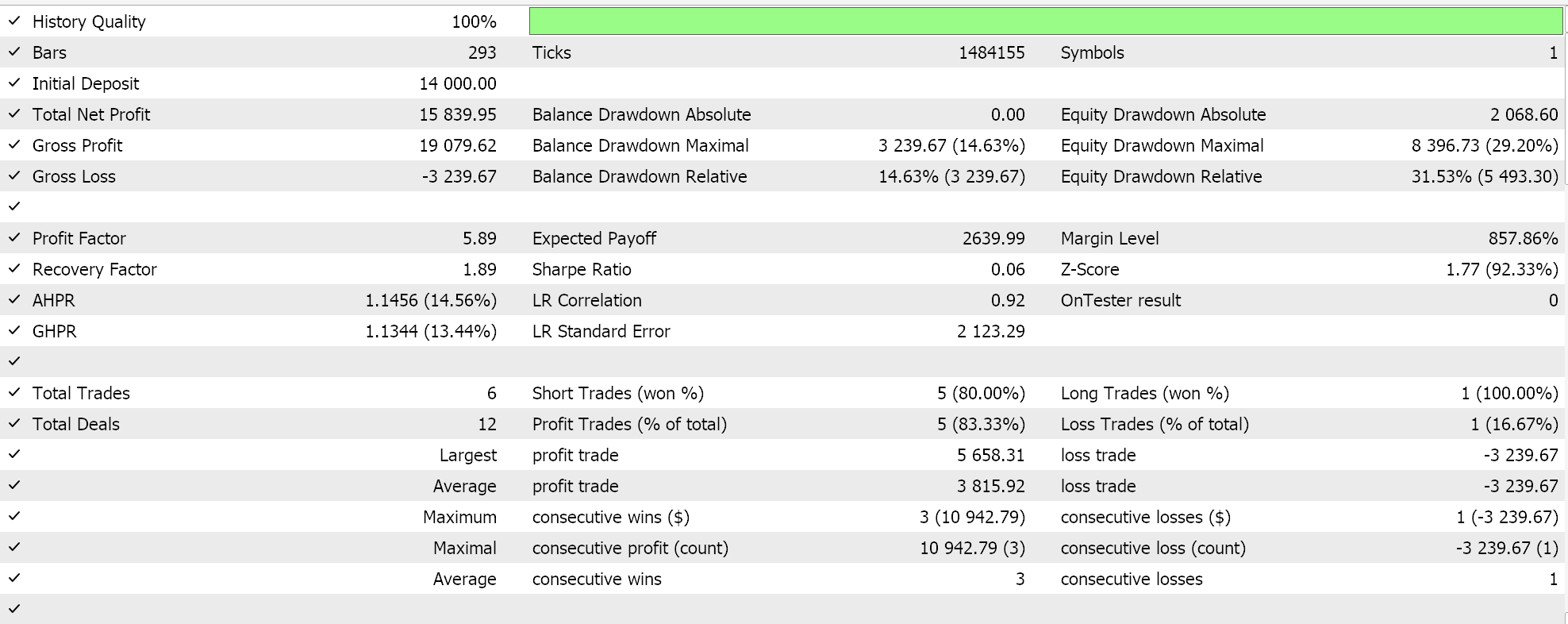
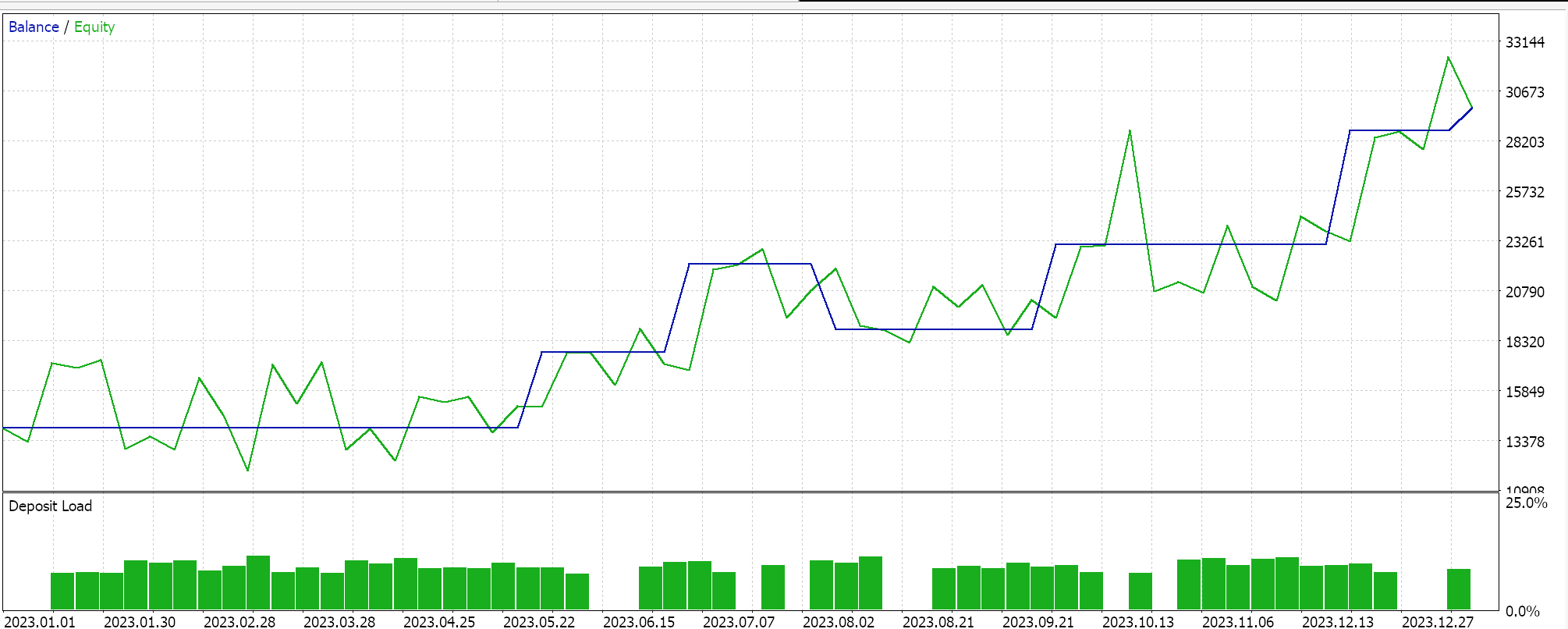
O código utilizado foi empregado na construção dos EAs com o Assistente. Mais detalhes podem ser encontrados aqui e aqui.

Considerações finais

Exploramos as funções de perda disponíveis no MQL5 para o desenvolvimento de algoritmos de aprendizado de máquina, como redes neurais. Embora o número de funções seja extenso, destacamos algumas principais que funcionam bem com funções de ativação específicas, abordadas nos artigos anteriores, com foco especial na prevenção de gradientes explosivos/desaparecendo e na eficiência do treinamento. Muitas das funções de perda disponíveis podem não ser adequadas para redes típicas de regressão e classificação, não apenas porque suas saídas não são compatíveis, mas também porque não atendem aos requisitos fundamentais dessas redes. Por esse motivo, não analisamos todas as funções de perda possíveis.