Reimaginando estratégias clássicas (Parte III): Prevendo máximas mais altas e mínimas mais baixas

Introdução

A inteligência artificial oferece possibilidades praticamente ilimitadas para aprimorar nossas estratégias de trading. No entanto, nem todas elas são eficazes. Nossa meta é ajudar os traders a identificar as estratégias que melhor atendem às suas necessidades, fornecendo as informações necessárias para que tomem decisões embasadas.

Dado o vasto número de possíveis combinações de estratégias, nenhum trader tem condições de avaliá-las todas antes de tomar decisões importantes. Por isso, nesta série de artigos, exploramos o espaço de busca de estratégias de trading, comparando a precisão de estratégias populares com modelos mais simples.

Neste artigo, analisamos detalhadamente uma estratégia clássica de price action baseada em "máximas mais altas" e "mínimas mais baixas". Treinamos diferentes modelos para prever dois tipos distintos de alvos. O primeiro, o mais simples possível, consistia em prever mudanças de preço. O segundo visava determinar se o preço de fechamento futuro estaria acima da máxima atual, abaixo da mínima atual ou entre esses dois valores.

Para comparar modelos de diferentes níveis de complexidade, utilizamos validação cruzada de séries temporais sem embaralhamento aleatório. Analisamos as variações na precisão para ambos os alvos. Nossos resultados indicam que modelos mais simples, que preveem mudanças no nível de preço, podem ser mais eficazes.

Visão geral da estratégia de negociação

Normalmente, traders que utilizam estratégias de price action analisam um título financeiro em busca de sinais de formação ou enfraquecimento de tendências fortes. Um sinal bem conhecido de uma tendência de alta em formação ocorre quando os preços de fechamento superam os extremos anteriores e continuam se movimentando em alta. Nesses casos, costuma-se falar em "máximas mais altas" ou "mínimas mais baixas", dependendo da direção do preço.

Por muitas gerações, os traders utilizaram essa estratégia simples para determinar pontos de entrada e saída. Os pontos de saída geralmente são definidos quando o preço não consegue ultrapassar seus extremos, o que indica que a tendência está perdendo força e pode potencialmente se reverter. Ao longo dos anos, foram adicionadas pequenas extensões a essa estratégia, mas sua essência permaneceu a mesma.

Uma das maiores desvantagens dessa estratégia ocorre quando o preço cai inesperadamente abaixo do extremo inferior. Essas mudanças adversas são conhecidas como "correções" e são difíceis de prever. Como resultado, a maioria dos traders não abre uma posição imediatamente quando o preço atinge um novo extremo. Em vez disso, eles aguardam para ver por quanto tempo o preço consegue se manter nesses níveis antes de tomar uma decisão, permitindo, essencialmente, que a tendência se manifeste. No entanto, esse método levanta algumas questões: por quanto tempo se deve esperar antes de concluir que a tendência se confirmou? E quanto tempo levará até que a tendência se reverta? São exatamente essas questões que os analistas da ação do preço (price action) enfrentam.

Visão geral da metodologia

Agora que estamos familiarizados com as fraquezas dessa estratégia de trading, compreendemos o desejo de muitos traders de utilizar IA para superar essas limitações. Como mencionado anteriormente, treinamos um grupo diversificado de classificadores para prever se o preço de fechamento ficará acima ou dentro da faixa atual. Para essa tarefa, selecionamos diferentes classificadores, incluindo AdaBoost, árvores de decisão e redes neurais. Nenhum dos modelos teve seus hiperparâmetros ajustados antes da comparação.

Associamos três resultados potenciais a três níveis categóricos: 1, 2 e 3, respectivamente:

• 1 indica que o preço de fechamento futuro será superior ao preço máximo atual.
• 2 indica que o preço de fechamento futuro será inferior ao preço mínimo atual.
• 3 indica que nem 1 nem 2 se confirmaram, ou seja, o preço futuro permanecerá entre a máxima e a mínima atuais.

Vale ressaltar que a nova meta que criamos é mais difícil de interpretar. Se nosso modelo prevê um estado 3, nem sempre podemos responder com clareza se os níveis de preços subirão ou cairão, pois isso depende do preço no momento. Isso torna nosso modelo não apenas menos transparente, mas também aparentemente menos preciso do que o modelo mais simples.

Normalmente, consideramos qualquer estratégia que possa superar o modelo mais básico. Uma estratégia complexa que não consiga superar um modelo simples pode não justificar o custo adicional de recursos, como tempo.

Análise exploratória de dados em python

Para começar, precisamos exportar os dados de mercado do MetaTrader 5. Abra o terminal e selecione o ícone "Símbolo". Em seguida, escolha "Barras" no menu de contexto, encontre o símbolo desejado e clique em "Exportar barras".

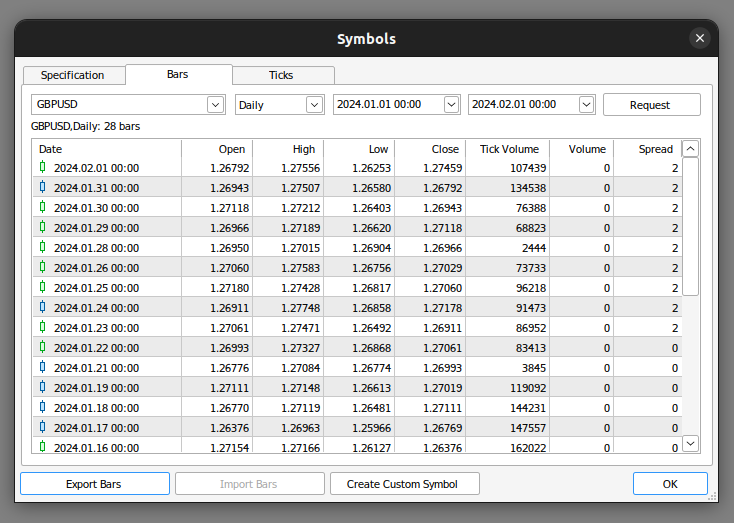
Fig. 1. Preparação para a exportação de dados de mercado

Agora que nossos dados estão prontos, iniciamos a visualização para avaliar se podem existir relações entre as variáveis analisadas.

Começamos importando as bibliotecas necessárias.

#import libraries
import pandas as pd
import numpy as np
import seaborn as sns
import matplotlib.pyplot as plt

Depois, carregamos os dados preparados anteriormente. Vale ressaltar que o terminal MetaTrader 5 nos fornece arquivos CSV separados por tabulação. Portanto, ao ler o arquivo, devemos especificar o parâmetro \t.

gbpusd = pd.read_csv("/home/volatily/market_data/GBPUSD_Daily_20160103_20240131.csv",sep="\t")

Renomeamos as colunas do nosso DataFrame.

#Rename the columns
gbpusd.rename(columns={"<DATE>":"Date","<OPEN>":"Open","<HIGH>":"High","<LOW>":"Low","<CLOSE>":"Close","<TICKVOL>":"TickVol","<VOL>":"Vol","<SPREAD>":"Spread"},inplace=True)

Definimos até que ponto no futuro queremos prever.

#Define how far into the future we want to forecast
look_ahead = 20

Agora, aplicamos nossas etiquetas conforme descrito anteriormente.

#This column will help us with our plots
gbpusd["Future Close"] = gbpusd["Close"].shift(-look_ahead)
#Let's mark the normal target
#If price rises, our target will be 1
#If price falls, our target will be 0
gbpusd["Price Target"] = 0
#Let's mark the new target
#If price makes a higher high, we will label 1
#If price makes a lower low, we will label 2
#If price fails to make either, we will label 3
gbpusd["New Target"] = 0

Rotulação de dados.

#Labeling the data
#If the future close was less than the current close, price depreciated, label 0
gbpusd.loc[gbpusd["Close"] > gbpusd["Close"].shift(-look_ahead),"Price Target"] = 0
#If the future close was greater than the current close, price depreciated, label 1
gbpusd.loc[gbpusd["Close"] < gbpusd["Close"].shift(-look_ahead),"Price Target"] = 1
#If price makes a higher high our label will be 1
gbpusd.loc[gbpusd["Close"].shift(-look_ahead) > gbpusd["High"],"New Target"] = 1
#If price makes a lower low our label will be 2
gbpusd.loc[gbpusd["Close"].shift(-look_ahead) < gbpusd["Low"],"New Target"] = 2
#Otherwise our label will be 3 
gbpusd.loc[gbpusd["Close"].shift(-look_ahead) < gbpusd["Low"],"New Target"] = 3

Podemos remover todas as linhas com valores ausentes.

#Drop the last look ahead rows
gbpusd = gbpusd[:-look_ahead]

A estratégia de trading pressupõe que existe uma relação entre o preço de fechamento e o preço máximo. Vamos visualizar se há alguma correlação entre o fechamento e a máxima.

#Plot a scattor plot so we can see if there may be any relationship between the close and the high
sns.scatterplot(data=gbpusd,x="Close",y="High",hue="Price Target")

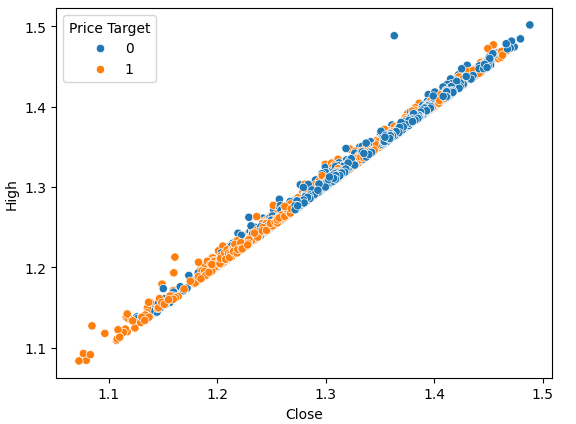
Fig. 2. Comparação gráfica do fechamento e da alta

Os gráficos de dispersão nos permitem visualizar as relações entre pares de variáveis dentro do sistema modelado.

Ao observar os dados, podemos notar imediatamente que há uma relação forte e quase linear entre o preço de fechamento e o preço máximo. Adicionamos cor ao gráfico para diferenciar os casos em que o preço subiu dos casos em que caiu. Como observado, não há uma separação clara entre esses dois casos. Os únicos pontos de divisão perceptíveis ocorrem em valores extremos. Por exemplo, quando o preço de fechamento cai abaixo do nível 1,1, ele sempre parece retornar.

Agora, construímos o mesmo gráfico de dispersão, mas desta vez colocando o preço mínimo no eixo Y.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Low",hue="Price Target")

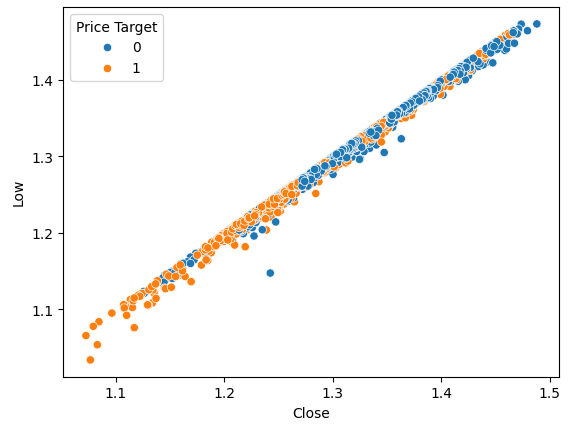
Fig. 3. Visualização da relação entre o preço de fechamento e a mínima

Como esperado, não observamos uma separação natural. Essa separação natural seria desejável, pois ajuda os modelos a aprenderem mais rapidamente os limites de tomada de decisão. Vamos verificar se nosso novo alvo nos ajuda a segmentar melhor os dados.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Low",hue="New Target")

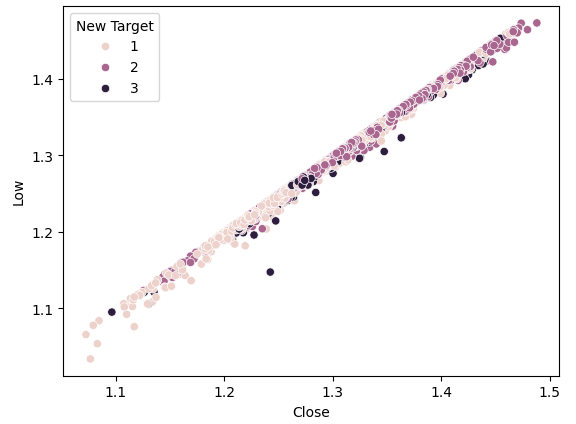
Fig. 4. Nossa nova meta não oferece mais separação

Como podemos ver, a separação ainda é tênue. Os pontos mais escuros, que representam o estado 3, estão distribuídos por todo o gráfico. Isso significa que existem casos nos dados nos quais as mesmas entradas resultam em resultados diferentes.

Para demonstrar como seria uma boa separação, vamos visualizar o preço atual no eixo X e o preço futuro no eixo Y. Colorimos os pontos em laranja para aumentos de preço e em azul para quedas de preço.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Future Close",hue="Price Target")

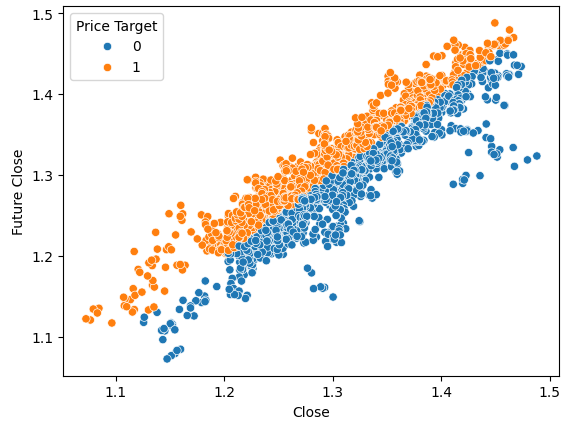
Fig. 5. Exemplo artificial de como é uma boa separação

Aqui vemos uma separação clara entre as duas classes. Isso era esperado, pois estamos usando a própria meta no gráfico. Nosso objetivo como especialistas em aprendizado de máquina é encontrar uma variável ou alvo que forneça um nível de separação próximo ao que vemos na figura 4.

Se fizermos o mesmo utilizando nosso novo alvo, veremos algo peculiar.

#Plot a scattor plot so we can see if there may be any relationship between the close and the low
sns.scatterplot(data=gbpusd,x="Close",y="Future Close",hue="New Target")

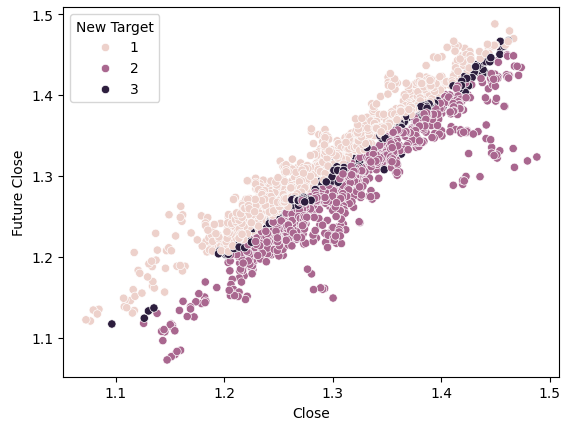
Fig. 6. Visualização da separação com um novo alvo

Observe que os pontos escuros e claros estão bem separados entre as metades superior e inferior do gráfico, representando casos em que o preço subiu e caiu, respectivamente. Entre esses dois grupos, há pontos classificados como estado 3, marcados por manchas escuras ao longo do centro, indicando momentos em que o preço oscilou.

Treinamento dos modelo

Agora importamos os modelos necessários e outras ferramentas de pré-processamento.

#Let's get a group of different models
from sklearn.ensemble import RandomForestClassifier
from sklearn.ensemble import BaggingClassifier
from sklearn.ensemble import AdaBoostClassifier
from sklearn.neighbors import KNeighborsClassifier
from sklearn.discriminant_analysis import LinearDiscriminantAnalysis
from sklearn.neural_network import MLPClassifier
from sklearn.svm import LinearSVC
#Import cross validation libraries
from sklearn.model_selection import TimeSeriesSplit
#Import accuracy metrics
from sklearn.metrics import accuracy_score
#Import preprocessors
from sklearn.preprocessing import RobustScaler

Definimos os parâmetros para a validação cruzada de nossas séries temporais. Lembre-se de que o intervalo deve ser pelo menos igual ao nosso horizonte de previsão.

#Splits
splits = 10
gap = look_ahead

Armazenamos todas as modelos em uma lista, para que possamos ajustá-los de forma programada.

#Store each of the models we need
cols = ["AdaBoostClassifier","Linear DiscriminantAnalysis","Bagging Classifier","Random Forest Classifier","KNeighborsClassifier","Neural Network Small","Neural Network Large"]
models = [AdaBoostClassifier(),LinearDiscriminantAnalysis(),BaggingClassifier(n_jobs=-1),RandomForestClassifier(n_jobs=-1),KNeighborsClassifier(n_jobs=-1),MLPClassifier(hidden_layer_sizes=(5,2),early_stopping=True,max_iter=1000),MLPClassifier(hidden_layer_sizes=(20,10),early_stopping=True,max_iter=1000)]
#Create data frames to store our accuracy with different models on different targets
index = np.arange(0,splits)
price_target = pd.DataFrame(columns=cols,index=index)
new_target = pd.DataFrame(columns=cols,index=index)

Criamos um objeto de divisão de séries temporais para a validação cruzada.

#Create the tscv splits
tscv = TimeSeriesSplit(n_splits=splits,gap=gap)

Definimos os preditores e os alvos para nossos modelos.

#Define the predictors and target
predictors = ["Open","High","Low","Close"]
target = "New Target"

Realizamos a validação cruzada.

#Now we perform cross validation
for j in (np.arange(len(models))):
    #We need to train each model
    model = models[j]
    for i,(train,test) in enumerate(tscv.split(gbpusd)):
        #Scale the data
        scaler = RobustScaler()
        X_train_scaled = scaler.fit_transform(gbpusd.loc[train[0]:train[-1],predictors])
        scaler = RobustScaler()
        X_test_scaled = scaler.fit_transform(gbpusd.loc[test[0]:test[-1],predictors])
        #Train the model
        model.fit(X_train_scaled,gbpusd.loc[train[0]:train[-1],target])
        #Measure the accuracy
        new_target.iloc[i,j] = accuracy_score(gbpusd.loc[test[0]:test[-1],target],model.predict(X_test_scaled))

Analisamos o desempenho de cada um de nossos modelos no alvo mais simples.

#Calculate the mean for each column when predicting price 
for i in np.arange(0,len(models)):
    print(f"{cols[i]} achieved accuracy: {price_target.iloc[:,i].mean()}")

AdaBoostClassifier achieved accuracy: 0.5190265486725664
Linear Discriminant Analysis achieved accuracy: 0.5579646017699115
Bagging Classifier achieved accuracy: 0.5075221238938052
Random Forest Classifier achieved accuracy: 0.5349557522123894
KNeighborsClassifier achieved accuracy: 0.536283185840708
Neural Network Small achieved accuracy: 0.45309734513274336
Neural Network Large achieved accuracy: 0.5446902654867257

A Análise Discriminante Linear (Linear Discriminant Analysis) apresentou os melhores resultados neste conjunto de dados específico, atingindo quase 56% de precisão. Agora, vejamos os resultados com o novo alvo.

#Calculate the mean for each column when predicting price 
for i in np.arange(0,len(models)):
    print(f"{cols[i]} achieved accuracy: {new_target.iloc[:,i].mean()}")

AdaBoostClassifier achieved accuracy: 0.45929203539823016
Linear DiscriminantAnalysis achieved accuracy: 0.4668141592920355
Bagging Classifier achieved accuracy: 0.4393805309734514
Random Forest Classifier achieved accuracy: 0.45929203539823016
KNeighborsClassifier achieved accuracy: 0.465929203539823
Neural Network Small achieved accuracy: 0.3920353982300885
Neural Network Large achieved accuracy: 0.4606194690265487

A Análise Discriminante Linear continua no topo da lista. Todos os modelos apresentaram resultados mais fracos com o novo alvo, mas a maior queda de desempenho foi observada na pequena rede neural.

Modelo	Variação no desempenho
AdaBoostClassifier	-14.32748538011695%
Linear Discriminant Analysis	-19.526066350710863%
Bagging Classifier	-22.09660842754366%
Random Forest Classifier	-16.730769230769248%
KNeighborsClassifier	-15.099715099715114%
Neural Network Small	-41.04193138500632%
Neural Network Large	-21.1502782931354%

Agora analisamos a matriz de erros do nosso modelo mais eficiente.

#Let's continue analysing the performance of our best model Linear Discriminant Analysis
from mlxtend.evaluate import confusion_matrix
from mlxtend.plotting import plot_confusion_matrix
model = LinearDiscriminantAnalysis()
model.fit(gbpusd.loc[0:1000,predictors],gbpusd.loc[0:1000,"New Target"])
cm = confusion_matrix(y_target=gbpusd.loc[1000:,"New Target"],y_predicted=model.predict(gbpusd.loc[1000:,predictors]),binary=True)
fig , ax = plot_confusion_matrix(cm)

Fig. 7. Matriz de erro para nosso modelo de análise discriminante linear

A matriz de erros nos ajuda a identificar quais classes são mais difíceis para nosso modelo prever. Como mostrado na imagem acima, nosso modelo apresentou os piores resultados ao prever a classe 3. No entanto, essa classe tem um pequeno conjunto de observações. Para lidar com esse problema, podemos precisar de dados que representem melhor toda a população. Isso pode ser alcançado obtendo mais dados históricos ou analisando timeframes menores.

Seleção de características

Às vezes, podemos melhorar o desempenho de nossos modelos removendo características desnecessárias. Vamos focar em nosso melhor modelo, a Análise Discriminante Linear (LDA), e identificar suas características mais importantes para verificar se podemos aumentar ainda mais seu desempenho.

#Now let us perform feature selection
from mlxtend.feature_selection import SequentialFeatureSelector

Existem vários algoritmos de seleção de características. Neste artigo, usamos um algoritmo de seleção progressiva. Embora existam diferentes versões desse algoritmo, o processo geral começa com um modelo nulo, que serve como referência. Em seguida, o algoritmo avalia cada uma das características disponíveis individualmente, escolhendo a primeira com maior impacto na melhoria do desempenho. Esse processo é repetido para os p-1 preditores restantes. Graças aos avanços recentes em computação paralela, esses algoritmos se tornaram mais acessíveis.

Ao reduzir nossos preditores de p para k, onde k<p, e selecionando características k de maneira criteriosa, podemos ou superar o modelo original ou criar um modelo com a mesma confiabilidade, mas mais rápido no treinamento. Além disso, reduzir o número de preditores utilizados pode diminuir a variabilidade dos coeficientes do nosso modelo.

No entanto, existem duas limitações importantes desse algoritmo que valem a pena ser discutidas. Primeiro, o novo modelo pode ser um pouco mais tendencioso devido à quantidade limitada de informações utilizadas em seu treinamento. Além disso, a escolha do primeiro preditor influencia a seleção dos seguintes. Se a primeira variável escolhida tiver pouca relação com o alvo, as características subsequentes podem acabar sendo pouco informativas devido a essa seleção inicial inadequada.

Em nossa análise, permitimos que o seletor de características escolhesse quantas variáveis considerasse importantes, mas ele selecionou apenas uma: o preço de abertura.

#Forward feature selection 
forward_feature_selection = SequentialFeatureSelector(LinearDiscriminantAnalysis(),
                                                     k_features =(1,4),
                                                     forward=True,
                                                     verbose=2,
                                                     scoring="accuracy",
                                                     cv=5,
                                                     n_jobs=-1).fit(gbpusd.loc[:,predictors],gbpusd.loc[:,"New Target"])

Agora queremos identificar a melhor característica.

#Best feature
forward_feature_selection.k_feature_names_

(Open,)

Vamos observar nossos novos níveis de precisão.

#Update the predictors and target
predictors = ["Open"]
target = "New Target"
best_features_for_new_target = pd.DataFrame(columns=["Linear Discriminant Analysis"],index=index)

Realizamos a validação cruzada utilizando o melhor preditor identificado.

#Now we perform cross validation
for i,(train,test) in enumerate(tscv.split(gbpusd)):
    #First initialize the model
    model = LogisticRegression()
    #Train the model
    model.fit(gbpusd.loc[train[0]:train[-1],predictors],gbpusd.loc[train[0]:train[-1],target])
    #Measure the accuracy
    best_features_for_new_target.iloc[i,0] = accuracy_score(gbpusd.loc[test[0]:test[-1],target],model.predict(gbpusd.loc[test[0]:test[-1],predictors]))

Avaliamos nossos novos níveis de precisão.

#New accuracy only using the open price
best_features_for_new_target.iloc[:,0].mean()

0.46548672566371685

E, por fim, analisamos a mudança na eficiência entre o modelo que utilizou todos os preditores e o modelo que usou apenas um.

-0.0013274336283186638

Como podemos ver, a variação de desempenho é de aproximadamente -0,2%. Isso significa que perdemos pouquíssima informação ao eliminar três outros preditores.

Implementação da estratégia em MQL5

Começamos importando as bibliotecas necessárias.

//+------------------------------------------------------------------+
//|                                   Forecasting Highs And Lows.mq5 |
//|                                        Gamuchirai Zororo Ndawana |
//|                                             https://www.mql5.com |
//+------------------------------------------------------------------+
#property copyright "Gamuchirai Zororo Ndawana"
#property link      "https://www.mql5.com"
#property version   "1.00"

//+------------------------------------------------------------------+
//|Libraries we need                                                 |
//+------------------------------------------------------------------+
#include <Trade/Trade.mqh> //Trade class
CTrade Trade;             //Initialize the class

Em seguida, definimos as variáveis de entrada para que o usuário final possa personalizar sua experiência.

//+------------------------------------------------------------------+
//| Input variables                                                  |
//+------------------------------------------------------------------+
input int fetch = 10; //How much data should we fetch?
input int look_ahead = 2; //Forecst horizon.
input int rsi_period = 20; //Forecst horizon.
int input  lot_multiple = 1; //How many times bigger than minimum lot?
input double stop_loss_values = 1; //How large should our stop loss be?

Precisamos de algumas variáveis globais que serão utilizadas em diferentes partes do nosso aplicativo.

//+------------------------------------------------------------------+
//| Global variables                                                 |
//+------------------------------------------------------------------+
vector state = vector::Zeros(3);//This vector will store the state of the system using binary mapping
double minimum_volume;//The smallest contract size allowed
vector input_data;//Input data
vector output_data;//Output data
vector rsi_data;//RSI output data
double variance;//This is the variance of our input data
int classes = 3;//The total number of output classes we have
vector mean_values = vector::Zeros(classes);//This vector will store the mean value for each class
vector probability_values = vector::Zeros(classes);//This vector will store the prior probability the target will belong each class
vector total_class_count = vector::Zeros(classes);//This vector will count the number of times each class was the target
int rsi_handler;//This will store our RSI handler
int forecast = 0;//Our model's forecast
double discriminant_values[3];//The discriminant function

Depois, definimos o procedimento de inicialização do nosso EA. Primeiro, verificamos se o usuário forneceu entradas válidas e, em seguida, configuramos nosso indicador técnico e inicializamos o estado do nosso sistema de trading.

//+------------------------------------------------------------------+
//| Expert initialization function                                   |
//+------------------------------------------------------------------+
int OnInit()
  {
//--- Validate inputs
   if(!valid_inputs())
     {
      //User passed invalid inputs
      Print("Invalid inputs were received!");
      return(INIT_FAILED);
     }
//--- Load input data
   rsi_handler = iRSI(_Symbol,PERIOD_CURRENT,rsi_period,PRICE_CLOSE);
//--- Market data
   minimum_volume = SymbolInfoDouble(_Symbol,SYMBOL_VOLUME_MIN);
//--- Update system state
   update_system_state(0);
//--- End of initialization
   return(INIT_SUCCEEDED);
  }

Também precisamos definir um procedimento de desinicialização para o nosso aplicativo.

//+------------------------------------------------------------------+
//| Expert deinitialization function                                 |
//+------------------------------------------------------------------+
void OnDeinit(const int reason)
  {
//--- Remove indicators
   IndicatorRelease(rsi_handler);
//--- Detach the Expert Advisor
   ExpertRemove();
//--- End of deinitialization
  }

Criamos uma função que nos ajuda a analisar se há sinais de entrada. Os sinais de entrada são considerados válidos se a previsão do modelo coincidir com a tendência em timeframes mais longos, como o semanal. Se esses dois fatores estiverem alinhados, calculamos o momento ideal para entrar na operação usando o indicador RSI.

//+------------------------------------------------------------------+
//| This function will analyse our entry signals                     |
//+------------------------------------------------------------------+
void analyse_entry(void)
  {
   Print("Higher Time Frame Trend");
   Print(iClose(_Symbol,PERIOD_W1,12) - iClose(_Symbol,PERIOD_CURRENT,0));
   if(iClose(_Symbol,PERIOD_W1,12) < iClose(_Symbol,PERIOD_CURRENT,0))
     {

      if(forecast == 1)
        {
         bullish_sentiment();
        }
     }
   if(iClose(_Symbol,PERIOD_W1,12) > iClose(_Symbol,PERIOD_CURRENT,0))
     {

      if(forecast == 2)
        {
         bearish_sentiment();
        }
     }
  }

Precisamos de duas funções especializadas para interpretar nosso indicador RSI: uma função analisará o indicador para identificar potenciais sinais de venda, enquanto a outra identificará oportunidades de compra.

//+------------------------------------------------------------------+
//| This function will analyze our RSI for sell signals              |
//+------------------------------------------------------------------+
void bearish_sentiment(void)
  {
   rsi_data.CopyIndicatorBuffer(rsi_handler,0,0,1);
   if(rsi_data[0] < 50)
     {
      Trade.Sell(minimum_volume * lot_multiple,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_BID),(SymbolInfoDouble(_Symbol,SYMBOL_BID) + stop_loss_values),(SymbolInfoDouble(_Symbol,SYMBOL_BID) - stop_loss_values));
      update_system_state(2);
     }
  }
//+------------------------------------------------------------------+
//| This function will analyze our RSI for buy signals               |
//+------------------------------------------------------------------+
void bullish_sentiment(void)
  {
   rsi_data.CopyIndicatorBuffer(rsi_handler,0,0,1);
   if(rsi_data[0] > 50)
     {
      Trade.Buy(minimum_volume * lot_multiple,_Symbol,SymbolInfoDouble(_Symbol,SYMBOL_ASK),(SymbolInfoDouble(_Symbol,SYMBOL_ASK) - stop_loss_values),(SymbolInfoDouble(_Symbol,SYMBOL_ASK) +stop_loss_values));
      update_system_state(2);
     }
  }

Agora definimos a função que verifica as entradas fornecidas pelo usuário durante a inicialização.

//+------------------------------------------------------------------+
//|This function will check the inputs the user passed               |
//+------------------------------------------------------------------+
bool valid_inputs(void)
  {
//--- For the inputs to be valid:
//--- The forecast horizon must be less than the data fetched
   return((fetch > look_ahead));
  }

Em seguida, desenvolvemos a função que inicializa nosso modelo LDA.

//+------------------------------------------------------------------+
//| This function will initialize our model                          |
//+------------------------------------------------------------------+
void initialize_model(void)
  {
//--- First fetch the input data
   fetch_input_data(look_ahead,fetch);
   fetch_output_data(0,fetch);
//--- Update the system state
   update_system_state(1);
//--- Fit the model
   fit_model();
  }

Para inicializar o modelo, primeiro precisamos obter os dados de entrada. É exatamente essa a função que estamos construindo. Vale notar que essa função simplesmente extrai o preço de abertura, pois nossa análise indicou que essa é a característica mais relevante que temos.

//+------------------------------------------------------------------+
//| This function will fetch our input data                          |
//+------------------------------------------------------------------+
void fetch_input_data(int start,int size)
  {
//--- Fetching input data
   Print("Fetching input data");
   input_data = vector::Zeros(fetch);
   input_data.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_OPEN,start,size);
   input_data.Resize(size);
   Print("Input data fetched");
  }

Em seguida, precisamos extrair nossas variáveis de saída e rotulá-las. Também registramos quantas vezes cada classe apareceu como alvo. Essas informações serão utilizadas posteriormente ao ajustarmos o modelo LDA.

//+------------------------------------------------------------------+
//| This function will fetch our output data                         |
//+------------------------------------------------------------------+
void fetch_output_data(int start,int size)
  {
//--- Fetching output data
   vector historic_high = vector::Zeros(size);
   vector historic_low = vector::Zeros(size);
   vector historic_close = vector::Zeros(size);
   historic_close.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_CLOSE,start,size+look_ahead);
   historic_low.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_HIGH,start,size+look_ahead);
   historic_high.CopyRates(_Symbol,PERIOD_CURRENT,COPY_RATES_LOW,start,size+look_ahead);
   output_data = vector::Zeros(size);
   output_data.Resize(size);
//--- Reset class counts
   total_class_count[0] = 0;
   total_class_count[1] = 0;
   total_class_count[2] = 0;
//--- Label the data
   for(int i = 0; i < size; i++)
     {
      //--- Price broke into a higher high
      if(historic_close[i + look_ahead] > historic_high[i])
        {
         output_data[i] = 1;
         total_class_count[0] += 1;
        }
      //--- Price broke into a lower low
      else
         if(historic_close[i + look_ahead] < historic_low[i])
           {
            output_data[i] = 2;
            total_class_count[1] += 1;
           }
         //--- Price was stuck in a range
         else
            if((historic_close[i + look_ahead] > historic_low[i]) && (historic_close[i + look_ahead] < historic_high[i]))
              {
               output_data[i] = 3;
               total_class_count[2] += 1;
              }
     }
//--- We fetched output data succesfully
   Print("Output data fetched");
   Print("Total class counts");
   Print(total_class_count);
  }

Agora, definimos o procedimento de ajuste do modelo LDA. Inicialmente, calculamos a média do preço de abertura para cada uma das três classes. No segundo estágio, precisamos calcular a distribuição inicial de probabilidades para que cada classe seja o alvo. Podemos estimar esse valor utilizando a contagem das classes realizada na etapa anterior. Por fim, devemos calcular a variância do preço de abertura para cada um dos três grupos.

//+------------------------------------------------------------------+
//| This function will fit the LDA algorithm                         |
//+------------------------------------------------------------------+
//--- Fit the model
void fit_model(void)
  {
//--- To fit the LDA model, we first need to know the mean value of X for each of our 3 classes
   double sum_class_one = 0;
   double sum_class_two = 0;
   double sum_class_three = 0;

//--- In this case we only have 1 input
   for(int i = 0; i < fetch;i++)
     {
      //--- Class 1
      if(output_data[i] == 1)
        {
         sum_class_one += input_data[i];
        }
      //--- Class 2
      else
         if(output_data[i] == 2)
           {
            sum_class_two += input_data[i];
           }
         //--- Class 3
         else
            if(output_data[i] == 3)
              {
               sum_class_three += input_data[i];
              }
     }
//--- Calculate the mean value for each class
   mean_values[0] = sum_class_one / total_class_count[0];
   mean_values[1] = sum_class_two / total_class_count[1];
   mean_values[2] = sum_class_three / total_class_count[2];
   Print("Mean values");
   Print(mean_values);
//--- Now we need to calculate class probabilities
   for(int i=0;i<classes;i++)
     {
      probability_values[i] = total_class_count[i] / fetch;
     }
   Print("Class probability values");
   Print(probability_values);
//--- Calculating the variance
   Print("Calculating the variance");
//--- Next we need to calculate the variance of the inputs within each class of y.
//--- This process can be simplified into 2 steps
//--- First we calculate the difference of each instance of x from the group mean.
   double squared_difference[3];
   for(int i =0; i < fetch;i++)
     {
      //--- If the output value was 1, find the input value that created the output
      //--- Calculate how far that value is from it's group mean and square the difference
      if(output_data[i] == 1)
        {
         squared_difference[0] = MathPow((input_data[i]-mean_values[0]),2);
        }

      else
         if(output_data[i] == 2)
           {
            squared_difference[1] = MathPow((input_data[i]-mean_values[1]),2);
           }

         else
            if(output_data[i] == 3)
              {
               squared_difference[2] = MathPow((input_data[i]-mean_values[2]),2);
              }
     }
//--- Show the squared difference values
   Print("Squared difference value for each output value of y");
   ArrayPrint(squared_difference);

//--- Next we calculate the variance as the average squared difference from the mean
   variance = (1.0/(fetch - 3.0)) * (squared_difference[0] + squared_difference[1] + squared_difference[2]);
   Print("Variance: ",variance);
  }

Agora precisamos de uma função para extrair previsões do nosso modelo. O modelo prevê um valor discriminante para cada um dos três possíveis resultados. O resultado com o maior valor discriminante será a previsão escolhida.

//+-------------------------------------------------------------------+
//| This model will fetch our model's prediction                      |
//+-------------------------------------------------------------------+
void model_forecast(void)
  {
//--- Obtain a forecast from our model
//--- First we need to fetch the most recent input data
   fetch_input_data(0,1);
//--- We need to calculate the discriminant function for each class
//--- The predicted class is the one with the largest discriminant function
   Print("Calculating discriminant values.");
   for(int i = 0; i < classes; i++)
     {
      discriminant_values[i] = (input_data[0] * (mean_values[i]/variance) - (MathPow(mean_values[i],2)/(2*variance)) + (MathLog(probability_values[i])));
     }
//--- Show the LDA prediction
   forecast = (ArrayMaximum(discriminant_values) +1);
   Print("LDA Forecast: ",forecast);
   ArrayPrint(discriminant_values);
  }

Precisamos de uma função para atualizar o estado do nosso sistema, garantindo que a função OnTick sempre saiba o que fazer a seguir.

//+-------------------------------------------------------------------+
//| This function will be used to update the state of the system      |
//+-------------------------------------------------------------------+
void update_system_state(int index)
  {
//--- Each column vector is set to 0 except column 0, the first column.
//--- If the first column is set to 1, then our model has not been trained
//--- If the second column is set to 1, then our model has been trained but we have no positions
//--- If the third column is set to 1, then we have a position we need to manage
//--- Update the system state
   state = vector::Zeros(3);
   state[index] = 1;
   Print("Updating system state");
   Print(state);
  }

Agora definimos a função OnTick, que será responsável por chamar todas as nossas funções nos momentos apropriados.

//+------------------------------------------------------------------+
//| Expert tick function                                             |
//+------------------------------------------------------------------+
void OnTick()
  {
//--- The model has not been trained
   if(state.ArgMax() == 0)
     {
      Print("Training the model.");
      initialize_model();
     }
//--- The model has been trained, but we have no positions
   else
      if(state.ArgMax() == 1)
        {
         Print("Finding An Entry.");
         model_forecast();
         analyse_entry();
        }
  }
//+------------------------------------------------------------------+

Fig. 8. Nosso EA

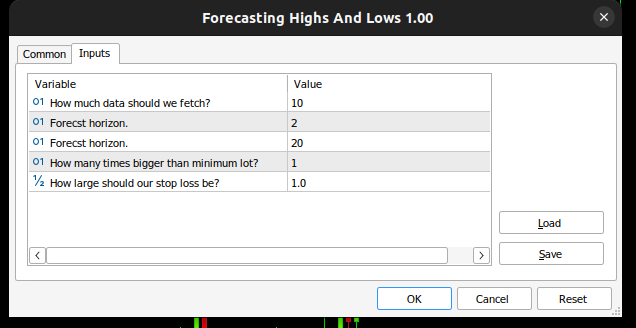
Fig. 9. Nosso EA baseado em LDA

 

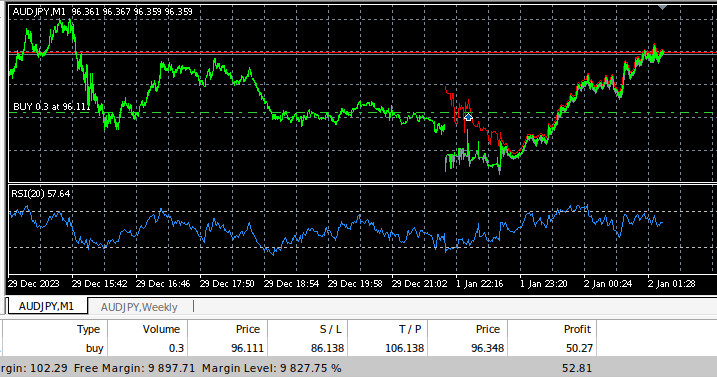
Fig. 10. Nosso EA em dados históricos

Considerações finais

Neste artigo, demonstramos por que pode ser mais vantajoso para os traders prever mudanças nos preços em vez de focar em máximas mais altas e mínimas mais baixas. Espero que, após ler este artigo, você tenha mais confiança para decidir se essa estratégia de trading é adequada para você, levando em consideração seu nível de tolerância ao risco e seus objetivos financeiros.

O algoritmo de Análise Discriminante Linear (LDA) modela a distribuição das variáveis de entrada dentro de cada classe utilizando o Teorema de Bayes para estimar probabilidades, assumindo uma distribuição normal com médias específicas para cada classe e variância comum. Assim, o LDA consegue distinguir eficientemente as características das classes ao calcular valores discriminantes que maximizam a separação entre os grupos e minimizam a variância dentro de cada classe. No entanto, as suposições do LDA podem limitar sua transparência e interpretabilidade. O modelo pode ter um desempenho inferior ao de modelos mais simples se não for ajustado adequadamente. Nossos testes utilizando configurações padrão para dados diários revelaram possíveis problemas de desempenho, sugerindo que melhores resultados poderiam ser alcançados com um volume maior de dados e mais recursos computacionais.

A repetição da análise com conjuntos de dados maiores pode fornecer mais insights, embora essa abordagem seja viável apenas se houver capacidade computacional suficiente. Utilizamos validação cruzada de séries temporais com 10 divisões, o que significa que cada modelo foi treinado 10 vezes. À medida que o tamanho do conjunto de dados aumenta, o tempo de treinamento do modelo tende a crescer exponencialmente.